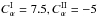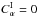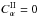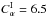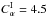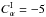| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 5 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201321093 | |
| Published online | 26 April 2013 | |
Resonances for activity waves in spherical mean field dynamos
1
School of Mathematics, University of Manchester,
Manchester
M13 9PL,
UK
e-mail:
moss@maths.manchester.ac.uk
2
Department of Physics, Moscow State University,
119999
Moscow,
Russia
e-mail:
sokoloff.dd@gmail.com
Received: 12 January 2013
Accepted: 19 March 2013
Context. It has been suggested that resonant phenomena may play a role in determining the properties of mean-field dynamos, such as operate in the Sun and other stars.
Aims. We tried to identify resonances which are expected to occur when a mean-field dynamo excites waves of quasi-stationary magnetic field in two distinct spherical layers.
Methods. We used a model with two physically separated dynamo active layers to study activity waves of the kind that determine cyclic magnetic activity of various stars, including the Sun, as a more general physical rather than a purely astronomical problem.
Results. We isolated some features that can be associated with resonances in the profiles of energy or frequency plotted versus a dynamo governing parameter. Rather unexpectedly however the resonances in spherical dynamos take a much less spectacular form than resonances in many more familiar branches of physics. In particular, we found that the magnitudes of resonant phenomena are much smaller than seem detectable by astronomical observations, and that plausibly any related effects in laboratory dynamo experiments (which of course are not in gravitating spheres!) can also be inferred to be likely to be small.
Conclusions. We discuss specific features relevant to resonant phenomena in spherical dynamos, and find parametric resonance to be the most pronounced type of resonance phenomena. Resonance conditions for these dynamo wave resonances are rather different from those found in more conventional branches of physics. We suggest that the relative insignificance of the phenomenon in this situation is because the phenomena of excitation and propagation of the activity waves are not well-separated from each other and this, together with the nonlinear nature of more-or-less realistic dynamos, suppresses the resonances and makes them much less pronounced than the resonant effects found, for example, in optics.
Key words: stars: activity / stars: magnetic field / dynamo
© ESO, 2013
1. Introduction
The well-known solar activity cycle is associated with propagation of a wave of quasistationary magnetic field somewhere within the solar convective envelope. This wave is believed to be excited and supported by electromagnetic induction effects driven by the joint action of differential rotation and mirror-asymmetric flows. This is known as dynamo action, e.g. Stix (2004). Correspondingly, the wave is known as a dynamo wave. More specifically, there are at least two, more or less independent, dynamo waves, one propagating equatorwards in each solar hemisphere.
For quite a long time, solar activity waves provided the unique example of dynamo wave propagation, and so the phenomenon was not investigated in a wider context. Even such a limited statement of the problem provides a quite rich range of instructive physical phenomena. From time to time the dynamo engine “misfires”, and solar grand minima, including the Maunder minimum in the XVIIth − early XVIIIth centuries, occur (see for review e.g. Soon & Yaskell 2003). At the end of the Maunder minimum, the dynamo wave propagated in one solar hemisphere only, and a so-called “mixed-parity” magnetic configuration appeared – see Sokoloff & Nesme-Ribes (1994). Analysis of XVIIIth century sunspot data by Arlt (2008) gives a hint (Illarionov et al. 2010) that from time to time magnetic field becomes concentrated near to the solar equator, rather than in two propagating belts in middle latitudes, and a configuration of quadrupole-like (instead of the usual dipole-like) symmetry then appears.
Recently the variety of physical phenomenon associated with dynamo wave propagation has enlarged substantially. The first attempts to isolate dynamo wave propagation from stellar activity data were undertaken in Berdyugina & Henry (2007) and Katsova et al. (2010), and generation of oscillating magnetic field, probably indicating dynamo wave propagation, was obtained in the VKS dynamo experiment (Monchaux et al. 2007). This opens new perspectives in the topic, in particular the opportunity to study dynamo waves as a physical, rather than a purely astronomical, phenomenon.
This change of viewpoint in the investigation of dynamo waves has attracted attention to these problems, which had previously remained underinvestigated. In particular, it was stressed by Gilman & Dikpati (2011) that resonance, which is a prominent and sometimes spectacular phenomenon in the conventional theory of various oscillations and wave propagations, might also play an important role in dynamo wave propagation. We share their view that the topic was not adequately addressed in previous studies, and only a few papers (including Kuzanyan & Sokoloff 1993; Moss 1996) have addressed the topic. The point is that the natural statement of the problem, as relevant to astronomical contexts, did not focus attention on this issue.
Here we present our findings associated with the problem of resonance phenomena in dynamo wave propagation. Our general conclusion can be formulated as follows. Resonances in dynamo systems do occur, and sometimes they can be isolated in the solutions of the governing equations (e.g. Kuzanyan & Sokoloff 1993; Moss 1996). However in general dynamo wave propagation as a physical phenomenon differs quite substantially from, say, the propagation of acoustic or electromagnetic waves. An important aspect is that conventional wave propagation can be easily separated from the wave excitation, whereas dynamo wave propagation is usually intimately associated with dynamo wave excitation. As a result, solutions of the dynamo equations usually fail to separate in any explicit way resonant phenomena from the more general phenomena of dynamo wave excitation. Apart from other aspects, our model is nonlinear, whereas that of Gilman & Dikpati (2011) is linear.
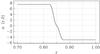 |
Fig. 1 Dependence of α on radius, at the north pole for a typical case where |
We illustrate the problem by numerical investigation of a dynamo model in which dynamo waves are excited in two adjacent spherical shells with different distributions of dynamo governing parameters. The magnetic field is continuous across the boundary between the two domains. A related model was discussed previously in Moss & Sokoloff (2007) and Moss et al. (2011) in a more specifically astronomical context.
2. The dynamo model
We consider a standard mean field dynamo equation (α2ω-dynamo)  (1)where η is the turbulent diffusivity and α represents the usual isotropic alpha-effect (for details of the model see Moss & Sokoloff (2007); the codes used there are in turn based on that of Moss & Brooke 2000). In Eq. (1) V is the velocity from the (differential) rotation and we only look for axisymmetric solutions. A simple algebraic α-quenching (in which α is reduced by a factor 1 + (B/B0)2, where B0 is a field strength at which dynamo saturation is expected) is used to suppress dynamo action as the magnetic field grows. Thus magnetic fields are measured in units of B0, the “equipartition value”, and energies are integrals over the relevant domains. Time is nondimensionalized in units of R2/η, where R is the stellar radius and η is the (constant) diffusivity.
(1)where η is the turbulent diffusivity and α represents the usual isotropic alpha-effect (for details of the model see Moss & Sokoloff (2007); the codes used there are in turn based on that of Moss & Brooke 2000). In Eq. (1) V is the velocity from the (differential) rotation and we only look for axisymmetric solutions. A simple algebraic α-quenching (in which α is reduced by a factor 1 + (B/B0)2, where B0 is a field strength at which dynamo saturation is expected) is used to suppress dynamo action as the magnetic field grows. Thus magnetic fields are measured in units of B0, the “equipartition value”, and energies are integrals over the relevant domains. Time is nondimensionalized in units of R2/η, where R is the stellar radius and η is the (constant) diffusivity.
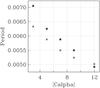 |
Fig. 2 Periods of oscillation in energy when dynamo action occurs in a single layer. Crosses: |
We solve the equation in spherical geometry for two adjacent dynamo active layers, the “deep” layer I with 0.7 ≤ r ≤ 0.85 and the “shallow” layer II with 0.85 ≤ r ≤ 1 (r is the fractional radius). We consider a very simple rotation profile with angular velocity linear in r, and α-profiles in each layer are proportional to cosθ where θ is the polar angle, so that θ = 90° is the equator.  and
and 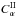 are dimensionless amplitudes of α in layers I and II correspondingly, and
are dimensionless amplitudes of α in layers I and II correspondingly, and 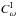 and
and 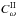 are dimensionless measures of the differential rotation, given that we assume the angular velocity to depend linearly on radius, so that its gradient is constant throughout the domain. Conventionally Cα = α0R/η, Cω = Ω0R2/η, where α0,Ω0 are typical values of the alpha coefficient and angular velocity. We take
are dimensionless measures of the differential rotation, given that we assume the angular velocity to depend linearly on radius, so that its gradient is constant throughout the domain. Conventionally Cα = α0R/η, Cω = Ω0R2/η, where α0,Ω0 are typical values of the alpha coefficient and angular velocity. We take 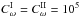 in the examples discussed below. α is continuous across the interface at r = 0.85. To be explicit, we show in Fig. 1 the radial dependence of α at the north pole, for a typical case. All solutions discussed have odd (“dipole-like”) parity.
in the examples discussed below. α is continuous across the interface at r = 0.85. To be explicit, we show in Fig. 1 the radial dependence of α at the north pole, for a typical case. All solutions discussed have odd (“dipole-like”) parity.
Our investigation is focussed on the more physical aspects of the problem, but it would be straightforward to rescale the results for particular celestial bodies, or to take a more realistic rotation curve.
 |
Fig. 3 Time variations of magnetic energy for |
 |
Fig. 4 The case |
 |
Fig. 5 Extracts from the time series of total energy for solutions outside of the resonant domain (upper panel, |
 |
Fig. 6 The case |
3. Looking for resonance in dynamo solutions
 |
Fig. 7 Parametric resonance: notation as in Fig. 4. The middle panel now includes the periods of oscillations in the upper layer II (shown by small solid circles). The dashed horizontal lines are values for the unperturbed model. The period of the total energy is plotted by solid dots in the middle panel. In each panel, quantities are plotted a functions of ω(P). |
3.1. Background
We obtained solutions for our model for various governing parameters. We first determined the periods when dynamo action occurs in one layer only, i.e. either 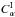 or
or 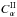 is zero. Note that the magnetic field does penetrate the passive layer, although its strength is substantially reduced there. Here we either take
is zero. Note that the magnetic field does penetrate the passive layer, although its strength is substantially reduced there. Here we either take 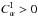 so that with
so that with  we obtain poleward migration, or
we obtain poleward migration, or 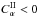 so that with
so that with  there is equatorward migration. The variations of period with
there is equatorward migration. The variations of period with 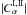 for these cases are shown in Fig. 2.
for these cases are shown in Fig. 2.
More generally, the model includes two interacting dynamo regions, which are physically separate but adjacent, which possess specific individual eigenfrequencies, so quite naturally the resulting time-series for the total magnetic energy and magnetic energy for the upper and lower layer can be more complicated than just a harmonic oscillation; see Fig. 3 where the result for a typical solution (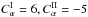 ) is shown.
) is shown.
3.2. Resonant solutions
We then set 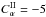 and allowed
and allowed 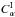 to vary, and plotted the period of the total energy (defined by a mean over O(1000) oscillations) The variations of toroidal field energies in the upper and lower layers, the (common) period and the total magnetic energy are shown in Fig. 4 as a function of
to vary, and plotted the period of the total energy (defined by a mean over O(1000) oscillations) The variations of toroidal field energies in the upper and lower layers, the (common) period and the total magnetic energy are shown in Fig. 4 as a function of 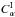 . We see a feature, in the form of a local peak of period, in the region
. We see a feature, in the form of a local peak of period, in the region 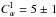 . A related feature appears in the plots of all three quantities (although it is maybe less pronounced in the lower panel). Examination of Fig. 3 shows that this feature does not correspond to
. A related feature appears in the plots of all three quantities (although it is maybe less pronounced in the lower panel). Examination of Fig. 3 shows that this feature does not correspond to 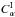 values for which the periods of the layers, taken individually, are equal. For
values for which the periods of the layers, taken individually, are equal. For 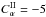 , periods are approximately equal when
, periods are approximately equal when 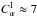 .
.
We show in Fig. 5 short samples of the time series of the total energy for solutions outside of the resonant domain ( , upper panel), and inside the domaon (
, upper panel), and inside the domaon ( , lower panel).
, lower panel).
3.3. Resonance with a subcritical dynamo layer
We recognize that the resonant behaviour was not very well pronounced in the previous results and thus try to explore and explain this situation. We do not doubt that resonance in its purely mathematical sense occurs in dynamo solutions. More specifically, if the governing equations for a kinematic dynamo problem have a degenerate eigenvalue Γn = γn + iωn (γn > 0), then it is more than plausible that the corresponding set of eigenvectors becomes insufficient to provide a basis, and the desired solution, apart from terms proportional to exp (γn + iωn)t, may contain resonant terms proportional to texp (γn + iωn)t. The point however is that the exponential growth of the solution as expγnt or texpγnt occurs just at the initial stage of the dynamo wave excitation and is a matter of more or less purely theoretical interest. A more practical issue is the amplitude of the steady-state oscillation obtained after the exponential growth is somehow saturated – here by the term 1 + (B/B0)2. The saturation reduces the growth rate γn to zero, and this is a much stronger effect than the additional power-law growth due to the resonance. The exceptional situation discussed by, say, Kuzanyan & Sokoloff (1993) and Moss (1996) addresses the cases where excitation of a particular solution without a resonance does not occur, and it is the existence of a resonance that allows this solution to develop. In contrast, resonances in acoustic or electromagnetic wave propagation occur when a wave can marginally propagate and does not grow (γ = 0), and the resonance is clearly recognisable as a growing (and then saturated) solution.
In another investigation, the lower layer was made much thinner (0.7 ≤ r ≤ 0.775), so a dynamo in this layer alone is subcritical (i.e. with 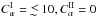 , dynamo action does not occur) and the upper layer correspondingly thicker, 0.775 ≤ r ≤ 1.0. We keep
, dynamo action does not occur) and the upper layer correspondingly thicker, 0.775 ≤ r ≤ 1.0. We keep 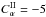 ,
, 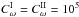 . There is again a (smaller) feature attributable to a resonance near
. There is again a (smaller) feature attributable to a resonance near 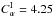 . See Fig. 6.
. See Fig. 6.
We conclude from Fig. 6 that the resonance here is of a similar nature to that in the previous case.
3.4. Parametric resonance
Now we seek the other kind of resonance, i.e. a parametric resonance in the dynamo wave driven by harmonic variations of the dynamo governing parameters. Our preliminary expectations here are twofold. The resonances recognized in Kuzanyan & Sokoloff (1993); Moss (1996) for galactic dynamos are parametric. Nevertheless, the parametric resonance suggested in Moss et al. (2002) to explain some details in the magnetic activity of stellar binary systems does not seem very spectacular.
We imposed a modulation α ∝ (1 + fcosωPt) in the region I, with 500 ≤ ωP ≤ 1500, f = 0.2, keeping 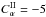 . We started from the unperturbed model which has
. We started from the unperturbed model which has 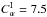 (i.e. outside of the resonant region discussed in Sect. 3.2). The corresponding period is P(E) = 0.00539, so ω(E) = 1166. Results are shown in Fig. 7, where resonant peaks are clearly recognizable.
(i.e. outside of the resonant region discussed in Sect. 3.2). The corresponding period is P(E) = 0.00539, so ω(E) = 1166. Results are shown in Fig. 7, where resonant peaks are clearly recognizable.
The feature at ωP ≈ 1150 is quite expected, as it satisfies the standard resonance condition ωP ≈ ω(E) = 2ω(B) (where ω(B) is the frequency of the magnetic field oscillations). The features near ωp ≈ 700 and ωp ≈ 900 have to be associated with rather unusual excitation conditions. Note that these resonant solutions do not settle to a completely steady (maybe modulated) oscillation, even when run for about 2000 oscillations. In the two anomalous cases the period is not quite stable, but the averaging process seems robust, in that averages over different temporal sub-ranges give the same values. Note that the energy in the upper and lower regions separately (top panel in Fig. 7) is the toroidal field energy only, whereas the “total energy” includes also the poloidal. Over long enough time intervals the average period in region II is slightly longer than that of the total energy (see middle panel of Fig. 7).
In general, parametric resonance effects seem to be much clearer and more pronounced than the resonances analysed in previous models (Sects. 3.2 and 3.3). However the peaks in energy profiles for parametric resonances are quite broad.
4. Discussion
The concept of resonance is one of the basic concepts of contemporary physics, and it looks a priori implausible that it should not be applicable to dynamo wave propagation. We have verified this natural expectation in the framework of activity waves generated by dynamo waves, in a quite traditional model of a two-layer mean-field spherical mean-field dynamo of the type conventionally considered as a model for periodic stellar magnetic activity.
We did find features in the profiles for energies or periods (frequencies) plotted versus a dynamo governing parameter that can be identified with a resonance. However, it looks noteworthy that the details resemble more discontinuities in the profiles of the behaviour of period and energy as 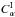 varies, rather than the conventional resonant peaks shown in physics textbooks. It is even difficult to claim that the resonance makes dynamo excitation more efficient and enhances, say, the total magnetic energy. The lower panel in Fig. 6 is instructive in this respect: the interaction here appears as a fall in total energy, rather than an increase. Of course, resonances are far from being the only effects that determine the relevant behaviour in, say, optics, and there are many cases where other effects make recognition of resonance peaks problematic. The point however is that it is not difficult to provide examples of pronounced resonant peaks in optics. When presenting our results, we have of course chosen the more pronounced examples of resonances for dynamo waves, admittedly from a rather small sample.
varies, rather than the conventional resonant peaks shown in physics textbooks. It is even difficult to claim that the resonance makes dynamo excitation more efficient and enhances, say, the total magnetic energy. The lower panel in Fig. 6 is instructive in this respect: the interaction here appears as a fall in total energy, rather than an increase. Of course, resonances are far from being the only effects that determine the relevant behaviour in, say, optics, and there are many cases where other effects make recognition of resonance peaks problematic. The point however is that it is not difficult to provide examples of pronounced resonant peaks in optics. When presenting our results, we have of course chosen the more pronounced examples of resonances for dynamo waves, admittedly from a rather small sample.
The parametric resonances present in the spherical dynamo models investigated here (Sect. 3.4) are much clearer than the other resonance features (Sects. 3.2 and 3.3). Perhaps this is a consequence of controlling by varying the frequency ωP, which governs the parametric excitation but, leaves unchanged the “nominal” parameters of the dynamo model for the vanishing modulation amplitude f = 0.
Our numerical experiment illuminates the unusual excitation conditions for parametric resonances in this situation. Perhaps, it can be said that the Mathieu equation is not a fully adequate model for parametric resonance in spherical dynamos. Isolation of the resonance condition here appears an attractive topic for dynamo theory, but it is however obviously beyond the scope of this paper. The transition time required for the dynamo system to achieve a resonant type solution can be long and a qualitative explanation in terms of an appropriate model equation also looks desirable.
We note also the existence of a quasi-resonant phenomenon in a case where one of the dynamo layers is passive, i.e. with the chosen parameters the lower layer taken in isolation does not support dynamo action.
Perhaps the basic differences between resonant phenomena for dynamo waves and those in more conventional branches of physics can be summarized as follows. It is difficult to separate dynamo wave propagation from dynamo wave excitation, while such processes are well separated in many other branches of physics. Correspondingly, eigenvalues of the linear (kinematic) dynamo problems take complex values. Coincidence of two complex quantities is a more severe requirement rather than equality of two real valued quantities. Dynamo self-excitation is in practice saturated by some back-reaction of the dynamo generated magnetic field on the hydrodynamics. This saturation determines the resulting magnetic energy and affects the periods of dynamo waves. The corresponding effects specific to dynamo action are more important than any potential resonant behaviour. In addition, the two layers where dynamo action occurs are separated hydrodynamically but magnetic field penetrates from one activity layer to the other, even if the dynamo action in one layer remains subcritical. Thus the very concept of the frequency of dynamo waves in one activity layer taken alone is not fully applicable.
We note that, whereas it looks a priori reasonable to expect that there will be some prominent features in stellar activity associated with resonance, surprisingly we find that the resonance phenomena in our spherical dynamo models are quite modest.
Our attention was initially drawn to the issue by Gilman & Dikpati (2011), and our intention was to investigate the generality of their results, and to draw attention to any novel behaviour. Our results are not so marked as those in Gilman & Dikpati (2011), plausibly because a linear problem was considered there, and our inclusion of a nonlinear saturation mechanism reduces these effects. We infer that the mechanism is unlikely to produce observable signatures.
In general, it seems that the situation under discussion reflects the every-day wisdom that small problems (here resonances) can only spoil your life in the absence of larger ones (in this case the other uncertainties associated with mean field dynamos are much larger).
Acknowledgments
D.S. is grateful to financial support from RFBR under grant 12-02-00170-a.
References
- Arlt, R. 2008, Sol. Phys., 247, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Berdyugina, S. V., & Henry, G. W. 2007, ApJ, 659, L157 [NASA ADS] [CrossRef] [Google Scholar]
- Gilman, P. A., & Dikpati, M. 2011, ApJ, 738, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Illarionov, E., Sokoloff, D., Arlt, R., & Khlystova, A. 2011, Astron. Nachr., 332, 590 [NASA ADS] [CrossRef] [Google Scholar]
- Katsova, M. M., Livshits, M. A., Soon, W., Baliunas, S. L., & Sokoloff, D. D. 2010, New Astron., 15, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Kuzanyan, K. M., & Sokoloff, D. D. 1993, Astrophys. Sp. Sci., 208, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Monchaux, R., Berhanu, M., Bourgoin, M., Moulin, M., et al. 2007, PRL, 98, 044502 [Google Scholar]
- Moss, D., 1996, A&A, 308, 381 [NASA ADS] [Google Scholar]
- Moss, D., & Brooke, J. 2000, MNRAS, 315, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., & Sokoloff, D. 2007, MNRAS, 377, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, D., Piskunov, N., & Sokoloff, D. 2002, A&A, 396, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moss, D., Sokoloff, D., & Lanza, A. F. 2011, A&A, 531, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sokoloff, D., & Nesme-Ribes, E. 1994, A&A, 288, 293 [NASA ADS] [Google Scholar]
- Soon, W. W.-H., & Yaskell, S. H. 2003, The Maunder Minimum: The Variable Sun-Earth Connection (Singapore: World Science) [Google Scholar]
- Stix, M. 2004, The Sun: An Introduction, 2nd edn. (Springer) [Google Scholar]
All Figures
 |
Fig. 1 Dependence of α on radius, at the north pole for a typical case where |
| In the text | |
 |
Fig. 2 Periods of oscillation in energy when dynamo action occurs in a single layer. Crosses: |
| In the text | |
 |
Fig. 3 Time variations of magnetic energy for |
| In the text | |
 |
Fig. 4 The case |
| In the text | |
 |
Fig. 5 Extracts from the time series of total energy for solutions outside of the resonant domain (upper panel, |
| In the text | |
 |
Fig. 6 The case |
| In the text | |
 |
Fig. 7 Parametric resonance: notation as in Fig. 4. The middle panel now includes the periods of oscillations in the upper layer II (shown by small solid circles). The dashed horizontal lines are values for the unperturbed model. The period of the total energy is plotted by solid dots in the middle panel. In each panel, quantities are plotted a functions of ω(P). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.