| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 8 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201220986 | |
| Published online | 25 April 2013 | |
Phase transitions in dense matter and the maximum mass of neutron stars
1
Institut d’Astronomie et d’Astrophysique, CP226, Université Libre de
Bruxelles,
1050
Brussels,
Belgium
e-mail: nchamel@ulb.ac.be
2 Dépt. de Physique, Université de Montréal, Montréal ( Québec),
H3C 3J7, Canada
Received: 21 December 2012
Accepted: 18 February 2013
Context. The recent precise measurement of the mass of pulsar PSR J1614−2230, as well as observational indications of even more massive neutron stars, has revived the question of the composition of matter at the high densities prevailing inside neutron-star cores.
Aims. We study the impact on the maximum possible neutron-star mass of an “exotic” core consisting of non-nucleonic matter. For this purpose, we study the occurrence of a first-order phase transition in nucleonic matter.
Methods. Given the current lack of knowledge of non-nucleonic matter, we consider the stiffest possible equation of state subject only to the constraints of causality and thermodynamic stability. The case of a hadron-quark phase transition is discussed separately. The purely nucleonic matter is described using a set of unified equations of state that have been recently developed to permit a consistent treatment of both homogeneous and inhomogeneous phases. We then compute the mass-radius relation of cold nonaccreting neutron stars with and without exotic cores from the Tolman-Oppenheimer-Volkoff equations.
Results. We find that even if there is a significant softening of the equation of state associated with the actual transition to an exotic phase, there can still be a stiffening at higher densities closer to the center of the star that is sufficient to increase the maximum possible mass. However, with quarks the maximum neutron-star mass is always reduced by assuming that the sound speed is limited by c/√3 as suggested by QCD calculations. In particular, by invoking such a phase transition, it becomes possible to support PSR J1614−2230 with a nucleonic equation of state that is soft enough to be compatible with the kaon and pion production in heavy-ion collisions.
Key words: stars: neutron / equation of state / gravitation / dense matter / methods: numerical
© ESO, 2013
1. Introduction
Born from the catastrophic gravitational core collapse of massive stars (mass M ≳ 8 M⊙) at the end point of their evolution, neutron stars are among the most compact objects in the universe (Haensel et al. 2007), with a radius of the order of 10 km and a mass of around 2 M⊙. A few meters below the surface at densities above ~104 g cm, matter is so compressed that all atoms are fully ionized and are arranged on a regular Coulomb lattice of nuclei, neutralized by a gas of degenerate electrons; this is the “outer crust”. Deeper in the star, nuclei become more and more neutron rich, as a result of electron capture, and at a density of about ~4 × 1011 g cm neutrons begin to drip out of the nuclei. This marks the transition to the inner crust, an inhomogeneous assembly of neutron-proton clusters and unbound neutrons, neutralized by the degenerate electron gas (Pethick & Ravenhall 1995; Chamel & Haensel 2008). When the density reaches about ~1014 g cm (about half the density found at the center of heavy nuclei), the crust dissolves into a uniform plasma of neutrons with a small admixture of protons, neutralized by electrons and, at slightly higher densities, muons.
The mass and radius of a neutron star are determined by the equation of state (EoS) over the full range of densities found in the star, i.e., by the relation between the pressure P and the mass-energy density ρ, although the core will play a dominating role. This has motivated many studies of purely nucleonic neutron-star matter (N*M), i.e., a homogeneous and electrically charged neutral liquid of nucleons and leptons in beta equilibrium. These studies consist of simple extensions of the large number of many-body calculations performed since the beginning of the 1950s on so-called nuclear matter, consisting of just neutrons and protons that interact via “realistic” forces fitted directly to experimental nucleon-nucleon phase shifts and to the properties of bound two- and three-nucleon systems (the Coulomb force being switched off). The EoS of purely nucleonic N*M has been determined in such many-body calculations up to the highest densities found in the most massive neutron stars. The maximum neutron-star mass obtained using different many-body methods and realistic forces is predicted to lie in the range between ~1.8−2.5 M⊙ (Li & Schulze 2008; Fuchs 2008) and is therefore compatible with the measured value 1.97 ± 0.04 M⊙ for the mass of the pulsar PSR J1614−2230 (Demorest et al. 2010).
However, the core of massive neutron stars is likely to contain not only nucleons and leptons but also other particles like hyperons, meson condensates, or even deconfined quarks (Page & Reddy 2006; Weber et al. 2007). Neutron stars with a hyperon core are sometimes referred to as “hyperon stars” (Glendenning 2000). Now according to Brueckner-Hartree-Fock calculations using realistic two- and three-body forces (Vidaña et al. 2011; Burgio et al. 2011; Schulze & Rijken 2011), the appearance of hyperons in dense matter softens the EoS considerably thus lowering the maximum neutron-star mass to an almost unique value around 1.3−1.4 M⊙. On the other hand, some relativistic mean-field calculations including hyperons can support neutron stars that are as massive as PSR J1614−2230 (Bednarek et al. 2012; Sulaksono & Agrawal 2012; Jiang et al. 2012; Weissenborn et al. 2012; Zhao & Jia 2012). This discrepancy can be understood at least partly from the fact that the maximum mass is very sensitive to the various hyperonic couplings, and these are determined very poorly since the limited nuclear and hypernuclear data that are relevant constrain the EoS only in the vicinity of the saturation density, whereas the maximum neutron-star mass is mostly determined by the EoS at much higher densities. Likewise, some relativistic mean-field models including meson condensates are able to predict the existence of massive neutron stars (Gupta & Arumugam 2012).
Another possibility for raising the maximum mass of neutron stars above ~2 M⊙ lies in the deconfinement of quarks in the core (such stars are generally called “hybrid stars”, see e.g. Glendenning 2000). However, most of the calculations on which this conclusion is based are phenomenological in the sense that they lack a direct relationship with quantum chromodynamics (QCD): see, e.g. Alford et al. (2007) and references therein. Even though recent perturbative QCD calculations lead to predicting compact stars compatible with PSR J1614−2230 (Kurkela et al. 2010), these calculations are not strictly valid for the densities prevailing in neutron stars, even in the most massive ones. In any case, whether the densities reached in neutron stars are high enough for deconfinement to occur is still an open question.
The EoS of neutron-star cores allowing for the presence of all kinds of particles (nucleons, leptons, hyperons, meson condensates, deconfined quarks, etc.) thus remains highly uncertain, and this situation is unlikely to be changed in the near future. Indeed, understanding the properties of high-density matter would require a consistent treatment of the various hadron species taking their internal structure into account based on QCD. Unfortunately, solving the equations of QCD in the nonperturbative regime prevailing in neutron-star cores appears as an extremely challenging problem. In comparison, the ambiguities in the EoS of purely nucleonic matter are much less acute, despite the divergences between different calculations at the higher densities found in neutron-star cores.
In this paper we do not deal with all the large uncertainties in the underlying physics of the EoS of the “exotic” non-nucleonic matter that might be found in neutron-star cores. Rather, we determine in all generality the optimal possible increase in the maximum neutron-star mass over what is found with purely nucleonic N*M. We only impose the constraints of causality and thermodynamic stability, i.e. the condition that at a given pressure a phase transition will occur only if the Gibbs free energy per nucleon is lowered. For the purely nucleonic N*M, we use a set of unified EoSs based on the nuclear energy-density functional theory (Goriely et al. 2010), as described in Sect. 2. In Sect. 3 we discuss the thermodynamics of a possible transition to an exotic phase, and then the EoS of such a phase. For the latter we consider first the case where the stiffness of the exotic phase is only limited by causality, i.e., the requirement that the speed of sound cannot exceed the speed of light, c. We then take account of the fact that, according to both perturbative QCD calculations at zero temperature (Kurkela et al. 2010) and non-pertubative lattice QCD calculations at finite temperatures (see e.g. Karsch 2007; Borsányi et al. 2010, and references therein), the speed of sound in a gas of deconfined quarks cannot exceed 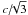 , and accordingly modify our causally limited EoS. The implications for the maximum neutron-star mass are discussed in Sect. 4, while in Sect. 5 we summarize our conclusions.
, and accordingly modify our causally limited EoS. The implications for the maximum neutron-star mass are discussed in Sect. 4, while in Sect. 5 we summarize our conclusions.
2. The nucleonic equation of state
To assess the role of a transition to a non-nucleonic phase we must begin with a purely nucleonic EoS that has been well adapted to the description of neutron stars whose cores are assumed to be non-exotic. Suitable such starting points are provided by the family of three EoSs that we have developed to provide a unified treatment of all parts of neutron stars. These EoSs are based on nuclear energy-density functionals that have all been derived from effective interactions that are generalizations of the conventional Skyrme forces in that they contain terms that depend simultaneously on momentum and density (Goriely et al. 2010). The parameters of this form of Skyrme force were determined primarily by fitting measured nuclear masses, which were calculated with the Hartree-Fock-Bogoliubov (HFB) method. For this it was necessary to supplement the Skyrme forces with a microscopic contact pairing force, phenomenological Wigner terms, and correction terms for the spurious collective energy. In fitting the mass data, we simultaneously constrained the Skyrme force to fit the zero-temperature EoS of homogeneous pure neutron matter (NeuM), as determined by many-body calculations with realistic two- and three-nucleon forces. Actually, several such calculations of the EoS of NeuM have been made, and while they all agree very closely at nuclear and subnuclear densities, they differ in the stiffness that they predict at the much higher densities that can be encountered towards the center of neutron stars. Functional BSk19 was fitted to a soft EoS of NeuM (the one labeled “UV14 plus TNI” in Wiringa et al. 1988, combined with the EoS of Friedman & Pandharipande 1981), BSk21 to a very stiff EoS (the one labeled “V18” in Li & Schulze 2008), while BSk20 was fitted to an EoS of intermediate stiffness (the one labeled “A18 + δ v + UIX” in Akmal et al. 1998, which we abbreviate as APR). All three EoSs are consistent with quantum Monte Carlo calculations (Gandolfi et al. 2012). Even though our EoSs were not fitted to symmetric nuclear matter, they are all consistent with the constraint of Danielewicz et al. (2002) deduced from heavy-ion collisions. Furthermore, the strength of the pairing force at each point in the nucleus in question was determined so as to exactly reproduce realistic 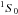 pairing gaps of homogeneous nuclear matter of the appropriate density and charge asymmetry (Chamel 2010). Finally, we imposed on these forces a number of supplementary realistic constraints, the most notable of which is the suppression of an unphysical transition to a spin-polarized configuration, both at zero and finite temperatures, at densities found in neutron stars and supernova cores (Chamel et al. 2009; Chamel & Goriely 2010; Goriely et al. 2010). The form of our functionals was flexible enough for us to satisfy all these constraints and at the same time fit the 2149 measured masses of nuclei with N and Z ≥ 8 given in the 2003 Atomic Mass Evaluation (AME, Wapstra et al. 2003) with an rms deviation as low as 0.58 MeV for all three models, i.e., for all three options for the high-density behavior of NeuM.
pairing gaps of homogeneous nuclear matter of the appropriate density and charge asymmetry (Chamel 2010). Finally, we imposed on these forces a number of supplementary realistic constraints, the most notable of which is the suppression of an unphysical transition to a spin-polarized configuration, both at zero and finite temperatures, at densities found in neutron stars and supernova cores (Chamel et al. 2009; Chamel & Goriely 2010; Goriely et al. 2010). The form of our functionals was flexible enough for us to satisfy all these constraints and at the same time fit the 2149 measured masses of nuclei with N and Z ≥ 8 given in the 2003 Atomic Mass Evaluation (AME, Wapstra et al. 2003) with an rms deviation as low as 0.58 MeV for all three models, i.e., for all three options for the high-density behavior of NeuM.
These functionals are very well adapted to a unified treatment of all parts of purely nucleonic neutron stars, given not only the NeuM constraints to which they have been subjected but also the precision fit to masses, which means that the presence of inhomogeneities and of protons is well represented. We used these functionals in Pearson et al. (2011, 2012) to calculate the properties of the outer and inner crusts, respectively, while in Chamel et al. (2011) we determined the maximum possible neutron-star mass for each functional. For this calculation we had to solve the Tolman-Oppenheimer-Volkoff (TOV) equations (Tolman 1939; Oppenheimer & Volkoff 1939) for different values of the central density, thereby obtaining the mass M of the star as a function of its radius R. The total mass of a neutron star depends largely on the core properties (although we always account for the crust using the EoS of Pearson et al. 2011, 2012, for the appropriate functionals) and thus on the EoS of homogeneous N*M: Fig. 1 shows the range of uncertainty spanned by our three functionals, BSk19 being the softest and BSk21 the stiffest. The corresponding uncertainties in the neutron-star mass for a given radius are shown in Fig. 2; from this same figure we can infer that BSk21 is stiff enough at high densities to support neutron stars as massive as PSR J1614−2230, but that functional BSk19 is too soft (BSk20 can also support PSR J1614−2230). It is worth noting that our functionals are consistent with the radius constraints of Steiner et al. (2010) inferred from observations of X-ray bursters and low-mass X-ray binaries.
 |
Fig. 1 Left panel a) range of energies per baryon (defined by e = ℰ/n − mnc2 where mn is the neutron mass) of nucleonic matter in beta equilibrium at zero temperature as a function of the baryon density for the unified Brussels-Montreal EoSs (Goriely et al. 2010). The shaded area reflects the different degrees of stiffness of these EoSs: the lower limit corresponds to BSk19, the upper to BSk21. Right panel b) corresponding range of pressures. |
 |
Fig. 2 Range of neutron-star masses and radii for the unified Brussels-Montreal EoSs (Goriely et al. 2010). The shaded area reflects the different degrees of stiffness of these EoSs: the lower limit corresponds to BSk19, the upper to BSk21. For comparison, we have indicated the measured mass of PSR J1614−2230 including estimated errors from Demorest et al. (2010). |
Since the softest of our Skyrme functionals that is compatible with the measured mass of PSR J1614−2230 is BSk20 (Chamel et al. 2011), the question arises as to whether it is not too stiff to be compatible with the analysis of K+ production (Fuchs et al. 2001; Sturm et al. 2001; Hartnack et al. 2006) and π−/π+ production ratio (Xiao et al. 2009) that have been measured in heavy-ion collisions. In particular, the former analysis suggests that the EoS of symmetric nuclear matter is much softer than what is obtained with BSk20 over the range 2n0 ≲ n ≲ 3n0, whereas the latter analysis concludes that over the range 2n0 ≲ n ≲ 3.5n0 the symmetry energy rises significantly less steeply than predicted for the APR EoS, on which BSk20 is based. These results, taken at face value, discriminate against both BSk20 and BSk21, and favor BSk19. Various exotic mechanisms, such as a “fifth force” (Wen et al. 2009) or variations of the gravitational constant (Wen et al. 2012), have been proposed to simultaneously account for both this result and the existence of PSR J1614−2230, but we shall see that the much more prosaic explanation of a transition to a non-nucleonic phase may suffice.
3. Transition to non-nucleonic phase in dense matter
3.1. Thermodynamic equilibrium
In view of the current uncertainties about the composition of matter at supernuclear densities, we simply assume that above a baryon density nN, nucleonic matter undergoes a first-order phase transition to some unknown exotic phase with a baryon density nX > nN. The exotic phase could consist of a pion condensate, a kaon condensate, hyperonic matter, or deconfined quarks (see e.g. Glendenning 2000; Haensel et al. 2007). In the region of coexisting phases, nN ≤ n ≤ nX, thermodynamic equilibrium requires the constancy of the pressure P and baryon chemical potential μ: 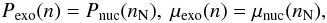 (1)where the subscripts “exo” and “nuc” are used to denote the exotic and nuclear-matter EoS, respectively. As a result, using the general expression
(1)where the subscripts “exo” and “nuc” are used to denote the exotic and nuclear-matter EoS, respectively. As a result, using the general expression 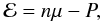 (2)valid at the zero temperature that we assume throughout this paper, we see that the energy density of the coexisting phases varies linearly with the baryon density in the range nN ≤ n ≤ nX according to
(2)valid at the zero temperature that we assume throughout this paper, we see that the energy density of the coexisting phases varies linearly with the baryon density in the range nN ≤ n ≤ nX according to  (3)At the density nX, which we always suppose to be lower than the central density ncen of the star, the phase transition has reduced the pressure from Pnuc(nX) to Pnuc(nN).
(3)At the density nX, which we always suppose to be lower than the central density ncen of the star, the phase transition has reduced the pressure from Pnuc(nX) to Pnuc(nN).
In this simple picture of a first-order phase transition, the two phases cannot coexist in the star because the densest phase will sink below the other. In hydrostatic equilibrium, the two phases would thus be spatially separated with the density varying discontinuously at the interface. In reality, the two distinct phases will generally rearrange themselves by forming a mixed phase in a finite region of the star (Tatsumi et al. 2011) unless the surface tension and the Coulomb interaction are sufficiently strong, as could be the case for the hadron-quark phase transition (see e.g. Heiselberg et al. 1993; Alford et al. 2001; Endo et al. 2006). The presence of a mixed phase leads to a smooth transition with the pressure increasing monotonically with the density instead of remaining constant. This situation generally increases the maximum neutron-star mass (see e.g. Glendenning 2000, Sect. 9.3). However, given the uncertainties pertaining to the EoS of the mixed phase, here we suppose the least favorable case of a first-order transition considered in Eqs. (1) and (3) which will provide a lower bound on the maximum mass (Rhoades & Ruffini 1974).
3.2. Equation of state for exotic matter
Causal limit of EoS. Instead of considering specific models of non-nucleonic matter, we suppose that the EoS of the exotic phase is the stiffest possible, being only constrained by Le Chatelier’s principle 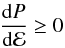 (4)and the causality requirement
(4)and the causality requirement 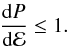 (5)Since the maximally compact stars are obtained for dP/dℰ = 1 (Rhoades & Ruffini 1974), we will assume that the pressure of the exotic phase at densities n > nX can be expressed as
(5)Since the maximally compact stars are obtained for dP/dℰ = 1 (Rhoades & Ruffini 1974), we will assume that the pressure of the exotic phase at densities n > nX can be expressed as 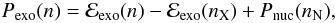 (6)recalling that Pnuc(nN) = Pexo(nX). After integrating the pressure by using Eq. (2) with μ = dℰ/dn, we find for the energy density of the exotic phase
(6)recalling that Pnuc(nN) = Pexo(nX). After integrating the pressure by using Eq. (2) with μ = dℰ/dn, we find for the energy density of the exotic phase ![\begin{eqnarray} \label{4} \mathcal{E}_{\rm exo}(n)=\frac{n_{\rm X} \mu_{\rm nuc}(n_{\rm N})}{2}\left[1+ \left(\frac{n}{n_{\rm X}}\right)^{2}\right]-P_{\rm nuc}(n_{\rm N}) . \end{eqnarray}](/articles/aa/full_html/2013/05/aa20986-12/aa20986-12-eq50.png) (7)Using Eqs. (3), (6), and (7), the baryon chemical potential in the exotic phase can be expressed as
(7)Using Eqs. (3), (6), and (7), the baryon chemical potential in the exotic phase can be expressed as 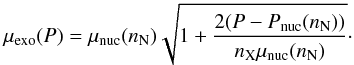 (8)From both Eqs. (7) and (8) it is seen that the EoS of the exotic phase is completely determined by the parameters nN and nX, and for any given pair of values of these parameters we have to determine the maximum possible neutron-star mass. But in this very general study we have a high degree of freedom in choosing the values of these parameters, and we do so in such a way as to obtain a maximum maximorum in the neutron-star mass, subject to certain physical constraints that we now discuss.
(8)From both Eqs. (7) and (8) it is seen that the EoS of the exotic phase is completely determined by the parameters nN and nX, and for any given pair of values of these parameters we have to determine the maximum possible neutron-star mass. But in this very general study we have a high degree of freedom in choosing the values of these parameters, and we do so in such a way as to obtain a maximum maximorum in the neutron-star mass, subject to certain physical constraints that we now discuss.
Dealing first with nN, we find that increasing values of this parameter lead to decreasing values of the maximum mass, as is to be expected intuitively. We therefore consider the lowest possible density nN consistent with nuclear data. In particular, we set nN = 0.2 fm, which is slightly higher than the highest density found in nuclei, as predicted by HFB calculations on more than 8000 nuclei1. Since much higher densities can be reached in heavy-ion collisions, the lack of any evidence of phase transitions might suggest that nN ≫ 0.2 fm. In fact, this is not necessarily the case because the conditions prevailing in neutron-star interiors are very different from those encountered in heavy-ion collisions. We do not discuss here the possibility of strange stars for which the exotic phase (strange-quark matter in this case) would be present in the entire star. At densities n < nN, we use the EoS of Pearson et al. (2011, 2012) for the outer and inner parts of the crust and the EoS of Goriely et al. (2010) for the purely nucleonic part of the core.
As for nX, we note first that the pressure of the exotic phase remains lower than that of the nucleonic phase from the baryon density nN up to some density nP > nX, but that it is higher thereafter, as shown in Fig. 3. Therefore the impact of a phase transition will be to increase the maximum neutron-star mass provided the central density ncen is substantially higher than nP. However, nP cannot be freely adjusted because of the requirement that the exotic phase should be energetically favored. More precisely, at a given pressure P, the equilibrium phase is found by minimizing the Gibbs free energy per baryon, which coincides with the baryon chemical potential. Now the baryon chemical potential of the exotic phase will rise more steeply than that of the nucleonic phase, and at some pressure PC the two phases will have the same baryon chemical potentials, μexo(PC) = μnuc(PC). This will occur when the density of the exotic phase reaches the value nC, such that Pexo(nC) = PC. For pressures P > PC, or equivalently for densities n > nC, the ground state of matter will once again be purely nucleonic. In order to exclude this unlikely possibility, we must have PC higher than the central pressure Pcen (or equivalently nC higher than ncen) in the most massive neutron stars. Fixing PC then completely determines the density nX, which is given by ![\begin{eqnarray} \label{5} n_{\rm X}= \frac{2 (P_{\rm C}-P_{\rm nuc}(n_{\rm N}))} {\mu_{\rm nuc}(n_{\rm N})} \Biggl[\left(\frac{\mu_{\rm nuc}(P_{\rm C})}{\mu_{\rm nuc}(n_{\rm N})}\right)^2-1\Biggr]^{-1} , \end{eqnarray}](/articles/aa/full_html/2013/05/aa20986-12/aa20986-12-eq64.png) (9)where we have used Eq. (8). At the same time, we confirmed the intuitively plausible result that the lower PC is, the greater the maximum possible mass, and accordingly we arranged for PC to be very close to Pcen. Now the maximum central pressure in a neutron star is approximately given by (Lattimer & Prakash 2011)
(9)where we have used Eq. (8). At the same time, we confirmed the intuitively plausible result that the lower PC is, the greater the maximum possible mass, and accordingly we arranged for PC to be very close to Pcen. Now the maximum central pressure in a neutron star is approximately given by (Lattimer & Prakash 2011) 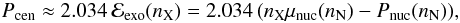 (10)where we have used Eq. (7). The optimum value of nX was therefore obtained by solving Eqs. (9) and (10) with Pcen = PC. However, since Eq. (10) is only approximately valid, we subsequently refined the value of PC by solving the TOV equations numerically in order to obtain a more accurate estimate of Pcen. With PC and nX determined, the density nC (for which Pexo(nC) = PC) can be obtained from Eqs. (6) and (7). The corresponding EoSs are as shown in Figs. 3 and 4. In particular, we note that at a given pressure the phase transition leads to a lowering of the baryon chemical potential.
(10)where we have used Eq. (7). The optimum value of nX was therefore obtained by solving Eqs. (9) and (10) with Pcen = PC. However, since Eq. (10) is only approximately valid, we subsequently refined the value of PC by solving the TOV equations numerically in order to obtain a more accurate estimate of Pcen. With PC and nX determined, the density nC (for which Pexo(nC) = PC) can be obtained from Eqs. (6) and (7). The corresponding EoSs are as shown in Figs. 3 and 4. In particular, we note that at a given pressure the phase transition leads to a lowering of the baryon chemical potential.
 |
Fig. 3 Upper panels: pressure as a function of the baryon number density (up to the highest central density ncen found in the most massive neutron stars) for the softest (BSk19, panel a) and the stiffest (BSk21, panel b) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a causally limited phase transition (solid lines). Lower panels: energy per baryon (defined by e = ℰ/n − mnc2 where mn is the neutron mass) as a function of the baryon density for the softest (BSk19, panel c) and the stiffest (BSk21, panel d) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a causally limited phase transition (solid lines). The shaded areas indicate the region of phase coexistence at densities nN ≤ n ≤ nX. |
 |
Fig. 4 Pressure as a function of the baryon chemical potential for the softest (BSk19, panel a) and the stiffest (BSk21, panel b) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a causally-limited phase transition (solid lines). The horizontal dotted line indicates the central pressure in the most massive neutron stars. |
 |
Fig. 5 Upper panels: pressure as a function of the baryon number density (up to the highest central density ncen found in the most massive neutron stars) for the softest (BSk19, panel a) and the stiffest (BSk21, panel b) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a quark phase transition (solid lines). Lower panels: energy per baryon (defined by e = ℰ/n − mnc2 where mn is the neutron mass) as a function of the baryon density for the softest (BSk19, panel c) and the stiffest (BSk21, panel d) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a quark phase transition (solid lines). The shaded areas indicate the region of phase coexistence at densities nN ≤ n ≤ nX. |
The density nP is completely determined by the nucleonic EoS, nN and nC, as follows. We first note that for the EoS given by Eq. (6) we have μ = dℰ/dn = dP/dn. Differentiating Eq. (2) thus leads to 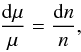 (11)which after integration using Eq. (1), yields
(11)which after integration using Eq. (1), yields 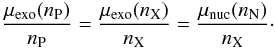 (12)Case of quark matter. The foregoing analysis may be invalid and the limiting EoS much softer if quark deconfinement takes place in the core of a neutron star. According to both perturbative QCD calculations at zero temperature (Kurkela et al. 2010) and nonperturbative lattice QCD calculations at finite temperatures (Karsch 2007; Borsányi et al. 2010), the speed of sound in quark matter is limited by
(12)Case of quark matter. The foregoing analysis may be invalid and the limiting EoS much softer if quark deconfinement takes place in the core of a neutron star. According to both perturbative QCD calculations at zero temperature (Kurkela et al. 2010) and nonperturbative lattice QCD calculations at finite temperatures (Karsch 2007; Borsányi et al. 2010), the speed of sound in quark matter is limited by 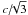 . Assuming that this result remains valid in the interior of neutron stars, the stiffest possible EoS is given by
. Assuming that this result remains valid in the interior of neutron stars, the stiffest possible EoS is given by ![\begin{eqnarray} \label{12} P_{\rm quark}(n)=\frac{1}{3}\left[\mathcal{E}_{\rm quark}(n)-\mathcal{E}_{\rm quark}(n_{\rm X})\right] + P_{\rm nuc}(n_{\rm N}) . \end{eqnarray}](/articles/aa/full_html/2013/05/aa20986-12/aa20986-12-eq70.png) (13)After integrating the pressure, we find for the energy density
(13)After integrating the pressure, we find for the energy density ![\begin{eqnarray} \label{13} \mathcal{E}_{\rm quark}(n)=\frac{3}{4} n_{\rm X} \mu_{\rm nuc}(n_{\rm N})\left[\frac{1}{3}+\left(\frac{n}{n_{\rm X}}\right)^{4/3}\right]-P_{\rm nuc}(n_{\rm N}) , \end{eqnarray}](/articles/aa/full_html/2013/05/aa20986-12/aa20986-12-eq71.png) (14)instead of Eq. (7). This equation of state ressembles that obtained with the simplest MIT bag model, which has been commonly used for describing the interior of compact stars (see e.g. Glendenning 2000; Haensel et al. 2007). In this model, quarks are treated as massless and noninteracting particles confined inside a “bag”. The pressure of the quarks is then given by
(14)instead of Eq. (7). This equation of state ressembles that obtained with the simplest MIT bag model, which has been commonly used for describing the interior of compact stars (see e.g. Glendenning 2000; Haensel et al. 2007). In this model, quarks are treated as massless and noninteracting particles confined inside a “bag”. The pressure of the quarks is then given by 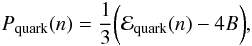 (15)where B is the bag pressure. Comparing Eqs. (13) and (15) yields the effective bag pressure
(15)where B is the bag pressure. Comparing Eqs. (13) and (15) yields the effective bag pressure 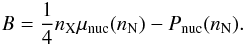 (16)As a matter of fact, Eq. (14) is also a fairly good approximation of more realistic quark matter EoSs (Zdunik et al. 2000; Gondek-Rosińska et al. 2000). Using Eqs. (13) and (14), the chemical potential is given by
(16)As a matter of fact, Eq. (14) is also a fairly good approximation of more realistic quark matter EoSs (Zdunik et al. 2000; Gondek-Rosińska et al. 2000). Using Eqs. (13) and (14), the chemical potential is given by ![\begin{eqnarray} \mu_{\rm quark}(P)=\mu_{\rm nuc}(n_{\rm N})\Biggl[\frac{4(P-P_{\rm nuc}(n_{\rm N}))}{\mu_{\rm nuc}(n_{\rm N}) n_{\rm X}}+1\Biggr]^{1/4}\cdot \end{eqnarray}](/articles/aa/full_html/2013/05/aa20986-12/aa20986-12-eq75.png) (17)Again, the EoS of the quark phase is completely determined by the parameters nN and nX, whose values must be specified. We choose the former as before, remarking that according to percolation simulations (Magas & Satz 2003) the density nN at which the hadron-quark phase transition begins could be very close to the saturation density. The density nX is still determined by maximizing the neutron-star mass, subject to the constraint that there be no reconversion of the exotic phase into nucleonic matter at the highest densities prevailing in the most massive neutron stars. However, the situation is now more complicated than in the previous case, where the stiffness of the EoS is limited only by causality. The EoS for quark matter is shown in Figs. 5 and 6, where it will be seen that it is possible to have equality of both the chemical potentials and the pressures of the two phases at the same density nC:
(17)Again, the EoS of the quark phase is completely determined by the parameters nN and nX, whose values must be specified. We choose the former as before, remarking that according to percolation simulations (Magas & Satz 2003) the density nN at which the hadron-quark phase transition begins could be very close to the saturation density. The density nX is still determined by maximizing the neutron-star mass, subject to the constraint that there be no reconversion of the exotic phase into nucleonic matter at the highest densities prevailing in the most massive neutron stars. However, the situation is now more complicated than in the previous case, where the stiffness of the EoS is limited only by causality. The EoS for quark matter is shown in Figs. 5 and 6, where it will be seen that it is possible to have equality of both the chemical potentials and the pressures of the two phases at the same density nC: 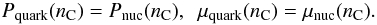 (18)It follows from Eq. (2) that the energy densities of the two phases are also equal
(18)It follows from Eq. (2) that the energy densities of the two phases are also equal 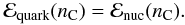 (19)We found numerically that this situation corresponds to the maximum possible neutron-star mass. It particularly needs to be emphasized that while nC is now less than ncen, the exotic phase is not reconverted into nucleonic matter: although it is on the point of doing so at nC, the EoS of quark matter immediately softens as n increases beyond nC. In any case, we see that while the pressure in the quark phase is higher than in the nucleonic phase at relatively low densities, the reverse is the case at the higher densities relevant to the maximum neutron-star mass that can be supported. We may thus anticipate that quark deconfinement will reduce the maximum neutron-star mass, assuming that the speed of sound is limited by
(19)We found numerically that this situation corresponds to the maximum possible neutron-star mass. It particularly needs to be emphasized that while nC is now less than ncen, the exotic phase is not reconverted into nucleonic matter: although it is on the point of doing so at nC, the EoS of quark matter immediately softens as n increases beyond nC. In any case, we see that while the pressure in the quark phase is higher than in the nucleonic phase at relatively low densities, the reverse is the case at the higher densities relevant to the maximum neutron-star mass that can be supported. We may thus anticipate that quark deconfinement will reduce the maximum neutron-star mass, assuming that the speed of sound is limited by 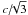 .
.
 |
Fig. 6 Pressure as a function of the baryon chemical potential for the softest (BSk19, panel a) and the stiffest (BSk21, panel b) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a quark phase transition (solid lines). The horizontal dotted line indicates the central pressure in the most massive neutron stars. |
 |
Fig. 7 Range of masses and radii of neutron stars with no quark cores (shaded areas), for maximally stiff EoSs and for EoSs satisfying thermodynamic stability. For comparison, we indicate the measured mass of PSR J1614−2230 including estimated errors from Demorest et al. (2010). The dotted area delimits the estimated range of masses of the soft X-ray transient GRO J0422 + 32 from Gelino & Harrison (2003). |
Concerning the low-density phase transition from nucleonic to quark matter, we see on comparing Figs. 3 and 5 that the density range nX − nN over which the two phases coexist is much narrower than in the case of the transition to the causally limited EoS.
The effective bag constants associated with the nucleonic EoSs BSk19, BSk20 and BSk21 (respectively 78.6, 65.5, and 56.7 MeV fm) lie in the range of values that have been generally adopted for studies of hybrid stars (see e.g. Haensel et al. 2007).
 |
Fig. 8 Range of masses and radii of neutron stars with quark cores (shaded areas), for maximally stiff quark EoSs and for EoSs satisfying thermodynamic stability. For comparison, we indicate the measured mass of PSR J1614−2230 including estimated errors from Demorest et al. (2010). |
Stability of nonrotating neutron stars with exotic cores.
4. Neutron-star maximum mass
For each of our three unified EoSs we have solved the TOV equations that describe the global structure of spherical nonrotating neutron stars (Tolman 1939; Oppenheimer & Volkoff 1939). As shown in a previous paper (Chamel et al. 2011), the impact of the rotation on the maximum neutron star mass is negligibly small for stars having rotation periods comparable to that of PSR J1614−2230. For simplicity, we have therefore ignored rotation. The resulting mass-radius relations are plotted in Figs. 7 and 8.
Global structure of nonrotating neutron stars.
Neutron stars with central densities ncen ≳ nX may be unstable with respect to radial oscillations due to the strong softening accompanying the phase transition in dense matter. Unstable configurations, which are characterized by the inequality (see e.g. Haensel et al. 2007) 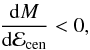 (20)are indicated in Tables 1 and 2 for each of our three functionals. For neutron stars with quark cores, no instabilities were found for BSk20 and BSk21, and unstable configurations for BSk19 were found to be restricted to a very narrow range of masses and radii.
(20)are indicated in Tables 1 and 2 for each of our three functionals. For neutron stars with quark cores, no instabilities were found for BSk20 and BSk21, and unstable configurations for BSk19 were found to be restricted to a very narrow range of masses and radii.
The numerical values of the maximum neutron-star masses Mmax are indicated in Tables 3 and 4 for each of our three functionals. We also show in these tables the corresponding radius, the highest baryonic density nN of the nucleonic phase, the lowest baryonic density nX of the exotic phase, and the central baryonic density ncen.
In Table 5 we summarize the results of Chamel et al. (2011) for the case of no exotic phase. Comparing with Table 3, we see that the result of allowing a transition to an exotic phase whose EoS is limited only by causality is always to increase the maximum possible neutron-star mass. Of particular interest is the case of functional BSk19, which can now support pulsar PSR J1614−2230. Thus this functional allows us to reconcile the existence of this pulsar with the K+ production (Fuchs et al. 2001; Sturm et al. 2001; Hartnack et al. 2006) and the π−/π+ production ratio measured in heavy-ion collisions (Xiao et al. 2009), without resorting to exotic explanations such as a “fifth force” (Wen et al. 2009) or variations on the gravitation constant (Wen et al. 2012): it is enough to suppose that nucleonic matter undergoes a transition at high densities to a phase whose EoS is limited only by causality.
On the other hand, comparing Tables 4 and 5 shows that the effect of quark deconfinement is to reduce the maximum possible neutron-star mass, assuming that the speed of sound is limited by 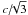 . We stress, however, that the maximum density of neutron stars may not be high enough for perturbative QCD to be valid, and that the EoS of deconfined quarks might well be limited only by causality.
. We stress, however, that the maximum density of neutron stars may not be high enough for perturbative QCD to be valid, and that the EoS of deconfined quarks might well be limited only by causality.
It is interesting to compare our results with those corresponding to the assumption of a maximally stiff EoS, i.e., to the assumption that the EoS is at the causal limit for all densities above nN (Zeldovich 1962; Nauenberg & Chapline 1973; Rhoades & Ruffini 1974; Malone et al. 1975; Brecher & Caporaso 1976; Hegyi et al. 1975; Hartle 1978; Lattimer et al. 1990; Kalogera & Baym 1996; Koranda et al. 1997; Sagert et al. 2012). The results are given in parentheses in Tables 3 and 4. We found, however, that such configurations are thermodynamically unstable. Not surprisingly, the maximum mass thus obtained ~3.7 M⊙ is very high. This upper bound has important consequences for identifying compact astrophysical sources. Taken at face value, it indicates that the soft X-ray transient GRO J0422 + 32, whose measured mass is 3.97 ± 0.95 M⊙ (Gelino & Harrison 2003), could be a neutron star. On the other hand, the requirement of thermodynamic stability imposes stringent constraints on the maximum neutron-star mass. In particular, the maximum mass is found to be reduced by about 1.6−1.7 M⊙ for the softest of our nucleonic EoSs, as compared to the maximally stiff EoS, as shown in Table 3 and Fig. 7. In this case, the identification of GRO J0422 + 32 as a neutron star is ruled out: it must be a black hole.
If the core of neutron stars is made of deconfined quark matter, the speed of sound in the maximally stiff EoS (obtained by setting nX = nN) will be limited by 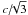 . In this case, the inequality Pquark(n) > Pnuc(n) for n > nN, hence also ℰquark(n) > ℰnuc(n), is still satisfied but only in a restricted density range, since the speed of sound in nucleonic matter generally exceeds
. In this case, the inequality Pquark(n) > Pnuc(n) for n > nN, hence also ℰquark(n) > ℰnuc(n), is still satisfied but only in a restricted density range, since the speed of sound in nucleonic matter generally exceeds 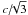 at high enough densities. For this reason, the reduction of the neutron-star maximum mass after imposing thermodynamic stability is found to be much less dramatic, amounting to ~0.6 M⊙ at most, as shown in Table 4 and Fig. 8.
at high enough densities. For this reason, the reduction of the neutron-star maximum mass after imposing thermodynamic stability is found to be much less dramatic, amounting to ~0.6 M⊙ at most, as shown in Table 4 and Fig. 8.
As a matter of fact, the maximum masses of neutron stars without and with quark cores are well approximated by the scaling relations (Hegyi et al. 1975; Hartle 1978; Witten 1984) 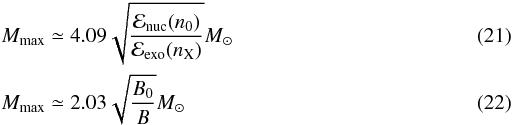 respectively, where B0 = 56 MeV fm.
respectively, where B0 = 56 MeV fm.
Summary of results from Chamel et al. (2011) for maximum neutron-star mass without an exotic phase.
5. Conclusions
We have investigated the impact of a phase transition in dense matter on the structure of neutron stars, considering the stiffest possible EoS constrained by i) causality and ii) thermodynamic stability, i.e., the condition that at a given pressure the exotic phase should have a lower Gibbs free energy per baryon than the nucleonic phase. The latter condition is found to severely limit the maximum mass.
Even if the phase transition is accompanied by a strong softening of the EoS, we find that in the causal limit the maximum possible neutron-star mass is always increased above the value determined for a purely nucleonic EoS. In particular, the softest of our three EoSs, BSk19, will then be able to support a neutron star as massive as PSR J1614−2230, provided the phase transition begins at a density nN as low as 0.2 fm. This shows, incidentally, that the existence of a two-solar mass neutron star is not necessarily incompatible with the soft nuclear-matter EoS that is suggested by the measurements of the kaon and pion productions in heavy-ion collisions (Fuchs et al. 2001; Sturm et al. 2001; Hartnack et al. 2006; Xiao et al. 2009).
On the other hand, the presence of deconfined quarks in dense matter will generally lower the maximum mass of neutron stars, assuming the speed of sound is limited by 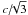 , as found by perturbative QCD calculations at zero temperature (Kurkela et al. 2010) and non-pertubative lattice QCD calculations at finite temperatures (see e.g. Karsch 2007; Borsányi et al. 2010, and references therein). In this case, only the stiffest of our nucleonic EoSs, BSk21, will be consistent with the recently measured mass of PSR J1614−2230. If confirmed, reported observations of significantly more massive neutron stars with M > 2 M⊙ (Clark et al. 2002; Freire et al. 2008; van Kerkwijk et al. 2011) will hardly be compatible with the presence of quark matter in neutron-star cores (see also Lattimer & Prakash 2011) unless the sound speed is significantly higher than
, as found by perturbative QCD calculations at zero temperature (Kurkela et al. 2010) and non-pertubative lattice QCD calculations at finite temperatures (see e.g. Karsch 2007; Borsányi et al. 2010, and references therein). In this case, only the stiffest of our nucleonic EoSs, BSk21, will be consistent with the recently measured mass of PSR J1614−2230. If confirmed, reported observations of significantly more massive neutron stars with M > 2 M⊙ (Clark et al. 2002; Freire et al. 2008; van Kerkwijk et al. 2011) will hardly be compatible with the presence of quark matter in neutron-star cores (see also Lattimer & Prakash 2011) unless the sound speed is significantly higher than 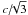 .
.
Considering the current knowledge of dense-nuclear matter properties, it would be difficult to understand the existence of neutron stars heavier than ~2.4−2.5 M⊙. This upper limit is considerably lower than estimates that did not impose the constraint of thermodynamical stability.
Acknowledgments
We are particularly grateful to P. Haensel and J. L. Zdunik for crucial remarks. We also had valuable discussions with M. Oertel, S. Reddy, P. Romatschke, and A. Sedrakian. The financial support of the FNRS (Belgium), the NSERC (Canada) and CompStar (a Research Networking Program of the European Science Foundation) is gratefully acknowledged.
References
- Akmal, A., Pandharipande, V. R., & Ravenhall, D. G. 1998, Phys. Rev. C, 58, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Rajagopal, K., Reddy, S., & Wilczek, F. 2001, Phys. Rev. D, 64, 074017 [NASA ADS] [CrossRef] [Google Scholar]
- Alford, M., Blaschke, D., Drago, A., et al. 2007, Nature, 445, E7 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bednarek, I., Haensel, P., Zdunik, J. L., Bejger, M., & Mańka, R. 2012, A&A, 543, A157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borsányi, S., Endrődi, G., Fodor, Z., et al. 2010, J. High Energy. Phys., 11, 77 [Google Scholar]
- Brecher, K., & Caporaso, G., 1976, Nature, 259, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Burgio, G. F., Schulze, H.-J., & Li, A. 2011, Phys. Rev. C, 83, 025804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N. 2010, Phys. Rev. C, 82, 061307 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Goriely, S. 2010, Phys. Rev. C, 82, 045804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., & Haensel, P. 2008, Liv. Rev. Rel., 11, 10 [Google Scholar]
- Chamel, N., Goriely, S., & Pearson, J. M. 2009, Phys. Rev. C, 80, 065804 [NASA ADS] [CrossRef] [Google Scholar]
- Chamel, N., Fantina, A. F., Pearson, J. M., & Goriely, S. 2011, Phys. Rev. C, 84, 062802 [Google Scholar]
- Clark, J. S., Goodwin, S. P., Crowther, P. A., et al. 2002, A&A, 392, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danielewicz, P., Lacey, R., & Lynch, W. G. 2002, Science, 298, 1592 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., & Hessels, J. W. T. 2010, Nature, 467, 1081 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Endo, T., Maruyama, T., Chiba, S., & Tatsumi, T. 2006, Prog. Theor. Phys., 115, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Freire, P. C. C., Ransom, S. M., Bégin, S., et al. 2008, ApJ, 675, 670 [NASA ADS] [CrossRef] [Google Scholar]
- Friedman, B., & Pandharipande, V. R. 1981, Nucl. Phys. A, 361, 502 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, C. 2008, J. Phys. G Nucl. Phys., 35, 014049 [Google Scholar]
- Fuchs, C., Faessler, A., Zabrodin, E., & Zheng, Y.-M. 2001, Phys. Rev. Lett., 86, 1974 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gandolfi, S., Carlson, J., & Reddy, S. 2012, Phys. Rev. C, 85, 032801 [NASA ADS] [CrossRef] [Google Scholar]
- Gelino, D. M., & Harrison, T. E. 2003, ApJ, 599, 1254 [NASA ADS] [CrossRef] [Google Scholar]
- Glendenning, N. K. 2000, Compact stars: nuclear physics, particle physics, and general relativity (New York: Springer Astronomy and astrophysics library) [Google Scholar]
- Gondek-Rosińska, D., Bulik, T., Zdunik, L., et al. 2000, A&A, 363, 1005 [NASA ADS] [Google Scholar]
- Goriely, S., Chamel, N., & Pearson, J. M. 2010, Phys. Rev. C, 82, 035804 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, N., & Arumugam, P. 2012, Phys. Rev. C, 85, 015804 [NASA ADS] [CrossRef] [Google Scholar]
- Haensel, P., Potekhin, A. Y., & Yakovlev, D. G. 2007, Astrophys. Space Sci. Lib., 326 [Google Scholar]
- Hartle, J. B. 1978, Phys. Rep., 46, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Hartnack, C., Oeschler, H., & Aichelin, J. 2006, Phys. Rev. Lett., 96, 012302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hegyi, D. J., Lee, T.-S. H., & Cohen, J. M. 1975, Seventh Texas Symposium on Relativistic Astrophysics, 262, 404 [NASA ADS] [Google Scholar]
- Heiselberg, H., Pethick, C. J., & Staubo, E. F. 1993, Phys. Rev. Lett., 70, 1355 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Jiang, W.-Z., Li, B.-A., & Chen, L.-W. 2012, ApJ, 756, 56 [Google Scholar]
- Kalogera, V., & Baym, G. 1996, ApJ, 470, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Karsch, F. 2007, Nucl. Phys. A, 783, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Koranda, S., Stergioulas, N., & Friedman, J. L. 1997 ApJ, 488, 799 [NASA ADS] [CrossRef] [Google Scholar]
- Kurkela, A., Romatschke, P., & Vuorinen, A. 2010, Phys. Rev. D, 81, 105021 [NASA ADS] [CrossRef] [Google Scholar]
- Lattimer J. M., & Prakash M. 2011, in From Nuclei to Stars, Festschrift in Honor of Gerald E Brown, ed. S. Lee, World Scientific, 275 [Google Scholar]
- Lattimer, J. M., Prakash, M., Masak, D., & Yahil, A. 1990, ApJ, 355, 241 [Google Scholar]
- Li, Z. H., & Schulze, H.-J. 2008, Phys. Rev. C, 78, 028801 [NASA ADS] [CrossRef] [Google Scholar]
- Magas, V., & Satz, H. 2003, EPJ C, 32, 115 [Google Scholar]
- Malone, R. C., Johnson, M. B., & Bethe, H. A. 1975, ApJ, 199, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Nauenberg, M., & Chapline, G., Jr. 1973, ApJ, 179, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Oppenheimer, J. R., & Volkoff, G. M. 1939, Phys. Rev., 55, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Page, D., & Reddy, S. 2006, Ann. Rev. Nucl. Part. Sci., 56, 327 [Google Scholar]
- Pearson, J. M., Goriely, S., & Chamel, N. 2011, Phys. Rev. C, 83, 065810 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, J. M., Chamel, N., Goriely, S., & Ducoin, C. 2012, Phys. Rev. C, 85, 065803 [NASA ADS] [CrossRef] [Google Scholar]
- Pethick, C. J., & Ravenhall, D. G. 1995, Ann. Rev. Nucl. Part. Sci., 45, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Rhoades, C. E., & Ruffini, R. 1974, Phys. Rev. Lett., 32, 324 [Google Scholar]
- Sagert, I., Tolos, L., Chatterjee, D., Schaffner-Bielich, J., & Sturm, C. 2012, Phys. Rev. C, 86, 045802 [NASA ADS] [CrossRef] [Google Scholar]
- Schulze, H.-J., & Rijken, T. 2011, Phys. Rev. C, 84, 035801 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, A. W., Lattimer, J. M., & Brown, E. F. 2010, ApJ, 722, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Sturm, C., Böttcher, I., Dȩbowski, M., et al. 2001, Phys. Rev. Lett., 86, 39 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Sulaksono, A., & Agrawal, B. K. 2012, Nucl. Phys. A, 895, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Tatsumi, T., Yasutake, N., & Maruyama, T. 2011 [arXiv:1107.0804] [Google Scholar]
- Tolman, R. C. 1939, Phys. Rev., 55, 364 [NASA ADS] [CrossRef] [Google Scholar]
- van Kerkwijk, M. H., Breton, R. P., & Kulkarni, S. R. 2011, ApJ, 728, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Vidaña, I., Logoteta, D., Providência, C., Polls, A., & Bombaci, I. 2011, Europhys. Lett., 94, 11002 [Google Scholar]
- Wapstra, A. H., Audi, G., & Thibault, C. 2003, Nucl. Phys. A, 729, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Weber, F., Negreiros, R., Rosenfield, P., & Stejner, M. 2007, Prog. Part. Nucl. Phys., 59, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Weissenborn, S., Chatterjee, D., & Schaffner-Bielich, J. 2012, Phys. Rev. C, 85, 065802 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, D.-H., Li, B.-A., & Chen, L.-W. 2009, Phys. Rev. Lett., 103, 211102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wen, D.-H., Yan, J., & Liu, X.-M. 2012, Int. J. Mod. Phys. D, 21, 50036 [NASA ADS] [CrossRef] [Google Scholar]
- Wiringa, R. B., Fiks, V., & Fabrocini, A. 1988, Phys. Rev. C, 38, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Witten, E. 1984, Phys. Rev. D, 30, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Xiao, Z., Li, B.-A., Chen, L.-W., Yong, G.-C., & Zhang, M. 2009, Phys. Rev. Lett., 102, 062502 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Zdunik, J. L., Haensel, P., Gondek-Rosińska, D., & Gourgoulhon, E. 2000, A&A, 356, 612 [NASA ADS] [Google Scholar]
- Zeldovich, Ya. B. 1962, Sov. Phys. JETP, 14, 1143 [Google Scholar]
- Zhao, X.-F., & Jia, H.-Y. 2012, Phys. Rev. C, 85, 065806 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Summary of results from Chamel et al. (2011) for maximum neutron-star mass without an exotic phase.
All Figures
 |
Fig. 1 Left panel a) range of energies per baryon (defined by e = ℰ/n − mnc2 where mn is the neutron mass) of nucleonic matter in beta equilibrium at zero temperature as a function of the baryon density for the unified Brussels-Montreal EoSs (Goriely et al. 2010). The shaded area reflects the different degrees of stiffness of these EoSs: the lower limit corresponds to BSk19, the upper to BSk21. Right panel b) corresponding range of pressures. |
| In the text | |
 |
Fig. 2 Range of neutron-star masses and radii for the unified Brussels-Montreal EoSs (Goriely et al. 2010). The shaded area reflects the different degrees of stiffness of these EoSs: the lower limit corresponds to BSk19, the upper to BSk21. For comparison, we have indicated the measured mass of PSR J1614−2230 including estimated errors from Demorest et al. (2010). |
| In the text | |
 |
Fig. 3 Upper panels: pressure as a function of the baryon number density (up to the highest central density ncen found in the most massive neutron stars) for the softest (BSk19, panel a) and the stiffest (BSk21, panel b) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a causally limited phase transition (solid lines). Lower panels: energy per baryon (defined by e = ℰ/n − mnc2 where mn is the neutron mass) as a function of the baryon density for the softest (BSk19, panel c) and the stiffest (BSk21, panel d) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a causally limited phase transition (solid lines). The shaded areas indicate the region of phase coexistence at densities nN ≤ n ≤ nX. |
| In the text | |
 |
Fig. 4 Pressure as a function of the baryon chemical potential for the softest (BSk19, panel a) and the stiffest (BSk21, panel b) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a causally-limited phase transition (solid lines). The horizontal dotted line indicates the central pressure in the most massive neutron stars. |
| In the text | |
 |
Fig. 5 Upper panels: pressure as a function of the baryon number density (up to the highest central density ncen found in the most massive neutron stars) for the softest (BSk19, panel a) and the stiffest (BSk21, panel b) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a quark phase transition (solid lines). Lower panels: energy per baryon (defined by e = ℰ/n − mnc2 where mn is the neutron mass) as a function of the baryon density for the softest (BSk19, panel c) and the stiffest (BSk21, panel d) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a quark phase transition (solid lines). The shaded areas indicate the region of phase coexistence at densities nN ≤ n ≤ nX. |
| In the text | |
 |
Fig. 6 Pressure as a function of the baryon chemical potential for the softest (BSk19, panel a) and the stiffest (BSk21, panel b) of our nucleonic EoSs (dashed lines) and for the corresponding EoSs with a quark phase transition (solid lines). The horizontal dotted line indicates the central pressure in the most massive neutron stars. |
| In the text | |
 |
Fig. 7 Range of masses and radii of neutron stars with no quark cores (shaded areas), for maximally stiff EoSs and for EoSs satisfying thermodynamic stability. For comparison, we indicate the measured mass of PSR J1614−2230 including estimated errors from Demorest et al. (2010). The dotted area delimits the estimated range of masses of the soft X-ray transient GRO J0422 + 32 from Gelino & Harrison (2003). |
| In the text | |
 |
Fig. 8 Range of masses and radii of neutron stars with quark cores (shaded areas), for maximally stiff quark EoSs and for EoSs satisfying thermodynamic stability. For comparison, we indicate the measured mass of PSR J1614−2230 including estimated errors from Demorest et al. (2010). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


