| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 9 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201220961 | |
| Published online | 16 May 2013 | |
A PCA approach to stellar effective temperatures⋆
1 Instituto de Astrofísica de Canarias 38205 La Laguna Tenerife Spain
e-mail: jbermejo@iac.es; aasensio@iac.es; callende@iac.es
2 Departamento de Astrofísica, Universidad de La Laguna, 38205 La Laguna, Tenerife, Spain
Received: 19 December 2012
Accepted: 8 March 2013
Context. The derivation of the effective temperature of a star is a critical first step in a detailed spectroscopic analysis. Spectroscopic methods suffer from systematic errors related to model simplifications. Photometric methods may be more robust, but are exposed to the distortions caused by interstellar reddening. Direct methods are difficult to apply, since fundamental data of high accuracy are hard to obtain.
Aims. We explore a new approach in which the spectrum is used to characterize a star’s effective temperature based on a calibration established by a small set of standard stars.
Methods. We perform principal component analysis on homogeneous libraries of stellar spectra, then calibrate a relationship between the principal components and the effective temperature using a set of stars with reliable effective temperatures.
Results. We find that our procedure gives excellent consistency when spectra from a homogenous set of observations are used. Systematic offsets may appear when combining observations from different sources. Using as reference the spectra of stars with high-quality spectroscopic temperatures in the Elodie library, we define a temperature scale for FG-type disk dwarfs with an internal consistency of about 50 K, in excellent agreement with temperatures from direct determinations and widely used scales based on the infrared flux method.
Key words: stars: fundamental parameters / catalogs / techniques: spectroscopic / stars: solar-type
Tables 2, 4, 5, and reduced spectra are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/553/A95
© ESO, 2013
1. Introduction
The photons we measure from a star provide information on the regions they were last emitted or scattered from, i.e. the atmosphere of the star. Accordingly, it is this shallow layer that matters for modeling and understanding a stellar spectrum. Stellar spectra are described with three basic atmospheric parameters: effective temperature (Teff), surface gravity (log g), and overall metallicity ([Fe/H]). The effective temperature corresponds to the temperature of a black body with the same total radiative energy of the star: 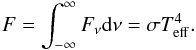 (1)In addition to the basic atmospheric parameters, we can infer a lot of information about a star from its spectrum, most notably its chemical composition from the strength of absorption lines associated with different elements.
(1)In addition to the basic atmospheric parameters, we can infer a lot of information about a star from its spectrum, most notably its chemical composition from the strength of absorption lines associated with different elements.
There are several ways to approach the task of determining the effective temperature of a star. One is by comparing the observed spectral energy distribution with model calculations (see, e.g., Ramírez et al. 2006). Another possibility consists in using photometric calibrations, such as those based on the infrared flux method (Blackwell & Lynas-Gray 1998; Alonso et al. 1996, 1999; Casagrande et al. 2010).
 |
Fig. 1 Elodie (upper panel) and S4N (lower panel) stellar parameters for all spectra in the sample. In the upper panels, the subsample of the Elodie library with the highest quality effective temperatures (QTeff = 4) is shown with filled-in black bars. |
The flux at the stellar surface (F at a distance equal to the stellar radius R) and that at the Earth (f at a distance d from the star) satisfy 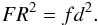 (2)Based on this property, the most straightforward method of deriving effective temperatures corresponds to measuring the bolometric flux of a star and its angular diameter (2R/d) and to using them with the Stefan-Boltzmann law (Eq. (1)). This method is, however, technologically challenging due to the tiny apparent sizes of stars in the sky – the nearest solar-like stars at merely a few pc from us are only a few milliarcseconds in diameter. Nevertheless, the Center for High Angular Resolution Astronomy (CHARA) array measurements (McAlister et al. 2005; ten Brummelaar et al. 2005) and other projects (Mozurkewich et al. 2003; Kervella & Fouqué 2008) have provided us with angular diameters with unprecedented quality for many giants and a handful of dwarf stars.
(2)Based on this property, the most straightforward method of deriving effective temperatures corresponds to measuring the bolometric flux of a star and its angular diameter (2R/d) and to using them with the Stefan-Boltzmann law (Eq. (1)). This method is, however, technologically challenging due to the tiny apparent sizes of stars in the sky – the nearest solar-like stars at merely a few pc from us are only a few milliarcseconds in diameter. Nevertheless, the Center for High Angular Resolution Astronomy (CHARA) array measurements (McAlister et al. 2005; ten Brummelaar et al. 2005) and other projects (Mozurkewich et al. 2003; Kervella & Fouqué 2008) have provided us with angular diameters with unprecedented quality for many giants and a handful of dwarf stars.
In this paper we introduce a new method of inferring the effective temperature of a star. Our procedure is inspired by the work by Cayrel et al. (2011), who derive effective temperatures by modeling the Hα line, correcting for systematic errors by linearly mapping their temperatures to a scale based on angular diameters and absolute fluxes. We condense the information on Teff contained in stellar spectra using principal component analysis (PCA). Then we map the principal components onto Teffs based on a set of reliable calibration stars. Once the calibration is performed, we can easily derive temperatures for other stars observed with the same instrument.
Since our procedure takes as input data continuum-normalized high-resolution spectra, it is immune to distortions in the spectral energy distributions due to interstellar reddening. Unlike χ2-fitting certain parts of the spectrum with high sensitivity to Teff, such as the Balmer lines, by using models, PCA is optimized to make use of all the information on the stellar effective temperature contained in the spectrum.
This paper is divided into five sections. Section 2 provides details of the libraries that we use in our work, and the PCA analysis we performed on them. Section 3 describes how we calibrate a relationship between PCA coefficients and stellar effective temperatures. Section 4 presents our results and Sect. 5 compares them with other temperature scales from the literature. In Sect. 6, we apply our preferred PCA transformation to more than 18 000 spectra from the Elodie archive. Finally, Sect. 7 gives a summary of the work and our conclusions.
2. The spectral libraries
Among the many spectral libraries available in the literature, we have selected two that cover quite homogeneously the entire visible range (from 390 to 680 nm): Elodie and S4N. As described below, these two libraries differ fundamentally in two aspects: their spectra were obtained with different instruments and processed independently, and they focus on different types of stars. S4N considers only stars in the immediate solar neighborhood, with distances to the Sun smaller than about 15 pc, whereas Elodie includes more distant stars.
2.1. Elodie
The Elodie library contains 1959 spectra of 1388 stars acquired with the Elodie spectrograph installed in the 1.93 m telescope at the Observatoire de Haute-Provence, France (Prugniel & Soubiran 2001; Prugniel et al. 2007)1. The spectra on the library have a signal-to-noise ratio (SNR) between 100 and 150. They cover the range between 3100 K to 50 000 K in effective temperature, − 0.25 to 4.9 in log g (with g in cm s-2) and − 3 to + 1 dex in [Fe/H]2. Histograms of these quantities are presented in the upper panel of Fig. 1.
The spectra have a resolving power R = λ/δλ = 42 000, with the flux normalized to a pseudo-continuum. We have performed our analysis both at a resolving power of R = 10 000 and 1000, finding slightly better results at lower resolution. Smoothing and resampling the spectra can only destroy information, but it is also possible that it helps reducing the impact of high-frequency instrumental distortions in the data. Working at low resolution offers additional advantages, since the computational effort required is signicantly smaller and opens up the application of the method to lower-resolution instruments.
In order to degrade the spectral resolution, we smear the spectra using Gaussian convolution3. Additionally, we ensure that all spectra have a consistent continuum normalization. Each spectrum is fitted with an 8th order polynomial. Data points for which the residual between the original spectrum and the fit are beyond 0.5 standard deviations below or 3 above the mean are discarded. This procedure is iterated ten times until the fit is close to the upper envelope of the spectrum. This process is arguably not optimal for locating the true stellar continuum, but it is consistently applied to all spectra.
Additional filtering is necessary, since some of the spectra show unwanted features, such as emission peaks or instrumental distortions, or correspond to outliers (for instance, when the temperature is outside the range considered in our analysis). To filter the data we first discard all spectra with emission peaks greater than 1.2 times the continuum and absorption features deeper than 0.1 times the continuum flux. After that we apply PCA to the spectra that have passed the first filter, and keep only those for which the difference between the spectra reconstructed with the first 5 principal components and the original spectrum is under 5%. This ensures that we are picking up “regular” stars which share properties with the rest of objects in the sample. That leaves us with a final set of 1245 spectra. In what follows we refer to this set of spectra as “Elodie”.
The atmospheric parameters of the Elodie stars (from the online database) have been obtained from a compilation of high resolution spectroscopic analyses in the literature. When multiple values are available from different sources, the library catalog adopts a weighted average, giving preference to data with smaller errors. The goal is to end up with a homogeneous set of values for all parameters. Quality flags (Q) are assigned to each parameter value according to the level of agreement across different sources. The better the agreement, the larger the quality flag. QTeff ranges from − 1 to 4; in this scale, 1 corresponds to the lowest and 4 to the highest quality, being − 1 and 0 special cases for internal determination of the effective temperature4, and values derived from B − V colors5, respectively.
2.2. S4N
The S4N library by Allende Prieto et al. (2004) includes spectra obtained with the Tull spectrograph (Tull et al. 1995) on the 2.7 m Harlan J. Smith telescope at the McDonald Observatory of the University of Texas at Austin, and FEROS, the Fiber-fed Extended Range Optical Spectrograph (Kaufer & Pasquini 1998) attached (at the time) to the 1.52 m telescope at the European Southern Observatory (La Silla, Chile). It includes 119 spectra of 119 stars (including the spectrum of the blue sky as a proxy for the Sun), which have a SNR of 150–600, and a resolving power R ≃ 50 000. It covers the range of − 0.9 to 0.5 in metallicity, 1.9 to 4.7 in log g and 4158 K to 7646 K in effective temperature, as illustrated in the lower panel of Fig. 1.
For consistency with the Elodie dataset, we have used the same wavelength grid and the same smoothing algorithm in S4N, resulting in a final resolution of R = 1000. Likewise, exactly the same continuum normalization process has been applied to the S4N spectra.
The original atmospheric parameters for the S4N library stars were obtained using several methods. The effective temperatures were calculated with the infrared flux method (IRFM) calibrations described by Alonso et al. (1996). We have recalculated the temperatures with the more recent B − V and b − y calibrations by Casagrande et al. (2010), adopting the latter as we explain in Sect. 5. The log g values were obtained with stellar evolution models, from the effective temperatures (derived from the Alonso et al. calibration) and the parallaxes measured by the Hipparcos mission (Perryman & ESA 1997), which are accurately known for all the S4N stars. The metallicity was then obtained by spectroscopic means, using Teff and log g as known parameters.
2.3. Combination
Both Elodie and S4N are spectroscopic libraries obtained with echelle spectrographs. Nevertheless, the instruments and the data processing are different in each case. We first attempted to use the full spectral region discussed in the preceding sections, but the results were significantly poorer than those for a single library. Therefore, we found it important to choose appropriate spectral windows instead of the entire wavelength range, so that the existing differences between libraries do not affect our results. The presence of the sought-after information in the spectra is a must, but nearly every feature in the spectrum responds to Teff, and PCA is designed for the very purpose of condensing such information. The discrepancies between the two libraries are dominated by instrumental or atmospheric (telluric) distortions.
The root mean squared error (rms) between two different stars in the same library (all wavelengths) is about 3%, whereas the mean difference between two different spectra of the same star in the same library is about 1% (derived from stars observed more than once in Elodie).
To select the wavelength regions that we consider in common for both surveys, we apply the following simple algorithm based on the fact that Elodie and S4N have 29 stars (and the same number of spectra) in common. Calculating the mean difference for those 29 spectra, we get what we can call a “mean difference spectrum” which is displayed in Fig. 2. Then, we selected the regions where this mean difference is small. The mean rms of the spectra we have in common in our spectral range is 0.8% (under 1%, which can be considered as a suitable threshold because this is the largest difference between different spectra of the same star in one of the databases). This criterion leads to the shaded regions in Fig. 2, that correspond to the windows [4449, 4907] Å, [5237, 6134] Å and [6368, 6790] Å.
 |
Fig. 2 Mean difference spectrum between Elodie and S4N for the 29 stars in common in both surveys. The dashed horizontal lines mark ±1% and the shadowed regions indicate the windows that we consider for the combined analysis of both databases. |
 |
Fig. 3 First 5 eigenvectors (ordered top to bottom) of the Elodie (left column) and S4N (right column) databases. |
2.4. PCA analysis
Principal component analysis is an algebraic and statistical tool which aims at finding the directions of largest variance in the data. Given a set of stellar spectra, we can apply PCA to them and describe each spectrum with far fewer numbers than the original data. In order to arrive at the new set of numbers (the principal components; PCs), we adopt a new basis set formed by the eigenvectors of the correlation matrix, and order them by decreasing eigenvalues. With just the projection of the data into the first 10 elements of the base we can reproduce optical low resolution spectra with a very small error (less than 2% in most cases). Not only is PCA a powerful compressing algorithm, but it also gives us information about the data.
We apply PCA and retain the first N principal components for each star in the sample; we typically work with ~10. Then we look for a calibration between the principal components of a subset of stars (the calibrators) and their effective temperatures. Finally, we use that calibration to infer the temperature of the rest of stars (test).
As a brief reminder of the procedure to compute the principal components, let us assume that the m × n matrix of data Y is built by stacking as rows the spectra of size m of all the n stars considered, where the average spectrum 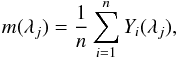 (3)with j = 1...m, has been subtracted from each observation. From the zero-mean data, we compute the correlation matrix:
(3)with j = 1...m, has been subtracted from each observation. From the zero-mean data, we compute the correlation matrix: 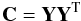 (4)and we diagonalize it. Note that it may be desirable to diagonalize the matrix YTY (along the observation direction, instead of the wavelength direction) if this has smaller dimensions. It is simple to transform back and forth from the eigenvectors in one representation to the other by appropriately multiplying by the data matrix Y (see, e.g., the discussion in Martínez González et al. 2008). The eigenvectors computed so far represent the directions in the space of spectra where we find the largest correlation. The first 5 eigenvectors obtained for Elodie and S4N are displayed in Fig. 3. Interestingly, we find that the fourth eigenvector of S4N contains a conspicuous peak at ~5000 Å. We believe this to be residuals from narcissus in one of the spectrographs, the picket fence described by Tull et al. (1995).
(4)and we diagonalize it. Note that it may be desirable to diagonalize the matrix YTY (along the observation direction, instead of the wavelength direction) if this has smaller dimensions. It is simple to transform back and forth from the eigenvectors in one representation to the other by appropriately multiplying by the data matrix Y (see, e.g., the discussion in Martínez González et al. 2008). The eigenvectors computed so far represent the directions in the space of spectra where we find the largest correlation. The first 5 eigenvectors obtained for Elodie and S4N are displayed in Fig. 3. Interestingly, we find that the fourth eigenvector of S4N contains a conspicuous peak at ~5000 Å. We believe this to be residuals from narcissus in one of the spectrographs, the picket fence described by Tull et al. (1995).
 |
Fig. 4 First 20 principal components of the first star in each library: HD 245 for Elodie (top) and the Sun for S4N (bottom). |
 |
Fig. 5 Teff versus the first 4 PCs of every star of Elodie (left panels) and S4N (right panel). |
Figure 4 shows the first 20 principal components for the first star of each library (HD 245 in the case of Elodie and the Sun in the case of S4N). As usual, they tend to decrease because the first PCs contain the most important information of the spectrum. The calibration we develop below builds on the data shown in Fig. 5, which shows the relationships between Teff and the first five principal components. Since these relations are, in general, not linear, more complicated expressions are necessary. This is discussed in Sect. 3.
3. Calibration
3.1. General considerations
Our goal is to find a suitable function that, given the principal components of a collection of stars, allows us to compute their effective temperature. Once that function has been established and tested for a calibration set, we can apply it to stars with unknown effective temperatures. There are three potential problems:
-
1.
First, it is important to include stars with spectra of sufficientquality. We verified that a calibration of the effective temperatureusing the entire Elodie sample (including stars withQTeff < 4) leads to a poor calibration. We also believe that spectra with different quality flags are subject to different systematic offsets. To solve this issue, we only used stars with QTeff = 4, ending up with a fairly homogeneous temperature scale.
-
2.
Second, we found difficulties in the simultaneous calibration of stars over a broad range of temperatures. It is obvious that it is of paramount importance to have a sample of stars spanning a sufficiently broad range of physical conditions, since otherwise the results will not be useful. Our calibration considers stars with temperatures between 5000 K and 7000 K and log g ≥ 3. In fact, there were only a few stars with temperatures outside this range in the libraries considered. The log g range was set to avoid giants; given their scarcity in our sample, they would cause a degradation in the calibration. After imposing the selection criteria described above, we ended up with 159 spectra in Elodie and 86 in S4N.
-
3.
Third, we found the application of standard regression algorithms inadequate. The final calibration procedure has to be general enough to be applied to stars of unknown effective temperature. Given that we include a large number of PCs in the regression, a regular linear regression algorithm based on a maximum-likelihood approach results in overfitting; it not only follows generic properties of the stars as representative examples of their classes, but it also includes peculiarities of individual stars in the calibration sample. To address this issue we employed a Bayesian non-parametric regression algorithm based on a Relevance Vector Machine (RVM; Tipping 2004), which uses Bayesian inference to learn about the data.
3.2. Bayesian calibration
Given that the RVM avoids overfitting, we propose a sufficiently general functional form for the calibration, and let the data decide on the optimal level of complexity for our sample. To this end, we write the effective temperature as 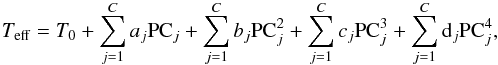 (5)where PCj is the jth principal component of a given star, C is the number of principal components that we consider, and T0, aj, bj, cj and dj are coefficients that we have to infer from the calibration data. For the sake of simplicity, we use a compact notation in which the vector w of length 4C + 1 is built by stacking all the coefficients together
(5)where PCj is the jth principal component of a given star, C is the number of principal components that we consider, and T0, aj, bj, cj and dj are coefficients that we have to infer from the calibration data. For the sake of simplicity, we use a compact notation in which the vector w of length 4C + 1 is built by stacking all the coefficients together 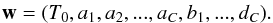 (6)The RVM is based on a Bayesian hierarchical approach to linear regression. The aim is to use the available data to compute the posterior distribution function for the vector of weights w and the noise variance σ2 (that can even be estimated from the same data). Therefore, a direct application of the Bayes theorem yields the posterior distribution function for the unknowns
(6)The RVM is based on a Bayesian hierarchical approach to linear regression. The aim is to use the available data to compute the posterior distribution function for the vector of weights w and the noise variance σ2 (that can even be estimated from the same data). Therefore, a direct application of the Bayes theorem yields the posterior distribution function for the unknowns 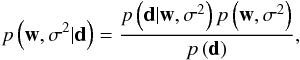 (7)where d is the data, which contains the principal components and the effective temperature, p(d | w,σ2) is the likelihood function that gives an idea of how well the model fits the data, p(w,σ2) is the prior distribution for the parameters and p(d) is the evidence (e.g., Gregory 2005). The key ingredient invoked by Tipping (2004) is to build a hierarchical prior for w. The prior for w will depend on a set of hyperparameters α, which are learned from the data during the inference process. The final posterior distribution is then, after following the standard procedure in Bayesian statistics of including a prior for the newly defined random variables, given by
(7)where d is the data, which contains the principal components and the effective temperature, p(d | w,σ2) is the likelihood function that gives an idea of how well the model fits the data, p(w,σ2) is the prior distribution for the parameters and p(d) is the evidence (e.g., Gregory 2005). The key ingredient invoked by Tipping (2004) is to build a hierarchical prior for w. The prior for w will depend on a set of hyperparameters α, which are learned from the data during the inference process. The final posterior distribution is then, after following the standard procedure in Bayesian statistics of including a prior for the newly defined random variables, given by 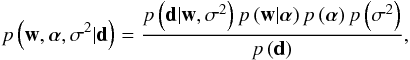 (8)where we have used the fact that the likelihood does depend directly on w and not on the particular choice of α, and that the priors for α and σ2 are independent.
(8)where we have used the fact that the likelihood does depend directly on w and not on the particular choice of α, and that the priors for α and σ2 are independent.
The transformation to a hierarchical approach allowed Tipping (2004) to regularize the regression problem by favoring the sparsest solutions, i.e., the solution that contains the least number of non-zero elements in w. This is done by defining the following prior 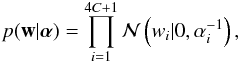 (9)where
(9)where 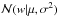 is a Gaussian distribution on the variable w with mean μ and variance σ2. When using an appropriate hyperprior p(α) (for instance, a sufficiently broad Gamma distribution), the marginal prior p(w) obtained by integrating out the α parameters strongly favors very small values of w, leading to a very sparse solution. The values of α are estimated from the data using a Type-II maximum likelihood approach (see Tipping 2004, for details).
is a Gaussian distribution on the variable w with mean μ and variance σ2. When using an appropriate hyperprior p(α) (for instance, a sufficiently broad Gamma distribution), the marginal prior p(w) obtained by integrating out the α parameters strongly favors very small values of w, leading to a very sparse solution. The values of α are estimated from the data using a Type-II maximum likelihood approach (see Tipping 2004, for details).
Applying this scheme, we find the values of the few non-zero elements of the vector w, together with their confidence intervals obtained with a set of calibration stars. Once these parameters are fixed, the next step is to apply the inferred model to a set of test stars and compare the calculated temperatures with the tabulated ones.
4. Results
We now discuss the results of applying the previous formalism to the calibration of effective temperature. The coefficients w are computed using a set of reliable stars for which we have good estimates of the temperature and apply the model to a set of stars of unknown temperatures. We first apply that calibration internally to Elodie and S4N (calibration and test spectra from the same library), and then externally (calibration and test spectra from different libraries).
It is interesting to point out that, when performing the internal calibration for just one library, we found that the spectral range that we used was not critical for obtaining reliable results. Similar results were obtained for different spectral ranges, unless they were too small. In any case, and in order to avoid further complications, we use the spectral range chosen in Sect. 2.3.
4.1. Elodie
As noted above, we considered 1245 spectra of 941 different stars that satisfied all the selection criteria described in Sect. 2. Of those stars, only 159 have been flagged as having the highest quality (QTeff = 4), temperatures between 5000 K and 7000 K, and values of log g ≥ 3.
Internal calibration with stars from Elodie and S4N.
 |
Fig. 6 Calculated temperatures vs. tabulated temperatures for the calibration group of stars (upper panel) and the test group of stars (lower panel) of the Elodie sample. |
Our first test is to calibrate with a subset of those spectra (the first 121, ordered by HD number), calculate the temperature of the rest of them (the remaining 38), and compare the calculated temperatures with the ones tabulated in the Elodie database. The results are summarized in Table 1, where we show the rms residual between the predicted temperatures and the original ones in the database as a function of the number of principal components included in the calibration of Eq. (5). This table presents the rms for the calibration with the best 159 spectra as well as the results from experiments using only spectra with QTeff = 3 (since those are the second best spectra in quality) for different number of PCs. One of the key results is that the rms for the test stars (those not used to build the calibration) is very similar to the rms for the calibration stars when only the QTeff = 4 stars are considered. This indicates that the regression is not overfitting the calibration data. An additional proof of this is that an accurate calibration is obtained independently from the number of PCs we use. The left-hand panel of Fig. 6 shows the tabulated Teff versus the predicted temperature for the calibration stars (upper panel) and test stars (lower panel).
It is clear from Table 1 that the rms values for the test stars with reduced quality (QTeff = 3) are higher than for the highest-quality stars, while this is not the case for the calibration stars. We interpret this as an indication that our calibration based only on stars with the highest quality temperatures is reliable, while this is not the case when including QTeff = 3 stars. Once we have verified that the method works, we use all the stars with QTeff = 4 as calibrators and infer the temperature of the sample (the complete set of 630 stars that passed all the filters and have tabulated temperatures between 5000 K and 7000 K). By doing so, we infer temperatures of QTeff = 4 quality for all of them. Table 2, includes the calculated temperatures for all the stars.
4.2. S4N
A total of 119 spectra of 119 different stars are available from this catalog. Once we apply the effective temperature and surface gravity filters we are left with 86 stars. Since we assume that all the Teff are equally well determined, we use the first 65 stars as a calibration set and the remaining 21 as a testing sample. As explained in Sect. 2.2, we adopt the Teff values we calculate for these stars using the Casagrande et al. (2010)b − y calibration.
The right panel in Fig. 6 shows the tabulated reference temperatures vs. those we calculate from our method for both the calibration (upper panel) and testing (lower panel) stars. As illustrated in the figure, there are two stars (one in the calibration set and the other in the testing set) for which the predicted temperatures differ significantly from the tabulated temperatures (marked with an open circle). Those two stars are HR 7578, a spectroscopic binary (Fekel & Beavers 1983), and HD 188512 (Alshain), a variable star that is evolving off the main sequence (Corsaro et al. 2012).
A summary of the results obtained is shown in Table 1 (the rms values have been calculated without taking into account the two stars mentioned above). The calibration and test rms values are very similar again, which suggests that the model is not overfitting the calibration data and that it is valid for all the spectra in the sample. The slightly larger values of the calibration rms as compared with the test rms is probably due to an small overestimation of the noise in the input data. Nevertheless, this does not strongly affect the calibration.
4.3. External application
Comparison of Teff in K in different catalogs.
We have tested that our method works internally both for Elodie and for S4N independently. Now we check whether we can use one library to calibrate the effective temperatures of the other one and homogenize the scales. We calibrate with Elodie (using just the QTeff = 4 spectra, in the range of 5000–7000 K and log g ≥ 3) and infer the temperatures of the stars in S4N.
We have compared the stars that Elodie and S4N have in common (out of 29 mentioned above there are 27 in the correct range of temperature and log g). The mean difference between the Elodie tabulated temperatures and the ones calculated projecting S4N onto Elodie is 88 K, with an rms of just 40 K. In other words, the inferred temperatures are highly correlated with the Elodie ones but with a systematic offset of 88 K.
5. Temperature scales
We have seen that both Elodie and S4N provide internally coherent temperature scales, and that our method is able to infer the temperature of a star, given its spectrum, with a reasonably small error. We have also seen that when we attempt to apply a PCA calibration based on Elodie spectra to S4N spectra, a systematic offset between the derived temperatures appears. In this section we examine whether the temperature scales used to calibrate our analysis of Elodie spectra, i.e. the Elodie QTeff = 4 literature-based temperatures, and those used for our analysis of the S4N spectra, i.e. the B − V/b − yCasagrande et al. (2010) IRFM-based calibrations, are compatible. We also compare with three additional sources of effective temperatures: the original scale of Alonso et al. (1996) adopted by Allende Prieto et al. (2004) in S4N, the spectroscopic temperatures derived by Katz et al. (1998) from Elodie spectra, and the direct determinations by Cayrel et al. (2011).
We selected the set of 29 stars that Elodie and S4N have in common, and calculated the mean difference and the rms between the effective temperatures from Alonso et al. (1996) or Casagrande et al. (2010), and those from Elodie. We find that, on average, the Elodie temperatures are higher than those of Alonso et al. (1996) by 70 K (with an rms scatter of 87 K), while they are cooler than those of Casagrande et al. (2010) by 28 K (rms scatter of 85 K) when their B − V calibration is used, or by 50 K (rms scatter of 58 K) when their b − y calibration is adopted. We embraced the Casagrande et al. (2010)b − y calibration for the analysis of S4N spectra due to the smaller scatter found in this comparison. Thus, the warmest scale is that by Casagrande et al. (2010), followed by the one based on classical high-resolution spectroscopic analyses, Elodie or Katz et al. (1998), and finally the one proposed by Alonso et al. (1996).
The Elodie QTeff = 4 or spectroscopic scale (and hence our method, which uses it for calibration), seems to be in good agreement with the recent results of Cayrel et al. (2011). These authors have calculated the effective temperature for 11 stars derived from angular diameters and bolometric fluxes, a technique which is expected to give the most fundamental measurement of the effective temperature. All their 11 stars are in S4N, and 7 are also in Elodie. Table 3 displays the Cayrel et al. (2011) direct effective temperatures, the Katz et al. (1998) and Casagrande et al. (2010) temperatures, those adopted in the original S4N paper obtained applying the Alonso et al. (1996) calibrations, as well as the temperatures calculated using the internal PCA calibration of Elodie. The Casagrande et al. (2010)b − y temperatures are, on average, 59 K warmer than the Cayrel et al. (2011) direct temperatures, whereas both Casagrande et al. (2010)B − V temperatures and the the Katz et al. (1998) temperatures are consistent with the Cayrel et al. (2011) temperatures, and the Alonso et al. (1996) values are somewhat lower.
Excluding the Sun, which is usually assigned a temperature of 5777 K, there are 6 stars in common for all six sources compared in Fig. 7 and Table 3. The mean (and standard deviation) of the differences between each of the following sources and the direct temperatures of Cayrel et al. (2011) for these stars are: − 17 (36) K for Katz et al. (1998), + 46(69) K for Casagrande et al. (2010) (b − y), + 15(34) K for Casagrande et al. (2010)B − V, − 42(90) K for Alonso et al. (1996), and + 32(54) K for our PCA calibration of Elodie spectra, consistent with the discussed systematics.
 |
Fig. 7 Differences between different estimates of the effective temperature and the direct values for six stars in common for the sources compared in Table 3. |
6. Application to the Elodie archive
We have mainly based our analysis on the Elodie library spectra made public by Prugniel & Soubiran (2001), and Prugniel et al. (2007), but in the 12 years (1994–2006) that this instrument was in operation, many more data were gathered, and these are publicly available from the Elodie archive (Moultaka et al. 2004).
We have downloaded 34 033 spectra from the Elodie archive, selected those in our range of interest (F- and G-type stars), and applied our PCA calibration to infer effective temperatures for them. We keep only 18 696 spectra for which the PCA components are within the range of our calibration, and for which the PCA reconstruction matches the original to better than 5%. The derived Teff values are provided in Table 4, available only in electronic form.
The 18 696 spectra we provide effective temperatures for correspond to 4039 unique stars, of which there are 2553 with just one spectrum. The remainder 1486 stars have between 2 and 368 spectra, with a median of 4 spectra per star. The derived effective temperatures for the 1486 stars with multiple spectra show a mean rms scatter of 32 K with a standard deviation of 58 K, and a median rms scatter of 18 K. Clearly the temperatures we provide for different Elodie spectra of the same star are in general highly consistent.
Table 5, only in electronic form, provides a single temperature for each object in the Archive, averaging the results when more than one spectra are available. Note that the archive includes some non-stellar spectra.
Our method is well-suited for application to very large sets of stellar spectra obtained as part of projects such as SEGUE/SDSS (Yanny et al. 2009), APOGEE (Eisenstein et al. 2011), RAVE (Siebert et al. 2011), GALAH (Zucker et al. 2013), Gaia-ESO (Gilmore et al. 2012), or Gaia (Lindegren et al. 2008). This only requires observations with the survey instrumentation of a suitable calibration sample, which may be a difficult enterprise for programs focusing on faint stars, since the best reference stars are quite bright.
7. Conclusions
We have developed a method to obtain effective temperatures from low-resolution spectroscopic data. We project the observed spectra onto the eigenvectors and use a calibration curve derived using a robust non-parametric regression on a set of stars with reliable temperatures.
Unlike the photometric or spectrophotometric methods, this procedure does not suffer from systematic errors associated with interstellar reddening. Also, given a certain Teff scale the method provides coherent Teff values on a homogeneous for all the sample. For instance, within the Elodie library, we carried out the calibration with only 159 spectra with well determined temperatures and obtained the temperatures of other 630 spectra with the same quality (see Table 2). We applied as well the calibration to nearly 19 000 spectra of some 4000 unique stars from the Elodie archive.
We checked the method internally for both Elodie and S4N spectra with excellent results. However, when applying the Elodie calibration to S4N spectra, we discovered that the method was overestimating the S4N temperatures by about 90 K. We also find that the IRFM-based Casagrande et al. (2010)B − V scale is very close to the Elodie (spectroscopic) scale, but that is not the case for their b − y calibration. We compared those scales with the direct temperatures provided by Cayrel et al. (2011) and found that the Elodie scale and the Casagrande et al. (2010)B − V calibration are in good agreement with them, whereas the Casagrande et al. (2010)b − y calibration presents an offset of about + 50 K.
One could use a third spectral library to check whether the method works properly in the spectral range used. We tried introducing the solar spectrum from (Kurucz et al. 1984), smoothed appropriately, and the temperature we obtained was 5789 K, which is in very good agreement with the real temperature, while the method returned a higher temperature for the S4N solar spectra (in line with the ~80 K offset expected from tests with stars in common between Elodie and S4N).
It would be useful to expand the set of reference (direct) Teff values. We have tried using the temperatures provided by Cayrel et al. (2011) but there was not enough information for a successful PCA mapping; the minimum number of calibration spectra required is about 50 spectra for our Teff range, or approximately one star per 40-K interval.
In addition to the practical application of our Elodie-based calibration of effective temperature, the most interesting outcome of this study is that our experiments demonstrate the potential of PCA to extract information from stellar spectra, and in particular a close connection between the most important principal components and the stellar effective temperatures.
For more detailed information check the webpage http://www.obs.u-bordeaux1.fr/m2a/soubiran/elodie_library.html
With the gconv IDL code available at http://hebe.as.utexas.edu/stools/
Determined with the TGMET software by Katz et al. (1998).
Acknowledgments
We are thankful to Luca Casagrande for useful comments on the manuscript. A.A.R. acknowledges financial support by the Spanish Ministry of Economy and Competitiveness through projects AYA2010-18029 (Solar Magnetism and Astrophysical Spectropolarimetry) and Consolider-Ingenio 2010 CSD2009-00038. A.A.R. also acknowledges financial support through the Ramón y Cajal fellowship. J.M.B. acknowledges financial support provided by the IAC summer research grants.
References
- Allen de Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso, A., Arribas, S., & Martinez-Roger, C. 1996, A&A, 313, 873 [NASA ADS] [Google Scholar]
- Alonso, A., Arribas, S., & Martínez-Roger, C. 1999, A&AS, 139, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blackwell, D. E., & Lynas-Gray, A. E. 1998, VizieR Online Data Catalog: J/A&AS/129/505 [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cayrel, R., van’t Veer-Menneret, C., Allard, N. F., & Stehlé, C. 2011, in SF2A-2011: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, eds. G. Alecian, K. Belkacem, R. Samadi, & D. Valls-Gabaud, 267 [Google Scholar]
- Corsaro, E., Grundahl, F., Leccia, S., et al. 2012, A&A, 537, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fekel, Jr., F. C., & Beavers, W. I. 1983, ApJ, 267, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 2005, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with Mathematica Support (Cambridge University Press) [Google Scholar]
- Katz, D., Soubiran, C., Cayrel, R., Adda, M., & Cautain, R. 1998, A&A, 338, 151 [NASA ADS] [Google Scholar]
- Kaufer, A., & Pasquini, L. 1998, in SPIE Conf. Ser. 3355, ed. S. D’Odorico, 844 [Google Scholar]
- Kervella, P., & Fouqué, P. 2008, A&A, 491, 855 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar flux atlas from 296 to 1300 nm (National Solar Observatory) [Google Scholar]
- McAlister, H. A., ten Brummelaar, T. A., Gies, D. R., et al. 2005, ApJ, 628, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Moultaka, J., Ilovaisky, S. A., Prugniel, P., & Soubiran, C. 2004, PASP, 116, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Mozurkewich, D., Armstrong, J. T., Hindsley, R. B., et al. 2003, AJ, 126, 2502 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The HIPPARCOS and TYCHO catalogues. Astrometric and photometric star catalogues derived from the ESA HIPPARCOS Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Prugniel, P., & Soubiran, C. 2001, A&A, 369, 1048 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prugniel, P., Soubiran, C., Koleva, M., & Le Borgne, D. 2007 [arXiv:astro-ph/0703658] [Google Scholar]
- Ramírez, I., Allen de Prieto, C., Redfield, S., & Lambert, D. L. 2006, A&A, 459, 613 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- ten Brummelaar, T. A., McAlister, H. A., Ridgway, S. T., et al. 2005, ApJ, 628, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Tipping, M. 2004, Bayesian inference: An introduction to principles and practice in machine learning (Springer) [Google Scholar]
- Tull, R. G., MacQueen, P. J., Sneden, C., & Lambert, D. L. 1995, PASP, 107, 251 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Elodie (upper panel) and S4N (lower panel) stellar parameters for all spectra in the sample. In the upper panels, the subsample of the Elodie library with the highest quality effective temperatures (QTeff = 4) is shown with filled-in black bars. |
| In the text | |
 |
Fig. 2 Mean difference spectrum between Elodie and S4N for the 29 stars in common in both surveys. The dashed horizontal lines mark ±1% and the shadowed regions indicate the windows that we consider for the combined analysis of both databases. |
| In the text | |
 |
Fig. 3 First 5 eigenvectors (ordered top to bottom) of the Elodie (left column) and S4N (right column) databases. |
| In the text | |
 |
Fig. 4 First 20 principal components of the first star in each library: HD 245 for Elodie (top) and the Sun for S4N (bottom). |
| In the text | |
 |
Fig. 5 Teff versus the first 4 PCs of every star of Elodie (left panels) and S4N (right panel). |
| In the text | |
 |
Fig. 6 Calculated temperatures vs. tabulated temperatures for the calibration group of stars (upper panel) and the test group of stars (lower panel) of the Elodie sample. |
| In the text | |
 |
Fig. 7 Differences between different estimates of the effective temperature and the direct values for six stars in common for the sources compared in Table 3. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


