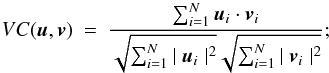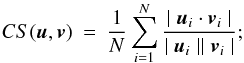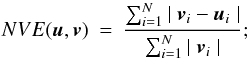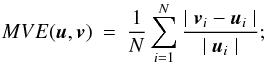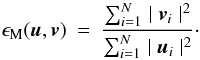| Issue |
A&A
Volume 553, May 2013
|
|
|---|---|---|
| Article Number | A43 | |
| Number of page(s) | 7 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201220787 | |
| Published online | 30 April 2013 | |
Reconstruction of the solar coronal magnetic field in spherical geometry
1
CNRS, Centre de Physique Théorique de l’École Polytechnique,
91128
Palaiseau Cedex,
France
e-mail: amari@cpht.polytechnique.fr
2
AIM, Unité Mixte de Recherche CEA – CNRS – Université Paris VII,
UMR 7158, Centre d’Études de
Saclay, 91191
Gif-sur-Yvette Cedex,
France
3
Institut d’Astrophysique Spatiale, 91405
Orsay Cedex,
France
4
Predictive Science Inc., San Diego, CA
92121,
USA
Received: 23 November 2012
Accepted: 26 February 2013
Context. High-resolution vector magnetographs either onboard spacecrafts or satellites (HMI/SDO, etc.) or ground based (SOLIS, etc.) now gives access to vector synoptic maps, composite magnetograms made of multiple interactive active regions, and full disk magnetograms. It thus become possible to reconstruct the coronal magnetic field on the full Sun scale.
Aims. We present a method for reconstructing the global solar coronal magnetic field as a nonlinear force-free field. It is based on a well-posed Grad-Rubin iterative scheme adapted to spherical coordinates
Methods. This method is a natural extension to spherical geometry of the one we previously developed in Cartesian geometry. It is implemented in the code XTRAPOLS, which is a massively parallel code. It allows dealing with the strong constraints put on the computational methods by having to handle the very large amounts of data contained in high-resolution large-scale magnetograms. The method exploits the mixed elliptic-hyperbolic nature of the Grad-Rubin boundary value problem. It uses a finite-difference method for the elliptic part and a method of characteristics for the hyperbolic part. The computed field guarantees to be divergence free up to round-off errors, by introducing a representation in terms of a vector potential satisfying specific gauge conditions. The construction of the latter – called here the restricted DeVore gauge – is described in detail in an appendix.
Results. We show that XTRAPOLS performs well by applying it to the reconstruction of a particular semi-analytic force-free field that has already been considered by various authors.
Key words: magnetic fields / magnetohydrodynamics (MHD) / methods: data analysis / Sun: corona
© ESO, 2013
1. Introduction
The problem of reconstructing the solar coronal magnetic field from photospheric boundary data has been a very active research topic during the past few years. This is mainly due to the arrival of high-resolution and low-noise vector magnetographs either on the ground, such as THEMIS and SOLIS, onboard present solar space missions, such as Hinode and SDO/HMI, and on future ones, such as EST and SOLAR-ORBITER. The various methods proposed so far to reconstruct the coronal field have been reviewed very recently (Aly & Amari 2007; Wiegelmann 2008; Schrijver et al. 2006). We just recall here that the most frequently used ones are (i) the optimization method (Wiegelmann 2004), which uses all photospheric data and tries to minimize a cost function measuring the difference between the computed transverse field and the measured one; (ii) the vertical integration method, which also uses all photospheric data (Song et al. 2006); (iii) the relaxation methods (Valori et al. 2005), in which the coronal field is obtained as the result of an MHD evolution driven by boundary conditions depending on the observed field; and (iv) the Grad-Rubin methods (Sakurai 1981; Amari et al. 1999, 2006; Wheatland 2007; Wheatland & Regnier 2009), which only use a part of the observational data. There is also a hybrid method called OGRM (Amari & Aly 2010) which combines a Grad-Rubin iterative scheme with an optimization scheme by selecting the most appropriate boundary values of the force-free function α at each step.
Up to now, these methods have been essentially applied to the reconstruction of the coronal field of an active region. On such a scale, the curvature of the solar surface does not play an important role, and the region can be represented by a half space. However, the recent observational progress recalled above allow us now to dispose of high-resolution composite vector magnetograms made of several active regions or embedded in a full disk vector magnetogram of synoptic vector magnetograms. Furthermore, vector magnetic fields are also currently measured by different technics on the whole surface of some stars (Donati et al. 2007), although at a lower resolution and with less accuracy. Reconstruction of the global coronal field of the Sun and the other stars thus becomes possible in principle, but this requires implementing the various methods in the spherical geometry context because surface sphericity can obviously no longer be neglected. This has already been done for the optimization method (Wiegelmann 2007; Tadesse et al. 2009) and for the vertical integration method (Song et al. 2007).
In the present paper we present a new numerical code, called XTRAPOLS, which allows reconstruction of the nonlinear force-free field outside of a spherical region. This code is based on an iterative Grad-Rubin scheme implemented in spherical coordinates. We favor this approach because it corresponds to a well-posed boundary value problem. Moreover, it has already proved to be quite efficient in the previously considered Cartesian context, and has allowed us to obtain significant quantitative results when applied to observational data (Bleybel et al. 2002; Régnier et al. 2002, 2005; Régnier & Amari 2004; DeRosa et al. 2009; Canou et al. 2009; Canou & Amari 2010, 2012; Petrie et al. 2011). XTRAPOLS is a massively parallel code, and as such will be able to handle the large amounts of data currently provided by the magnetographs, with fields being measured on a very large scale and with very high resolution.
The paper is organized as follows. In Sect. 2 we describe the basic elements on which XTRAPOLS rests. We formulate the Grad-Rubin iterative scheme in the context of spherical geometry, explain the particular gauge that is used in the vector potential formulation such that ∇·B = 0 (the construction of the gauge is detailed in Appendix A), and explain some particular technical points. Section 3 is devoted to testing our code. We first describe the semi-analytical force-free magnetic field (Low & Lou 1990) that is used as the test case, and thus present the results obtained in the numerical reconstruction of that field with various numerical resolutions. Finally Sect. 4 gathers our concluding remarks together.
2. Method
We present in this section our method for reconstructing the coronal field in the domain D extending outside the sphere of radius r0. We denote as r the position vector, and use spherical coordinates (r,θ,ϕ) related in the standard way to the Cartesian coordinates (x,y,z).
2.1. The Grad-Rubin iterative scheme
In our calculations the unbounded domain D is replaced by the bounded numerical box Ωb. The latter is chosen to be the spherical shell Ωb = { r: 0 < r0 < r < r1 } ⊂ R3 and it is thus bounded by the two spherical surfaces S0 = { r = r0 } (with inner unit normal 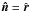 ) and S1 = { r = r1 } (with inner unit normal
) and S1 = { r = r1 } (with inner unit normal 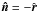 ). The Grad-Rubin scheme in Ωb is identical to the one in a Cartesian box previously described in details in Amari et al. (2006). It alternates between solving an hyperbolic problem and an elliptic one.
). The Grad-Rubin scheme in Ωb is identical to the one in a Cartesian box previously described in details in Amari et al. (2006). It alternates between solving an hyperbolic problem and an elliptic one.
The hyperbolic problem is defined by 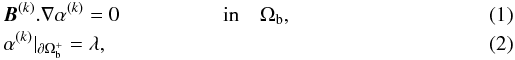 and the elliptic one by
and the elliptic one by 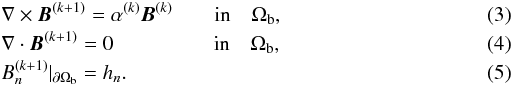 Here hn and λ are the given boundary values for
Here hn and λ are the given boundary values for 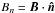 and α, respectively, and
and α, respectively, and 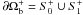 is the part of ∂Ωb where hn > 0.
is the part of ∂Ωb where hn > 0.
Equation (1) means that α(k) keeps a constant value all along a magnetic line of B(k). To determine α(k), we have thus to fix its value λ at only one of the two footpoints of the latter. Here we have chosen the footpoint located on the part 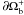 of ∂Ωb of positive polarity. But we could have just as well chosen to fix its value at the footpoint located on the part
of ∂Ωb of positive polarity. But we could have just as well chosen to fix its value at the footpoint located on the part 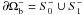 of ∂Ωb of negative polarity, where hn < 0.
of ∂Ωb of negative polarity, where hn < 0.
The iterative process is started by choosing B(0) to coincide with the unique potential field Bπ whose normal component on the boundary is hn; i.e., B(0) is the solution of
2.2. Vector potential formulation
To address the ∇·B = 0 constraint, XTRAPOLS introduces a vector potential A(k) and ensures that the iterated numerical field B(k) = ∇ × A(k). To determine A(k) in a unique way, we impose the gauge conditions ![\begin{eqnarray} \label{EqAtBound} && \nabla\cdot\bA^{(k)} = 0 \;\;\;\;\;\;\;\; \mbox{in} \;\; \Omega_{\rm b} , \\[2mm] && \bA^{(k)}_{\rm t} = \bA_{\po {\rm t}}\;\;\;\; \;\;\;\;\;\; \mbox{on} \;\; \partial\Omega_{\rm b} , \end{eqnarray}](/articles/aa/full_html/2013/05/aa20787-12/aa20787-12-eq33.png) where Xt denotes the component of X tangent to the boundary, and Aπ is a specific vector potential of the current-free field Bπ; i.e.,
where Xt denotes the component of X tangent to the boundary, and Aπ is a specific vector potential of the current-free field Bπ; i.e., 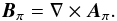 (11)Here, Aπ is chosen to be the “restricted DeVore gauge” (RDVG) described in detail in Appendix A. Aπ is thus required to satisfy
(11)Here, Aπ is chosen to be the “restricted DeVore gauge” (RDVG) described in detail in Appendix A. Aπ is thus required to satisfy ![\begin{eqnarray} \label{GaugeApo1} && A_{\po r}(r,\theta,\varphi)= 0 , \\[2mm] \label{GaugeApo2} && {{\nabla}\cdot}\bA_{\po}(r_{0},\theta,\varphi) = 0 , \end{eqnarray}](/articles/aa/full_html/2013/05/aa20787-12/aa20787-12-eq38.png) which implies that
which implies that 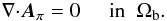 (14)To compute Aπ on the boundary S0 ∪ S1:
(14)To compute Aπ on the boundary S0 ∪ S1:
-
We introduce a scalar potential χπ(r,θ,ϕ) such that
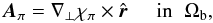 (15)where ∇ ⊥ is the orthoradial component of the gradient. This representation is allowed by Eqs. (12), (13).
(15)where ∇ ⊥ is the orthoradial component of the gradient. This representation is allowed by Eqs. (12), (13). -
We impose χπ(r0,θ,ϕ) as the unique solution with zero average value of the equation
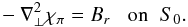 (16)Solving this equation determines Aπ on S0.
(16)Solving this equation determines Aπ on S0. -
We introduce the standard representation Bπ = ∇ψπ in Ωb, and compute the scalar potential ψπ by solving the boundary value problem
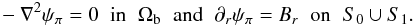 (17)
(17) -
χπis thus given by
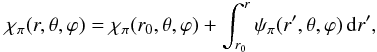 (18)from which we get Aπ on S1 by Eq. (15).
(18)from which we get Aπ on S1 by Eq. (15).
2.3. Some specific technical points
In our vector potential formulation, α is determined by solving 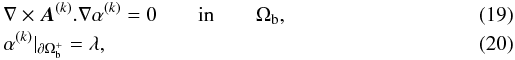 which is just a rewriting of Eqs. (1), (2). The boundary value of α is thus directly imposed at each iterative step, rather than being progressively increased to its nominal value through a second iterative loop as was done in Amari et al. (1999). In other words, we only keep the inner Grad-Rubin iteration loop in the two-level iteration procedure used in that paper.
which is just a rewriting of Eqs. (1), (2). The boundary value of α is thus directly imposed at each iterative step, rather than being progressively increased to its nominal value through a second iterative loop as was done in Amari et al. (1999). In other words, we only keep the inner Grad-Rubin iteration loop in the two-level iteration procedure used in that paper.
Equations (19), (20) are solved by the method of characteristics. For the field B(k), the characteristic 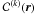 passing through the point r is represented here by the function X(k)(s,r) that solves (Amari et al. 1999, 2006)
passing through the point r is represented here by the function X(k)(s,r) that solves (Amari et al. 1999, 2006)  The parameter s running along
The parameter s running along 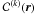 is thus taken to vanish at r and to increase in the direction of B(k), and it takes negative values on that part of
is thus taken to vanish at r and to increase in the direction of B(k), and it takes negative values on that part of 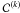 comprised between the footpoint located on
comprised between the footpoint located on 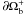 and r.
and r.
For any node rh ∈ Ωb at which α(k) is defined, one has 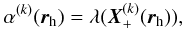 (23)where
(23)where 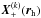 is the intersection of
is the intersection of 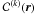 with
with 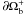 . Because λ is only known at nodes that do not generally coincide with
. Because λ is only known at nodes that do not generally coincide with 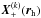 , we use an interpolation from the four nearest neighbors. We define the location of α(k) on the cell vertices. We use either a high-order Adams-Bashford integration scheme with adaptive step size or a fourth-order Runge Kutta scheme, which also allows us to capture the ending point of the characteristics accurately at the limits of the computational box.
, we use an interpolation from the four nearest neighbors. We define the location of α(k) on the cell vertices. We use either a high-order Adams-Bashford integration scheme with adaptive step size or a fourth-order Runge Kutta scheme, which also allows us to capture the ending point of the characteristics accurately at the limits of the computational box.
Computation of the elliptic part of each iterative step is done on a spherical grid. As for the hyperbolic part, we found that computing the characteristics on the spherical grid led to some awkward behavior near the poles (i.e., for θ near 0 and π). We thus used a somewhat more elaborate method that turned out to be robust, but slower than the previous one. It consists in writing the equation of the characteristics in Cartesian coordinates and computing a characteristic by performing at each point in Ωb a mapping from spherical to Cartesian coordinates and a mapping back to spherical ones.
The algorithm is parallel in the following sense. The elliptic solver is performed by full domain decomposition with our iterative preconditioned conjugate gradient algorithm to get A and B. The global field as well as the global mesh are therefore known for the hyperbolic part and for each process (each spherical subdomain Ωi). But each process can consider the calculation of alpha independently for each set of starting point in Ωi. Although it is not full parallelism in the sense that the magnetic field B(k) is global, it clearly speeds up the calculation and does not overload the memory too much since only one global field is needed by each process.
Finally we point out that our convergence criterion for the sequence of fields B(k) is chosen to be 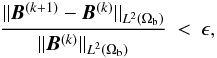 (24)where ϵ = 10-6 and we have introduced the L2(Ωb)-norm of a vector B, defined by
(24)where ϵ = 10-6 and we have introduced the L2(Ωb)-norm of a vector B, defined by 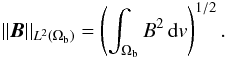 (25)As shown in Sect. 3.2, a total number of iterations of about 30–50 is sufficient to achieve convergence in most cases, and the stopping criteria is robust with respect to changes in the data put as boundary conditions.
(25)As shown in Sect. 3.2, a total number of iterations of about 30–50 is sufficient to achieve convergence in most cases, and the stopping criteria is robust with respect to changes in the data put as boundary conditions.
3. The test case
3.1. The Low and Lou solutions
For testing the quality of our reconstructing method, we used the semi-analytic Low & Lou (1990) force-free magnetic field, BLL, which has now become a standard benchmark. To describe that particular field, we first set up a new Cartesian coordinate system (x′,y′,z′) centered on some point O′ and define associated spherical coordinates (r′,θ′,ϕ′) in the standard way. Expressed in these coordinates, BLL is axisymmetric with respect to the axis O′z′ and mirror-symmetric with respect to the equatorial plane { z′ = 0 } , so it admits the usual representation 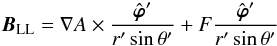 (26)in terms of the poloidal flux function A(r′,θ′) and the current function F(r′,θ′). Both A and F are taken to have the form
(26)in terms of the poloidal flux function A(r′,θ′) and the current function F(r′,θ′). Both A and F are taken to have the form 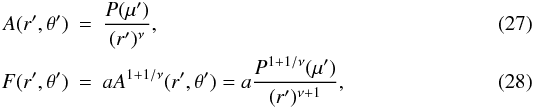 respectively, where a and ν are real constants, μ′ = cosθ′, and P is a solution of a nonlinear ordinary differential equation satisfying P(± 1) = 0. We take here a solution that generates a quadrupolar field and has the “stretching parameter” ν = 1.
respectively, where a and ν are real constants, μ′ = cosθ′, and P is a solution of a nonlinear ordinary differential equation satisfying P(± 1) = 0. We take here a solution that generates a quadrupolar field and has the “stretching parameter” ν = 1.
Next we fix the position of the auxiliary coordinate system (O′;x′,y′,z′) with respect to our original coordinate system (O;x,y,z). This is done by imposing the simple relations x′ = x, y′ = y − d, and z′ = z, with d > 0 a constant, from which we get r′ = (r2 + d2 − 2drsinθsinϕ)1/2, cosθ′ = (r/r′)cosθ, and tanϕ′ = (rsinθsinϕ − d)/rsinθcosϕ. Straightforward but somewhat heavy algebra thus allows computing the components of BLL in both the Cartesian coordinates (x,y,z) and the spherical ones (r,θ,ϕ). Clearly, the latter depend on ϕ.
A similar shifting procedure applied to the Low-Lou field has already been used in Wiegelmann (2007), and we choose for d the value selected in that paper. It will thus be possible to compare our results with those reported in the latter.
Various error diagnostics (see text for definitions) evaluating XTRAPOLS when applied to the reconstruction of BLL from its boundary data for three numerical resolutions.
3.2. Results
Table 1 shows some of the diagnostics, often called figures of merit, already used for Cartesian coordinates calculations in Amari et al. (1999, 2006) and in Schrijver et al. (2006). If u and v are two vectors, and N is the number of computational nodes, we introduce
The various quantities above are evaluated for u equal to the exact solution BLL and v equal to a numerical solution obtained with XTRAPOLS. They have to be compared to the reference values
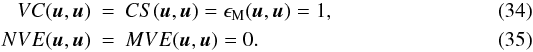 We also found important to report the values of the L∞(Ωb)-norm of ∇·B,
We also found important to report the values of the L∞(Ωb)-norm of ∇·B, ![\begin{eqnarray} \norm{\nabla\cdot\B}_{L^{\infty}(\Omega_{\rm b})} = \sup_{\r\in\Omega_{\rm b}}[|(\nabla\cdot\B)(\r)|], \label{} \end{eqnarray}](/articles/aa/full_html/2013/05/aa20787-12/aa20787-12-eq122.png) (36)as well as the CPU time, both figures providing additional measures of the quality of the solution.
(36)as well as the CPU time, both figures providing additional measures of the quality of the solution.
To compare with the Cartesian case, we show only the cases – corresponding to “Case 3” in Wiegelmann (2007) – where the surfaces S0 and S1, on which we impose boundary conditions corresponding to the Low-Lou solution, are fixed by setting r0 = 1 and r1 = 2.57, respectively, where S1 may be considered as some kind of source-surface, although we do not require the field to be radial on it.
 |
Fig. 1 Convergence properties of the method XTRAPOLS applied to the field BLL for various resolutions: (top) 20 × 40 × 80; (middle) 40 × 80 × 160; (bottom) 80 × 160 × 360. The norm of the solution reaches its asymptotic value in about 20 iterations. |
 |
Fig. 2 Set of field lines of various solutions. Top: exact solution; middle: potential (current-free) solution; bottom: solution computed with our algorithm with a resolution of 80 × 160 × 320. |
Figure 1 shows the convergence properties of XTRAPOLS. We have drawn the rate of convergence on a logarithmic scale as functions of the number of iterations, as well as the L2(Ωb)-norm of the iterates expressed in nondimensional units. It should be noted that
-
The convergence rate appears to exhibit a regular decrease fromthe very beginning of the computation.
-
The number of iterations necessary to reach a relative error of 10-5, say, decreases when the resolution increases. We needed 40 iterations at the lowest resolution, 32 at the intermediate one, and only 27 at the highest one.
-
There is a strong variation in the L2 norm of the solution (therefore of the total magnetic energy) at the first iteration, at which point the potential state is left over. This might be related to the fact that no progressive injection of α at the boundary (no two-level iteration loop) has been achieved. After a very short “adaptation” step, this wide behavior is damped, and ||B(k)||L2(Ωb) exhibits a smooth increase similar to the one obtained in Amari et al. (2006).
-
Our convergence criterion ϵ = 10-6 appears to be relatively strong since ||B(k)||L2(Ωb) has already reached its asymptotic value, on the order of 0.01, at about iteration 20.
-
These results, which are complementary to the one above, show the benefit of increasing resolution on the value of the L2-norm of the solution.
As shown in Fig. 2, the field lines of the numerically computed nonlinear force-free configuration are very similar to those of the exact solution. They are quite far from those of the potential (current-free) solution.
4. Discussion
In this paper, we have presented a method for reconstructing the solar coronal magnetic field on the full Sun scale. This method is an adaptation to spherical coordinates of the Grad-Rubin algorithm, based on a well-posed formulation, which we have developed over the years in Cartesian coordinates. We implemented this algorithm in the massively parallel code XTRAPOLS, and tested its efficiency by applying it to reconstructing of a nonaxisymmetric version of the Low-Lou force-free field in spherical coordinates. This reconstruction has been shown to be quite successful. In particular, our results are comparable to those obtained by Wiegelmann (2007) for his “type 3” boundary conditions. We did not consider here the other types of boundary conditions studied in that paper.
Our results show that the code has good convergence properties, as confirmed by the various diagnostics and by the fact that the L2-norm of the solutions, and then the energy, approaches an asymptotic value quite rapidly. But there is not much improvement in some of the diagnostics when the numerical resolution becomes higher. This does not imply, however, that there is no interest in increasing the resolution. For instance, one may want the reconstruction to catch not only the gross structure of the magnetic field, but also the small-scale features that are associated with the active regions and are expected to have a negligible influence on the large-scale field. Unfortunately, the Low-Lou solution, which currently appears as the only analytical solution useful for testing a code, does not exhibit such multi-scale magnetic field and electric current density. The efficiency of the code in such a situation will then be tested by applying it to actual data. This is the next step in our program, and the results will be presented in forthcoming papers.
Our method allows us to deal with the very large amount of data provided nowadays by various vector magnetographs on the ground or onboard satellites, such as SOLIS and HMI. These instruments are currently used for studying transequatorial loops connecting active regions and for building up synoptic maps and composite maps made of full disk maps embedded in synoptics ones. It is important to note that the reliability of a reconstruction depends as much on the quality of these magnetograms as on the accuracy of the numerical algorithm. This quality depends in particular on the method that is used to invert Stokes parameters and then on the assumption made on the value of the filling factor that has to be introduced to deal with both strong (active) and weak (quiet) field regions.
Acknowledgments
We acknowledge support from NASA’s Heliophysics Theory Program, the STEREO/SECCHI Consortium, and the Centre National d’Études Spatiales. The numerical simulations performed in this paper have been done on the IBM Power 6 supercomputer of the Institute I.D.R.I.S of the Centre National de la Recherche Scientifique. We also thank the anonymous referee for his/her helpful remarks that helped improve the clarity of the paper.
References
- Aly, J. J., & Amari, T. 2007, Geophys. Astrophys. Fluid Dyn., 101, 249 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Amari, T., & Aly, J.-J. 2010, A&A, 522, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amari, T., Boulmezaoud, T. Z., & Mikic, Z. 1999, A&A, 350, 1051 [NASA ADS] [Google Scholar]
- Amari, T., Boulmezaoud, T. Z., & Aly, J. J. 2006, A&A, 446, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bleybel, A., Amari, T., van Driel-Gesztelyi, L., & Leka, K. D. 2002, A&A, 395, 685 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canou, A., & Amari, T. 2010, ApJ, 715, 1566 [NASA ADS] [CrossRef] [Google Scholar]
- Canou, A., & Amari, T. 2012, in EAS Pub. Ser., 55, 125 [Google Scholar]
- Canou, A., Amari, T., Bommier, V., et al. 2009, ApJ, 693, L27 [NASA ADS] [CrossRef] [Google Scholar]
- DeRosa, M. L., Schrijver, C. J., Barnes, G., et al. 2009, ApJ, 696, 1780 [Google Scholar]
- DeVore, C. R. 2000, ApJ, 539, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Jardine, M. M., Gregory, S. G., et al. 2007, MNRAS, 380, 1297 [NASA ADS] [CrossRef] [Google Scholar]
- Low, B. C., & Lou, Y. Q. 1990, ApJ, 352, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Petrie, G. J. D., Canou, A., & Amari, T. 2011, Sol. Phys., 274, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Régnier, S., & Amari, T. 2004, A&A, 425, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Régnier, S., Amari, T., & Kersalé, E. 2002, A&A, 392, 1119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Régnier, S., Amari, T., & Canfield, R. C. 2005, A&A, 442, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakurai, T. 1981, Sol. Phys., 69, 343 [NASA ADS] [CrossRef] [Google Scholar]
- Schrijver, C. J., Derosa, M. L., Metcalf, T. R., et al. 2006, Sol. Phys., 235, 161 [Google Scholar]
- Song, M. T., Fang, C., Tang, Y. H., Wu, S. T., & Zhang, Y. A. 2006, ApJ, 649, 1084 [NASA ADS] [CrossRef] [Google Scholar]
- Song, M. T., Fang, C., Zhang, H. Q., et al. 2007, ApJ, 666, 491 [NASA ADS] [CrossRef] [Google Scholar]
- Tadesse, T., Wiegelmann, T., & Inhester, B. 2009, A&A, 508, 421 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valori, G., Kliem, B., & Keppens, R. 2005, A&A, 433, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wheatland, M. 2007, Sol. Phys., 245, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Wheatland, M. S., & Regnier, S. 2009, ApJ, 700, L88 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T. 2004, Sol. Phys., 219, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T. 2007, Sol. Phys., 240, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Wiegelmann, T. 2008, J. Geophys. Res. (Space Physics), 113, 3 [Google Scholar]
Appendix A: DeVore and restricted DeVore gauges in spherical geometry
The gauge used in the main text for representing the potential field is the spherical analog of the gauge introduced by DeVore (2000) in the Cartesian context. We explain in this appendix how to construct this gauge for an arbitrary magnetic field B occupying the domain Ωb, with the value r1 = ∞ being allowed (in which case Ωb = D). We also give formulae valid when B is axisymmetric. Although they are not used explicitly in the present paper, they have proved to be useful in some auxiliary computations we did on the Low & Lou (1990) force-free magnetic field, and we think that they may also be useful to some readers.
A.1. DeVore gauge
As is well known, the conditions 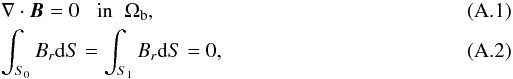 satisfied by the magnetic field B, allow the introduction of a vector potential A0 such that
satisfied by the magnetic field B, allow the introduction of a vector potential A0 such that 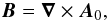 (A.3)and all the other gauges have the form A = A0 + ∇f. We first define the “DeVore gauge” (DVG) A1 by the condition
(A.3)and all the other gauges have the form A = A0 + ∇f. We first define the “DeVore gauge” (DVG) A1 by the condition 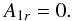 (A.4)A1can thus be obtained from A0 by requiring the arbitrary function f to satisfy
(A.4)A1can thus be obtained from A0 by requiring the arbitrary function f to satisfy 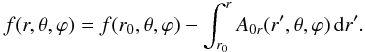 (A.5)Note that f is determined by the latter equation only up to an additive function of (θ,ϕ).
(A.5)Note that f is determined by the latter equation only up to an additive function of (θ,ϕ).
In DVG we have 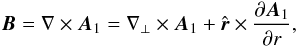 (A.6)where the indice ⊥ indicates an orthoradial component. As ∇ ⊥ × A1 is collinear to
(A.6)where the indice ⊥ indicates an orthoradial component. As ∇ ⊥ × A1 is collinear to 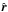 , we can write
, we can write 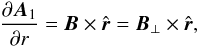 (A.7)and we get by a mere integration
(A.7)and we get by a mere integration 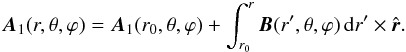 (A.8)This expression leaves the surface function A1(r0,θ,ϕ) undetermined.
(A.8)This expression leaves the surface function A1(r0,θ,ϕ) undetermined.
A.2. Restricted DVG
Taking the divergence of both members of Eq. (A.8) leads to 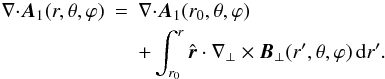 (A.9)Using the gauge arbitrariness still in A1, we set A = A1 + ∇ ⊥ f(θ,ϕ), and choose f such that
(A.9)Using the gauge arbitrariness still in A1, we set A = A1 + ∇ ⊥ f(θ,ϕ), and choose f such that 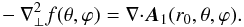 (A.10)We thus get a particular form A of the DVG for which
(A.10)We thus get a particular form A of the DVG for which 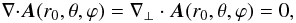 (A.11)and
(A.11)and 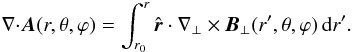 (A.12)We refer to A as the restricted DeVore gauge (RDVG).
(A.12)We refer to A as the restricted DeVore gauge (RDVG).
Note that 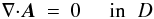 (A.13)in the case where ∇ ⊥ × B ⊥ = 0 in Ωb (no radial current).
(A.13)in the case where ∇ ⊥ × B ⊥ = 0 in Ωb (no radial current).
Condition (A.11) allows a new potential χ(θ,ϕ) to be introduced such that 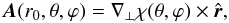 (A.14)hence
(A.14)hence 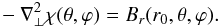 (A.15)This equation determines χ(θ,ϕ) from Br(r0,θ,ϕ) up to an additive constant whose value may be fixed, e.g., by requiring that
(A.15)This equation determines χ(θ,ϕ) from Br(r0,θ,ϕ) up to an additive constant whose value may be fixed, e.g., by requiring that 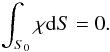 (A.16)
(A.16)
A.3. The case of a potential field
Consider the case of a potential magnetic field Bπ in Ωb (∇ × Bπ = 0). Then we can introduce the alternative representation 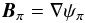 (A.17)in terms of the scalar potential ψπ. The latter satisfies Laplace equation
(A.17)in terms of the scalar potential ψπ. The latter satisfies Laplace equation 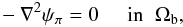 (A.18)and can then be determined (up to a constant) by solving this equation along with the boundary condition
(A.18)and can then be determined (up to a constant) by solving this equation along with the boundary condition 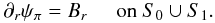 (A.19)On the other hand, the RDVG Aπ for Bπ does satisfy ∇·Aπ = 0 (see Eq. (A.13)), and we can introduce a scalar potential χπ(r,θ,ϕ), defined up to an additive function f(r), such that
(A.19)On the other hand, the RDVG Aπ for Bπ does satisfy ∇·Aπ = 0 (see Eq. (A.13)), and we can introduce a scalar potential χπ(r,θ,ϕ), defined up to an additive function f(r), such that 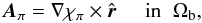 (A.20)while χπ(r0,θ,ϕ) is determined by Eqs. (A.15), (A.16). Using Eqs. (A.20) and (A.17) in Eq. (A.8) for Aπ,
(A.20)while χπ(r0,θ,ϕ) is determined by Eqs. (A.15), (A.16). Using Eqs. (A.20) and (A.17) in Eq. (A.8) for Aπ, 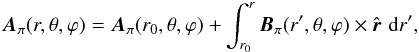 (A.21)we obtain
(A.21)we obtain 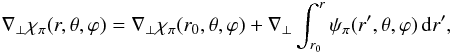 (A.22)whence after integration
(A.22)whence after integration 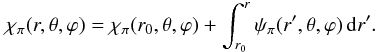 (A.23)No constant of integration needs to be introduced here as is immediately seen by setting r = r0.
(A.23)No constant of integration needs to be introduced here as is immediately seen by setting r = r0.
A.4. The case of an axisymmetric magnetic field
Let us consider an arbitrary magnetic field B that is axisymmetric in Ωb with respect to the z-axis – that is to say B is left invariant by the rotations about that axis. Then B has the standard representation 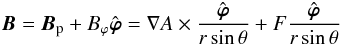 (A.24)in terms of the two scalar functions A(r,θ) – the poloidal flux function – and F(r,θ) – the poloidal current function. A(r,θ) is defined up to an additive constant, which we may fix by imposing
(A.24)in terms of the two scalar functions A(r,θ) – the poloidal flux function – and F(r,θ) – the poloidal current function. A(r,θ) is defined up to an additive constant, which we may fix by imposing 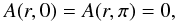 (A.25)where the first equality is a mere consequence of the fact that B has zero flux through any sphere of radius r, r0 ≤ r ≤ r1. Moreover, the regularity of B at the two poles of the sphere requires that
(A.25)where the first equality is a mere consequence of the fact that B has zero flux through any sphere of radius r, r0 ≤ r ≤ r1. Moreover, the regularity of B at the two poles of the sphere requires that 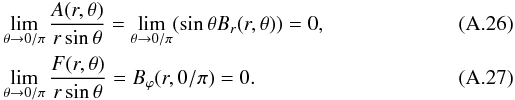 To construct a vector potential for B satisfying the DVG condition, we first consider the poloidal part Bp. Noticing that
To construct a vector potential for B satisfying the DVG condition, we first consider the poloidal part Bp. Noticing that 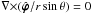 , we can write
, we can write 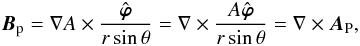 (A.28)with
(A.28)with 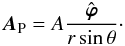 (A.29)Owing to Eq. (A.26), this quantity is well defined even when θ = 0,π, with
(A.29)Owing to Eq. (A.26), this quantity is well defined even when θ = 0,π, with 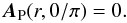 (A.30)Clearly we have
(A.30)Clearly we have  in the whole D, and then AP even satisfies the RDVG conditions.
in the whole D, and then AP even satisfies the RDVG conditions.
Next we consider the toroidal part of the field, for which we have to compute a vector AT such that  Let us try to find a solution to these equations of the form
Let us try to find a solution to these equations of the form 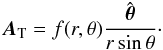 (A.35)Injecting this form into Eq. (A.33), we get
(A.35)Injecting this form into Eq. (A.33), we get 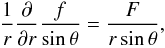 (A.36)hence
(A.36)hence 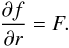 (A.37)Taking for instance the particular solution
(A.37)Taking for instance the particular solution 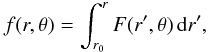 (A.38)we obtain
(A.38)we obtain 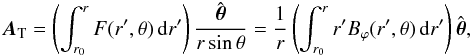 (A.39)which is a well defined quantity for θ = 0,π owing to Eq. (A.27), with
(A.39)which is a well defined quantity for θ = 0,π owing to Eq. (A.27), with 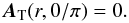 (A.40)Reciprocally, the AT we have constructed gives back the toroidal field Bϕ. It is then a solution to our problem, which actually turns out to also satisfy the RDVG conditions. We indeed have
(A.40)Reciprocally, the AT we have constructed gives back the toroidal field Bϕ. It is then a solution to our problem, which actually turns out to also satisfy the RDVG conditions. We indeed have 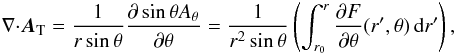 (A.41)
(A.41)
whence 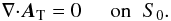 (A.42)The field B thus admits the vector potential
(A.42)The field B thus admits the vector potential 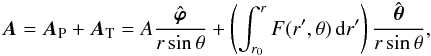 (A.43)such that
(A.43)such that ![\appendix \setcounter{section}{1} \begin{eqnarray} && A_{r} = 0 , \\[2mm] && ({{\nabla}\cdot}\bA)(r_{0},\theta) = 0 , \\[2mm] && \bA(r,0/\pi,\varphi) = 0 , \\[2mm] && \bA(r_{0},\theta,\varphi) = \frac{A(r_{0},\theta)}{r_{0}\sin\theta}{\hat{\bsvph}}(\varphi) , \end{eqnarray}](/articles/aa/full_html/2013/05/aa20787-12/aa20787-12-eq205.png) and is a RDVG vector potential.
and is a RDVG vector potential.
As an application, consider the axisymmetric force-free field BLL (Low & Lou 1990) centered on O (i.e., without the shift in y introduced in Sect. 3.1). For this field, 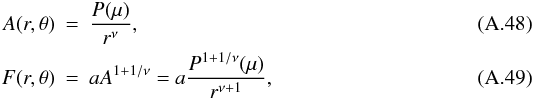 where μ = cosθ, and P(± 1) = 0, and from the formulae above we immediately get
where μ = cosθ, and P(± 1) = 0, and from the formulae above we immediately get  (A.50)
(A.50)
All Tables
Various error diagnostics (see text for definitions) evaluating XTRAPOLS when applied to the reconstruction of BLL from its boundary data for three numerical resolutions.
All Figures
 |
Fig. 1 Convergence properties of the method XTRAPOLS applied to the field BLL for various resolutions: (top) 20 × 40 × 80; (middle) 40 × 80 × 160; (bottom) 80 × 160 × 360. The norm of the solution reaches its asymptotic value in about 20 iterations. |
| In the text | |
 |
Fig. 2 Set of field lines of various solutions. Top: exact solution; middle: potential (current-free) solution; bottom: solution computed with our algorithm with a resolution of 80 × 160 × 320. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.