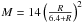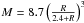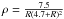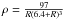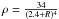EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) A101 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number A101
Number of page(s) 4
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201220781
Published online 16 May 2013

© ESO, 2013

1. Introduction

The Coma cluster of galaxies (A1656) is the most massive well-studied regular gravitationally bound aggregation of matter in the observable Universe. In his classic work Zwicky (1933, 1937) applied the virial theorem to the cluster and showed that dark matter dominates the system. Zwicky estimated its mass as 3 × 1014 M⊙, when normalized to the Hubble constant h = 0.71 used hereafter.

Decades later, The & White (1986) found an order of magnitude higher value, 2 × 1015 M⊙, with a generalization of the virial theorem that must be used when the observed sample does not include the entire system. Hughes (1989, 1998) obtained a similar value (1 − 2) × 1015 M⊙ with X-ray data under the assumption that the cluster’s hot intergalactic gas is in hydrostatic equilibrium. In a similar way, Colles (2006) reports the mass 4.4 × 1014 M⊙ inside the radius of 1.4 Mpc. A weak-lensing analysis gives 2.6 × 1015 M⊙ (Kubo et al. 2007) within 4.8 Mpc radius. Geller et al. (1999, 2011) extended mass estimates to the outskirts of the cluster using the caustic technique (Diaferio & Geller 1997; Diaferio 1999) and find the mass 2.4 × 1015 M⊙ within the 14 Mpc radius. Here the 2σ error is 1.2 × 1015 M⊙, so it does not contradict the apparently higher mass within 4.8 Mpc.

In this paper, we re-examine the mass estimation of the Coma cluster using the data above and a new theory model that describes the cluster as a bound spherical system embedded in the cosmic background of dark energy. We find that dark energy strongly affects the cluster structure at large distances R ≥ 14 Mpc from the cluster center and must be taken into account in the mass estimate.

Basic theory is outlined in Sect. 2, three characteristic masses of a regular cluster are introduced in Sect. 3, a new matter mass profile is defined in Sect. 4, the upper bound on the total size of the Coma cluster is calculated and discussed in Sect. 5, and the results are summarized in Sect. 6.

2. Local dynamical effects of dark energy

We adopt the ΛCDM cosmology that identifies dark energy with Einstein’s cosmological constant Λ and treats it as a perfectly uniform vacuum-like fluid with the constant density ρDE = 0.71 × 10-29 g cm-3. The dark energy background produces antigravity that is stronger than the matter gravity in the present Universe as a whole. This makes the cosmological expansion accelerate, as discovered by Riess et al. (1998) and Perlmutter et al. (1999).

The cosmic antigravity can be stronger than gravity not only globally, but also locally on scales of  ~ 1–10 Mpc (Chernin et al. 2000, 2006; Chernin 2001; Byrd et al. 2007, 2012), as studied using the HST observations made by Karachentsev’s team (e.g., Chernin et al. 2010, 2012a).

The local weak-field dynamical effects of dark energy can be adequately described in terms of Newtonian mechanics (e.g., Chernin 2008). Such an approach borrows from general relativity the major result: the effective gravitating density of a uniform medium is given by the sum 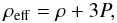(1)where ρ and P are the fluid’s density and pressure (c = 1 hereafter). In the ΛCDM model, the dark energy equation of state is PDE = −ρDE, and its effective gravitating density 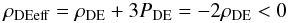(2)is negative, producing antigravity. Einstein’s “law of universal antigravity” says that a point mass M within uniform dark energy generates an acceleration a(r) that includes, in addition to the Newtonian term aN(r) = −GM/r2, the antigravity effect of dark energy 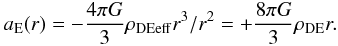(3)Then a test particle at the distance R from the center of a spherical matter mass MM (beyond the mass) has the radial acceleration in the reference frame of the mass center: 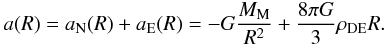(4)Equation (4) comes from the Schwarzschild-de Sitter spacetime in the weak field approximation. The net acceleration a(R) is zero at the distance (Chernin et al. 2000; Chernin 2001, 2008) (5)Gravity dominates at distances R < RZG, while antigravity is stronger than gravity at R > RZG. A gravitationally bound system with the mass MM can only exist inside its zero-gravity sphere of the radius RZG.

3. Three masses of a regular cluster

The presence of dark energy in the spherical volume of a regular cluster like Coma may be quantified by its effective gravitating mass within a given clustrocentric radius R: (6)The matter (dark matter and baryons) content of the cluster is characterized by the mass MM(R) inside radius R: 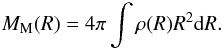(7)Here ρ(R) is the matter density within the cluster. The sum 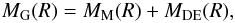(8)is the total gravitating mass within the radius R. It is this mass that can be directly measured by the methods cited in Sect. 1, which are all related to gravitation and give the gravitating mass MG(R), rather than the matter mass MM(R), which can, however, be derived from the data of Sect. 1 using Eq. (8): MM = MG − MDE. So one has for R = 1.4 Mpc: (9)For R = 4.8 Mpc, 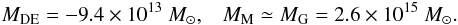(10)And for R = 14 Mpc, 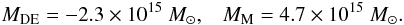(11)As we see, in the inner cluster at R = 1.4 and 4.8 Mpc, the dark energy contributes practically nothing compared to the gravitating mass, so MG ≃ MM here. But (curiously) the absolute value of the dark energy mass MDE nearly equals the gravitating mass MG at R = 14 Mpc; as a result, the matter mass MM ≃ 2MG ≃ 2 | MDE |  at this radius. The difference between the Eq. (11) estimate and the observed value of MG is at the level of 4σ (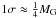, Sect. 1).

In the outer regions of the Coma cluster, 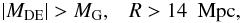(12)where the antigravity effect is thus significant.

4. Matter mass profile

Our estimate of the Coma matter mass within R = 14 Mpc (Eq. (11)) may be compared with estimates following from traditional matter density profiles for dark halos.

4.1. NFW and Hernquist profiles

The popular NFW profile (Navarro et al. 2005) is 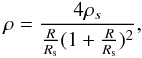(13)where R is again the distance from the cluster center, ρs = ρ(Rs), and Rs are constant parameters. At small radii, R ≪ Rs, the matter density goes to infinity, ρ ∝ 1/R as R goes to zero. At long distances, R ≫ Rs, the density slope is ρ ∝ 1/R3. With this profile, the matter mass profile is (14)To find the parameters ρs and Rs, we use the small-radii data of Sect. 1: M1 = 4.4 × 1014 M⊙ at R1 = 1.4 Mpc, M2 = 2.6 × 1015 M⊙ at R2 = 4.8 Mpc. At these radii, the gravitating masses are nearly equal to the matter masses there (cf. Sect. 3). The values of M1, R1 and M2, R2, together with Eq. (14) lead to two logarithmic equations for the two parameters of the profile, which can easily be solved: Rs = 4.7 Mpc,ρs = 1.8 × 10-28 g/cm3. Then we find the matter mass within R = 14 Mpc, 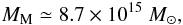(15)to be considerably larger (over 70%) than given by Eq. (11).

Another widely used density profile (Hernquist 1990) is 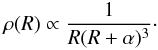(16)Its small-radius behavior is the same as in the NFW profile: ρ → ∞, as R goes to zero. The slope at large radii is different: ρ ∝ 1/R4. The corresponding mass profile is (17)The parameters M0 and α can be found from the same data as above on M1, R1 and M2,R2: M0 = 1.4 × 1016 M⊙,α = 6.4 Mpc, giving another value for the mass within 14 Mpc: 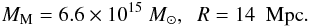(18)Now the difference from the figure of Eq. (11) is about 40%.

thumbnail Fig. 1

Matter mass M vs. radius R for three profiles. 1) NFW mass profile of Eq. (14): – dashed line; 2) Hernquist profile of Eq. (17): – thin line; 3) New mass profile of Eq. (19): – thick line. Here R is in Mpc and M is in 1015 M⊙. The values of the matter mass at radii R = 1.4,4.8,14 Mpc are also shown as given by Eqs. (9)–(11) with 1σ error bars.

4.2. A modified mass profile

In a search for a more suitable mass profile for the Coma cluster, we try a modified version of Hernquist’s relation: (19)The power of three is used now instead of the power of two in Eq. (17). This mass profile comes from the density profile: 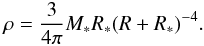(20)The density goes to a constant as R goes to zero; at large radii, ρ ∝ 1/R4, as in Hernquist’s profile.

The parameters M∗ and R∗ are found again from the data for the radii of 1.4 and 4.8 Mpc: M∗ = 8.7 × 1015 M⊙,R∗ = 2.4 Mpc. The new profile leads to a lower matter mass at 14 Mpc: 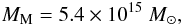(21)which is equal to the Eq. (11) value within 15% accuracy. The three profiles can be found in Figs. 1 and 2.

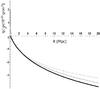thumbnail Fig. 2

Matter density ρ vs. radius R. 1) NFW density profile (Eq. (13)):  – dashed line; 2) Hernquist profile (Eq. (16)):  – thin line; 3) New density profile (Eq. (20)): – thick line.

5. Discussion

We now discuss some implications of the above results.

5.1. Upper limits to size and mass

The strong effect of dark energy at large radii puts an absolute upper limit on the total size of the cluster. The system can be gravitationally bound only if gravity dominates in its volume (as we mentioned in Sect. 2). In terms of the three different masses, this criterion may be given in the form 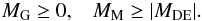(22)Both inequalities are met, if the system is not larger than its zero-gravity radius (Eq. (5)): R ≤ Rmax = RZG.

If the radius of a system with matter mass MM is equal to the maximal radius R = Rmax, its mean matter density (see Bisnovatyi-Kogan & Chernin 2012) is 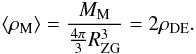(23)This relation and the new profile (Eq. (19)) now lead to Rmax and the corresponding matter mass, Mmax = MM(Rmax): 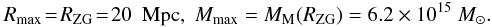(24)For comparison, the other profiles lead to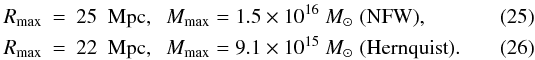

5.2. Close to the maximal size?

Our studies of nearby systems like the Local Group and the Virgo and Fornax clusters (e.g., Chernin et al. 2010, 2012a) suggest their sizes are not far from the zero-gravity radii. Around them, flows of galaxies are seen (Karachentsev et al. 2009; Nasonova et al. 2011), the systems are located in the gravity-dominated regions (R < RZG), and the outflows are at R > RZG. If the local systems have nearly maximal sizes, this may explain the apparent underdensity of the local universe (Chernin et al. 2012b).

It is tempting to ask if the matter distribution could extend to somewhere near the maximal distance of 20 Mpc in the Coma cluster as well. If so, its mass would be near the upper limit evaluated above, and still consistent with the theory of large-scale structure formation that claims the range 2 × 1015 < M < 1016 M⊙ for the most massive bound objects in the Universe (Holz & Perlmutter 2012; Busha et al. 2005). Another implication is the predicted (Eq. (23)) mean matter density of the system  =  twice the dark energy density, which does not depend on the density profile assumed (Merafina et al. 2012; Bisnovatyi-Kogan & Chernin 2012). Its observational confirmation would directly indicate the key role of dark energy for the structure of the system. Using the cosmological matter density parameter Ωm = 0.27, its mean density contrast would be 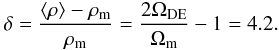(27)Another general prediction (Chernin et al. 2006) is that at distances R > RZG any galaxy in the outflow should have a velocity higher than (28)Here depends on the dark energy density alone. Furthermore, within the simplified model of the Einstein-Straus vacuole, one expects the flow to reach the global Hubble rate at the edge of the vacuole ( ≈ 1.7 RZG, Teerikorpi & Chernin 2010; Hartwick 2011).

The situation is complicated by the fact that the Coma cluster is not isolated, but lies within the CfA Great Wall.

5.3. Dark energy estimator

We have assumed that the dark energy density inside the Coma cluster is equal to its global value. One can reverse the argument and consider the local dark energy density as an unknown constant ρx. Its value may be independently estimated using our concept of three cluster masses.

The data (Geller et al. 1999, 2011) give the gravitating mass MG within R = 14 Mpc. The mass MM at the same radius may be found by extrapolating the data from R = 1.4 Mpc and R = 4.8 Mpc using a reasonable matter density profile (Sect. 4). Then with the masses MG and MM known for R = 14 Mpc, we may find the dark energy mass, MDE(R) = MG − MM, at the same radius. Finally, the dark energy density inside the cluster is estimated from 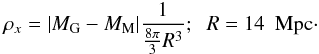(29)With the density profiles of Eqs. (13) and (16) in Sect. 4, Eq. (29) gives for the local dark energy density the values 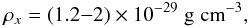(30)equal to the global value ρDE within an order-of-magnitude accuracy. (To avoid a circular argument, we do not use the profile of Eq. (20) here, as was partly suggested from considerations related to the global value itself.)

6. Conclusions

Three masses that characterize the structure of a regular cluster (like Coma) are defined as functions of the radius R: the matter (dark matter and baryons) mass MM(R), the dark-energy effective gravitating mass MDE (negative), and the total gravitating mass MG(R) = MM + MDE. Of these masses, only the gravitating mass MG reveals itself directly in observations at various distances from the cluster center. The dark energy mass MDE may be derived using the known global value of the dark energy density. The mass 2.4 × 1015 M⊙ measured at R = 14 Mpc by Geller et al. (1999, 2011) is the gravitating mass MG inside this radius. The corresponding matter mass is MM ≃ 2 MG.

At small radii, R ≪ 14 Mpc, dark energy effects are almost negligible,  | MDE | ≪ MM, and the gravitating mass MG is practically equal to the matter mass MM. At large radii R ≥ 14 Mpc, the antigravity effects are strong and  | MDE | ≥ MG.

A new matter-mass profile for the Coma cluster reproduces the observational data well and accounts for the dark energy effects in the radius range from 1.4 to 14 Mpc and beyond: , where the constants M∗ and R∗ can be found from the data for small radii.

The available observational data and the new mass profile give upper limits for the Coma cluster total size, R ≲ 20 Mpc, and total matter mass, MM ≲ 6.2 × 1015 M⊙.

Acknowledgments

We thank Yu. N. Efremov, I. D. Karachentsev, D. I. Makarov, O. G. Nasonova, and A. V. Zasov for many useful discussions. A.C. appreciates partial support from the RFBR grant 13-02-00137. The work of G.B.-K. was partly supported by RFBR grant 11-02-00602, the RAN Program “Formation and evolution of stars and galaxies”, and Russian Federation President Grant for Support of Leading Scientific Schools NSh-3458.2010.2. We also thank the anonymous referee for useful comments.

References

  1. Bisnovatyi-Kogan, G. S., & Chernin, A. D. 2012, Ap&SS, 338, 337 [NASA ADS] [CrossRef] [Google Scholar]
  2. Busha, M. T., Evrard, A. E., Adams, F. C., & Wechsler, R. H. 2005, MNRAS, 363, L11 [NASA ADS] [Google Scholar]
  3. Byrd, G. G., Chernin, A. D., & Valtonen, M. J. 2007, Cosmology: Foundations and Frontiers, Moscow, URSS [Google Scholar]
  4. Byrd, G. G., Chernin, A. D., Teerikorpi, P., & Valtonen, M. J. 2012, Paths to Dark Energy: Theory and Observation (Berlin: de Gruyter) [Google Scholar]
  5. Chernin, A. D. 2001, Physics-Uspekhi, 44, 1099 [NASA ADS] [CrossRef] [Google Scholar]
  6. Chernin, A. D. 2008, Physics-Uspekhi, 51, 267 [Google Scholar]
  7. Chernin, A. D., Teerikorpi, P., & Baryshev, Yu. V. 2000, Adv. Space Res., 31, 459, 2003 [NASA ADS] [CrossRef] [Google Scholar]
  8. Chernin, A. D., Teerikorpi, P., & Baryshev, Yu. V. 2006, A&A, 456, 13 [Google Scholar]
  9. Chernin, A. D., Karachentsev, I. D., Nasonova, O. G., et al. 2010, A&A, 520, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Chernin, A. D., Teerikorpi, P., Valtonen, M. J., et al. 2012a, Astron. Rep., 56, 653 [NASA ADS] [CrossRef] [Google Scholar]
  11. Chernin, A. D., Teerikorpi, P., Valtonen, M. J., et al. 2012b, A&A, 539, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Colles, M. 2006, in Encyclopedia of Astronomy and Astrophysics, ed. P. Murdin, IOP Pubs. Ltd, UK, 245 [Google Scholar]
  13. Diaferio, A. 1999, MNRAS, 309, 610 [NASA ADS] [CrossRef] [Google Scholar]
  14. Diaferio, A., & Geller, M. J. 1997, ApJ, 481, 633 [NASA ADS] [CrossRef] [Google Scholar]
  15. Geller, M. J., Diaferio, A., & Kurtz, M. J. 1999, ApJ, 517, L23 [NASA ADS] [CrossRef] [Google Scholar]
  16. Geller, M. J., Diaferio, A., & Kurtz, M. J. 2011, AJ, 142, 143 [Google Scholar]
  17. Hartwick, F. D. A. 2011, AJ, 141, 198 [NASA ADS] [CrossRef] [Google Scholar]
  18. Hernquist, L. 1990, ApJ, 356, 359 [NASA ADS] [CrossRef] [Google Scholar]
  19. Holz, D. E., & Perlmutter, S. 2012, ApJ, 755, L36 [NASA ADS] [CrossRef] [Google Scholar]
  20. Hughes, J. P. 1989, ApJ, 337, 21 [NASA ADS] [CrossRef] [Google Scholar]
  21. Hughes, J. P. 1998, Untangling Coma Berenices: A New Vision of an Old Cluster, Proc. meeting held in Marseilles, June 17–20, 1997, eds. A. Mazure, F. Casoli, F. Durret, & D. Gerbal, Word Scientific, 175 [Google Scholar]
  22. Karachentsev, I. D., Kashibadze, O. G., Makarov, D. I., et al. 2009, MNRAS, 393, 1265 [NASA ADS] [CrossRef] [Google Scholar]
  23. Kubo, J. M., Stebbins, A., Annis, J., et al. 2007, ApJ, 671, 1466 [NASA ADS] [CrossRef] [Google Scholar]
  24. Merafina, M., Bisnovatyi-Kogan, G. S., & Tarasov, S. O. 2012, A&A, 541, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Nasonova, O. G., de Freitas Pacheco, J. A., & Karachentsev, I. D. 2011, A&A, 532, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Navarro, J., Frenk, C. S., & White, S. D. M. 2005, ApJ, 463, 563 [Google Scholar]
  27. Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
  28. Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  29. Rines, K., & Diaferio, A. 2006, AJ, 132, 1275 [NASA ADS] [CrossRef] [Google Scholar]
  30. Rines, K., Geller, M. J., Diaferio, A., Kurtz, M. J., & Jarrett, T. H. 2004, AJ, 128, 1078 [NASA ADS] [CrossRef] [Google Scholar]
  31. Teerikorpi, P., & Chernin, A. D. 2010, A&A, 516, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. The, L. S., & White, S. D. M. 1986, AJ, 92, 1248 [NASA ADS] [CrossRef] [Google Scholar]
  33. Zwicky, F. 1933, Helvetica Phys. Acta, 6, 110 [Google Scholar]
  34. Zwicky, F. 1937, ApJ, 86, 217 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

thumbnail Fig. 1

Matter mass M vs. radius R for three profiles. 1) NFW mass profile of Eq. (14): – dashed line; 2) Hernquist profile of Eq. (17): – thin line; 3) New mass profile of Eq. (19): – thick line. Here R is in Mpc and M is in 1015 M⊙. The values of the matter mass at radii R = 1.4,4.8,14 Mpc are also shown as given by Eqs. (9)–(11) with 1σ error bars.
In the text
thumbnail Fig. 2

Matter density ρ vs. radius R. 1) NFW density profile (Eq. (13)):  – dashed line; 2) Hernquist profile (Eq. (16)):  – thin line; 3) New density profile (Eq. (20)): – thick line.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.