EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 553 (May 2013) A&A, 553 (2013) A65 Full HTML
Free Access
Issue
A&A
Volume 553, May 2013
Article Number A65
Number of page(s) 11
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201219630
Published online 06 May 2013

© ESO, 2013

1. Introduction

Solar flares are interpreted as transient energy release events in solar active regions (ARs) and are known to exhibit robust statistical properties that obey well-defined power laws. Numerous flare observations over a series of solar cycles (Datlowe et al. 1974; Lin et al. 1984; Sturrock et al. 1984; Dennis 1985; Vilmer 1987; Crosby et al. 1993; Biesecker 1994; Bromund et al. 1995; Aschwanden et al. 2000; Polygiannakis et al. 2002) have reported that the distribution functions of flare peak flux, total energy, and event duration follow power laws with exponents in the ranges of (−1.59, −1.80), (−1.39, −1.50), and (−2.25, −2.80), respectively.

The consistency of the flaring activity in terms of scaling laws and indices triggered a phenomenological approach in reproducing and modeling its statistical behavior. Lu & Hamilton (1991) and Lu et al. (1993) constructed the first model of solar flare occurrence in this direction, assuming that the solar corona is in a statistically stationary self-organized critical (SOC) state. ARs are thus considered nonlinear dissipative dynamical systems, externally driven by magnetic flux emergence and the photospheric velocity field, while instabilities are locally triggered, giving rise to flaring and sub-flaring activity. These instabilities are considered to be the source of the fragmented energy release in the solar corona. Cellular automata (CA) are a convenient way of modeling the magnetic energy release in this context, leading to avalanche-like simulated flare events.

Various enhanced SOC models were developed since then. Vlahos et al. (1995) and Georgoulis et al. (1995) suggested that an initial instability might trigger secondary ones, thus affecting sites beyond the closest vicinity of the original event. Isotropic and anisotropic relaxation mechanisms and instability criteria were introduced by Georgoulis & Vlahos (1996), producing a double power-law scaling behavior: the flatter power law resembled intermediate and large flares, while the steeper one described low-energy events. Furthermore, the external driver of the system followed a power law itself, thus mimicking the effect of the emerging magnetic flux from the convection zone in addition to the photospheric shuffling. Georgoulis & Vlahos (1998) attempted to model the stresses that are randomly built up within ARs through a highly variable, inhomogenous external driver. This provided a systematic study of the power law indices’ variability as a function of the driver’s properties. In parallel, Macpherson & MacKinnon (1999) attempted to identify the features that control the power-law indices obtained from self-organizing models of flare occurrence by continuously enhancing previous SOC models (MacKinnon et al. 1996; MacKinnon & Macpherson 1997).

Despite their compatibility with numerous flare observations, SOC models still need to interpret the underlying physical nature of the instability criterion, the selected threshold value, and the redistribution rules. Lu (1995) showed that a 1D nonlinear diffusion equation can be driven to lead to the SOC state, thus yielding power law distributions in dissipated energies. Isliker et al. (1998, 2000, 2001) tried to connect the magnetohydrodynamic (MHD) and CA approaches by physically interpreting numerous CA elements, such as the grid variable, the time step, the finite spatial resolution, the energy release process, and by determining the role of diffusivity. This work revealed specific physical inconsistencies in the CA modeling, such as the uncontrolled value of the magnetic field divergence (∇·B) and the inability to derive important secondary variables (e.g., the current density and the electric field). An extended CA model (X-CA) introduced by Isliker et al. (2002) aimed at overcoming these weaknesses. Liu et al. (2002) used a 1D sandpile model to obtain a nonlinear hyperdiffusion equation and conducted a renormalization analysis on the extracted critical exponents. Bélanger et al. (2007) expanded Liu’s work by using a 2D hyperdiffusion equation, which led to SOC similarly to the corresponding discrete 2D model. Morales & Charbonneau (2008) used parallel magnetic field lines of uniform strength as basic dynamical elements and drove the system through discrete, localized deformations. The appearing tangential discontinuities led to flares, when a specific angle threshold was exceeded. By design, such a model guarantees a zero magnetic field divergence and can be conceivably linked with actual coronal loop characteristics.

Dimitropoulou et al. (2011) constructed a static integrated flare model (S-IFM hereafter), using for the first time observed vector magnetograms as initial conditions, which allowed calculations in physical units and direct comparison with observations. This was not possible in a number of previous models, as explained by Georgoulis et al. (2001). In the context of the S-IFM, the magnetic field from the photospheric boundary of observed vector magnetograms was extrapolated and was resampled on a 32 × 32 × 32 grid through a nonlinear force-free optimization algorithm (Wiegelmann 2008) with preprocessing at the photospheric level (see Appendix A.1, module EXTRA). The unstable locations were identified where the approximated magnetic field Laplacian Gav(r) at site r exceeded a specific threshold Gcr (see Appendix A.2, module DISCO). This imposed instability criterion in terms of the Laplacian of the magnetic field implied an almost zero resistivity in the solar corona, except in regions where the magnetic field discontinuities (and the local currents) reached the critical value. These locations dissipate magnetic energy. Adopting the Lu & Hamilton (1991) approach, the magnetic field was redistributed in the case that magnetic discontinuities had been identified, causing the instabilities to completely relax (see Appendix A.3, module RELAX). The complete relaxation of the primary and all subsequent secondary instabilities triggered during this process defined an avalanche event, interpreted as a “flare”. To further load the system, we added a random magnetic field increment δB(r) at a random site r within the grid, perpendicular to the existing magnetic field B(r), and only after a previously triggered avalanche had completely decayed (see Appendix A.4, module LOAD). This condition is compatible with the localized excitation of Alfvén waves, or even the plasma upflow from the active-region photosphere. The magnetic field increment was forced to be significantly smaller than the magnetic field magnitude to allow the system to reach the SOC state, without this state being influenced by the loading process itself (Bak et al. 1987). Finally, the condition ∇·(B(r) + δB(r)) = 0 was imposed during the loading process to keep the magnetic field divergence at a minimum.

Time in the S-IFM remained the only quantity expressed in arbitrary model units because the photospheric vector magnetogram did not change during the simulation. The S-IFM demonstrated that all examined ARs reached the SOC state under the imposed driving and redistribution rules, as indicated by the asymptotic stabilization of the volume average 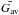of the critical quantity Gav. The retrieved distribution functions for event duration were best described by either double power laws or power laws with exponential rollover, while the peak energy and total energy clearly followed single power laws. All power-law indices agreed well with observations and fell into the observed ranges. Although it mimicked photospheric convection as proposed by Parker (1988, 1989, 1993), or even coronal turbulence and current sheet interaction through either localized Alfvén waves or larger-scale turbulent flows (Einaudi et al. 1996; Rappazzo et al. 2008), the S-IFM was, in fact, a static model. Therefore, it could not realistically simulate either photospheric convection or systematic photospheric flows (e.g., shear), which are are known to be the drivers of most coronal instabilities (Regnier & Priest 2007).

This work aims to address this significant drawback as well as to relate our model’s evolution to physical temporal units. To do so, the random loading mechanism applied in the S-IFM is now replaced by a naturally evolving system. In particular, the dynamic integrated flare model (D-IFM) presented here describes the evolution of an observed solar active region (NOAA AR 8210) on the MHD timescale, using an ensemble of seven 3D magnetic field configurations that were extrapolated from seven subsequent vector magnetograms of this AR. The extrapolated magnetic field configurations have already reached the SOC state through the S-IFM and are used as initial condition and driving mechanism in the context of the D-IFM.

According to the above summary, the D-IFM comprises a deterministic model (each D-IFM run generates reproducible results as long as the subsequent input magnetic configurations remain the same). Still, the D-IFM does not aim to reproduce the exact flaring activity of NOAA AR 8210 but, rather, to provide statistical data for the flare distribution functions (duration, peak energy, total energy). To acquire the amount of data adequate for such a statistical study, we further developed the seven subsequent magnetic configurations through the S-IFM until 50 additional flares were generated by each one of them. This number of additional flares was chosen such that the resulting new sequence of seven configurations was uncorrelated with the previous one. We then again applied the D-IFM model to the new sequence. The same process was repeated until sufficient statistics are achieved.

The structure of this work is as follows: Sect. 2 describes NOAA AR 8210 with its observed flaring activity and characteristics. Section 3 explains the D-IFM concept in detail and introduces the dynamic driving mechanism (Sect. 3.1, module INTER). Section 4 presents our results and discusses our findings. Finally, Sect. 5 summarizes our key conclusions, while Sect. 6 discusses the strengths and weaknesses of the dynamic model, its relation with previous results and also suggests possible future enhancements. The Appendix provides a technical summary of the reused modules from the static model, as introduced by Dimitropoulou et al. (2011).

2. NOAA AR 8210

We have used a timeseries of seven vector magnetograms from NOAA AR 8210 recorded on 01/05/1998 from the University of Hawaii Imaging Vector Magnetograph (IVM). The IVM obtains Stokes images in photospheric lines with 7 pm spectral resolution, 1.1 arcsec spatial resolution (~ 0.55 arcsec per pixel) over a field of 4.7 arcmin2 and polarimetric precision of 0.1% (Mickey et al. 1996). Table 1 shows the magnetogram sequence with the corresponding acquisition UT times, starting from 18:58 and ending at 23:16. Assuming that the D-IFM simulation starts at time t = 0 s, we provide the corresponding model times t in seconds in the third column of the Table.

Table 1

NOAA AR 8210 magnetogram sequence, UT time of IVM acquisition, and respective D-IFM time in seconds of each snapshot.

Table 2

Characteristics of three major flares produced by NOAA AR 8210 on 01/05/1998 (from 18:58 until 23:16 UT) as recorded by GOES.

To remove the intrinsic azimuthal ambiguity of 180°, we used the non-potential magnetic field calculation (NPFC) method of Georgoulis (2005). For computational convenience we furthermore rebinned the disambiguated magnetograms into a 32 × 32 regular grid. The original IVM magnetograms had linear dimensions of 512 × 512 pixels2 with 0.55 arcsec per pixel. Rebinning the original magnetograms to a 32 × 32 grid yields a pixel size of 0.55 × 16 = 8.8 arcsec. Furthermore, we spatially coaligned the sequence of our magnetograms using the first magnetogram as a reference. This allows the evolution of the field vector from one snapshot to the next in a consistent way. The upper row of Fig. 1 depicts the subsequent magnetograms of NOAA AR 8210 after the azimuthal ambiguity removal and the rebinning process.

The flare productivity of NOAA AR 8210 is documented in the solar X-ray flare catalog from the GOES satellite1 (item 3). On 01/05/1998 and for the examined UT time interval (18:58-23:16), GOES recorded three significant flares: two of class C and one of class M. The starting, peak, and ending flare times are shown in Table 2.

thumbnail Fig. 1

Upper row: the vertical magnetic field components of the sequence of NOAA AR 8210 magnetograms in 32 × 32 grid resolution. Lower row: the same sequence after the S-IFM has been applied for 4 × 105 iterations. The i-values correspond to the indices of Table 1.

3. Model

It is prerequisite for applying the D-IFM to the IVM vector magnetogram sequence that all snapshots are extrapolated in 3D into the corona and that they are already in the SOC state. For this reason, we first applied the S-IFM model (see Dimitropoulou et al. 2011 and the appendix for a detailed description) to the seven vector magnetogram snapshots. The algorithm ran for 4 × 105 iterations, which is sufficient for all NOAA AR 8210 snapshots to independently reach the SOC state. We thus obtained seven 3D 32 × 32 × 32 configurations denoted by SOC:i, 0, (i = 1,2,...,7). We refer to this first S-IFM run as static (IFM) original run (SOR) hereafter. As demonstrated in Fig. 1 by comparing the upper (IVM data) with the lower (SOC:i, 0, (i = 1,2,...,7)) row, the photospheric layer is not significantly impacted by the SOR process.

Each snapshot of the SOC:i, 0, (i = 1,2,...,7) sequence was then developed through the S-IFM (excluding the extrapolation step, since this only needs to take place during the SOR). The static algorithm was forced to pause every time 50 additional flares were triggered and completely relaxed for every snapshot. The output of these static (IFM) intermediate runs (SIRs hereafter) is a series of additional magnetic configuration groups SOC:i, j, (i = 1,2,...,7), where j is the index of the SIR performed. In total we allowed for jmax = 16   235 SIRs, thus collecting an equal number of SOC:i, j, (i = 1,2,...,7, j = 1,2,...,jmax) sequence groups – all in an SOC state. As highlighted in the introduction, the need for having subsequent SIRs derives from the fact that the D-IFM aims to achieve sufficient statistics for the flare distribution functions (duration, peak energy, total energy). To acquire this amount of data requires numerous D-IFM runs (jmax = 16   235 in this work), each on a distinct seven-element magnetic configuration sequence.

We then applied the D-IFM algorithm to each of the 3D magnetic configuration sequences SOC:i, j, (i = 1,2,...,7, j = 0,2,...,jmax) as a separate simulation, i.e., there are jmax D-IFM runs, each one for a fixed j and using the sequence SOC:i, j, (i = 1,2,...,7) as input and driver. The D-IFM follows in principle the same concept as the S-IFM, namely it generates magnetic instabilities in the system through a loading mechanism, which are then relaxed through magnetic field redistribution. The complete relaxation of the primary (from the loading) and all subsequent secondary instabilities (through the imposed magnetic field redistribution, following Lu & Hamilton 1991) comprises an avalanche or “flare” event. The total number of 16 236 D-IFM simulations provides an adequate sample of 90   971 flaring events. In the statistical analysis, the total duration, total energy, and peak energy of each event are calculated and their distribution functions are constructed.

The basic difference between the S-IFM and the D-IFM is the loading process. In the D-IFM, it is implemented by means of a cubic spline interpolation (module INTER) of the magnetic field for all transitions SOC:i, j → SOC:i + 1, j, (i = 1,2,...,6) with j fixed for each D-IFM run. The time interval between two subsequent interpolation steps, the number of the interpolation steps per transition from one configuration to the subsequent one, and the reasoning for selecting cubic spline interpolation are explained in detail in the technical description of the module INTER (Sect. 3.1).

The new driving mechanism introduced in the D-IFM is more physical than the S-IFM driver because it reflects the observed photospheric evolution. As we will see below, this dynamical evolution allows for both physical time units, at least for the start times of simulated flares, and multiple perturbation sites. The latter is important, because we show that SOC persists even in this driver case, which is clearly different from conventional, single-site perturbed SOC models. Regarding the former, following each interpolation step the entire grid is scanned for possible instabilities. If one or more are detected, a collective avalanche starts, involving all identified unstable locations. The onset of each avalanche is labeled by a unique MHD time stamp (starting time). Point taken, the avalanche is relaxed “instantly” (i.e., by means of “infinitesimal”, arbitrary model units, or time steps), as the sequence of magnetic reconnection events needed to adjust the field takes place on kinetic timescales that are much shorter than the MHD ones. Therefore, as in the S-IFM, D-IFM flare durations are measured in time steps with arbitrary units. The peak and total released energies of flares are measured in physical units as in the S-IFM. Figure 2 provides a graphical representation of the D-IFM concept.

thumbnail Fig. 2

Graphic overview of the D-IFM. A total number of 16   236 SOC:i, j (i = 1,2,...,7, j = 0,1,2,...,jmax, jmax = 16   235) sequence groups are created by advancing the previous group through the S-IFM for 50 additional avalanches (vertical direction). Each group is then provided as input to the D-IFM (horizontal direction). Event duration, flare peak, and total energies are accumulated in the database from all D-IFM runs.

3.1. INTER: a magnetic field interpolator acting as driver

INTER is a magnetic field interpolator that calculates the magnetic field components at intermediate times between two subsequent configurations SOC:i, j and SOC:i + 1, j for given j. Cubic-spline interpolation was selected for this purpose. The main reason for selecting cubic spline interpolation instead of, e.g., linear interpolation is that in the linear interpolation differentiability is not ensured at the endpoints of the subintervals, which means that the interpolating function is not smooth. From the physical demands of our model, it is clear that the interpolating function must be continuously differentiable, because the physical quantity interpolated is the magnetic field, which needs to follow a smooth transition throughout the entire D-IFM simulation. Cubic spline interpolation is continuously differentiable up to order 2. Moreovr, Isliker et al. (2000) present a detailed analysis in favor of the cubic spline interpolation.

The interval τ between two interpolation steps acquires physical units within the D-IFM. As shown in Sect. 2, rebinning the original magnetograms to a 32 × 32 grid yields a pixel size of 8.8 arcsec. At this scale, at just one grid-site above the lower boundary we reach a height of about 6.4 Mm in the solar atmosphere that is clearly in the lower corona. Although Regnier et al. (2008) have demonstrated that there is no typical coronal Alfvén speed above ARs, but rather a dynamic Alfvén speed range varying mainly with height and depending on the overall AR magnetic configuration, we selected an indicative Alfvén speed of 103  km   s-1 throughout our grid. This is considered a reasonable approximation, since especially for NOAA AR 8210, Regnier et al. (2008) showed that the highest Alfvén speed at the base of the corona is ~ 70   000  km   s-1, decreasing rapidly with height, and reaching the value of 600 km s-1 at a height of about 70 Mm (z ~ 11 in our grid, where z is the grid height, taking values in the range 0 ≤ z ≤ 31). At a given height, though, there are very limited variations in the Alfvén-speed values. This is attributed to the complex topology of NOAA AR 8210, which does not significantly influence the Alfvén speed distribution.

With the above-mentioned assumptions (8.8 arcsec per pixel as spatial resolution and 103  km   s-1 as a first approximation of the Alfvén speed), we obtained a time step τ ~ 6.4 s for our interpolation. This time step corresponds to the Alfvén crossing time of a distance equal to the linear scale of our grid-size.

These assumptions allow us to assign physical time stamps to each of the interpolation steps during the transition from SOC:i, j to SOC:i + 1, j on the MHD time scale. For imax = 7 snapshots, the number of transitions k from one magnetic configuration to the subsequent one takes the maximum value of kmax = 6. Assuming that the model time stamps for two subsequent snapshots are t(SOC:i,   j) and t(SOC:i + 1,   j) (see third column of Table 1), the number of interpolation steps sk is defined as 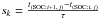for each transition k. These data are summarized in Table 3.

We also assumed that when an avalanche is triggered by the magnetic field loading, it is relaxed in zero MHD time (t does not increase), because magnetic reconnection − the cause of the redistribution − takes place on kinetic timescales. This leaves us with arbitrary model time step units for the duration of each flare (as in the S-IFM), but the time of event occurrence acquires an MHD timescale stamp for the first time in the D-IFM.

Initially, INTER calculates the magnetic field B(r) per site r for the number of time steps sk per transition k. After each interpolation step magnetic instabilities may occur at any site within the grid (DISCO), and the magnetic field will be redistributed to relax them in ΔtMHD = 0 (RELAX). After each flare, INTER recalculates the remaining number of interpolation steps and uses the redistributed magnetic field B(r) per site r after the relaxation as the starting point for the new interpolation toward the subsequent SOC:i, j.

Table 3

Interpolation map of the D-IFM.

To construct a database of 90   971 events, we performed a total of 16   236 D-IFM simulations, one for each of the j sequence groups SOC:i,   j, (i = 1,2,...,7,j = 0,2,...,jmax) already in the SOC state.

An important consideration in this new loading process through INTER is whether we sustain the magnetic field divergence close to zero. For the LOAD module of the S-IFM (Appendix A.4), we had imposed the condition 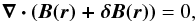(1)As discussed in Dimitropoulou et al. (2011), however, condition (1) implies deviations from a divergence-free magnetic field in the selected site’s vicinity. This is a known problem, which can be tackled by working with the vector potential A, with ∇ × A = B, instead of the magnetic field B directly (see e.g. Lu et al. 1993; Galsgaard 1996; Isliker et al. 2000, 2001). But because our study uses observed vector magnetograms as initial conditions and driver, we naturally work with the magnetic fields rather than their generated vector potential. Thus, Eq. (1) only provides a low-order approximation of a divergence-free magnetic field. To monitor how effective condition (1) is for the S-IFM, Dimitropoulou et al. (2011) introduced a weighted nabla dot B (WNDB) monitoring parameter as the average value of the following expression over all grid points: 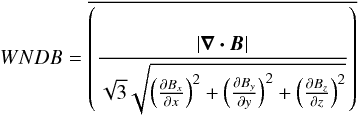where Bx, By, Bz are the components of B(r). By definition, WNDB is a dimensionless quantity, lying in the range 0 ≤ WNDB ≤ 1. Monitoring WNDB during our S-IFM simulations provides evidence on whether LOAD keeps the magnetic field within the volume approximately divergence-free. We used the same variable to monitor the departure of the magnetic field divergence from zero both for the S-IFM (SOR and SIRs) runs preparing the SOC:i,   j, (i = 1,2,...,7) groups, and for each of the D-IFM runs. Appendix A.3 discusses how the magnetic field redistribution rules during the avalanche relaxation guarantee that ∇·B is not increased beyond the WNDB value after the loading phase (LOAD for S-IFM, INTER for D-IFM) has been completed. The respective results provided in Sect. 4 show that our model does not depart more than 25% from the divergence-free condition for the magnetic field vector.

3.2. Model parameters

We combined the above-described modules in one consistent model (D-IFM) that monitors the flare duration, the peak energy, and the total energy for each snapshot group. The distribution functions were determined for the cumulative data from all groups. If an instability was identified (DISCO) after a magnetic field interpolation step (INTER), the possible chain of instabilities that follows was left to completely relax (RELAX) throughout the grid before the next interpolation starts (INTER). This rule takes into account that the lifetime of a flare is much shorter than the evolution (MHD) timescale of an AR. Note that if multiple sites become unstable after the interpolation, we regarded all triggered relaxation processes as one single flare event. Successive grid scans may be required for an instability to be completely relaxed. Each scanning corresponds to one time step, therefore the relaxation of an event may be accomplished in more than one time steps. Each loading/interpolation step triggers a new iteration. The interval between two subsequent interpolation steps is defined as τ = 6.4 s (Sect. 3.1). Switching from the magnetic configuration i to i + 1 comprises a transition in our model (with j fixed).

We considered the number of time steps needed for the entire subsequent burst activity to have ended as the total avalanche (flare) duration. The same concept applies to the recorded flare peak energy, which is defined as the maximum energy recorded during the relaxation time-steps within the grid. Finally, regarding the flare total energy, we summed up the released energy from all bursting sites during the avalanche.

The simulation results presented in the next section were performed using a 32 × 32 × 32 cubic grid with open boundaries in the relaxation events (see Isliker et al. 2001 for a detailed discussion on open-boundary conditions).

4. Results

After applying the S-IFM to all seven initially extrapolated IVM magnetograms for 4 × 105 iterations, we found that all of them (SOC:i, 0, (i = 1,2,...,7)) have reached the SOC state. Dimitropoulou et al. (2011) have shown that whether the SOC state is reached is indicated by the asymptotic stabilization of the volume average 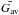of the critical quantity Gav. The system was verified to remain in the SOC-state after the first application of the D-IFM (SOC:i, 0, (i = 1,2,...,7)) and for all subsequent runs (for all j = 1,2,...,16   235 groups).

thumbnail Fig. 3

Distributions of the event duration a), the peak energy Epeakb), and the total energy Etotalc) determined from the accumulated event data of the 16 236 D-IFM simulations. The main graph is plotted with linearly equispaced bins, while the inset graphs are plotted in equally spaced logarithmic bins.

The SOC state is known to exhibit robust power-law behavior for the frequency distribution of the modeled avalanche parameters. In the framework of the D-IFM it is interesting to investigate whether this feature still persists with the new driving process that allows multiple-site driving, leading to a collective nature of avalanches. To define the best-fitting functions we applied least-squares fits and calculated the chi-square goodness-of-fits.

Figure 3 depicts the distribution functions of duration (Fig. 3a), peak energy (Fig. 3b), and total energy (Fig. 3c) for the 90   971 events within our database in linearly equispaced bins. The duration distribution follows a double power law with index − 2.15 ± 0.15 for the flatter part and − 3.60 ± 0.09 for the steeper part. Both the peak and total energy distribution functions follow single power laws with indices − 1.65 ± 0.11 and − 1.47 ± 0.13, respectively. The inset graphs per frame depict the same distributions in equally spaced logarithmic bins. All results were derived with a 95% significance level.

Although our findings agree well with both previous models and observations, it is crucial to verify that we have a physically sound magnetic field. Indeed, neither loading in the S-IFM (Eq. (1)) nor spline interpolation, acting as the loading mechanism in D-IFM simulations, guarantee a zero-divergence field.

WNDB is therefore calculated to monitor the magnetic field divergence throughout the loading and the redistribution process for both static and dynamic simulations. Figure 4 shows the WNDB evolution for the 4 × 105 S-IFM iterations applied to the initial i = 6 snapshot for the preparation of SOC:6, 0. We note that the magnetic field exhibits an average departure from zero divergence that barely exceeds 20%. Figure 5 shows that WNDB during the (jmax)th D-IFM simulation retains more or less the same value (<22% in all simulations), meaning that neither the interpolation process nor the S-IFM simulations used for the generation of more snapshot groups cause an uncontrollable increase of | ∇·B |. This is one of the reasons why the spline interpolation was selected, namely to achieve a smooth magnetic-field loading process in all interpolation steps and transitions.

Motivated by Georgoulis & Vlahos (1998), who investigated the variability of the scaling indices as a result of the driver’s variability, we investigated whether the magnetic field increments δB(r) as determined by the spline interpolation mechanism follow any specific scaling law. Figure 6 depicts the δB(r) distribution function for one of the simulation series (j = 5). The magnetic field increments resulting from the interpolation process follow a distribution function that can be either fitted by a double power law with index − 2.33 ± 0.19 for the flat part and − 3.18 ± 0.21 for the steep part of the distribution (frame a), or alternatively by a power law with exponential rollover (with index − 1.37 ± 0.19) (frame b) for the small- and medium-magnitude increments. The same analysis was conducted for several j-groups, always yielding single/double power laws or power laws with exponential rollover distributions for δB(r). The derived power-law indices do not differ significantly from the results presented in Fig. 6. This finding is indicative of the scale-independent nature of the physical driving process, as given by the spline interpolation of the magnetic field.

thumbnail Fig. 4

Evolution of WNDB during the 4 × 105 iterations of the S-IFM application to the i = 6 IVM magnetogram for the preparation of the SOC:6,0 snapshot.

thumbnail Fig. 5

Evolution of WNDB during the jmax = 16   250 D-IFM simulation.

thumbnail Fig. 6

Magnetic increment δB(r) distribution function during the D-IFM simulation for j = 5. The graph is plotted with linearly equispaced bins. a) depicts the double power law fitting to the distribution. b) depicts fitting by a power law with an exponential rollover.

Figure 7 shows a 3D representation of the emerging magnetic discontinuities during a large avalanche recorded during the D-IFM run j = 1800. This flare occurred at MHD time stamp t = 2547 s of our D-IFM simulation, namely during transition k = 1. A total of 3250 generated instabilities were relaxed in 112 model time steps without the MHD time progressing until the flare completely decayed. The photospheric layer is shown isolated from the corona at the bottom part of the figure, so that the photospheric magnetic field evolution is clearly visible. The subsequent frames in this figure depict avalanche snapshots indicative for the onset, peak, and decay phases of the simulated flare. The avalanche sets off with 12 discontinuities (Fig. 7a), evolves further with 74 discontinuities (Fig. 7b), peaks with 104 discontinuities (Fig. 7c) , and decays with 86, 41, and 11 discontinuities (Figs. 7d–f), respectively.

Finally, we note that the average flare occurrence rate, as obtained by dividing the total number of simulated events (90 971) by the number of dynamic runs (16 250), yields the value 5.6 during the observation period (4.3 h), which is comparable to the number of the observed flares (3) for the timeframe under examination (see Table 2). This is an indication that the system has not been under-/overdriven during the simulation.

thumbnail Fig. 7

3D representation of the emerging magnetic discontinuities during an avalanche generated in the course of the D-IFM simulation for j = 1800. The total duration of this event is 112 steps. During the early stages, the avalanche generates 12 discontinuities a), evolves with 74 discontinuities b), peaks with 104 discontinuities c), and decays with 86 discontinuities d), 41 discontinuities e), and 11 discontinuities f).

5. Conclusions

This study provides a statistical simulation of the flaring activity for NOAA AR 8210 based on observational data in terms of a dynamic CA model. In our modeling process we applied the static integrated flare model (S-IFM) of Dimitropoulou et al. (2011) to a sequence of seven IVM magnetograms captured on 01/05/1998 between 18:58 and 23:16. The S-IFM simulation runs for 4 × 105 iterations in order to allow all snapshots to reach the SOC state.

The generated SOC:i, 0, i = (1,2,...,7)) group is provided as input to the dynamic integrated flare model (D-IFM) introduced in this work. We dynamically evolved our system through spline interpolation of the magnetic field taking the SOC-driven snapshots SOC:i, 0 (i = (1,2,...,7)) as anchor points. The interpolated magnetic field effectively acts as the driver of our system by gradually adding magnetic field increments δB(r) in every interpolation step and throughout the grid (module INTER, Sect. 3.1).

After each interpolation step we identified the unstable locations that will dissipate magnetic energy in the grid where the approximated magnetic field Laplacian Gav(r) at site r exceeds a specific threshold Gcr (module DISCO, see Appendix A.2 for details).

If magnetic discontinuities were identified, the magnetic field was redistributed such that the instabilities were completely relaxed (module RELAX see Appendix A.3 for details).

When no discontinuities were found after interpolation and all identified instabilities throughout the grid were relaxed, the algorithm continues to interpolate until all transitions are covered. For statistical data collection we advanced the SOC:i, 0 (i = (1,2,...,7)) group by repeating the first step for 50 additional avalanches to construct SOC:i, 1 (i = (1,2,...,7)), and we again applied the dynamical interpolation, instability identification, and relaxation as described above. The same process was repeated 16 235 times, yielding 90 971 avalanches for statistical analysis.

Our results show that under the imposed driving and redistribution rules in the D-IFM, the peak energy and total energy clearly follow single power laws, whereas the event duration follows a double power law distribution. The duration distribution follows a double power law with index − 2.15 ± 0.15 for the flatter part and − 3.60 ± 0.09 for the steeper part. The indices of the single power laws fitting to the peak and total energy distribution are − 1.65 ± 0.11 and − 1.47 ± 0.13, respectively. These power laws lie in the well-known ranges documented consistently in numerous past studies, including Georgoulis et al. (2001) at least for the peak and total energy. In this study, Georgoulis et al. compared their SOC model with data from the Danish Wide Angle Telescope for Cosmic Hard X-rays (WATCH) collected during the maximum of solar cycle 21. Figure 1 in the cited work shows that the peak and total energy of the observed flares follow single power-law distribution functions with indices − 1.59 and − 1.39, respectively, whereas the flare duration distribution function was considered to either follow a double power law (with index − 1.15 for the flat and − 2.25 for the steep part) or a power law with exponential rollover (with power law index − 1.09).

6. Discussion

The D-IFM was developed to enhance previous SOC models of solar flares. First and foremost, the initial and boundary conditions are not arbitrary, but stem from real solar magnetograms. While this is also a feature of the S-IFM, the newly introduced D-IFM furthermore features a dynamical evolution in real time, commensurate to the observed photospheric evolution of observed magnetogram timeseries. An NLFF field extrapolation was used to reconstruct the initial 3D magnetic configuration for each magnetogram. Although NLFF field extrapolation models include significant uncertainties (DeRosa et al. 2009), they provide physical, divergence-free field solutions, and equilibrium configurations via the minimization of the Lorentz force.

The D-IFM generally follows the principles of Lu & Hamilton (1991). Given the use of a magnetic field vector, the rules obeyed during both the magnetic field redistribution and the driving of the system are designed to maintain the magnetic field divergence within acceptable limits. This was not the case in the early CA models (Vlahos 1995; Georgoulis & Vlahos 1996, 1998) and has only been touched in advanced CA approaches through the use of the vector potential A instead of the magnetic field B in combination with an improved way of calculating the derivatives (Isliker et al. 2000, 2001).

Given that the simulation commences from observed magnetograms, it is possible for our CA model to remove the restriction of arbitrary energy units (see e.g. the remarks in Georgoulis et al. 2001). Going one step further, our model evolution is anchored to a sequence of magnetic snapshots stemming from IVM magnetograms. This methodology allows us to assign physical time stamps to each of the interpolation steps during the transition from one anchor point to the next on the MHD timescale. It should be noted that the triggered avalanches are still unresolved in real time, thought to be evolving on reconnection (i.e., kinetic) timescales.

The interpolation-based driving mechanism effectively mimics a variety of physical processes that affect the flaring activity. In addition to photospheric convection (Parker 1988, 1989, 1993), localized Alfvén waves, coronal turbulence, and current sheet interaction (Einaudi et al. 1996; Rappazzo et al. 2008), which were also simulated by the S-IFM, the dynamic driving through magnetic field interpolation based on subsequent photospheric observations now allows for a realistic simulation of systematic photospheric flows (e.g. shear). This enhancement is important because (1) it has been argued that the distribution and energy content of magnetic discontinuities in a given photospheric boundary can explain the statistical properties of flares (Vlahos & Georgoulis 2004) and (2) investigating possible correlations between the photospheric driver and the corresponding coronal active region reveals the strong nonlinearity in the magnetic fields of active regions that hinders correlations between the fractal dimensions and thus the complexity of photospheric and coronal structures (Dimitropoulou et al. 2009). The latter patterns, however, have a crucial impact on the expected dynamical activity of the system, specifically the magnetic energy release and the subsequent particle acceleration processes (Vlahos et al. 2004). D-IFM now provides the means for future investigation of these aspects.

One of our key findings is that the D-IFM’s spline-interpolation driving mechanism naturally gives rise to a power-law distribution of magnetic field increments, qualitatively similar to the variable driver described in Georgoulis & Vlahos (1998). In that study, the peak and total energy distribution functions followed double power laws with a “knee point” that distinguishes between the steeper and flatter parts of the distribution. The steeper part corresponds to a “soft” flare population (dubbed nanoflares), while the flatter part is attributed to microflares and flares. The soft, nanoflare population was attributed by Georgoulis & Vlahos (1998) to the application of anisotropic, small-scale relaxation rules. In the absence of anisotropic relaxation, one expects a global scale-invariance of the distribution functions reflected by robust scaling laws. As a result, the steepening feature in the peak and total energy distribution functions does not appear in the D-IFM model, which is a purely isotropic model in its relaxation process. In the D-IFM the variable driver follows a power-law distribution for the magnetic field increments, which results in scale-invariance in the distribution functions for the total and peak energies, which follow single power laws.

Although this work overcomes major drawbacks of many previous CA models, there are still some points that can lead to discrepancies, such as the arbitrary determination of the threshold value Gcr that can slightly influence the exponents of the inferred power laws and the extent of the duration and energy ranges. Gcr cannot incur any qualitative changes to the distribution functions, a feature well-known in SOC models. Nonetheless, the histogram method of Dimitropoulou et al. (2011) (Appendix A.2) manages to reduce the arbitrariness of the Gcr-selection.

Variations in the indices of the flare distribution functions can also be expected by the application of a dynamic range of Alfvén speeds, which would be more realistic than a single Alfvén speed value throughout the active-region corona. Such a distribution – at least depending on height – would accordingly alter the interpolation step duration while driving the system, and could thus cause modifications in the inferred distribution functions. A dynamic Alfvén speed range is an improvement of the D-IFM that is considered for future implementation.

In conclusion, the validity of the CA models regarding the simulation of physical processes in complex systems remains a long-standing question. Isliker et al. (1998) demonstrated that the essence of CA modeling is to describe complex systems, which comprise a large number of interacting subsystems, assuming that the global dynamics described statistically are not sensitive to the fine structure of the elementary processes. MHD approaches are based on a precise description of elementary processes through detailed differential equations. The CA approach does not provide insight into the local processes or over short-time intervals, but it reproduces the global statistics. MHD reveals details about the local processes, but coupling them to a global description is a formidable task. It is therefore evident that both approaches can be considered to be complementary rather than competing. There have been various attempts to either combine them (e.g. Longope & Noonan 2000), or interpret CA models as discretized MHD equations (Isliker et al. 1998; Vassiliadis et al. 1998). More refined CA models, such as the X-CA model described by Isliker et al. (2001), have achieved consistency with MHD to a greater extent. Our CA model will opt to incorporate and use meaningful modeling developments into a continuously improving dynamic integrated flare model.

Acknowledgments

We are grateful to Thomas Wiegelmann, who kindly contributed his NLFF extrapolation code to this analysis. Xenophon Moussas and Dafni Strintzi are acknowledged for their constructive comments in the course of this work. Additionally, IVM Survey data are made possible through the staff of the U. of Hawaii, supported by the Air Force Office of Scientific Research, contract F49620-03-C-0019. IVM Survey data are based upon work supported by the National Science Foundation under Grant No. 0454610. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation (NSF).

References

  1. Aschwanden, M. J., Tarbell, T. D., Nightingale, R. W., et al. 2000, ApJ, 535, 1047 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bak, P., Tang, C., & Wiesenfeld, K. 1987, Phys. Rev. Lett., 59, 381 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  3. Bélanger, E., Vincent, A., & Charbonneau, P. 2007, Sol. Phys., 245, 141 [Google Scholar]
  4. Biesecker, D. A. 1994, Ph. D. Thesis, University of New Hampshire [Google Scholar]
  5. Bromund, K. R., McTiernan, J. M., & Kane, S. R. 1995, ApJ, 455, 733 [NASA ADS] [CrossRef] [Google Scholar]
  6. Crosby, N. B., Aschwanden, M. J., & Dennis, B. R. 1993, Sol. Phys., 143, 275 [NASA ADS] [CrossRef] [Google Scholar]
  7. Datlowe, D. W., Elcan, M. J., & Hudson, H. S. 1974, Sol. Phys., 39, 155 [NASA ADS] [CrossRef] [Google Scholar]
  8. Dennis, B. R. 1985, Sol. Phys., 100, 465 [NASA ADS] [CrossRef] [Google Scholar]
  9. DeRosa, M. L., Schrijver, C. J., Barnes, G., et al. 2009, ApJ, 696, 1780 [Google Scholar]
  10. Dimitropoulou, M., Georgoulis, M., Isliker, H., et al. 2009, A&A, 505, 1245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Dimitropoulou, M., Isliker, H., Vlahos, L., & Georgoulis, M. 2011, A&A, 529, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Einaudi, G., Velli, M., Politano, H., & Pouquet, A. 1996, ApJ, 457, L113 [NASA ADS] [CrossRef] [Google Scholar]
  13. Galsgaard, K. 1996, A&A, 315, 312 [NASA ADS] [Google Scholar]
  14. Georgoulis, M. K. 2005, ApJ, 629, 69 [Google Scholar]
  15. Georgoulis, M. K., & Vlahos, L. 1996, ApJ, 469, L135 [NASA ADS] [CrossRef] [Google Scholar]
  16. Georgoulis, M. K., & Vlahos, L. 1998, ApJ, 336, 721 [Google Scholar]
  17. Georgoulis, M. K., Kluiving, R., & Vlahos, L. 1995, Phys. A, 218, 191 [CrossRef] [Google Scholar]
  18. Georgoulis, M. K., Vilmer, N., & Corsby, N. B. 2001, A&A, 367, 326 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Isliker, H., Anastasiadis, A., Vassiliadis, D., & Vlahos, L. 1998, A&A, 335, 1085 [NASA ADS] [Google Scholar]
  20. Isliker, H., Anastasiadis, A., & Vlahos, L. 2000, A&A, 363, 1134 [NASA ADS] [Google Scholar]
  21. Isliker, H., Anastasiadis, A., & Vlahos, L. 2001, A&A, 377, 1068 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Isliker, H., Anastasiadis, A., & Vlahos, L. 2002, ESA SP, 506, 6411 [Google Scholar]
  23. Lin, R. P., Schwartz, R. A., Kane, S. R., Pelling, R. M., & Hurly, K. C. 1984, ApJ, 283, 421 [NASA ADS] [CrossRef] [Google Scholar]
  24. Liu, H. L., Charbonneau, P., Pouquet, A., Bogdan, T. J., & McIntosh, S. W. 2002, Phys. Rev. E, 66, 056111 [NASA ADS] [CrossRef] [Google Scholar]
  25. Longope, D. W., & Noonan, E. J. 2000, ApJ, 542, 1088 [NASA ADS] [CrossRef] [Google Scholar]
  26. Lu, E. T. 1995, Phys. Rev. Lett., 74, 2511 [NASA ADS] [CrossRef] [Google Scholar]
  27. Lu, E. T., & Hamilton, R. J. 1991, ApJ, 380, L89. [NASA ADS] [CrossRef] [Google Scholar]
  28. Lu, E. T., Hamilton, R. J., McTiernan, J. M., & Bromund, K. R. 1993, ApJ, 412, 841 [NASA ADS] [CrossRef] [Google Scholar]
  29. MacKinnon, A. L., & Macpherson, K. P. 1997, A&A, 326, 1228 [NASA ADS] [Google Scholar]
  30. MacKinnon, A. L., Macpherson, K. P., & Vlahos, L. 1996, A&A, 310, L9 [NASA ADS] [Google Scholar]
  31. Macpherson, K. P., & MacKinnon, A. L. 1999, A&A, 350, 1050 [Google Scholar]
  32. Mickey, D. L., Canfield, R. C., LaBonte, B. J., et al. 1996, Sol. Phys., 168, 229M [Google Scholar]
  33. Morales, L., & Charbonneau, P. 2008, ApJ, 682, 654 [NASA ADS] [CrossRef] [Google Scholar]
  34. Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
  35. Parker, E. N. 1989, Sol. Phys., 121, 271 [NASA ADS] [CrossRef] [Google Scholar]
  36. Parker, E. N. 1993, ApJ, 414, 389 [NASA ADS] [CrossRef] [Google Scholar]
  37. Polygiannakis, J. M., Nikolopoulou, A., Preka-Papadima, P., Moussas, X., & Hilaris, A. 2002, ESA SP, 505, 541 [NASA ADS] [Google Scholar]
  38. Priest, E. R., Hornig, G., & Pontin, D. I. 2003, J. Geophys. Res. Space Phys., 108(A7), 1285 [NASA ADS] [CrossRef] [Google Scholar]
  39. Rappazzo, A. F., Velli, M., Einaudi, G., & Dahlburg, R. B. 2008, ApJ, 677, 1348 [NASA ADS] [CrossRef] [Google Scholar]
  40. Regnier, S., & Priest, E. R. 2007, A&A, 468, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Regnier, S., Priest, E. R., & Hood, A. W. 2008, A&A, 491, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Shimizu, T. 1995, PASJ, 47, 251 [NASA ADS] [Google Scholar]
  43. Sturrock, S., Kaufmann, P., Moore, P. L., & Smith, D. F. 1984, Sol. Phys., 94, 341 [NASA ADS] [CrossRef] [Google Scholar]
  44. Vilmer, N. 1987, Sol. Phys., 111, 207 [NASA ADS] [CrossRef] [Google Scholar]
  45. Vlahos, L., & Georgoulis, M. K. 2004, ApJ, 603, 61 [Google Scholar]
  46. Vlahos, L., Georgoulis, M. K., Kluiving, R., & Paschos, P. 1995, A&A, 299, 897 [NASA ADS] [Google Scholar]
  47. Vlahos, L., Isliker, H., & Lepreti, F. K. 2004, ApJ, 608, 540 [NASA ADS] [CrossRef] [Google Scholar]
  48. Wiegelmann, T. 2004, Sol. Phys., 219, 87 [NASA ADS] [CrossRef] [Google Scholar]
  49. Wiegelmann, T. 2008, J. Geophys. Res., 113, 3S02 [Google Scholar]
  50. Wiegelmann, T., Inhester, B., & Sakurai, T. 2006, Sol. Phys., 233, 215 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: S-IFM model

Appendix A.1: EXTRA: a nonlinear force-free extrapolation module

The first step is to extrapolate the photospheric magnetic fields. As explained in Dimitropoulou et al. (2009), a physically meaningful treatment is the nonlinear force-free (NLFF) field extrapolation. Our method of choice is based on the optimization technique introduced by Wheatland et al. (2000) and further developed by T. Wiegelmann and collaborators (Wiegelmann 2004, 2008; Wiegelmann et al. 2006). This technique reconstructs force-free magnetic fields from their boundary values by minimizing the Lorentz force and the divergence of the magnetic field vector in the extrapolation volume: (A.1)In this functional, w(x,   y,   z) is a weighting function and V denotes the extrapolation volume. A force-free state is reached when L → 0 for w > 0. For w(x,   y,   z) = 1, the magnetic field must be available on all six boundaries of our cubic box for the optimization algorithm to work. However, photospheric vector magnetograms pertain only to the bottom boundary, whereas the magnetic field vector on the top and lateral boundaries is unknown. The weighting function is therefore used to minimize the dependence of the interior solution from the unknown boundaries. In this study we introduced a buffer zone of ten grid points expanding to the lateral and top boundaries of the computational box. We then chose w(x,   y,   z) = 1 in the inner domain and let w drop to zero with a cosine-profile in the buffer zone toward the lateral and top boundaries of the computational box. This technique was first described by Wiegelmann (2004).

An additional useful attribute of Wiegelmann’s NLFF field extrapolation code is the preprocessing option it offers. As the photospheric magnetic field is in principle inconsistent with the force-free approximation, a preprocessing procedure was developed by Wiegelmann et al. (2006) to drive photospheric fields closer to an NLFF field equilibrium. Preprocessing minimizes the forces and torques in the system, thus satisfying the force-free requirements more closely.

Although NLFF extrapolation methods have been greatly improved in recent years, such models still include numerous uncertainties (DeRosa et al. 2009). Additional constraints stem from the measurements (signal-to-noise ratio, inadequate resolution of the 180° ambiguity) or from physical origins (the non-force-free nature of the photospheric vector magnetograms), which are not adequately handled in the course of the extrapolation. These uncertainties are unavoidably conveyed to our simulations.

Appendix A.2: DISC: a module for identifying magnetic-field instabilities

The DISCO module used in the D-IFM is identical to the one introduced in the S-IFM (refer to Dimitropoulou et al. 2011, Sect. 3.2). For reasons of completeness, we herein present only its basic principles. We assume that instabilities occur if the magnetic field stress exceeds a critical threshold. For every site r within our grid, we calculate the magnetic field stress Gav(r) as 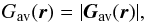where 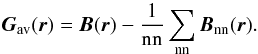In the above definitions nn is the number of nearest neighbors for each site r and Bnn(r) is the magnetic field vector of these neighbors. Depending on the location of each site within the volume, the number of nearest neighbors nn can be nn = 3,4,5,6. The physical reason for selecting this criterion is that strong magnetic stresses favor magnetic reconnection in three dimensions, even in the absence of null points (Priest et al. 2003).

Following Isliker et al. (1998), Dimitropoulou et al. (2011) showed mathematically that the selection of Gav as the critical quantity relates to the diffusive term of the induction equation: 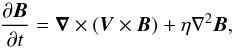(A.2)where V is the plasma velocity and η the resistivity.

In the physical picture, we assume an almost zero resistivity value everywhere within the corona, except in the regions where the discontinuities (and the local currents) reach a critical value. In these regions current-driven instabilities will enhance the resistivity by many orders of magnitude, and the second term in equation (A.2) will become dominant.

Although there are several ways to determine the threshold value for the critical quantity (Dimitropoulou et al. 2011), we choose Gcr = 10  G by applying the histogram method: we construct the histogram of the Gav values in our grid. We then fit a Gaussian to this histogram and define the threshold Gcr as the field stress value, above which the histogram deviates from the Gaussian.

Every site r = (i,   j,   k) for which the inequality Gavi,   j,   k ≥ Gcr is satisfied is considered unstable and undergoes magnetic field restructuring under the rules implemented in the RELAX module.

Appendix A.3: RELAX: a redistribution module for magnetic energy

The redistribution module in the D-IFM remains the same as in Dimitropoulou et al. (2011). If the instability criterion Gavi,   j,   k ≥ Gcr is met at a specific site i,   j,   k, the vicinity of the unstable location undergoes a field restructuring, which follows the rules of Lu & Hamilton (1991): 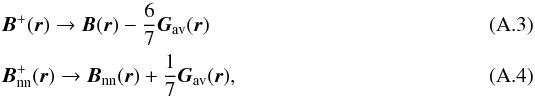where the superscript + denotes the field components after the redistribution. Isliker et al. (1998) showed that the redistribution rules (A.3) and (A.4) implement local diffusion and after redistribution, 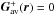, so the instability at location r has been relaxed.

It is worth mentioning at this point that the above redistribution rules maintain the zero-divergence requirement for the magnetic field, as discussed also in Dimitropoulou et al. (2011).

Appendix A.4: LOAD: the driver of the static model

The module LOAD is only used in the S-IFM. In the D-IFM it is replaced by the module INTER (Sect. 3.1). With the module LOAD, after the system is completely relaxed, we introduce a driving mechanism in the static model that adds a magnetic field increment δB(r) at one randomly selected site r within the grid. The driving process complies with the following conditions:

  • 1.

    B(r)·δB(r) = 0.(A.5) This condition implies that the magnetic field increment is always perpendicular to the existing magnetic field B(r) at the randomly selected site r. Figure A.1 provides a sketch of the suggested situation, depicting the directions of the plasma velocity V, the magnetic field B, and the perpendicular magnetic field increment δB. We note that the condition described by Eq. (A.5) is compatible with two physical scenarios: (a) that Alfven waves may have been excited locally, or (b) that, according to the convective term ∇ × (V × B) of the induction Eq. (A.2), a magnetized plasma upflow occurs in the AR, out from the photosphere.

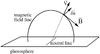
    thumbnail Fig. A.1

    Typical configuration of a magnetic loop anchored in the photosphere. The magnetic field vector B is perpendicular to an assumed plasma outflow velocity V. The model driver requires that the magnetic field increments δB are always perpendicular to the existing magnetic field B.

  • 2.

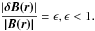    (A.6) This is a typical condition known to allow the system to reach the SOC state, without this state being influenced by the loading process (Bak et al. 1987). As also shown by Lu & Hamilton (1991), decreasing the driving rate by making the magnetic field increments even smaller increases the average time between subsequent events. For the results presented here we have used a fixed ϵ = 0.3.

  • 3.

    ∇·(B(r) + δB(r)) = 0(A.7) This condition should guarantee that the divergence of the magnetic field is approximately kept to zero during the loading process, as is also the case in the redistribution of the magnetic field (RELAX module). To implement the condition, a first-order, left finite-difference scheme is used. Condition (A.7) does not provide a guarantee for a divergence-free magnetic field in the selected site’s vicinity, but rather a low-order approximation toward a divergence-free magnetic field. As discussed in Sect. 3.1, the WNDB variable is introduced to monitor the departure from zero magnetic field divergence both in the static and dynamic models.

All Tables

Table 1

NOAA AR 8210 magnetogram sequence, UT time of IVM acquisition, and respective D-IFM time in seconds of each snapshot.

In the text
Table 2

Characteristics of three major flares produced by NOAA AR 8210 on 01/05/1998 (from 18:58 until 23:16 UT) as recorded by GOES.

In the text
Table 3

Interpolation map of the D-IFM.

In the text

All Figures

thumbnail Fig. 1

Upper row: the vertical magnetic field components of the sequence of NOAA AR 8210 magnetograms in 32 × 32 grid resolution. Lower row: the same sequence after the S-IFM has been applied for 4 × 105 iterations. The i-values correspond to the indices of Table 1.
In the text
thumbnail Fig. 2

Graphic overview of the D-IFM. A total number of 16   236 SOC:i, j (i = 1,2,...,7, j = 0,1,2,...,jmax, jmax = 16   235) sequence groups are created by advancing the previous group through the S-IFM for 50 additional avalanches (vertical direction). Each group is then provided as input to the D-IFM (horizontal direction). Event duration, flare peak, and total energies are accumulated in the database from all D-IFM runs.
In the text
thumbnail Fig. 3

Distributions of the event duration a), the peak energy Epeakb), and the total energy Etotalc) determined from the accumulated event data of the 16 236 D-IFM simulations. The main graph is plotted with linearly equispaced bins, while the inset graphs are plotted in equally spaced logarithmic bins.
In the text
thumbnail Fig. 4

Evolution of WNDB during the 4 × 105 iterations of the S-IFM application to the i = 6 IVM magnetogram for the preparation of the SOC:6,0 snapshot.
In the text
thumbnail Fig. 5

Evolution of WNDB during the jmax = 16   250 D-IFM simulation.
In the text
thumbnail Fig. 6

Magnetic increment δB(r) distribution function during the D-IFM simulation for j = 5. The graph is plotted with linearly equispaced bins. a) depicts the double power law fitting to the distribution. b) depicts fitting by a power law with an exponential rollover.
In the text
thumbnail Fig. 7

3D representation of the emerging magnetic discontinuities during an avalanche generated in the course of the D-IFM simulation for j = 1800. The total duration of this event is 112 steps. During the early stages, the avalanche generates 12 discontinuities a), evolves with 74 discontinuities b), peaks with 104 discontinuities c), and decays with 86 discontinuities d), 41 discontinuities e), and 11 discontinuities f).
In the text
thumbnail Fig. A.1

Typical configuration of a magnetic loop anchored in the photosphere. The magnetic field vector B is perpendicular to an assumed plasma outflow velocity V. The model driver requires that the magnetic field increments δB are always perpendicular to the existing magnetic field B.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.