| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A133 | |
| Number of page(s) | 5 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201321257 | |
| Published online | 16 April 2013 | |
Sparsity and the Bayesian perspective
1 Laboratoire AIM, UMR CEA-CNRS-Paris 7, Irfu, Service d’Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette Cedex, France
e-mail: jstarck@cea.fr
2 Department of Statistics, Stanford University, Stanford CA, 94305, USA
3 GREYC CNRS-ENSICAEN-Université de Caen, 6 Bd du Maréchal Juin, 14050 Caen Cedex, France
4 Laboratoire d’Astrophysique, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
Received: 7 February 2013
Accepted: 15 February 2013
Sparsity has recently been introduced in cosmology for weak-lensing and cosmic microwave background (CMB) data analysis for different applications such as denoising, component separation, or inpainting (i.e., filling the missing data or the mask). Although it gives very nice numerical results, CMB sparse inpainting has been severely criticized by top researchers in cosmology using arguments derived from a Bayesian perspective. In an attempt to understand their point of view, we realize that interpreting a regularization penalty term as a prior in a Bayesian framework can lead to erroneous conclusions. This paper is by no means against the Bayesian approach, which has proven to be very useful for many applications, but warns against a Bayesian-only interpretation in data analysis, which can be misleading in some cases.
Key words: methods: statistical / cosmic background radiation / methods: data analysis
© ESO, 2013
1. Introduction
Bayesian methodology is extremely popular in cosmology. It proposes a very elegant framework for dealing with uncertainties and for using our knowledge under the form of priors in order to solve a given inverse problem (Hobson et al. 2010; Mielczarek et al. 2009). The huge success of Bayesian methods in cosmology is well illustrated in Trotta (2008) with a figure on the number of papers with the word “Bayesian” in the title as a function of the publication year. Bayesian techniques have been used for many applications such as model selection (Kilbinger et al. 2010; Trotta 2012), primordial power spectrum analysis (Kawasaki & Sekiguchi 2010), galactic surveys design (Watkinson et al. 2012), or cosmological parameters estimations (March et al. 2011). Bayesian methods are now commonly used at almost every step in the cosmic microwave background (CMB) pipeline experiments, for point source removal (Argüeso et al. 2011; Carvalho et al. 2012), noise level estimation (Wehus et al. 2012), component separation (Dickinson et al. 2009), cosmological parameter estimation (Efstathiou et al. 2010), non-Gaussianity studies (Elsner & Wandelt 2010; Feeney et al. 2012), or inpainting (Bucher & Louis 2012; Kim et al. 2012).
Sparsity has recently been proposed for CMB data analysis for component separation (Bobin et al. 2013) and inpainting (Abrial et al. 2007; Abrial et al. 2008; Starck et al. 2013). The sparsity-based inpainting approach has been successfully used for two different CMB studies, the CMB weak-lensing on Planck simulated data (Perotto et al. 2010; Plaszczynski et al. 2012), and the analysis of the integrated Sachs-Wolfe effect (ISW) on WMAP data (Dupé et al. 2011; Rassat et al. 2012). In both cases, the authors showed using Monte-Carlo simulations that the statistics derived from the inpainted maps can be trusted at a high confidence level, and that sparsity-based inpainting can indeed provide an easy and effective solution to the problem of large Galactic mask. However, even if these simulations have shown that sparsity-based inpainting does not destroy CMB weak-lensing, ISW signals, or large-scale anomalies in the CMB, the CMB community is very reluctant to use this concept.
This has lead to very animated discussions in conferences. During these discussions it has come up that cosmologists often resort to a Bayesian interpretation of sparsity. Hence, they summarize the sparse regularization to the maximum a posteriori (MAP) estimator assuming the solution follows a Laplacian distribution. From this perspective, several strong arguments against the use of sparsity for CMB analysis were raised:
-
1.
Sparsity consists in assuming an anisotropic and anon-Gaussian prior, which is unsuitable for the CMB, which isGaussian and isotropic.
-
2.
Sparsity violates rotational invariance.
-
3.
The ℓ1 norm that is used for sparse inpainting arose purely out of expediency because under certain circumstances it reproduces the results of the ℓ0 pseudo-norm (which arises naturally in the context of strict, as opposed to weak, sparsity) without requiring combinatorial optimization.
-
4.
There is no mathematical proof that sparse regularization preserves/recovers the original statistics.
The above arguments result from a Bayesian point of view of the sparsity concept. In this paper we explain in detail why the above arguments are not rigorously valid and why sparsity is not in contradiction with a Bayesian interpretation.
2. Sparse regularization of inverse problems
2.1. Inverse problem regularization
Many data processing problems can be formalized as a linear inverse problem, 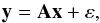 (1)where y ∈ Fm is a vector of noisy measurements (real with F=R, or complex F=C), ε is an m-dimensional vector of additive noise, x is the perfect n-dimensional unobserved vector of interest, and A:Fn → Fm is a linear operator. For example, the inpainting problem corresponds to the case where we want to recover some missing data, in which case A is a binary matrix with fewer rows than columns (m < n), and contains only one value equal to 1 per row, with all other values equal to 0.
(1)where y ∈ Fm is a vector of noisy measurements (real with F=R, or complex F=C), ε is an m-dimensional vector of additive noise, x is the perfect n-dimensional unobserved vector of interest, and A:Fn → Fm is a linear operator. For example, the inpainting problem corresponds to the case where we want to recover some missing data, in which case A is a binary matrix with fewer rows than columns (m < n), and contains only one value equal to 1 per row, with all other values equal to 0.
Finding x when the values of y and A are known is a linear inverse problem. When it does not have a unique and stable solution, it is ill-posed and a regularization is necessary to reduce the space of candidate solutions.
A very popular regularization in astronomy is the well-known Bayesian maximum entropy method (MEM), which is based on the principle that we want to select the simplest solution which fits the data. Sparsity has recently emerged as very powerful approach for regularization (Starck et al. 2010).
2.2. Strict and weak sparsity
A signal x considered as a vector in Fn is said to be sparse if most of its entries are equal to zero. If k numbers of the n samples are equal to zero, where k < n, then the signal is said to be k-sparse. Generally, signals are not sparse in direct space, but can be sparsified by transforming them to another domain. Think for instance of a purely sinusoidal signal which is 1-sparse in the Fourier domain, while it is clearly dense in the original one. In the so-called sparsity synthesis model, a signal can be represented as the linear expansion 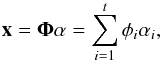 (2)where α are the synthesis coefficients of x, Φ = (φ1,...,φt) is the dictionary whose columns are t elementary waveforms φi also called atoms. In the language of linear algebra, the dictionary Φ is a b × t matrix whose columns are the normalized atoms, supposed here to be normalized to a unit ℓ2-norm, i.e.,
(2)where α are the synthesis coefficients of x, Φ = (φ1,...,φt) is the dictionary whose columns are t elementary waveforms φi also called atoms. In the language of linear algebra, the dictionary Φ is a b × t matrix whose columns are the normalized atoms, supposed here to be normalized to a unit ℓ2-norm, i.e., ![\hbox{$\forall i\in[1,t],\left\Vert \phi_{i}\right\Vert _2^2=\sum_{n=1}^{n}\left|\phi_{i}[n]\right|^{2}=1$}](/articles/aa/full_html/2013/04/aa21257-13/aa21257-13-eq29.png) .
.
A signal can be decomposed in many dictionaries, but the best one is the one with the sparsest (most economical) representation of the signal. In practice, it is convenient to use dictionaries with fast implicit transforms (such as the Fourier transform, wavelet transforms, etc.) which allow us to directly obtain the coefficients and reconstruct the signal from these coefficients using fast algorithms running in linear or almost linear time (unlike matrix-vector multiplications). The Fourier, wavelet, and discrete cosine transforms are among the most popular dictionaries.
Most natural signals however are not exactly sparse but rather concentrated near a small set. Such signals are termed compressible or weakly sparse in the sense that the sorted magnitudes |α(i)|, i.e., |α(1)| > |α(2)|,..., > |α(t)|, of the sequence of coefficients α decay quickly according to a power law, i.e., 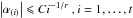 , where C is a constant. The larger r is, the faster the amplitudes of coefficients decay, and the more compressible the signal is. In turn, the non-linear ℓ2 approximation error of α (and x) from its M largest entries in magnitude also decrease quickly. One can think, for instance, of the wavelet coefficients of a smooth signal away from isotropic singularities, or the curvelet coefficients of a piecewise regular image away from smooth contours. A comprehensive account on sparsity of signals and images can be found in Starck et al. (2010).
, where C is a constant. The larger r is, the faster the amplitudes of coefficients decay, and the more compressible the signal is. In turn, the non-linear ℓ2 approximation error of α (and x) from its M largest entries in magnitude also decrease quickly. One can think, for instance, of the wavelet coefficients of a smooth signal away from isotropic singularities, or the curvelet coefficients of a piecewise regular image away from smooth contours. A comprehensive account on sparsity of signals and images can be found in Starck et al. (2010).
2.3. Sparse regularization for inverse problems
In the following, for a vector z we denote 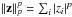 for p ≥ 0. In particular, for p ≥ 1, this is the pth power of the ℓp norm, and for p = 0, we get the ℓ0 pseudo-norm which counts the number of non-zero entries in z. The ℓ0 regularized problem amounts to minimizing
for p ≥ 0. In particular, for p ≥ 1, this is the pth power of the ℓp norm, and for p = 0, we get the ℓ0 pseudo-norm which counts the number of non-zero entries in z. The ℓ0 regularized problem amounts to minimizing 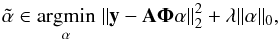 (3)where λ is a regularization parameter. A solution
(3)where λ is a regularization parameter. A solution 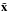 is reconstructed as
is reconstructed as 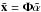 . Clearly, the goal of Eq. (3) is to minimize the number of non-zero coefficients describing the sought after signal while ensuring that the forward model is faithful to the observations.
. Clearly, the goal of Eq. (3) is to minimize the number of non-zero coefficients describing the sought after signal while ensuring that the forward model is faithful to the observations.
 |
Fig. 1 Left: amplitude (absolute value) of the spherical harmonic coefficients versus their index, when the coefficients are sorted from the largest amplitude to the smallest. Right: same plot with the y-axis in log. |
Solving Eq. (3) is however known to be NP-hard. The ℓ1 norm has been proposed as a tight convex relaxation of Eq. (3) leading to the minimization problem 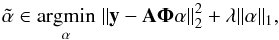 (4)where λ is again a regularization parameter different from that of Eq. (3). There has been a tremendous amount of work where researchers spanning a wide range of disciplines have studied the structural properties of minimizers of Eq. (4) and its equivalence with Eq. (3). Equation (4) is computationally appealing and can be efficiently solved, and it has also been proved that under appropriate circumstances, Eq. (4) produces exactly the same solutions as Eq. (3), see e.g., Donoho (2006b) and the overview in the monograph (Starck et al. 2010).
(4)where λ is again a regularization parameter different from that of Eq. (3). There has been a tremendous amount of work where researchers spanning a wide range of disciplines have studied the structural properties of minimizers of Eq. (4) and its equivalence with Eq. (3). Equation (4) is computationally appealing and can be efficiently solved, and it has also been proved that under appropriate circumstances, Eq. (4) produces exactly the same solutions as Eq. (3), see e.g., Donoho (2006b) and the overview in the monograph (Starck et al. 2010).
3. Sparsity prior and Bayesian prior
3.1. Bayesian framework
In the Bayesian framework, a prior is imposed on the object of interest through a probability distribution. For instance, assume that coefficients α are i.i.d. Laplacian with the scale parameter τ, i.e., the density Pα(α) ∝ e− τ∥α∥1, and the noise ε is zero-mean white Gaussian with variance σ2, i.e., the conditional density 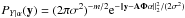 . By traditional Bayesian arguments, the MAP estimator is obtained by maximizing the conditional posterior density Pα | Y(α) ∝ PY | α(y)Pα(α), or equivalently by minimizing its anti-log version
. By traditional Bayesian arguments, the MAP estimator is obtained by maximizing the conditional posterior density Pα | Y(α) ∝ PY | α(y)Pα(α), or equivalently by minimizing its anti-log version 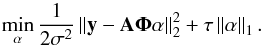 (5)This is exactly Eq. (4) by identifying λ = 2σ2τ. This resemblance has led Bayesian cosmologists to raise the four criticisms mentioned in the introduction. But as we will discuss shortly, their central argument is not used in the right sense, which can yield misleading conclusions.
(5)This is exactly Eq. (4) by identifying λ = 2σ2τ. This resemblance has led Bayesian cosmologists to raise the four criticisms mentioned in the introduction. But as we will discuss shortly, their central argument is not used in the right sense, which can yield misleading conclusions.
3.2. Should ℓ1 regularization be the MAP?
In Bayesian cosmology, the following shortcut is often made: if a prior is at the basis of an algorithm, then to use this algorithm, the resulting coefficients must be distributed according to this prior. But it is a false logical chain in general, and high-dimensional phenomena completely invalidate it.
For instance, Bayesian cosmologists claim that ℓ1 regularization is equivalent to assuming that the solution is Laplacian and not Gaussian, which would be unsuitable for the case of CMB analysis. This argument however assumes that a MAP estimate follows the distribution of the prior. But it is now well-established that MAP solutions substantially deviate from the prior model, and that the disparity between the prior and the effective distribution obtained from the true MAP estimate is a permanent contradiction in Bayesian MAP estimation (Nikolova 2007). Even the supposedly correct ℓ2 prior would yield an estimate (Wiener, which coincides with the MAP and posterior conditional mean) whose covariance is not that of the prior.
In addition, rigorously speaking, this MAP interpretation of ℓ1 regularization is not the only possible interpretation. More precisely, it was shown in Gribonval et al. (2011a) and Baraniuk et al. (2010) that solving a penalized least squares regression problem with penalty ψ(α) (e.g. the ℓ1 norm) should not necessarily be interpreted as assuming a Gibbsian prior Cexp(−ψ(α)) and using the MAP estimator. In particular, for any prior Pα, the conditional mean can also be interpreted as a MAP with some prior Cexp(−ψ(α)). Conversely, for certain penalties ψ(α), the solution of the penalized least squares problem is indeed the conditional posterior mean, with a certain prior Pα(α) which is generally different from Cexp(−ψ(α)).
In summary, the MAP interpretation of such penalized least-squares regression can be misleading, and using a MAP estimation, the solution does not necessarily follow the prior distribution, and an incorrect prior does not necessarily lead to a wrong solution. What we are claiming here are facts that were stated and proved as rigorous theorems in the literature.
3.3. Compressed sensing: the Bayesian interpretation inadequacy
A beautiful example to illustrate this is the compressed sensing scenario (Donoho 2006a; Candès & Tao 2006), which tells us that a k-sparse, or compressible n-dimensional signal x can be recovered either exactly, or to a good approximation, from much less random measurements m than the ambient dimension n, if m is sufficiently larger than the intrinsic dimension of x. Clearly, the underdetermined linear problem, y = Ax, where A is drawn from an appropriate random ensemble, with fewer equations than unknown, can be solved exactly or approximately, if the underlying object x is sparse or compressible. This can be achieved by solving a computationally tractable ℓ1-regularized convex optimization program.
If the underlying signal is exactly sparse, in a Bayesian framework, this would be a completely absurd way to solve the problem, since the Laplacian prior is very different from the actual properties of the original signal (i.e., k coefficients different from zero). In particular, what compressed sensing shows is that we can have prior A be completely true, but utterly impossible to use for computation time or any other reason, and we can use prior B instead and get the correct results. Therefore, from a Bayesian point of view, it is rather difficult to understand not only that the ℓ1 norm is adequate, but also that it leads to the exact solution.
3.4. The prior misunderstanding
Considering the chosen dictionary Φ as the spherical harmonic transform, the coefficients α are now α = {al,m}l = 0,...,lmax,m = −l,...,l. The standard CMB theory assumes that the values of al,m are the realizations of a collection of heteroscedastic complex zero-mean Gaussian random variables with variances Cl/2, where Cl is the true power spectrum. Using a ℓ1 norm is then interpreted in the Bayesian framework as having a Laplacian prior on each al,m which contradicts the underlying CMB theory. However, as argued above, from the regularization point of view, the ℓ1 norm merely promotes a solution x such that its spherical harmonic coefficients are (nearly) sparse. There is no assumption at all on the properties related to a specific al,m. In fact, there is no randomness here and the al,m values do not even have to be interpreted as a realization of a random variable. Therefore, whatever the underlying distribution for a given al,m (if its exists), it need not be interpreted as Laplacian under the ℓ1 regularization. The CMB can be Gaussian or not, isotropic or not, and there will be no contradiction with the principle of using the ℓ1 norm to solve the reconstruction problem (e.g., inpainting). What is important is that the sorted absolute values of the CMB spherical harmonics coefficients presents a fast decay. This is easily verified using a CMB map, data, or simulation. This is well illustrated by Fig. 1 which shows this decay for the nine-year WMAP data set. As we can see, the compressibility assumption is completely valid.
4. Discussion of the Bayesian criticisms
-
Sparsity consists in assuming an anisotropy and a non-Gaussianprior, which is unsuitable for the CMB, which is Gaussian andisotropic. We have explained in the previous section that thisMAP interpretation of ℓ1 regularization is misleading, and also that there is no assumption at all on the underlying stochastic process. The CMB sparsity-based recovery is a purely data-driven regularization approach; the sorted absolute values of the spherical harmonic coefficients presents a fast decay, as seen on real data or simulations, and this motivates the sparse regularizations.
There is no assumption that the CMB is Gaussian or isotropic, but there is also no assumption that it is non-Gaussian or anisotropic. In this sense, using the ℓ1-regularized inpainting to test if the CMB is indeed Gaussian and isotropic may be better than other methods, including Wiener filtering, which in the Bayesian framework assumes Gaussianity and isotropy. Furthermore, the Wiener estimator will also require knowing the underlying power spectrum (i.e., the theoretical Cl) which is an even stronger prior.
-
Sparsity violates rotational invariance. The criticicism here is that linear combinations of independent exponentials are not independent exponentials; therefore, isotropy is necessarily violated, unless the alm are Gaussian. But again, our arguments for ℓ1 regularization are borrowed from approximation theory and harmonic analysis, and this does not contradict the idea that the alm coefficients can be realizations of a sequence of heteroscedastic Gaussian variables. The ℓ1 norm regularization will be adequate if the sorted coefficients amplitudes follow a fast decay, which is always verified with CMB data. Indeed, as we already mentioned, a set of parameters xi, where each xi is a realization of a Gaussian process of mean 0 and variance Vi, can present a fast decay when we plot the sorted absolute values of xi. In the case of CMB spherical harmonic coefficients verifying this is straightforward.
-
Theℓ1 norm that is used for sparse inpainting arose purely out of expediency because under certain circumstances it reproduces the results of the ℓ0 pseudo-norm. First, we would like to correct a possible misunderstanding: ℓ1 regularization can provably recover both strictly and weakly sparse signals, while being stable to noise. In the strictly sparse case, ℓ1 norm minimization can recover the right solution although the prior is not correct from a Bayesian point of view. In the compressible case, the recovery is up to a good approximation, as good as an oracle that would give the best M-term approximation of the unknown signal (i.e., ℓ0-solution). What is criticized as an “expedient” prior is basically at the heart of regularization theory, for instance here ℓ1 provides strong theoretical recovery guarantees under appropriate conditions. A closer look at the literature of inverse problems shows that these guarantees are possible beyond the compressed sensing scenario.
-
There is no mathematical proof that sparse regularization preserves/recovers the original statistics. This is true, but this argument is not specific to ℓ1 regularized inpainting. Even worse, as detailed and argued in the previous section, the posterior distribution generally deviates from the prior, and even if one uses the MAP with the correct Gaussian prior, the MAP estimate (Wiener) will not have the covariance of the prior.
Another point to mention is that the CMB is never a pure Gaussian random field, even if the standard ΛCDM cosmological model is truly valid. We know that the CMB is at least contaminated by non-Gaussian secondary anisotropies such as weak-lensing or kinetic Sunyaev-Zel’dovich (SZ) effects. Therefore the original CMB statistics are likely to be better preserved by an inpainting method that does not assume Gaussianity (but nonetheless allows it), rather than by a method which has an explicit Gaussian assumption. Moreover, if the CMB is not Gaussian, then one can clearly anticipate that the Wiener estimate does not preserve the original statistics.
Finally, it appears unfair to criticize sparsity-regularised inverse problems on the mathematical side. A quick look at the literature shows the vitality of the mathematics community, both pure and applied, and the large amount of theoretical guarantees (deterministic and frequentist statistical settings) that have been devoted to ℓ1 regularization. In particular, theoretical guarantees of ℓ1-based inpainting can be found in King et al. (2013) on the Cartesian grid, and of sparse recovery on the sphere in Rauhut & Ward (2012).
5. Conclusions
We have shown that Bayesian cosmologists’ criticisms about sparse inpainting are based on a false logical chain, which consists in assuming that if a prior is at the basis of an algorithm, then to use this algorithm, the resulting coefficients must be distributed according to this prior. Compressed sensing theory is a nice counter-example, where it is mathematically proved that other prior, than the true one can lead, under some conditions, to the correct solution. Therefore, we cannot understand how a regularization penalty has an impact on a solution of an inverse problem just by expressing the prior which derives this penalty. To understand this we also need to take into account the operator involved in the inverse problem, and this requires much deeper mathematical developments than a simple Bayesian interpretation. Compressed sensing theory shows that for some operators, beautiful geometrical phenomena allow us to recover perfectly the solution of an underdetermined inverse problem. Similar results were derived for a random sampling on the sphere (Rauhut & Ward 2012).
We do not claim in this paper that sparse inpainting is the best solution for inpainting, but we have showed that the arguments raised against it are incorrect, and that if Bayesian methodology offers a very elegant framework that is extremely useful for many applications, we should be careful not to be monolithic in the way we address a problem. In practice, it may be useful to use several inpainting methods to better understand the CMB statistics, and it is clear that sparsity based inpainting does not require making any assumptions about the Gaussianity nor about the isotropy, nor does it need to have a theoretical Cℓ as an input.
Acknowledgments
The authors thank Benjamin Wandelt, Mike Hobson, Jason McEwen, Domenico Marinucci, Hiranya Peiris, Roberto Trotta, and Tom Loredo for the useful and animated discussions. This work was supported by the French National Agency for Research (ANR -08-EMER-009-01), the European Research Council grant SparseAstro (ERC-228261), and the Swiss National Science Foundation (SNSF).
References
- Abrial, P., Moudden, Y., Starck, J., et al. 2007, J. Fourier Anal. Appl., 13, 729 [Google Scholar]
- Abrial, P., Moudden, Y., Starck, J., et al. 2008, Statist. Methodol., 5, 289 [Google Scholar]
- Argüeso, F., Salerno, E., Herranz, D., et al. 2011, MNRAS, 414, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Baraniuk, R., Cevher, V., & Wakin, M. 2010, Proc. IEEE, 98, 959 [CrossRef] [Google Scholar]
- Bobin, J., Starck, J.-L., Sureau, F., & Basak, S. 2013, A&A, 550, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bucher, M., & Louis, T. 2012, MNRAS, 424, 1694 [NASA ADS] [CrossRef] [Google Scholar]
- Candès, E., & Tao, T. 2006, IEEE Trans. Info. Theory, 52, 5406 [CrossRef] [Google Scholar]
- Carvalho, P., Rocha, G., Hobson, M. P., & Lasenby, A. 2012, MNRAS, 427, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Dickinson, C., Eriksen, H. K., Banday, A. J., et al. 2009, ApJ, 705, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Donoho, D. 2006a, IEEE Trans. Info. Theory, 52, 1289 [CrossRef] [Google Scholar]
- Donoho, D. 2006b, Comm. Pure Appl. Math., 59, 907 [CrossRef] [MathSciNet] [Google Scholar]
- Dupé, F.-X., Rassat, A., Starck, J.-L., & Fadili, M. J. 2011, A&A, 534, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efstathiou, G., Ma, Y.-Z., & Hanson, D. 2010, MNRAS, 407, 2530 [NASA ADS] [CrossRef] [Google Scholar]
- Elsner, F., & Wandelt, B. D. 2010, ApJ, 724, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Feeney, S. M., Johnson, M. C., McEwen, J. D., Mortlock, D. J., & Peiris, H. V. 2012 [arXiv:1210.2725] [Google Scholar]
- Gribonval, R., Cevher, V., & Davies, M. E. 2011 [arXiv:1102.1249] [Google Scholar]
- Hobson, M. P., Jaffe, A. H., Liddle, A. R., Mukeherjee, P., & Parkinson, D. 2010, Bayesian Methods in Cosmology [Google Scholar]
- Kawasaki, M., & Sekiguchi, T. 2010, J. Cosmol. Astropart. Phys., 2010, 013 [Google Scholar]
- Kilbinger, M., Wraith, D., Robert, C., et al. 2010, MNRAS, 405, 2381 [NASA ADS] [Google Scholar]
- Kim, J., Naselsky, P., & Mandolesi, N. 2012, ApJ, 750, L9 [NASA ADS] [CrossRef] [Google Scholar]
- King, E. J., Kutyniok, G., & Zhuang, X. 2013, J. Math. Imaging Vision, submitted [Google Scholar]
- March, M. C., Trotta, R., Berkes, P., Starkman, G. D., & Vaudrevange, P. M. 2011, MNRAS, 418, 2308 [NASA ADS] [CrossRef] [Google Scholar]
- Mielczarek, J., Szydlowski, M., & Tambor, P. 2009 [arXiv:0901.4075] [Google Scholar]
- Nikolova, M. 2007, Inverse Problems and Imaging, 1, 399 [CrossRef] [Google Scholar]
- Perotto, L., Bobin, J., Plaszczynski, S., Starck, J., & Lavabre, A. 2010, A&A, 519, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plaszczynski, S., Lavabre, A., Perotto, L., & Starck, J.-L. 2012, A&A, 544, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rassat, A., Starck, J.-L., & Dupe, F. X. 2012, A&A, submitted [Google Scholar]
- Rauhut, H., & Ward, R. 2012, J. Approx. Theory, 164 [Google Scholar]
- Starck, J.-L., Murtagh, F., & Fadili, M. 2010, Sparse Image and Signal Processing (Cambridge University Press) [Google Scholar]
- Starck, J.-L., Fadili, M. J., & Rassat, A. 2013, A&A, 550, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Trotta, R. 2008, Contemp. Phys., 49, 71 [Google Scholar]
- Trotta, R. 2012, in Astrostatistics and Data Mining, eds. L. M. Sarro, L. Eyer, W. O’Mullane, & J. De Ridder (New York: Springer), Springer Series in Astrostatistics, 2, 3 [Google Scholar]
- Watkinson, C., Liddle, A. R., Mukherjee, P., & Parkinson, D. 2012, MNRAS, 424, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Wehus, I. K., Næss, S. K., & Eriksen, H. K. 2012, ApJS, 199, 15 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Left: amplitude (absolute value) of the spherical harmonic coefficients versus their index, when the coefficients are sorted from the largest amplitude to the smallest. Right: same plot with the y-axis in log. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


