A Fourier domain model for estimating astrometry errors due to static and quasi-static optical surface errors

B. Ellerbroek

doi:10.1051/0004-6361/201321092

Home

All issues

Volume 552 (April 2013)

A&A, 552 (2013) A41

Full HTML

Free Access

Issue		A&A Volume 552, April 2013


Article Number		A41
Number of page(s)		7
Section		Astronomical instrumentation
DOI		https://doi.org/10.1051/0004-6361/201321092
Published online		20 March 2013

A&A 552, A41 (2013)

A Fourier domain model for estimating astrometry errors due to static and quasi-static optical surface errors

B. Ellerbroek

TMT Observatory CorporationInstrumentation Department, 1111 S. Arroyo Pkwy. Ste. 200, Pasadena, CA, 91107 USA
e-mail: brente@caltech.edu

Received: 12 January 2013
Accepted: 25 February 2013

Abstract

Context. The wavefront aberrations due to optical surface errors in adaptive optics systems and science instruments can be a significant error source for high precision astrometry.

Aims. This report derives formulas for evaluating these errors which may be useful in developing astrometry error budgets and optical surface quality specifications.

Methods. A Fourier domain approach is used, and the errors on each optical surface are modeled as “phase screens” with stationary statistics at one or several conjugate ranges from the optical system pupil. Three classes of error are considered: (i) errors in initially calibrating the effects of static surface errors; (ii) the effects of beam translation, or “wander,” across optical surfaces due to (for example) instrument boresighting error; and (iii) quasistatic surface errors which change from one observation to the next.

Results. For each of these effects, we develop formulas describing the position estimation errors in a single observation of a science field, as well as the differential error between two separate observations. Sample numerical results are presented for the three classes of error, including some sample computations for the Thirty Meter Telescope and the NFIRAOS first-light adaptive optics system.

Key words: astrometry / instrumentation: high angular resolution / instrumentation: adaptive optics

© ESO, 2013

1. Introduction

High precision astrometry is becoming an increasingly important capability for large, and future extremely large, optical and near-infra-red astronomical telescopes (Yelda et al. 2010; Fritz et al. 2010; Trippe et al. 2010). Astrometric accuracies of 40 to 100 micro arc seconds (μas) have now been reported for observations both without and with adaptive optics (Lazorenko et al. 2009; Cameron et al. 2009), and requirements for future systems are specified in the 10 to 50 μas range (TMT Science Requirements Document, at http://www.tmt.org/documents). Much as for high contrast imaging, performance at this level will require the careful evaluation of the full range of possible error sources, some of which have been considered negligible up to now. One sample astrometry error budget includes at least 35 different terms, grouped into the five categories of: reference star catalog errors, atmospheric refraction effects, atmospherc turbulence effects, focal plane measurement errors, and opto-mechanical errors (Schoeck 2011). This final category places challenging requirements on the design, fabrication, and alignment of science instruments (and adaptive optical systems) in order to control this systematic error source.

The purpose of this paper is to describe a set of engineering formulas for estimating the astrometry errors due to surface errors in opto-mechanical systems. These formulas can be used to develop quantitative error budgets and the corresponding optical surface specifications. A Fourier domain approach is used, and the phase errors on each optical surface are modeled as “phase screens” with shift-invariant statistics at one or several conjugate ranges from the optical system pupil. The image distortion errors inherit this property of stationarity, and some steps of the work consequently resemble previous analysis of tilt anisoplanatism in adaptive optical (AO) systems (Roddier et al. 1993). The errors are evaluated as weighted integrals of the power spectral densities (PSDs) of the errors on each optical surface, where the values of the weighting functions depend upon parameters including the telescope aperture diameter, science field-of-view (FoV) diameter, conjugate range to the optical surface, and the category of optical surface effect evaluated.

Section 2 formulates a model for the three different types of optical surface effects considered in the analysis. These are:

the static calibration undersampling error from using only a finite number of reference sources to sample the image distortion pattern in the focal plane;
the error due to random or systematic beam wander translation across the static errors on each surface, which could occur due to an instrument boresighting error or image derotation; and
quasi-static errors due to time-varying optical surface errors, for example a calibration error on a deformable mirror in a multi-conjugate AO (MCAO) system.

We develop a notation to keep track of these various errors, both for a single observation of a science field and the differential error between two successive observations. We formulate a model for on-sky calibration of the errors (using known reference stars in the image) in terms of removing the low-order modes of the image distortion pattern, such as global tip/tilt and plate scale.

The analytical methods used to evaluate these errors are developed in Sects. 3 through 5. Section 3 describes our standard geometrical optics model for the image distortion due to a set of optical surface errors. Section 4 transforms this model into the spatial frequency domain, and Sect. 5 then focuses the analysis on the special case of a circular, unobscured aperture and a circular FoV.

Section 6 next details the explicit formulas for each of the three different optical surface effects introduced in Sect. 2 and presents sample numerical results. These include: (i) a multiplicative “transfer function” relating the PSD of quasi-static errors on an optical surface to the resulting position estimation errors, and (ii) the errors due to beam wander or calibration undersampling of static optical surface errors with a power law PSD. Finally, Sect. 7 is a brief summary of the key results.

2. Astrometry error models and metrics

The two-dimensional image distortion map at the focal plane of an instrument will be denoted Θ(ϕ,p), where ϕ is a two-dimensional line-of-sight (LOS) through the instrument optics, and p is a set of error profiles for each optical surface of the instrument. The error profiles are sums of static and quasi-static components, s and q. The line-of-sight ϕ is a sum of o, the intended LOS for the origin of the science field, δ, the unintended shift in the LOS due to (for example) boresighting error, and α, the relative location of a particular object in the science field.

The estimate of the image distortion map will be denoted Θ_c(ϕ,p). This calibration estimate is based upon the measured image of an array of reference sources; it includes the effect of static error profiles s and can be translated to account for the known value of o, but it is ignorant of the error sources q and δ. The resulting two-dimensional position estimation error in a single image of the science field takes the form 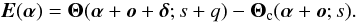$E (α) = Θ (α + o + δ; s + q) - Θ_{c} (α + o; s) .$ $\begin{equation} \vec{E}(\bm{\alpha}) = \bm{\Theta}(\bm{\alpha}+\vec{o}+\bm{\delta}; s+q)-\bm{\Theta}_{\rm c}(\bm{\alpha}+\vec{o};s). \label{eq1} \end{equation}$ (1)Similarly, the differential error between two separate images is given by $\begin{matrix} Δ E (α) & = & [Θ (α + o' + δ'; s + q') - Θ_{c} (α + o'; s)] \\ - [Θ (α + o + δ; s + q) - Θ_{c} (α + o; s)], \end{matrix}$ $\begin{eqnarray} \label{eq2} \Delta\vec{E}({\bm\alpha}) & = & \left[{\bm\Theta}({\bm\alpha}+\vec{o}\arcmin +{\bm\delta}\arcmin ; s+q\arcmin )-{\bm\Theta}_{\rm c}({\bm\alpha}+\vec{o}\arcmin ;s)\right] \nonumber \\ & & -\left[{\bm\Theta}({\bm\alpha}+\vec{o} +{\bm\delta} ; s+q )-{\bm\Theta}_{\rm c}({\bm\alpha}+\vec{o} ;s)\right], \end{eqnarray}$ (2)where the quasistatic surface errors and boresighting errors can take two different, uncorrelated values in the two exposures (but the static errors s remain the same).

Since we will be using a geometrical optics model, the distortion map Θ(ϕ,p) is linear in p. The formula for the error E can therefore be decomposed into the sum of 3 terms, namely: $\begin{matrix} E (α) & = & Θ (α + o + δ; q) + [Θ (α + o + δ; s) - Θ (α + o; s)] \\ + [Θ (α + o; s) - Θ_{c} (α + o; s)] \\ = & Q (α) + W (α) + C (α) . \end{matrix}$ $\begin{eqnarray} \label{eq3} \vec{E}({\bm\alpha}) & = & {\bm\Theta}({\bm\alpha}+\vec{o}+{\bm\delta};q) +\left[{\bm\Theta}({\bm\alpha}+\vec{o}+{\bm\delta};s)-{\bm\Theta}({\bm\alpha}+\vec{o};s)\right] \nonumber \\ & & \quad +\left[{\bm\Theta}({\bm\alpha}+\vec{o};s)-{\bm\Theta}_{\rm c}({\bm\alpha}+\vec{o};s)\right] \nonumber \\ & = & \vec{Q}({\bm\alpha}) + \vec{W}({\bm\alpha}) + \vec{C}({\bm\alpha}). \end{eqnarray}$ (3)Here Q is the two-dimensional quasistatic error, W is the two-dimensional error due to wander in the LOS, and C is the two-dimensional calibration error. 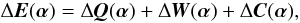Similarly, the differential error ΔE can be written as $Δ E (α) = Δ Q (α) + Δ W (α) + Δ C (α),$ $\begin{equation} \Delta \vec{E}({\bm\alpha}) = \Delta \vec{Q}({\bm\alpha}) + \Delta \vec{W}({\bm\alpha}) + \Delta \vec{C}({\bm\alpha}), \label{eq4} \end{equation}$ (4)where the three individual terms are defined by the formulas $\begin{matrix} Δ Q (α) & = & Θ (α + o' + δ'; q') - Θ (α + o + δ; q), \\ Δ W (α) & = & [Θ (α + o' + δ'; s) - Θ (α + o'; s)] \\ - [Θ (α + o + δ; s) - Θ (α + o; s)], \\ Δ C (α) & = & [Θ (α + o'; s) - Θ_{c} (α + o'; s)] \\ - [Θ (α + o; s) - Θ_{c} (α + o; s)] . \end{matrix}$ $\begin{eqnarray} \label{eq5} \Delta \vec{Q}({\bm\alpha}) & = & {\bm\Theta}({\bm\alpha}+\vec{o}\arcmin+{\bm\delta}\arcmin ;q\arcmin )- {\bm\Theta}({\bm\alpha}+\vec{o} +{\bm\delta} ;q ), \\ \label{eq6} \Delta \vec{W}({\bm\alpha}) & = & \left[{\bm\Theta}({\bm\alpha}+\vec{o}\arcmin +{\bm\delta}\arcmin ;s)- {\bm\Theta}({\bm\alpha}+\vec{o}\arcmin ;s)\right] \nonumber \\ & & \quad-\left[{\bm\Theta}({\bm\alpha}+\vec{o}+{\bm\delta};s)- {\bm\Theta}({\bm\alpha}+\vec{o};s)\right], \\ \label{eq7} \Delta \vec{C}({\bm\alpha}) & = & \left[{\bm\Theta}({\bm\alpha}+\vec{o}\arcmin ;s)- {\bm\Theta}_{\rm c}({\bm\alpha}+\vec{o}\arcmin ;s)\right] \nonumber \\ & & \quad-\left[{\bm\Theta}({\bm\alpha}+\vec{o};s)- {\bm\Theta}_{\rm c}({\bm\alpha}+\vec{o};s)\right]. \end{eqnarray}$ We are interested in developing formulas for the mean-square value of f, where f is any of these six effects of optical surface errors. 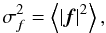We write $σ_{f}^{2} = ⟨ {| f |}^{2} ⟩,$ $\begin{equation} \sigma_f^2=\left\langle\left|\vec{f}\right|^2\right\rangle, \label{eq8} \end{equation}$ (8)where the angle brackets denote ensemble averaging over the statistics of the optical surface errors and the unknown line of sight errors δ. Note that measurement noise is not included in the analysis.

For some observations, it may be possible to estimate and partially correct for the effects of the surface errors using the known locations of astrometric reference stars in the science field. One star can be used to calibrate a global tip/tilt error, three stars can be used to calibrate plate scale and rotation, and so on. We model this image postprocessing in terms of a low-order mode removal operator P, defined by the formula $P f (α) = f (α) - \frac{\sum_{j} [^{\int} d β Ω (β) m \begin{matrix} T \\ j \end{matrix} (β) f (β)^{]} m j (α)}{\int d β Ω (β)} \cdot$ $\begin{equation} P\vec{f}({\bm\alpha})=\vec{f}({\bm\alpha})- \frac{\sum_j\left[\int {\rm d}{\bm\beta}\Omega({\bm\beta})\vec{m}_j^T({\bm\beta})\vec{f}({\bm\beta})\right] \vec{m}_j({\bm\alpha})}{\int {\rm d}{\bm\beta}\,\Omega({\bm\beta})}\cdot \label{eq9} \end{equation}$ (9)Here the { 0,1 } -valued function Ω defines the science FoV, and the functions m_j are the orthogonal low-order distortion modes removed from the image. This is an idealized, best case correction, as it neglects possible errors due to measurement noise, imperfectly known positions of the reference stars, and the aliasing of higher-order distortion modes into an estimate obtained using a finite number of reference stars. If the modes are defined to be orthonormal over the FoV, it follows that the field-averaged, mean-square value of Pf is given by $\begin{matrix} σ_{Pf}^{2} & = & \frac{⟨^{\int} d α Ω (α) {| P f (α) |}^{2} ⟩}{\int d α Ω (α)} \\ = & σ_{f}^{2} - \sum_{j} ⟨ {[\frac{\int d α Ω (α) m \begin{matrix} T \\ j \end{matrix} (α) f (α)}{\int d α Ω (α)}]}^{2} ⟩ . \end{matrix}$ $\begin{eqnarray} \label{eq10} \sigma_{Pf}^2 & = & \frac{\left\langle \int {\rm d}{\bm\alpha}\,\Omega({\bm\alpha}) \left\vert P\vec{f}({\bm\alpha})\right\vert^2\right\rangle}{ \int {\rm d}{\bm\alpha}\,\Omega({\bm\alpha})} \nonumber \\ & = & \sigma_f^2-\sum_j \left\langle\left[\frac{\int {\rm d}{\bm\alpha}\, \Omega({\bm\alpha})\vec{m}_j^T({\bm\alpha})\vec{f}({\bm\alpha})}{ \int {\rm d}{\bm\alpha}\,\Omega({\bm\alpha})}\right]^2\right\rangle. \end{eqnarray}$ (10)Even if the error f is approximated as spatially stationary, the point-wise value of the image distortion variance is no longer spatially invariant (i.e., independent of α) after low order modes have been removed.

3. Image distortion maps due to optical surface errors

We will use first-order, geometric optics to model the focal plane image distortions due to optical surface errors, an accurate approximation for the case of AO-assisted observations with near-diffraction-limited resolution. The image distortion in the direction α due to the set of optical error profiles p is defined to be the rms best-fit tilt to the wavefront aberration in this direction, namely $Θ (α; e) = (\frac{λ}{2 π}) {[\int d r A (r) r r T]}^{-1} [\int d r A (r) r φ (r; α,p)] .$ $\begin{equation} {\bm\Theta}({\bm\alpha};e)=\left(\frac{\lambda}{2\pi}\right) \left[\int {\rm d}\vec{r}\,A(\vec{r})\vec{r}\vec{r}^T\right]^{-1} \left[\int {\rm d}\vec{r}\,A(\vec{r})\vec{r}\phi(\vec{r};{\bm\alpha},p)\right]. \label{eq11} \end{equation}$ (11)Here r denotes coordinates in the pupil plane, A(r) is a { 0,1 } -valued pupil function, and φ(r;α,p) is the wavefront aberration profile in the direction α due to the optical surface errors p. Other models for image motion as a function of the aberration φ are possible, for example the aperture-averaged value of the gradient, but the rms best-fit tilt is a good approximation to the measured motion of the central core of a well-corrected PSF (Ellerbroek 2009).

If we restrict attention to the case of a circular, unobscured pupil function of diameter D, the first integral in Eq. (11) may be evaluated with the result $Θ (α; p) = (\frac{λ}{D}) (\frac{32}{π^{2} D^{3}}) [\int d r A (r) r φ (r; α,p)] .$ $\begin{equation} {\bm\Theta}({\bm\alpha};p)=\left(\frac{\lambda}{D}\right)\left(\frac{32}{\pi^2 D^3}\right) \left[\int {\rm d}\vec{r}\,A(\vec{r})\vec{r}\phi(\vec{r};{\bm\alpha},p)\right]. 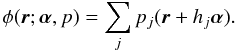\label{eq12} \end{equation}$ (12)Next, the wavefront aberration profile φ will be modeled using first-order optics as a sum of the contributions from each individual optical phase errors p_j at conjugate range h_j: $φ (r; α,p) = \sum_{j} p_{j} (r + h_{j} α) .$ $\begin{equation} \phi(\vec{r};{\bm\alpha},p)=\sum_j p_j(\vec{r}+h_j{\bm\alpha}). \label{eq13} \end{equation}$ (13)Substituting Eq. (13) into Eq. (12), we obtain the result 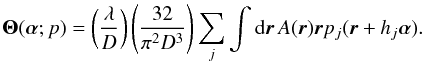$Θ (α; p) = (\frac{λ}{D}) (\frac{32}{π^{2} D^{3}}) \sum_{j} \int d r A (r) r p_{j} (r + h_{j} α) .$ $\begin{equation} {\bm\Theta}({\bm\alpha};p)=\left(\frac{\lambda}{D}\right)\left(\frac{32}{\pi^2 D^3}\right) \sum_j\int {\rm d}\vec{r}\,A(\vec{r})\vec{r}p_j(\vec{r}+h_j{\bm\alpha}). \label{eq14} \end{equation}$ (14)

4. Fourier domain analysis

The mean-square image distortion errors introduced in Sect. 2 can be evaluated most easily in the angular frequency domain if we assume that the optical phase errors p are spatially invariant, i.e., have shift-invariant statistics that can be described in terms of a PSD function. Of course, this assumption introduces approximations at several different levels. Phase errors on actual optical surfaces cannot be fully defined in terms of a spatial PSD because (i) each optical surface is unique, not part of an infinite ensemble of possible surfaces; and (ii) optical surfaces have finite dimension. At the same time, the use of PSD models to specify and characterize optical surface errors has been established for at least several decades (Lawson et al. 1995), and the use of Fourier domain methods to study the performance of finite aperture adaptive optics systems and high contrast imaging systems has met with considerable success (Jolissaint et al. 2006). As with these previous efforts, the intent here is to develop practical formulas for optical surface specifications and error budgeting.

Using Eq. (14) above, the Fourier transform of the image distortion profile Θ is described by the expression $\begin{matrix} ℱ [Θ (α; p)] (κ) & = & \int d α Θ (α; p) \exp (- 2 π i α \cdot κ) \\ = & (\frac{λ}{D}) (\frac{32}{π^{2} D^{3}}) \sum_{j} \int d r h_{j}^{-2} A (r) r \\ \times \exp (2 π i r \cdot κ / h_{j}) ℱ (p_{j}) (κ / h_{j}) \\ = & (\frac{λ}{D}) (\frac{32}{π^{2} D^{3}}) \sum_{j} h_{j}^{-2} ℱ {[A (r) r]}^{*} (κ / h_{j}) \end{matrix}$ $\begin{eqnarray} {\cal F}\left[{\bm\Theta}({\bm\alpha};p)\right]({\bm\kappa}) & = & \int {\rm d}{\bm\alpha}\,{\bm\Theta}({\bm\alpha};p)\exp(-2\pi {\rm i}{\bm\alpha}\cdot{\bm\kappa}) \nonumber \\ & = & \left(\frac{\lambda}{D}\right)\left(\frac{32}{\pi^2 D^3}\right) \sum_j \int {\rm d}\vec{r}\,h_j^{-2} A(\vec{r})\vec{r} \nonumber \\ & & \times\, \exp(2\pi {\rm i} \vec{r}\cdot{\bm\kappa}/h_j) {\cal F}(p_j)({\bm\kappa}/h_j) \nonumber \\ & = & \left(\frac{\lambda}{D}\right)\left(\frac{32}{\pi^2 D^3}\right) \sum_j h_j^{-2}{\cal F}\left[A(\vec{r})\vec{r}\right]^*({\bm\kappa}/h_j) \nonumber \\ & & \times\, {\cal F}(p_j)({\bm\kappa}/h_j), \label{eq15} \end{eqnarray}$ (15)where κ is a two-dimensional angular frequency variable. This result is essentially the Fourier convolution theorem. If the random optical phase errors p_j are shift-invariant, then the PSD of Θ is expressed in terms of their power spectra Φ_{p_j} by the formula $\begin{matrix} Φ_{Θ} (κ) & = & {(\frac{λ}{D})}^{2} {(\frac{32}{π^{2} D^{3}})}^{2} \sum_{j} h_{j}^{-2} Φ_{p_{j}} (κ / h_{j}) \\ \times ℱ [A (r) r] (κ / h_{j}) ℱ {[A (r) r]}^{*} (κ / h_{j}) . \end{matrix}$ $\begin{eqnarray} \label{eq16} \Phi_\Theta({\bm\kappa}) & = & \left(\frac{\lambda}{D}\right)^2\left(\frac{32}{\pi^2 D^3}\right)^2 \sum_j h_j^{-2} \Phi_{p_j}({\bm\kappa}/h_j) \nonumber \\ & & \times\,{\cal F}\left[A(\vec{r})\vec{r}\right]({\bm\kappa}/h_j){\cal F}\left[A(\vec{r})\vec{r}\right]^*({\bm\kappa}/h_j). \end{eqnarray}$ (16)The quasi-static and beam-wander errors Q, W, and ΔW introduced in Sect. 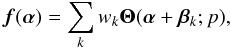2 can be expressed as sums of the form $f (α) = \sum_{k} w_{k} Θ (α + β_{k}; p),$ $\begin{equation} \vec{f}({\bm\alpha}) = \sum_k w_k {\bm\Theta}({\bm\alpha}+{\bm\beta}_k;p), \label{eq17} \end{equation}$ (17)where the possibility of only a single term with w₁ = 1 is included. Using the Fourier shift theorem we have $ℱ (f) (κ) = [\sum_{k} w_{k} \exp (2 π i β_{k} \cdot κ)] ℱ (Θ) (κ),$ $\begin{equation} {\cal F}(\vec{f})({\bm\kappa})= \left[\sum_k w_k\exp(2\pi {\rm i} {\bm\beta}_k\cdot{\bm\kappa})\right]{\cal F}({\bm\Theta})({\bm\kappa}), \label{eq18} \end{equation}$ (18)so that the power spectrum of f is given by $Φ_{f} (κ) = {| \sum_{k} w_{k} \exp (2 π i β_{k} \cdot κ) |}^{2} Φ_{Θ} (κ) .$ $\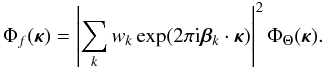begin{equation} \Phi_f({\bm\kappa})=\left|\sum_k w_k\exp(2\pi {\rm i} {\bm\beta}_k\cdot{\bm\kappa})\right|^2 \Phi_\Theta({\bm\kappa}). \label{eq19} \end{equation}$ (19)The two-axis mean-square value of f is then $σ_{f}^{2} = \int d κ tr [Φ_{f} (κ)^{]},$ $\begin{equation} \sigma_f^2=\int {\rm d}{\bm\kappa}\,\mbox{tr}\left[\Phi_f({\bm\kappa})\right], \label{eq20} \end{equation}$ (20)where tr denotes the trace of a matrix (recall that Φ_f is a 2 × 2 matrix).

PSD methods may also be used to evalute the expected value of the inner product integrals appearing in Eq. (10) above for the mean-square value of Pf, the position estimation error remaining after low-order mode removal. Using Parseval’s theorem, we have: $⟨ {[\frac{\int d α Ω (α) m \begin{matrix} T \\ j \end{matrix} (α) f (α)}{\int d α Ω (α)}]}^{2} ⟩ = \frac{\int d κ ℱ (m j)^{*} (κ) Φ_{f} (κ) ℱ (m j) (κ)}{{[^{\int} d α Ω (α)^{]}}^{2}} \cdot$ $\begin{equation} \left\langle\left[\frac{\int {\rm d}{\bm\alpha}\,\Omega({\bm\alpha})\vec{m}_j^T({\bm\alpha})\vec{f}({\bm\alpha})}{ \int {\rm d}{\bm\alpha}\,\Omega({\bm\alpha})}\right]^2\right\rangle = \frac{\int {\rm d}{\bm\kappa}\,{\cal F}(\vec{m}_j)^*({\bm\kappa})\Phi_f({\bm\kappa}) {\cal F}(\vec{m}_j)({\bm\kappa})}{\left[\int {\rm d}{\bm\alpha}\,\Omega({\bm\alpha})\right]^2}\cdot \label{eq21} \end{equation}$ (21)It remains to develop a Fourier domain model for the calibration errors C and ΔC. For this purpose, suppose that the image distortion function Θ(α;p) is sampled using an infinite grid of reference sources with one-dimensional angular spacing d, and that the image distortion map is estimated from these samples using Fourier interpolation. The calibration Θ_c(α;p) is correct for the Fourier modes of the distortion with angular frequencies less than 1/2d in each component, but it aliases the higher frequency modes. 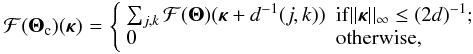More formally, $\begin{matrix} ℱ (Θ_{c}) (κ) & = & {\begin{matrix} \end{matrix} \end{matrix}$ $\begin{eqnarray} {\cal F}({\bm\Theta}_{\rm c})({\bm\kappa}) \!& = &\! \left\{\begin{array}{ll} \sum_{j,k} {\cal F}({\bm\Theta})({\bm\kappa}+d^{-1}(j,k)) & {\rm if} ||{\bm\kappa}||_\infty \leq (2d)^{-1} ; \\ 0 & \mbox{otherwise,} \end{array}\right. \nonumber \\ & & \label{eq22} \end{eqnarray}$ (22)where the sum is taken over all pairs of integers j and k, and ||κ||_∞ = max(| κ₁|, ∥ κ₂|). 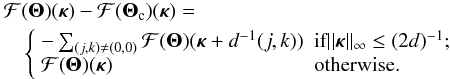The Fourier transform of the calibration error is then given by $\begin{matrix} ℱ (Θ) (κ) - ℱ (Θ_{c}) (κ) = \\ {\begin{matrix} \end{matrix} \end{matrix}$ $\begin{eqnarray} \label{eq23} \lefteqn{{\cal F}({\bm\Theta})({\bm\kappa})-{\cal F}({\bm\Theta}_{\rm c})({\bm\kappa})=} \nonumber \\ & & \left\{\begin{array}{ll} -\sum_{(j,k)\neq (0,0)} {\cal F}({\bm\Theta})({\bm\kappa}+d^{-1}(j,k)) & \mbox{if} ||{\bm\kappa}||_\infty \leq (2d)^{-1} ; \\ {\cal F}({\bm\Theta})({\bm\kappa}) & \mbox{otherwise.} \end{array}\right. \end{eqnarray}$ (23)For a linear combination of image distortions defined as in Eq. (17) above, using Eq. (18) we obtain $\begin{matrix} ℱ (f) (κ) - ℱ (f c) (κ) = \\ [\sum_{k} w_{k} \exp (2 π i β_{k} \cdot κ)] [ℱ (Θ) (κ) - ℱ (Θ_{c}) (κ)] . \end{matrix}$ $\begin{eqnarray} \label{eq24} \lefteqn{{\cal F}(\vec{f})({\bm\kappa})-{\cal F}(\vec{f}_{\rm c})({\bm\kappa}) =} \nonumber \\ & & \qquad \left[\sum_k w_k \exp(2\pi {\rm i} {\bm\beta}_k\cdot{\bm\kappa})\right] \left[{\cal F}({\bm\Theta})({\bm\kappa})-{\cal F}({\bm\Theta}_{\rm c})({\bm\kappa})\right]. \end{eqnarray}$ (24)From Eq. (23) (and intuition) it follows that the calibration error is not shift-invariant, since the Fourier components of the error are not statistically independent at distinct angular frequencies. 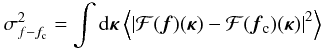However, the mean-square value of the error can still be expressed in the Fourier domain as $σ_{f - f_{c}}^{2} = \int d κ ⟨ {| ℱ (f) (κ) - ℱ (f c) (κ) |}^{2} ⟩$ $\begin{equation} \sigma^2_{f-f_{\rm c}}=\int {\rm d}{\bm\kappa}\left\langle\left\vert{\cal F}(\vec{f})({\bm\kappa})- {\cal F}(\vec{f}_{\rm c})({\bm\kappa})\right\vert^2\right\rangle \label{eq25} \end{equation}$ (25)on account of the Plancheral theorem. Using Eqs. (23), (24), and the fact that the distortion function Θis shift invariant, the mean-square calibration error now becomes $\begin{matrix} σ_{f - f_{c}}^{2} & = & \int | | κ | |_{\infty} \leq (2 d)^{-1} d κ {| \sum_{k} w_{k} \exp (2 π i β_{k} \cdot κ) |}^{2} \\ \times \sum_{(j,k) \neq (0, 0)} Φ_{Θ} (κ + δ^{-1} (j,k)) \\ + \int_{| | κ | |_{\infty} > (2 d)^{-1}} d κ {| \sum_{k} w_{k} \exp (2 π i β_{k} \cdot κ) |}^{2} Φ_{Θ} (κ) \\ = & \int | | κ | |_{\infty} > (2 d)^{-1} d κ {{| \sum_{k} w_{k} \exp (2 π i β_{k} \cdot κ) |}^{2} \end{matrix}$ $\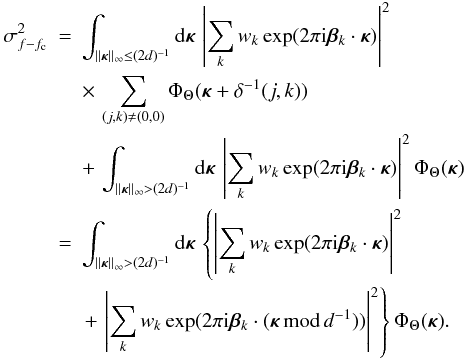begin{eqnarray} \sigma^2_{f-f_{\rm c}} & = & \int_{||{\bm\kappa}||_\infty \leq (2 d)^{-1}} {\rm d}{\bm\kappa}\, \left|\sum_k w_k\exp(2\pi {\rm i}{\bm\beta}_k\cdot{\bm\kappa})\right|^2 \nonumber \\ & & \times\,\sum_{(j,k)\neq(0,0)} \Phi_\Theta({\bm\kappa}+\delta^{-1}(j,k)) \nonumber \\ & & + \,\int_{||{\bm\kappa}||_\infty > (2 d)^{-1}} {\rm d}{\bm\kappa}\, \left|\sum_k w_k\exp(2\pi {\rm i}{\bm\beta}_k\cdot{\bm\kappa})\right|^2 \Phi_\Theta({\bm\kappa}) \nonumber \\ & = & \int_{||{\bm\kappa}||_\infty > (2 d)^{-1}} {\rm d}{\bm\kappa}\, \left\{\left|\sum_k w_k\exp(2\pi {\rm i}{\bm\beta}_k\cdot{\bm\kappa})\right|^2 \right. \nonumber \\ & & \left. +\, \left|\sum_k w_k\exp(2\pi {\rm i}{\bm\beta}_k\cdot({\bm\kappa}\,\mbox{mod}\,d^{-1}))\right|^2\right\} \Phi_\Theta({\bm\kappa}). \label{eq26} \end{eqnarray}$ (26)Here κmod d^-1 is the component-wise remainder of κ when divided by d^-1. Equation (26) is a somewhat awkward expression, and we will only evaluate it explicitly for the calibration error C (i.e., f = Θ) as opposed to ΔC.

5. Specializing to circular apertures and fields

The special case of a circular, unobscured aperture function A(r) and a circular science FoV Ω(α) is generally sufficient for error budgeting purposes. The Fourier transform of the function A(r)r appearing in Eq. (15) then takes the form $ℱ [A (r) r] (ν) = \frac{i D^{3} J_{2} (πDν)}{4 Dν} (\begin{matrix} \cos φ \\ \sin φ \end{matrix}),$ $\begin{equation} {\cal F}\left[A(\vec{r})\vec{r}\right]({\bm\nu})=\frac{iD^3J_2(\pi D\nu)}{4D\nu} \left(\begin{array}{c}\cos\phi \\ \sin\phi\end{array}\right), \label{eq27} \end{equation}$ (27)where D is the aperture diameter, J₂ is a Bessel function of the first kind, and φ is the angle of the vector ν. Substituting Eq. (27) back into Eq. 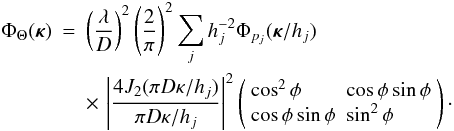(16) now yields $\begin{matrix} Φ_{Θ} (κ) & = & {(\frac{λ}{D})}^{2} {(\frac{2}{π})}^{2} \sum_{j} h_{j}^{-2} Φ_{p_{j}} (κ / h_{j}) \\ \times {| \frac{4 J_{2} (πDκ / h_{j})}{πDκ / h_{j}} |}^{2} (\begin{matrix} \end{matrix}) \cdot \end{matrix}$ $\begin{eqnarray} \label{eq28} \Phi_\Theta({\bm\kappa}) & = & \left(\frac{\lambda}{D}\right)^2\left(\frac{2}{\pi}\right)^2 \sum_j h_j^{-2} \Phi_{p_j}({\bm\kappa}/h_j) \nonumber \\ & & \times\, \left\vert\frac{4J_2(\pi D\kappa/h_j)}{\pi D\kappa/h_j}\right\vert^2 \left(\begin{array}{ll} \cos^2\phi & \cos\phi\sin\phi \\ \cos\phi\sin\phi & \sin^2\phi \end{array}\right)\cdot \end{eqnarray}$ (28)For a circular FoV of radius ρ, it is reasonable to decompose the image distortion profile in terms of the orthonormal basis functions $\begin{matrix} m 2 j - 1 (α) = (Z_{j} (α / ρ), 0) \\ m 2 j (α) = (0, Z_{j} (α / ρ)), \end{matrix}$ $\begin{eqnarray} \label{eq29} &&\vec{m}_{2j-1}({\bm\alpha})=(Z_j({\bm\alpha}/\rho),0) \\ \label{eq30} &&\vec{m}_{2j }({\bm\alpha})=(0,Z_j({\bm\alpha}/\rho)), \end{eqnarray}$ where the functions Z_i are the orthonormal Zernike polynomials on the unit radius disk as used by Noll (1976). Using Eq. (21) and Noll’s formulas for ℱ(Z_i) in terms of Bessel functions, we obtain the result $\begin{matrix} \sum_{j} ⟨ {[\frac{\int d α m \begin{matrix} T \\ j \end{matrix} (α) f (α) Ω (α)}{\int d α Ω (α)}]}^{2} ⟩ = \\ \int d κ Tr Φ_{f} (κ) \sum_{n = 0}^{N} {| \frac{(n + 1) J_{n + 1} (2 πρκ)}{πρκ} |}^{2} \end{matrix}$ $\begin{eqnarray} \label{eq31} \lefteqn{\sum_j \left\langle\left[\frac{\int {\rm d}{\bm\alpha}\,\vec{m}_j^T({\bm\alpha})\vec{f}({\bm\alpha})\Omega({\bm\alpha})}{ \int {\rm d}{\bm\alpha}\,\Omega({\bm\alpha})}\right]^2\right\rangle =} \nonumber \\ & & \qquad\qquad\int {\rm d}{\bm\kappa}\,\mbox{Tr}\Phi_f({\bm\kappa})\sum_{n=0}^N \left\vert\frac{(n+1)J_{n+1}(2\pi\rho\kappa)}{\pi\rho\kappa}\right\vert^2 \end{eqnarray}$ (31)for the projection of the function f onto the first N radial orders of the distortion modes. For example, N = 0 corresponds to global tip/tilt removal, N = 1 adds modes for plate scale, animorphic plate scale, and image rotation, and so on.

6. Final formulas and sample numerical results

Using the general results developed in Sects. 3 through 5 above, we can now derive and evaluate expressions for the three error terms of quasi-static distortion, beam wander across static surface distortions, and calibration undersampling error.

6.1. Quasi-static errors

In Sect. 2, the position estimation error due to the effects of the quasi-static optics figure error q is denoted Q, and the residual error after low-order mode removal is written as PQ. This corresponds to the case f = Θ, and by Eq. (19) the particular value of the LoS error o + δ is unimportant. Substituting Eqs. (20), (28), and (31) into Eq. (10) yields the result 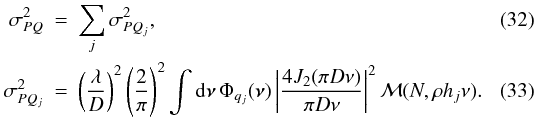$\begin{matrix} σ_{PQ}^{2} & = & \sum_{j} σ_{P Q_{j}}^{2}, \\ σ_{P Q_{j}}^{2} & = & {(\frac{λ}{D})}^{2} {(\frac{2}{π})}^{2} \int d ν Φ_{q_{j}} (ν) {| \frac{4 J_{2} (πDν)}{πDν} |}^{2} ℳ (N,ρ h_{j} ν) . \end{matrix}$ $\begin{eqnarray} \label{eq32} \sigma_{PQ}^2 & = & \sum_j\sigma_{PQ_j}^2, \\ \label{eq33} \sigma_{PQ_j}^2 & = & \left(\frac{\lambda}{D}\right)^2\left(\frac{2}{\pi}\right)^2 \int {\rm d}{\bm\nu}\,\Phi_{q_j}({\bm\nu})\left\vert\frac{4J_2(\pi D\nu)}{\pi D\nu}\right\vert^2 {\cal M}(N,\rho h_j\nu). 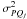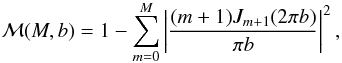\end{eqnarray}$ Here $σ_{P Q_{j}}^{2}$ $\hbox{$\sigma_{PQ_j}^2$}$ is the mean-square position estimation error due to the surface errors on optical surface number j at conjugate range h_j, D is the aperture diameter, ρ is the diameter of the FoV, ν = κ/h_j, and the mode removal filter ℳ is defined by $ℳ (M,b) = 1 - \sum_{m = 0}^{M} {| \frac{(m + 1) J_{m + 1} (2 πb)}{πb} |}^{2},$ $\begin{equation} {\cal M}(M,b)=1 - \sum_{m=0}^M \left\vert\frac{(m+1)J_{m+1}(2\pi b)}{\pi b}\right\vert^2, \label{eq34} \end{equation}$ (34)where M is the maximum radial order of the modes removed from the image distortion map.

Quasi-static wavefront errors are unpredictable almost by definition, so reliable information on their PSD may not necessarily be available. However, it is still possible to develop a “sensitivity” function to describe the magnitude of the error introduced by one unit of rms wavefront error as a function of spatial frequency. For the higher-order, tip/tilt/piston removed wavefront errors, this sensitivity function is given by the formula $T_{P Q_{j}} (ν) = (\frac{λ}{D}) (\frac{2}{π}) | \frac{4 J_{2} (πDν)}{πDν} | {[ℳ (N,ρ h_{j} ν) / ℳ (1,Dν)^{]}}^{1 / 2},$ $\begin{equation} T_{PQ_j}({\bm\nu})=\left(\frac{\lambda}{D}\right)\left(\frac{2}{\pi}\right)\left\vert\frac{4J_2(\pi D\nu)}{\pi D\nu}\right\vert \left[{\cal M}(N,\rho h_j\nu)/{\cal M}(1,D\nu)\right]^{1/2}, \label{eq35} \end{equation}$ (35)where the factor of ℳ(1,Dν) is included to filter out the tip/tilt/piston modes of the wavefront error on a circular aperture of diameter D.

Figure 1 plots this sensitivity function (in units of μas per nm) for quasi-static wavefront errors on the deformable mirror DM11.2 in the NFIRAOS first light AO system for the Thirty Meter Telescope (Herriot et al. 2012). The relevant parameter values for this instrument are D = 30 m, ρ = 30 arcsec, h_j = 11.2 km, and N = 0 or 1. The maximum value of the sensitivity function is approximately 3 μas nm^-1 with global tip-tilt removal (N = 0), and approximately 0.15 assuming that the plate scale and rotation modes (N = 1) can also be calibrated using reference stars. Results such as this can be used to help specify the requirements on deformable mirror stability in AO systems used for high precision astrometry.

Fig. 1

Sensitivity function relating quasi-static wavefront errors on the deformable mirror DM11.2 in the TMT AO system NFIRAOS to the resulting image distortion after low-order mode correction using reference stars. See the text for further parameter values.

Finally, if the random quasi-static wavefront aberrations have the same variance and are uncorrelated for two separate science exposures, the value of the differential error due to the two independent quasi-static errors in two images is simply 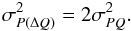$σ_{P (Δ Q)}^{2} = 2 σ_{PQ}^{2} .$ $\begin{equation} \sigma_{P(\Delta Q)}^2 = 2\sigma_{PQ}^2. \label{eq36} \end{equation}$ (36)

6.2. Error due to beam wander effects

The position estimation error in a single exposure due to a beam wander across the optical surface errors is the function W(α) defined as the first term within square brackets in Eq. (3). Using Eqs. (10), (20), (19), (16) and (31) above, we can again evaluate the mean-square value of the error as sum of contributions from each optical surface, with each contribution expressed as a weighted integral of the surface error PSD. For a fixed value of the beam wander δ, the contribution from surface number j is given by the formula $\begin{matrix} σ_{P W_{j}}^{2} (δ) & = & {(\frac{λ}{D})}^{2} {(\frac{2}{π})}^{2} \int d ν Φ_{s_{j}} (ν) {| \frac{4 J_{2} (πDν)}{πDν} |}^{2} \\ \times 2 ℜ [1 - \exp (2 π i h_{j} ν \cdot δ)^{]} ℳ (N,ρ h_{j} ν) . \end{matrix}$ $\begin{eqnarray} \label{eq37} \sigma_{PW_j}^2({\bm\delta}) & = & \left(\frac{\lambda}{D}\right)^2\left(\frac{2}{\pi}\right)^2 \int {\rm d}{\bm\nu}\,\Phi_{s_j}({\bm\nu})\left\vert\frac{4J_2(\pi D\nu)}{\pi D\nu}\right\vert^2 \nonumber \\[-0.5mm] & & \times 2\Re\left[1-\exp(2\pi {\rm i} h_j{\bm\nu}\cdot{\bm\delta})\right]{\cal M}(N,\rho h_j\nu). \end{eqnarray}$ (37)If the beam wander vector is treated as a zero-mean, normally distibuted random error, the expected error averaged over all realizations of δ is then given by $\begin{matrix} σ_{P W_{j}}^{2} & = & 2 {(\frac{λ}{D})}^{2} {(\frac{2}{π})}^{2} \int d ν Φ_{s_{j}} (ν) {| \frac{4 J_{2} (πDν)}{πDν} |}^{2} \end{matrix}$ $\begin{eqnarray} \sigma_{PW_j}^2 & = & 2\left(\frac{\lambda}{D}\right)^2\left(\frac{2}{\pi}\right)^2 \int {\rm d}{\bm\nu}\,\Phi_{s_j}({\bm\nu})\left\vert\frac{4J_2(\pi D\nu)}{\pi D\nu}\right\vert^2 \nonumber \\[-0.5mm] & & \times\left[1-\exp(-2\pi^2 h_j^2\nu^2\sigma_\delta^2)\right]{\cal M}(N,\rho h_j\nu), \label{eq38} \end{eqnarray}$ (38)where σ_δ is the one-axis rms value of the beam wander.

A common functional form for the fabrication errors on an optical surface is a (two-dimensional) power law PSD, Φ(ν) = cν^−p. If the optical surface is specified to have a piston-tip/tilt-focus removed rms OPD equal to σ_OPD on a clear aperture of radius equivalent to R_C for the image of the surface in telescope object space, the coefficient c may be evaluated with the result 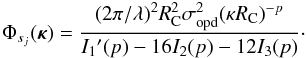$Φ_{s_{j}} (κ) = \frac{(2 π / λ)^{2} R_{C}^{2} σ_{opd}^{2} (κ R_{C})^{- p}}{I_{1}' (p) - 16 I_{2} (p) - 12 I_{3} (p)} \cdot$ $\begin{equation} \Phi_{s_j}({\bm\kappa})=\frac{(2\pi/\lambda)^2 R_{\rm C}^2\sigma_{\rm{opd}}^2(\kappa R_{\rm C})^{-p}}{ I_1\arcmin (p)-16 I_2(p) -12 I_3(p)}\cdot \label{eq39} \end{equation}$ (39)Here the quantities I₁′(p) and I_n(p) are similar to the integrals computed by Noll (1976) for the case of Kolmogorov turbulence with p = 11/3, and are given by the expressions $\begin{matrix} I_{1}' (p) & = & \frac{π^{p} Γ (p + 1)}{{Γ [(p + 2) / 2]}^{2} Γ [(p + 4) / 2] Γ (p / 2) \sin [π (p - 2) / 2]} \\ I_{n} (p) & = & \frac{π^{p - 1} Γ (p + 1) Γ [(2 n - p) / 2]}{4 {Γ [(p + 2) / 2]}^{2} Γ [(2 n + 2 + p) / 2]} \cdot \end{matrix}$ $\begin{eqnarray} \label{eq40} I_1\arcmin (p)\! & = & \!\frac{\pi^p \Gamma(p+1)}{ \left\{\Gamma\left[(p\!+\!2)/2\right]\right\}^2\Gamma[(p\!+\!4)/2]\Gamma(p/2)\sin\left[\pi(p\!-\!2)/2\right]} \\ \label{eq41} I_n(p) & = & \frac{\pi^{p-1}\Gamma(p+1)\Gamma[(2n-p)/2]}{4\left\{\Gamma[(p+2)/2]\right\}^2\Gamma[(2n+2+p)/2]}\cdot \end{eqnarray}$ By substituting Eq. (39) into Eq. (38) and applying the change of variable ν → Dν, we finally obtain $\begin{matrix} σ_{P W_{j}}^{2} & = & \frac{64 π (D / R_{C})^{p - 2} (σ_{opd} / D)^{2}}{I_{1}' (p) - 16 I_{2} (p) - 12 I_{3} (p)} \int_{0}^{\infty} d ν ν^{1 - p} {| \frac{4 J_{2} (πν)}{πν} |}^{2} \\ \times ℳ (N, h_{j} ρν / D) {1 - \exp [- 2 π^{2} ν^{2} (h_{j} σ_{δ} / D)^{2}]} . \end{matrix}$ $\begin{eqnarray} \label{eq42} \sigma_{PW_j}^2 & = & \frac{64\pi (D/R_{\rm C})^{p-2}(\sigma_{\mbox{opd}}/D)^2}{I_1\arcmin (p)-16I_2(p)-12I_3(p)} \int_0^\infty {\rm d}\nu\,\nu^{1-p}\left\vert\frac{4J_2(\pi \nu)}{\pi\nu}\right\vert^2 \nonumber \\ & & \times\, {\cal M}(N,h_j\rho\nu/D)\left\{1-\exp\left[-2\pi^2\nu^2(h_j\sigma_\delta/D)^2\right]\right\}. \end{eqnarray}$ (42)Equation (42) suggests the definition of a normalized sensitivity coefficient s_{PW_j} according to the formula $s_{P W_{j}} = σ_{P W_{j}} / [(D / R_{C})^{(p - 2) / 2} (σ_{OPD} / D)] .$ $\begin{equation} s_{PW_j}=\sigma_{PW_j}/[(D/R_{\rm C})^{(p-2)/2}(\sigma_{\rm{OPD}}/D)]. \label{eq42a} \end{equation}$ (43)We recall that D is the diameter of the telescope aperture, the rms optical path error over the clear aperture of surface j is σ_OPD, and the radius of this surface is equivalent to R_C when imaged into telescope object space. The normalization defined in Eq. (43) expresses the fact that the rms image distortion due to beam wander on surface j will scale linearly with the rms optical path error within the beamprint (i.e., with (D/R_C)^{(p − 2)/2}σ_OPD), and inversely with the diameter of the telescope (D). According to Eq. (42), the resulting sensitivity coefficient s_{PW_j} is a function of the surface error power law p, the order of low-order mode removal N, the normalized FoV diameter hρ/D, and the normalized beam wander hσ_δ/D.

Fig. 2

Normalized astrometry error for beam wander with global tip/tilt removed. See Eq. (43) for the definition of this sensitivity coefficient.

Fig. 3

Normalized astrometry error for beam wander with global tip/tilt and plate scale removed. See Eq. (43) for the definition of this sensitivity coefficient.

The trends in the error due to beam wander across optical surface errors are plotted in Figs. 2 and 3. From the plotted results, we see that

Larger random beam wanders always cause larger position estimation errors, although the trend begins to asymptote for normalized jitters beyond the range of 0.3–1.0;
Larger fields of view also cause a larger error, although this effect also begins to asymptote for normalized fields of view greater than about 1.0. This result implies that surface errors on optics located far from a pupil (i.e., with a large absolute value of h) have the greatest impact on astrometric accuracy.
The expontent of the PSD power law has a relatively smaller effect, with a steeper PSD (more negative exponent) generally yielding a modestly larger error;
The error is always reduced by removing the plate scale modes from the image distortion profile, with a greater reduction obtained for smaller normalized fields of view.

The differential error between two separate exposures due to two random, uncorrelated beam wanders can be evalulated similarly, beginning with Eq. (6) for ΔW. In this case the function f is a linear combination of four terms, so that the final formula is somewhat more elaborate:

\begin{matrix} σ_{P (Δ W)_{j}}^{2} & = & \frac{64 π (D / R_{C})^{p - 2} (σ_{opd} / D)^{2}}{I_{1}' (p) - 16 I_{2} (p) - 12 I_{3} (p)} \int_{0}^{\infty} d ν ν^{1 - p} {| \frac{4 J_{2} (πν)}{πν} |}^{2} \\ \times ℳ (N, h_{j} ρν / D) {2 - 2 \exp [- 2 π^{2} ν^{2} {(\frac{h_{j} σ_{δ}}{D})}^{2}] \\ - J_{0} (\frac{2 πν | o - o' |}{D}) {\begin{matrix} ⎧ \\ ⎪ \\ ⎪ \\ ⎨ \\ ⎪ \\ ⎪ \\ ⎩ \end{matrix} 1 - \exp [- 2 π^{2} ν^{2} {(\frac{h_{j} σ_{δ}}{D})}^{2}] \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix}}^{2} \begin{matrix} ⎫ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎬ \\ ⎪ \\ ⎪ \\ ⎪ \\ ⎭ \end{matrix} \cdot \end{matrix}

$\begin{eqnarray} \sigma_{P(\Delta W)_j}^2 & = & \frac{64\pi (D/R_{\rm C})^{p-2}(\sigma_{\mbox{opd}}/D)^2}{I_1\arcmin (p)-16I_2(p)-12I_3(p)} \int_0^\infty {\rm d}\nu\,\nu^{1-p}\left\vert\frac{4J_2(\pi \nu)}{\pi\nu}\right\vert^2 \nonumber \\ & & \times\, {\cal M}(N,h_j\rho\nu/D) \left\{2-2\exp\left[-2\pi^2\nu^2\left(\frac{h_j\sigma_\delta}{D}\right)^2\right]\right. \nonumber \\ & & \left.-\,J_0\left(\frac{2\pi\nu\vert \vec{o}-\vec{o}\arcmin \vert}{D}\right) \left\{1-\exp\left[-2\pi^2\nu^2\left(\frac{h_j\sigma_\delta}{D}\right)^2\right]\right\}^2\right\}\cdot \nonumber \\ & & \label{eq43} \end{eqnarray}$ (44)If the two offset vectors o and o′ are identical, it may be verified that this expression simplifies to Eq. (42) with σ_δ replaced by

\sqrt{2} σ_{δ}

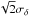$\hbox{$\sqrt{2}\sigma_\delta$}$ (as expected).

6.3. Calibration undersampling error

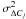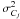The last two terms to consider are the calibration errors C and ΔC. The function f consists of only a single term for C, but two terms for ΔC. On account of Eq. (26), this means that the formula for $σ_{Δ C_{j}}^{2}$ $\hbox{$\sigma_{\Delta C_j}^2$}$ is much less tractable than for $σ_{C_{j}}^{2}$ $\hbox{$\sigma_{C_j}^2$}$ , so we have only considered the simpler case of the error in a single exposure¹.

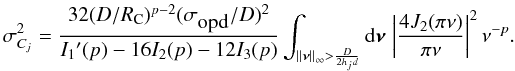Substituting Eq. (39) for a power law PSD into Eq. (26), the formula for the mean-square calibration error due to surface number j becomes $σ_{C_{j}}^{2} = \frac{32 (D / R_{C})^{p - 2} (σ_{opd} / D)^{2}}{I_{1}' (p) - 16 I_{2} (p) - 12 I_{3} (p)} \int_{| | ν | |_{\infty} > \frac{D}{2 h_{j} d}} d ν {| \frac{4 J_{2} (πν)}{πν} |}^{2} ν^{- p} .$ $\begin{equation} \sigma_{C_j}^2 = \frac{32 (D/R_{\rm C})^{p-2}(\sigma_{\mbox{opd}}/D)^2}{I_1\arcmin (p)-16I_2(p)-12I_3(p)} \int_{\vert\vert{\bm\nu}\vert\vert_\infty > \frac{D}{2 h_j d}} {\rm d}{\bm\nu}\, \left\vert\frac{4J_2(\pi\nu)}{\pi\nu}\right\vert^2 \nu^{-p}. \label{eq44} \end{equation}$ (45)Note that domain of integration is still two-dimensional, consisting of all spatial frequency vectors ν with ||ν||_∞ = max(ν₁,ν₂) > (2h_jd/D)^-1. Since the integrand in Eq. (45) is radially symmetric, we replace the square “hole” in the domain of integration with an equal-area disk so that the integral can be converted into polar coordinates and simplied. 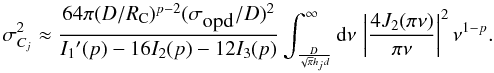The final formula for the calibration error becomes $σ_{C_{j}}^{2} \approx \frac{64 π (D / R_{C})^{p - 2} (σ_{opd} / D)^{2}}{I_{1}' (p) - 16 I_{2} (p) - 12 I_{3} (p)} \int_{\frac{D}{\sqrt{π} h_{j} d}}^{\infty} d ν {| \frac{4 J_{2} (πν)}{πν} |}^{2} ν^{1 - p} .$ $\begin{equation} \sigma_{C_j}^2 \approx \frac{64\pi(D/R_{\rm C})^{p-2}(\sigma_{\mbox{opd}}/D)^2}{I_1\arcmin (p)-16I_2(p)-12I_3(p)} \int_{\frac{D}{\sqrt{\pi}h_j d}}^\infty {\rm d}\nu\,\left\vert\frac{4J_2(\pi\nu)}{\pi\nu}\right\vert^2 \nu^{1-p}. \label{eq45} \end{equation}$ (46)Figure 4 plots the calibration error sensitivity coefficient $s_{C_{j}} = σ_{C_{j}} / [(D / R_{C})^{(p - 2) / 2} (σ_{OPD} / D)],$ $\begin{equation} s_{C_j}=\sigma_{C_j}/[(D/R_{\rm C})^{(p-2)/2}(\sigma_{\rm{OPD}}/D)], \label{eq45a} \end{equation}$ (47)as a function of the calibration Nyquist frequency D/(h_jd) for several different power laws p. We see that for calibration to provide a meaningful improvement, the calibration Nyquist frequency must exceed 1, or equivalently the reference source spacing d must satisfy d < D/h_j. The rms error then falls as the Nyquist frequency to the power −(p + 1)/2, as would be expected from Eq. (46) and the asymptotic behavior of the Bessel function J₂. Smoother optical surface errors, with larger values of p, are consequently easier to calibrate.

Fig. 4

Normalized rms position estimation error due calibration undersampling. See Eq. (47) for the definition of this sensitivity coefficient.

7. Conclusions

We have derived a Fourier domain model for evaluating the position estimation errors due to optical surface errors in astronomical instrumentation and associated adaptive optics systems. Using analytical methods very similar to those used earlier to study adaptive optics, the errors can be evaluated as a sum of weighted integrals of the surface error PSD on each optical element. Separate formulas have been developed for: (i) quasi-static surface errors; (ii) the error due to beam wander across static surface errors; and (iii) the calibration undersampling error for a finite number of bright, regularly spaced reference sources. The benefits of on-sky calibration using a number of known reference stars in the science image has also been modeled. It is hoped that these results may be useful for developing optical surface specifications and astrometry error budgets.

There are several aspects of this basic model which could be revisited for greater generality and improved accuracy. Characterizing quasi-static surface errors in terms of a PSD may be challenging, since these errors are difficult to model almost by definition. The assumption that surface errors are uncorrelated between different optical surfaces will not necessarily apply to MCAO system, although these correlations will not matter in the important special case that only the ground-layer DM is adjusted to compensate for the static errors on other surfaces. Finally, the current model for calibration, which is based upon a grid of regularly spaced, bright reference sources, is restricted to laboratory source simulators and cannot be used to evaluate the performance of more sophisticated on-sky calibration methods using images of dense star fields. It remains to be seen whether Fourier domain methods are applicable in these cases with an acceptable level of accuracy, or if more computationally intensive approaches such as Monte Carlo simulations may be required instead.

¹

According to Eq. (7), the error ΔC is identically zero if the offset vectors o and o′ are identical.

Acknowledgments

The basic model for astrometry errors described in Sect. 2 above was developed in conversations with Glen Herriot and Matthias Schoeck, and we would also like to thank the referee for providing many helpful suggestions in his review. The TMT Project gratefully acknowledges the support of the TMT collaborating institutions. They are the Association of Canadian Universities for Research in Astronomy (ACURA), the California Institute of Technology, the University of California, the National Astronomical Observatory of Japan, the National Astronomical Observatories of China and their consortium partners, and the Department of Science and Technology of India and their supported institutes. This work was supported as well by the Gordon and Betty Moore Foundation, the Canada Foundation for Innovation, the Ontario Ministry of Research and Innovation, the National Research

Council of Canada, the Natural Sciences and Engineering Research Council of Canada, the British Columbia Knowledge Development Fund, the Association of Universities for Research in Astronomy (AURA) and the US National Science Foundation.

References

Cameron, P. B., Britton, M. C., & Kulkarni, S. R. 2009, AJ, 137, 83 [Google Scholar]
Ellerbroek, B. L. 2009, in Adaptive Optics: Methods, Analysis and Applications, eds. B. L. Ellerbroek, & J. Christou (Washington D.C.: OSA) [Google Scholar]
Fritz, T., Gillessen, S., Trippe, S., et al. 2010, MNRAS, 401, 1177 [NASA ADS] [CrossRef] [Google Scholar]
Herriot, G., Andersen, D., Atwood, J., et al. 2012, in Adaptive Optics Systems III, eds. B. L. Ellerbroek, E. Marchetti, & J.-P. Veran (Bellingham: SPIE), 84471 [Google Scholar]
Jolissaint, L., Veran, J.-P., & Conan, R. 2006, J. Opt. Soc. Am A, 23, 382 [NASA ADS] [CrossRef] [Google Scholar]
Lawson, J. K., Wolfe, C. R., Manes, K. R., et al. 1995, in Optical Manufacturing and Testing, eds. V. J. Doherty, & H. P. Stahl (Bellingham: SPIE), 38 [Google Scholar]
Lazorenko, P. F., Mayor, M., Dominik, M., et al. 2009, A&A, 505, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Noll, R. J. 1976, J. Opt. Soc. Am., 66, 207 [NASA ADS] [CrossRef] [Google Scholar]
Roddier, F., Northcott, M. J., Graves, J. E., McKena, D. L., & Roddier, D. 1993, J. Opt. Soc. Am. A, 10, 957 [Google Scholar]
Schoeck, M. 2011, in Adaptive Optics for Extremely Large Telescopes 2, eds. J.-P. Veran, T. Fusco, & Y. Clenet (Paris: ONERA), 721 [Google Scholar]
Trippe, S., Davies, R., Eisenhauer, F., et al. 2010, MNRAS, 402, 1126 [NASA ADS] [CrossRef] [Google Scholar]
Yelda, S., Lu, J. R., Ghez, A. M., et al. 2010, ApJ, 725, 331 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

	Fig. 1 Sensitivity function relating quasi-static wavefront errors on the deformable mirror DM11.2 in the TMT AO system NFIRAOS to the resulting image distortion after low-order mode correction using reference stars. See the text for further parameter values.
In the text

	Fig. 2 Normalized astrometry error for beam wander with global tip/tilt removed. See Eq. (43) for the definition of this sensitivity coefficient.
In the text

	Fig. 3 Normalized astrometry error for beam wander with global tip/tilt and plate scale removed. See Eq. (43) for the definition of this sensitivity coefficient.
In the text

	Fig. 4 Normalized rms position estimation error due calibration undersampling. See Eq. (47) for the definition of this sensitivity coefficient.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Cameron, P. B., Britton, M. C., & Kulkarni, S. R. 2009, AJ, 137, 83 [Google Scholar]

[2] Ellerbroek, B. L. 2009, in Adaptive Optics: Methods, Analysis and Applications, eds. B. L. Ellerbroek, & J. Christou (Washington D.C.: OSA) [Google Scholar]

[3] Fritz, T., Gillessen, S., Trippe, S., et al. 2010, MNRAS, 401, 1177 [NASA ADS] [CrossRef] [Google Scholar]

[4] Herriot, G., Andersen, D., Atwood, J., et al. 2012, in Adaptive Optics Systems III, eds. B. L. Ellerbroek, E. Marchetti, & J.-P. Veran (Bellingham: SPIE), 84471 [Google Scholar]

[5] Jolissaint, L., Veran, J.-P., & Conan, R. 2006, J. Opt. Soc. Am A, 23, 382 [NASA ADS] [CrossRef] [Google Scholar]

[6] Lawson, J. K., Wolfe, C. R., Manes, K. R., et al. 1995, in Optical Manufacturing and Testing, eds. V. J. Doherty, & H. P. Stahl (Bellingham: SPIE), 38 [Google Scholar]

[7] Lazorenko, P. F., Mayor, M., Dominik, M., et al. 2009, A&A, 505, 903 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[8] Noll, R. J. 1976, J. Opt. Soc. Am., 66, 207 [NASA ADS] [CrossRef] [Google Scholar]

[9] Roddier, F., Northcott, M. J., Graves, J. E., McKena, D. L., & Roddier, D. 1993, J. Opt. Soc. Am. A, 10, 957 [Google Scholar]

[10] Schoeck, M. 2011, in Adaptive Optics for Extremely Large Telescopes 2, eds. J.-P. Veran, T. Fusco, & Y. Clenet (Paris: ONERA), 721 [Google Scholar]

[11] Trippe, S., Davies, R., Eisenhauer, F., et al. 2010, MNRAS, 402, 1126 [NASA ADS] [CrossRef] [Google Scholar]

[12] Yelda, S., Lu, J. R., Ghez, A. M., et al. 2010, ApJ, 725, 331 [NASA ADS] [CrossRef] [Google Scholar]