| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A113 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201220867 | |
| Published online | 12 April 2013 | |
Comparison of solar horizontal velocity fields from SDO/HMI and Hinode data
1
Institut de Recherche en Astrophysique et Planétologie, Université de
Toulouse, CNRS,
14 avenue Édouard Belin,
31400
Toulouse,
France
e-mail:
thierry.roudier@irap.omp.eu
2
LESIA, Observatoire de Paris, Section de Meudon, 92195
Meudon,
France
3
CALMIP, DTSI Université Paul Sabatier, Université de Toulouse,
31062
Toulouse,
France
4
Lockheed Martin Advance Technology Center,
Palo Alto, CA-94304,
USA
5
Astronomical Institute, Faculty of Mathematics and Physics,
Charles University in Prague, V
Holešovičkách 2, 18000, Prague 8, Czech Republic
6
Astronomical Institute, Academy of Sciences of the CzechRepublic
(v. v. i.), Fričova
298, 25165
Ondřejov, Czech
Republic
7
National Solar Observatory, Sunspot, NM
88349,
USA
8
Max-Planck-Institut für Sonnensystemforschung,
Max-Planck-Strasse
2, 37191
Katlenburg-Lindau,
Germany
9
Institut für Astrophysik, Georg-August-Universität Göttingen,
Friedrich-Hund-Platz
1, 37077
Göttingen,
Germany
Received:
7
December
2012
Accepted:
6
March
2013
Context. The measurement of the Sun’s surface motions with a high spatial and temporal resolution is still a challenge.
Aims. We wish to validate horizontal velocity measurements all over the visible disk of the Sun from Solar Dynamics Observatory/ Helioseismic and Magnetic Imager (SDO/HMI) data.
Methods. Horizontal velocity fields are measured by following the proper motions of solar granules using a newly developed version of the coherent structure tracking (CST) code. The comparison of the surface flows measured at high spatial resolution (Hinode, 0.1 arcsec) and low resolution (SDO/HMI, 0.5 arcsec) allows us to determine corrections to be applied to the horizontal velocity measured from HMI white light data.
Results. We derive horizontal velocity maps with spatial and temporal resolutions of respectively 2.5 Mm and 30 min. From the two components of the horizontal velocity vx and vy measured in the sky plane and the simultaneous line of sight component from SDO/HMI dopplergrams vD, we derive the spherical velocity components (vr, vθ, vϕ). The azimuthal component vϕ gives the solar differential rotation with a high precision (± 0.037 km s-1) from a temporal sequence of only three hours.
Conclusions. By following the proper motions of the solar granules, we can revisit the dynamics of the solar surface at high spatial and temporal resolutions from hours to months and years with the SDO data.
Key words: Sun: atmosphere / Sun: granulation
© ESO, 2013
1. Introduction
The dynamics of the Sun’s surface is one of the major elements in understanding the time evolution of its magnetic activity. It is a real challenge to measure the surface motions at all spatial and temporal scales and compare them to those coming from the simulations. Recently, the Helioseismic and Magnetic Imager (HMI) on board the Solar Dynamics Observatory (SDO) allowed us a new step in that direction. By following the proper motions of the solar granules, representative of solar plasma evolution, it is possible to define the flow field on the solar surface (Roudier et al. 2012) from a small spatial scale of 2.5 Mm up to nearly 85% of the solar radius (Fig. 6 of that paper). We measured the velocities in a cartesian coordinate system, where x and y denote the coordinates in the sky plane with x parallel to the direction of the solar rotation and z directed towards the observer along the line of sight. Beyond 0.85 R⊙, the vx and vy components appeared to be noisy, but the vx component showed a trend indicative of the solar rotation. In order to identify whether improvements could be made in the determination of the horizontal velocities beyond that limit, we used simultaneous observations of the Sun in white light at low (SDO/HMI) and high (Hinode) spatial resolution.
In this paper, we describe a comparison between velocity fields projected on the sky plane that are obtained in the south pole region with Hinode data and SDO/HMI data using the coherent structure tracking (CST) code (Rieutord et al. 2007; Roudier et al. 2012). In the next section we discuss the corrections done in order to get an accurate velocity close to the solar limb. From the vx, vy and Doppler observations, we describe the transformation to the local surface velocities vr, vθ, vϕ. Finally, we present an application to measure solar differential rotation with a short time sequence (3 h) up to high latitudes with low noise. Discussion and conclusions follow.
2. Observations
2.1. Hinode observations
We used data sets from the Solar Optical Telescope (SOT), onboard the Hinode1 mission (e.g., Suematsu
et al. 2008; Ichimoto et al. 2004). The SOT
has a 50 cm primary mirror with a spatial resolution of about 0.2′′ at a
wavelength of 550 nm. For our study, we used blue continuum observations at 450.45 nm.
from the Hinode/SOT Broadband Filter Imager (BFI). The observations were recorded
continuously on December 10, 2011, from 16:11:33 to 19:07:05 UT. To get the limb as
reference, the south pole was observed at the position reported in the FITS header of
Hinode, i.e, Xcent = −10.08″ and
Ycent = −969.84″. The time step was 45 sec and the field
of view was 111.6″ × 111.6″ with a pixel size of 0
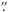 1089. After
alignment, the useful field of view reduced to 104″ × 82″. To remove the effects of the
oscillations, we applied a subsonic Fourier filter. This filter was defined by a cone in
k-ω space, where k and
ω are spatial and temporal frequencies. All Fourier components such
that
ω/k ≥ Vcut−off = 7 km s-1
were removed so as to keep only convective motions (Title
et al. 1989).
1089. After
alignment, the useful field of view reduced to 104″ × 82″. To remove the effects of the
oscillations, we applied a subsonic Fourier filter. This filter was defined by a cone in
k-ω space, where k and
ω are spatial and temporal frequencies. All Fourier components such
that
ω/k ≥ Vcut−off = 7 km s-1
were removed so as to keep only convective motions (Title
et al. 1989).
 |
Fig. 1 vx computed from LCT and CST on Hinode observations on December 10, 2011. |
2.2. SDO/HMI observations
The HMI (Scherrer et al. 2012; Schou et al. 2012) onboard the SDO provides
uninterrupted observations over the entire disk. This gives a unique opportunity for
mapping surface flows on various scales (spatial and temporal). Using the SDO/HMI white
light data on December 10, 2011, from 16:11:15 to 19:06:45 UT, we derived horizontal
velocity fields from image granulation tracking using the newly developed version of the
CST code (Roudier et al. 2012). The time step was 45
seconds with a pixel size of 0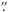 5. The solar
differential rotation discussed in Sect. 6 was determined from SDO/HMI white light and
Doppler data taken on August 30, 2010 from 8:00:45 to 11:09:45 UT.
5. The solar
differential rotation discussed in Sect. 6 was determined from SDO/HMI white light and
Doppler data taken on August 30, 2010 from 8:00:45 to 11:09:45 UT.
 |
Fig. 2 Angular rotation (sidereal) computed from LCT and CST on Hinode observation on December 10, 2011. |
 |
Fig. 3 SDO (left) and Hinode (right) observations on December 10, 2011, at 16:11:15 and 16:11:33 respectively. The location of the Hinode field is shown on the SDO image. |
3. Hinode south pole flow field
Measuring the solar rotation near the poles is a difficult task because there are few solar structures at high latitudes suitable for tracking. However, the Hinode images allow us to follow solar granules with good contrast up to the solar limb. First, we compare results of two methods to measure the solar motion close to the south pole using Hinode observations: local correlation tracking (LCT, November & Simon 1988) and CST (Rieutord et al. 2007; Roudier et al. 2012). Both methods track the horizontal motions of granules in the field of view. More precisely, the LCT method of obtaining the horizontal velocity uses a spatial window that simultaneously accounts for the solar granules and integranular structures and may cover several granules. In contrast, the CST method measures the velocities by following the trajectory of each granule, i.e., solar plasma, during the life of the coherent object, which is defined by its appearance and disappearance if the granule does not split or merge. The data were aligned and the P angle evolution corrected by 0.018°/hour in order to get a perfect co-alignment with SDO data used in the following. On December 10, 2011, the B0 angle was − 0.25°, resulting in insignificant projection effects with a negligible evolution during the observation period. Figure 1 shows good agreement of the vx component from the LCT and CST up to latitude 75°. Close to the limb, the effect of the spatial window used in the LCT prevents correct velocity determination. Figure 2 gives a solar sidereal rotation rate close to the pole of around 11°/day, which corresponds to a polar period of 32.73 days. This is in agreement with previous determinations (Beck 2000).
 |
Fig. 4 vx component from Hinode and SDO Hinode (0.1′′) and SDO (0.5′′), same field and duration. |
 |
Fig. 5 vy component from Hinode (0.1′′) and SDO (0.5′′) same field and duration. |
4. Comparison of the velocities from SDO and Hinode
Our main goal is to compare the surface flows measured with a high spatial resolution (Hinode, 0.1′′) and a low resolution (SDO, 0.5′′). We extracted the same field of view from the SDO data set as the Hinode one and performed a very precise co-alignment of both sequences. To get the best co-alignment, the south polar region was observed and the solar limb was taken as an absolute reference. An additional check was performed after the alignment process by locating the brightest features (facular points) at the beginning and end of both sequences (Hinode and SDO). A very good match of the structures indicated very good alignment of both sequences during the 3 h. We then applied the CST to both sequences to get the horizontal velocities (vx and vy) over the entire field of view. Figures 4 and 6 show a good agreement up to 78° of southern latitude. This indicates that SDO observations can be used to determine the solar rotation in the central meridian region up to significantly high latitudes. However, as shown in Fig. 5, the meridional component measured on SDO data exhibits an offset of 0.4 km s-1 relative to the Hinode component, which was used as the reference (because the velocity is close to zero at the limb). Figure 5 shows a good correspondence between Hinode and SDO velocities when the 0.4 km s-1 offset is removed (curve marked as SDO−0.4). We tried to elucidate the origin of that offset by determining all possible errors as listed in Table II of Strous (2000). The estimation on the SDO measurement gives a total error on the vy component of around 0.034 km s-1, which is ten times smaller than the measured offset.
 |
Fig. 6 Angular solar rotation from Hinode and SDO Hinode (0.1′′) and SDO (0.5′′), same field and duration. |
 |
Fig. 7 Comparison of vx, angular solar rotation and vy and from Hinode (0.1′′), Hinode (0.5′′) and SDO (0.5′′). |
As described above, one of the major differences between the two sequences is the pixel size, which is 0.1′′ and 0.5′′ for Hinode and SDO, respectively. In order to analyze the sequences under the same conditions, we degraded the pixel size of the Hinode observation to the SDO one: 0.5′′. We then applied CST to the Hinode degraded sequence to get the horizontal velocities, which were also k-ω filtered. Figure 7 still shows good agreement for the vx component and, in the same way, for the siderial angular rotation, at the latitudes up to 78°. The offset of 0.4 km s-1 observed in vy component of the Hinode data at 0.5′′ is clearly visible in Fig. 7. We conclude that the offset is caused by the combination of the lower spatial resolution and decreasing contrast to the limb. One has to bear in mind that we only observe the south pole region in detail, where vy is practically identical to the radial component of the flow. Thus, our observation can be generalized so that the radial component is always affected by the offset and we can correct for it. Indeed, different processes play a role in generating that radial component: at very high heliocentric angles, one pixel covers several granules. The granule part close to the limb is of lower contrast: it tends to be lost in the segmented images. This introduces an artificial radial motion of some granules that we see as the offset in the vy component on the central meridian when comparing high-resolution (Hinode) and low-resolution (SDO) measurements. This radial effect was previously observed in our measurements, but its origin was not identified. Since we now have the origin of that error, we can measure it and correct for it all over the Sun. One way to get the radial offset is to average the radial velocity component over a circle centered on the solar disk. Due to the B0 angle, the radial correction is not necessarily symmetrical in the northern and southern hemispheres of the Sun. This is why we treat the average process in the northern and southern regions of the Sun separately. Figure 8 shows, for example, the plot of the measured average radial component in the southern part and the overplotted fit obtained by using a polynomial function of the fifth degree. Figure 9 shows the entire profile of the correction of the radial velocity to be applied to the velocities vx and vy all over the Sun (north and south), allowing a good representation of the velocity field around 90% of the solar radius. In the following, this correction is applied systematically to all velocity fields.
 |
Fig. 8 Determination of the radial offset close to the south solar limb and the adjusted function. |
 |
Fig. 9 Entire profile of the correction of the radial velocity to be applied on the velocities vx and vy all over the Sun. |
 |
Fig. 10 Coordinate systems used throughout this paper: velocity components in the sky plane vx and vy and the line of sight velocity vDop (left); velocity components on the solar surface vr,vϕ,vθ (right). |
 |
Fig. 11 vx, vy, vDop velocity maps for the three-hour sequence on August 30, 2010, and the intensity at the beginning of the sequence. |
5. Determination of the spherical components of the velocity
From the velocity components vx and
vy measured in the sky plane and the
simultaneous line of sight velocity vD measured
from the SDO/HMI dopplergrams (e.g., Fig. 11), we can
derive the spherical velocity components vr,
vθ,
vϕ, projected onto spherical coordinates
r, θ, ϕ using
 The
system of coordinates is also shown in Fig. 10. We
note that ϕ is along the longitude and θ is along the
latitude. The co-alignment of all components has been checked carefully by using the
information from FITS headers of the SDO data. Before using the dopplergrams, some data
reduction had to be applied. First, the dopplergrams were averaged over the same time
interval as the vx and
vy sequence, here three hours. The
limbshift had to be be corrected (Ulrich 2010) and,
in this case, we used the limbshift function determined by the SDO team over the month of
August 2010 (Scherrer, priv. comm.).
The
system of coordinates is also shown in Fig. 10. We
note that ϕ is along the longitude and θ is along the
latitude. The co-alignment of all components has been checked carefully by using the
information from FITS headers of the SDO data. Before using the dopplergrams, some data
reduction had to be applied. First, the dopplergrams were averaged over the same time
interval as the vx and
vy sequence, here three hours. The
limbshift had to be be corrected (Ulrich 2010) and,
in this case, we used the limbshift function determined by the SDO team over the month of
August 2010 (Scherrer, priv. comm.).
 |
Fig. 12 vr(θ,ϕ),vθ(θ,ϕ),vθ(θ,ϕ) for the three-hour sequence on August 30, 2010. |
By defining z = 1−cosρ, where ρ is heliocentric angle, the limb-shift correction (in km s-1) is given by limb-shift (z) = −0.664z + 0.775z2 + 0.284z3. The mean velocity of the central region of the dopplergrams was taken as zero origin. The dopplergrams were resampled to the same size as the vx and vy components.
To convert the vx and
vy velocities in the sidereal system
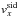 and
and
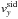 , the Earth’s
orbital displacement was taken into account. This correction depends on the
P angle as
, the Earth’s
orbital displacement was taken into account. This correction depends on the
P angle as 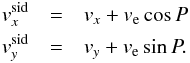 On
August 30, 2010, it was 0.13 km s-1 on
vx and 0.04 km s-1 on
vy, where ve is
the Earth velocity component projected on the Sun’s surface.
On
August 30, 2010, it was 0.13 km s-1 on
vx and 0.04 km s-1 on
vy, where ve is
the Earth velocity component projected on the Sun’s surface.
Figure 12 shows the resulting velocities vr,vθ,vϕ for the three-hour sequence on August 30, 2010. The vr map exhibits the radial component where the downflow is visible in the sunspot regions. Close to disk center we observe a lower contrast of vr, due to the low contrast in Doppler velocity in this part of the Sun because of the mostly horizontal flow on the Sun’s surface. The vr component is not well determined close to the limb because the projection effects are predominant. The vϕ component clearly shows the solar differential rotation with a lower velocity close to the pole. To our knowledge, this is the first time that we can measure and visualize the solar differential rotation with a three-hour time sequence. The latitudinal component vθ map allows us to essentially observe motion on supergranulation scales with a comparatively short time sequence.
 |
Fig. 13 Solar differential rotation on August 30, 2010, computed for the four different angles: 2° (top left), 10° (top right), 20° (bottom left), 40° (bottom right) either side of the central meridian. |
6. Determination of the solar differential rotation
One of the first scientific applications of the CST algorithm on SDO/HMI data described in Roudier et al. (2012) was to determine the solar rotation from the granule displacements. From the longitudinal velocity component vϕ, it is possible to calculate the solar differential rotation. In order to reduce the noise, we average vϕ over bands in longitudes. Figure 13 shows the computed differential rotation averaged over bands limited to longitude of (− 2,2), (− 10,10), (− 20,20), (− 40,40) degrees. The overplotted continuous line represents the solar rotation measured by the spectroscopic method (Howard & Harvey 1970), which is our reference to evaluate the noise of our measurements. The noise level is found to be 0.94, 0.37, 0.27, 0.267 °/day for the set of above-mentioned longitudinal bands. Thus, the average equatorial solar rotation determined for these four bands around the central meridian is 1.99 km s-1 ± (0.133, 0.052, 0.038, 0.037) km s-1 for the different longitudinal bands.
Our results show that, for the first time, using the CST we can get a determination of the solar rotation with a time sequence as short as three hours at very high precision, namely, 1.9% in the best case.
7. Discussion and conclusion
The comparison between high and low spatial resolution observations from the Hinode and SDO satellites allowed us to quantify the quality of the horizontal velocities determined over the full Sun. We found that the differential rotation along the central meridian is well determined up to latitude 60°. With a longer time series, higher latitudes will be reached on depending the B0 angle. Comparison of the meridional components shows an offset of 0.4 km s-1 due to a combination of three factors: the low spatial resolution, the limb gradient contrast, and the segmentation process. However, we describe a way to measure and correct for the radial effect all over the Sun and get nearly a full Sun velocity measurement. From the velocities vx and vy measured in the sky plane and the simultaneous line of sight velocity from SDO/HMI dopplergrams, we derived the spherical velocity components (vr,vθ,vϕ). From the longitudinal component, it is possible to get the solar differential rotation with high precision (± 0.037 km s-1) using a temporal sequence of only three hours. This is remarkable because other methods require at least one month of data. That particularity opens a new field of study of the solar rotation and motions over the solar surface. In this way, we can revisit the dynamics of the solar surface at high spatial and temporal resolution from hours to months and years with the SDO data. In particular, it will be of great interest to compare CST convective velocities with numerical simulations and constraints from helioseismology (Gizon & Birch 2012).
Acknowledgments
We thank the Hinode team for letting us use their data. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner and with NASA and STFC (UK) as international partners. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway). We thank the HMI team members for their hard work.We thank the German Data Center for SDO and BAS2000 for providing SDO/HMI data.We thank F. Rincon for his private comments. This work was granted access to the HPC resources of CALMIP under the allocation 2011-[P1115]. L.G. acknowledges support from DFG Collaborative Research Center 963 “Astrophysical Flow Instabilities and Turbulence” (Project A1). This work was supported by the CNRS Programme National Soleil Terre. M. Š is supported by the Czech Science Foundation (grant P209/12/P568).
References
- Beck, J. G. 2000, Sol. Phys., 191, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Birch, A. C. 2012, Proc. National Academy of Science, 109, 11896 [Google Scholar]
- Howard, R., & Harvey, J. 1970, Sol. Phys., 12, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Ichimoto, K., Tsuneta, S., Suematsu, Y., et al. 2004, in Optical, Infrared, and Millimeter Space Telescopes, ed. J. C. Mather, SPIE Conf., 5487, 1142 [Google Scholar]
- November, L. J., & Simon, G. W. 1988, ApJ, 333, 427 [Google Scholar]
- Rieutord, M., Roudier, T., Roques, S., & Ducottet, C. 2007, A&A, 471, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Malherbe, J. M., et al. 2012, A&A, 540, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Strous, L. H. 2000, Sol. Phys., 195, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Sol. Phys., 249, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Title, A. M., Tarbell, T. D., Topka, K. P., et al. 1989, ApJ, 336, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Ulrich, R. K. 2010, ApJ, 725, 658 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 vx computed from LCT and CST on Hinode observations on December 10, 2011. |
| In the text | |
 |
Fig. 2 Angular rotation (sidereal) computed from LCT and CST on Hinode observation on December 10, 2011. |
| In the text | |
 |
Fig. 3 SDO (left) and Hinode (right) observations on December 10, 2011, at 16:11:15 and 16:11:33 respectively. The location of the Hinode field is shown on the SDO image. |
| In the text | |
 |
Fig. 4 vx component from Hinode and SDO Hinode (0.1′′) and SDO (0.5′′), same field and duration. |
| In the text | |
 |
Fig. 5 vy component from Hinode (0.1′′) and SDO (0.5′′) same field and duration. |
| In the text | |
 |
Fig. 6 Angular solar rotation from Hinode and SDO Hinode (0.1′′) and SDO (0.5′′), same field and duration. |
| In the text | |
 |
Fig. 7 Comparison of vx, angular solar rotation and vy and from Hinode (0.1′′), Hinode (0.5′′) and SDO (0.5′′). |
| In the text | |
 |
Fig. 8 Determination of the radial offset close to the south solar limb and the adjusted function. |
| In the text | |
 |
Fig. 9 Entire profile of the correction of the radial velocity to be applied on the velocities vx and vy all over the Sun. |
| In the text | |
 |
Fig. 10 Coordinate systems used throughout this paper: velocity components in the sky plane vx and vy and the line of sight velocity vDop (left); velocity components on the solar surface vr,vϕ,vθ (right). |
| In the text | |
 |
Fig. 11 vx, vy, vDop velocity maps for the three-hour sequence on August 30, 2010, and the intensity at the beginning of the sequence. |
| In the text | |
 |
Fig. 12 vr(θ,ϕ),vθ(θ,ϕ),vθ(θ,ϕ) for the three-hour sequence on August 30, 2010. |
| In the text | |
 |
Fig. 13 Solar differential rotation on August 30, 2010, computed for the four different angles: 2° (top left), 10° (top right), 20° (bottom left), 40° (bottom right) either side of the central meridian. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


