EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 552 (April 2013) A&A, 552 (2013) A33 Full HTML
Free Access
Issue
A&A
Volume 552, April 2013
Article Number A33
Number of page(s) 3
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201220699
Published online 20 March 2013

© ESO, 2013

1. Introduction

We here continue our previous investigations of inelastic A + A∗(n) atom-Rydberg atom collision processes (where the principal quantum number was n ≫ 1 and A was the ground-state atom), which influence the excited atom populations in stellar atmospheres. We consider the processes that can be interpreted as resulting from a resonant energy exchange between the subsystem A + A+, in which A+ is the core of the Rydberg atom A∗(n), and the outer electron of this atom. There are two groups of such processes. The first group involves the chemi-ionization processes (Janev & Mihajlov 1980; Mihajlov et al. 1996, 1997), which connect the block of atomic Rydberg states with the continuum. The second group comprises the so-called (n − n′)-mixing processes within the above mentioned block of atomic Rydberg states (Mihajlov 1982; Mihajlov et al. 2004, 2008), i.e. the excitation and deexcitation processes that imply transitions between the Rydberg states with the principal quantum numbers n and n′ ≠ n.

The chemi-ionization processes in A∗(n) + A collisions, together with their inverse processes, have been studied for both A = H and A = He cases, which are especially important for stellar atmospheres. Mihajlov et al. (2003, 2007) studied the influence of these processes on the excited hydrogen atom populations and the spectral line profiles in the atmosphere of an M red dwarf (Teff = 3800 K) using the PHOENIX code. Mihajlov et al. (1997, 2011, 2003) studied the potential influence of these processes on the excited hydrogen and helium atom populations in the atmospheres of Sun and of some DB white dwarfs.

However, the possible influence of the (n − n′)-mixing processes in A∗(n) + A collisions on the excited-atom populations in stellar atmospheres has only been studied for the A = H case in the context of the atmosphere of the Sun (Mihajlov et al. 2005). In the above mentioned studies concerning the solar atmosphere, the necessary calculations were performed within the corresponding non-local thermodynamic equilibrium (non-LTE) model proposed by Vernazza et al. (1981). The findings of these studies have shown that the efficiency of these processes in a major part of the solar photosphere is dominant with respect to the efficiency of the relevant concurrent excitation and deexcitation processes for n = 4,5 and 6, and is comparable with them for n = 7 and 8. The above mentioned studies concluded that the excitation and deexcitation processes in H∗(n) + H collisions should be included ab initio into future non-LTE models of the solar atmosphere. The importance and effects of the atom-Rydberg atom (n − n′)-mixing processes have also been analyzed in Barklem (2007) and Mashonkina (2009).

We found no non-LTE models similar to that of Vernazza et al. (1981) for the Sun that would have provided all data necessary for calculations as in Mihajlov et al. (2005), in relation to the atmospheres of DB white dwarfs and other similar helium-rich stellar atmospheres. However, since the influence of strong electromagnetic emission is the same in helium-rich atmospheres as in the Sun, the distribution shape of the helium excited-atom population probably deviates considerably from the Boltzmann distribution. Taking this into account and because the data on the relative efficiencies of atom-Rydberg atom processes and the relevant concurrent processes would be useful for future non-LTE stellar-atmosphere models, the chemi-ionization processes in He∗(n) + He collisions were studied in Mihajlov et al. (2003) in the context of DB white dwarf atmospheres, within the models proposed by Koester (1980). In the current study, for the same reason and using the same models, the efficiencies of the excitation processes 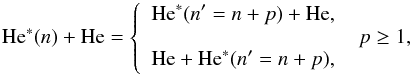He∗(n)+He={He∗(n′=n+p)+He,     p≥1,He+He∗(n′=n+p),\begin{equation} \label{eq:aa1} \textrm{He}^{*}(n)+\textrm{He} = \left\lbrace \begin{array}{ll} \displaystyle{ \textrm{He}^{*}(n'=n + p)+\textrm{He},}\\ \displaystyle{ \qquad \qquad \qquad \qquad \qquad p\ge 1,}\\ \displaystyle{ \textrm{He}+\textrm{He}^{*}(n'=n + p),} \end{array} \right. 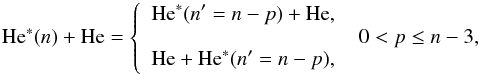\end{equation}(1)and the inverse deexcitation processes He∗(n)+He={He∗(n′=n−p)+He,     0<p≤n−3,He+He∗(n′=n−p),\begin{equation} \label{eq:aa2} \textrm{He}^{*}(n)+\textrm{He} = \left\lbrace \begin{array}{ll} \displaystyle{ \textrm{He}^{*}(n'=n - p)+\textrm{He},}\\ \displaystyle{ \qquad \qquad \qquad \qquad \qquad 0<p\le n-3,}\\ \displaystyle{ \textrm{He}+\textrm{He}^{*}(n'=n - p),} \end{array} \right. \end{equation}(2)(where n + p and n − p are the principal quantum numbers of the final Rydberg states) are compared for 3 ≤ n ≤ 8 with the efficiencies of the relevant concurrent processes. 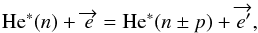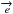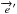Here, we consider the well-known electron-excited-atom collision excitation/deexcitation processes He∗(n)+−0→e=He∗(n±p)+−0→e′,\begin{equation} \label{eq:ea} \textrm{He}^{*}(n)+\overrightarrow{e} =\textrm{He}^{*}(n \pm p)+\overrightarrow{e'}, \end{equation}(3)where −0→e\hbox{$\overrightarrow{e}$} and −0→e′\hbox{$\overrightarrow{e}'$} denote a free electron in the initial and final states, respectively. The necessary calculations were performed using the models in Koester (1980) for DB white dwarf atmospheres with log  g = 8 and Teff = 12 000 K and Teff = 14 000 K.

2. Theoretical remarks

As several of the above mentioned studies have reported, the same dipole resonant mechanism (DRM) causes the non-elastic (n − n′)-mixing and chemi-ionization processes in A∗(n) + A collisions. The DRM was also discussed in detail in Mihajlov et al. (2012). For the (n − n′)-mixing processes (1) and (2), with A = He, the DRM assumes that they occur in the region Rn;n ± p ≪ rn, where R is the internuclear distance and rn ~ n2 is the characteristic radius of atom He∗(n), in the vicinity of the corresponding resonant points Rn;n ± p. These parameters are found to be the roots of the equation U2(R) − U1(R) = εn ± p − εn, where εn and εn ± p denote the energies of the Rydberg states | n > and | n ± p > with the principal quantum numbers n and n ± p; and U1(R) and U2(R) are the adiabatic energies of the electronic ground state | 1;R > and the first excited state | 2;R > of the molecular ion 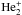He2+\hbox{$\textrm{He}_{2}^{+}$}. We took the potential curves U1(R) and U2(R) from Ignjatović et al. (2009) and following the foundational work of Janev & Mihajlov (1979), which focuses on the (n − n′)-mixing processes, we assumed that the processes (1) and (2) are caused exclusively by the transitions | n > → |n + p > and | n > → |n − p > of the outer electron, which occur simultaneously with the transitions | 2;R > → |1;R > and | 1;R > → |2;R >, respectively, in the subsystem He+ + He, close to the resonant points Rn;n ± p. This fact is responsible for the resonant character of the processes in (1) and (2).

For A = H only chemi-ionization processes with n ≥ 4 and (n − n′)-mixing processes with min(n,n′) ≥ 4 can be described on the basis of the DRM, which caused by the existence of the stable negative ion H−. In contrast, for A = He, the excited helium state with n = 3 can be taken as the lower boundary of the block of Rydberg states. This was also used in Mihajlov et al. (2003), who focused on the chemi-ionization processes in DB white dwarf atmospheres.

The processes (1) and (2) are characterized by the excitation and deexcitation rate coefficients Kn;n + p(T) and Kn;n − p(T), where T is the local temperature of the atomic particles in the considered stellar atmosphere. In accordance with the aim of this work, these rate coefficients are defined as the quantities that determine the mean rates of transition (per single excited atom) caused by the processes (1) and (2) between whole shells with a given n and n ± p. They are determined here using a method similar to that described in Mihajlov et al. (2008): the excitation rate coefficients Kn;n + p(T) are calculated directly and numerically in the semi-classical way, while the deexcitation rate coefficients Kn;n − p(T) are determined later according to the principle of thermodynamical balance. All necessary expressions are given in Mihajlov et al. (2008).

Table 1

Excitation rate coefficients K3;3 + p(T) for 1 ≤ p ≤ 5 in [10-9 cm3 s-1].

For the DB white dwarf atmospheres considered here, the values of Kn;n + p(T) and Kn;n − p(T), which are used in Eqs. (1) and (2) for all necessary temperatures, can be calculated in principle by fitting the values of Kn;n + p(T) presented in Table 2 of Mihajlov et al. (2008), but only for the region 4 ≤ n ≤ 8. Bearing this in mind, Table 1 shows the values of the excitation rate coefficients K3;n + p(T) when 1 ≤ p ≤ 5. These values, together with Table 1 in Mihajlov et al. (2008), enable the calculation of Kn;n + p(T) and Kn;n − p(T) for the entire block, 3 ≤ n ≤ 8.

The concurrent electron-Rydberg atom processes (3) are characterized here by the rate coefficients αn;n ± p(Te = T), where Te denotes the electron temperature, which in the general case is not equal to the atomic temperature. In the current study, the values of αn;n ± p(T) are determined from the corresponding expressions given in Vriens & Smeets (1980) and Johnson (1972). We note that ion-atom non elastic collisional processes, although they are also characterized by long-range interaction, cannot be concurrent. The reason is the huge difference in masses of electron and ion, which causes the impact ion-atom velocity to be several orders of magnitudes lower than electron-atom impact velocity.

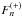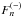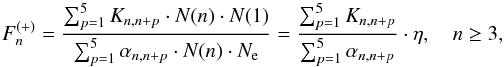To estimate the relative efficiency of processes (1) and (2) and the concurrent processes (3), it is sufficient to study the behavior of quantities Fn(+)\hbox{$F_{n}^{(+)}$} and Fn(−)\hbox{$F_{n}^{(-)}$} in the considered DB white dwarf atmospheres, which are given by the expressions Fn(+)=∑p=15Kn,n+p·N(n)·N(1)∑p=15αn,n+p·N(n)·Ne=∑p=15Kn,n+p∑p=15αn,n+p·η, n≥3,\begin{equation} F_{n}^{(+)}=\frac{\sum_{p=1}^{5} K_{n,n+p}\cdot N(n)\cdot N(1)} {\sum_{p=1}^{5} \alpha_{n,n+p}\cdot N(n)\cdot N_{\rm e}} = \frac{\sum_{p=1}^{5} K_{n,n+p}}{\sum_{p=1}^{5} \alpha_{n,n+p}}\cdot\eta, \quad n\ge 3, \label{eq:F+} \end{equation}(4)and Fn(−)=∑p=1n−3Kn,n−p·N(n)·N(1)∑p=1n−3αn,n−p·N(n)·Ne=∑p=1n−3Kn,n−p∑p=1n−3αn,n−p·η, n≥4,\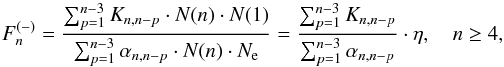begin{equation} F_{n}^{(-)}=\frac{\sum_{p=1}^{n-3} K_{n,n-p}\cdot N(n)\cdot N(1)} {\sum_{p=1}^{n-3} \alpha_{n,n-p}\cdot N(n)\cdot N_{\rm e}} = \frac{\sum_{p=1}^{n-3} K_{n,n-p}}{\sum_{p=1}^{n-3} \alpha_{n,n-p}}\cdot\eta, \quad n\ge 4, \label{eq:F-} \end{equation}(5)where N(n), N(1), and Ne are the local densities of all Rydberg helium atoms in the states with a given n ≥ 3, of a helium atom in the ground state, and of free electrons, respectively; and the products Kn,n ± p·N(n)·N(1) and αn,n ± p·N(n)·Ne are the partial atom- and electron-Rydberg atom excitation/deexcitation fluxes. The factor η is defined here by the relation 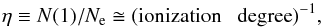η≡N(1)/Ne≅(ionizationdegree)-1,\begin{equation} \eta \equiv N(1)/N_{\rm e} \cong (\mbox{ionization \; degree})^{-1}, \label{eq:eta} \end{equation}(6)and its behavior in the atmospheres of the considered DB white dwarfs (which is very important for the studied processes) is presented in Fig. 1.

thumbnail Fig. 1

Parameters (temperature T – full line and η = N(1)/Ne – dotted) for DB white dwarf atmosphere models with log  g = 8 and Teff = 12 000 K and 14 000 K from Koester (1980) as functions of log  τ, where τ is the Rosseland optical depth.

thumbnail Fig. 2

Behavior of quantities Fn(+)\hbox{$F_{n}^{(+)}$}, given by Eq. (4) with 3 ≤ n ≤ 8, on the basis of DB white dwarf atmosphere models from Koester (1980) for log  g = 8 and Teff = 12 000 K and 14 000 K, as functions of log  τ, where τ is the Rosseland optical depth.

3. Results and discussion

Figure 2 illustrates the behavior of the quantity Fn(+)\hbox{$F_{n}^{(+)}$} with 3 ≤ n ≤ 8 in the DB white dwarf atmospheres described by the models presented in Koester (1980), for log  g = 8 and Teff = 12 000 K and 14 000 K. All results were obtained using the data from Koester (1980), and these quantities are presented as functions of log τ, where τ is the Rosseland optical depth. Figure 2 unambiguously shows that for DB white dwarf atmospheres with Teff ≲ 14 000 K, the excitation processes (1) in the lower part of the Rydberg block (3 ≤ n ≤ 8) must be taken into account as a new important factor that influences the helium Rydberg-state populations. Figure 2 shows that in the parts of the atmosphere where the ionization degree is ≲10-3, the processes (1) with n = 3,4, and 5 are dominant with respect to the known concurrent processes (3); for n = 6 and 7 they are dominant in the parts where the ionization degree is ≲10-4; and in the remaining parts their efficiency is comparable with the efficiency of the processes (3). Even the efficiency of the processes (1) with n = 8 is close to, or at least comparable with, the efficiency of the processes (3) in the parts where the ionization degree is <10-4.

These facts are especially important for the considered DB white dwarf atmospheres, because for any temperature from the relevant temperature regions, the corresponding Boltzman distribution of the excited helium atom populations will have a distinct minimum (known as the “bottleneck”) only in the region 3 ≤ n < 8. Thus, it is correct to expect that even a considerable perturbation of the mentioned distribution would not result in a significant change in the position of this minimum. Hence, it follows that the excitation processes (1) should by all means be taken into account in any future non-LTE model of DB white dwarf atmospheres with similar parameters.

Examining the behavior of the quantities 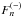Fn(−)\hbox{$F_{n}^{(-)}$} with 4 ≤ n ≤ 8 in the same DB white dwarf atmospheres would lead to the same conclusions, including the necessity of introducing the deexcitation processes (2) into the mentioned models. For this reason, the efficiencies of the considered (n − n′)-mixing processes are only illustrated in Fig. 2.

Finally, we emphasize that these results are relevant not only to the atmospheres of the DB white dwarfs mentioned here, but also to a considerably wider range of helium-rich stellar atmospheres. For instance, an entire array of white dwarfs of other types, as described in Wegner & Koester (1985), Dufour et al. (2006, 2007), have similar parameters. Consequently, processes (1) and (2) must be just as important as the concurrent processes (3). Overall, the findings suggest that the considered atom-Rydberg atom (n − n′)-mixing processes (1) and (2) should be included ab initio in the modeling of the helium-rich white dwarf atmospheres.

Acknowledgments

The authors are grateful to the Ministry of Education, Science and Technological Development of the Republic of Serbia for the support of this work within the projects 176002, III4402.

References

  1. Barklem, P. S. 2007, A&A, 466, 327 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Dufour, P., Bergeron, P., Schmidt, G. D., et al. 2006, ApJ, 651, 1112 [NASA ADS] [CrossRef] [Google Scholar]
  3. Dufour, P., Bergeron, P., Liebert, J., et al. 2007, ApJ, 663, 1291 [NASA ADS] [CrossRef] [Google Scholar]
  4. Ignjatović, L. M., Mihajlov, A. A., Sakan, N. M., Dimitrijević, M. S., & Metropoulos, A. 2009, MNRAS, 396, 2201 [NASA ADS] [CrossRef] [Google Scholar]
  5. Janev, R. K., & Mihajlov, A. A. 1979, Phys. Rev. A, 20, 1890 [NASA ADS] [CrossRef] [Google Scholar]
  6. Janev, R. K., & Mihajlov, A. A. 1980, Phys. Rev. A, 21, 819 [NASA ADS] [CrossRef] [Google Scholar]
  7. Johnson, L. C. 1972, ApJ, 174, 227 [NASA ADS] [CrossRef] [Google Scholar]
  8. Koester, D. 1980, A&AS, 39, 401 [NASA ADS] [Google Scholar]
  9. Mashonkina, L. 2009, Phys. Scr. T, 134, 014004 [NASA ADS] [CrossRef] [Google Scholar]
  10. Mihajlov, A. A. 1982, in Proceedings of international conference on plasma physics. G [Google Scholar]
  11. Mihajlov, A. A., Dimitrijević, M. S., & Djurić, Z. 1996, Phys. Scri., 53, 159 [Google Scholar]
  12. Mihajlov, A. A., Ignjatović, L. M., Vasilijević, M. M., & Dimitrijević, M. S. 1997, A&A, 324, 1206 [NASA ADS] [Google Scholar]
  13. Mihajlov, A. A., Jevremović, D., Hauschildt, P., et al. 2003, A&A, 403, 787 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Mihajlov, A. A., Ignjatović, L. M., Djurić, Z., & Ljepojević, N. N. 2004, J. Phys. B At. Mol. Phys., 37, 4493 [Google Scholar]
  15. Mihajlov, A. A., Ignjatović, L. M., & Dimitrijević, M. S. 2005, A&A, 437, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Mihajlov, A. A., Jevremović, D., Hauschildt, P., et al. 2007, A&A, 471, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Mihajlov, A. A., Ignjatović, L. M., Srećković, V. A., & Djurić, Z. 2008, J. Quant. Spec. Radiat. Transf., 109, 853 [NASA ADS] [CrossRef] [Google Scholar]
  18. Mihajlov, A. A., Ignjatović, L. M., Srećković, V. A., & Dimitrijević, M. S. 2011, ApJS, 193, 2 [NASA ADS] [CrossRef] [Google Scholar]
  19. Mihajlov, A. A., Srećković, V. A., Ignjatović, L. M., & Klyucharev, A. N. 2012, J. Cluster Sci., 23, 47 [CrossRef] [Google Scholar]
  20. Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
  21. Vriens, L., & Smeets, A. H. M. 1980, Phys. Rev. A, 22, 940 [NASA ADS] [CrossRef] [Google Scholar]
  22. Wegner, G., & Koester, D. 1985, ApJ, 288, 746 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Excitation rate coefficients K3;3 + p(T) for 1 ≤ p ≤ 5 in [10-9 cm3 s-1].

In the text

All Figures

thumbnail Fig. 1

Parameters (temperature T – full line and η = N(1)/Ne – dotted) for DB white dwarf atmosphere models with log  g = 8 and Teff = 12 000 K and 14 000 K from Koester (1980) as functions of log  τ, where τ is the Rosseland optical depth.
In the text
thumbnail Fig. 2

Behavior of quantities Fn(+)\hbox{$F_{n}^{(+)}$}, given by Eq. (4) with 3 ≤ n ≤ 8, on the basis of DB white dwarf atmosphere models from Koester (1980) for log  g = 8 and Teff = 12 000 K and 14 000 K, as functions of log  τ, where τ is the Rosseland optical depth.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.