Theoretical formulation of Doppler redistribution in scattering polarization within the framework of the velocity-space density matrix formalism

L. Belluzzi; E. Landi Degl’Innocenti; J. Trujillo Bueno

doi:10.1051/0004-6361/201220588

Home

All issues

Volume 552 (April 2013)

A&A, 552 (2013) A72

Full HTML

Free Access

Issue		A&A Volume 552, April 2013


Article Number		A72
Number of page(s)		14
Section		Astrophysical processes
DOI		https://doi.org/10.1051/0004-6361/201220588
Published online		28 March 2013

A&A 552, A72 (2013)

Theoretical formulation of Doppler redistribution in scattering polarization within the framework of the velocity-space density matrix formalism

L. Belluzzi¹^,2, E. Landi Degl’Innocenti³ and J. Trujillo Bueno¹^,2^,4

¹ Instituto de Astrofísica de Canarias, C. Vía Láctea s/n, 38205 La Laguna Tenerife, Spain
e-mail: belluzzi@iac.es
² Departamento de Astrofísica, Facultad de Física, Universidad de La Laguna, 38206, La Laguna Tenerife, Spain
³ Dipartimento di Fisica e Astronomia, Università di Firenze, Largo E. Fermi 2, 50125 Firenze, Italy
⁴ Consejo Superior de Investigaciones Científicas, Spain

Received: 18 October 2012
Accepted: 25 January 2013

Abstract

Within the framework of the density matrix theory for the generation and transfer of polarized radiation, velocity density matrix correlations represent an important physical aspect that, however, is often neglected in practical applications when adopting the simplifying approximation of complete redistribution on velocity. In this paper, we present an application of the non-LTE problem for polarized radiation taking such correlations into account through the velocity-space density matrix formalism. We consider a two-level atom with infinitely sharp upper and lower levels, and we derive the corresponding statistical equilibrium equations, neglecting the contribution of velocity-changing collisions. Coupling such equations with the radiative transfer equations for polarized radiation, we derive a set of coupled equations for the velocity-dependent source function. This set of equations is then particularized to the case of a plane-parallel atmosphere. The equations presented in this paper provide a complete and solid description of the physics of pure Doppler redistribution, a phenomenon generally described within the framework of the redistribution matrix formalism. The redistribution matrix corresponding to this problem (generally referred to as R_I) is derived starting from the statistical equilibrium equations for the velocity-space density matrix and from the radiative transfer equations for polarized radiation, thus showing the equivalence of the two approaches.

Key words: atomic processes / line: formation / polarization / radiative transfer / scattering / stars: atmospheres

© ESO, 2013

1. Introduction

When polarization phenomena are considered, the usual description of the excitation state of an atomic system in terms of the population of its energy levels is not adequate, and it is necessary to specify the population of each magnetic sublevel, as well as the quantum interference (or coherence) that might be present between pairs of them. Whenever the magnetic sublevels of a given energy level are unevenly populated and/or quantum interference between pairs of them are present, the atomic system is said to be polarized. Atomic polarization is generally induced whenever an atomic system is excited by means of a physical process which is not spatially isotropic.

A powerful theoretical tool that allows the description of the full excitation state of an atomic system in a very compact way is the so-called density operator (see Fano 1957). The most natural basis for defining the matrix elements of the density operator is the basis of the eigenvectors of the total angular momentum | αJM ⟩, with J the total angular momentum, M its projection along the quantization axis, and α a set of inner quantum numbers. On this basis, the elements of the density matrix are given by $⟨ αJM | ρ̂ | α^{'} J^{'} M^{'} ⟩ \equiv ρ (αJM, α^{'} J^{'} M^{'}),$ $\begin{equation} \langle \alpha J M | \, \hat{\rho} \, |\alpha^{\prime} J^{\prime} M^{\prime} \rangle \equiv \rho(\alpha J M, \alpha^{\prime} J^{\prime} M^{\prime}) , \end{equation}$ (1)with $\hbox{$\hat{\rho}$}$ the density operator. The diagonal elements represent the populations of the magnetic sublevels, the off-diagonal elements the quantum interference (or coherence) between different magnetic sublevels (see Landi Degl’Innocenti & Landolfi 2004, hereafter LL04). For the sake of simplicity, in this paper we only consider interference between pairs of magnetic sublevels pertaining to the same J-level, which is a good approximation for the investigation of many solar spectral lines (see LL04 and Belluzzi & Trujillo Bueno 2011, for a detailed discussion of the importance of interference between different J-levels in determining the wing polarization of multiplet lines). We thus consider only the density matrix elements of the form ρ(αJM,αJM′). In general it is convenient to work in terms of the multipole moments of the density matrix (or spherical statistical tensors) $ρ_{Q}^{K} (αJ) = \sum_{M M^{'}} (- 1)^{J - M} \sqrt{2 K + 1} (\begin{matrix} J & J & K \\ M & - M^{'} & - Q \end{matrix}) ρ (αJM,αJ M^{'}),$ $\begin{equation} \rho^K_Q(\alpha J) = \sum_{M M^{\prime}} (-1)^{J-M} \sqrt{2K + 1} \, \left( \begin{array}{ccc} J & J & K \\ M & -M^{\prime} & -Q \end{array} \right) \, \rho(\alpha J M, \alpha J M^{\prime}) , \end{equation}$ (2)which transform as irreducible tensors under a rotation of the reference system.

Since the radiation field experienced by an atom depends on its velocity because of the Doppler effect, the density matrix will also depend on the velocity ν of the atom. Indicating with $ρ_{Q}^{K} (αJ; ν)$ $\hbox{$\rho^K_Q(\alpha J; \vec{\varv})$}$ the ν-dependent spherical statistical tensor of the atomic system, and with f(ν) the velocity distribution function of the atoms in a given point of the plasma, a complete statistical description of the atom is given by the product $f (ν) ρ_{Q}^{K} (αJ; ν)$ $\hbox{$f(\vec{\varv}) \, \rho^K_Q(\alpha J; \vec{\varv})$}$ , generally referred to as velocity-space density matrix. The need for introducing this quantity was put forward by Landi Degl’Innocenti (1996), who pointed out the importance of velocity density matrix correlations in polarized radiative transfer. The statistical equilibrium equations for the velocity-space density matrix can be written in the form (see Sect. 13.2 of LL04) $\frac{d}{d t} [f (ν) ρ_{Q}^{K} (αJ; ν)^{]} = f (ν) {(\frac{d}{d t} ρ_{Q}^{K} (αJ; ν))}_{0} + {(\frac{δ}{δt} [f (ν) ρ_{Q}^{K} (αJ; ν)^{]})}_{vel . chang . coll .} .$ $\begin{equation} \frac{\rm d}{{\rm d} t} \left[ f(\vec{\varv}) \, \rho^K_Q(\alpha J; \vec{\varv}) \right] = f(\vec{\varv}) \left( \frac{\rm d}{{\rm d} t} \, \rho^K_Q(\alpha J;\vec{\varv}) \right)_{0} + \left( \frac{\delta}{{\delta} t} \left[ f(\vec{\varv}) \, \rho^K_Q(\alpha J; \vec{\varv}) \right] \right)_{\rm vel. \, chang. \, coll.} \! . \label{Eq:Gen_SEE} \end{equation}$ (3)The first term on the righthand side is due to processes that, as a first approximation, are not effective in changing the velocity of the atom: these include radiative processes (absorption and emission of photons), inelastic and superelastic collisions with electrons, and depolarizing collisions with neutral hydrogen atoms¹. The second term, which can be regarded as a generalization of the Boltzmann term which is met in the kinetic theory of gases, is due to collisions that are able to modify the velocity of the atom (velocity-changing collisions). Such collisions, which are characterized by very small impact parameters and by rather large exchange of kinetic energy, generally induce transitions between different energy levels, and thus affect the atomic density matrix. Because of the generalized Boltzmann term, Eq. (3) is extremely complicated, and two different approximations are generally introduced.

The first one consists in neglecting the generalized Boltzmann term (velocity-coherence approximation). As discussed in Sect. 13.2 of LL04, this is a good approximation in the outer layers of a stellar atmosphere, where the number density of perturbers responsible for velocity-changing collisions (typically short-range collisions with hydrogen atoms or ions) is sufficiently low, and this kind of collisions are indeed negligible. Under this approximation, the ν-dependence of the density matrix is only due to the fact that atoms moving with different velocities may experience, because of the Doppler effect, different radiation fields.

The second approximation is to assume that velocity-changing collisions are so efficient in reshuffling the atomic velocities that any velocity density matrix correlation is lost (complete redistribution on velocity approximation). In this case, the velocity-space density matrix is given by $f (ν) ρ_{Q}^{K} (αJ)$ $\hbox{$f(\vec{\varv}) \, \rho^K_Q(\alpha J)$}$ , the density matrix being independent of ν. Since velocity-changing collisions also contribute to depolarize the atomic system, when the complete redistribution on velocity approximation is justified, polarization phenomena are generally negligible. For this reason, it is customary to consider an intermediate approach which consists in neglecting the generalized Boltzmann term, still assuming a velocity-independent density matrix.

The general problem of interpreting the spectropolarimetric profiles of lines formed in an optically thick plasma, such as a stellar atmosphere, requires the self-consistent solution of the statistical equilibrium equations and of the radiative transfer equations, taking into account polarization phenomena, both in the atomic system and in the radiation field (see Trujillo Bueno 2003). This problem has been referred to as the non-LTE problem of the second kind (see LL04), so to distinguish it from the usual non-LTE problem where polarization phenomena are neglected. A detailed discussion of the general non-LTE problem of the second kind, under the approximation of complete redistribution on velocity, is presented in Chapter 14 of LL04.

In this paper, we present an application of the non-LTE problem of the second kind under the velocity-coherence approximation previously discussed. We consider the basic case of a two-level atom with infinitely sharp upper and lower levels. Starting from the statistical equilibrium equations for the velocity-space density matrix (Sect. 3), and from the radiative transfer equations for polarized radiation (Sect. 4), we derive a set of coupled equations for the velocity-dependent source function (Sect. 5). This set of coupled equations is then specified to the particular case of a Maxwellian distribution of velocities, and it is finally applied to the particular case of a plane-parallel atmosphere (Sect. 6). From the same equations we also derive the redistribution phase-matrix corresponding to this physical problem (generally referred to as R_I), thus showing the equivalence of this widely applied approach to the one described in this paper (Sect. 7).

The more realistic case of partial frequency redistribution, assuming a two-level model atom with infinitely-sharp and unpolarized lower level, and with a naturally and/or collisionally broadened upper level, has been considered by several authors (e.g., Omont et al. 1972, 1973; Domke & Hubeny 1988; Bommier 1997a,b; Sampoorna 2012), providing expressions for the ensuing redistribution matrix. In this paper we show, for the academic case of a two-level atom with infinitely-sharp upper and lower levels, how the phenomenon of pure Doppler redistribution can be rigorously described through the velocity-space density matrix formalism. This formalism allows us to describe the physics of the atom-photon interaction in a very transparent way (e.g., it allows us to clearly identify correlations between atoms located at different points of the plasma), and it highlights the underlying approximations (e.g., the neglect of velocity-changing collisions). The equations that are obtained are very general, and can be applied to arbitrary velocity distributions. Moreover, they are able to account for the presence of atomic polarization in the lower level of the considered transition, and they are suitable for a generalization to the multilevel case. The application of the velocity-space density matrix formalism for the description of a two-level atom with broadened upper level is presently under investigation, and is not discussed in this paper.

2. Formulation of the problem: hypotheses and approximations

We consider a two-level atom with an unpolarized lower level and we suppose that the radiation field incident on the atom is weak, in the sense that the average number of photons per mode, $\hbox{$\bar n$}$ , is much smaller than unity, which justifies to neglect stimulated emission.

We suppose that a collection of such atoms is distributed within a static medium of arbitrary shape. In this medium the atoms interact with a magnetic field, B, and with a population of colliding particles having a Maxwellian distribution of velocities characterized by the temperature T. No restriction is made on the spatial variation within the medium of the temperature T of the colliders, of the densities of the atoms and colliders, and of the magnetic field vector B. We suppose that the magnetic field is weak (in the sense that the associated Larmor frequency ν_L is much lower than the frequency width Δν_P of the absorption profile) and that the broadening of both the upper and lower levels is much smaller than Δν_P, so that they can be considered as infinitely sharp, and the flat-spectrum approximation is satisfied².

The atoms are characterized by an arbitrary velocity distribution f(ν) that, for the sake of simplicity, we assume to be constant throughout the medium. Taking velocity density matrix correlations into account, at any point P of the medium, of coordinate x, the atom is thus described by the velocity-space density matrix $f (ν) {}^{[}ρ_{Q}^{K} (αJ; ν)^{]}_{x}$ $\hbox{$f(\vec \varv) \left[ \rho^K_Q(\alpha J; \vec{\varv}) \right]_{\vec{x}}$}$ , where (αJ) = (α_uJ_u) for the upper level and (αJ) = (α_ℓJ_ℓ) for the lower level. Neglecting velocity-changing collisions (i.e. assuming the velocity-coherence approximation described in Sect. 1), the velocity-space density matrix evolves with time according to the equation $\frac{d}{d t} (f (ν) {[ρ_{Q}^{K} (αJ; ν)^{]}}_{x}) = f (ν) {(\frac{d}{d t} {[ρ_{Q}^{K} (αJ; ν)^{]}}_{x})}_{0},$ $\begin{equation} \frac{\rm d}{{\rm d} t} \left( f(\vec \varv) \left[ \rho^K_Q(\alpha J; \vec \varv) \right]_{\vec x} \right) = f(\vec \varv) \left( \frac{\rm d}{{\rm d} t} \left[ \rho^K_Q(\alpha J; \vec \varv) \right]_{\vec x} \right)_{0} , \end{equation}$ (4)which is solved by $\begin{matrix} \frac{d}{d t} f (ν) = 0, \\ \frac{d}{d t} {[ρ_{Q}^{K} (αJ; ν)^{]}}_{x} = {(\frac{d}{d t} {[ρ_{Q}^{K} (αJ; ν)^{]}}_{x})}_{0} . \end{matrix}$ $\begin{eqnarray} \label{Eq:SEE_rho} &&\frac{\rm d}{{\rm d} t} \, f(\vec{\varv}) = \, 0 , \\ &&\frac{\rm d}{{\rm d} t} \, \left[ \rho^K_Q(\alpha J; \vec{\varv}) \right]_{\vec x} = \, \left( \frac{\rm d}{{\rm d} t} \left[ \rho^K_Q(\alpha J; \vec{\varv}) \right]_{\vec x} \right)_{0}. \end{eqnarray}$ As previously pointed out, the term on the righthand side of Eq. (5) contains the “ordinary” processes due to the atom-radiation interaction and to collisions. The value of ${}^{[}ρ_{Q}^{K} (αJ; ν)^{]}_{x}$ $\hbox{$\left[ \rho^K_Q(\alpha J; \vec \varv) \right]_{\vec x}$}$ can thus be found by solving the statistical equilibrium equations presented in LL04, taking properly into account the explicit dependence of the radiative and collisional rates on the velocity of the atom. The velocity distribution f(ν), on the other hand, remains undetermined, and can only be established by means of different physical considerations. In many cases, it can simply be assumed to be a Maxwellian, possibly centered at a non-zero velocity, like in the case of the solar wind. In the next Sections, if not explicitly specified, we consider an arbitrary velocity distribution f(ν).

In terms of scattering processes, our model allows us to describe coherent scattering in the atom rest frame, with purely Doppler redistribution in the observer frame. Within the framework of the redistribution matrix formalism, following the terminology introduced by Hummer (1962), this kind of process, in the case of a Maxwellian velocity distribution, is described by the R_I redistribution function.

3. The statistical equilibrium equations

Referring to the geometry of Fig. 1, in the “fixed” (or laboratory) reference system Σ, the statistical equilibrium equation for the multipole moments of the upper level is the same as Eq. (14.2) of LL04, with the only difference that the radiative and collisional rates now depend explicitly on the velocity ν of the atom. We thus have $\begin{matrix} {(\frac{d}{d t} {[ρ_{Q}^{K} (α_{u} J_{u}; ν)^{]}}_{x})}_{0} & = & - 2 π i ν_{L} g_{α_{u} J_{u}} \sum_{Q^{'}} 𝒦_{Q Q^{'}}^{K} {[ρ_{Q^{'}}^{K} (α_{u} J_{u}; ν)^{]}}_{x} \\ + \sum_{K^{'} Q^{'}} T_{A} (α_{u} J_{u} KQ, α_{ℓ} J_{ℓ} K^{'} Q^{'}) {[ρ_{Q^{'}}^{K^{'}} (α_{ℓ} J_{ℓ}; ν)^{]}}_{x} \\ - \sum_{K^{'} Q^{'}} [R_{E} (α_{u} J_{u} KQ K^{'} Q^{'}) + R_{S}^{} (α_{u} J_{u} KQ K^{'} Q^{'})^{]} {[ρ_{Q^{'}}^{K^{'}} (α_{u} J_{u}; ν)^{]}}_{x} \\ + \sqrt{\frac{2 J_{ℓ} + 1}{2 J_{u} + 1}} C_{I}^{(K)} (α_{u} J_{u}, α_{ℓ} J_{ℓ}) {[ρ_{Q}^{K} (α_{ℓ} J_{ℓ}; ν)^{]}}_{x} \\ - [C_{S}^{(0)} (α_{ℓ} J_{ℓ}, α_{u} J_{u}) + D^{(K)} (α_{u} J_{u})^{]} {[ρ_{Q}^{K} (α_{u} J_{u}; ν)^{]}}_{x}, \end{matrix}$ $\begin{eqnarray} \label{Eq:SEE} \left( \frac{\rm d}{{\rm d} t} \left[ \rho^K_Q(\alpha_u J_u ;\vec \varv ) \right]_{\vec x} \right)_{0} & = & -2 \pi {\rm i} \,\nu_{\rm L} \, g_{\alpha_u J_u} \, \sum_{Q'} \, {\mathcal K}^K_{QQ'} \, \left[ \rho^K_{Q'}(\alpha_u J_u ; \vec \varv ) \right]_{\vec x} \nonumber\\ &&\quad + \sum_{K'Q'} \, {\mathbb T}_{\! \rm A}(\alpha_u J_u KQ, \alpha_\ell J_\ell K'Q') \, \left[ \rho^{K'}_{Q'}(\alpha_\ell J_\ell ; \vec \varv ) \right]_{\vec x} \nonumber\\ &&\quad - \sum_{K'Q'} \, \left[ {\mathbb R}_{\rm E}(\alpha_u J_u KQK'Q') + {\mathbb R}_{\rm S}^{\phantom K}(\alpha_u J_u KQK'Q') \right] \left[ \rho^{K'}_{Q'}(\alpha_u J_u ; \vec \varv ) \right]_{\vec x} \nonumber\\ &&\quad + \, \sqrt{\frac{2J_\ell+1}{2J_u+1}} \, C_{\rm I}^{(K)}(\alpha_u J_u, \alpha_\ell J_\ell) \, \left[ \rho^K_Q(\alpha_\ell J_\ell ; \vec \varv ) \right]_{\vec x} \nonumber\\ &&\quad - \left[ C_{\rm S}^{(0)}(\alpha_\ell J_\ell, \alpha_u J_u) \, + D^{\, (K)}(\alpha_u J_u) \right] \left[ \rho^K_Q(\alpha_u J_u ; \vec \varv ) \right]_{\vec x} , \end{eqnarray}$ (7)where all the rates are evaluated at point x, ν_L is the Larmor frequency at the same point, and g_{α_uJ_u} is the Landé factor of the upper level.

Fig. 1

Geometry of the problem. At each point P of the medium, the magnetic field vector B is specified by the angles θ_B and χ_B, defined in the fixed reference system Σ ≡ (xyz). The polarization unit vector e_a(Ω) specifies the reference direction for positive Q of the radiation flowing through P in the direction Ω, specified by the angles θ and χ in the fixed reference system.

The kernel $𝒦_{Q Q^{'}}^{K}$ $\hbox{${\mathcal K}^K_{QQ'}$}$ is given by (see Eq. 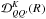(7.79) of LL04) $𝒦_{Q Q^{'}}^{K} = \sum_{Q^{′′}} 𝒟_{Q^{′′} Q}^{K} (R_{B})^{*} Q^{′′} 𝒟_{Q^{′′} Q^{'}}^{K} (R_{B}),$ $\begin{equation} {\mathcal K}^K_{QQ^{\prime}} = \sum_{Q^{\prime \prime}} \, {\mathcal D}^K_{Q^{\prime \prime} Q}(R_B)^{\ast} \; Q^{\prime \prime} \; {\mathcal D}^K_{Q^{\prime \prime} Q^{\prime}} (R_B) , \end{equation}$ (8)where $𝒟_{Q Q^{'}}^{K} (R)$ $\hbox{${\mathcal D}^K_{QQ^{\prime}}(R)$}$ are rotation matrices, and R_B is the rotation that carries the local “magnetic” reference system (having the z-axis aligned with the magnetic field) into the “fixed” reference system Σ. In terms of Euler angles one simply has (see Fig. 1 for the definition of the angles) $\begin{matrix} R_{B} \equiv (- γ_{B}, - θ_{B}, - χ_{B}), \end{matrix}$ $\begin{eqnarray*} R_B \equiv (-\gamma_B,-\theta_B,-\chi_B) \nonumber , \end{eqnarray*}$ where γ_B is an arbitrary angle that can be set to zero. The main properties and the explicit expressions of the components of $𝒦_{Q Q^{'}}^{K}$ $\hbox{${\mathcal K}^K_{QQ^{\prime}}$}$ are given in Appendix 19 of LL04. The assumptions that we have introduced yield two basic simplifications in Eq. (7):

because stimulation effects are neglected, the relaxation rate R_S iszero;
because lower-level polarization is neglected, the statistical tensors of the lower level reduce to $ρ_{Q}^{K} (α_{ℓ} J_{ℓ}; ν) = ρ_{0}^{0} (α_{ℓ} J_{ℓ}; ν) δ_{K 0} δ_{Q 0}$ $\hbox{$\rho^K_Q(\alpha_\ell J_\ell ; \vec \varv ) = \rho^0_0(\alpha_\ell J_\ell ; \vec \varv ) \, \delta_{K0} \, \delta_{Q0}$}$ .

This implies that the only radiative rate needed in Eq. (7) is the absorption rate, T_A(α_uJ_uKQ,α_ℓJ_ℓ 0 0). Taking into account that the upper and lower levels of the atom are infinitely sharp, such rate, in the fixed reference frame, is given by (cf. Eq. (10.9) of LL04) $T_{A} (α_{u} J_{u} KQ, α_{ℓ} J_{ℓ} 0 0) = \sqrt{3 (2 J_{ℓ} + 1)} B (α_{ℓ} J_{ℓ} \to α_{u} J_{u}) (- 1)^{1 + J_{ℓ} + J_{u} + Q} {\begin{matrix} 1 & 1 & K \\ J_{u} & J_{u} & J_{ℓ} \end{matrix}} {[J_{- Q}^{K} (ν_{0})^{]}}_{c . f .},$ $\begin{equation} {\mathbb T}_{\rm A}(\alpha_u J_u K Q, \alpha_\ell J_\ell \, 0 \, 0) = \sqrt{3 (2 J_\ell + 1)} \; B(\alpha_\ell J_\ell \rightarrow \alpha_u J_u) \, (-1)^{1 + J_\ell + J_u + Q} \left\{ \! \begin{array}{ccc} 1 & 1 & K \\ J_u & J_u & J_\ell \end{array} \right\} \, \left[ J^K_{-Q}(\nu_0) \right]_{\rm c.f.} \;\, , \end{equation}$ (9)where ${}^{[}J_{- Q}^{K} (ν_{0})^{]}_{c . f .}$ $\hbox{$\left[ J^K_{-Q}(\nu_0) \right]_{\rm c.f.}$}$ is the radiation field tensor calculated in the atom rest frame, or comoving frame (it describes the radiation field as “seen” by the atom, and it actually depends on its velocity ν in the fixed reference frame), and where ν₀ is the frequency of the transition between the upper and lower level of the atom. In the comoving frame, the radiation field tensor is given by (see Eq. (5.157) of LL04) ${[J_{- Q}^{K} (ν_{0})^{]}}_{c . f .} = 􏽉 \frac{dΩ}{4 π} \sum_{i = 0}^{3} 𝒯_{- Q}^{K} (i, Ω) {[S_{i} (ν_{0}, Ω)]}_{c . f .},$ $\begin{equation} \left[ J^K_{-Q}(\nu_0) \right]_{\rm c.f.} = \oint \frac{{\rm d} \Omega}{4 \pi} \, \sum_{i=0}^3 \, {\mathcal T}^K_{-Q}(i, \vec\Omega) \, \left[ S_{\! i}(\nu_0, \vec\Omega) \right]_{\rm c.f.} , \end{equation}$ (10)where [S_i(ν₀,Ω)]_c.f. are the Stokes parameters of the radiation propagating along the direction Ω at the frequency ν₀, as defined in the comoving frame. In the limit ν/ c ≪ 1 aberration and further relativistic effects can be neglected and the radiation field tensor in the comoving frame can be calculated from the Stokes parameters in the fixed reference frame just taking into account the Doppler effect evaluated to first order in ν/ c. This brings to the following expression ${[J_{- Q}^{K} (ν_{0})^{]}}_{c . f .} = 􏽉 \frac{dΩ}{4 π} \sum_{i = 0}^{3} 𝒯_{- Q}^{K} (i, Ω) S_{i} (ν_{0} + ν_{0} \frac{ν \cdot Ω}{c}, Ω),$ $\begin{equation} \left[ J^K_{-Q}(\nu_0) \right]_{\rm c.f.} = \oint \frac{{\rm d} \Omega}{4 \pi} \, \sum_{i=0}^3 \, {\mathcal T}^K_{-Q}(i, \vec\Omega) \; S_{\! i} \left( \nu_0 + \nu_0 \frac{\vec\varv \cdot \vec\Omega}{c}, \vec\Omega \right) , \label{Eq:JKQ_cf} \end{equation}$ (11)where now S_i are the Stokes parameters measured in the fixed frame.

As far as the inelastic and superelastic collisional rates, $C_{I}^{(K)} (α_{u} J_{u}, α_{ℓ} J_{ℓ})$ $\hbox{$C_{\rm I}^{(K)} (\alpha_u J_u, \alpha_\ell J_\ell)$}$ , and $C_{S}^{(0)} (α_{ℓ} J_{ℓ}, α_{u} J_{u})$ $\hbox{$C_{\rm S}^{(0)} (\alpha_\ell J_\ell,\alpha_u J_u)$}$ are concerned, we suppose that they do not depend on the velocity ν of the atom undergoing the collision. This is a very good approximation, since such collisions are due to electrons, which travel with velocities much higher (typically by two orders of magnitude) than the velocity of the atom. Concerning depolarizing collisions (elastic collisions), basically due to neutral perturbers such as hydrogen atoms, the approximation can be more questionable. For this reason, from now on we denote such rates with the symbol D^(K)(α_uJ_u;ν).

Taking into account these remarks, and recalling the expression of the radiative rate R_E (cf. Eq. (7.14e) of LL04), which obviously does not depend on the velocity of the atom, being due to spontaneous de-excitation processes, we can rewrite Eq. (7) in the form $\begin{matrix} {(\frac{d}{d t} {[ρ_{Q}^{K} (α_{u} J_{u}; ν)^{]}}_{x})}_{0} & = & - 2 π i ν_{L} g_{α_{u} J_{u}} \sum_{Q^{'}} 𝒦_{Q Q^{'}}^{K} {[ρ_{Q^{'}}^{K} (α_{u} J_{u}; ν)^{]}}_{x} \\ - [A (α_{u} J_{u} \to α_{ℓ} J_{ℓ}) + C_{S}^{(0)} (α_{ℓ} J_{ℓ}, α_{u} J_{u}) + D^{(K)} (α_{u} J_{u}; ν)^{]} {[ρ_{Q}^{K} (α_{u} J_{u}; ν)^{]}}_{x} \\ + \sqrt{\frac{2 J_{ℓ} + 1}{2 J_{u} + 1}} [B (α_{ℓ} J_{ℓ} \to α_{u} J_{u}) w_{J_{u} J_{ℓ}}^{(K)} (- 1)^{Q} {[J_{- Q}^{K} (ν_{0})^{]}}_{c . f .} + δ_{K 0} δ_{Q 0} C_{I}^{(0)} (α_{u} J_{u}, α_{ℓ} J_{ℓ})] {[ρ_{0}^{0} (α_{ℓ} J_{ℓ}, ν)^{]}}_{x}, \end{matrix}$ $\begin{eqnarray} \left( \frac{\rm d}{{\rm d} t} \, \left[ \rho^K_Q(\alpha_u J_u ; \vec\varv ) \right]_{\vec x} \right)_0 & = & -2\pi \, {\rm i} \, \nu_{\rm L} \, g_{\alpha_u J_u} \, \sum_{Q'} \, {\mathcal K}^K_{QQ'} \, \left[ \rho^K_{Q'}(\alpha_u J_u ; \vec\varv ) \right]_{\vec x} \nonumber\\ &&\quad- \left[ A(\alpha_u J_u \rightarrow \alpha_\ell J_\ell) +C_{\rm S}^{(0)}(\alpha_\ell J_\ell, \alpha_u J_u) +D^{(K)}(\alpha_u J_u ; \vec\varv ) \right] \left[ \rho^K_Q(\alpha_u J_u ; \vec\varv ) \right]_{\vec x}\nonumber \\ &&\quad + \, \sqrt{\frac{2J_\ell + 1}{2J_u + 1}} \; \left[ B(\alpha_\ell J_\ell \rightarrow \alpha_u J_u) \, w^{(K)}_{J_u J_\ell} \; (-1)^Q \, \left[ J^K_{-Q}(\nu_0) \right]_{\rm c.f.} + \delta_{K0} \, \delta_{Q0} \; C_{\rm I}^{(0)}(\alpha_u J_u, \alpha_\ell J_\ell) \right] \left[ \rho^0_0(\alpha_\ell J_\ell , \vec\varv ) \right]_{\vec x} , \end{eqnarray}$ (12)where the symbol $w_{J_{u} J_{ℓ}}^{(K)}$ $\hbox{$w^{(K)}_{J_u J_\ell}$}$ is given by Eq. (10.11) of LL04.

Since the colliding particles have a Maxwellian distribution of velocities, we can apply the Einstein-Milne relation to connect the collisional rates due to inelastic and superelastic collisions (cf. Eq. (10.49) of LL04). Next we divide both members by A(α_uJ_u → α_ℓJ_ℓ) and introduce the usual notations (cf. Eqs. (10.51) and (10.28) of LL04) $ϵ = \frac{C_{S}^{(0)} (α_{ℓ} J_{ℓ}, α_{u} J_{u})}{A (α_{u} J_{u} \to α_{ℓ} J_{ℓ})}, δ_{u}^{(K)} (ν) = \frac{D^{(K)} (α_{u} J_{u}; ν)}{A (α_{u} J_{u} \to α_{ℓ} J_{ℓ})}, H_{u} = \frac{2 π ν_{L} g_{α_{u} J_{u}}}{A (α_{u} J_{u} \to α_{ℓ} J_{ℓ})} \cdot$ $\begin{equation} \epsilon = \frac{C_{\rm S}^{(0)}(\alpha_\ell J_\ell, \alpha_u J_u)} {A(\alpha_u J_u \rightarrow \alpha_\ell J_\ell)} \, , \quad \delta^{(K)}_{\,u}(\vec\varv \,)=\frac{D^{(K)}(\alpha_u J_u;\vec\varv \,)} {A(\alpha_u J_u \rightarrow \alpha_\ell J_\ell)} \, , \quad H_u = \frac{2\pi\nu_{\rm L} \; g_{\alpha_u J_u}} {A(\alpha_u J_u \rightarrow \alpha_\ell J_\ell)} \cdot \end{equation}$ (13)Recalling the relations between the Einstein coefficients (Eqs. (7.8) of LL04), we obtain, for stationary situations $\begin{matrix} [1 + ϵ + δ_{u}^{(K)} (ν)^{]} {[ρ_{Q}^{K} (α_{u} J_{u}; ν)^{]}}_{x} + i H_{u} \sum_{Q^{'}} 𝒦_{Q Q^{'}}^{K} {[ρ_{Q^{'}}^{K} (α_{u} J_{u}; ν)^{]}}_{x} = \\ \frac{c^{2}}{2 h ν_{0}^{3}} \sqrt{\frac{2 J_{u} + 1}{2 J_{ℓ} + 1}} [w_{J_{u} J_{ℓ}}^{(K)} (- 1)^{Q} [J_{- Q}^{K} (ν_{0})]_{c . f .} + δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0})^{]} {[ρ_{0}^{0} (α_{ℓ} J_{ℓ}; ν)^{]}}_{x}, \end{matrix}$ $\begin{eqnarray} &&\left[ 1 + \epsilon + \delta_{\,u}^{\, (K)}(\vec\varv \,) \right] \left[ \rho^K_Q(\alpha_u J_u ; \vec\varv ) \right]_{\vec x} \, + \, {\rm i} \, H_u \sum_{Q'} \, {\mathcal K}^K_{QQ'} \, \left[ \rho^K_{Q'}(\alpha_u J_u ; \vec\varv ) \right]_{\vec x} = \nonumber\\ && \frac{c^2}{2h\nu_0^3} \, \sqrt{\frac{2J_u+1}{2J_\ell+1}} \; \left[ w^{\, (K)}_{J_u J_\ell} \; (-1)^Q \, [J^K_{-Q}(\nu_0)]_{\rm c.f.} + \delta_{K0} \, \delta_{Q0} \; \epsilon \, B_T(\nu_0) \right] \left[ \rho^0_0(\alpha_\ell J_\ell ; \vec\varv ) \right]_{\vec x} , \end{eqnarray}$ (14)where $B_{T} (ν_{0}) = \frac{2 h ν_{0}^{3}}{c^{2}} \exp (- \frac{h ν_{0}}{k_{B} T})$ $\begin{equation} B_T(\nu_0)=\frac{2 h \nu_0^3}{c^2} \, {\rm exp} \left( -\frac{h \nu_0}{k_{\rm B}T} \right) \end{equation}$ (15)is the Planck function in the Wien limit (consistently with the fact that stimulated emission is neglected).

In view of the following applications, it is convenient to rewrite the previous equation for the time evolution of the density matrix in a more compact form, by introducing suitable “source functions” for the different statistical tensors. Defining $𝒮_{Q}^{K} (ν, x) = \frac{2 h ν_{0}^{3}}{c^{2}} \sqrt{\frac{2 J_{ℓ} + 1}{2 J_{u} + 1}} \frac{{[ρ_{Q}^{K} (α_{u} J_{u}; ν)^{]}}_{x}}{{[ρ_{0}^{0} (α_{ℓ} J_{ℓ}; ν)^{]}}_{x}},$ $\begin{equation} {\mathcal S}^K_Q(\vec\varv, \vec x \,)=\frac{2h \nu_0^3}{c^2} \, \sqrt{\frac{2J_\ell+1}{2J_u+1}} \;\, \frac{\left[ \rho^K_Q(\alpha_u J_u; \vec\varv ) \right]_{\vec x}} {\left[ \rho^0_0(\alpha_\ell J_\ell; \vec\varv ) \right]_{\vec x}} , \end{equation}$ (16)such equation becomes $[1 + ϵ + δ_{u}^{(K)} (ν)^{]} 𝒮_{Q}^{K} (ν, x) + i H_{u} \sum_{Q^{'}} 𝒦_{Q Q^{'}}^{K} 𝒮_{Q^{'}}^{K} (ν, x) = w_{J_{u} J_{ℓ}}^{(K)} (- 1)^{Q} {[J_{- Q}^{K} (ν_{0})^{]}}_{c . f .} + δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0}) .$ $\begin{equation} \left[ 1 + \epsilon + \delta_{\,u}^{\,(K)} (\vec\varv \,) \right] {\mathcal S}^K_Q(\vec\varv, \vec x\,) + {\rm i} \, H_u \sum_{Q'} \, {\mathcal K}^K_{QQ'}\,{\mathcal S}^K_{Q'}(\vec \varv, \vec x\,) = w^{\,(K)}_{J_u J_\ell} \; (-1)^Q \, \left[ J^K_{-Q}(\nu_0) \right]_{\rm c.f.} + \delta_{K0} \, \delta_{Q0} \; \epsilon \, B_T(\nu_0) . \label{Eq:SF_SEE} \end{equation}$ (17)The quantities $𝒮_{Q}^{K} (ν, x)$ $\hbox{${\mathcal S}^K_Q(\vec\varv, \vec x \,)$}$ are the obvious generalization of the irreducible components of the two-level atom source function, introduced in LL04. Now we also have an explicit dependence on ν. This is because atoms having different velocities may have, in general, different source functions since, even at the same point in the medium, they experience, due to the Doppler effect, different radiation fields.

4. The radiative transfer equation

We consider now the radiative transfer equation. From Eq. (6.83) of LL04 we have, neglecting stimulated emission $\frac{d}{d s} S_{i} (ν, Ω) = - \sum_{j = 0}^{3} K_{ij}^{A} S_{j} (ν, Ω) + ε_{i} (i = 0, ..., 3),$ $\begin{equation} \frac{\rm d}{{\rm d} s} \, S_{\! i}(\nu,\vec\Omega) = - \sum_{j=0}^3 \, K_{ij}^{\, \rm A} \; S_{\!\! j}(\nu,\vec\Omega) \, + \, \varepsilon_i \qquad (i=0,\ldots,3) , \end{equation}$ (18)where S_i(ν,Ω) are the Stokes parameters of the radiation flowing through point x in the direction Ω, defined with respect to the unit vectors e_a(Ω), e_b(Ω) of Fig. 1, $K_{ij}^{A}$ $\hbox{$K_{ij}^{\rm A}$}$ is the absorption matrix, and ε_i are the emission coefficients in the four Stokes parameters. The explicit expressions of the radiative transfer coefficients for the case we are concerned with can be derived by a simple generalization of the results contained in Sect. 14.2 of LL04. Since we have assumed that the lower level is unpolarized, and that the Zeeman splitting is negligible with respect to Δν_D, the absorption matrix $K_{ij}^{A}$ $\hbox{$K_{ij}^{\rm A}$}$ is proportional to the identity matrix, i.e., it is of the form $K_{ij}^{A} = η_{0}^{A} (ν, Ω) δ_{ij} .$ $\begin{equation} K_{ij}^{\rm A} = \eta^{\, \rm A}_0(\nu, \vec{\Omega}) \, \delta_{ij} . \end{equation}$ (19)Due to the Doppler effect, an atom with velocity ν absorbs radiation propagating in direction Ω only at the frequency ν₀(1 + ν·Ω/c) (we assumed that the upper and lower levels are infinitely sharp). The absorption coefficient $η_{0}^{A} (ν, Ω)$ $\hbox{$\eta^{\rm A}_0(\nu, \vec{\Omega})$}$ is thus given by $η_{0}^{A} (ν, Ω) = k_{L}^{A} (x) p (ν, Ω),$ $\begin{equation} \eta_0^{\, \rm A}(\nu, \vec{\Omega}) = k_{\rm L}^{\, \rm A}(\vec{x}) \, p(\nu, \vec{\Omega}) , \label{Eq:abs_coef} \end{equation}$ (20)with $p (ν, Ω) = \int d^{3} ν f (ν) δ (ν_{0} + ν_{0} \frac{ν \cdot Ω}{c} - ν),$ $\begin{equation} p(\nu, \vec{\Omega}) = \int {\rm d}^3 \vec{\varv} \, f(\vec{\varv}) \, \delta \left( \nu_0 + \nu_0 \frac{\vec{\varv} \cdot \vec{\Omega}}{c} - \nu \right) , \label{Eq:abs_prof} \end{equation}$ (21)where δ is the Dirac-delta. The quantity $k_{L}^{A} (x)$ $\hbox{$k_{\rm L}^{\, \rm A}(\vec{x})$}$ is the frequency-integrated absorption coefficient of the line, given by $k_{L}^{A} (x) = \frac{h ν_{0}}{4 π} 𝒩_{ℓ} (x) B (α_{ℓ} J_{ℓ} \to α_{u} J_{u}),$ $\begin{equation} k_{\rm L}^{\, \rm A}(\vec{x}) = \frac{h \nu_0}{4 \pi} \, {\mathcal N}_{\ell}(\vec{x}) \; B(\alpha_\ell J_\ell \rightarrow \alpha_u J_u) , \end{equation}$ (22)with $\hbox{${\mathcal N}_{\ell}(\vec{x})$}$ the number density of atoms in the lower level at point x.

The expression for the emission coefficient in the four Stokes parameters is obtained from Eq. (7.16e) of LL04 (where the velocity-independent density matrix has now to be substituted with the velocity-space density matrix, and where, consistently with our assumptions, the profile φ(ν₀ − ν) is now a Dirac-delta). Considering that, due to the Doppler effect, the atoms having velocity ν emit, along the direction Ω, at the frequency ν₀(1 + ν·Ω/c), we have $ε_{i} (ν, Ω) = k_{L}^{A} (x) \int d^{3} ν f (ν) δ (ν_{0} + ν_{0} \frac{ν \cdot Ω}{c} - ν) \sum_{KQ} w_{J_{u} J_{ℓ}}^{(K)} 𝒯_{Q}^{K} (i, Ω) 𝒮_{Q}^{K} (ν, x) .$ $\begin{equation} \varepsilon_i(\nu,\vec \Omega) = k_{\rm L}^{\, \rm A}(\vec{x}) \int {\rm d}^3 \vec \varv \; f(\vec \varv) \; \delta \left(\nu_0 + \nu_0 \, \frac{\vec \varv \cdot \vec \Omega}{c}-\nu \right) \; \sum_{KQ} \; w^{\, (K)}_{J_u J_\ell} \; {\mathcal T}^K_{\,Q}(i,\vec\Omega) \; {\mathcal S}^K_Q(\vec \varv, \vec x) . \label{Eq:emis_coef} \end{equation}$ (23)Obviously, the preceding expressions imply that the only contribution to the opacity and emissivity of the medium comes from transitions between the two levels of the model atom. The case where a source of continuum opacity (and emissivity) is also present is formally more complicated and is not treated here.

The radiative transfer equation can be formally solved.

Fig. 2

Geometry of the transfer process. A ray with direction Ω enters the medium at point x₀ , where its Stokes parameters are $S_{i}^{(b)} (ν, Ω)$ $\hbox{$S_{\! i}^{\rm (b)}(\nu,\vec\Omega)$}$ . At point x, the Stokes parameters are given by Eq. (24).

Referring to Fig. 2, and using Eq. (8.18) of LL04, the Stokes parameters at point x of the radiation at frequency ν, flowing along the direction Ω can be expressed in the form $S_{i} (ν, Ω) = \int_{x_{0}}^{x} d s^{'} \int d^{3} ν f (ν) δ (ν_{0} + ν_{0} \frac{ν \cdot Ω}{c} - ν) k_{L}^{A} (x^{'}) e^{- τ_{ν} (x, x^{'})} \sum_{KQ} w_{J_{u} J_{ℓ}}^{(K)} 𝒯_{Q}^{K} (i, Ω) 𝒮_{Q}^{K} (ν, x^{'}) + e^{- τ_{ν} (x, x_{0})} S_{i}^{(b)} (ν, Ω),$ $\begin{equation} S_{\! i}(\nu,\vec\Omega) = \int_{\vec x_0}^{\vec x} {\rm d}s' \int {\rm d}^3 \vec \varv \; f(\vec \varv) \; \delta \left( \nu_0 + \nu_0 \, \frac{\vec \varv \cdot \vec \Omega}{c} -\nu \right) k_{\rm L}^{\, \rm A}(\vec x^{\,\prime}) \; {\rm e}^{-\tau_\nu(\vec x,\vec x')} \sum_{KQ}\; w^{\, (K)}_{J_u J_\ell} \; {\mathcal T}^K_{\,Q}(i,\vec\Omega) \; {\mathcal S}^K_Q(\vec \varv , \vec x^{\,\prime}) + \, {\rm e}^{-\tau_\nu(\vec x,\vec x_0)} \; S_{\! i}^{\rm (b)}(\nu,\vec\Omega) , \label{Eq:RT_formal-sol} \end{equation}$ (24)where $S_{i}^{(b)} (ν, Ω)$ $\hbox{$S_{\! i}^{\rm (b)}(\nu,\vec\Omega)$}$ is the Stokes vector of the radiation entering the medium at point x₀ along the direction Ω, s′ is the coordinate of x′ reckoned along Ω (s′ = |x′ − x₀ |), and τ_ν(x,x′) is the optical depth at frequency ν between points x and x′, $τ_{ν} (x, x^{'}) = \int_{x^{'}}^{x} d s^{′′} η_{0}^{A} (ν, Ω) = \int_{x^{'}}^{x} d s^{′′} k_{L}^{A} (x^{′′}) \int d^{3} ν f (ν) δ (ν_{0} + ν_{0} \frac{ν \cdot Ω}{c} - ν) .$ $\begin{equation} \tau_\nu(\vec x,\vec x^{\,\prime}) = \int_{\vec x'}^{\vec x} \! {\rm d} s^{\prime \prime} \eta^{\, \rm A}_0(\nu,\vec{\Omega}) = \int_{\vec x'}^{\vec x} \! {\rm d} s^{\prime \prime} k_{\rm L}^{\, \rm A}(\vec x^{\,\prime\prime}) \int {\rm d}^3 \vec{\varv} \, f(\vec{\varv}) \, \delta \left( \nu_0 + \nu_0 \frac{\vec{\varv} \cdot \vec{\Omega}}{c} - \nu \right) . \label{Eq:opt_depth} \end{equation}$ (25)It is now possible to find the expression for the radiation field tensor at point x. Substituting Eq. (24) into Eq. (11), we obtain two contributions and we can thus write ${[J_{Q}^{K} (ν_{0})^{]}}_{c . f .} = {[J_{Q}^{K} (ν_{0})^{]}}_{I} + {[J_{Q}^{K} (ν_{0})^{]}}_{E},$ $\begin{equation} \left[ J^K_Q(\nu_0) \right]_{\rm c.f.} = \left[ J^K_Q(\nu_0) \right]_{\rm I} \, + \, \left[ J^K_Q(\nu_0) \right]_{\rm E} , \label{Eq:JKQ_IE} \end{equation}$ (26)where the “internal” part ${}^{[}J_{Q}^{K} (ν_{0})^{]}_{I}$ $\hbox{$\left[ J^K_Q(\nu_0) \right]_{\rm I}$}$ is given by ${[J_{Q}^{K} (ν_{0})^{]}}_{I} = 􏽉 \frac{dΩ}{4 π} \sum_{i = 0}^{3} 𝒯_{Q}^{K} (i, Ω) \int_{x_{0}}^{x} d s^{'} \int d^{3} ν^{'} f (ν^{'}) δ (ν_{0} \frac{ν^{'} - ν}{c} \cdot Ω) k_{L}^{A} (x^{'}) e^{- τ_{ν^{'}} (x, x^{'})} \sum_{K^{'} Q^{'}} w_{J_{u} J_{ℓ}}^{(K^{'})} 𝒯_{Q^{'}}^{K^{'}} (i, Ω) 𝒮_{Q^{'}}^{K^{'}} (ν^{'}, x^{'}),$ $\begin{equation} \left[ J^K_Q(\nu_0) \right]_{\rm I} = \oint \frac{{\rm d}\Omega}{4\pi} \; \sum_{i=0}^3 \; {\mathcal T}^K_{\,Q}(i,\vec\Omega) \int_{\vec x_0}^{\vec x} \! {\rm d} s' \int {\rm d}^3 \vec\varv^{\, \prime} f(\vec\varv^{\, \prime}) \, \delta \left( \nu_0 \frac{\vec\varv^{\, \prime} - \vec\varv}{c} \cdot \vec \Omega \right) \; k_{\rm L}^{\, \rm A}(\vec x^{\,\prime}) \;\, {\rm e}^{-\tau_{\nu^\prime}(\vec x,\vec x')} \; \sum_{K'Q'} \; w^{\, (K')}_{J_u J_\ell} \; {\mathcal T}^{K'}_{\,Q'}(i,\vec\Omega) \; {\mathcal S}^{K'}_{Q'}(\vec\varv^{\, \prime},\vec x^{\,\prime}) , \label{Eq:JKQ_I1} \end{equation}$ (27)where $ν^{'} = ν_{0} + ν_{0} \frac{ν \cdot Ω}{c},$ $\begin{equation} \nu^{\prime} = \nu_0 + \nu_0 \, \frac{\vec\varv \cdot \vec\Omega}{c} , \label{Eq:nup} \end{equation}$ (28)and the “external” part ${}^{[}J_{Q}^{K} (ν_{0})^{]}_{E}$ $\hbox{$\left[ J^K_Q(\nu_0) \right]_{\rm E}$}$ , originating from the boundary conditions, by ${[J_{Q}^{K} (ν_{0})^{]}}_{E} = 􏽉 \frac{dΩ}{4 π} \sum_{i = 0}^{3} 𝒯_{Q}^{K} (i, Ω) e^{- τ_{ν^{'}} (x, x_{0})} S_{i}^{(b)} (ν^{'}, Ω) .$ $\begin{equation} \left[ J^K_Q(\nu_0) \right]_{\rm E} = \oint \frac{{\rm d}\Omega}{4\pi} \; \sum_{i=0}^3 \; {\mathcal T}^K_{\,Q}(i,\vec\Omega) \; {\rm e}^{-\tau_{\nu^\prime}(\vec x,\vec x_0)} \; S_{\! i}^{\rm (b)}(\nu^{\prime},\vec\Omega) . \end{equation}$ (29)Equation (27) can be cast in a simpler form by changing the double integral in dΩ and ds′ into a volume integral. Since $d^{3} x^{'} = (x - x^{'})^{2} dΩ d s^{'},$ $\begin{equation} {\rm d}^3 \vec x^{\,\prime} = (\vec x-\vec x^{\,\prime})^2 \; {\rm d}\Omega \, {\rm d} s' , \end{equation}$ (30)we get ${[J_{Q}^{K} (ν_{0})^{]}}_{I} = \int d^{3} x^{'} \frac{k_{L}^{A} (x^{'}) e^{- τ_{ν^{'}} (x, x^{'})}}{4 π (x - x^{'})^{2}} \int d^{3} ν^{'} f (ν^{'}) δ (ν_{0} \frac{ν^{'} - ν}{c} \cdot Ω) \sum_{i = 0}^{3} 𝒯_{Q}^{K} (i, Ω) \sum_{K^{'} Q^{'}} w_{J_{u} J_{ℓ}}^{(K^{'})} 𝒯_{Q^{'}}^{K^{'}} (i, Ω) 𝒮_{Q^{'}}^{K^{'}} (ν^{'}, x^{'}) .$ $\begin{equation} \left[ J^K_Q(\nu_0) \right]_{\rm I} = \int \! {\rm d}^3 \vec x^{\,\prime} \; \frac{k_{\rm L}^{\, \rm A}(\vec x^{\,\prime}) \; {\rm e}^{-\tau_{\nu^\prime}(\vec x,\vec x')}} {4\pi(\vec x-\vec x^{\,\prime})^2} \int {\rm d}^3 \vec\varv^{\, \prime} \, f(\vec\varv^{\, \prime}) \, \delta \left( \nu_0 \frac{\vec\varv^{\, \prime} - \vec\varv}{c} \cdot \vec\Omega \right) \sum_{i=0}^3 \; {\mathcal T}^K_{\,Q}(i,\vec\Omega) \sum_{K'Q'} \; w^{\, (K')}_{J_u J_\ell} \; {\mathcal T}^{K'}_{\,Q'}(i,\vec\Omega) \; {\mathcal S}^{K'}_{Q'}(\vec\varv^{\, \prime}, \vec x^{\,\prime}) . \label{Eq:JKQ_I} \end{equation}$ (31)

5. Coupled equations for the velocity dependent irreducible components of the source function

We can now substitute the expression of the radiation field tensor at point x into the statistical equilibrium equation. From Eqs. (17), (26), and (31) we obtain $\begin{matrix} [1 + ϵ + δ_{u}^{(K)} (ν)^{]} 𝒮_{Q}^{K} (ν, x) + i H_{u} \sum_{Q^{'}} 𝒦_{Q Q^{'}}^{K} 𝒮_{Q^{'}}^{K} (ν, x) = δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0}) + w_{J_{u} J_{ℓ}}^{(K)} (- 1)^{Q} {[J_{- Q}^{K} (ν_{0})^{]}}_{E} \\ + \int d^{3} x^{'} \frac{k_{L}^{A} (x^{'})}{4 π (x - x^{'})^{2}} \int d^{3} ν^{'} f (ν^{'}) \sum_{K^{'} Q^{'}} G_{KQ, K^{'} Q^{'}} (ν, x; ν^{'}, x^{'}) 𝒮_{Q^{'}}^{K^{'}} (ν^{'}, x^{'}), \end{matrix}$ $\begin{eqnarray} \label{Eq:Coupled_SF1} &&\left[ 1+ \epsilon+ \delta_{\,u}^{\, (K)}(\vec \varv) \right] {\mathcal S}^K_Q(\vec\varv, \vec x\,) + {\rm i} \, H_u \sum_{Q'} \, {\mathcal K}^K_{QQ'} \, {\mathcal S}^K_{Q'} (\vec\varv, \vec x\,) = \delta_{K0} \, \delta_{Q0} \; \epsilon \, B_T(\nu_0) + w^{\, (K)}_{J_u J_\ell} \, (-1)^Q \left[ J^K_{-Q}(\nu_0) \right]_{\rm E} \nonumber\\ &&\quad + \int \! {\rm d}^3 \vec x^{\,\prime} \, \frac{k_{\rm L}^{\, \rm A}(\vec x^{\,\prime})} {4\pi(\vec x-\vec x^{\,\prime})^2} \int \! {\rm d}^3 \vec\varv^{\, \prime} \, f(\vec\varv^{\, \prime}) \! \sum_{K'Q'} G_{KQ,K'Q'}(\vec\varv, \vec x \, ; \vec\varv^{\, \prime}, \vec x^{\,\prime}) \; {\mathcal S}^{K'}_{Q'}(\vec\varv^{\, \prime},\vec x^{\,\prime}) , \end{eqnarray}$ (32)where $G_{KQ, K^{'} Q^{'}} (ν, x; ν^{'}, x^{'}) = e^{- τ_{ν^{'}} (x, x^{'})} δ (ν_{0} \frac{ν^{'} - ν}{c} \cdot Ω) w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} \sum_{i = 0}^{3} (- 1)^{Q} 𝒯_{- Q}^{K} (i, Ω) 𝒯_{Q^{'}}^{K^{'}} (i, Ω) .$ $\begin{equation} G_{KQ,K'Q'}(\vec\varv, \vec x \, ; \vec\varv^{\, \prime},\vec x^{\,\prime}) = {\rm e}^{-\tau_{\nu^\prime}(\vec x,\vec x')} \, \delta \left( \nu_0 \frac{\vec\varv^{\, \prime} - \vec\varv}{c} \cdot \vec \Omega \right) \, w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \, \sum_{i=0}^3 \; (-1)^Q \; {\mathcal T}^K_{-Q}(i,\vec\Omega) \, {\mathcal T}^{K'}_{\,Q'}(i,\vec\Omega) . \label{Eq:GKQ} \end{equation}$ (33)The quantities G_KQ,K′Q′(ν,x ;ν′,x′) appearing in this equation represent a factor (having the dimension of the inverse of a frequency) which weights the amount of coupling between the statistical tensor $ρ_{Q}^{K}$ $\hbox{$\rho^K_Q$}$ of the atoms having velocity ν at point x and the statistical tensor $ρ_{Q^{'}}^{K^{'}}$ $\hbox{$\rho^{K'}_{Q'}$}$ of the atoms having velocity ν′ at point x′. They are a generalization of similar quantities introduced in LL04 and can be referred to as velocity dependent multipole coupling coefficients. The Dirac-delta appearing in their expression is responsible for the fact that two such multipoles can be coupled only if the velocity difference, ν− ν′ is perpendicular to the unit vector Ω which specifies the direction x − x′.

Equation (32) is a system of linear, non-homogeneous, integral equations in the unknowns $𝒮_{Q}^{K} (ν, x)$ $\hbox{${\mathcal S}^K_Q(\vec\varv, \vec x\,)$}$ , the velocity dependent irreducible components of the source function, which can in principle be solved once the properties of the medium and the boundary conditions are specified. When the values of these components are known at each point, the Stokes parameters of the radiation emerging from the medium can be computed by applying Eq. (24). It should be remarked that, owing to a property of the tensor $𝒯_{Q}^{K}$ $\hbox{${\mathcal T}^K_Q$}$ , whose proof can be found in Appendix 20 of LL04, it can be shown that Eq. (32) decouples in two different sets of equations involving, respectively, the components with K = 0,2 and those with K = 1. In the latter set, the only source term is $[J_{- Q}^{1} (ν_{0})]_{E}$ $\hbox{$[ J^1_{-Q}(\nu_0)]_{\rm E}$}$ , which vanishes unless the boundary radiation field has some contribution arising from circular polarization. Excluding this case of limited interest, all the components $𝒮_{Q}^{1} (ν, x)$ $\hbox{${\mathcal S}^1_Q(\vec\varv, \vec x\,)$}$ are everywhere zero in the medium.

For further developments it is however more practical to rewrite Eq. (32) in an alternative form by substitution of Eq. (33) and by introducing the compact symbol Γ_KQ,K′Q′(Ω), whose main properties are collected in Appendix 20 of LL04. Its definition, that we recall here for completeness, is the following $Γ_{KQ, K^{'} Q^{'}} (Ω) = \sum_{i = 0}^{3} (- 1)^{Q} 𝒯_{- Q}^{K} (i, Ω) 𝒯_{Q^{'}}^{K^{'}} (i, Ω) .$ $\begin{equation} \Gamma_{K Q, K' Q'} (\vec \Omega) = \sum_{i=0}^3 \; (-1)^Q \; {\mathcal T}^K_{-Q}(i,\vec\Omega) \, {\mathcal T}^{K'}_{\,Q'}(i,\vec\Omega) . \end{equation}$ (34)With these transformations we obtain $\begin{matrix} [1 + ϵ + δ_{u}^{(K)} (ν)^{]} 𝒮_{Q}^{K} (ν, x) + i H_{u} \sum_{Q^{'}} 𝒦_{Q Q^{'}}^{K} 𝒮_{Q^{'}}^{K} (ν, x) = δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0}) + w_{J_{u} J_{ℓ}}^{(K)} (- 1)^{Q} {[J_{- Q}^{K} (ν_{0})^{]}}_{E} \\ + \int d^{3} x^{'} \frac{k_{L}^{A} (x^{'})}{4 π (x - x^{'})^{2}} e^{- τ_{ν^{'}} (x, x^{'})} \int d^{3} ν^{'} f (ν^{'}) δ (ν_{0} \frac{ν^{'} - ν}{c} \cdot Ω) \sum_{K^{'} Q^{'}} w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} Γ_{KQ, K^{'} Q^{'}} (Ω) 𝒮_{Q^{'}}^{K^{'}} (ν^{'}, x^{'}) . \end{matrix}$ $\begin{eqnarray} \label{Eq:Coupled_SF2} && \left[ 1+ \epsilon+ \delta_{\,u}^{\, (K)}(\vec\varv) \right] \, {\mathcal S}^K_Q(\vec\varv, \vec x) \, + \, {\rm i} \, H_u \sum_{Q'} \, {\mathcal K}^K_{QQ'} \, {\mathcal S}^K_{Q'}(\vec\varv, \vec x) = \delta_{K0} \, \delta_{Q0} \, \epsilon \, B_T(\nu_0) \, + \, w^{\, (K)}_{J_u J_\ell} \, (-1)^Q \left[ J^K_{-Q}(\nu_0) \right]_{\rm E}\nonumber\\ && + \int \! {\rm d}^3 \vec x^{\,\prime} \, \frac{k_{\rm L}^{\, \rm A}(\vec x^{\,\prime})} {4\pi(\vec x-\vec x^{\,\prime})^2} \, {\rm e}^{-\tau_{\nu^\prime}(\vec x,\vec x')} \, \int \! {\rm d}^3 \vec\varv^{\, \prime} \, f(\vec\varv^{\, \prime}) \, \delta \left( \nu_0 \frac{\vec\varv^{\, \prime} - \vec\varv}{c} \cdot \vec \Omega \right) \sum_{K'Q'} w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \, \Gamma_{K Q, K' Q'} (\vec \Omega) \, {\mathcal S}^{K'}_{Q'}(\vec\varv^{\, \prime}, \vec x^{\,\prime}) . 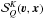\end{eqnarray}$ (35)This is a very general set of coupled equations for the velocity-dependent source function that in principle can be solved numerically by suitable discretization of $𝒮_{Q}^{K} (ν, x)$ $\hbox{$\mathcal{S}^K_Q(\vec{\varv},\vec{x})$}$ over the velocity-space and the physical-space.

We now assume that the velocity distribution f(ν) is a Maxwellian characterized by the thermal velocity ν_t (possibly containing the contribution of microturbulent velocities) $f (ν) = \frac{1}{ν_{t}^{3} π^{3 / 2}} e^{- ν^{2} / ν_{t}^{2}} .$ $\begin{equation} f(\vec{\varv}) = \frac{1}{\varv_t^3 \, \pi^{3/2}} \, {\rm e}^{-\varv^2/ \varv_t^2} . \end{equation}$ (36)For fixed x and x′ (which implies a fixed direction Ω joining x′ with x), and for a fixed velocity ν, we introduce a right-handed, Cartesian coordinate system (e_a,e_b,e_c) in the velocity space. The unit vector e_c is directed along Ω (coinciding with it), while the other two vectors are perpendicular to Ω and for the rest arbitrary. In this system we obviously have $ν = ν_{a} e_{a} + ν_{b} e_{b} + ν_{c} e_{c}, ν^{'} = ν_{a}^{'} e_{a} + ν_{b}^{'} e_{b} + ν_{c}^{'} e_{c} .$ $\begin{equation} \vec\varv = \varv_{\rm a} \, \vec e_{\rm a} + \varv_{\rm b} \, \vec e_{\rm b} + \varv_{\rm c} \, \vec e_{\rm c} , \qquad \vec\varv^{\, \prime} = \varv^\prime_{\rm a} \, \vec e_{\rm a} + \varv^\prime_{\rm b} \, \vec e_{\rm b} + \varv^\prime_{\rm c} \, \vec e_{\rm c} . \end{equation}$ (37)With these positions, we can perform the following formal substitution in the integral in d³ν′ $\int d^{3} ν^{'} f (ν^{'}) δ (ν_{0} \frac{ν^{'} - ν}{c} \cdot Ω) \to \int \frac{d ν_{a}^{'}}{ν_{t}} \int \frac{d ν_{b}^{'}}{ν_{t}} \int \frac{d ν_{c}^{'}}{ν_{t}} \frac{e^{- (ν_{a}^{' 2} + ν_{b}^{' 2} + ν_{c}^{' 2}) / ν_{t}^{2}}}{π^{3 / 2}} δ (ν_{0} \frac{ν_{c}^{'} - ν_{c}}{c}) \cdot$ $\begin{equation} \int {\rm d}^3 \vec\varv^{\, \prime} \, f(\vec\varv^{\, \prime}) \, \delta \left( \nu_0 \frac{\vec\varv^{\, \prime} - \vec\varv}{c} \cdot \vec \Omega \right) \rightarrow \int \frac{{\rm d} \varv^\prime_{\rm a}}{\varv_{\rm t}} \int \frac{{\rm d} \varv^\prime_{\rm b}}{\varv_{\rm t}} \int \frac{{\rm d} \varv^\prime_{\rm c}}{\varv_{\rm t}} \; \frac{{\rm e}^{-(\varv_{\rm a}^{\prime \, 2} + \varv_{\rm b}^{\prime \, 2} + \varv_{\rm c}^{\prime \, 2})/ \varv_{\rm t}^2}}{\pi^{3/2}} \; \delta \left( \nu_0 \frac{\varv_{\rm c}^{\prime} - \varv_{\rm c}}{c} \right) \cdot \end{equation}$ (38)Due to the presence of the Dirac’s delta, the integral in $d ν_{c}^{'}$ $\hbox{${\rm d} \varv_{\rm c}^{\prime}$}$ is immediately performed, and the last term on the righthand side of Eq. (35) acquires the form $\int d^{3} x^{'} \frac{k_{L}^{A} (x^{'})}{4 π (x - x^{'})^{2}} e^{- τ_{ν^{'}} (x, x^{'})} \int \frac{d ν_{a}^{'}}{ν_{t}} \int \frac{d ν_{b}^{'}}{ν_{t}} \frac{e^{- (ν_{a}^{' 2} + ν_{b}^{' 2} + ν_{c}^{2}) / ν_{t}^{2}}}{π^{3 / 2}} \frac{1}{Δ ν_{D}} \sum_{K^{'} Q^{'}} w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} Γ_{KQ, K^{'} Q^{'}} (Ω) 𝒮_{Q^{'}}^{K^{'}} (ν_{*}^{'}, x^{'}),$ $\begin{equation} \int \! {\rm d}^3 \vec x^{\,\prime} \, \frac{k_{\rm L}^{\, \rm A}(\vec x^{\,\prime})} {4\pi(\vec x-\vec x^{\,\prime})^2} \; {\rm e}^{-\tau_{\nu^{\prime}}(\vec x,\vec x')} \, \int \frac{{\rm d}\varv_{\rm a}^{\prime}}{\varv_{\rm t}} \int \frac{{\rm d}\varv_{\rm b}^{\prime}}{\varv_{\rm t}} \; \frac{{\rm e}^{-(\varv_{\rm a}^{\prime \, 2} +\varv_{\rm b}^{\prime \, 2} + \varv_{\rm c}^2)/\varv_{\rm t}^2}}{\pi^{3/2}} \frac{1}{\Delta \nu_{\rm D}} \sum_{K'Q'} w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \, \Gamma_{K Q, K' Q'} (\vec \Omega) \, {\mathcal S}^{K'}_{Q'}(\vec\varv^{\, \prime}_{\ast}, \vec x^{\,\prime}) , \end{equation}$ (39)where the vector $ν_{*}^{'}$ $\hbox{$\vec \varv^{\, \prime}_{\ast}$}$ in the argument of $𝒮_{Q^{'}}^{K^{'}}$ $\hbox{${\mathcal S}^{K'}_{Q'}$}$ has components $(ν_{a}^{'}, ν_{b}^{'}, ν_{c})$ $\hbox{$(\varv^\prime_{\rm a}, \varv^\prime_{\rm b}, \varv_{\rm c})$}$ , and where the Doppler width Δν_D is given by $Δ ν_{D} = ν_{0} \frac{ν_{t}}{c} \cdot$ $\begin{equation} \Delta \nu_{\rm D} = \nu_0 \frac{\varv_t}{c} \cdot \end{equation}$ (40)We also observe that under the assumption that the velocity distribution is a Maxwellian characterized by the thermal velocity ν_t, the absorption coefficient (see Eq. (20)) does not depend any longer on the propagation direction of the radiation (Ω), and it is given by $η_{0}^{A} (ν) = k_{L}^{A} (x) p_{M} (ν - ν_{0}),$ $\begin{equation} \eta_0^{\, \rm A}(\nu) = k_{\rm L}^{\, \rm A}(\vec{x}) \, p_{\rm M}(\nu - \nu_0) , \end{equation}$ (41)with $p_{M} (ν - ν_{0}) = \frac{1}{\sqrt{π} Δ ν_{D}} e^{- (ν - ν_{0})^{2} / Δ ν_{D}^{2}} .$ $\begin{equation} p_{\rm M}(\nu- \nu_0) = \frac{1}{\sqrt{\pi} \, \Delta \nu_{\rm D}} \, {\rm e}^{-(\nu - \nu_0)^2/\Delta \nu_{\rm D}^2} . \end{equation}$ (42)Under the same assumption, the optical depth τ_ν(x,x′) (see Eq. (25)) is given by $τ_{ν} (x, x^{'}) = p_{M} (ν - ν_{0}) \int_{x^{'}}^{x} d s^{′′} k_{L}^{A} (x^{′′}) .$ $\begin{equation} \tau_\nu(\vec x,\vec x^{\,\prime}) = p_{\rm M}(\nu - \nu_0) \int_{\vec x'}^{\vec x} \! {\rm d} s^{\prime \prime} k_{\rm L}^{\, \rm A}(\vec x^{\,\prime\prime}) . \end{equation}$ (43)

6. Equations for a plane-parallel semi-infinite stellar atmosphere

We now consider the particular case of a plane-parallel, semi-infinite stellar atmosphere. In this case all the physical quantities of the medium depend on a single coordinate, the height in the atmosphere, that we assume as the z-axis of our fixed reference system of Fig. 1. As a consequence, the irreducible components of the velocity-dependent source function only vary with the height z. We keep assuming that the velocity distribution is Maxwellian and we introduce the line optical depth t_L through the equation $d t_{L} = - \frac{k_{L}^{A} (z)}{Δ ν_{D}} d z .$ $\begin{equation} {\rm d} t_{\rm L} = -\frac{k_{\rm L}^{\, \rm A}(z)} {\Delta \nu_{\rm D}} \, {\rm d} z . \end{equation}$ (44)Assuming that the stellar atmosphere is not illuminated by external sources of radiation, Eq. (35) takes the form $\begin{matrix} [1 + ϵ + δ_{u}^{(K)} (ν)] 𝒮_{Q}^{K} (ν, t_{L}) + i H_{u} \sum_{Q^{'}} 𝒦_{Q Q^{'}}^{K} 𝒮_{Q^{'}}^{K} (ν, t_{L}) = δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0}) \\ + \int_{0}^{\infty} d t_{L}^{'} \int_{- \infty}^{\infty} d x^{'} \int_{- \infty}^{\infty} d y^{'} \frac{1}{4 π (x - x^{'})^{2}} e^{- τ_{ν^{'}} (x, x^{'})} \int \frac{d ν_{a}^{'}}{ν_{t}} \int \frac{d ν_{b}^{'}}{ν_{t}} \frac{e^{- (ν_{a}^{' 2} + ν_{b}^{' 2} + ν_{c}^{2}) / ν_{t}^{2}}}{π^{3 / 2}} \sum_{K^{'} Q^{'}} w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} Γ_{KQ, K^{'} Q^{'}} (Ω) 𝒮_{Q^{'}}^{K^{'}} (ν_{*}^{'}, t_{L}^{'}), \end{matrix}$ $\begin{eqnarray} \label{Eq:Coupled_SF_PP1} && \Big[ 1 \, + \, \epsilon + \delta_{\,u}^{\, (K)}(\vec\varv \,) \Big] \, {\mathcal S}^K_Q(\vec\varv, t_{\rm L}) + {\rm i} \, H_u \sum_{Q'} \, {\mathcal K}^K_{QQ'} \, {\mathcal S}^K_{Q'}(\vec\varv, t_{\rm L}) = \, \delta_{K0} \, \delta_{Q0} \; \epsilon \, B_T(\nu_0) \nonumber \\ && +\int_0^\infty \! {\rm d} t'_{\rm L} \! \int_{-\infty}^{\infty} \!\! {\rm d} x' \! \int_{-\infty}^{\infty} \!\! {\rm d} y' \, \frac{1}{4\pi(\vec x - \vec x^{\,\prime})^2} \, {\rm e}^{-\tau_{\nu^\prime}(\vec x,\vec x')} \, \int \frac{{\rm d}\varv_{\rm a}^\prime}{\varv_{\rm t}} \int \frac{{\rm d}\varv_{\rm b}^\prime}{\varv_{\rm t}} \; \frac{{\rm e}^{-(\varv_{\rm a}^{\prime \, 2} +\varv_{\rm b}^{\prime \, 2} + \varv_{\rm c}^2)/\varv_{\rm t}^2}}{\pi^{3/2}} \sum_{K'Q'} w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \, \Gamma_{K Q, K' Q'} (\vec \Omega) \, {\mathcal S}^{K'}_{Q'}(\vec\varv^{\, \prime}_{\ast},t'_{\rm L}) , \end{eqnarray}$ (45)where the indices K and K′ are restricted to the values 0 and 2.

Fig. 3

Geometry for the plane-parallel atmosphere. In the reference system Σ we consider a fixed point P located at height z corresponding to line optical depth t_L. The point P′ lies on the plane Γ parallel to the x–yplane; its height is z′ corresponding to line optical depth $t_{L}^{'}$ $\hbox{$t'_{\rm L}$}$ . The cylindrical coordinates (r,α) define the position of P′ in the plane Γ. The angles θ and χ specify the direction Ω.

The integral over x′ and y′ can be performed by introducing cylindrical coordinates and following a procedure similar to the one developed in Appendix 21 of LL04. Referring to the geometry of Fig. 3 (which represents the case $t_{L}^{'} > t_{L}$ $\hbox{$t'_{\rm L}>t_{\rm L}$}$ or z′ < z), and introducing the cylindrical coordinates r and α of the point P′, one has $d x^{'} d y^{'} = r d r d α .$ $\begin{equation} {\rm d} x' \, {\rm d} y' = r \; {\rm d} r \, {\rm d} \alpha . \end{equation}$ (46)On the other hand $(x - x^{'})^{2} = (z - z^{'})^{2} + r^{2},$ $\begin{equation} (\vec x-\vec x^{\,\prime})^2=(z-z')^2 + r^2 , \end{equation}$ (47)and $r = (z - z^{'}) \tan θ, d r = \frac{z - z^{'}}{\cos^{2} θ} d θ .$ $\begin{equation} r = (z-z') \tan \theta , \qquad {\rm d} r = \frac{z-z'}{\cos^2 \! \theta} \, {\rm d} \theta . \end{equation}$ (48)From these relations we get $\frac{d x^{'} d y^{'}}{(x - x^{'})^{2}} = \tan θ d θ d α,$ $\begin{equation} \frac{{\rm d} x' \, {\rm d} y'}{(\vec x - \vec x^{\,\prime})^2} \, = \, \tan \theta \; {\rm d} \theta \, {\rm d} \alpha , \end{equation}$ (49)and since χ = α + π, the double integral over x′ and y′ can be transformed into an integral over the angles θ and χ specifying the direction Ω. In Eq. (45) one can then perform the formal substitution $\int_{- \infty}^{\infty} d x^{'} \int_{- \infty}^{\infty} d y^{'} \frac{1}{4 π (x - x^{'})^{2}} \to \frac{1}{4 π} \int_{0}^{2 π} d χ \int_{0}^{π / 2} d θ \tan θ .$ $\begin{equation} \int_{-\infty}^{\infty} \!\! {\rm d} x' \! \int_{-\infty}^{\infty} \!\! {\rm d} y' \, \frac{1}{4\pi(\vec x-\vec x^{\,\prime})^2} \rightarrow \frac{1}{4 \pi} \int_0^{2 \pi} \! {\rm d} \chi \int_0^{\pi/2} \! {\rm d} \theta \;\, \tan\theta . \end{equation}$ (50)Moreover, introducing the reduced frequency distance from line center through the usual expression $ξ = \frac{ν - ν_{0}}{Δ ν_{D}},$ $\begin{equation} \xi = \frac{\nu - \nu_0}{\Delta \nu_{\rm D}} , \end{equation}$ (51)and the normalized profile $ϕ (ξ) = \frac{1}{\sqrt{π}} e^{- ξ^{2}},$ $\begin{equation} \varphi(\xi) = \frac{1}{\sqrt{\pi}} \, {\rm e}^{-\xi^2} , \label{Eq:abs_prof_red} \end{equation}$ (52)one has $τ_{ν^{'}} (x, x^{'}) = \frac{(t_{L}^{'} - t_{L}) ϕ (ξ^{'})}{\cos θ},$ $\begin{equation} \tau_{\nu'}(\vec x, \vec x^{\, \prime}) = \frac{(t'_{\rm L} - t_{\rm L}) \, \varphi(\xi')}{\cos \theta} , \end{equation}$ (53)with (recalling Eq. (28)) $ξ^{'} = \frac{ν^{'} - ν_{0}}{Δ ν_{D}} = \frac{ν_{0} ν_{c}}{Δ ν_{D} c} \cdot$ $\begin{equation} \xi' = \frac{\nu' - \nu_0}{\Delta \nu_{\rm D}} = \frac{\nu_0 \, \varv_{\rm c}}{\Delta \nu_{\rm D} \, c} \cdot \end{equation}$ (54)Taking into account these transformations, and performing a similar analysis for the case $t_{L}^{'} < t_{L}$ $\hbox{$t'_{\rm L} < t_{\rm L}$}$ , Eq. (45) becomes $\begin{matrix} [1 + ϵ + δ_{u}^{(K)} (ν)] 𝒮_{Q}^{K} (ν, t_{L}) + i H_{u} \sum_{Q^{'}} 𝒦_{Q Q^{'}}^{K} 𝒮_{Q^{'}}^{K} (ν, t_{L}) = δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0}) \\ + \int_{0}^{\infty} d t_{L}^{'} \frac{1}{4 π} \int_{0}^{2 π} d χ \int_{θ_{1}}^{θ_{2}} d θ | \tan θ | e^{- (t_{L}^{'} - t_{L}) ϕ (ξ^{'}) / \cos θ} \int \frac{d ν_{a}^{'}}{ν_{t}} \int \frac{d ν_{b}^{'}}{ν_{t}} \frac{e^{- (ν_{a}^{' 2} + ν_{b}^{' 2} + ν_{c}^{2}) / ν_{t}^{2}}}{π^{3 / 2}} \sum_{K^{'} Q^{'}} w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} Γ_{KQ, K^{'} Q^{'}} (Ω) S_{Q^{'}}^{K^{'}} (ν_{*}^{'}, t_{L}^{'}), \end{matrix}$ $\begin{eqnarray} && \Big[ 1 \, + \epsilon+ \delta_{\,u}^{\, (K)}(\vec\varv \,) \Big] {\mathcal S}^K_Q(\vec\varv, t_{\rm L}) + {\rm i} \, H_u \sum_{Q'} \, {\mathcal K}^K_{QQ'} \, {\mathcal S}^K_{Q'}(\vec\varv, t_{\rm L}) = \, \delta_{K0} \, \delta_{Q0} \; \epsilon \, B_T(\nu_0) \nonumber \\ &&\quad + \int_0^{\infty} \! {\rm d} t'_{\rm L} \; \frac{1}{4 \pi} \int_0^{2 \pi} \! {\rm d} \chi \int_{\theta_1}^{\theta_2} \! {\rm d} \theta \, |\tan\theta \,| \; {\rm e}^{- (t'_{\rm L} - t_{\rm L}) \, \varphi(\xi') / \cos \theta} \, \int \frac{{\rm d}\varv_{\rm a}^\prime}{\varv_{\rm t}} \int \frac{{\rm d}\varv_{\rm b}^\prime}{\varv_{\rm t}} \; \frac{{\rm e}^{-(\varv_{\rm a}^{\prime \, 2} + \varv_{\rm b}^{\prime \, 2} + \varv_{\rm c}^2)/\varv_{\rm t}^2}}{\pi^{3/2}} \sum_{K'Q'} w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \Gamma_{K Q, K' Q'} (\vec \Omega) S^{K'}_{Q'}(\vec\varv^{\, \prime}_{\ast}, t'_{\rm L}) , \end{eqnarray}$ (55)the interval (θ₁,θ₂) being (0,π/2) if $t_{L}^{'} > t_{L}$ $\hbox{$t'_{\rm L} > t_{\rm L}$}$ and (π/2,π) if $t_{L}^{'} < t_{L}$ $\hbox{$t'_{\rm L} < t_{\rm L}$}$ .

It is now necessary to specify the unit vectors e_a and e_b that have been left undefined. For a given direction Ω we set $\begin{matrix} e_{a} & = & e_{θ} = \cos θ \cos χ i + \cos θ \sin χ j - \sin θ k, \\ e_{b} & = & e_{χ} = - \sin χ i + \cos χ j, \\ e_{c} & = & e_{r} = Ω = \sin θ \cos χ i + \sin θ \sin χ j + \cos θ k . \end{matrix}$ $\begin{eqnarray} \vec e_{\rm a} & = & \vec e_\theta = \cos \theta \, \cos \chi \, \vec i + \cos \theta \, \sin \chi \, \vec j -\sin \theta \, \vec k , \nonumber \\ \vec e_{\rm b} & = & \vec e_\chi = -\sin \chi \, \vec i + \cos \chi \, \vec j , \nonumber\\ \vec e_{\rm c} & = & \vec e_r = \vec \Omega = \sin \theta \, \cos \chi \, \vec i + \sin \theta \, \sin \chi \, \vec j +\cos \theta \, \vec k. \end{eqnarray}$ (56)Given the velocity components $ν_{a}^{'}$ $\hbox{$\varv'_{\rm a}$}$ and $ν_{b}^{'}$ $\hbox{$\varv'_{\rm b}$}$ , the velocity $ν_{*}^{'}$ $\hbox{$\vec\varv^{\, \prime}_{\ast}$}$ is thus given by $\begin{matrix} ν_{*}^{'} = ν_{a}^{'} e_{a} + ν_{b}^{'} e_{b} + ν_{c} e_{c} & = & [(\cos θ ν_{a}^{'} + \sin θ ν_{c}) \cos χ - \sin χ {ν_{b}^{'}}^{]} i \\ + [(\cos θ ν_{a}^{'} + \sin θ ν_{c}) \sin χ + \cos χ {ν_{b}^{'}}^{]} j \\ - [\sin θ ν_{a}^{'} - \cos θ ν_{c}] k . \end{matrix}$ $\begin{eqnarray} \vec\varv^{\, \prime}_{\ast} = \varv'_{\rm a} \, \vec e_{\rm a} + \varv'_{\rm b} \, \vec e_{\rm b} + \varv_{\rm c} \, \vec e_{\rm c} & = & \left[ (\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c}) \cos \chi - \sin \chi \, \varv'_{\rm b} \right] \, \vec i \nonumber \\ &&\quad +\left[ (\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c}) \sin \chi + \cos \chi \, \varv'_{\rm b} \right] \, \vec j \nonumber\\ &&\quad -\left[ \sin \theta \, \varv'_{\rm a} - \cos \theta \, \varv_{\rm c} \right] \, \vec k.\nonumber \end{eqnarray}$ This equation allows us to find the modulus, $ν_{*}^{'}$ $\hbox{$\varv'_{\ast}$}$ , polar angle, θ_∗, and azimuth, χ_∗, of the velocity $ν_{*}^{'}$ $\hbox{$\vec\varv^{\, \prime}_{\ast}$}$ in terms of $ν_{a}^{'}$ $\hbox{$\varv'_{\rm a}$}$ , $ν_{b}^{'}$ $\hbox{$\varv'_{\rm b}$}$ , and ν_c. One gets $\begin{matrix} ν_{*}^{'} = \sqrt{ν_{a}^{' 2} + ν_{b}^{' 2} + ν_{c}^{2}}, \\ ν_{*}^{'} \cos θ_{*} = - \sin θ ν_{a}^{'} + \cos θ ν_{c}, \\ ν_{*}^{'} \sin θ_{*} \cos χ_{*} = (\cos θ ν_{a}^{'} + \sin θ ν_{c}) \cos χ - \sin χ ν_{b}^{'}, \\ ν_{*}^{'} \sin θ_{*} \sin χ_{*} = (\cos θ ν_{a}^{'} + \sin θ ν_{c}) \sin χ + \cos χ ν_{b}^{'}, \end{matrix}$ $\begin{eqnarray} && \varv'_{\ast} = \sqrt{\varv_{\rm a}^{\prime 2} + \varv_{\rm b}^{\prime 2} + \varv_{\rm c}^2} , \nonumber \\ &&\varv'_{\ast} \, \cos \theta_{\ast} = -\sin \theta \, \varv'_{\rm a} + \cos \theta \, \varv_{\rm c} , \nonumber \\ &&\varv'_{\ast} \, \sin \theta_{\ast} \, \cos \chi_{\ast} = (\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c}) \cos \chi -\sin \chi \, \varv'_{\rm b} , \\ &&\varv'_{\ast} \, \sin \theta_{\ast} \, \sin \chi_{\ast} = (\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c}) \sin \chi + \cos \chi \, \varv'_{\rm b} \nonumber , \end{eqnarray}$ (57)the combination of the last two equations giving $ν_{*}^{'} \sin θ_{*} e^{i χ_{*}} = (\cos θ ν_{a}^{'} + \sin θ ν_{c} + i ν_{b}^{'}) e^{i χ},$ $\begin{equation} \varv'_{\ast} \, \sin \theta_{\ast} \, {\rm e}^{\, {\rm i} \, \chi_{\ast}} = (\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c} + {\rm i} \, \varv'_{\rm b}) \, {\rm e}^{\, {\rm i} \, \chi} , \end{equation}$ (58)or $e^{- i χ_{*}} = \frac{\cos θ ν_{a}^{'} + \sin θ ν_{c} - i ν_{b}^{'}}{\sqrt{(\cos θ ν_{a}^{'} + \sin θ ν_{c})^{2} + ν_{b}^{' 2}}} e^{- i χ} .$ $\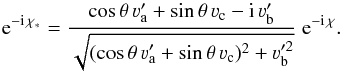begin{equation} {\rm e}^{- {\rm i} \, \chi_{\ast}} = \frac{\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c} - {\rm i} \, \varv'_{\rm b}} {\sqrt{(\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c})^2 + \varv_{\rm b}^{\prime 2}}} \; {\rm e}^{- {\rm i} \, \chi} . \label{Eq:exp_chiast} \end{equation}$ (59)The previous equations can also be inverted to give $\begin{matrix} ν_{a}^{'} & = & ν_{*}^{'} \sin θ_{*} \cos θ \cos (χ_{*} - χ) - ν_{*}^{'} \cos θ_{*} \sin θ, \\ ν_{b}^{'} & = & ν_{*}^{'} \sin θ_{*} \sin (χ_{*} - χ), \\ ν_{c} & = & ν_{*}^{'} \sin θ_{*} \sin θ \cos (χ_{*} - χ) + ν_{*}^{'} \cos θ_{*} \cos θ . \end{matrix}$ $\begin{eqnarray} \varv'_{\rm a} & = & \varv'_{\ast} \, \sin \theta_{\ast} \, \cos \theta \, \cos(\chi_{\ast} - \chi) - \varv'_{\ast} \, \cos \theta_{\ast} \, \sin \theta , \nonumber \\ \varv'_{\rm b} & = & \varv'_{\ast} \, \sin \theta_{\ast} \, \sin(\chi_{\ast} - \chi) , \nonumber \\ \varv_{\rm c} & = & \varv'_{\ast} \, \sin \theta_{\ast} \, \sin \theta \, \cos(\chi_{\ast} - \chi) + \varv'_{\ast} \, \cos \theta_{\ast} \, \cos \theta . \end{eqnarray}$ (60)We now consider the simplified case of cylindrical symmetry. This implies the absence of a deterministic magnetic field (the case of a turbulent magnetic feld can be handled with a slight modification of the formalism; see Sect. 14.2 of LL04, and Appendix A of Trujillo Bueno & Manso Sainz 1999). In a cylindrically symmetric environment the velocity-dependent irreducible components of the source function, $𝒮_{Q}^{K} (ν, t_{L})$ $\hbox{${\mathcal S}^K_Q(\vec\varv, t_{\rm L})$}$ , have a dependence on the azimuth χ_ν of the velocity of the form $\begin{matrix} 𝒮_{Q}^{K} (ν, t_{L}) = 𝒮_{Q}^{K} (ν, θ_{ν}, χ_{ν}, t_{L}) = 𝒮_{Q}^{K} (ν, θ_{ν}, 0, t_{L}) e^{- i Q χ_{ν}}, \end{matrix}$ $\begin{eqnarray} {\mathcal S}^K_Q(\vec{\varv}, t_{\rm L}) = {\mathcal S}^K_Q(\varv,\theta_{\varv},\chi_{\varv},t_{\rm L}) = {\mathcal S}^K_Q(\varv,\theta_{\varv},0,t_{\rm L}) \, {\rm e}^{-{\rm i} \, Q \, \chi_{\varv} }, \end{eqnarray}$ (61)where $𝒮_{Q}^{K} (ν, θ_{ν}, 0, t_{L})$ $\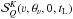hbox{${\mathcal S}^K_Q(\varv,\theta_{\varv},0, t_{\rm L})$}$ is the value of the source function corresponding to χ_ν = 0. Taking into account this property, we can limit ourselves to find the coupled equations for the quantities $𝒮_{Q}^{K} (ν, θ_{ν}, 0, t_{L})$ $\hbox{${\mathcal S}^K_Q(\varv,\theta_{\varv},0,t_{\rm L})$}$ , thus finding $\begin{matrix} [1 + ϵ + δ_{u}^{(K)} (ν)^{]} 𝒮_{Q}^{K} (ν, θ_{ν}, 0, t_{L}) = δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0}) \\ + \int_{0}^{\infty} d t_{L}^{'} \frac{1}{4 π} \int_{0}^{2 π} d χ \int_{θ_{1}}^{θ_{2}} d θ | \tan θ | e^{- (t_{L}^{'} - t_{L}) ϕ (ξ^{'}) / \cos θ} \int \frac{d ν_{a}^{'}}{ν_{t}} \int \frac{d ν_{b}^{'}}{ν_{t}} \frac{e^{- (ν_{a}^{' 2} + ν_{b}^{' 2} + ν_{c}^{2}) / ν_{t}^{2}}}{π^{3 / 2}} \\ \times \sum_{K^{'} Q^{'}} w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} Γ_{KQ, K^{'} Q^{'}} (Ω) e^{- i Q^{'} χ_{*}} 𝒮_{Q^{'}}^{K^{'}} (ν_{*}^{'}, θ_{*}, 0, t_{L}^{'}), \end{matrix}$ $\begin{eqnarray} \label{Eq:Coupled_SF_PP2} && \left[ 1 + \epsilon+ \delta_{\,u}^{\, (K)}(\vec\varv \,) \right] \, {\mathcal S}^K_Q(\varv, \theta_{\varv}, 0, t_{\rm L}) = \delta_{K0} \, \delta_{Q0} \; \epsilon \, B_T(\nu_0) \nonumber\\ && + \int_0^{\infty} \! {\rm d} t'_{\rm L} \; \frac{1}{4 \pi} \int_0^{2 \pi} \! {\rm d} \chi \int_{\theta_1}^{\theta_2} \! {\rm d} \theta \, |\tan\theta \,| \; {\rm e}^{-(t'_{\rm L} - t_{\rm L}) \, \varphi(\xi') / \cos \theta} \, \int \frac{{\rm d}\varv_{\rm a}^{\prime}}{\varv_{\rm t}} \int \frac{{\rm d}\varv_{\rm b}^{\prime}}{\varv_{\rm t}} \; \frac{{\rm e}^{-(\varv_{\rm a}^{\prime \, 2} +\varv_{\rm b}^{\prime \, 2} + \varv_{\rm c}^2)/\varv_{\rm t}^2}}{\pi^{3/2}} \nonumber\\ && \qquad \qquad \times \sum_{K'Q'} w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \, \Gamma_{K Q, K' Q'} (\vec \Omega) \, {\rm e}^{-{\rm i} \, Q' \chi_{\ast}} \, {\mathcal S}^{K'}_{Q'} \! (\varv^{\, \prime}_{\ast}, \theta_{\ast}, 0, t'_{\rm L}), \end{eqnarray}$ (62)where, according to Eq. (59), $e^{- i Q^{'} χ_{*}} = {[\frac{\cos θ ν_{a}^{'} + \sin θ ν_{c} - i ν_{b}^{'}}{\sqrt{(\cos θ ν_{a}^{'} + \sin θ ν_{c})^{2} + ν_{b}^{' 2}}}]}^{Q^{'}} e^{- i Q^{'} χ} .$ $\begin{equation} \label{Eq:exp_Qchiast} {\rm e}^{-{\rm i} \, Q' \chi_{\ast}} = \left[ \frac{\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c} - {\rm i} \, \varv'_{\rm b}} {\sqrt{(\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c})^2 + \varv_{\rm b}^{\prime 2}}} \right]^{Q'} \, {\rm e}^{-{\rm i}\, Q' \chi} . \end{equation}$ (63)We remind that the quantity ν_c appearing in this equation is defined by $ν_{c} = ν \cdot Ω = ν (\cos θ_{ν} \cos θ + \sin θ_{ν} \sin θ \cos χ) .$ $\begin{equation} \varv_{\rm c} = \vec\varv \cdot \vec \Omega = \varv \, (\cos \theta_{\varv} \cos \theta + \sin \theta_{\varv} \sin \theta \cos \chi) . \end{equation}$ (64)From Eq. (63), one can notice that the integrand in Eq. (62) is an odd function of $ν_{b}^{'}$ $\hbox{$\varv'_{\rm b}$}$ . When integrating over $ν_{b}^{'}$ $\hbox{$\varv'_{\rm b}$}$ from − ∞ to ∞, one can thus perform the following substitutions $\begin{matrix} {[\frac{\cos θ ν_{a}^{'} + \sin θ ν_{c} - i ν_{b}^{'}}{\sqrt{(\cos θ ν_{a}^{'} + \sin θ ν_{c})^{2} + ν_{b}^{' 2}}}]}^{\pm 1} & \to & \frac{\cos θ ν_{a}^{'} + \sin θ ν_{c}}{\sqrt{(\cos θ ν_{a}^{'} + \sin θ ν_{c})^{2} + ν_{b}^{' 2}}}, \\ {[\frac{\cos θ ν_{a}^{'} + \sin θ ν_{c} - i ν_{b}^{'}}{\sqrt{(\cos θ ν_{a}^{'} + \sin θ ν_{c})^{2} + ν_{b}^{' 2}}}]}^{\pm 2} & \to & \frac{(\cos θ ν_{a}^{'} + \sin θ ν_{c})^{2} - ν_{b}^{' 2}}{(\cos θ ν_{a}^{'} + \sin θ ν_{c})^{2} + ν_{b}^{' 2}} \cdot \end{matrix}$ $\begin{eqnarray} \left[ \frac{\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c} - {\rm i} \, \varv'_{\rm b}}{\sqrt{(\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c})^2 + \varv_{\rm b}^{\prime 2}}} \right]^{\pm 1} & \rightarrow & \frac{\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c}} {\sqrt{(\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c})^2 + \varv_{\rm b}^{\prime 2}}} , \nonumber \\ \left[ \frac{\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c} - {\rm i} \, \varv'_{\rm b}}{\sqrt{(\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c})^2 + \varv_{\rm b}^{\prime 2}}} \right]^{\pm 2} & \rightarrow& \frac{(\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c})^2 - \varv_{\rm b}^{\prime 2}}{(\cos \theta \, \varv'_{\rm a} + \sin \theta \, \varv_{\rm c})^2 + \varv_{\rm b}^{\prime 2}} \cdot \end{eqnarray}$ (65)Finally, one can notice that the structure of Eq. (62) is such to be consistent with our hypothesis on the behavior of the source function with the azimuth of the velocity. This is easily proven by considering the fact that the quantity Γ_KQ,K′Q′(Ω) depends on the angle χ through an exponential of the form exp [i(Q′ − Q)χ].

It is convenient to perform a change of variables in the integral appearing in Eq. (62). Once the values of ν and θ_ν (the velocity vector appearing as the argument of the density matrix element for which we write the statistical equilibrium equation) and the direction Ω (through the angles θ and χ) are specified, the velocity component ν_c is fixed. We can then transform the double integral in the variables $(d ν_{a}^{'}, d ν_{b}^{'})$ $\hbox{$({\rm d} \varv'_{\rm a}, {\rm d} \varv'_{\rm b})$}$ in a double integral over the variables $(ν_{*}^{'}, θ_{*})$ $\hbox{$(\varv'_{\ast},\theta_{\ast})$}$ . For this we have to consider the formal transformation $\int \frac{d ν_{a}^{'}}{ν_{t}} \int \frac{d ν_{b}^{'}}{ν_{t}} \to \frac{1}{ν_{t}^{2}} \int d ν_{*}^{'} \int d (\cos θ_{*}) \frac{1}{| 𝒥 |},$ $\begin{equation} \int \frac{{\rm d} \varv_{\rm a}^\prime}{\varv_{\rm t}} \int \frac{{\rm d} \varv_{\rm b}^\prime}{\varv_{\rm t}} \rightarrow \frac{1}{\varv_{\rm t}^2} \, \int {\rm d} \varv'_{\ast} \int {\rm d} (\cos \theta_*) \, \frac{1}{|\, {\mathcal J}\, |} , \label{Eq:int_transf} \end{equation}$ (66)where $\hbox{${\mathcal J}$}$ is the determinant of the Jacobian of the transformation, namely $𝒥 = \det (\begin{matrix} \frac{d ν_{*}^{'}}{d ν_{a}^{'}} & \frac{d ν_{*}^{'}}{d ν_{b}^{'}} \\ \frac{d (\cos θ_{*})}{d ν_{a}^{'}} & \frac{d (\cos θ_{*})}{d ν_{b}^{'}} \end{matrix}) .$ $\begin{equation} {\mathcal J} = {\rm det} \left( \begin{array}{cc} \displaystyle{\frac{{\rm d} \varv'_{\ast}}{{\rm d} \varv'_{\rm a}}} & \displaystyle{\frac{{\rm d} \varv'_{\ast}}{{\rm d} \varv'_{\rm b}}} \\ & \\ \displaystyle{\frac{{\rm d} (\cos\theta_{\ast})}{{\rm d} \varv'_{\rm a}}} & \displaystyle{\frac{{\rm d} (\cos\theta_{\ast})}{{\rm d} \varv'_{\rm b}}} \end{array} \right) . \end{equation}$ (67)On the other hand, from the equations relating $ν_{*}^{'}$ $\hbox{$\varv'_{\ast}$}$ and θ_∗ with $ν_{a}^{'}$ $\hbox{$\varv'_{\rm a}$}$ and $ν_{b}^{'}$ $\hbox{$\varv'_{\rm b}$}$ , we have $\frac{d ν_{*}^{'}}{d ν_{a}^{'}} = \frac{ν_{a}^{'}}{ν_{*}^{'}}, \frac{d ν_{*}^{'}}{d ν_{b}^{'}} = \frac{ν_{b}^{'}}{ν_{*}^{'}}, \frac{d (\cos θ_{*})}{d ν_{a}^{'}} = \frac{- \sin θ}{ν_{*}^{'}}, \frac{d (\cos θ_{*})}{d ν_{b}^{'}} = 0,$ $\begin{equation} \frac{{\rm d} \varv'_{\ast}}{{\rm d} \varv'_{\rm a}} = \frac{\varv'_{\rm a}}{\varv'_{\ast}} , \qquad \frac{{\rm d} \varv'_{\ast}}{{\rm d} \varv'_{\rm b}} = \frac{\varv'_{\rm b}}{\varv'_{\ast}} , \qquad \frac{{\rm d} (\cos \theta_{\ast})}{{\rm d} \varv'_{\rm a}} = \frac{-\sin \theta}{\varv'_{\ast}} , \qquad \frac{{\rm d} (\cos \theta_{\ast})}{{\rm d} \varv'_{\rm b}} = 0 , \end{equation}$ (68)so that we obtain $\frac{1}{| 𝒥 |} = \frac{ν_{*}^{' 2}}{\sin θ | ν_{b}^{'} |} \cdot$ $\begin{equation} \frac{1}{|\, {\mathcal J}\, |} = \frac{\varv_{\ast}^{\prime 2}}{\sin \theta \, | \, \varv'_{\rm b} \, |} \cdot \end{equation}$ (69)This equation, together with the relationships previously developed among the components of the velocity, allows us to rewrite Eq. (66) in the form $\int \frac{d ν_{a}^{'}}{ν_{t}} \int \frac{d ν_{b}^{'}}{ν_{t}} \to \int \frac{d ν_{*}^{'}}{ν_{t}} \frac{ν_{*}^{'}}{ν_{t}} \int d θ_{*} \frac{1}{\sin θ | \sin (χ_{*} - χ) |},$ $\begin{equation} \int \frac{{\rm d} \varv_{\rm a}^\prime}{\varv_{\rm t}} \int \frac{{\rm d} \varv_{\rm b}^\prime}{\varv_{\rm t}} \rightarrow \int \frac{{\rm d} \varv'_{\ast}}{\varv_{\rm t}} \, \frac{\varv'_{\ast}}{\varv_{\rm t}} \int {\rm d} \theta_{\ast} \frac{1}{\sin \theta \, |\sin (\chi_{\ast} - \chi) \,|} , \end{equation}$ (70)where $| \sin (χ_{*} - χ) | = \sqrt{1 - {(\frac{ν_{c} - ν_{*}^{'} \cos θ_{*} \cos θ}{ν_{*}^{'} \sin θ_{*} \sin θ})}^{2}} \cdot$ $\begin{equation} |\sin (\chi_{\ast} - \chi) \,| = \sqrt{1 - \left( \frac{\varv_{\rm c} - \varv'_{\ast} \, \cos \theta_{\ast} \, \cos \theta}{\varv'_{\ast} \, \sin \theta_{\ast} \, \sin \theta } \right)^2 } \cdot \end{equation}$ (71)Substituting this result into Eq. (62), and inverting the order of the integrals, it is possible to rewrite the same equation in a different form. Performing the following change of notations on the integration variables: $ν_{*}^{'} \to ν^{'}$ $\hbox{$\varv'_{\ast} \rightarrow \varv'$}$ , $θ_{*} \to θ_{ν}^{'}$ $\hbox{$\theta_{\ast} \rightarrow \theta'_{\varv}$}$ , one gets $[1 + ϵ + δ_{u}^{(K)} (ν)^{]} 𝒮_{Q}^{K} (ν, θ_{ν}, 0, t_{L}) = δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0}) + \int_{0}^{\infty} d t_{L}^{'} \int \frac{d ν^{'}}{ν_{t}} \frac{ν^{'}}{ν_{t}} \int d θ_{ν}^{'} \sum_{K^{'} Q^{'}} 𝒜_{Q Q^{'}}^{K K^{'}} (ν, θ_{ν}, t_{L}, ν^{'}, θ_{ν}^{'}, t_{L}^{'}) 𝒮_{Q^{'}}^{K^{'}} (ν^{'}, θ_{ν}^{'}, 0, t_{L}^{'}),$ $\begin{equation} \left[ 1+ \epsilon+ \delta_{\,u}^{\, (K)}(\vec\varv \,) \right] {\mathcal S}^K_Q(\varv, \theta_{\varv}, 0, t_{\rm L}) = \delta_{K0} \, \delta_{Q0} \; \epsilon \, B_T(\nu_0) +\int_0^{\infty} \! {\rm d} t'_{\rm L} \; \int \frac{{\rm d} \varv'}{\varv_{\rm t}} \, \frac{\varv'}{\varv_{\rm t}} \int {\rm d} \theta'_{\varv} \sum_{K' Q'} {\mathcal A}^{K K'}_{Q Q'} (\varv, \theta_{\varv}, t_{\rm L}, \varv', \theta'_{\varv}, t'_{\rm L}) \, {\mathcal S}^{K'}_{Q'} \! (\varv', \theta'_{\varv}, 0, t'_{\rm L}) , \end{equation}$ (72)where the kernel, $𝒜_{Q Q^{'}}^{K K^{'}} (ν, θ_{ν}, t_{L}, ν^{'}, θ_{ν}^{'}, t_{L}^{'})$ $\hbox{${\mathcal A}^{K K'}_{Q Q'} (\varv, \theta_{\varv}, t_{\rm L}, \varv', \theta'_{\varv},t'_{\rm L})$}$ is given by $𝒜_{Q Q^{'}}^{K K^{'}} (ν, θ_{ν}, t_{L}, ν^{'}, θ_{ν}^{'}, t_{L}^{'}) = \frac{1}{4 π} \frac{1}{π^{3 / 2}} \int_{0}^{2 π} d χ \int_{θ_{1}}^{θ_{2}} d θ \frac{1}{| \cos θ |} e^{- (t_{L}^{'} - t_{L}) ϕ (ξ^{'}) / \cos θ} e^{- (ν^{'} / ν_{t})^{2}} w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} Γ_{KQ, K^{'} Q^{'}} (Ω) \frac{e^{- i Q^{'} χ_{*}}}{| \sin (χ_{*} - χ) |}$ $\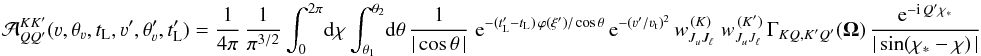begin{equation} {\mathcal A}^{K K'}_{Q Q'} (\varv, \theta_{\varv}, t_{\rm L}, \varv', \theta'_{\varv}, t'_{\rm L}) = \frac{1}{4 \pi} \, \frac{1}{\pi^{3/2}} \int_0^{2 \pi} \! {\rm d}\chi \int_{\theta_1}^{\theta_2} \! {\rm d} \theta \, \frac{1}{|\cos \theta \,|} \; {\rm e}^{- (t'_{\rm L} - t_{\rm L}) \, \varphi(\xi') / \cos \theta} \, {\rm e}^{-(\varv' / \varv_{\rm t})^2} \, w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \, \Gamma_{K Q, K' Q'} (\vec \Omega) \, \frac{{\rm e}^{-{\rm i}\, Q'\chi_{\ast}}}{|\sin (\chi_{\ast} - \chi) \,|} \end{equation}$ (73)and can be more conveniently expressed in the form $𝒜_{Q Q^{'}}^{K K^{'}} (ν, θ_{ν}, t_{L}, ν^{'}, θ_{ν}^{'}, t_{L}^{'}) = \frac{1}{4 π} \frac{1}{π^{3 / 2}} \int_{0}^{2 π} d χ \int_{θ_{1}}^{θ_{2}} d θ \frac{1}{| \cos θ |} e^{- (t_{L}^{'} - t_{L}) ϕ (ξ^{'}) / \cos θ} e^{- (ν^{'} / ν_{t})^{2}} w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} Γ_{KQ, K^{'} Q^{'}} (Ω) e^{- i Q^{'} χ} \frac{e^{- i Q^{'} (χ_{*} - χ)}}{| \sin (χ_{*} - χ) |} \cdot$ $\begin{equation} {\mathcal A}^{K K'}_{Q Q'} (\varv, \theta_{\varv}, t_{\rm L}, \varv', \theta'_{\varv}, t'_{\rm L}) = \frac{1}{4 \pi} \, \frac{1}{\pi^{3/2}} \int_0^{2 \pi} \! {\rm d}\chi \int_{\theta_1}^{\theta_2} \! {\rm d}\theta \, \frac{1}{|\cos \theta \,|} \; {\rm e}^{-(t'_{\rm L} - t_{\rm L}) \, \varphi(\xi') / \cos \theta} \; {\rm e}^{-(\varv' / \varv_{\rm t})^2} w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \, \Gamma_{K Q, K' Q'} (\vec \Omega) \, {\rm e}^{-{\rm i} \, Q' \chi} \, \frac{{\rm e}^{-{\rm i} \, Q'(\chi_{\ast}-\chi)}} {|\sin (\chi_{\ast}-\chi) \,|} \cdot \label{Eq:kernel_PP} \end{equation}$ (74)The quantities cos(χ_∗ − χ) and sin(χ_∗ − χ) appearing (implicitly or explicitly) in this equation are related to the other variables through the equations $\begin{matrix} \cos (χ_{*} - χ) & = & \frac{ν_{c} - ν^{'} \cos θ_{ν}^{'} \cos θ}{ν^{'} \sin θ_{ν}^{'} \sin θ}, \\ \sin (χ_{*} - χ) & = & \pm \sqrt{1 - {(\frac{ν_{c} - ν^{'} \cos θ_{ν}^{'} \cos θ}{ν^{'} \sin θ_{ν}^{'} \sin θ})}^{2}} \cdot \end{matrix}$ $\begin{eqnarray} \cos(\chi_{\ast} -\chi) & = & \frac{\varv_{\rm c} - \varv' \, \cos \theta'_{\varv} \, \cos \theta}{\varv' \, \sin \theta'_{\varv} \, \sin \theta} , \\ \sin(\chi_{\ast} -\chi) & = & \pm \sqrt{1 - \left( \frac{\varv_{\rm c} - \varv' \, \cos \theta'_{\varv} \, \cos \theta} {\varv' \, \sin \theta'_{\varv} \, \sin \theta} \right)^2 } \cdot \end{eqnarray}$ Concerning the ± sign appearing in this last expression, it is important to note that it is connected with the sign of the velocity component, $ν_{b}^{'}$ $\hbox{$\varv'_{\rm b}$}$ , that has now disappeared from the equations, due to change of variables that we have performed. Equation (74) has then, more properly, to be written as $\begin{matrix} 𝒜_{Q Q^{'}}^{K K^{'}} (ν, θ_{ν}, t_{L}, ν^{'}, θ_{ν}^{'}, t_{L}^{'}) = \frac{1}{4 π} \frac{1}{π^{3 / 2}} \int_{0}^{2 π} d χ \int_{θ_{1}}^{θ_{2}} d θ \frac{1}{| \cos θ |} e^{- (t_{L}^{'} - t_{L}) ϕ (ξ^{'}) / \cos θ} e^{- (ν^{'} / ν_{t})^{2}} w_{J_{u} J_{ℓ}}^{(K)} w_{J_{u} J_{ℓ}}^{(K^{'})} \\ \times Γ_{KQ, K^{'} Q^{'}} (Ω) e^{- i Q^{'} χ} \frac{1}{| \sin (χ_{*} - χ) |} [e^{- i Q^{'} (χ_{*}^{(-)} - χ)} + e^{- i Q^{'} (χ_{*}^{(+)} - χ)}], \end{matrix}$ $\begin{eqnarray} && {\mathcal A}^{K K'}_{Q Q'}(\varv, \theta_{\varv}, t_{\rm L}, \varv', \theta'_{\varv}, t'_{\rm L}) = \frac{1}{4 \pi} \, \frac{1}{\pi^{3/2}} \int_0^{2 \pi} \! {\rm d}\chi \int_{\theta_1}^{\theta_2} \! {\rm d}\theta \, \frac{1}{|\cos \theta \, |} \; {\rm e}^{-(t'_{\rm L} - t_{\rm L}) \, \varphi(\xi') / \cos \theta} \; {\rm e}^{-(\varv' / \varv_{\rm t})^2} w^{\, (K)}_{J_u J_\ell} \; w^{\, (K')}_{J_u J_\ell} \nonumber\\ && \times \Gamma_{K Q, K' Q'} (\vec \Omega) \, {\rm e}^{-{\rm i} \, Q' \chi} \, \frac{1}{|\sin (\chi_{\ast} - \chi) \,|} \left[ {\rm e}^{-{\rm i}\, Q' (\chi_{\ast}^{(-)}-\chi)} + {\rm e}^{-{\rm i}\, Q' (\chi_{\ast}^{(+)}-\chi)} \right] , \end{eqnarray}$ (77)where $χ_{*}^{(-)}$ $\hbox{$\chi_{\ast}^{(-)}$}$ and $χ_{*}^{(+)}$ $\hbox{$\chi_{\ast}^{(+)}$}$ are the values of χ_∗ corresponding, respectively, to negative or positive $ν_{b}^{'}$ $\hbox{$\varv'_{\rm b}$}$ . With easy algebra we find $\begin{matrix} [e^{- i Q^{'} (χ_{*}^{(-)} - χ)} + e^{- i Q^{'} (χ_{*}^{(+)} - χ)}] & = & 2, for Q^{'} = 0, \\ [e^{- i Q^{'} (χ_{*}^{(-)} - χ)} + e^{- i Q^{'} (χ_{*}^{(+)} - χ)}] & = & 2 \cos (χ_{*} - χ), for Q^{'} = \pm 1, \\ [e^{- i Q^{'} (χ_{*}^{(-)} - χ)} + e^{- i Q^{'} (χ_{*}^{(+)} - χ)}] & = & 2 [2 \cos^{2} (χ_{*} - χ) - 1], for Q^{'} = \pm 2. \end{matrix}$ $\begin{eqnarray} \left[ {\rm e}^{-{\rm i} \, Q' (\chi_{\ast}^{(-)}-\chi)} + {\rm e}^{-{\rm i} \, Q' (\chi_{\ast}^{(+)}-\chi)} \right] & =& 2 , \qquad \qquad \qquad \qquad \qquad {\rm for \;} Q'=0 , \nonumber \\ \left[ {\rm e}^{-{\rm i} \, Q' (\chi_{\ast}^{(-)}-\chi)} + {\rm e}^{-{\rm i} \, Q' (\chi_{\ast}^{(+)}-\chi)} \right] & =& 2 \cos(\chi_{\ast} -\chi) , \qquad \qquad \quad \, {\rm for \;} Q' = \pm 1 , \\ \left[ {\rm e}^{-{\rm i} \, Q' (\chi_{\ast}^{(-)}-\chi)} + {\rm e}^{-{\rm i} \, Q' (\chi_{\ast}^{(+)}-\chi)} \right] & =& 2 \, [ 2 \, \cos^2(\chi_{\ast} -\chi) - 1] , \qquad \! {\rm for \;} Q' = \pm 2 \nonumber . \end{eqnarray}$ (78)We conclude observing that the equations for the velocity-independent source function derived in Chapter 14 of LL04 under the approximation of complete redistribution on velocity can be recovered, as a particular case, from the equations presented in this work. Indeed, they can be obtained starting from Eq. (35), assuming that the source function $𝒮_{Q}^{K}$ $\hbox{${\mathcal S}^K_Q$}$ and the depolarizing rate $δ_{u}^{(K)}$ $\hbox{$\delta_u^{(K)}$}$ do not depend on the velocity, performing the integral in d³ν′ appearing in the last term, and averaging over the velocity distribution f(ν).

7. The R_I redistribution phase-matrix

We now analyze the basic equations that underly this physical problem, following an alternative approach. Instead of eliminating the “radiation field variables” in order to obtain a set of coupled equations for the velocity-dependent density matrix elements, we can eliminate the “density matrix variables” in order to obtain equations which directly involve the Stokes parameters of the radiation field. This brings us to the definition of a suitable redistribution phase-matrix, referred to in the literature as R_I in the case of a Maxwellian distribution of velocities.

Neglecting the magnetic field contribution, Eq. (17) can be easily solved for $𝒮_{Q}^{K} (ν, x)$ $\hbox{${\mathcal S}^K_Q(\vec\varv, \vec x)$}$ . One gets $𝒮_{Q}^{K} (ν, x) = \frac{w_{J_{u} J_{ℓ}}^{(K)} (- 1)^{Q} [J_{- Q}^{K} (ν_{0})]_{c . f .} + δ_{K 0} δ_{Q 0} ϵ B_{T} (ν_{0})}{1 + ϵ + δ_{u}^{(K)} (ν)} \cdot$ $\begin{equation} {\mathcal S}^K_Q(\vec\varv, \vec x\,) = \frac{w^{\, (K)}_{J_u J_\ell} \; (-1)^Q \, [ J^K_{-Q}(\nu_0)]_{\rm c.f.} + \delta_{K0} \, \delta_{Q0} \; \epsilon \, B_T(\nu_0)}{1+ \epsilon+ \delta_{\,u}^{\, (K)}(\vec\varv \,)} \cdot \end{equation}$ (79)We can now substitute this expression for the velocity-dependent source function into Eq. (23), giving the emission coefficient for the Stokes parameters at frequency ν into the direction Ω. Taking also into account Eqs. (11) and (21), the expression of the emission coefficient can be cast in the form $ε_{i} (ν, Ω) = k_{L}^{A} (x) {\frac{ϵ}{1 + ϵ} p (ν, Ω) B_{T} (ν_{0}) + \frac{1}{1 + ϵ} \int d^{3} ν f (ν) δ (ν_{0} + ν_{0} \frac{ν \cdot Ω}{c} - ν) 􏽉 \frac{d Ω^{'}}{4 π} \sum_{j = 0}^{3} P_{ij}^{(c)} (Ω, Ω^{'}, ν) S_{j} (ν_{0} + ν_{0} \frac{ν \cdot Ω^{'}}{c}, Ω^{'})},$ $\begin{equation} \varepsilon_i(\nu, \vec \Omega) = k_{\rm L}^{\rm A}(\vec{x}) \left\{ \frac{\epsilon}{1 + \epsilon} \, p(\nu,\vec{\Omega}) \, B_T(\nu_0) + \frac{1}{1 + \epsilon} \int {\rm d}^3 \vec\varv \, f(\vec\varv \,) \, \delta \left( \nu_0 + \nu_0 \frac{\vec\varv \cdot \vec \Omega}{c} - \nu \right) \oint \frac{{\rm d} \vec \Omega'}{4 \pi} \sum_{j=0}^3 P_{ij}^{({\rm c})}(\vec \Omega, \vec \Omega', \vec \varv) \, S_{\! j} \left( \nu_0 + \nu_0 \frac{\vec\varv \cdot \vec \Omega'}{c}, \vec\Omega' \right) \right\} , \label{Eq:eps_red1} \end{equation}$ (80)where $P_{ij}^{(c)} (Ω, Ω^{'}, ν)$ $\hbox{$P_{ij}^{({\rm c})}(\vec \Omega, \vec \Omega', \vec \varv)$}$ is the scattering phase matrix (corrected for depolarizing collisions) which is given by $P_{ij}^{(c)} (Ω, Ω^{'}, ν) = \sum_{KQ} {[1 + \frac{δ_{u}^{(K)} (ν)}{1 + ϵ}]}^{-1} W_{K} (J_{ℓ}, J_{u}) (- 1)^{Q} 𝒯_{Q}^{K} (i, Ω) 𝒯_{- Q}^{K} (j, Ω^{'}),$ $\begin{equation} P_{ij}^{({\rm c})}(\vec \Omega, \vec \Omega', \vec \varv) = \sum_{KQ} \left[ 1+ \frac{\delta_u^{(K)}(\vec\varv \, )}{1 + \epsilon} \right]^{-1} W_K(J_\ell,J_u) \, (-1)^Q \, {\mathcal T}^K_Q (i, \vec \Omega) \, {\mathcal T}^K_{-Q}(j,\vec \Omega') , \end{equation}$ (81)with $W_{K} (J_{ℓ}, J_{u}) = {}^{(}{w_{J_{u} J_{ℓ}}^{(K)}}^{)}^{2}$ $\hbox{$W_K(J_{\ell},J_u) = \left( w^{(K)}_{J_u J_{\ell}} \right)^2$}$ . We now assume that the velocity distribution is Maxwellian, and we perform the integral in d³ν, neglecting the velocity dependence of the depolarizing collisions³. Under this hypothesis, the scattering phase matrix does not depend any longer on ν and can thus be simply written as $P_{ij}^{(c)} (Ω, Ω^{'})$ $\hbox{$P_{ij}^{({\rm c})}(\vec \Omega, \vec \Omega')$}$ . It is convenient to perform an inversion of the two integrals (first we perform the integral in d³ν and then the one in dΩ′) and to introduce a right-handed triplet of unit vectors, (u₁,u₂,u₃), defined in the following way: u₁ is the unit vector along the direction that bisects the angle Θ (0 ≤ Θ ≤ π) formed by Ω and Ω′; u₂ is perpendicular to u₁, lying, as u₁, in the plane defined by Ω and Ω′, and being directed in such a way that it has a positive component along Ω . Finally, u₃ is defined accordingly. The unit vectors u₁ and u₂ are given by $u_{1} = \frac{Ω + Ω^{'}}{2 \cos (Θ / 2)}, u_{2} = \frac{Ω - Ω^{'}}{2 \sin (Θ / 2)},$ $\begin{equation} \vec u_1 = \frac{\vec \Omega + \vec \Omega'}{2 \, \cos(\Theta/2)} , \qquad \vec u_2 = \frac{\vec \Omega - \vec \Omega'}{2 \, \sin(\Theta/2)} , \end{equation}$ (82)with the inverse formulae $Ω = \cos (Θ / 2) u_{1} + \sin (Θ / 2) u_{2}, Ω^{'} = \cos (Θ / 2) u_{1} - \sin (Θ / 2) u_{2} .$ $\begin{equation} \vec \Omega = \cos(\Theta/2) \, \vec u_1 + \sin(\Theta/2) \, \vec u_2 , \qquad \vec \Omega' = \cos(\Theta/2) \, \vec u_1 - \sin(\Theta/2) \, \vec u_2 . \end{equation}$ (83)Writing ν= ν₁ u₁ + ν₂ u₂ + ν₃ u₃, the delta function appearing in Eq. (80) is satisfied when $\frac{c}{ν_{0}} (ν - ν_{0}) = \cos (Θ / 2) ν_{1} + \sin (Θ / 2) ν_{2} .$ $\begin{equation} \frac{c}{\nu_0} \, (\nu - \nu_0) = \cos(\Theta/2) \, \varv_1 + \sin(\Theta/2) \, \varv_2 . \label{Eq:int_delta} \end{equation}$ (84)Taking into account this relation between ν₁ and ν₂, the Stokes parameter S_j(ν₀ + ν₀ ν·Ω′/c,Ω′), also appearing in Eq. (80), can be written as S_j(ν′,Ω′), where the frequency ν′ only depends on ν₂, being given by $ν^{'} = ν - 2 \frac{ν_{0}}{c} \sin (Θ / 2) ν_{2} .$ $\begin{equation} \nu' = \nu -2 \frac{\nu_0}{c} \, \sin(\Theta/2) \, \varv_2 \;\ . \label{Eq:nuprime} \end{equation}$ (85)Integrating first in dν₃ and then in dν₁ (this latter integral being performed taking into account the Dirac-delta), one is left with the expression $ε_{i} (ν, Ω) = k_{L}^{A} (x) {\frac{ϵ}{1 + ϵ} p_{M} (ν - ν_{0}) B_{T} (ν_{0}) + \frac{1}{1 + ϵ} 􏽉 \frac{d Ω^{'}}{4 π} \sum_{j = 0}^{3} P_{ij}^{(c)} (Ω, Ω^{'}) \frac{1}{π Δ ν_{D} \cos (Θ / 2)} \int \frac{d ν_{2}}{ν_{t}} e^{- (ν_{1}^{2} + ν_{2}^{2}) / ν_{t}^{2}} S_{j} (ν^{'}, Ω^{'})},$ $\begin{equation} \varepsilon_i(\nu, \vec \Omega) = k_{\rm L}^{\rm A}(\vec{x}) \left\{ \frac{\epsilon}{1 + \epsilon} \, p_{\rm M}(\nu - \nu_0) \, B_T(\nu_0) + \frac{1}{1 + \epsilon} \oint \frac{{\rm d} \vec \Omega'}{4 \pi} \sum_{j=0}^3 P_{ij}^{({\rm c})} (\vec \Omega, \vec \Omega') \frac{1}{\pi \, \Delta \nu_{\rm D} \, \cos(\Theta/2)} \, \int \frac{{\rm d} \varv_2}{\varv_{\rm t}} \, {\rm e}^{-(\varv_1^2 + \varv_2^2)/\varv_{\rm t}^2} \, S_{\! j} (\nu', \vec \Omega') \right\} , \label{Eq:eps_red2} \end{equation}$ (86)where ν₁ follows from Eq. (84), being given by $ν_{1} = \frac{1}{\cos (Θ / 2)} (\frac{c}{ν_{0}} (ν - ν_{0}) - \sin (Θ / 2) ν_{2}) .$ $\begin{equation} \varv_1= \frac{1}{\cos(\Theta/2)} \left( \frac{c}{\nu_0} \, (\nu - \nu_0) - \sin(\Theta/2) \, \varv_2 \right) . \label{Eq:v1} \end{equation}$ (87)This equation can be written in an alternative form by a change of variable in the second integral, passing from the variable ν₂ to the variable ν′. This can be done by taking into account that (see Eq. (85)) $\frac{d ν_{2}}{ν_{t}} = - \frac{1}{2 Δ ν_{D} \sin (Θ / 2)} d ν^{'},$ $\begin{equation} \frac{{\rm d} \varv_2}{\varv_{\rm t}} = -\frac{1}{2 \, \Delta \nu_{\rm D} \, \sin(\Theta/2)} \, {\rm d}\nu' , \end{equation}$ (88)and that, starting from Eqs. (85) and (87), the quantity $(ν_{1}^{2} + ν_{2}^{2}) / ν_{t}^{2}$ $\hbox{$(\varv_1^2 + \varv_2^2)/\varv_{\rm t}^2$}$ can be written, after some algebra, in the form $\frac{ν_{1}^{2} + ν_{2}^{2}}{ν_{t}^{2}} = \frac{1}{Δ ν_{D}^{2} \sin^{2} Θ} [(ν - ν_{0})^{2} + (ν^{'} - ν_{0})^{2} - 2 (ν - ν_{0}) (ν^{'} - ν_{0}) \cos Θ^{]} .$ $\begin{equation} \frac{\varv_1^2 + \varv_2^2}{\varv_{\rm t}^2} = \frac{1}{\Delta \nu_{\rm D}^2 \sin^2 \! \Theta} \left[ (\nu - \nu_0)^2 + (\nu' - \nu_0)^2 - 2 \, (\nu-\nu_0) (\nu' - \nu_0) \, \cos \! \Theta \right] . \end{equation}$ (89)Moreover, by introducing the reduced variables ξ and ξ′, defined by $ξ = \frac{ν - ν_{0}}{Δ ν_{D}}, ξ^{'} = \frac{ν^{'} - ν_{0}}{Δ ν_{D}},$ $\begin{equation} \xi = \frac{\nu - \nu_0}{\Delta \nu_{\rm D}} , \qquad \xi'= \frac{\nu' - \nu_0}{\Delta \nu_{\rm D}} , \end{equation}$ (90)taking into account that ε_i(ξ,Ω) = ε_i(ν,Ω) dν/dξ = ε_i(ν,Ω) Δν_D, and recalling the definition of the absorption profile ϕ(ξ) (see Eq. (52)), Eq. (86) can be written in the following form $ε_{i} (ξ, Ω) = k_{L}^{A} (x) {\frac{ϵ}{1 + ϵ} ϕ (ξ) B_{T} (ν_{0}) + \frac{1}{1 + ϵ} 􏽉 \frac{d Ω^{'}}{4 π} \sum_{j = 0}^{3} P_{ij}^{(c)} (Ω, Ω^{'}) \frac{1}{π \sin Θ} \int d ξ^{'} e^{- (ξ^{2} + ξ^{' 2} - 2 ξ ξ^{'} \cos Θ) / \sin^{2} Θ} S_{j} (ξ^{'}, Ω^{'})}$ $\begin{equation} \varepsilon_i(\xi, \vec \Omega) = k_{\rm L}^{\rm A}(\vec{x}) \left\{ \frac{\epsilon}{1 + \epsilon} \, \varphi(\xi) \, B_T(\nu_0) + \frac{1}{1 + \epsilon} \oint \frac{{\rm d} \vec \Omega'}{4 \pi} \sum_{j=0}^3 P_{ij}^{({\rm c})} (\vec \Omega, \vec \Omega') \frac{1}{\pi \, \sin \! \Theta} \, \int {\rm d}\xi' \, {\rm e}^{-(\xi^2 + \xi^{\prime 2} - 2 \, \xi \xi' \cos \! \Theta) / \! \sin^2 \Theta} \, S_{\! j} (\xi', \vec \Omega') \right\} \end{equation}$ (91)or, using the lexicon of “redistribution functions”, $ε_{i} (ξ, Ω) = k_{L}^{A} (x) {\frac{ϵ}{1 + ϵ} ϕ (ξ) B_{T} (ν_{0}) + \frac{1}{1 + ϵ} 􏽉 \frac{d Ω^{'}}{4 π} \int d ξ^{'} \sum_{j = 0}^{3} {[R_{I} (ξ, Ω, ξ^{'}, Ω^{'})]}_{ij} S_{j} (ξ^{'}, Ω^{'})},$ $\begin{equation} \varepsilon_i(\xi, \vec \Omega) = k_{\rm L}^{\rm A}(\vec{x}) \left\{ \frac{\epsilon}{1 + \epsilon} \, \varphi(\xi) \, B_T(\nu_0) + \frac{1}{1 + \epsilon} \oint \frac{{\rm d} \vec{\Omega'}}{4 \pi} \int {\rm d}\xi' \, \sum_{j=0}^3 \left[ R_{\rm I}(\xi,\vec \Omega,\xi',\vec \Omega') \right]_{ij} \, S_{\! j} (\xi', \vec \Omega') \right\} , \end{equation}$ (92)where ${[R_{I} (ξ, Ω, ξ^{'}, Ω^{'})]}_{ij} = \frac{1}{π \sin Θ} P_{ij}^{(c)} (Ω, Ω^{'}) e^{- (ξ^{2} + ξ^{' 2} - 2 ξ ξ^{'} \cos Θ) / \sin^{2} Θ} .$ $\begin{equation} \left[ R_{\rm I}(\xi,\vec \Omega,\xi',\vec \Omega') \right]_{ij} = \frac{1}{\pi \sin \Theta} P_{ij}^{({\rm c})} (\vec \Omega, \vec \Omega') \, {\rm e}^{-(\xi^2 + \xi^{\prime 2} - 2 \, \xi \xi' \cos \! \Theta) / \! \sin^2 \! \Theta} . \label{Eq:RI} \end{equation}$ (93)This redistribution matrix was first proposed heuristically by Dumont et al. (1977). We also observe that for a 0 → 1 transition (for which W₀ = W₂ = 1), and in the absence of depolarizing collisions ( $δ_{u}^{(K)} = 0$ $\hbox{$\delta_u^{(K)}=0$}$ ), the redistribution matrix element [R_I] ₀₀ corresponds to the redistribution function R_I derived by Hummer (1962) for the unpolarized case (see his Eqs. (2.21.2) and (2.21.4))⁴.

8. Conclusions

In this paper we have derived the equations for the non-LTE problem of the second kind, taking velocity density matrix correlations into account. We considered the basic case of a two-level atom with infinitely sharp upper and lower levels, and we derived the statistical equilibrium equations for the velocity-space density matrix, neglecting the generalized Boltzmann term (which is a good approximation in the outer layers of a stellar atmosphere). Taking the Doppler effect into account, we derived a set of coupled equations for the velocity-dependent multipole components of the source function. Such equations show a coupling between the atoms at point x, moving with velocity ν, and the atoms at point x′, moving with velocity ν′, such that the difference ν− ν′ (the relative velocity) is perpendicular to the direction x − x′. This is a clear consequence of the Doppler effect and of the fact that we considered a resonant transition between two infinitely sharp atomic levels, an academic case that nevertheless allows us to investigate in detail the physics of pure Doppler redistribution in scattering polarization.

Starting from the statistical equilibrium equations for the velocity-space density matrix, and from the radiative transfer equations for polarized radiation, we derived the redistribution matrix corresponding to this physical problem. This redistribution matrix (heuristically proposed by Dumont et al. 1977) provides an alternative, equivalent description of the problem, and represents the generalization to the polarized case of the (angle-dependent) R_I redistribution function derived by Hummer (1962). If, on the one hand, the redistribution matrix formalism allows a very simple and intuitive description of redistribution phenomena, on the other hand, the velocity-space density matrix formalism provides a very transparent picture of the physics of the atom-photon interaction. The above-mentioned correlations between atoms located at different points of the plasma remain actually “hidden” in the redistribution matrix formalism. It should also be observed that only the average effect of such correlations is taken into account if the approximate “angle-averaged” $R_{I}^{AA}$ $\hbox{$R_{\rm I}^{\rm AA}$}$ redistribution matrix is considered. The velocity-space density matrix formalism has also the advantage of being suitable for taking lower-level polarization into account, and for describing multilevel atomic systems. An important point to remark is the appearance, in the statistical equilibrium equations for the velocity-space density matrix, of the generalized Boltzmann term. This term allows the inclusion of the effect of velocity-changing collisions into the problem, and points out the limits of applicability of any theoretical approach in which it is neglected. Velocity-changing collisions are a complex and not yet deeply investigated physical aspect that, however, may play an important role in the lower layers of stellar atmospheres. We point out that the equations that have been derived in Sect. 5 (in particular Eq. (35)) are very general, and can be applied to arbitrary velocity distributions and to plasma structures of any geometry.

¹

Depolarizing collisions are elastic collisions due to long-range interactions, and are thus ineffective in changing appreciably the velocity of the atom.

²

The applicability of the flat-spectrum approximation follows from the two inequalities γ_u,γ_ℓ ≪ Δν_P, with γ_u and γ_ℓ the inverse lifetimes of the upper and lower level, respectively, and ν_L ≪ Δν_P. The latter obviously implies an upper limit on the magnetic field intensities that can be handled by this formalism.

³

This is a non-trivial approximation. Indeed, if the colliding hydrogen atoms have a root mean square velocity w, an atom that is moving with velocity ν “sees”, in his rest frame, that the hydrogen atoms have a root mean square velocity $\sqrt{ν^{2} + w^{2}}$ $\hbox{$\sqrt{\varv^2 + w^2}$}$ . This can lead to an important dependence of the quantities δ^(K) on ν.

⁴

The discrepancy by a factor 16π² is due to the different normalization of the redistribution functions.

Acknowledgments

Financial support by the Spanish Ministry of Economy and Competitiveness and the European FEDER Fund through project AYA2010-18029 (Solar Magnetism and Astrophysical Spectropolarimetry) is gratefully acknowledged. One of the authors (ELD) wishes to acknowledge the Research Area of the Instituto de Astrofísica de Canarias (IAC) for helping to finance a six months sabbatical leave at the IAC, during which part of this work was carried out.

References

Belluzzi, L., & Trujillo Bueno, J. 2011, ApJ, 743, 3 [NASA ADS] [CrossRef] [Google Scholar]
Bommier, V. 1997a, A&A, 328, 706 [NASA ADS] [Google Scholar]
Bommier, V. 1997b, A&A, 328, 726 [NASA ADS] [Google Scholar]
Domke, H., & Hubeny, I. 1988, ApJ, 334, 527 [NASA ADS] [CrossRef] [Google Scholar]
Dumont, S., Omont, A., Pecker, J. C., & Rees, D. E. 1977, A&A, 54, 675 [NASA ADS] [Google Scholar]
Fano, U. 1957, Rev. Mod. Phys., 29, 74 [Google Scholar]
Hummer, D. G. 1962, MNRAS, 125, 21 [NASA ADS] [CrossRef] [Google Scholar]
Landi Degl’ Innocenti, E. 1996, Sol. Phys., 164, 21 [NASA ADS] [CrossRef] [Google Scholar]
Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) (LL04) [Google Scholar]
Omont, A., Smith, E. W., & Cooper, J. 1972, ApJ, 175, 185 [Google Scholar]
Omont, A., Smith, E. W., & Cooper, J. 1973, ApJ, 182, 283 [NASA ADS] [CrossRef] [Google Scholar]
Sampoorna, M. 2012, ApJ, 745, 189 [NASA ADS] [CrossRef] [Google Scholar]
Trujillo Bueno, J. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 551 [Google Scholar]
Trujillo Bueno, J., & Manso Sainz, R. 1999, ApJ, 516, 436 [NASA ADS] [CrossRef] [Google Scholar]

All Figures

	Fig. 1 Geometry of the problem. At each point P of the medium, the magnetic field vector B is specified by the angles θ_B and χ_B, defined in the fixed reference system Σ ≡ (xyz). The polarization unit vector e_a(Ω) specifies the reference direction for positive Q of the radiation flowing through P in the direction Ω, specified by the angles θ and χ in the fixed reference system.
In the text

	Fig. 2 Geometry of the transfer process. A ray with direction Ω enters the medium at point x₀ , where its Stokes parameters are $S_{i}^{(b)} (ν, Ω)$ $\hbox{$S_{\! i}^{\rm (b)}(\nu,\vec\Omega)$}$ . At point x, the Stokes parameters are given by Eq. (24).
In the text

Fig. 3

Geometry for the plane-parallel atmosphere. In the reference system Σ we consider a fixed point P located at height z corresponding to line optical depth t_L. The point P′ lies on the plane Γ parallel to the x–yplane; its height is z′ corresponding to line optical depth $t_{L}^{'}$ $\hbox{$t'_{\rm L}$}$ . The cylindrical coordinates (r,α) define the position of P′ in the plane Γ. The angles θ and χ specify the direction Ω.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Belluzzi, L., & Trujillo Bueno, J. 2011, ApJ, 743, 3 [NASA ADS] [CrossRef] [Google Scholar]

[2] Bommier, V. 1997a, A&A, 328, 706 [NASA ADS] [Google Scholar]

[3] Bommier, V. 1997b, A&A, 328, 726 [NASA ADS] [Google Scholar]

[4] Domke, H., & Hubeny, I. 1988, ApJ, 334, 527 [NASA ADS] [CrossRef] [Google Scholar]

[5] Dumont, S., Omont, A., Pecker, J. C., & Rees, D. E. 1977, A&A, 54, 675 [NASA ADS] [Google Scholar]

[6] Fano, U. 1957, Rev. Mod. Phys., 29, 74 [Google Scholar]

[7] Hummer, D. G. 1962, MNRAS, 125, 21 [NASA ADS] [CrossRef] [Google Scholar]

[8] Landi Degl’ Innocenti, E. 1996, Sol. Phys., 164, 21 [NASA ADS] [CrossRef] [Google Scholar]

[9] Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) (LL04) [Google Scholar]

[10] Omont, A., Smith, E. W., & Cooper, J. 1972, ApJ, 175, 185 [Google Scholar]

[11] Omont, A., Smith, E. W., & Cooper, J. 1973, ApJ, 182, 283 [NASA ADS] [CrossRef] [Google Scholar]

[12] Sampoorna, M. 2012, ApJ, 745, 189 [NASA ADS] [CrossRef] [Google Scholar]

[13] Trujillo Bueno, J. 2003, in Stellar Atmosphere Modeling, eds. I. Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 551 [Google Scholar]

[14] Trujillo Bueno, J., & Manso Sainz, R. 1999, ApJ, 516, 436 [NASA ADS] [CrossRef] [Google Scholar]

Theoretical formulation of Doppler redistribution in scattering polarization within the framework of the velocity-space density matrix formalism

1. Introduction

2. Formulation of the problem: hypotheses and approximations

3. The statistical equilibrium equations

4. The radiative transfer equation

5. Coupled equations for the velocity dependent irreducible components of the source function

6. Equations for a plane-parallel semi-infinite stellar atmosphere

7. The RI redistribution phase-matrix

8. Conclusions

Acknowledgments

References

All Figures

7. The R_I redistribution phase-matrix