| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A53 | |
| Number of page(s) | 8 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219658 | |
| Published online | 22 March 2013 | |
Simulations of micrometeoroid interactions with the Earth atmosphere
1
Dipartimento di Fisica e AstronomiaUniversità di Firenze,
Largo Fermi 2,
50125
Firenze,
Italy
e-mail:
giacomo.briani@csnsm.in2p3.fr
2
Dipartimento di Fisica, Università di Pisa,
Largo Pontecorvo 3,
50127
Pisa,
Italy
3
Istituto Nazionale di Fisica Nucleare (INFN), sezione di Pisa,
Largo Pontecorvo 3, 50127
Pisa,
Italy
4
INAF – Istituto di Radioastronomia, via Gobetti 101,
40129
Bologna,
Italy
5
Alta S. p. A., via A. Gherardesca 5, 56121 Ospedaletto,
Pisa,
Italy
Received:
23
May
2012
Accepted:
6
February
2013
Aims. Micrometeoroids (cosmic dust with size between a few μm and ~1 mm) dominate the annual extraterrestrial mass flux to the Earth. We investigate the range of physical processes occurring when micrometeoroids traverse the atmosphere. We compute the time (and altitude) dependent mass loss, energy balance, and dynamics to identify which processes determine their survival for a range of entry conditions.
Methods. We develop a general numerical model for the micrometeoroid-atmosphere interaction. The equations of motion, energy, and mass balance are simultaneously solved for different entry conditions (e.g. initial radii, incident speeds and angles). Several different physical processes are taken into account in the equation of energy and in the mass balance, in order to understand their relative roles and evolution during the micrometeoroid-atmosphere interaction. In particular, to analyze the micrometeoroid thermal history we include in the energy balance: collisions with atmospheric particles, micrometeoroid radiation emission, evaporation, melting, sputtering and kinetic energy of the ablated mass.
Results. Low entry velocities and grazing incidence angles favor micrometeoroid survival. Among those that survive, our model distinguishes (1) micrometeoroids who reach the melting temperature and for which melting is the most effective mass loss mechanism, and (2) micrometeoroids for which ablation due to evaporation causes most of the the mass loss. Melting is the most effective cooling mechanism. Sputtering-induced mass loss is negligible.
Key words: meteorites, meteors, meteoroids / Earth
© ESO, 2013
1. Introduction
Micrometeoroids (hereafter referred to as μMETs) with dimensions between ~25 μm and ~1 mm represent (by mass) the majority population of Solar system minor bodies at a distance of 1 AU from the Sun (Grün et al. 1985) and dominate the annual mass flux of extraterrestrial matter entering the Earth’s atmosphere, i.e. 4 ± 2 × 107 kg/yr, (Love & Brownlee 1993). μMETs can survive the interaction with the atmosphere and reach the Earth surface, becoming micrometeorites. A large number of micrometeorites, ≥105, have been recovered in Greenland (Maurette et al. 1987) and Antarctica (Maurette et al. 1991; Engrand & Maurette 1998; Duprat et al. 2007; Cordier et al. 2011; van Ginneken et al. 2012) over the past three decades. Many of these recovered μMETs are, however, less altered than expected: unmelted micrometeorites account for between 10 and 30% for particles >100 μm, ~50% for sizes between 50 and 100 μm and up to 78% in the size range 25−50 μm (Genge et al. 2008). In the CONCORDIA collection, which comprises micrometeorites collected in 2000, 2002 and 2006 at Dome C, Antarctica, unmelted micrometeorites represent between 33 and 36% of all the particles (Dobrica et al. 2009, 2010).
When interacting with the Earth’s atmosphere, μMETs are subjected to effects of different physical processes. These include collisions with atmospheric atoms and molecules, deceleration, temperature variations, ablation of μMET mass and sputtering, and excitation and ionization of atmospheric atoms and molecules. Several models have been proposed to analyze different aspects of the μMET – atmosphere interaction. In many cases, models for the μMET-atmosphere interaction focus on specific processes or are aim to explain particular meteor observations. Flynn (1989) modeled the μMET – atmosphere interaction using the US Standard Atmosphere values for the atmospheric density instead of the exponential approximation proposed by Whipple (1950) and Fraundorf (1980), but assuming that the μMET mass remains constant during the interaction. Love & Brownlee (1991) analyzed the heating experienced by μMETs. Their model includes vaporization and ablation of the μMET material but not sputtering, and they did not analyze how the different processes evolve during the μMET atmospheric flight. Campbell-Brown & Koschny (2004) tuned their model to explain light curves of faint meteors (μMETs in the size range 10 μm–2 mm). In particular, they modeled the μMET fragmentation to explain sudden increases observed in the light curves and to characterize the size of the grains that constitute the μMETs. Rogers et al. (2005) compared the mass loss due to sputtering to that due to ablation. They assumed,however, that all the energy transferred to a μMET by the collisions with atmospheric particles can be used by sputtering, rather than only a fraction of it, as should be the case because other physical properties (temperature increment, evaporation, etc.) depend on the collision energy. Szasz et al. (2008) added the treatment of sputtering proposed by Tielens et al. (1994) to the model of Love & Brownlee (1991) to model μMET head echoes recorded by the UHF European Incoherent Scatter facility. Vondrak et al. (2008) proposed a detailed model of the differential ablation of the μMET elements. They included thermal ablation (i.e. vaporization and melting) and sputtering and focused their analysis on the height at which the different μMET chemical constituents (e.g. Na, Mg, Si, Ca, Fe) are released in the atmosphere.
We approach the problem of the μMET – atmosphere interaction in a holistic way, considering those physical processes that can be the most important and highlighting their relative contributions with different atmospheric entry conditions and their evolution during the μMET atmospheric flight. This work is, however, not an exhaustive analysis of the μMET-atmosphere interaction. Our goals are (a) to highlight the necessity of a general study (b) to propose a model that includes different physical processes and to analyze their respective contributions and (c) to delineate the most critical aspects of the problem.
2. The model: properties of micrometeoroids and atmosphere
We treat μMETs as homogeneous, constant density spheres, with radius rμMET. Their initial radii are assumed to be between 25 μm and 500 μm. The upper limit of 500 μm is required by the assumption of isothermality: we assume that a μMET is sufficiently small to achieve a uniform internal temperature TμMET through thermal conduction. Actually, thermal gradients develop within μMETs due to endothermic reactions (e.g. phase transitions, see Flynn 1995) and are observed in recovered micrometeorites (Genge 2006a) as well as in experimental simulations (Toppani et al. 2001). But a treatment of μMET internal temperature distribution is beyond the scope of the present work (a qualitative discussion is presented in Sect. 6). Since we also assume constant emissivity, the μMET size must be larger than the wavelength of the emitted and absorbed radiation. A μMET generally absorbs radiation in the visible and ultraviolet (VIS-UV) in the spctral range 200−800 nm and emits infrared (IR) radiation (at temperatures of ~1000 K) with wavelength ≈3 μm (Coulson & Wickramasinge 2003), so the simulations terminate when rμMET < 5 μm. Micrometeoritic structure and compositions are particularly difficult issues. To treat the thermal processes occurring during their atmospheric passage (Greshake et al. 1998; Genge et al. 2008), we assume the μMETs have the composition of carbonaceous chondritic micrometeorites (which represent ~84% of the recovered micrometeorites, see e.g. Genge 2006b and Levison et al. 2009). In particular, we assume that μMETs are predominantly silicates. We choose the values of their thermodynamic parameters accordingly, as described below. As specified above, the μMET density ρμMET is assumed to be constant during the atmospheric flight. We used two different values for ρμMET, 3 and 1 g/cm3, to span the range of density measured for recovered micrometeorites (Genge et al. 2008). Similar values are adopted in Campbell-Brown & Koschny (2004) and Rogers et al. (2005).
The present-day Earth atmosphere is represented by the altitude profiles of density and the concentration of neutral components from the MSISE-90 model (Hedin 1991). We include six atmospheric species: N2, O, O2, Ar, He, H. We neglect the effects of charge accumulation in our models and therefore do not include atmospheric ions. Such processes are left for a future development.
The atmospheric properties determine also how a μMET moves in the atmosphere. Because the mean free path of an atmospheric particle, at heights between 60 and 200 km (those of interest in this work), is always longer than the μMET radius, we apply the free molecular flow regime. In other words, μMETs always interact with single atmospheric atoms and molecules, and there is not a gas layer that protects them from collisions (Sorasio et al. 2001; Campbell-Brown & Koschny 2004).
3. The model equations
The two dimensional micrometeroid trajectory is described by the time dependent
h (height from the Earth surface) and z (angle with
respect to the zenith direction). The equations describing their evolution are:
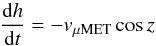 (1)and
(1)and 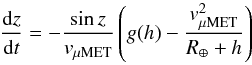 (2)where
vμMET is the μMET velocity,
g(h) is the gravitational acceleration at height
h and R⊕ is the radius of the Earth. The
initial value, h = 400 km, applies to the present-day terrestrial
atmosphere: the ambient density above this height is negligible. For the entry angle,
different values were simulated (0°, 45° and 70°); for
angles greater than 70°, μMETs tend to skip back to space. The
initial value (vin) of the μMET velocity
vμMET was left as a free parameter, the
observed range is from 11.2 km s-1 to 72.8 km s-1 (Ceplecha et al. 1998).
(2)where
vμMET is the μMET velocity,
g(h) is the gravitational acceleration at height
h and R⊕ is the radius of the Earth. The
initial value, h = 400 km, applies to the present-day terrestrial
atmosphere: the ambient density above this height is negligible. For the entry angle,
different values were simulated (0°, 45° and 70°); for
angles greater than 70°, μMETs tend to skip back to space. The
initial value (vin) of the μMET velocity
vμMET was left as a free parameter, the
observed range is from 11.2 km s-1 to 72.8 km s-1 (Ceplecha et al. 1998).
Collisions with atmospheric atoms and molecules determine the μMET
velocity vμMET. We model this neglecting the
thermal velocity of atmospheric particles (~370 m/s for Tatm =
160 K at h = 100 km) relative to
vμMET using the equation of motion:
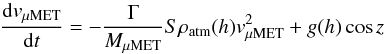 (3)where
(3)where
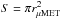 is the
μMET geometric cross section,
MμMET is its mass, and
ρatm(h) is the altitude dependent atmospheric
density. The drag coefficient Γ describes the momentum transfer efficiency in a single
collision to a μMET; its value is 0 ≤ Γ ≤ 2 (Γ = 2 for elastic collisions)
and we assume Γ = 1 (Campbell-Brown & Koschny
2004; Rogers et al. 2005).
is the
μMET geometric cross section,
MμMET is its mass, and
ρatm(h) is the altitude dependent atmospheric
density. The drag coefficient Γ describes the momentum transfer efficiency in a single
collision to a μMET; its value is 0 ≤ Γ ≤ 2 (Γ = 2 for elastic collisions)
and we assume Γ = 1 (Campbell-Brown & Koschny
2004; Rogers et al. 2005).
The core of our model is the description of how μMETs acquire energy and
of the changes thus produced. μMETs acquire energy by collisions with
atmospheric gas. Since
vth ≪ vμMET,
the heating rate is given by: 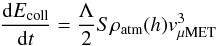 (4)where
Λ, heat transfer coefficient, parameterizes the fraction of the kinetic energy of an
incoming atmospheric particle that is transferred to the target μMET. Its
value depends on the μMET temperature and on the μMET Mach
number
ℳμMET ≡ vμMET/vth
(Hood & Horanyi 1991; Melosh & Goldin 2008). However, in the limit where
ℳμMET ≫ 1, Λ ≈ 1 (see Sect. 6 for a discussion) and we therefore assume Λ = 1, as do other recent studies
(e.g. Campbell-Brown & Koschny 2004; Rogers et al. 2005). Two other possible heating sources
are solar irradiation (Moses 1992; McAuliffe & Christou 2006), and atmosphere
radiation. We did not include these sources in our energy balance because they are
negligible for bodies as small as μMETs. We estimated the contributions of
solar and atmosphere radiation for
rin = 500 μm,
vin = 11.2 km s-1,
zin = 45°,
ρμMET = 3 g/cm3. The energy is 2
orders of magnitude larger than that gained from collisions at h = 262 km
and 1 order of magnitude larger at h = 170 km. However, this energy
acquired by radiation does not provoke either a reduction in the size of the
μMET size or a temperature increase. Energy acquired by radiation becomes
negligible, as in previous models (Moses 1992), when
denser atmospheric layers are reached where the collisions dominate. In our example
(rin = 500 μm,
vin = 11.2 km s-1,
zin = 45°,
ρμMET = 3 g/cm3) collisions
start to dominate at h = 128 km and the maximum energy acquired by
collisions overcomes that from radiation by 3 orders of magnitude. Thus, the
μMET’s temperature is regulated by the collisions: their peak
temperatures and final sizes do not change when radiation effects are included.
(4)where
Λ, heat transfer coefficient, parameterizes the fraction of the kinetic energy of an
incoming atmospheric particle that is transferred to the target μMET. Its
value depends on the μMET temperature and on the μMET Mach
number
ℳμMET ≡ vμMET/vth
(Hood & Horanyi 1991; Melosh & Goldin 2008). However, in the limit where
ℳμMET ≫ 1, Λ ≈ 1 (see Sect. 6 for a discussion) and we therefore assume Λ = 1, as do other recent studies
(e.g. Campbell-Brown & Koschny 2004; Rogers et al. 2005). Two other possible heating sources
are solar irradiation (Moses 1992; McAuliffe & Christou 2006), and atmosphere
radiation. We did not include these sources in our energy balance because they are
negligible for bodies as small as μMETs. We estimated the contributions of
solar and atmosphere radiation for
rin = 500 μm,
vin = 11.2 km s-1,
zin = 45°,
ρμMET = 3 g/cm3. The energy is 2
orders of magnitude larger than that gained from collisions at h = 262 km
and 1 order of magnitude larger at h = 170 km. However, this energy
acquired by radiation does not provoke either a reduction in the size of the
μMET size or a temperature increase. Energy acquired by radiation becomes
negligible, as in previous models (Moses 1992), when
denser atmospheric layers are reached where the collisions dominate. In our example
(rin = 500 μm,
vin = 11.2 km s-1,
zin = 45°,
ρμMET = 3 g/cm3) collisions
start to dominate at h = 128 km and the maximum energy acquired by
collisions overcomes that from radiation by 3 orders of magnitude. Thus, the
μMET’s temperature is regulated by the collisions: their peak
temperatures and final sizes do not change when radiation effects are included.
The rise in temperature due to collisional heating drives evaporation and melting of the
μMET, which reduce its mass and dimensions. Here the word “evaporation”
refers to sublimation and that mass is assumed to be lost immediately. We assume that the
evaporation begins as soon as μMETs start to acquire energy from collisions
(Moses 1992; Campbell-Brown & Koschny 2004; Rogers et
al. 2005) with the temperature dependent mass loss rate being modeled using the
Knudsen-Langmuir formula (Bronshten 1983):
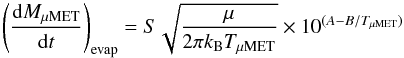 (5)where
kB is the Boltzmann constant. Here the relation
log 10(psat) = A − B/TμMET
(solution of the Clausius-Clapeyron equation) is used to evaluate the μMET
saturated vapor pressure. We assume A = 10.6 and
B = 13 500 K (Love & Brownlee
1991). We adopt μ = 45 amu for the mean atomic mass of the
μMET constituents that is appropriate for a chondritic composition (Love & Brownlee 1991).
(5)where
kB is the Boltzmann constant. Here the relation
log 10(psat) = A − B/TμMET
(solution of the Clausius-Clapeyron equation) is used to evaluate the μMET
saturated vapor pressure. We assume A = 10.6 and
B = 13 500 K (Love & Brownlee
1991). We adopt μ = 45 amu for the mean atomic mass of the
μMET constituents that is appropriate for a chondritic composition (Love & Brownlee 1991).
Melting also drives mass loss. At high temperatures, between ~1500 and ~2000 K, portions of
the body undergo pass from a solid to a liquid and we assume that this melted mass is also
completely lost. We note, however, that the very complex composition of chondritic
μMETs means that they have a range of melting points, so different parts
within a μMET can begin melting while others remain solid. We model melting
using a term proportional to the heating, as suggested by Campbell-Brown & Koschny (2004). To enforce the condition that the rate of
mass loss due to melting is different from zero only if
TμMET ≈ Tmelt = μMET
melting temperature, we employ a parametric coefficient Pspall,
defined as ![\begin{eqnarray*} P_\mathrm{spall}&=&0.5 + \frac{\arctan(T_\mathrm{\mu MET}-T_\mathrm{fus})}{\pi} \;\;\; \mathrm{for} \;\;\; T_\mathrm{\mu MET} < T_\mathrm{melt} \\[-1mm] P_\mathrm{spall}&=&0.5 + \frac{\arctan[4(T_\mathrm{\mu MET}-T_\mathrm{fus})]}{4\pi} \;\;\; \mathrm{for} \;\;\; T_\mathrm{\mu MET} > T_\mathrm{melt}. \end{eqnarray*}](/articles/aa/full_html/2013/04/aa19658-12/aa19658-12-eq60.png) This
coefficient was introduced by Campbell-Brown &
Koschny (2004), but in their work its value rapidly reaches 1 for
TμMET > Tmelt,
(i.e. all the heat is used to melt the μMET mass). Since melting is only
one of the processes included in the energy balance (8), we adopt a form of Pspall that limits its value to
0.625 (the two different expressions make Pspall a continuous
function of TμMET, to avoid problems in the
numerical integration). The assumed value for the μMET melting temperature
is Tmelt = 1623 K. This is similar to values adopted in previous
studies (Bonny & Balageas 1990; Love & Brownlee 1991; Flynn 1992; Scarsi 2004) and is
the melting point of silicates that are the dominant phases in μMETs. The
rate of mass loss caused by melting is thus given by
This
coefficient was introduced by Campbell-Brown &
Koschny (2004), but in their work its value rapidly reaches 1 for
TμMET > Tmelt,
(i.e. all the heat is used to melt the μMET mass). Since melting is only
one of the processes included in the energy balance (8), we adopt a form of Pspall that limits its value to
0.625 (the two different expressions make Pspall a continuous
function of TμMET, to avoid problems in the
numerical integration). The assumed value for the μMET melting temperature
is Tmelt = 1623 K. This is similar to values adopted in previous
studies (Bonny & Balageas 1990; Love & Brownlee 1991; Flynn 1992; Scarsi 2004) and is
the melting point of silicates that are the dominant phases in μMETs. The
rate of mass loss caused by melting is thus given by 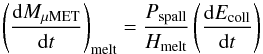 (6)where
Hmelt = 2.65 × 105 J/kg is the latent heat of
melting for stony meteoroids (Love & Brownlee
1991).
(6)where
Hmelt = 2.65 × 105 J/kg is the latent heat of
melting for stony meteoroids (Love & Brownlee
1991).
Sputtering is the ejection of atoms or molecules (targets) by collisions with incident
particles (projectiles) of sufficient kinetic energy. This mechanism has been proposed to
explain high altitude meteors (Brosch et al. 2001) and
previous studies suggest that it can cause significant mass loss (Rogers et al. 2005). We require the sputtering yield Y,
i.e. the number of target atoms or molecules removed by each projectile impact. To calculate
Y we chose a semi-empirical formula from Draine & Salpeter (1979), again using μ = 45 amu as mass
of the target particles and U0 = 5.7 eV as their binding energy
(this value is that indicated for a silicate compound in Draine & Salpeter 1979). Using s for the total number of
atmospheric species considered, the rate of mass loss by sputtering is: 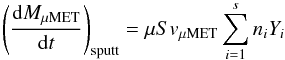 (7)where
ni is the number density of the
ith atmospheric species.
(7)where
ni is the number density of the
ith atmospheric species.
In summary, evaporation, melting, and sputtering are considered in the energy balance. As emphasized by Love & Brownlee (1991), it is essential to include all three to properly evaluate the μMET temperature. An important feature of our model is that the contributions of melting and evaporation are evaluated individually. The problem is to estimate the fraction η of the incoming energy that is used for sputtering and not for the other processes. Popova et al. (2007) proposed that particles removed by sputtering have a kinetic energy varying from 0% of the energy supplied by collisions (when the μMET entry velocity is <20 km s-1) to 20% (when μMETs enter the atmosphere at 70 km s-1), and that the rest of the energy contributes to the rise of μMET temperature that causes the emission of radiation and ablation. Based on this, and considering that a part of the incoming energy must be used to remove these particles, we assume η = 0.15 for every value of the μMET entry speed.
Beyond processes responsible for the mass loss, the rise of μMET temperature causes intense emission of radiation. This cooling process is fundamental for the μMET thermal balance, unlike larger meteoroids. As described in Sect. 2, we assume μMETs have a constant emissivity, ϵ = 0.9, as suggested in Campbell-Brown & Koschny (2004).
Finally we add a term for the kinetic energy of the ablated mass. As proposed in Campbell-Brown & Koschny (2004), we assume that
the ablated μMET mass leaves with a speed determined by the
μMET temperature TμMET . The
energy balance is thus given by: 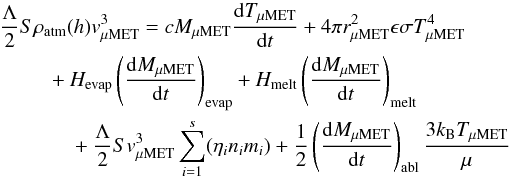 (8)where
σ is the Stefan-Boltzmann constant,
ηi,
ni and
mi are the sputtering coefficient, number
density and mass, respectively, of the atmospheric components. The expression for the energy
used in sputtering takes into account that, depending on the collision velocity, sputtering
is caused by only some of the atmospheric species (i.e. if Y is zero for
the ith species, then ηi = 0).
For the thermodynamic properties of μMETs we adopt values used in Bronshten (1983) and Love
& Brownlee (1991) for stony meteoroids: c = 103
J/(kg K) is the μMET specific heat,
Hevap = 6.05 × 106 J/kg is the latent heat of
vaporization. The variation of each term in Eq. (8) is followed throughout the numerical integrations so it is possible to see
which are most responsible for determining the μMET fate and valuate how
their roles change with different entry conditions and time during flight.
(8)where
σ is the Stefan-Boltzmann constant,
ηi,
ni and
mi are the sputtering coefficient, number
density and mass, respectively, of the atmospheric components. The expression for the energy
used in sputtering takes into account that, depending on the collision velocity, sputtering
is caused by only some of the atmospheric species (i.e. if Y is zero for
the ith species, then ηi = 0).
For the thermodynamic properties of μMETs we adopt values used in Bronshten (1983) and Love
& Brownlee (1991) for stony meteoroids: c = 103
J/(kg K) is the μMET specific heat,
Hevap = 6.05 × 106 J/kg is the latent heat of
vaporization. The variation of each term in Eq. (8) is followed throughout the numerical integrations so it is possible to see
which are most responsible for determining the μMET fate and valuate how
their roles change with different entry conditions and time during flight.
4. Numerical integration and validation of our code
Numerical integrations were performed using the RK4 method with an adaptive step size. For each quantity (i.e., μMET height, angle with respect to the vertical, speed, radius, mass and temperature) we required a minimum relative variation of 5 × 10-5, and the maximum relative variation allowed was 10-3. If the relative variations were too small, the integration step size is doubled with an imposed upper limit of 1 s; if the variations are too large then the calculated values are rejected and the integration step size halved with a lower limit of 10-10 s. We verified that the code reproduced the results of previous studies. Several temperature vs time profiles are shown in Love & Brownlee (1991). They use different initial temperatures and atmospheric properties than we do but we choose the difference between μMET peak temperatures as parameter for a comparison (i.e. the difference between the peak temperatures of μMETs that have equal entry speed, angle and density, but with different initial size). Introducing the set of equations of Love & Brownlee (1991) in our code, we obtain peak temperature differences that differ from the original ones for less than 9%. A second comparison was made with Rogers et al. (2005), who focused on the sputtering-induced mass loss. We computed the fractional mass lost by sputtering for μMETs with ρμMET = 3 g/cm3 and for μMETs with ρμMET = 1 g/cm3, considering value of entry speed ranging between 20 and 70 km s-1 using the same set of equations of Rogers et al. (2005). The maximum difference between our results and those of Rogers et al. (2005) is 6%.
5. Results
Our simulations highlight how decisive entry conditions are1. Table 1 summarizes the maximum values of vin that permits the survival of μMETs with different initial radii, incidence angles, and densities. It is evident that 1) smaller μMETs can have greater values of entry speed than greater μMETs; 2) less dense μMETs can sustain greater entry speeds than denser μMETs and 3) μMETs with large entry angle (i.e. far from the vertical) can survive higher entry speed than μMETs with small entry angle (i.e. close to the vertical).
 |
Fig. 1 Evolution of μMET radius with height assuming rin = 50 μm, zin = 45° and ρμMET = 3 g/cm3. |
Maximum values of entry velocity for which μMETs are able to survive and reach the Earth surface.
Figure 1 (all figures refer to μMETs with ρμMET = 3 g/cm3) shows the radius evolution of a 50 μm μMET for different values of vin. In the case of zin = 45°, for vin = 11.2 km s-1 the final μMET size is 28 μm, i.e. the μMET lost ~82% of its initial mass, while for vin = 16 km s-1 the final μMET radius is 7 μm (the mass lost is 99%). Another important feature evident in Fig. 1 is that μMETs experience most of their alteration within a limited height interval (~15 km for the cases displayed in Fig. 1), corresponding to a duration of only few seconds.
The same is true for the time evolution of μMET’s velocity. After a first phase in which the velocity remains almost constant, μMETs are suddenly decelerated when they encounter sufficiently dense atmospheric layers (Fig. 2). The height at which μMETs start to be decelerated is higher for larger entry radii and higher initial velocities but the time interval in which μMETs change from their initial to their final velocity is generally short. A μMET with rin = 50 μm, vin = 11.2 km s-1, zin = 45° and ρμMET = 3 g/cm3 is slowed down to 1 km s-1 in ~4 s, and then reaches its final velocity of ~100 m/s within ~30 s. In contrast, for rin = 300 μm, vin = 12 km s-1, zin = 45° and ρμMET = 3 g/cm3, a μMET is slowed down to 1 km s-1 in only ~2.5 s. Those μMETs with grazing trajectories or lower density experience lesser variation. For a very oblique entry, they decelerate more gradually. In particular, the μMET’s velocity (and therefore the rate of collisions) is reduced before the beginning of intensive ablation. Hence the maximum temperature is lower and the final radius is greater than for more nearly vertical entry. Similarly, μMETs with low density values (1 g/m3) are decelerated at higher altitude where the atmospheric density is low.
 |
Fig. 2 Evolution of μMET velocity with height A) and time B) assuming rin = 50 μm, zin = 45° and ρμMET = 3 g/cm3. |
Typical thermal histories are shown in Fig. 3A. The almost impulsive temperature rise is followed by cooling with the whole process lasting only a few seconds. The initial slight temperature decrease is due to efficient radiative emission and to the scarcity of collisions in the highest strata. μMET temperature would not decrease in the first phases of atmospheric entry if we included solar and atmospheric radiative heating but, as previously discussed, this contribution has negligible effects on μMET peak temperatures and final sizes (Sect. 3). At h ~100−120 km, the μMET temperature rapidly rises because of collisions, then after the maximum, TμMET decreases very rapidly because the collisional heating is reduced as μMETs slow down and shrink. Taking the full width at half the maximum (FWHM) temperature to compare the duration of the heating pulse, μMETs in Fig. 3A suffer heating pulses of 5.78 s (for vin = 11.2 km s-1), 5.25 s (for vin = 12 km s-1) and 3.15 s (for vin = 16 km s-1). Figure 3A shows that peak temperatures are reached earlier for higher entry velocities but the altitude of peak temperature is about the same: 86 km for vin = 11.2 km s-1, 88 km for vin = 16 km s-1. Figure 3A and B show that higher entry speeds as well as larger initial radii imply higher peak temperature, but the differences are small. Comparing Fig. 3A with Fig. 1 shows that the final radius is most sensitive to differences in entry speed. This is due to the melting process that both limits the maximum temperature values (Fig. 3B) and generates significant mass loss.
 |
Fig. 3 Typical time variation of the μMET temperature. A) Results for rin = 50 μm, zin = 45° and ρμMET = 3 g/cm3. B) Results for vin = 11.2 km s-1, zin = 45° and ρμMET = 3 g/cm3. The truncated dashed and solid curves correspond to μMETs that do not survive atmospheric passage. See text for discussion. |
Figure 3B shows temperature profiles for different values of the initial radius (with vin = 11.2 km s-1). Again, higher peak temperatures are reached for larger rin. Figure 3B shows the clear difference between two classes of profiles. For rin ≤ 100 μm the temperature curves have a regular, rounded shape. In contrast, for rin between 200 and 500 μm the top of the curves is due to melting of μMET material. This is a general characteristic of our results. It is not linked only to different entry radii, but it appears for several combinations of entry conditions. These two classes of temperature profiles imply different final states for μMETs. When the peak temperature is below the melting point and the temperature profile does not flatten, then the μMET survives after experiencing minor melting. These could correspond to the recovered unmelted and partially melted micrometeorites (see e.g. Genge et al. 2008). The other class of temperature profiles, with flatten peak near the melting point, correspond to μMETs for which most of the mass is melted. The difference between these two classes can be seen also analyzing the history of the energy producing the temperature variation, i.e. the term cMμMET(dTμMET/dt) included in the energy balance. This term is displayed in Fig. 4, normalized to the incoming energy (Eq. (4)), for the same cases as Fig. 3. These curves cross zero around 40 s, i.e. when the μMET temperatures reach their peak value and then start to decrease. As shown in the insert in Fig. 4, when μMETs reach the melting temperature there is an interval during which no energy is used to alter their temperature. In contrast, curves corresponding to unmelted or partially melted μMETs vary smoothly.
 |
Fig. 4 Fraction of the absorbed energy used to change the μMET temperature. These curves are proportional to dTμMET/dt so negative values mean that temperature is decreasing, positive values that it is increasing. The insert shows the transition from positive to negative values at around 40 s, coinciding with peak temperature and the start of μMET cooling by intense ablation. |
Figure 5 shows the distribution of the energy that μMETs gain from collisions in the different processes considered in the energy balance. In the first part of the trajectory most of the energy goes into raising the μMET’s temperature (black, thin line). At high temperature, ≳1000 K, ablative processes (evaporation and melting) and the kinetic energy of the ablated mass become important. However, the relative importance of the different processes change with different entry conditions. For the smallest μMETs (Fig. 5A) the radiative losses dominate. This happens in two phases. At the very beginning, not shown in Fig. 5, when μMETs suffer relatively few collisions, their temperature (Tin = 330 K) is sufficient to produce significant emission. Then when the μMET speed and radius are greatly reduced, so is the energy acquired by collisions, the μMET temperature is near its peak values, and the radiative loss dominates.
 |
Fig. 5 Variation of the energy going into different processes relative to the absorbed energy. A) Unmelted or partially melted μMET. B) Almost completely melted μMET. C) Completely destroyed μMET. See text for discussion. Noise in the temperature variation lines is due to the numerical integration and occurs when the calculation is performed on very small step sizes (of the order of 10-5 s, used when μMET size, velocity and temperature vary significantly). |
Figure 5A shows the typical case for a partially melted or unmelted μMET. In the case shown, melting accounts for only about 0.1% of the incoming energy, while up to about 25% goes into evaporation. Sputtering is negligible, reaching about the same level as melting and terminating abruptly when μMETs have slowed enough that the incident kinetic energy of atmospheric particles is below the sputtering threshold. For the case shown in Fig. 5B ablation processes (evaporation and melting) are more important than in the previous case. There is a time interval during which both evaporation and melting consume more energy than radiative losses. Consequently, more mass is lost (see Fig. 6) and the kinetic energy removed by the ablated mass is important for the energy balance. Sputtering is still unimportant because of the low initial velocity (vin = 11.2 km s-1 in Fig. 5B). Instead, for vin = 14 km s-1 (with rin = 500 μm, zin = 70° and ρμMET = 3 g/cm3), we find an increase of about two order of magnitude, with the fraction of incident energy going into sputtering reaching ~10%. This is also found for μMETs that do not survive atmospheric passage, as shown in Fig. 5C; sputtering accounts for more than 10% in the energy balance, and melting and evaporation are more important than radiative losses.
 |
Fig. 6 Relative contribution to the mass loss of processes. The solid line (labeled “mass lost”) shows the fraction of the total mass lost. A) Evaporation dominates the mass loss, the final mass of this μMET is 47% of the initial mass. B) Melting dominates the mass loss, the final mass is <1% of the initial mass. C) A μMET that is completely destroyed by melting. |
The analysis of the mass balance (Fig. 6) confirms what we find from the energy balance. In Fig. 6A (unmelted or partially melted μMET) melting accounts for ~20% of the total mass lost. For these μMETs, mass loss is mainly from evaporation; sputtering is negligible. The situation is opposite for the case shown in Fig. 6B: melting is the main cause of mass loss, while evaporation driven mass loss is much lower (~16% for the case of Fig. 6B). In summary, sputtering is significant for greater entry velocities but, in our models, it is never the principal mechanism for mass loss. In the case of Fig. 6C (relative to a μMET completely destroyed) sputtering is responsible for ~0.1% of the total mass lost. Even in the most extreme case, vin = 70 km s-1 and rin = 500 μm, it accounts for a modest 1% of the mass loss.
6. Discussion
We have assumed constant values for both the drag Γ (Eq. (3)) and the heat transfer Λ (Eq. (4)) coefficients, a choice that is valid in a free molecular flow regime (see e.g. Sorasio et al. 2001 and Popova et al. 2007) at high ℳμMET. These coefficients are, however, dependent on the μMET temperature and the μMET Mach number (Hood & Horanyi 1991; Melosh & Goldin 2008). Thus, to test the sensitivity of our model to these parameters we performed simulations with different values of Γ and Λ for rin = 100 μm, vin = 12 km s-1, zin = 45° and ρμMET = 3 g/cm3. Increasing Γ means the μMETs are decelerated more effectively, so they are less heated by collisions, reach lower peak temperatures (peak temperature for Γ = 2 is 55 K lower than for Γ = 1) and have larger final radii (rfin = 67 μm for Γ = 2, while rfin = 30 μm for Γ = 1). In contrast, for Γ < 0.6 our test μMET is destroyed; for Γ = 0.6 its peak temperature is 15 K higher than in the case Γ = 1 and the final radius is 6 μm. We find that μMET peak temperatures and final radii are more dependent on Λ. Decreasing Λ from 1 to 0.1 yields lower peak temperatures, decreasing from 1604 K to 1255 K. The final radius is 99 μm for Λ = 0.1, i.e. μMET size is unaffected by the interaction with the atmosphere as also found by Campbell-Brown & Koschny (2004). However, such low values of Λ are unlikely for the cases considered here. To estimate at what Λ the μMETs experience the most intense alteration at peak temperatures, we use the expression of Hood & Horanyi (1991):
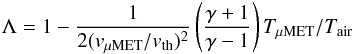 where
γ = 7/5 is the ratio of the specific heats of the
terrestrial atmospheric gases and Tair is the atmospheric
temperature. Since vth is computed as
where
γ = 7/5 is the ratio of the specific heats of the
terrestrial atmospheric gases and Tair is the atmospheric
temperature. Since vth is computed as
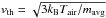 (kB = Boltzmann constant and mavg
= mean mass of atmospheric particles) the value of Λ is determined by the ratio
(kB = Boltzmann constant and mavg
= mean mass of atmospheric particles) the value of Λ is determined by the ratio
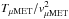 . In our
simulations the maximum TμMET is always reached
before vμMET is significantly reduced, and when
vμMET decreases, so does
TμMET. Thus, Λ remains close to 1. This is
illustrated in Table 2.
. In our
simulations the maximum TμMET is always reached
before vμMET is significantly reduced, and when
vμMET decreases, so does
TμMET. Thus, Λ remains close to 1. This is
illustrated in Table 2.
Values of the heat transfer coefficient Λ for three test case μMETs with zin = 45° and ρμMET = 3 g/cm3.
The coefficient η, the fraction of the absorbed energy going into sputtering, is also important but choosing its value is very difficult since previous theoretical (e.g. Sigmund 1981) and experimental (e.g. Nakles 2004) studies have treated sputtering as an isolated process. For instance, the mean mass of μMET atoms and their binding energy are necessary parameters for specifying the sputtering yield Y, and its contribution to the energy balance. We note that a simplified treatment of the structure and composition of the μMETs, as in this work, only approximates the sputtering contribution and this process is probably more important for less compact μMETs than those treated here. Any treatment of the sputtering yield and heating hinges on several critical points: the evaluation of the different processes that cause the removal of a particle from a solid body (May et al. 2000), the sputtering yield dependence on the projectile incidence angle (Jurac et al. 1998), which particles are ejected from the target (atoms? molecules? both? See Tielens et al. 1994) and the speed at which they leave the target (Popova et al. 2007). Coulson (2002) assumed a Maxwellian distribution for the speed of sputtered particles. This produces a momentum transfer to μMETs about 11 times greater than the case of collisions alone, with consequent significant decreases of the μMET speed, peak temperature and ablation. In our model, we do not include any impulsive reaction sustained by μMETs from removed fragments since we assume isotropic ablative mass loss, although we do account for their kinetic energy in the energy balance.
Finally the atmospheric component number density also affects sputtering. We find that sputtering-induced mass loss is always a small fraction (≤0.01) of the total amount. This contrasts with the results of Rogers et al. (2005), who find that sputtering accounts for up to about 40% of the mass loss for μMETs with ρμMET = 3 g/cm3 and up to half for μMETs with ρμMET = 1 g/cm3. We suggest that the difference between our results and those obtained by Rogers et al. (2005) is due to their assumption that all the energy transferred to μMETs by collisions with atmospheric particles produces sputtering, rather than only a fraction of it (i.e. they assume η = 1) and to their overestimate of the number densities of the atmospheric components that are systematically two order of magnitude greater than those we obtained from the same atmospheric model (the MSISE-90 model).
Our model assumes that μMETs are homogeneous and that all have the same composition. Recovered micrometeorites are, however, complex aggregates of different phases (e.g. silicates, sulfides, carbonaceous material) and show a wide range of compositions. More realistic μMETs could be modeled assuming different proportions of the constituent phases. This would require modeling μMETs of different densities and with different melting temperatures. Our results show that a lower μMET density favors their survival (see Table 1) because they are decelerated at higher altitude, in less dense atmospheric layers. Qualitatively, we expect that lower melting temperatures correspond to those μMETs that are mainly composed of more fragile phases, i.e. phases easily removed by the atmospheric frictional heating, as carbonaceous material and that higher melting temperatures correspond to those mainly composed of refractory phases, such as silicates, that are less affected by the atmospheric frictional heating. Vondrak et al. (2008) modeled the differential ablation of the μMET constituents, but without considering heterogeneities and retaining the hypothesis of uniform μMET temperature. We too assumed that μMETs have a uniform temperature at each instant of their atmospheric flight, as in previous models (Love & Brownlee 1991; Campbell-Brown & Koschny 2004). The problem of internal temperature gradients was treated by Szydlik & Flynn (1992), Flynn (1995), Szydlik & Flynn (1997), Genge & Grady (2000). However, in all these studies, the μMET radius is kept constant as are the thermal conductivity and heat capacity (i.e. they assume homogeneous composition). A model for the simulation of the atmospheric passage of heterogeneous, multiphase μMETs and of their internal temperature distribution would be a major advance.
7. Conclusions
To summarize, we list here our major conclusions. For any initial radius, a higher entry velocity and a more nearly normal incidence yield more severe heating for μMETs, and therefore greater destruction rate. For fixed entry velocity and angle, the larger the radius, the greater the amount of mass lost. For all the μMETs simulated in this work radiation emission is the most important process at greatest altitude, before μMETs encounter atmospheric layers sufficiently dense to activate ablation processes (evaporation and melting). Melting is the most effective process that limits the increase of the μMET temperature and produces significant mass loss. In all cases, the contribution of sputtering is found to be negligible in both the energy and the mass balance but could be more important for more fragile μMETs than those simulated here. For the smallest μMETs simulated in this work (rin = 25 μm), radiation is the dominant cooling process during all their atmospheric flight, allowing the survival of these small μMETs. Ablative processes are more important for larger μMETs, i.e. these lose a larger fraction of their mass than small μMETs and only low entry velocities and grazing entry angles insure survival during atmospheric passage.
Our model shows that, among μMETs that are not completely destroyed, two types can be distinguished based on their temperature evolution. The first group is those μMETs that show smooth temperature curves, i.e. that are not completely melted during atmospheric flight and therefore reach the surface as unmelted or partially melted micrometeorites (most of the mass lost by these μMETs is due to evaporation). The second comprises μMETs with flattened temperature curves near the maximum temperature. As we have shown, these differences are due to the importance of the melting process in the energy and the mass balance equations.
We view this model as a first step in a broader study of μMETs-atmosphere interactions. The necessary refinements require a broadly multidisciplinary approach that combines the physics with laboratory studies of the material properties from chemistry and mineralogy, for the alteration sustained by μMETs in flight, with detailed numerical hydrodynamic simulations of the composite materials typical of real samples. Finally, the analysis of the biochemical aspects, i.e. related to the organic molecules present in μMETs, could improve the understanding of what role μMETs played in the emergence of life on
Earth (and, by extension, extrasolar planets). For example, although its is beyond the scope of the present paper, this type of modeling can be applied to the case of the interaction of μMETs with the primordial terrestrial atmosphere to assess the role of μMETs as conveyors of pre-biotic molecules (Briani 2010).
We presented preliminary results of our model in a previous work (Briani et al. 2007). In the present paper we correct a few errors in the model equations. We changed the expression for Pspall so that its maximum value is 0.65; we changed the equation for the rate of mass loss due to sputtering (7) so that we now include sputtering caused only by those atmospheric molecules that collide with the μMET with sufficient energy (Draine & Salpeter 1979). In addition, we present here a more detailed analysis of how the considered physical processes evolve during the μMET flight.
Acknowledgments
We thank M. D’Orazio and L. Folco for valuable discussions and F. Savini for assistance. We thank F. Rietmeijer for a careful review of a first version of the manuscript. This work was supported in part by MIUR.
References
- Bonny, P., & Balageas, D. 1990, LPSC, 21, 111 [Google Scholar]
- Briani, G. 2010, Ph.D. Thesis, Università di Firenze, Florence, Italy, and Muséum National d’Histoire Naturelle, Paris, France [Google Scholar]
- Briani, G., Pupillo, G., Aiello, S., et al. 2007, Mem. Sos. Astron. It. Suppl., 11, 89 [Google Scholar]
- Bronshten, V. 1983, Physics of meteoric phenomena (D. Reidel Publishing Company) [Google Scholar]
- Brosch, N., Schijvarg, L. S., Podolak, M., & Rosenkrantz, M. R. 2001, in Meteoroids 2001, ESA SP, 495, 165 [Google Scholar]
- Campbell-Brown, M. D., & Koschny, D. 2004, A&A, 418, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceplecha, Z., Borovicka, J., Graham elford, W., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Cordier, C., Folco, L., & Taylor, S. 2011, Geochim. Cosmochim. Acta, 75, 1199 [NASA ADS] [CrossRef] [Google Scholar]
- Coulson, S. G. 2002, MNRAS, 332, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Coulson, S. G., & Wickramasinge, N. C. 2003, MNRAS, 343, 1123 [NASA ADS] [CrossRef] [Google Scholar]
- Dobrica, E., Engrand, C., Duprat, J., et al. 2009, M&PS, 44, 1643 [NASA ADS] [Google Scholar]
- Dobrica, E., Engrand, C., Duprat, J., & Gounelle, M. 2010, M&PSA, 73, 5213 [Google Scholar]
- Draine, B. T., & Salpeter, E. E. 1979, ApJ, 231, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Duprat, J., Engrand, C., Maurette, M., et al. 2007, AdSpR, 39, 605 [Google Scholar]
- Engrand, C., & Maurette, M. 1998, M&PS, 33, 565 [NASA ADS] [Google Scholar]
- Flynn, G. J. 1989, LPSC, 19, 673 [NASA ADS] [Google Scholar]
- Flynn, G. J. 1992, in Asteroids, Comets, Meteors, eds. A. W. Harris, & E. Bowell, 195 [Google Scholar]
- Flynn, G. J. 1995, LPSC, 26, 405 [Google Scholar]
- Fraundorf, P. 1980, Geophys. Res. Lett., 10, 765 [NASA ADS] [CrossRef] [Google Scholar]
- Genge, M. J. 2006a, Geochim. Cosmochim. Acta, 70, 2603 [NASA ADS] [CrossRef] [Google Scholar]
- Genge, M. J. 2006b, LPSC, 37, 1759 [Google Scholar]
- Genge, M. J., & Grady, M. M. 2000, LPSC, 31, 1361 [Google Scholar]
- Genge, M., Engrand, C., Gounelle, M., & Taylor, S. 2008, M&PS, 43, 497 [Google Scholar]
- Greshake, A., Kloeck, W., Arndt, P., et al. 1998, M&PS, 33, 267 [Google Scholar]
- Grün, E., Zook, H. A., Fechtig, H., & Giese, R. H. 1985, Icarus, 62, 244 [NASA ADS] [CrossRef] [Google Scholar]
- Hedin, A. 1991, J. Geophys. Res., 96, 1159 [Google Scholar]
- Hood, L. L., & Horanyi, M. 1991, Icarus, 93, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Jurac, S., Johnson, R. E., & Donn, B. 1998, ApJ, 503, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Bottke, W. F., Gounelle, M., et al. 2009, Nature, 460, 364 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Love, S. G., & Brownlee, D. E. 1991, Icarus, 89, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Love, S. G., & Brownlee, D. E. 1993, Science, 262, 550 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maurette, M., Jehanno, C., Robin, E., & Hammer, C. 1987, Nature, 328, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Maurette, M., Olinger, C., Michel-Levy, M. C., et al. 1991, Nature, 351, 44 [NASA ADS] [CrossRef] [Google Scholar]
- May, P. W., Pineau des Forêts, G., Flower, D. R., et al. 2000, MNRAS, 318, 809 [NASA ADS] [CrossRef] [Google Scholar]
- McAuliffe, J. P., & Christou, A. A. 2006, Icarus, 180, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Melosh, H. J., & Goldin, T. J. 2008, LPSC, 39, 2457 [Google Scholar]
- Moses, J. I. 1992, Icarus, 99, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Nakles, M. R. 2004, Ph.D. Thesis, Virginia Polytechnic Institute and State University [Google Scholar]
- Popova, O. P., Strelkov, A. S., & Sidneva, S. N. 2007, AdSpR, 39, 567 [NASA ADS] [Google Scholar]
- Rogers, L. A., Hill, K. A., & Hawkes, R. L. 2005, Planet. Space Sci., 53, 1341 [NASA ADS] [CrossRef] [Google Scholar]
- Scarsi, P. 2004, NCimC, 27, 359 [NASA ADS] [Google Scholar]
- Sigmund, P. 1981, Sputtering by particle bombardment, ed. R. Behrisch (Berlin: Springer-Verlag) [Google Scholar]
- Sorasio, G., Mendis, G. A., & Rosemberg, M. 2001, Planet. Space Sci., 49, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Szasz, C., Kero, J., Pellinen-Wannberg, A., et al. 2008, EM&P, 102, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Szydlik, P. P., & Flynn, G. J. 1992, LPSC, 23, 1399 [Google Scholar]
- Szydlik, P. P., & Flynn, G. J. 1997, M&PSA, 32, 127 [NASA ADS] [Google Scholar]
- Tielens, A. G. G., McKee, C. F., Seab, C. G., & Hollenbach, D. J. 1994, ApJ, 431, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Toppani, A., Libourel, G., Engrand, C., & Maurette, M. 2001, M&PS, 36, 1377 [Google Scholar]
- van Ginneken, M., Folco, L., Cordier, C., & Rochette, P. 2012, M&PS, 47, 228 [Google Scholar]
- Vondrak, T., Plane, J. M. C., Broadley, S., & Janches, D. 2008, Atmos. Chem. Phys., 8, 7015 [Google Scholar]
- Whipple, F. L. 1950, PNAS, 36, 687 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Maximum values of entry velocity for which μMETs are able to survive and reach the Earth surface.
Values of the heat transfer coefficient Λ for three test case μMETs with zin = 45° and ρμMET = 3 g/cm3.
All Figures
 |
Fig. 1 Evolution of μMET radius with height assuming rin = 50 μm, zin = 45° and ρμMET = 3 g/cm3. |
| In the text | |
 |
Fig. 2 Evolution of μMET velocity with height A) and time B) assuming rin = 50 μm, zin = 45° and ρμMET = 3 g/cm3. |
| In the text | |
 |
Fig. 3 Typical time variation of the μMET temperature. A) Results for rin = 50 μm, zin = 45° and ρμMET = 3 g/cm3. B) Results for vin = 11.2 km s-1, zin = 45° and ρμMET = 3 g/cm3. The truncated dashed and solid curves correspond to μMETs that do not survive atmospheric passage. See text for discussion. |
| In the text | |
 |
Fig. 4 Fraction of the absorbed energy used to change the μMET temperature. These curves are proportional to dTμMET/dt so negative values mean that temperature is decreasing, positive values that it is increasing. The insert shows the transition from positive to negative values at around 40 s, coinciding with peak temperature and the start of μMET cooling by intense ablation. |
| In the text | |
 |
Fig. 5 Variation of the energy going into different processes relative to the absorbed energy. A) Unmelted or partially melted μMET. B) Almost completely melted μMET. C) Completely destroyed μMET. See text for discussion. Noise in the temperature variation lines is due to the numerical integration and occurs when the calculation is performed on very small step sizes (of the order of 10-5 s, used when μMET size, velocity and temperature vary significantly). |
| In the text | |
 |
Fig. 6 Relative contribution to the mass loss of processes. The solid line (labeled “mass lost”) shows the fraction of the total mass lost. A) Evaporation dominates the mass loss, the final mass of this μMET is 47% of the initial mass. B) Melting dominates the mass loss, the final mass is <1% of the initial mass. C) A μMET that is completely destroyed by melting. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


