| Issue |
A&A
Volume 552, April 2013
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 7 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219600 | |
| Published online | 18 March 2013 | |
Long quasi-periodic oscillations of sunspots and nearby magnetic structures
1 University of Turku, 20014 Turku, Finland
e-mail: vvsvid.smirnova@yandex.ru
2 Central (Pulkovo) Astronomical Observatory, Russian Academy of Sciences, 196140 Saint Petersburg, Russia
3 Sobolev Astronomical Institute, Saint Petersburg State University, 198504 Saint Petersburg, Russia
4 Aalto University, Metsähovi Radio Observatory, 02540 Kylmälä, Finland
5 Bauman Moscow State Technical University, 105005 Moscow, Russia
Received: 15 May 2012
Accepted: 8 February 2013
Aims. Simultaneous study of long quasi-periodic oscillations in sunspots (using line-of-sight magnetic field data) and nearby magnetic structures located above them (using radio emission data at 37 GHz) was the basic aim of this work.
Methods. Data from the ground-based radio-telescope (Metsähovi Radio Observatory, Aalto University, Finland) and the Helioseismic and Magnetic Imager instrument on-board the Solar Dynamics Observatory spacecraft were obtained and analyzed. We used the wavelet (Morlet) analysis and the fast Fourier transform (FFT) method to obtain the oscillation periods.
Results. Long-period oscillations in intervals of 200–400 min were found both in radio and in magnetic field data. The interpretation of these oscillations and their propagation to higher levels of the solar atmosphere are discussed in the context of a “shallow sunspot” model.
Key words: Sun: oscillations / sunspots / Sun: radio radiation
© ESO, 2013
1. Introduction
Quasi-periodic oscillations in solar active regions play an important role in the investigation of physical processes and plasma parameters in the solar atmosphere. Oscillatory phenomena have been observed in different solar structures (sunspots, pores, coronal loops, faculae) by ground-based and cosmic instruments for several tens of years (Kobrin et al. 1976; Ofman 2000; Loukitcheva et al. 2006; Dorotovič et al. 2008; Foullon et al. 2004, 2009; Yuan et al. 2011).
In the past few years the periodic variations of sunspot parameters and nearby magnetic structures connected with them have been investigated with great interest.
Quasi-periodic oscillations in sunspots with periods of 3–5 min are widely known and have been detected at different atmospheric levels (Thomas et al. 1984; Banerjee et al. 2002; Balthasar & Collados 2005; Kobanov et al. 2006; Tlatov & Riehokainen 2009; Abramov-Maximov et al. 2011; Botha et al. 2011; Reznikova et al. 2012). These oscillations are interpreted as the propagation of acoustic slow or fast magnetohydrodynamic waves excited by turbulence flows in the convective zone (Nakariakov 2007; Bogdan 2000; Bogdan et al. 2003; Parchevsky & Kosovichev 2009; Felipe et al. 2010; Zhugzhda 2008).
Long quasi-periodic oscillations with periods of 20–40, 60–80, 100–120, and 160–180 min were detected in sunspots at radio wavelengths (Gelfreikh et al. 2006; Bakunina et al. 2009; Chorley et al. 2010, 2011; Kislyakova et al. 2011; Smirnova et al. 2011).
Variations of line-of-sight velocities, recorded as Doppler shifts of spectral lines with periods of 40–45, 60–80, and 160–180 min were detected by Efremov et al. (2009). Subsequently, using SOHO/MDI space data, the same authors obtained long-term oscillations of the sunspot magnetic field with periods in the range 250–480 min (Efremov et al. 2010). More recently, they found the lowest modes of these oscillations with periods of up to 12–28 h that depend on the magnetic field strength of sunspots (Efremov et al. 2012).
The observed phenomenon has been interpreted by authors in the context of a “shallow-spot” model (Solov’ev & Kirichek 2008, 2009; Kshevetskii & Solov’ev 2008). According to this model, time-variations of line-of-sight velocities and magnetic field strength in sunspots are associated with the slow quasi-periodic vertical displacement of a sunspot as a whole.
The main goal of our study was to investigate long quasi-periodic oscillations in sunspots and the surrounding magnetic structures near sunspots. We used observational data obtained from the ground-based Metsähovi radio-telescope at 37 GHz and from the space-based observations of the line-of-sight component of the magnetic field, provided by the Helioseismic and Magnetic Imager (HMI) onboard the Solar Dynamics Observatory (SDO).
The observations and data reduction are described in Sect. 2. Observational tests are presented in Sect. 3. We presented results in Sect. 4. The discussion and our conclusions are given in Sects. 5 and 6.
2. Observations and data analysis
 |
Fig. 1 Example of tracks from the active region NOAA 11261 and the sky area obtained from the Metsähovi radio telescope at 37 GHz on 2011/08/03 04:22:30-14:52:24 UT. The beam sequentially scans the chosen region and the indicated area of the sky during 1–2 min. |
2.1. Metsähovi instrument and radio data
The Metsähovi RT-14 telescope, which is operated by the Metsähovi Radio Observatory (MRO), Aalto University (Helsinki Region, Finland, GPS: N 60 13.04 E 24 23.35), is a Cassegrain-type of antenna with a diameter of 13.7 meters. The working range of the telescope is 2–150 GHz (13.0 cm–2.0 mm). The antenna can provide solar mapping, partial solar mapping, and tracking of any selected point on the solar disk. The beam size of the telescope is 2.4′ at 37 GHz. The sensitivity of the receiver is good enough for 0.1 sfu resolution. In the temperature scale the resolution is better than 100 K and is limited by short-term changes in atmospheric attenuation. The estimated quiet-Sun level at 37 GHz is 7800 K (Urpo 1982). The cadence between two partial solar radio maps is typically 1–2 min, depending on the size of the selected active region.
Figure 1 shows an example of the tracks obtained from the active region NOAA 11261 and the sky area on 2011/08/03 04:22:30-14:52:24 UT. The active region track (top-right panel) has two radio-bursts. The sky area track (right-bottom panel) has two sharp peaks associated with clouds during the observations. This example was eliminated from the analysis, because the radio-bursts and clouds distorted the oscillation image. For our analysis we chose only tracks that did not contain the radio-bursts and influences from clouds.
2.2. SDO/HMI instrument and magnetic field data
The Helioseismic and Magnetic Imager (HMI) instrument is part of the Solar Dynamics Observatory (SDO). It enables us to study the photospheric magnetic field variations. It provides one-arcsecond-resolution full-disk Doppler velocity images and the line-of-sight component of the magnetic field every 45 s (Scherrer et al. 2012). A detailed description of the HMI instrument and the data processing is presented in Schou & Larson (2011), Schou et al. (2012), Wachter et al. (2012), and Couvidat et al. (2012).
 |
Fig. 2 Left panel: SDO/HMI magnetogram of a full solar disk. Right panel: contour of the sunspot umbra at the level of 1000 G, obtained from the active region NOAA 11251. |
We obtained full-disk images of the line-of-sight magnetic field component in the interval of 13–18 h (HMI magnetograms), using the Joint Science Operation Centre (JSOC) HMI-AIA Science Data Processing with a cadence of 3 min. The HMI data were chosen in association with bright radio sources observed with the Metsähovi 37 GHz radio-telescope.
To select the SDO/HMI objects we used the radio observations as a base list to provide the maximum overlap of the space- and ground-based time-series. This provided a good opportunity to investigate simultaneously the oscillatory processes in different atmospheric levels – from the photosphere to the lower corona.
The SDO/HMI data processing consisted of averaging the magnetic field inside some chosen areas marked by contours or by boxes (see in Fig. 2). Areas with positive and negative polarities were analyzed separately.
We used the technique described in Torrence & Compo (1998) to analyze time-series by the sixth order wavelet Morlet function.
2.2.1. Trends and artifacts
The typical trend associated with the well-known fluctuation effects of the Earth’s atmospheric absorption coefficient, which affects the intensity of radio emission during the whole observational day, is shown in Fig. 3. Figure 4 shows a typical form of the initial time-series obtained from HMI magnetograms. We removed these trends with a polynomial approximation and obtained normalized tracks for all radio and HMI data.
 |
Fig. 3 Observed Metsähovi track obtained from the active region NOAA 11243 on 2011/06/30. |
 |
Fig. 4 Initial SDO/HMI time-series obtained for the same day and active region. |
 |
Fig. 5 SDO/HMI time-series obtained from the active region NOAA 11251 observed on 2011/07/14–2011/07/17. Cadence: 24 min. |
 |
Fig. 6 Periodogram obtained from the Fourier analysis of the SDO/HMI time-series (see Fig. 4). Two peaks are defined at 12 and 24 h. |
Artificial variations of the magnetic field obtained from HMI magnetograms were also detected (Fig. 5). The magnetic field strength of this sunspot, re-calculated for the disk center, reached more than 3050 G. Figure 6 shows the periodogram for this time-series. Two harmonics were found – 12 and 24 h. The amplitude of the 12-hour harmonic was about ten times less than the 24-h.
We confirmed that these two periods are artifacts associated with SDO spacecraft orbital features and the Zeeman effect, as reported by Liu et al. (2012). In agreement with their results, these 12- and 24-hour artificial harmonics have a significant effect only for strong magnetic fields of more than 2000 G.
But in the active regions presented here (except for NOAA 11251, which test-analyzed) the magnetic field strength values were lower than 2000 G, and the tracks are not very long. Therefore, we assumed that the influence of the 12- and 24-hour artifacts is not significant and can be removed from our data with a polynomial fitting.
3. Observational tests
Before proceeding with our analysis, we first performed three tests to demonstrate that the observed variations are not artifacts:
-
1.
we analyzed and compared the signal amplitudes of active andquiet regions obtained from SDO/HMI data;
-
2.
we analyzed and compared time-series from radio and magnetic field data of a chosen active region to demonstrate a correlation of temporal structures;
-
3.
and we analyzed and compared the time-series obtained from magnetograms of two distant sunspots to check the data-processing method.
The superposed time-series obtained from NOAA 11243 on 2011/06/30 and a quiet region at the equator are presented in Fig. 7. In this case we analyzed areas with the same size. Figure 7 shows that the amplitude of the signal from the quiet area is smaller than that from the active region. The formal correlation coefficient obtained for these time-series is equal to − 0.12. For that reason, we assume that the signal from the active region is real and significant for the statistical study.
 |
Fig. 7 Comparison of signals from the active region NOAA 11243 (solid line) and from the quiet solar region (dashed line). Both regions were analyzed inside the same box area. |
 |
Fig. 8 Superposition of time-series obtained from SDO/HMI magnetic field data (solid line) and the Metsähovi track at 37 GHz (dashed line). The active region NOAA 11243 was observed on 2011/06/30. |
In Fig. 8 one can see two superposed tracks for the same active region, obtained from Metsähovi radio and SDO/HMI data on 2011/06/30. We found a good correlation between the tracks. The correlation coefficient in this case is equal to 0.65. Moreover, we found that the best correlation coefficient is 0.72, but then the radio time-series should be shifted with regard to the magnetic field time-series. The estimated delay of the radio time-series (lag) is in range of 15–18 min.
 |
Fig. 9 SDO/HMI magnetic field time-series obtained from the magnetograms of the two distant sunspots NOAA 11242 (N17, W29) and NOAA 11243 (N16, E38). Date of observations: 2011/06/30. |
Additionally we analyzed two distant sunspots to investigate the existence of correlation between the phase of their long-period variations.
Two active regions were considered: NOAA 11242 and NOAA 11243. The regions were visible at the same time on the solar disk with coordinates N17W29 and N16E38. We analyzed the averaged magnetic field obtained from the magnetograms over a period of 13.5 h (Fig. 9).
The estimated correlation coefficient is − 0.35. It shows no correlation between these time-series. However, these sunspots have the same long-period oscillations (see Table 1). Because the analyzed sunspots were spatially separated and are not physically connected to each other, their variations are not in phase.
Accordingly, we can conclude that our data processing method gives real, independent results for every investigated sunspot.
Results.
4. Results
The main results of this study are presented in Table 1. The first four columns contain dates, temporal intervals of observations, active region numbers and the instrument, with which the data were obtained. Period intervals obtained from wavelet power spectra are shown in Col. 5 and periods from the Fourier periodograms are presented in Col. 6. In Col. 7 one can see the correlation coefficients obtained from the analysis of the radio and magnetic field time-series. We provide a lag analysis to investigate the delay between time-series. The first value of Col. 7 is the correlation coefficient with zero lag, the second value is the maximum coefficient with the lag and the third is the value of the lag measured in minutes. Column 8 contains the highest values of the line-of-sight component of the magnetic field and re-calculated values for the disk center. The estimated brightness temperature variations obtained from radio maps before and after active-region tracking are presented in Col. 9.
The same period intervals were found both in radio intensity at 37 GHz and in the magnetic field variations.
 |
Fig. 10 a) Metsähovi track obtained from the active region NOAA 11243. The duration of observations is about 11 hours with a cadence of 2 min. b) Wavelet power spectrum: the range of detected periods is 200–400 min. c) Global wavelet spectrum with a significance level of 95%. |
 |
Fig. 11 a) SDO/HMI time-series obtained from the magnetorgrams of the active region NOAA 11243 with a cadence of 3 min. The duration of the time-series is about 13 h. The magnetic field was average in a box with a size of [32 × 40] pixels. b) Wavelet power spectrum. c) Global wavelet spectrum with a significance level of 95%. |
In Fig. 10 one can see the low-frequency variations of the radio intensity in the active region NOAA 11243 (2011/06/30) observed at 37 GHz during 11 h. This was a bipolar sunspot group with a complex magnetic structure. The most powerful component of the wavelet spectrum corresponds to the interval of periods 200–400 min with a maximum at 334 min. Note that the duration of observations was limited and the long-period component in the wavelet spectrum lies in the region where edge effects are important, but it is clear from Fig. 10 (panels a and c) that the long-periodic interval found is clearly significant.
Furthermore, we analyzed several parts (boxes) of the active region 11243 obtained from HMI magnetograms. In Fig. 11 we show a wavelet power spectrum of magnetic field variations obtained inside the box 32 × 40. Long periods were defined in intervals of 80–130 and 200–400 min. A direct comparison of the radio and magnetic field time-series for this region is shown in Fig. 8.
The other results presented in Table 1 were obtained in the same manner.
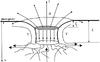 |
Fig. 12 Structure of magnetic field B in observed and subsurface layers (Solov’ev & Kirichek 2009). The dashed lines show the mass flows near the sunspot in accordance with local helioseismology data. L is the depth, counted downward from photosphere, ζ is the Wilson depression. L indicates the level of lower magnetic boundary, from which the magnetic flux tube of the sunspot sharply expands downward. The magnetic field in deeper layers is weakened and entangled in the convection motion. It decreases in a diffuse irregular form. |
The study presented here is another independent confirmation of the reality of long-period oscillations of sunspots, obtained from original radio observations at 37 GHz as well as from corresponding data of SDO/HMI.
5. Discussion
Ground-based observations of the Sun are naturally limited by the duration of daylight. For this reason, we cannot study oscillations with periods of more than 4–5 h. But, as was mentioned above, the oscillatory spectrum of long-period sunspot oscillations covers a wider range of periods (Efremov et al. 2012). It suggests that the oscillatory process in sunspots has a complex, multi-mode character. In terms of the shallow sunspot model (Solov’ev & Kirichek 2008, 2009) this principal statement can be explained as follows.
According to the model, the magnetic structure of a sunspot is limited both laterally and from below: at the depth of about 4 Mm, the magnetic flux tube of a sunspot expands sharply downward (as is shown in Fig. 12), and in deeper layers the magnetic field of the sunspot flux tube turns out to be relatively weak. It continues into the deep layers, supposedly because of the entangling impact of convective motion. The model defines this level as a “lower magnetic boundary of a sunspot” at a depth L. In accordance with data of local helioseismology (Zhao et al. 2001; Kosovichev 2006) at a depth of more than 4 Mm, a wide extended zone of overheated gas (with plasma at 1000 K hotter than the environment) is located.
We also found that the shallow sunspot model agrees with the sunspot structure obtained in 3D magnetohydrodynamic simulations suggested by Rempel et al. (2009) and Cheung et al. (2010). In these simulations, the authors have taken into account the formation of the active regions (spots) beginning from a depth of 6–7 Mm in the convective zone to the photosphere. The result of this type of simulation is shown in Fig. 1 of Rempel et al. (2009). The figure shows a well-formed sunspot pair at the photospheric level and the upper convective zone of the simulated magnetic field structure. It seems to be close to the scheme presented in Fig. 12 of this article.
Two basic parameters determine the period of shallow sunspot oscillations: the magnetic field strength in a quasi-cylindrical part of the sunspot flux tube and the plasma mass involved in the oscillations. The second one depends on the behavior of the vertical plasma displacement ξ along the vertical and near the lower magnetic boundary of a sunspot L, i.e., the amount of oscillating mass is determined by the form of function ξ(h) and its value at the lower boundary: ξ(L) (see Fig. 12 and the description to it). When the oscillation geometry is such that the vertical plasma displacements do not vanish at the lower boundary, ξ(L) ≠ 0, the underlying dense layers at the depths h > L will be strongly perturbed by the vertical periodic displacements of the sunspot tube as a whole; hence, the effective gas mass involved in the long-period oscillations grows dramatically in this case. Accordingly, the period of these oscillations will increase greatly and can rise to tens of hours. In another case, when the vertical displacements are negligible near the lower boundary, ξ(L) = 0, the lowest more dense parts of the sunspot tube with a strong magnetic field do not take part in the oscillations on this mode, and the period of this oscillatory mode will be limited to a time interval of approximately 1 to 6 h. Evidently, with the ground-based observations we can reveal the modes of the second type only, as seen in the present work.
In connection with the discussion of long-period oscillations, another important question can arise: why are the sunspot oscillations at the level of the photosphere and deeper clearly manifested at relatively high heights where radio emission is generated? According to the atmospheric model proposed by Vernazza et al. (1981), these heights are about 2000 km above the photosphere.
To answer this, we note firstly, that the propagation velocities of any perturbation in the solar atmosphere above the sunspot are very high: the sound speed is about 107 cm/s, the Alfven velocity is higher, around 108 cm/s. The typical coronal loop length lies in the range of 100–300 Mm. Hence, the time in the interval 3–45 min is needed for the magnetic structure of active regions to relax to some state of equilibrium (Roberts 2000; Nakariakov & Stepanov 2007). Lags obtained in our analysis (see Col. 8 in Table 1) are within this interval.
When we discuss the time - variations of the magnetic field at the level of the photosphere with periods of few hours and more, we take into account that for the magnetic structures above the sunspot these time-variation are very slow quasi-static processes: at every moment of time the magnetic system over the spot stays in equilibrium, or more exactly: the system passes slowly through the continuous series of equilibrium states in accordance with the quasi-static variations of the boundary conditions. Hence, the slow time-variations in the magnetic field of a sunspot are followed by the relatively rapid adjustment of the spatial structure in the active region that is connected with the magnetic flux of the sunspot. Therefore, all physical parameters of the region where the radio emission is generated are to be automatically changed through variations of the field at the base level. The values of temperature, density, pressure, and magnetic field in this region vary according to the magneto-hydrostatic space distribution, following changes in boundary conditions. In other words, the radio emission intensity is inevitably modulated in amplitude with the period of the sunspot field time-variations.
Thus, the first modulation mechanism of radio emission at high levels is the magneto-hydrostatic rebuilding of magnetic structures caused by slow time-variation of the boundary field.
But there is an alternative mechanism that could be applied to explain the phenomenon of quasi-periodic modulation of radio emission in the region near the sunspot, even in the absence of a magnetic field. Kshevetskii and Solov’ev (2008) have used the shallow-spot model as a purely hydrodynamic piston, with no magnetic field, to study the propagation of internal gravity waves generated by the oscillating of the piston. They found with numerical calculations that the internal gravity waves propagate from the source (the oscillating spot) at a small angle to the photosphere and the highest density is reached at a height of about of 3000 km. This is close to the height of the 8 mm radio emission generation derived from the Vernazza model. The highest radio intensity should be shifted from the center of the sunspot by at least a few tens of thousands of kilometers. Such a spatial distribution corresponds well to the position of nominal radio maximum, shifted normally from the sunspot. Both these mechanisms (acting together or independently) could explain the effect of amplitude modulation of the radio emission by slow long-periodic sunspot oscillations.
6. Conclusions
Sunspot oscillations with periods in the interval of 60–120 min have previously been obtained and discussed (Smirnova et al. 2011; Chorley et al. 2010; Gelfreikh et al. 2006) using 17 GHz (Nobeyama Radiohelograph), 37 GHz (Metsähovi), and 96 GHz data (RT-7.5 BMSTU, Moscow region). These results were obtained on the basis of time-series with durations of 8 h or shorter.
Long sessions of radio observations (9.5–11 h) were organized during the Summer of 2011 at the Metsähovi radio-telescope. This enabled us to detect oscillations of longer periods of up to 150–400 min in radio emission. We obtained more than 20 long tracks of radio sources connected with sunspots. But we chose only four radio tracks that satisfied our data selection conditions.
Results obtained in this study from these longer time-series very clearly show the existence of long quasi-periodic (200–400 min) radio emission oscillations that are connected with the corresponding sunspots and nearby magnetic structures. These oscillations have been detected simultaneously at the photospheric level (in SDO/HMI magnetograms) and at the level of the chromosphere – low corona where radio emission at 37 GHz is generated. We stress that in this study we selected the sunspots on the basis of radio observations.
As a rule, the positions of nominal radio maxima do not coincide with the sunspot position. These maxima were usually situated above the distributed magnetic field structures of the opposite polarity in the unipolar case and somewhere between the spots in the bipolar case. In both cases, complicated magnetic structures consisting of magnetic loops and arches are present in the radio source regions.
Therefore, we assume that the oscillations explain not only the sunspot (umbra) magnetic field variations, but that these oscillations propagate to the heights where the radio emission at 37 GHz originates.
Acknowledgments
We thank Dr. E. Valtaoja for the valuable advice and support. We thank the referee for very useful critiques and advice. Part of work was supported by the Vilho, Yrjö ja Kalle Väisälän Fund. The work was partially supported by the programs of the Presidium of Russian Academy of Science: P-19 and P-22. Part of the work was supported by the Federal Target Program “Research and scientific-pedagogical cadres Innovative Russia” in 2009–2013.
References
- Abramov-Maximov, V. E., Gelfreikh, G. B., Kobanov, N. I., Shibasaki, K., & Chupin, S. A. 2011, Sol. Phys., 270, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Bakunina, I. A., Abramov-Maximov, V. E., Lesovoy, S. V., et al. 2009, in IAU Symp. 257, eds. N. Gopalswamy, & D. F. Webb, 155 [Google Scholar]
- Balthasar, H., & Collados, M. 2005, A&A, 429, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banerjee, D., O’Shea, E., Doyle, J. G., & Goossens, M. 2002, in Multi-Wavelength Observations of Coronal Structure and Dynamics, eds. P. C. H. Martens, & D. Cauffman, 19 [Google Scholar]
- Bogdan, T. 2000, Sunspot Oscillations and Seismology, ed. P. Murdin [Google Scholar]
- Bogdan, T. J., Carlsson, M., Hansteen, V. H., et al. 2003, ApJ, 599, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Botha, G. J. J., Arber, T. D., Nakariakov, V. M., & Zhugzhda, Y. D. 2011, ApJ, 728, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Cheung, M. C. M., Rempel, M., Title, A. M., & Schüssler, M. 2010, ApJ, 720, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Chorley, N., Hnat, B., Nakariakov, V. M., Inglis, A. R., & Bakunina, I. A. 2010, A&A, 513, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chorley, N., Foullon, C., Hnat, B., Nakariakov, V. M., & Shibasaki, K. 2011, A&A, 529, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Couvidat, S., Schou, J., Shine, R. A., et al. 2012, Sol. Phys., 275, 285 [NASA ADS] [CrossRef] [Google Scholar]
- Dorotovič, I., Erdélyi, R., & Karlovský, V. 2008, in IAU Symp. 247, eds. R. Erdélyi, & C. A. Mendoza-Briceno, 351 [Google Scholar]
- Efremov, V. I., Parfinenko, L. D., & Soloviev, A. A. 2009, Cosm. Res., 47, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Efremov, V. I., Parfinenko, L. D., & Solov’ev, A. A. 2010, Sol. Phys., 267, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Efremov, V. I., Parfinenko, L. D., & Solov’ev, A. A. 2012, Cosm. Res., 50, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Felipe, T., Khomenko, E., Collados, M., & Beck, C. 2010, ApJ, 722, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Foullon, C., Verwichte, E., & Nakariakov, V. M. 2004, A&A, 427, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Foullon, C., Verwichte, E., & Nakariakov, V. M. 2009, ApJ, 700, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Gelfreikh, G. B., Nagovitsyn, Y. A., & Nagovitsyna, E. Y. 2006, PASJ, 58, 29 [NASA ADS] [Google Scholar]
- Kislyakova, K. G., Zaitsev, V. V., Urpo, S., & Riehokainen, A. 2011, Astron. Rep., 55, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Kobanov, N. I., Kolobov, D. Y., & Makarchik, D. V. 2006, Sol. Phys., 238, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kobrin, M. M., Pakhomov, V. V., & Prokofeva, N. A. 1976, Sol. Phys., 50, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G. 2006, Adv. Space Res., 38, 876 [NASA ADS] [CrossRef] [Google Scholar]
- Kshevetskii, S. P., & Solov’ev, A. A. 2008, Astron. Rep., 52, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Y., Hoeksema, J. T., Scherrer, P. H., et al. 2012, Sol. Phys., 279, 295 [Google Scholar]
- Loukitcheva, M. A., Solanki, S. K., & White, S. 2006, in Solar Activity and its Magnetic Origin, eds. V. Bothmer, & A. A. Hady, IAU Symp., 233, 104 [Google Scholar]
- Nakariakov, V. M. 2007, Adv. Space Res., 39, 1804 [NASA ADS] [CrossRef] [Google Scholar]
- Nakariakov, V. M., & Stepanov, A. V. 2007, in Lecture Notes in Physics, eds. K.-L. Klein, & A. L. MacKinnon (Berlin: Springer Verlag), 725, 221 [Google Scholar]
- Ofman, L. 2000, in Last Total Solar Eclipse of the Millennium, eds. W. Livingston, & A. Özgüç, ASP Conf. Ser., 205, 147 [Google Scholar]
- Parchevsky, K. V., & Kosovichev, A. G. 2009, ApJ, 694, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., Schüssler, M., Cameron, R. H., & Knölker, M. 2009, Science, 325, 171 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Reznikova, V. E., Shibasaki, K., Sych, R. A., & Nakariakov, V. M. 2012, ApJ, 746, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B. 2000, Sol. Phys., 193, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Schou, J., Bush, R. I., et al. 2012, Sol. Phys., 275, 207 [Google Scholar]
- Schou, J., & Larson, T. P. 2011, in AAS/Solar Physics Division Abstracts #42, 1605 [Google Scholar]
- Schou, J., Scherrer, P. H., Bush, R. I., et al. 2012, Sol. Phys., 275, 229 [Google Scholar]
- Smirnova, V., Riehokainen, A., Ryzhov, V., Zhiltsov, A., & Kallunki, J. 2011, A&A, 534, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solov’ev, A. A., & Kirichek, E. A. 2008, Astrophys. Bull., 63, 180 [Google Scholar]
- Solov’ev, A. A., & Kirichek, E. A. 2009, Astron. Rep., 53, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, J. H., Cram, L. E., & Nye, A. H. 1984, ApJ, 285, 368 [Google Scholar]
- Tlatov, A. G., & Riehokainen, A. 2009, in Solar Polarization 5: In Honor of Jan Stenflo, eds. S. V. Berdyugina, K. N. Nagendra, & R. Ramelli, ASP Conf. Ser., 405, 449 [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Am. Meteorol. Soc., 79, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Urpo, S. 1982, Ph.D. Thesis, Helsinki University of Technology, Espoo, Finland [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Wachter, R., Schou, J., Rabello-Soares, M. C., et al. 2012, Sol. Phys., 275, 261 [Google Scholar]
- Yuan, D., Nakariakov, V. M., Chorley, N., & Foullon, C. 2011, A&A, 533, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhao, J., Kosovichev, A. G., & Duvall, Jr., T. L. 2001, ApJ, 557, 384 [NASA ADS] [CrossRef] [Google Scholar]
- Zhugzhda, Y. D. 2008, Sol. Phys., 251, 501 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Example of tracks from the active region NOAA 11261 and the sky area obtained from the Metsähovi radio telescope at 37 GHz on 2011/08/03 04:22:30-14:52:24 UT. The beam sequentially scans the chosen region and the indicated area of the sky during 1–2 min. |
| In the text | |
 |
Fig. 2 Left panel: SDO/HMI magnetogram of a full solar disk. Right panel: contour of the sunspot umbra at the level of 1000 G, obtained from the active region NOAA 11251. |
| In the text | |
 |
Fig. 3 Observed Metsähovi track obtained from the active region NOAA 11243 on 2011/06/30. |
| In the text | |
 |
Fig. 4 Initial SDO/HMI time-series obtained for the same day and active region. |
| In the text | |
 |
Fig. 5 SDO/HMI time-series obtained from the active region NOAA 11251 observed on 2011/07/14–2011/07/17. Cadence: 24 min. |
| In the text | |
 |
Fig. 6 Periodogram obtained from the Fourier analysis of the SDO/HMI time-series (see Fig. 4). Two peaks are defined at 12 and 24 h. |
| In the text | |
 |
Fig. 7 Comparison of signals from the active region NOAA 11243 (solid line) and from the quiet solar region (dashed line). Both regions were analyzed inside the same box area. |
| In the text | |
 |
Fig. 8 Superposition of time-series obtained from SDO/HMI magnetic field data (solid line) and the Metsähovi track at 37 GHz (dashed line). The active region NOAA 11243 was observed on 2011/06/30. |
| In the text | |
 |
Fig. 9 SDO/HMI magnetic field time-series obtained from the magnetograms of the two distant sunspots NOAA 11242 (N17, W29) and NOAA 11243 (N16, E38). Date of observations: 2011/06/30. |
| In the text | |
 |
Fig. 10 a) Metsähovi track obtained from the active region NOAA 11243. The duration of observations is about 11 hours with a cadence of 2 min. b) Wavelet power spectrum: the range of detected periods is 200–400 min. c) Global wavelet spectrum with a significance level of 95%. |
| In the text | |
 |
Fig. 11 a) SDO/HMI time-series obtained from the magnetorgrams of the active region NOAA 11243 with a cadence of 3 min. The duration of the time-series is about 13 h. The magnetic field was average in a box with a size of [32 × 40] pixels. b) Wavelet power spectrum. c) Global wavelet spectrum with a significance level of 95%. |
| In the text | |
 |
Fig. 12 Structure of magnetic field B in observed and subsurface layers (Solov’ev & Kirichek 2009). The dashed lines show the mass flows near the sunspot in accordance with local helioseismology data. L is the depth, counted downward from photosphere, ζ is the Wilson depression. L indicates the level of lower magnetic boundary, from which the magnetic flux tube of the sunspot sharply expands downward. The magnetic field in deeper layers is weakened and entangled in the convection motion. It decreases in a diffuse irregular form. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


