| Issue |
A&A
Volume 551, March 2013
|
|
|---|---|---|
| Article Number | A120 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220009 | |
| Published online | 05 March 2013 | |
Characterization of potentially habitable planets: Retrieval of atmospheric and planetary properties from emission spectra
1
Univ. Bordeaux, LAB, UMR 5804,
33270
Floirac,
France
e-mail: philip.vonparis@dlr.de
2
CNRS, LAB, UMR 5804, 33270
Floirac,
France
3
Institut für Planetenforschung, Deutsches Zentrum für Luft- und Raumfahrt, Rutherfordstr.
2, 12489
Berlin,
Germany
4
Institut für Methodik der Fernerkundung, Deutsches Zentrum für Luft-und
Raumfahrt, Oberpfaffenhofen, 82234
Weßling,
Germany
Received:
13
July
2012
Accepted:
23
December
2012
Context. An increasing number of potentially habitable terrestrial planets and planet candidates are found by ongoing planet search programs. The search for atmospheric signatures to establish planetary habitability and the presence of life might be possible in the future.
Aims. We want to quantify the accuracy of retrieved atmospheric parameters (composition, temperature, pressure) that might be obtained from infrared emission spectroscopy.
Methods. We use synthetic observations of the atmospheres of hypothetical potentially habitable planets. These were constructed with a parametrized atmosphere model, a high-resolution radiative transfer model and a simplified noise model. The simulated observations were used to fit the model parameters. Furthermore, classic statistical tools such as χ2 statistics and least-square fits were used to analyze the simulated observations.
Results. When adopting the design of currently planned or proposed exoplanet characterization missions, we find that emission spectroscopy could provide weak limits on the surface conditions of terrestrial planets, hence their potential habitability. However, these mission designs are unlikely to allow the composition of the atmosphere of a habitable planet to be characterized, even though CO2 is detected. Upon increasing the signal-to-noise ratios by about a factor of 2−5 (depending on spectral resolution) compared to current mission designs, the CO2 content could be characterized to within two orders of magnitude. The detection of the O3 biosignature remains marginal. The atmospheric temperature structure could not be constrained. Therefore, a full atmospheric characterization seems to be beyond the capabilities of such missions when using only emission spectroscopy during secondary eclipse or target visits. Other methods such as transmission spectroscopy or orbital photometry are probably needed in order to give additional constraints and break degeneracies.
Key words: planets and satellites: atmospheres / techniques: spectroscopic / methods: data analysis
© ESO, 2013
1. Introduction
The possibility of finding potentially habitable or even inhabited terrestrial planets is one of the exciting motivations in the search for extrasolar planets. So far, more than 50 planets with (minimum) masses below ten Earth masses are known among the more than 800 detected extrasolar planets. Furthermore, recent studies based on radial-velocity planet searches have claimed that the number of low-mass, potentially terrestrial planets is rather large (e.g., Howard et al. 2010; Wittenmyer et al. 2011). For short-period orbits with periods <50 days, 11−17% of all stars host at least one low-mass planet. Estimates inferred from microlensing surveys imply that the mean number of planets per star is larger than one (Cassan et al. 2012).
Emission spectroscopy of potentially habitable planets: Science goals (species to be detected and characterized) and requirements in terms of spectral resolution and S/N for two European exoplanet characterization missions.
Already, some potentially habitable (candidate) super-Earths in or very close to the habitable zone (HZ) of their central star have been discovered (Udry et al. 2007; Mayor et al. 2009; Borucki et al. 2011; Pepe et al. 2011; Bonfils et al. 2013; Anglada-Escudé et al. 2012; Delfosse et al. 2013; Borucki et al. 2012; Tuomi et al. 2013). Detection of potentially habitable terrestrial planets is therefore within reach of present-day instrumentation. The next step would be to search such potentially habitable worlds for indications of the presence of life, so-called biomarkers. To be detectable remotely from Earth, such biomarkers are necessarily surface or atmospheric spectral signatures.
Several studies have addressed the issue of atmospheric biosignatures (e.g., Sagan et al. 1993; Schindler & Kasting 2000; Des Marais et al. 2002; Selsis et al. 2002) or the response of spectra when changing atmospheric composition of the central star (e.g., Segura et al. 2003, 2005; Kaltenegger et al. 2007; Vasquez et al. 2013). Further studies have focused not only on the spectral response, but also on signal detectability (e.g., Kaltenegger & Traub 2009; Deming et al. 2009; Belu et al. 2011; Rauer et al. 2011; von Paris et al. 2011). These studies calculated signal-to-noise ratios (S/Ns) and suggest observation strategies using the instrument capabilities of the planned James Webb Space Telescope (JWST). Since exoplanet characterization is not the design-driving purpose of JWST, dedicated exoplanet space mission concepts have been developed. Some of them have already been proposed to ESA or NASA. The concepts include coronographs such as SEE-COAST or ACCESS (e.g., Schneider et al. 2009; Trauger et al. 2008), interferometers such as Darwin (e.g., Léger et al. 1996; Cockell et al. 2009a,b), and near- to mid-IR spectrographs such as EChO or FINESSE (e.g., Tinetti et al. 2012; Tessenyi et al. 2012; Swain 2012). The ultimate aim of these missions is to characterize the atmospheres of (habitable) exoplanets spectroscopically. The Darwin mission, which is no longer pursued by ESA, was explicitly designed for the investigation of terrestrial, potentially habitable planets. The main focus of EChO, currently in competition for the ESA M3 launch slot, is the observation of hot Jupiter and hot Neptune planets. However, an additional science opportunity is the possibility of observing (in case they would be discovered) nearby (habitable) terrestrial planets around low-mass stars (Tinetti et al. 2012). Table 1 states the current mission design of Darwin and EChO with the aimed spectral resolution and S/N for reaching the scientific goals and opportunities regarding terrestrial planets. For Darwin, these S/N goals limit the number of potential targets to 40 (20) for R = 5 (R = 20) (see, e.g., Léger et al. 1996). In the case of EChO, tens to hundreds of transits need to be accumulated in order to achieve the stated aims, depending on the IR magnitude of the host star (Tinetti et al. 2012). Because of mission lifetime constraints, EChO is limited to M-type stars brighter than about K ≈ 9m. Currently, there are only three transit host stars satisfying these criteria, all orbited by hot Neptunes or hot super-Earths.
However, the difficulty of characterizing the atmospheres of small, potentially low-mass exoplanets even with high spectral resolution and good S/Ns is illustrated by the case of GJ 1214 b. Numerous studies using both ground- and space-based spectroscopy and spectrophotometry (e.g, Bean et al. 2010, 2011; Désert et al. 2011; Croll et al. 2011; Crossfield et al. 2011; de Mooij et al. 2012; Berta et al. 2012) aimed at constraining the range of possible atmospheric scenarios. Most observations favor a cloud-free water vapor atmosphere. However, a data point presented by de Mooij et al. (2012) seems to favor a hydrogen-rich atmosphere with a possible low-altitude cloud layer.
In view of such difficulties, several methods have recently been proposed to allow for an efficient search for sets of atmospheric parameters that produce a reasonable fit to the data. Studies by, e.g., Madhusudhan & Seager (2009), Lee et al. (2012), or Line et al. (2012) focus on hot Jupiter planets, with both primary and secondary eclipse data from real observations, whereas Benneke & Seager (2012) investigated the potential of transmission spectroscopy in detail to characterize the atmospheres of hypothetical super-Earths. These studies have shown that it should be feasible to constrain the atmospheric composition and temperature structure for hot Jupiters and super-Earths; however, given the current data quality, both in terms of spectral coverage and S/Ns, the error bars on retrieved atmospheric parameters are rather large.
Such retrieval studies could provide valuable clues to the design of the aforementioned space missions and should be taken into account when calculating integration times or allocating observations. Therefore, we present here for the first time a study of the possible retrieval of atmospheric and planetary parameters for hypothetical habitable terrestrial planets from emission spectra. The focus of the study will be on the possible constraints on surface conditions and detection of important molecules in the context of life, such as ozone and water. In contrast to the work by, e.g., Lee et al. (2012) or Benneke & Seager (2012), we do not use a Bayesian optimal estimation approach here but rather focus on straightforward χ2 calculations and nonlinear least-squares fits to illustrate the difficulties of atmospheric retrieval for habitable planets. From there, we quantitatively investigate the potential of planned or near-future space instrumentation to characterize habitable planets.
The paper is organized as follows. Section 2 presents atmospheric scenarios and models used. Results will be shown in Sect. 3 and discussed in Sect. 4. Conclusions are given in Sect. 5.
2. Models and atmospheric scenarios
2.1. Parametric atmosphere model
We use a semi-empirical parametric atmosphere model to describe the temperature structure and chemical composition of an arbitrary terrestrial, cloud-free habitable atmosphere, similar to the approach presented in Madhusudhan & Seager (2009), Line et al. (2012) or Lee et al. (2012). Simple, analytical 1D models have been proposed recently (Robinson & Catling 2012), which might also be applicable to the retrieval problem.
The model atmosphere is divided into 50 layers, with a higher resolution in log (p) in the lower atmosphere where the temperature gradient is expected to be larger. We make the following assumptions regarding our temperature structure:
-
The lower atmosphere is convective, i.e. a troposphere exists. The temperature gradient is given by the wet adiabatic lapse rate, taking the release of latent heat by condensation of water into account:
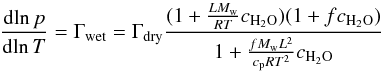 (1)where
(1)where
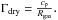 (cp heat capacity of the atmosphere,
Rgas the universal gas constant) is the dry adiabatic
lapse rate in pressure coordinates, cH2O is
the concentration of water, Mw the molar mass of water,
L the latent heat, and
(cp heat capacity of the atmosphere,
Rgas the universal gas constant) is the dry adiabatic
lapse rate in pressure coordinates, cH2O is
the concentration of water, Mw the molar mass of water,
L the latent heat, and 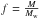 the mass ratio between dry air and water. Throughout this work, we took
L = 583 cal g-1, its value at 300 K.
the mass ratio between dry air and water. Throughout this work, we took
L = 583 cal g-1, its value at 300 K. -
Above the tropopause, the atmosphere is in radiative equilibrium. The temperature gradient is assumed to be linear in lnp, given by a linear interpolation between the tropopause temperature and the temperature at the model lid.
 |
Fig. 1 Illustration of the parameterized temperature structure. |
For  ,
the temperature T(n) in a layer
n (starting at the layer above the surface, with
nsurface = 50) is calculated via (see Eq. (1))
,
the temperature T(n) in a layer
n (starting at the layer above the surface, with
nsurface = 50) is calculated via (see Eq. (1)) 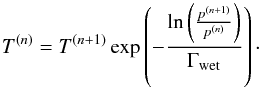 (2)For
(2)For
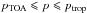 ,
the temperature profile is calculated with
,
the temperature profile is calculated with 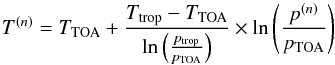 (3)where
Ttrop (the temperature of the tropopause at
ptrop) is calculated based on the values of
Tsurf, psurf, and
ptrop (see Eq. (2)).
(3)where
Ttrop (the temperature of the tropopause at
ptrop) is calculated based on the values of
Tsurf, psurf, and
ptrop (see Eq. (2)).
The atmosphere is assumed to be composed of four species: CO2, H2O, the so-called biomarker O3 as well as N2. We chose CO2 and H2O because they are the main greenhouse gases on Venus, Earth and Mars, and both are generally accepted constituents of the atmospheres of potentially habitable planets. N2 is a major atmospheric species for all terrestrial-like atmospheres in the solar system (i.e., Venus, Earth, Mars, Titan). We chose O3 as the biomarker in our model atmospheres because it is usually considered to be a very prominent bioindicator (e.g., Sagan et al. 1993; Schindler & Kasting 2000; Selsis et al. 2002), thanks to its strong mid-IR absorption band centered at 9.6 μm. On Earth, O3 is an indirect biomarker because its presence is due to the large O2 amount in the atmosphere, which itself is produced by the biosphere. Our model atmospheres do not contain O2, which would affect the temperature structure in our model mainly through its contribution to the heat capacity (Eq. (1)) and the spectrum by a pressure broadening effect on spectral lines and potential collision-induced absorption, similar to N2, but the effect would be rather small.
The following assumptions are used for the atmospheric composition.
-
CO2, O3, and N2 are assumed to follow isoprofiles. While CO2 and N2 are indeed isoprofiles (at least on Earth, Venus, and Mars, where neither species significantly condenses), assuming an isoprofile for O3 is a simplifying assumption made in this work. Because O3 is formed by a 3-body reaction that requires both a pressure that is high enough and atomic oxygen produced by UV photolysis at low pressure levels, its abundance exhibits a very distinct maximum at mid-altitudes, as confirmed by many photochemical model studies. The terrestrial O3 profile can be approximated by a Gaussian profile without taking interactive photochemistry into account (e.g., von Paris et al. 2011). Instead of one parameter for the O3 isoprofile, this would introduce at least three parameters into the model, namely the location of the maximum, the concentration at the maximum, and the full width at half maximum of the Gaussian which would complicate retrieval further (see also discussion of the effect on spectra in Sect. 2.3).
-
H2O and O3 are assumed to be minor species, meaning they are only present at a level of several 10-2 or less. Therefore, they are neglected in calculating of the heat capacity or the mean molecular weight of the atmosphere.
-
Up to ptrop, H2O is calculated based on a fixed, constant relative humidity h, i.e. the partial pressure of water is obtained from pH2O(T) = hpvap,H2O(T), with the saturation vapor pressure according to local temperature. At ptrop, we assume a cold trap. For pressures lower than ptrop, H2O remains at the cold trap value. Using a constant relative humidity h in our model is also a simple assumption. On Earth, h is a function of altitude, longitude, and latitude and is highly variable. Standard globally-averaging 1D models often use, e.g., the profile of Manabe & Wetherald (1967), which decreases monotonically with altitude. However, since the hydrological cycle on Earth is already difficult to model correctly, it will be much harder for exoplanets where no topographic or other constraints are available. Therefore, assuming a fixed, constant relative humidity is justified in a first step.
-
N2 is a filling gas which means that its concentration is adjusted such that the sum over all species is unity at the surface.
The possibility of constraining surface conditions and molecular absorption bands could be limited substantially by the presence of clouds (e.g., Tinetti et al. 2006; Kitzmann et al. 2011). In that sense, the cloud-free model used in this work illustrates upper limits on detectability.
To calculate the heat capacity in Eq. (1),
we used the respective values for N2 and CO2, taken at 300 K. The
values are (in units of cal K-1 mol-1),
cp,N2 = 6.953 and
cp,CO2 = 9.215. The atmospheric
altitude profile is then constructed by assuming hydrostatic equilibrium, given the mean
atmospheric weight, temperature-pressure profile and surface gravity. The surface gravity
is calculated from the planetary mass and radius (mP and
rP, respectively). At any given value of
mP, rP is obtained from a
mass−radius relationship for rocky planets of Sotin et al.
(2007)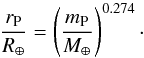 (4)(M⊕,
R⊕: Earth mass and radius).
(4)(M⊕,
R⊕: Earth mass and radius).
All of the eight parameters (4 T/p, 3 chemical, 1 planetary) are uncorrelated in our model. In reality, this is not the case. For example, the surface temperature is of course related to surface pressure and atmospheric composition via the greenhouse effect. In turn, the chemical composition is influenced by atmospheric temperature through equilibrium chemistry, photochemistry, and temperature-dependent surface processes (e.g., outgassing, weathering). However, for the purpose of illustrating a retrieval algorithm, a (self-) consistent atmospheric modeling would be computationally too expensive. Self-consistency is interesting when it allows the number of parameters to be decreased. In the case of the cool planetary atmospheres considered here, that are far from the thermodynamic equilibrium, self-consistency is out of reach: it implies, among other things, 3D time-dependent modeling with a realistic treatment of clouds and topography. Not only can this not be used for retrieval, but in practice it also increases the number of model parameters.
2.2. Target scenario
For our analysis, we used modern Earth as the reference case for an inhabited planet. We chose model parameters so as to approximately reproduce the modern Earth temperature profile (see Table 2). The relative humidity was set to h = 0.5 throughout the troposphere, CO2 to 3.55 × 10-4 and O3 to 10-7. An O3 concentration of 3.75 × 10-7 would reproduce the atmospheric column amount of modern Earth. The planetary mass mP was fixed at 1 M⊕ (so the model planet has a radius of 1 R⊕, see Eq. (4)).
Target model parameters used in this work.
Figure 2 shows the temperature-pressure and water-pressure profiles in comparison with a modern Earth reference case. This reference case was obtained with a consistent 1D radiative-convective climate model, coupled to photochemistry (for a detailed description, see Rauer et al. 2011 or Grenfell et al. 2011).
Despite the simplicity of the model, the general agreement between the target profile and the modern Earth reference is fairly good. Also, the water profiles agree qualitatively well, even though the target profile is calculated with constant relative humidity.
 |
Fig. 2 Temperature and water profiles of the target scenario, in comparison to modern Earth. |
2.3. Planetary spectra
The line-by-line code MIRART-SQuIRRL (Schreier & Böttger 2003) was used to calculate high-resolution synthetic radiance spectra of the model atmospheres described above. Line parameters were taken from the Hitran 2008 database (Rothman et al. 2009). The zenith angle was fixed at 38°. To obtain disk-integrated emission spectra, the radiance spectra were multiplied by π. For the purpose of this work, collision-induced self-continua of CO2 (Wordsworth et al. 2010) and N2 (Borysow & Frommhold 1986; Lafferty et al. 1996) have been included.
The resulting high-resolution emission spectrum for our target model of Table 2 is shown in Fig. 3. It is compared to a spectrum obtained using global mean modern Earth profiles (see Sect. 2.2). The water features (around the 6.3 μm band and in the rotation band longwards of around 16 μm) do not differ by much, indicating that the choice of relative humidity is indeed not critical. Some noticeable differences, however, occur in the optically thin window region between 8−12 μm (due to different surface temperatures, modern Earth 288 K, our target scenario 290 K and the different O3 profile) and around 7.7 μm (due to a strong methane absorption band, with methane not included in our model atmospheres). Near the 15 μm CO2 band, some differences in the spectra are apparent that are due to the slightly different temperature structure in the stratosphere (see Fig. 2).
 |
Fig. 3 High-resolution emergent spectrum for the target model of Table 2 and a comparison with modern Earth (taken from Grenfell et al. 2011). |
For modern Earth, the O3 band probes the upper troposphere and lower stratosphere, at pressures of about 10-2 to 10-1 bar, where temperatures increase with altitude. An isoprofile that would reproduce the atmospheric column amount of O3 therefore results in less emission from the O3 band since the contribution function would peak closer to the tropopause. This would imply that assuming an O3 isoprofile would underestimate the emission of the O3 band. However, many atmospheric modeling studies have shown that, e.g., planets orbiting around M and K stars would not show a strong stratospheric inversion (e.g., Segura et al. 2003; Grenfell et al. 2007). In these cases, an O3 isoprofile would actually overestimate the O3 band. Therefore, since we do not include the influence of the central star in our model (see above), assuming an O3 isoprofile is justified for the sake of model simplicity.
2.4. Observational model
The measured quantity for spectral observations is the number of photons in a wavelength bin. To translate the calculated high-resolution spectra from Sect. 2.3 into a number of photons, we place the hypothetical target planet at a distance of 10 pc. We furthermore assume an ideal detector (i.e., throughput and quantum efficiency of unity) with a 10 m2 collecting surface (i.e., about 3.6 m circular telescope aperture) and an integration time of one hour. Then, the spectra were binned to equidistant bins, corresponding to different spectral resolutions (R = 5−100) at 10 μm (i.e., bin sizes of 2−0.1 μm), over a spectral range of 5−20 μm, thus yielding a noise-free spectrum IF.
When comparing observed spectra and models to estimate atmospheric or planetary
properties, it is important to consider the S/N per bin of the observations. We take the
noise source NS to be constant over wavelength. This is of
course an approximation, since many individual, wavelength-dependent terms contribute to
the overall noise (e.g., photon noise of both star and planet, thermal noise of the
telescope and instrument, zodiacal light, etc.). However, this approach yields a simple
tool for calculating synthetic observations independent of telescope and instrument
configurations. We define NS as 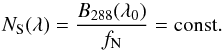 (5)where
B288 is a blackbody emitter of one Earth radius
(R⊕) with a temperature of 288 K at a distance of 10 pc,
λ0 = 10 μm, and
fN an arbitrary noise factor.
(5)where
B288 is a blackbody emitter of one Earth radius
(R⊕) with a temperature of 288 K at a distance of 10 pc,
λ0 = 10 μm, and
fN an arbitrary noise factor.
To construct noisy spectra IN, we added a Gaussian noise of
amplitude 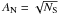 to IF:
to IF:  (6)where
i is the wavelength bin and ℛi is drawn
randomly from the standard normal distribution
(6)where
i is the wavelength bin and ℛi is drawn
randomly from the standard normal distribution  .
The S/N per bin i is then
.
The S/N per bin i is then 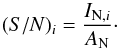 (7)To reproduce the
EChO and Darwin S/N specifications at the respective spectral resolution (see Table 1), we adapted the noise factor
fN in Eq. (5)
accordingly (e.g., for EChO, fN = 5 × 10-3 at
R = 10 to produce a mean S/N per bin of 5−6). Figure 4 shows examples of synthetic spectra generated in this
way.
(7)To reproduce the
EChO and Darwin S/N specifications at the respective spectral resolution (see Table 1), we adapted the noise factor
fN in Eq. (5)
accordingly (e.g., for EChO, fN = 5 × 10-3 at
R = 10 to produce a mean S/N per bin of 5−6). Figure 4 shows examples of synthetic spectra generated in this
way.
 |
Fig. 4 Example spectra of the target model (see Table 2 and Fig. 3) for different mission designs as summarized in Table 1. |
2.5. Fit models
When analyzing (noisy) observations and comparing them to a model, one standard quantity
that is usually evaluated is the sum of the weighted squared residuals, the so-called
χ2. The χ2 is defined as
 (8)with
x the vector of parameters (in our case, eight parameters, see Sect. 2.1), Oi the
noisy observation, Mi the parameter-dependent
model value, σi the noise level (obtained
from Eq. (5), i.e.,
(8)with
x the vector of parameters (in our case, eight parameters, see Sect. 2.1), Oi the
noisy observation, Mi the parameter-dependent
model value, σi the noise level (obtained
from Eq. (5), i.e.,
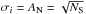 )
in a respective spectral bin i, and N is the number of
data points.
)
in a respective spectral bin i, and N is the number of
data points.
The χ2 as defined above in Eq. (8) is the log-likelihood in the case of Gaussian measurement errors,
which we assume here. The nσ uncertainties on retrieved model parameters
are then calculated by  . This means that a
3σ uncertainty corresponds to a distance of
Δχ2 = 9 from the minimum χ2
value (
. This means that a
3σ uncertainty corresponds to a distance of
Δχ2 = 9 from the minimum χ2
value ( ). Finding a
best-fit model corresponding to a certain minimum
). Finding a
best-fit model corresponding to a certain minimum  , however,
does not guarantee a good fit corresponding to the global minimum. Two quantities are
generally used to check the quality of a fit, namely the p value and the
reduced
, however,
does not guarantee a good fit corresponding to the global minimum. Two quantities are
generally used to check the quality of a fit, namely the p value and the
reduced  . The
p value is the probability of generating a worse (i.e., larger)
χ2 than the one calculated if the chosen parameters were the
true ones. All parameter vectors x with
. The
p value is the probability of generating a worse (i.e., larger)
χ2 than the one calculated if the chosen parameters were the
true ones. All parameter vectors x with
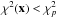 would be considered
a good fit, with
would be considered
a good fit, with 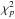 the
χ2 value corresponding to the chosen p. A
standard threshold is p = 0.01; i.e., the false-alarm probability is 1%.
Based on the χ2, the
the
χ2 value corresponding to the chosen p. A
standard threshold is p = 0.01; i.e., the false-alarm probability is 1%.
Based on the χ2, the  is
calculated via
is
calculated via 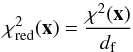 (9)where
df is the number of the degrees of freedom obtained from
df = N − P
(P number of parameters). To be considered a good fit,
(9)where
df is the number of the degrees of freedom obtained from
df = N − P
(P number of parameters). To be considered a good fit,
 should be
close to unity.
should be
close to unity.
In this work, we used two different approaches for comparing modeled spectra with the synthetic observations. First, to fit the observations, we used the IDL fitting routine MPFIT (Markwardt 2009), which is an implementation of the nonlinear least-squares Levenberg-Marquardt (LM) algorithm (Moré 1978). MPFIT uses the χ2 value to calculate best-fitting parameters. However, since it is based on a Newton-type method, it might find a local minimum that could be quite far from the actual global minimum of the χ2. Newton-type solvers are to some extent dependent on the initial parameter guess.
Second, we calculated the χ2 for a large number of parameter combinations to produce a χ2 map of the parameter space. With these maps, local minima in the χ2 and potential degeneracies between model parameters could be visualized easily. Such a method was used, e.g., by Lee et al. (2012), Cochran et al. (2011), Fabrycky et al. (2012), or Ford et al. (2012), in addition to formal fitting procedures. Error bars or uncertainties on retrieved parameters were then calculated from the χ2 maps.
For many parameters (e.g., eight in the full model described in Sect. 2.1), producing χ2 maps is not practical, in terms of both calculation time and visualization. In such cases, the LM algorithm (or other algorithms, such as Monte-Carlo) is essential to estimate parameter values.
3. Results
3.1. Surface conditions
In this section, we show the χ2 maps in the
Tsurf-pdry plane, i.e., the
parameters relevant to surface habitability. The maps represent slices of the parameter
space with all other six parameters (planetary mass, atmospheric composition, upper
atmospheric T/p profile) held
constant at the true parameters used when generating the synthetic spectra (see Table
2). This means that uncertainties on surface
conditions cannot be assigned based on such slicing, since for real observations, the
model parameters are not known exactly a priori. However, these
χ2 maps illustrate the difficulty trying to infer surface
conditions from observations. The χ2 values were calculated
for 20 synthetic observations, each with the specified S/N per bin, but with a different
realization of the noise. The median χ2 of these 20
observations is plotted to illustrate the general shape of the
χ2 map at the chosen S/N. If we were to combine these 20
observations (equivalent to adding transits), we would increase the S/N by a factor of
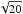 .
.
 |
Fig. 5 χ2 maps for EChO (Tinetti et al. 2012, upper panel) and Darwin (Léger et al. 1996, R = 5) specifications. Symbols show the grid points considered. |
Figure 5 shows the χ2
maps for the EChO (upper) and Darwin (lower) low-resolution configuration, corresponding
to a spectral resolution of R = 10 (Tinetti et al. 2012) and R = 5 (Léger et al. 1996), respectively. The mean S/N per bin is approximately six in
the upper part and 12 in the lower part, i.e. close to the respective S/N goals stated in
Table 1. The different colors in the
χ2 maps represent increasing confidence levels of 1, 2, 3
and 5σ, corresponding to a distance of 1, 4, 9 and 25 to the minimum
 (see Sect.
2.5). For EChO, at a 3σ level
(i.e., blue area in the χ2 maps), surface temperatures can be
inferred to be higher than 280 K and lower than 300 K, indicating a habitable surface with
relatively high confidence. However, for the extraordinary claim of the detection of
(inhabited) habitable planets, one would instead need the 5σ uncertainty
level. This barely excludes surface temperatures below the freezing point of water (273 K)
in the EChO case, while surface habitability can be inferred at the 5σ
level for the presented Darwin specifications. In contrast, surface pressure is less
constrained in both cases (about a factor of 4), but still within reasonable values for
habitability.
(see Sect.
2.5). For EChO, at a 3σ level
(i.e., blue area in the χ2 maps), surface temperatures can be
inferred to be higher than 280 K and lower than 300 K, indicating a habitable surface with
relatively high confidence. However, for the extraordinary claim of the detection of
(inhabited) habitable planets, one would instead need the 5σ uncertainty
level. This barely excludes surface temperatures below the freezing point of water (273 K)
in the EChO case, while surface habitability can be inferred at the 5σ
level for the presented Darwin specifications. In contrast, surface pressure is less
constrained in both cases (about a factor of 4), but still within reasonable values for
habitability.
Figure 6 shows the χ2 maps for the medium resolution Darwin cases (R = 20, Léger et al. 1996 and Cockell et al. 2009a). The mean S/N per bin in these cases is 20 and 10 (see stated S/N goals in Table 1). It is clearly seen that the relatively high spectral resolution, together with the high projected S/N per bin allows for a secure >5σ characterization of surface conditions (but keep in mind the idealized setup of the χ2 maps in this section).
 |
Fig. 6 χ2 maps for Darwin spec (R = 20, upper: Léger et al. 1996, lower: Cockell et al. 2009a). Symbols show the grid points considered. |
In summary, in the idealized case presented here, the retrieval of surface conditions is possible with a high S/N (on the order of 5 and more). The 1σ uncertainties are relatively small, but the optimistic case considered here underestimates retrieval uncertainties. Adding free parameters, such as atmospheric composition, stratospheric temperature structure, and planetary mass, to the fit will only increase the uncertainties of the retrieval. Furthermore, it should be kept in mind that the cloud-free nature of our model implies that retrieval possibilities for surface conditions might be overestimated.
3.2. Atmospheric composition
The detection of atmospheric species is another major goal for exoplanet characterization. Habitability in terms of surface conditions does not necessarily imply an inhabited planet, so the search for atmospheric biomarker species holds the greatest potential for actually finding extraterrestrial life. Therefore, in this section, we show the χ2 maps for the atmospheric composition (i.e., h, CO2 and O3), again, as above, with all other parameters held constant at the true values. As in Sect. 3.1, the different colors in the χ2 maps represent increasing confidence levels and the median χ2 of the 20 synthetic observations is plotted.
Figure 7 shows the χ2 maps for the EChO resolution (R = 10) in the respective CO2-h (upper) and CO2-O3 (lower) plane. The S/N is chosen to be equal to the EChO goal of five (see Table 1). It is clearly seen that the presence of water can be securely inferred from the spectrum, since h = 0 is excluded at high confidence. Also, CO2 can be detected clearly, since the minimum CO2 mixing ratio is about 10-5. O3 is detected at the 1σ level, but O3 concentrations of 10-10 are compatible with the observations at the 2σ level, making the detection somewhat marginal. However, even 2σ constraints would be very useful for potential selection of candidates that would be subjected to further, more detailed follow-up observations.
 |
Fig. 7 χ2 contours for ECho specifications from Table 1. White symbols show the considered grid points. |
The goal of exoplanet space missions (such as EChO, Darwin, Finesse), however, is not only to detect atmospheric species (strong lower limits), but also the characterization (a quantitative estimate of the concentration, meaning strong upper limits). As implied by Fig. 7, 5σ uncertainties on CO2 concentration cover about three orders of magnitude, and the humidity is only constrained to about a factor of 9 (with h = 1 and h = 0 excluded at high confidence). Therefore, it seems unlikely that an S/N of about five at spectral resolution R = 10 will allow for accurate characterization of Earth-like atmospheres.
In Fig. 8, we show the χ2 maps with the same spectral resolution (R = 10) but with a S/N sufficient to limit the 5σ uncertainties of the atmospheric composition to below one order of magnitude. The S/N per bin (~28) is five times higher than the value stated in Table 1, but allows for the characterization of H2O, CO2, and O3 in this ideal model exercise (all parameters except composition fixed). An increase S/N from 5 to 28 translates into a factor of about 30 in integration time if read-out noise is not the dominant noise source, because S/N then scales with the square root of the integration time.
 |
Fig. 8 χ2 contours for ECho resolution, with increased S/N of 28. White symbols show the considered grid points. |
In Figs. 9 and 10, we show analogous χ2 maps for the Darwin low-resolution (R = 5, see Table 1) and medium-resolution (R = 20, see Table 1) cases. Since at low resolution, the aim is to constrain CO2, we only show the CO2-O3 plane in Fig. 9. Results in Fig. 9 suggest that an S/N of around 12 is not sufficent at R = 5 to constrain CO2 better than about two orders of magnitude. To obtain one order of magnitude uncertainty at the 5σ level, an increase in S/N to more than 25 is needed (lower part of Fig. 9).
 |
Fig. 9 χ2 contours for Darwin low-resolution specification (upper) and needed S/N (lower). White symbols show the considered grid points. |
At medium spectral resolution of R = 20, Cockell et al. (2009a,b) state that an S/N of 10 is aimed for to characterize the atmosphere with respect to CO2, H2O, and O3. We therefore show both the CO2-h (left column) and the CO2-O3 (right column) planes in Fig. 10. As can be inferred from the upper panel (S/N of 10) in Fig. 10, except for CO2, atmospheric composition cannot be constrained with these specifications. An increase to an S/N of about 20 (lower panel) is needed to better constrain H2O and O3 at the 5σ level (although O3 is already constrained at the 3σ level for an S/N of 10). This S/N at R = 20 corresponds to the stated O3 characterization aim of Léger et al. (1996) in Table 1.
An increase of about a factor of 2 in S/N then translates into a factor 4 for Darwin in terms of the exposure time necessary for a specific target. This significantly reduces the number of potential target stars.
 |
Fig. 10 χ2 contours for Darwin high-resolution specifications (upper) and needed S/N (lower). White symbols show considered grid points. |
To further illustrate the difficulty of obtaining firm constraints on O3 concentration, we show in Figs. 11 and 12 sample noisy observations together with spectra of model atmospheres containing various amounts of O3, but otherwise the seven remaining parameters fixed at the “correct” values. Figure 11 shows a synthetic observation at R = 10 and a mean S/N per bin of about six, i.e. the current EChO specifications. It is clearly seen that increasing the O3 concentration from 10-10 to 10-6 changes the O3 band (within 2σ in the bin); however, the change in overall χ2 is not significant, as expected from Fig. 7.
 |
Fig. 11 Influence of O3 on synthetic observations (upper panel, noisy spectrum in black) and corresponding χ2 values (lower panel, diamonds). EChO resolution and S/N. |
In Fig. 12, the effect of O3 is shown with the same S/N of about six, but at a spectral resolution of R = 100. As expected, the higher resolution clearly improves the accuracy for O3 retrieval.
 |
Fig. 12 Influence of O3 on synthetic observations (upper panel, noisy spectrum in black) and corresponding χ2 values (lower panel, diamonds). R = 100 and S/N of 6. |
Our results therefore imply that the current Darwin design is probably overly optimistic with respect to how many habitable terrestrial planets could be characterized and searched for atmospheric biomarkers with emission spectroscopy. Even putting aside the current paucity of targets, since no transiting HZ planet are known so far and only a few candidate super-Earths in or near the HZ have been discovered (see Introduction), EChO is probably also unlikely to constrain atmospheric composition with the current S/N and R goals.
Best-fit parameters after 100 randomly initialized fits, with associated 3σ uncertainties and fit statistics.
3.3. Complete retrieval of planetary parameters
In this section, we performed a nonlinear least-squares fit to one specific synthetic observation using MPFIT (see above, Sect. 2.5). All eight model parameters were allowed to vary, as is the case for real observations, and we initialized the fit with a random guess of the parameters. Upper and lower boundaries for the fit parameters are stated in Table 4. The numerical values for the parameter boundaries are mostly motivated by the fact that we aim at investigating habitable, terrestrial planets, which puts constraints on the planetary mass and the surface temperature. In total, 100 randomly initialized fits were performed.
Parameter range used for initial guess and retrieval iteration.
Minimizing the χ2 determines the best-fitting, optimal
parameter vector xopt corresponding to
 . The 100 fit
results were used to determine xopt. Uncertainties were then
estimated based on the distance Δχ2 to
. The 100 fit
results were used to determine xopt. Uncertainties were then
estimated based on the distance Δχ2 to
 (see Sect.
2.5).
(see Sect.
2.5).
Figures 13 and 14 illustrate how this is done. They show the χ2 values as a function of the respective parameter values for all points evaluated by MPFIT during the fitting procedure, a total of about 20 000 points. We chose the R = 5, S/N = 12 case, i.e. the low-resolution Darwin aim (see Table 1). Indicated are the Δχ2 = 1, Δχ2 = 4, Δχ2 = 9 and Δχ2 = 25 thresholds, corresponding respectively to 1, 2, 3 and 5σ uncertainties in the estimated parameter value. Also clearly seen are the local minima for Tsurf, CO2 and O3. Interestingly, the high O3 concentrations essentially correspond to zero CO2, indicating a strong correlation between both species at low spectral resolution. Furthermore, this also suggests that CO2 cannot be detected in this scenario, since no firm lower limits are found (see below, Table 3).
 |
Fig. 13 χ2 values as a function of parameter values: temperature profile, for R = 5, S/N = 12 (Darwin). Horizonal lines indicate 1, 2, 3, and 5σ uncertainties. |
 |
Fig. 14 χ2 values as a function of parameter values: composition and mass, for R = 5, S/N = 12 (Darwin). Horizonal lines indicate 1, 2, 3, and 5σ uncertainties. |
As stated in Sect. 2.5, a best-fit model found by a
fitting method does not necessarily correspond to a good fit. Therefore, Table 3 shows the quality of the fits as indicated by the
p value and the  value. Except
for the R = 5 observations where there are as many parameters as there
are data points (df = 0, hence by definition
value. Except
for the R = 5 observations where there are as many parameters as there
are data points (df = 0, hence by definition
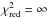 , Eq.
(9)), the
, Eq.
(9)), the
 indicates
that good fits are indeed obtained by MPFIT. Also, as stated in Sect. 2.5, MPFIT depends on initial conditions. This is indicated in Table
3 by the fact that fewer than 100% of the
best-fits are actually good fits, when adopting a p value of 0.01.
However, generally, most estimates of xopt are good fits, even
though we used a Newton-type algorithm.
indicates
that good fits are indeed obtained by MPFIT. Also, as stated in Sect. 2.5, MPFIT depends on initial conditions. This is indicated in Table
3 by the fact that fewer than 100% of the
best-fits are actually good fits, when adopting a p value of 0.01.
However, generally, most estimates of xopt are good fits, even
though we used a Newton-type algorithm.
In Table 3, we present the found parameters, as well as the 3σ uncertainties (i.e., Δχ2 = 9, see Figs. 13 and 14) for several combinations of spectral resolution and S/N. We use mission specifications as indicated by Table 1, as well as simulations with increased S/N.
Table 3 shows that the temperature profile is largely unconstrained by the observations. This is apparent from the found values of TTOA and ptrop which are, within 3σ, compatible with the boundaries imposed in Table 4. Only at R = 20 with an S/N = 20 do fit results seem to indicate at least lower limits for TTOA.
Limits on surface temperatures are tighter, with the fit results in most cases excluding cold surfaces with high confidence. However, for the nominal EChO and Darwin R = 5 cases, surface temperatures around 260 K are compatible with the data, which is inconsistent with surface habitability. Even at R = 20 and S/N = 10, surface temperatures above 273 K are only marginally inferred from the fit. Additionally, for the Darwin R = 5 and the EChO nominal cases (R = 5, S/N = 12 and R = 10, S/N = 5, respectively), upper limits for Tsurf are consistent with surface temperatures on the order of 400 K, which is higher than the limit of extremophilic life on Earth (e.g., Rothschild & Mancinelli 2001). Surface pressure is relatively well constrained to within a few bars at R = 20 and, with an increased S/N of 28, also at R = 10. For the Darwin R = 5 cases, however, the entire pressure range of Table 4 is compatible with the noisy observations. In summary, surface habitability in terms of surface temperature could be inferred in most of the cases, but the temperature profile remains unconstrained.
The planetary mass is generally well-fitted to within a factor of two or better to the true value, indicating that, combined with further constraints based on discovery data, it is probably not a critical parameter in our model. Of course, this is because mass correlates with radius (see Eq. (4)), which then directly influences the emitting surface, hence the number of photons detected. Based on our assumed mass-radius relationship (see Eq. (4)), the uncertainties in planetary radius range from of 10% to 50%, which is close to current uncertainties in transit surveys.
With respect to atmospheric composition, Table 3 implies that the most difficult parameter for the retrieval is actually the humidity h. Most cases only allow for weak lower limits, indicating that a significant detection is missing. Also, giving firm upper and lower limits to characterize the humidity is only marginally possible for the R = 20, S/N = 20 case.
The CO2 concentration cannot be constrained for the EChO nominal case, and even a detection is only marginal. At an increased S/N of 26, the EChO resolution allows for CO2 characterization within two orders of magnitude. For the Darwin R = 5 cases, only upper limits to CO2 could be provided, with lower limits not allowing for a conclusive detection. At R=20, in contrast, clear upper limits are found. O3 cannot be characterized accurately with either R = 5 or R = 10 nominal S/Ns, but upon increasing the S/N at the EChO resolution, relatively strong upper limits are found. A spectral resolution of R = 20 allows for relatively firm upper O3 limits; however a detection is rather marginal at S/N = 10.
These results imply that even with increased S/N (with respect to the current mission design, Table 1), both Darwin and EChO are unlikely to be able to provide accurate constraints on atmospheric composition and temperature structure, even though surface temperature and, to some extent, surface pressure are in principle accessible, confirming results from Sects. 3.1 and 3.2.
In Fig. 15, we present scatter plots of the best-fit parameters at both the projected Darwin and EChO designs from Table 1 to investigate possible correlations between fit parameters. The most obvious correlations are between CO2, O3, and pdry (upper panels). The CO2 and O3 concentrations are generally lower at higher surface pressures. This is related to the depth of the 15 μm and 9.6 μm bands, respectively. The apparent correlation between CO2 and O3 is interesting for the discussion of possible false-positive detections of both species (see also discussion below). Correlations between CO2 and O3 with TTOA and ptrop become apparent (middle panels), at least at better S/N and higher spectral resolution. At higher values of ptrop, the CO2 and O3 concentrations are systematically lower. This is related to the parametrization of the model stratosphere. Both species are best probed in bands originating in the lower stratosphere. Since higher ptrop values mean warmer stratospheres (all other parameters being equal, see e.g. Eq. (3) and Fig. 1), higher ptrop therefore translates into lower concentrations of CO2 and O3. An analogous argument is valid for the apparent weak correlation between CO2 and O3 with TTOA. As stated above, there also is a weak correlation between planetary mass and Tsurf. However, Tsurf does not show any strong correlation with surface pressure or atmospheric composition (bottom panels).
 |
Fig. 15 Scatter plots of best-fit parameters from 100 randomly initialized fits. Black: EChO case, R = 10, S/N = 6; red: Darwin medium-resolution case, R = 20, S/N = 10. |
4. Discussion
4.1. Atmospheric model
In reality, a full atmospheric model that is able to reproduce observations of terrestrial, potentially habitable planets should contain many more parameters than the one presented here (see Sect. 2.1).
One important factor is the presence of clouds in the atmosphere that have been omitted in the present work (see Sect. 2.1). Clouds could alter the atmospheric temperature profiles and have a potentially strong influence on surface temperatures (e.g., Forget & Pierrehumbert 1997; Kitzmann et al. 2010). Furthermore, they also affect the spectral appearance of a planet in emission spectra (e.g., Tinetti et al. 2006). They could mask molecular absorption bands and inhibit the probing of the lower atmosphere and surface (hence, the retrieval of surface conditions). On Earth, many different types of clouds exist in terms of, e.g., vertical and horizontal cloud extension, optical properties, or composition. Cloud cover is highly variable both spatially and temporarily. This adds many complications both for atmospheric modeling and spectral retrieval since many single observations must usually be added to obtain reasonable S/N.
In addition, many more radiatively active species besides the ones considered in this work could have an impact on temperature structure and emission spectra. In particular, the biomarker species nitrous oxide could be detectable at least in high-resolution spectra given specific planetary scenarios (e.g., early Earth, Grenfell et al. 2011). SO2 and other sulfur species have been proposed in anoxic atmospheres or atmospheres with high volcanic activity (e.g., Kaltenegger & Sasselov 2010; Domagal-Goldman et al. 2011). Given appropriate concentrations of larger than ≈10-3, H2 could also be detectable due to distinct collision-induced absorption (e.g., Borysow 1991). Additionally, the impact of the stellar radiation on the temperature profile should be taken into account since variations are potentially large even for fixed atmospheric composition (e.g., Kitzmann et al. 2010).
Furthermore, many photochemical studies have shown that the influence of central star on atmospheric composition cannot be neglected. As an example, the biomarker-relevant gases methane and chloromethane could build up to high concentrations given a suitable stellar UV radiation environment, such as on planets around M dwarf stars (e.g., Segura et al. 2005). The CO concentration was shown to increase for planets orbiting M dwarfs (e.g., Rauer et al. 2011). However, using (photo-)chemical models introduces many more additional parameters, e.g., number of important species for catalytic cycles, planetary surface fluxes, stellar and orbital parameters, and geochemical cycles which would complicate the retrieval of planetary properties. Constraining CO2 concentrations to within a few orders of magnitude might indicate the existence of a silicate weathering cycle that controls CO2 (Abbot et al. 2012). Still, the potential importance of using consistent modeling tools is demonstrated by Selsis (2000) or Rauer et al. (2011) among others. Coupling temperature structure, stellar radiation, and atmospheric photochemistry could cause biosignatures, such as the O3 band, to disappear in the emission spectra.
Planetary and orbital properties, such as rotation rate, obliquity and eccentricity, induce diurnal and seasonal variability in the emission and reflectance spectra, which again poses a problem for the retrieval, because of both additional free parameters and, in the case of thermal spectra, severe degeneracies between obliquity and thermal inertia (e.g., Gaidos & Williams 2004; Cowan et al. 2012). Surface properties, e.g., oceans, continents, vegetation, ice and snow cover, also influence planetary spectra (e.g., Hu et al. 2012). Numerous studies have shown how to retrieve such information from spectrophotometry of Earth in the visible spectral range (e.g., Oakley & Cash 2009; Fujii et al. 2010; Livengood et al. 2011). However, in a full planetary model these properties would increase the number of free parameters, hence render retrieval more complex and most likely prohibit conclusions on habitability.
The bulk properties of a planet, e.g. its mass-radius relationship, does not necessarily follow the one obtained for rocky, terrestrial planets used here (Sotin et al. 2007). The masses and radii of super-Earths discovered so far span a wide range (e.g., Léger et al. 2009; Charbonneau et al. 2009; Lissauer et al. 2011; Batalha et al. 2011). Assuming different bulk compositions for the planet then leads to very different mass-radius relationships (e.g., Fortney et al. 2007).
Regarding the parametric nature of our model, note that self-consistent modeling could provide a better constraint on CO2 and, indirectly, on O3, since detecting O3 has a lot to do with constraining CO2 (see discussion below). Therefore, the retrieval results presented here might be conservative. Future studies could use real observations of Earth or Mars, or results from consistent modeling studies, as target scenarios and investigate whether accurate and correct retrieval is possible in such more realistic cases.
4.2. Observational constraints
To reduce the number of fit parameters and break existing degeneracies in emission spectra, observational constraints and additional information must be used when interpreting the spectra. Many important planetary properties could be determined beforehand, such as mass and radius. Measurements of the planetary mass are available through a number of methods, such as astrometry (e.g., Malbet et al. 2011), radial velocity, transit timing variations in multiple systems (e.g., Lissauer et al. 2011) or dynamical models (e.g., Beust et al. 2008; Mayor et al. 2009). The planetary radius could be estimated for transiting planets.
In addition, for transiting planets it is possible to combine emission spectroscopy with transmission spectroscopy. Transmission spectroscopy is, to first order, sensitive to atmospheric scale height, hence mean atmospheric weight and planetary gravity, and only weakly dependent on the vertical temperature structure. Thus, degeneracies between temperature and atmospheric composition could be broken (see, e.g., Benneke & Seager 2012). Thanks to the broad spectral range covered by EChO, such transmission observations could be performed with the same mission as the emission spectroscopy, in contrast to Darwin, which would need to rely on other observation facilities. Another complementary method, especially on non-transiting planets, could be to use phase curves and the variation spectrum (e.g., Harrington et al. 2006; Seager & Deming 2009; Selsis et al. 2011; Maurin et al. 2012), a technique that could be used by the Darwin misson.
Broadband optical photometry (over a spectral range of about 0.2–2 μm)
could be used to measure the reflected light IR of the planet,
which would impose constraints on the Bond albedo AB and the
planetary radius (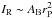 ). Since
AB depends strongly on atmospheric composition and surface
pressure through absorption of stellar radiation and Rayleigh scattering and Eq. (4) relates mass and radius, such measurements
could in principle provide useful additional constraints. However, the contrast in
reflected light between star and planet is on the order of
10-8–10-10 for terrestrial, habitable-zone planets. As a result,
observations would be very challenging and, consequently, constraints may actually be
fairly weak.
). Since
AB depends strongly on atmospheric composition and surface
pressure through absorption of stellar radiation and Rayleigh scattering and Eq. (4) relates mass and radius, such measurements
could in principle provide useful additional constraints. However, the contrast in
reflected light between star and planet is on the order of
10-8–10-10 for terrestrial, habitable-zone planets. As a result,
observations would be very challenging and, consequently, constraints may actually be
fairly weak.
The orbital period of the planet is determined from the discovery data rather precisely. The orbital distance is determined from the orbital period based on stellar mass (and/or radius, for transiting planets). Combining orbital distance with the stellar energy distribution obtained either from spectroscopy or stellar model atmospheres (e.g., Buser & Kurucz 1992 or Hauschildt et al. 1999), it is possible to compute the stellar energy input on the planet. Then, assuming global energy conservation for the planet, it would be possible to eliminate the model scenarios that would be prohibited, thus possibly limiting the parameter space.
4.3. Real observations
In practice, many of these potential limits on parameters are rather difficult to obtain. For example, detecting and verifying a planetary signal is very challenging for low-mass planets (see, e.g., Ferraz-Mello et al. 2011; Pont et al. 2011; Hatzes et al. 2011 for the CoRoT-7 system; Vogt et al. 2010; Tuomi 2011; Gregory 2011 for the GL 581 system). Also, uncertainties on stellar parameters, usually derived from stellar models, are the main problem for derived planetary parameters such as radius and mass, as is for example the case for GJ 1214 b (e.g., Carter et al. 2011; Sada et al. 2010; Berta et al. 2011) where the estimated planetary radius changes by 15%, depending on the adopted stellar model.
Other practical concerns are instrumental constraints, such as available filters, wavelength coverage and spectral resolution of the telescopes used for the observations, or large gaps in time between observations. Constraints obtained with the same mission (or instrument, even) are usually preferable to constraints obtained with different observational setups due to systematic noise.
4.4. Biomarker and bioindicators
Here, we have considered ozone as a biomarker, since on Earth it is mainly produced from oxygen photochemistry, and the oxygen is provided by the biosphere. However, interpreting the presence of ozone as a bioindicator is not necessarily straightforward. In other words, a 2σ detection of ozone is not equivalent to a 2σ detection of life. Many studies have shown that ozone can be produced abiotically (e.g., Selsis et al. 2002; Segura et al. 2007; Domagal-Goldman & Meadows 2010). Additionally, it has been shown that ozone persists in the atmospheres of Earth-like planets even at drastically reduced oxygen concentrations and that ozone concentrations depend crucially on the UV radiation field of the central star (e.g., Segura et al. 2003; Grenfell et al. 2007). Very thin ozone layers have indeed been detected in the atmospheres of both Venus and Mars (e.g., Lebonnois et al. 2006; Montmessin et al. 2011), although concentrations are far too low to be detectable on exoplanets.
The absence of ozone in observations, however, does not imply that ozone is not present in the atmosphere, because a masking of absorption features is certainly possible, as shown by, e.g., Schindler & Kasting (2000), Selsis et al. (2002), or von Paris et al. (2011).
The most promising way to identify biospheric signatures in atmospheric spectra therefore seems the simultaneous presence of species such as water, ozone, oxygen, and methane, as proposed by, e.g., Sagan et al. (1993) or Selsis et al. (2002).
5. Conclusions
In this work, we have investigated the possibility of retrieving planetary properties (such as atmospheric composition, temperature structure, radius) from emission spectra. We used a parametric atmosphere model to create arbitrary atmospheres of hypothetical habitable planets. The atmospheric profiles were then used to calculate synthetic, noisy observations. Based on these observations, we tried to fit the model parameters and investigate potential degeneracies.
We used two design concepts (in terms of S/N and spectral resolution) of exoplanet space missions. Results imply that surface conditions can be characterized relatively well (to within ~10 K at 3σ) with S/Ns between 10 and 30, depending on spectral resolution. This would allow for an assessment of the potential habitability of the target planet. However, even with high S/Ns on the order of 20 or higher, emission spectra did not allow for accurate determination of atmospheric composition. The biosignature of O3, as well as the atmospheric H2O content, is not well constrained with current mission designs. Also, the temperature structure could not be retrieved.
Since achieving such high S/Ns (or even higher values) is rather difficult in the foreseeable future, single-visit emission spectroscopy alone is most likely not capable of characterizing the atmospheres of potentially habitable planets. To obtain higher accuracy on the retrieved parameters of habitable planets, emission spectroscopy must be combined with other techniques, e.g. transmission spectroscopy, phase curves or photometry in the visible spectral range. An investigation of such possibilities and of whether this would allow for atmospheric characterization is the subject of future studies.
Acknowledgments
P. von Paris, P. Hedelt and F. Selsis acknowledge support from the European Research Council (Starting Grant 209622: E3ARTHs). This research has been supported in part by the Helmholtz Association through the research alliance “Planetary Evolution and Life”. Stimulating discussions with H. Rauer and Sz. Csizmadia are gratefully acknowledged. We further acknowledge helpful comments by the referee. We thank A. Borysow for making the Fortran programs freely available to calculate the collision-induced absorption coefficients for N2.
References
- Abbot, D. S., Cowan, N. B., & Ciesla, F. J. 2012, ApJ, 756, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Vogt, S. S., et al. 2012, ApJ, 751, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. M., Borucki, W. J., Bryson, S. T., et al. 2011, ApJ, 729, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Kempton, E., & Homeier, D. 2010, Nature, 468, 669 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bean, J. L., Désert, J.-M., Kabath, P., et al. 2011, ApJ, 743, 29 [Google Scholar]
- Belu, A. R., Selsis, F., Morales, J., et al. 2011, A&A, 525, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benneke, B., & Seager, S. 2012, ApJ, 753, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, Z. K., Charbonneau, D., Bean, J., et al. 2011, ApJ, 736, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Berta, Z. K., Charbonneau, D., Désert, J.-M., et al. 2012, ApJ, 747, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Beust, H., Bonfils, X., Delfosse, X., & Udry, S. 2008, A&A, 479, 277 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borucki, W. J., Koch, D. G., Basri, G., et al. 2011, ApJ, 736, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D. G., Batalha, N., et al. 2012, ApJ, 745, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A. 1991, Icarus, 92, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Borysow, A., & Frommhold, L. 1986, ApJ, 311, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Buser, R., & Kurucz, R. L. 1992, A&A, 264, 557 [NASA ADS] [Google Scholar]
- Carter, J. A., Winn, J. N., Holman, M. J., et al. 2011, ApJ, 730, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Cassan, A., Kubas, D., Beaulieu, J.-P., et al. 2012, Nature, 481, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cochran, W. D., Fabrycky, D. C., Torres, G., et al. 2011, ApJS, 197, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Cockell, C. S., Herbst, T., Léger, A., et al. 2009a, Exp. Astron., 23, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Cockell, C. S., Léger, A., Fridlund, M., et al. 2009b, Astrobiology, 9, 1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Cowan, N. B., Voigt, A., & Abbot, D. S. 2012, ApJ, 757, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Croll, B., Albert, L., Jayawardhana, R., et al. 2011, ApJ, 736, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Crossfield, I. J. M., Barman, T., & Hansen, B. M. S. 2011, ApJ, 736, 132 [NASA ADS] [CrossRef] [Google Scholar]
- de Mooij, E. J. W., Brogi, M., de Kok, R. J., et al. 2012, A&A, 538, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delfosse, X., Bonfils, X., Forveille, T., et al. 2013, A&A, in press, DOI: 10.1051/0004-6361/201219013 [Google Scholar]
- Deming, D., Seager, S., Winn, J., et al. 2009, PASP, 121, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Des Marais, D. J., Harwit, M. O., Jucks, K. W., et al. 2002, Astrobiology, 2, 153 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Désert, J., Bean, J., Miller-Ricci Kempton, E., et al. 2011, ApJ, 731, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Domagal-Goldman, S., & Meadows, V. 2010, ASP Conf. Ser., 430, 152 [NASA ADS] [Google Scholar]
- Domagal-Goldman, S. D., Meadows, V. S., Claire, M. W., & Kasting, J. F. 2011, Astrobiology, 11, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Fabrycky, D. C., Ford, E. B., Steffen, J. H., et al. 2012, ApJ, 750, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraz-Mello, S., Tadeu Dos Santos, M., Beaugé, C., Michtchenko, T. A., & Rodríguez, A. 2011, A&A, 531, A161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ford, E. B., Fabrycky, D. C., Steffen, J. H., et al. 2012, ApJ, 750, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Forget, F., & Pierrehumbert, R. T. 1997, Science, 278, 1273 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Fortney, J. J., Marley, M. S., & Barnes, J. W. 2007, ApJ, 659, 1661 [NASA ADS] [CrossRef] [Google Scholar]
- Fujii, Y., Kawahara, H., Suto, Y., et al. 2010, ApJ, 715, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E., & Williams, D. M. 2004, New Astron., 10, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C. 2011, MNRAS, 415, 2523 [NASA ADS] [CrossRef] [Google Scholar]
- Grenfell, J. L., Grießmeier, J.-M., Patzer, B., et al. 2007, Astrobiology, 7, 208 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Grenfell, J. L., Gebauer, S., von Paris, P., et al. 2011, Icarus, 211, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Harrington, J., Hansen, B. M., Luszcz, S. H., et al. 2006, Science, 314, 623 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hatzes, A. P., Fridlund, M., Nachmani, G., et al. 2011, ApJ, 743, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Howard, A. W., Marcy, G. W., Johnson, J. A., et al. 2010, Science, 330, 653 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hu, R., Ehlmann, B. L., & Seager, S. 2012, ApJ, 752, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., & Sasselov, D. 2010, ApJ, 708, 1162 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Kaltenegger, L., Traub, W. A., & Jucks, K. W. 2007, ApJ, 658, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Kitzmann, D., Patzer, A. B. C., von Paris, P., et al. 2010, A&A, 511, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitzmann, D., Patzer, A. B. C., von Paris, P., Godolt, M., & Rauer, H. 2011, A&A, 531, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lafferty, W. J., Solodov, A. M., Weber, A., Olson, W. B., & Hartmann, J. 1996, Appl. Opt., 35, 5911 [NASA ADS] [CrossRef] [Google Scholar]
- Lebonnois, S., Quémerais, E., Montmessin, F., et al. 2006, J. Geophys. Res., 111, 9 [Google Scholar]
- Lee, J.-M., Fletcher, L. N., & Irwin, P. G. J. 2012, MNRAS, 420, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Mariotti, J. M., Mennesson, B., et al. 1996, Icarus, 123, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Léger, A., Rouan, D., Schneider, J., et al. 2009, A&A, 506, 287 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Line, M. R., Zhang, X., Vasisht, G., et al. 2012, ApJ, 749, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Lissauer, J. J., Fabrycky, D. C., Ford, E. B., et al. 2011, Nature, 470, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Livengood, T. A., Deming, L. D., A’Hearn, M. F., et al. 2011, Astrobiology, 11, 907 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N., & Seager, S. 2009, ApJ, 707, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Malbet, F., Léger, A., Shao, M., et al. 2011, Exp. Astron., 109 [Google Scholar]
- Manabe, S., & Wetherald, R. T. 1967, J. Atmosph. Sci., 24, 241 [Google Scholar]
- Markwardt, C. B. 2009, ASP Conf. Ser., 411, 251 [Google Scholar]
- Maurin, A. S., Selsis, F., Hersant, F., & Belu, A. 2012, A&A, 538, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montmessin, F., Bertaux, J.-L., Lefèvre, F., et al. 2011, Icarus, 216, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Moré, J. 1978, Lect. Notes Math., 630, 105 [CrossRef] [Google Scholar]
- Oakley, P. H. H., & Cash, W. 2009, ApJ, 700, 1428 [NASA ADS] [CrossRef] [Google Scholar]
- Pepe, F., Lovis, C., Ségransan, D., et al. 2011, A&A, 534, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pont, F., Aigrain, S., & Zucker, S. 2011, MNRAS, 411, 1953 [NASA ADS] [CrossRef] [Google Scholar]
- Rauer, H., Gebauer, S., von Paris, P., et al. 2011, A&A, 529, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robinson, T. D., & Catling, D. C. 2012, ApJ, 757, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spectr. Rad. Transf., 110, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Rothschild, L. J., & Mancinelli, R. L. 2001, Nature, 409, 1092 [NASA ADS] [CrossRef] [Google Scholar]
- Sada, P. V., Deming, D., Jackson, B., et al. 2010, ApJ, 720, L215 [NASA ADS] [CrossRef] [Google Scholar]
- Sagan, C., Thompson, W. R., Carlson, R., Gurnett, D., & Hord, C. 1993, Nature, 365, 715 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schindler, T. L., & Kasting, J. F. 2000, Icarus, 145, 262 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
- Schneider, J., Boccaletti, A., Mawet, D., et al. 2009, Exp. Astron., 23, 357 [Google Scholar]
- Schreier, F., & Böttger, U. 2003, Atmosph. Ocean. Opt., 16, 262 [Google Scholar]
- Seager, S., & Deming, D. 2009, ApJ, 703, 1884 [Google Scholar]
- Segura, A., Krelove, K., Kasting, J. F., et al. 2003, Astrobiology, 3, 689 [Google Scholar]
- Segura, A., Kasting, J. F., Meadows, V., et al. 2005, Astrobiology, 5, 706 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Segura, A., Meadows, V. S., Kasting, J. F., Crisp, D., & Cohen, M. 2007, A&A, 472, 665 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Selsis, F. 2000, ESA SP, 451, 133 [Google Scholar]
- Selsis, F., Despois, D., & Parisot, J.-P. 2002, A&A, 388, 985 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Selsis, F., Wordsworth, R. D., & Forget, F. 2011, A&A, 532, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sotin, C., Grasset, O., & Mocquet, A. 2007, Icarus, 191, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Swain, M. R. 2012, AAS Meet. Abstracts, 220, 505.05 [Google Scholar]
- Tessenyi, M., Ollivier, M., Tinetti, G., et al. 2012, ApJ, 746, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Tinetti, G., Meadows, V. S., Crisp, D., et al. 2006, Astrobiology, 6, 881 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tinetti, G., Beaulieu, J. P., Henning, T., et al. 2012, Exp. Astron., 34, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Trauger, J., Stapelfeldt, K., Traub, W., et al. 2008, SPIE Conf. Ser., 7010 [Google Scholar]
- Tuomi, M. 2011, A&A, 528, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tuomi, M., Anglada-Escude, G., Gerlach, E., et al. 2013, A&A, 549, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udry, S., Bonfils, X., Delfosse, X., et al. 2007, A&A, 469, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vasquez, M., Schreier, F., Gimeno Garcia, S., et al. 2013, A&A, 549, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogt, S. S., Butler, R. P., Rivera, E. J., et al. 2010, ApJ, 723, 954 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- von Paris, P., Cabrera, J., Godolt, M., et al. 2011, A&A, 534, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wittenmyer, R. A., Tinney, C. G., Butler, R. P., et al. 2011, ApJ, 738, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Wordsworth, R., Forget, F., & Eymet, V. 2010, Icarus, 210, 992 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Emission spectroscopy of potentially habitable planets: Science goals (species to be detected and characterized) and requirements in terms of spectral resolution and S/N for two European exoplanet characterization missions.
Best-fit parameters after 100 randomly initialized fits, with associated 3σ uncertainties and fit statistics.
All Figures
 |
Fig. 1 Illustration of the parameterized temperature structure. |
| In the text | |
 |
Fig. 2 Temperature and water profiles of the target scenario, in comparison to modern Earth. |
| In the text | |
 |
Fig. 3 High-resolution emergent spectrum for the target model of Table 2 and a comparison with modern Earth (taken from Grenfell et al. 2011). |
| In the text | |
 |
Fig. 4 Example spectra of the target model (see Table 2 and Fig. 3) for different mission designs as summarized in Table 1. |
| In the text | |
 |
Fig. 5 χ2 maps for EChO (Tinetti et al. 2012, upper panel) and Darwin (Léger et al. 1996, R = 5) specifications. Symbols show the grid points considered. |
| In the text | |
 |
Fig. 6 χ2 maps for Darwin spec (R = 20, upper: Léger et al. 1996, lower: Cockell et al. 2009a). Symbols show the grid points considered. |
| In the text | |
 |
Fig. 7 χ2 contours for ECho specifications from Table 1. White symbols show the considered grid points. |
| In the text | |
 |
Fig. 8 χ2 contours for ECho resolution, with increased S/N of 28. White symbols show the considered grid points. |
| In the text | |
 |
Fig. 9 χ2 contours for Darwin low-resolution specification (upper) and needed S/N (lower). White symbols show the considered grid points. |
| In the text | |
 |
Fig. 10 χ2 contours for Darwin high-resolution specifications (upper) and needed S/N (lower). White symbols show considered grid points. |
| In the text | |
 |
Fig. 11 Influence of O3 on synthetic observations (upper panel, noisy spectrum in black) and corresponding χ2 values (lower panel, diamonds). EChO resolution and S/N. |
| In the text | |
 |
Fig. 12 Influence of O3 on synthetic observations (upper panel, noisy spectrum in black) and corresponding χ2 values (lower panel, diamonds). R = 100 and S/N of 6. |
| In the text | |
 |
Fig. 13 χ2 values as a function of parameter values: temperature profile, for R = 5, S/N = 12 (Darwin). Horizonal lines indicate 1, 2, 3, and 5σ uncertainties. |
| In the text | |
 |
Fig. 14 χ2 values as a function of parameter values: composition and mass, for R = 5, S/N = 12 (Darwin). Horizonal lines indicate 1, 2, 3, and 5σ uncertainties. |
| In the text | |
 |
Fig. 15 Scatter plots of best-fit parameters from 100 randomly initialized fits. Black: EChO case, R = 10, S/N = 6; red: Darwin medium-resolution case, R = 20, S/N = 10. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


