| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201220587 | |
| Published online | 30 January 2013 | |
Calibrating Milky Way dust extinction using cosmological sources
1
Department of PhysicsStockholm University, AlbaNova University
Center,
10691
Stockholm,
Sweden
e-mail: edvard@fysik.su.se
2
The Oskar Klein Centre for Cosmoparticle Physics, Stockholm
University, 10691
Stockholm,
Sweden
Received:
18
October
2012
Accepted:
13
December
2012
We constrain the light extinction properties of Milky Way dust. We investigated the correlations between dust column density as inferred from infrared data and the observed colours of celestial objects at cosmological distances with low levels of colour dispersion. Results derived using colours of quasars, brightest central galaxies, and luminous red galaxies are broadly consistent, indicating a proportionality constant between the reddening E(B − V) ≡ AB − AV and the dust column density DT (given in units of MJy/sr) of p = E(B − V)/DT ~ 0.02 and a reddening parameter RV ≡ AV/E(B − V) ~ 3 with fractional uncertainties of approximately 10%. The data do not provide any evidence for spatial variations in the dust properties, except for a possible hint of scatter in the dust extinction properties at the longest optical wavelengths.
Key words: dust, extinction / Galaxy: general
© ESO, 2013
1. Introduction
Astronomical data need to be corrected for extinction from dust in the Milky Way. Typical values (albeit with large variations) for the reddening E(B − V) ≡ AB − AV is 0.02 with AV ~ 0.06, see Fig. 1. In this paper, we reinvestigate the relationship between the Milky Way reddening and the dust maps generated in Schlegel et al. (1998) using colours of quasi-stellar objects (QSOs) observed within the Sloan Digital Sky Survey (SDSS). We also compare with results from SDSS observations of brightest central galaxies (BCGs) and luminous red galaxies (LRGs). Compared with the original investigation in Schlegel et al. (1998), the improved statistics and multiple band photometry give us the possibility to decrease the errors on a linear relation while simultaneously constraining the properties of Milky Way dust, in this case the total to selective extinction ratio RV ≡ AV/E(B − V).
We also performed a simple check to investigate if there are deviations from the linear relationship, in other words whether regions with high dust column density have more or less reddening than the linear prediction. No such effect is found, nor do we find any firm evidence of scatter in the dust properties as a function of the line-of-sight.
While noting that there is still room for non-linear behaviour, as well as scatter in dust properties at angular positions and scales not probed by the data, we conclude that at the positions and scales studied in this paper, it is a fair assumption that the reddening is linear to the dust column density DT (in units of MJy/sr) with proportionality constant p = E(B − V)/DT ~ 0.02 and RV ~ 3. The relative errors are of the order of 10% and are mainly limited by uncertainties in the filter response functions and the source spectral templates.
This agrees well with the results of Berry et al. (2011) where SDSS photometry of 73 million stars is used to obtain the dust extinction towards each star giving a three-dimensional dust map of the Milky Way in the direction of the observed stripes. The results from this analysis are consistent with RV = 3.0, with a statistical and systematic error of 0.1 and a scatter of 0.2.
In Peek & Graves (2010), the colours of passively evolving galaxies from the SDSS are used to obtain corrections to the results of Schlegel et al. (1998). They find that the reddening in regions of low dust temperature are underpredicted with maximum deviations in E(B − V) of 45 millimagnitudes.
Schlafly et al. (2010) use the blue edge of SDSS main-sequence stars to recalibrate the reddening induced by the dust maps of Schlegel et al. (1998). They find that the reddening is best described by a Fitzpatrick extinction curve with RV = 3.1, whereas the extinction curve originally employed in Schlegel et al. (1998) generically overestimates the reddening. Similar results were obtained in Schlafly & Finkbeiner (2011) where very similar methods were used, but the reddening was measured by comparing the observed colours of SDSS stars to the colours predicted from their spectral features.
In the following, all limits are given as 95.4% confidence levels (CL) corresponding to
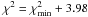 for
one parameter and
for
one parameter and 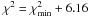 for
two parameters.
for
two parameters.
 |
Fig. 1 Galactic dust extinction represented as E(B − V) and plotted with degree resolution for Galactic latitudes |b| > 20°, together with the corresponding probability distribution function. This dust map peaks at E(B − V) ~ 0.016 mag, with a mean value of 0.048 mag and a median value of 0.028 mag. Data taken from Schlegel et al. (1998). |
2. Method
We used the temperature corrected dust maps from Schlegel et al. (1998) to derive a reddening map by correlating the dust maps to the observed colours of celestial objects, preferably with a low intrinsic colour dispersion. The dust map, given as the dust column density DT in units of MJy/sr, is derived from Infrared Astronomical Satellite (IRAS) data, in principle allowing for a resolution of approximately five arcminutes. However, these data are calibrated and temperature corrected using degree resolution Cosmic Background Explorer (COBE) Diffuse Infrared Background Experiment (DIRBE) data. We note that in Kohyama et al. (2010), IRAS data are used to estimate the dust temperature in order to reach a resolution of five arcminutes also for the temperature corrected data of the Cygnus region. However, no all sky map data have yet been produced using this technique.
As a first attempt, we assumed that the observed colour, e.g.
E(B − V), is proportional to the dust
column density 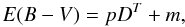 (1)where we set out to
derive the proportionality constant p, and m represents an
arbitrary offset that is marginalised over (possibly caused by calibration errors giving the
wrong mean colour) and the dust column density is given in units of MJy/sr, making
p dimensionless. In Schlegel et al.
(1998), a value of the reddening parameter
RV = 3.1 was assumed, yielding a value of
the proportionality constant p = 0.0184 ± 0.0014 for Mg2-calibrated BCGs.
(1)where we set out to
derive the proportionality constant p, and m represents an
arbitrary offset that is marginalised over (possibly caused by calibration errors giving the
wrong mean colour) and the dust column density is given in units of MJy/sr, making
p dimensionless. In Schlegel et al.
(1998), a value of the reddening parameter
RV = 3.1 was assumed, yielding a value of
the proportionality constant p = 0.0184 ± 0.0014 for Mg2-calibrated BCGs.
Note that this can, in principle, be done for any set of filters X and
Y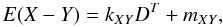 (2)and that multiple
colour data thus can be used to infer dust properties.
(2)and that multiple
colour data thus can be used to infer dust properties.
2.1. Fitting for RV and p
Since SDSS data allow for multiple colour combinations, we are also able to fit for the properties of the Milky Way dust and relax any prior assumptions on the reddening parameter RV. The SDSS [u,g,r,i,z] filters have central wavelengths at [3543,4770,6231,7625,9134] Å and we thus expect g − r and/or u − r to correspond the most closely to B − V.
For each source and filter, we calculate the transmitted flux using a redshifted source template. This is done for a grid of dust models in order to compute how each dust model will affect a given colour. Note that in doing this, we need to calculate the transmitted flux for each dust model separately since k-corrections will depend on the dust model. In practice, we have created tables that list the necessary k-corrections over a grid of redshifts AV and RV for each filter that we interpolate between. After calculating how a given dust model affects each source template in each filter, we can compare with the actual observed colours E(X − Y) allowing us to constrain the parameters p and RV.
 |
Fig. 2 Dust extinction curves for different values of RV shown together with the (arbitrary normalised) SDSS filter transmission curves. Top: extinction curve for the CCM parametrisation. Bottom: extinction curve for the Fitzpatrick parametrisation. |
Normalising such that zero column density corresponds to zero reddening, i.e.
m = 0 in Eq. (1),
defining
f(λ) ≡ A(λ)/AV
and using 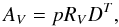 (3)we can write
(3)we can write
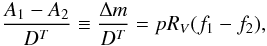 (4)and
(4)and 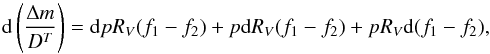 (5)showing how uncertainties
in DT, Δm, and the dust
extinction curve f(λ) translates into uncertainties in
p and RV. In the
following, we will make use of the Milky Way extinction curves
f(λ) as parametrised in Cardelli et al. (1989, CCM) and Fitzpatrick (1999,
FTZ), plotted in Fig. 2 together with the
(arbitrarily normalised) SDSS filter transmission curves. The extinction curve of O’Donnell (1994) gives results very close to those
derived using the CCM paramterisation.
(5)showing how uncertainties
in DT, Δm, and the dust
extinction curve f(λ) translates into uncertainties in
p and RV. In the
following, we will make use of the Milky Way extinction curves
f(λ) as parametrised in Cardelli et al. (1989, CCM) and Fitzpatrick (1999,
FTZ), plotted in Fig. 2 together with the
(arbitrarily normalised) SDSS filter transmission curves. The extinction curve of O’Donnell (1994) gives results very close to those
derived using the CCM paramterisation.
We now turn to the expected degeneracy between
RV and p and how this can
be broken using multiple colour data. In the CCM-model, we have
f = a + b/RV
and
f1 − f2 = (a1 − a2) + (b1 − b2)/RV ≡ Δa + Δb/RV.
Setting
d(Δm/DT) = 0
in Eq. (5) and putting
d(Δa) = d(Δb) = 0, i.e. no systematic error in the
extinction curves, we obtain 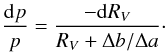 (6)This can be
integrated to give
(6)This can be
integrated to give 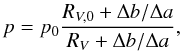 (7)describing the
relation between different values of RV and
p giving the same extinction per unit column density
Δm/DT.
The degeneracy lines for the SDSS standard colours u − g
(dark red), g − r (red),
r − i (orange) and
i − z (yellow) are plotted in Fig. 3, displaying the power of multiple colour data to break
the degeneracy between p and
RV. We see that p is
anti-correlated with RV, if the difference
(AX − AY)/AV
is decreasing more slowly than
1/RV with
RV, which is the case for the three reddest
SDSS standard colours. The slopes of these curves compare well with the confidence
contours derived from data in the forthcoming sections.
(7)describing the
relation between different values of RV and
p giving the same extinction per unit column density
Δm/DT.
The degeneracy lines for the SDSS standard colours u − g
(dark red), g − r (red),
r − i (orange) and
i − z (yellow) are plotted in Fig. 3, displaying the power of multiple colour data to break
the degeneracy between p and
RV. We see that p is
anti-correlated with RV, if the difference
(AX − AY)/AV
is decreasing more slowly than
1/RV with
RV, which is the case for the three reddest
SDSS standard colours. The slopes of these curves compare well with the confidence
contours derived from data in the forthcoming sections.
 |
Fig. 3 Degeneracy between parameters p and RV for SDSS colours u − g (dark red), g − r (red), r − i (orange) and i − z (yellow). The degeneracy lines correspond to a reddening equivalent to p = 0.02 and RV = 3.0. It is evident that multiple colours allow the degeneracy to be broken. |
3. Error analysis
We first note that constant filter calibration errors do not affect our results, since we are marginalising over any constant offset between the observed and theoretically calculated colours. However, we may get systematic effects if the spectral template is wrong and/or if the shape of the filter response function is incorrectly modeled since this will change the effective wavelength of the filters. We assume that this will induce fractional uncertainties in the effective wavelengths of [0.02, 0.01, 0.01, 0.01, 0.01] in [u,g,r,i,z] filters (Doi et al. 2010). We note that this error will be a true systematic error since the effect will be correlated between all source redshifts and colours. For comparison, for our QSO template, effective wavelengths will vary by ~2 − 3% when varying the source redshift and dust parameters. Schlegel et al. (1998) calculate their reddening estimates to have a dispersion of ~16%. Attributing a major part of this dispersion to a scatter in the dust column density, we assume a fractional uncertainty of 10% in the dust map values DT. Since this uncertainty is treated as a statistical error, and we are systematics dominated, the exact value of this fractional error does not affect the end result. A possible problem not taken into account in this paper is that the dust map may be contaminated by the extragalactic background at low values (Yahata et al. 2007).
We incorporate uncertainties using a Monte Carlo-based approach as follows:
-
We pick a random value for the shift in the effective wavelengthfor each filter and compute the corresponding colour offset. Wealso randomise the value for DT at each sky position within the given uncertainties.
-
We derive the likelihood over a grid of fitted parameters. In doing this, we use the statistical sources of error from observational uncertainties and the intrinsic colour dispersion of the sources.
-
We repeat N times (we use N ~ 50) to obtain N likelihood functions.
-
We compute the mean of the N likelihood functions.
In this way we take full account of the different correlations between sources of error, and the resulting confidence contours correctly incorporate both statistical and systematic effects. As noted in Sect. 1, the dominating source of error is the possibility of shifts in the effective filter wavelengths, originating in uncertainties in the filter response functions and the source spectral templates.
4. Quasar analysis
It is well known that QSOs form a relatively homogeneous group of objects in terms of colours and spectral features. They also have large flux at short wavelengths which means that we can use blue colours, e.g. u − r, even for high redshift sources, which allows us to effectively break the degeneracy between p and RV as shown in Fig. 3. We use the fifth edition of the SDSS Quasar Catalog (Schneider et al. 2007) consisting of 77 429 objects. The area covered by the catalogue is 5740 deg2, see Fig. 4. QSOs have also been used successfully to constrain the amount and properties of dust in galaxies at cosmological distances (Östman et al. 2006, 2008) and for intergalactic dust (Östman & Mörtsell 2005).
 |
Fig. 4 Top: angular positions of the SDSS QSOs used in this analysis with darker colours corresponding to higher observed surface densities of QSOs, reflecting the given survey strategy. Bottom: restframe QSO template spectrum shown with arbitrary normalised SDSS filter transmission curves. |
We are primarily interested in the colours of QSOs, so it is important to understand how the objects in the SDSS QSO catalogue are chosen in order to assess whether there are selection effects that need to be considered. The QSO candidate selection is based on the position of sources in multidimensional SDSS colour space. In terms of colours, QSOs are mainly identified as being outside the four-dimensional stellar loci points in [u,g,r,i,z] space (Richards et al. 2002). Since the method is purely differential, any general colour bias will not affect the end result; however, we need to make sure that the selection does not depend on the dust column. Since the selection is made after correcting for the extinction maps in Schlegel et al. (1998), assuming that these provide a fair model for the extinction, there is no reason that the selection should be severely affected by Milky Way dust extinction. By applying an extra colour cut of included objects where the (uncorrected) colour is less than 2σ off the mean value, as evaluated in bins of different dust column density, we are guaranteed a sample not correlated with the dust column, unless initial dust corrections are grossly incorrect.
Only QSOs in the redshift range 0.5 < z < 3.0 are considered as QSOs outside this range are less accurately described by the spectral template used, created by combining the Hubble Space Telescope radio-quiet composite spectrum (Telfer et al. 2002) with the SDSS median composite spectrum (Vanden Berk et al. 2001) as described in Östman et al. (2006, 2008). Generally, all colours are relatively homogeneous at z ≲ 2. Typically, at z ~ 1, we have σ(u − g) = 0.15, σ(g − r) = 0.13, σ(r − i) = 0.093, and σ(i − z) = 0.11. However, when the Lyman-α emission is being redshifted into the observed filters, the dispersion increases. We thus cut the u-band data at z > 3000/1210 − 1 ~ 1.5 and the g-band data at z > 4000/1210 − 1 ~ 2.3.
In order to display the close to linear relationship between the observed QSO colour and the dust density, in Fig. 5 we show the observed QSO g − r colour as a function of Galactic dust column density at redshifts z ~ 0.95, z ~ 1.72 and z ~ 2.48.
 |
Fig. 5 Observed g − r colour as a function of Galactic dust column density for SDSS QSOs at three different redshifts. Note the almost perfect linear relationship between the observed colour and the dust density. |
Results for the full fit of p and RV are shown in Fig. 6 for the CCM dust extinction parametrisation (top panel) and the Fitzpatrick parametrisation (bottom panel). Solid colours correspond to 95.4% CL for two parameters. Our constraints are p = 0.0205 ± 0.0015 and RV = 3.10 ± 0.43 (CCM) and p = 0.0190 ± 0.0015 and RV = 3.25 ± 0.37 (FTZ) (95.4% CL for one parameter). Although consistent at the 95.4% CL, compared to the r − i and i − z colours, we have on average less extinction in u − g and more extinction in g − r for the CCM parametrisation. For Fitzpatrick dust, compared to g − r and r − i, u − g has less extinction and i − z more extinction on average.
Albeit with very limited resolution, multiple colour data allow us to derive the dust extinction curve directly from the data, without the need to assume any specific dust extinction parametrisation. For each colour, we fit the slope kXY in Eq. (2), apply the necessary k-corrections, and normalise the extinction to zero in the V-band. In Fig. 7 we show the dust law as derived from QSO colours compared to the extinction curves for some fiducial dust models. Assuming the errors to be accurately represented by the uncertainty of the slope in the linear fit, the error bars are too small to be visible. However, this assumption is valid only in the case that the relation between the reddening and the dust column density indeed is linear and constant over the field. Furthermore, the dominating source of error of possible systematic shifts in the effective central filter wavelengths have not been included. Note that since the normalisation is arbitrary, only the shape of the derived extinction curve is relevant.
5. Brightest central galaxies analysis
The brightest galaxies at the centre of galaxy clusters are empirically known to be relatively homogeneous in colour. Since high-luminosity early-type galaxies are generally redder than low-luminosity galaxies (usually attributable to higher metallicity), the colour dispersion can be further reduced using colour-magnitude relations. In this paper, however, we defer from employing any such calibration.
We have used data from the MaxBCG catalogue of 13 823 galaxy clusters from the SDSS (Koester et al. 2007). In order to extract the full photometric data for the BCGs, we retrieved all objects within 6 arcsec from the BCG positions. We managed to identify and retrieve [u,g,r,i,z] data for 13 796 BCGs with redshifts 0.046 < z < 0.37. The angular positions of the BCGs are depicted in Fig. 8. Generally, all colours involving the u-band are not very well-determined. Typically (at z ~ 0.2), we have σ(u − g) = 0.32, σ(g − r) = 0.059, σ(r − i) = 0.029, and σ(i − z) = 0.042.
 |
Fig. 6 Constraints on p and RV as derived from the observed colours of SDSS QSOs and the measured dust column density at the angular position of each QSO. Solid colours correspond to 95.4% CL for two parameters. Top: results for CCM dust corresponding to 95.4% CL for one parameter of p = 0.0205 ± 0.0015 and RV = 3.10 ± 0.43. Bottom: results for Fitzpatrick dust corresponding to 95.4% CL for one parameter of p = 0.0190 ± 0.0015 and RV = 3.25 ± 0.37. |
 |
Fig. 7 Empirical dust law as derived from QSO colours (diamonds) compared to the extinction curves of CCM dust with p = 0.01,RV = 5.0 (dotted curve), p = 0.02,RV = 3.0 (dashed curve), and p = 0.03,RV = 1.0 (dash-dotted curve). |
 |
Fig. 8 Top: angular positions of the SDSS BCGs used in this analysis with darker colours corresponding to higher observed surface densities of BCGs. Bottom: rest-frame BCG template spectrum shown together with arbitrarily normalised SDSS filter transmission curves. Note that the same template is used for the LRG analysis. |
 |
Fig. 9 Constraints on p and RV as derived from the observed colours of SDSS BCGs and the measured dust column density at the angular position of each BCG. Solid colours correspond to 95.4% CL for two parameters. Top: results for CCM dust corresponding to 95.4% CL for one parameter of p = 0.0205 ± 0.0030 and RV = 2.89 ± 0.88. Bottom: results for Fitzpatrick dust corresponding to 95.4% CL for one parameter of p = 0.0177 ± 0.0020 and RV = 3.42 ± 0.48. |
 |
Fig. 10 Empirical dust law as derived from BCG colours (diamonds) compared to the extinction curves of CCM dust with p = 0.01,RV = 5.0 (dotted curve), p = 0.02,RV = 3.0 (dashed curve), and p = 0.03,RV = 1.0 (dash-dotted curve). |
 |
Fig. 11 Constraints on p and RV as derived from the observed colours of SDSS LRGs and the measured dust column density at the angular position of each LRG. Solid colours correspond to 95.4% CL for two parameters. Top: results for CCM dust corresponding to 95.4% CL for one parameter of p = 0.026 ± 0.004 and RV = 1.95 ± 0.35. Bottom: results for Fitzpatrick dust corresponding to 95.4% CL for one parameter of p = 0.019 ± 0.0025 and RV = 3.16 ± 0.36. |
 |
Fig. 12 Empirical dust law as derived from LRG colours (diamonds) compared to the extinction curves of CCM dust with p = 0.01,RV = 5.0 (dotted curve), p = 0.02,RV = 3.0 (dashed curve), and p = 0.03,RV = 1.0 (dash-dotted curve). |
 |
Fig. 13 Differences between the CCM and FTZ dust extinction curves. |
We cut all colours involving the the u-band at z > 0.15 since the colour dispersion becomes very large at those redshifts. For consistency with the QSO and LRG analysis, we reject objects with uncorrected colours more than 2σ off the mean value, as evaluated in bins of different dust column density. Results for fitting p and RV to the BCG data are shown in Fig. 9. Our constraints are p = 0.0205 ± 0.0030 and RV = 2.89 ± 0.88 (CCM), and p = 0.0177 ± 0.0020 and RV = 3.42 ± 0.48 (FTZ) (95.4% CL for one parameter). Like the QSO constraints, compared to r − i and i − z that give p = 0.02 for RV = 3, we have less extinction in u − g and more extinction in g − r for the CCM parametrisation. For Fitzpatrick dust, g − r and r − i give p = 0.02 at RV = 3 while u − g has less extinction and i − z more extinction. In Fig. 10 we show the empirically derived dust law.
6. Luminous red galaxies
Since LRGs are also known to be homogeneous in terms of colours, we have extracted data for 114 151 LRGs from the SDSS data base. Generally, all colours involving the u-band are not well-determined. Typically, at z ~ 0.3 we have σ(u − g) = 0.84, σ(g − r) = 0.086, σ(r − i) = 0.043, and σ(i − z) = 0.056. We therefore do not use any colours involving the u-band in this analysis. As discussed in Sect. 4, we reject objects with uncorrected colours more than 2σ off the mean value, as evaluated at different dust column values, in order for the final sample to be unbiased by dust extinction. Fitting for p and RV gives the results shown in Fig. 11. Our constraints are p = 0.026 ± 0.004 and RV = 1.95 ± 0.35 (CCM), and p = 0.019 ± 0.0025 and RV = 3.16 ± 0.36 (FTZ) (95.4% CL for one parameter). Compared to the QSO and BCG analysis, the absence of the u-band pushes best-fit values towards higher p and lower RV. Assuming RV = 3, compared to r − i and i − z that give p = 0.02, we have more extinction in g − r for the CCM parametrisation. For Fitzpatrick dust, r − i gives p = 0.02 while g − r and i − z have more extinction. In Fig. 12 we show the derived dust law.
7. Discussion
As seen in the previous sections, there are slight differences in the preferred values of
p and RV, depending on the
dust parametrisation and the data set used. Generally, for the CCM parametrisation with
RV = 3, for
r − i and i − z we get
p = 0.02. We have more extinction (higher p) in
g − r and less in
u − g. For Fitzpatrick dust,
r − i gives p = 0.02 while
g − r and i − z have
more extinction and u − g less. How can we understand
these differences? First, we need to understand the differences between the CCM and FTZ dust
extinction parametrisations. In Fig. 13, we plot
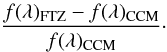 (8)The reason that the we need
higher p for i − z for the FTZ model is
that the extinction curve is flatter there compared to the CCM model. We also see that it is
steeper for g − r which means that we get a lower
p for that colour. That is, we need a dust law that is slightly steeper
for g − r and flatter for
u − g compared to CCM. As for the differences between
the data sets, comparing BCGs and LRGs, we see that the differences can be explained by
having a flatter template spectrum for LRGs in the region covering
g − r, compared to the BCG template. Comparing BCGs and
QSOs, the differences can be resolved by having either the BCG template flatter for
u − g and g − r or the
QSO template steeper in the same wavelength region.
(8)The reason that the we need
higher p for i − z for the FTZ model is
that the extinction curve is flatter there compared to the CCM model. We also see that it is
steeper for g − r which means that we get a lower
p for that colour. That is, we need a dust law that is slightly steeper
for g − r and flatter for
u − g compared to CCM. As for the differences between
the data sets, comparing BCGs and LRGs, we see that the differences can be explained by
having a flatter template spectrum for LRGs in the region covering
g − r, compared to the BCG template. Comparing BCGs and
QSOs, the differences can be resolved by having either the BCG template flatter for
u − g and g − r or the
QSO template steeper in the same wavelength region.
8. RV-variations
It is not unreasonable to assume that the distributions of grain sizes, and thus the resulting value of RV, is different in high- and low-density environments. Whether grains are generally larger or smaller in high-density environments depends on whether grain-grain collisions are more likely to cause coalescence or shattering. We therefore check for any evidence of correlations between RV and the dust column density by dividing our sample into subsamples with different column densities. Note, however, that a high column density does not necessarily correspond to a high physical density. In Fig. 14 we show constraints from dividing the QSO sample into two regions with low (DT < 3 MJy sr-1) and high (DT > 3 MJy sr-1) dust column density. Our constraints for CCM are p = 0.020 ± 0.0016 and RV = 3.06 ± 0.56 (DT < 3 MJy sr-1), and p = 0.019 ± 0.0019 and RV = 3.09 ± 0.65 (DT > 3 MJy sr-1). For Fitzpatrick dust, p = 0.019 ± 0.0016 and RV = 3.28 ± 0.37 (DT < 3 MJy sr-1), and p = 0.018 ± 0.0018 and RV = 3.23 ± 0.41 (DT > 3 MJy sr-1) (95.4% CL for one parameter). This simple test does not provide evidence for any correlation between the dust column density and dust properties.
8.1. σ(RV) and σ(AV)
If dust has spatially varying properties, depending on the size of the regions we would
expect the colour dispersion to be higher behind regions with high column density
DT. For filters X and
Y we can write the colour
E(X − Y) as a combination of the
intrinsic colour Ei(X − Y)
and the dust induced colour
Ed(X − Y)
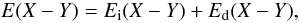 (9)and the corresponding
colour dispersion
(9)and the corresponding
colour dispersion ![\begin{equation} \sigma[E(X-Y)]^2= \sigma[E_{\rm i}(X-Y)]^2+ \sigma[E_{\rm d}(X-Y)]^2 , \end{equation}](/articles/aa/full_html/2013/02/aa20587-12/aa20587-12-eq124.png) (10)where
(10)where
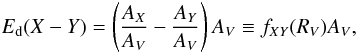 (11)and
(11)and
![\begin{eqnarray} \sigma[E_{\rm d}(X\!-\!Y)]^2 \! &=&\! \left[\left(\frac{R_V}{f_{XY}}\frac{\partial f_{XY}}{\partial R_V}\right )^2\left(\frac{\sigma_{R_V}}{R_V}\right)^2\!+\! \left(\frac{\sigma_{A_V}}{A_V}\right)^2\right]E_{\rm d}(X\!-\!Y)^2\\ \nonumber &\equiv& g[X,Y,R_V,\sigma(R_V),\sigma(A_V)])E_{\rm d}(X-Y)^2 . \end{eqnarray}](/articles/aa/full_html/2013/02/aa20587-12/aa20587-12-eq126.png) (12)In
Fig. 15, we plot the variance
σ [E(X − Y)] 2
as a function of
Ed(X − Y)2 for
each standard colour of the QSO sample, expecting the variance at zero
Ed(X − Y)2 to
give the intrinsic colour variance
σ [Ei(X − Y)] 2
and the slope to be related to the scatter in
RV and
AV through the function
g [X,Y,RV,σ(RV),σ(AV)]
(using the CCM dust extinction parametrisation). As can be seen, there are no obvious
correlations between
σ [E(X − Y)] 2
and Ed(X − Y)2
(or
σ [E(X − Y)] 2
and the dust column density DT). Assuming
σRV/RV
and
σAV/AV
to be constant, although the results depicted in Fig. 15 indicate that this assumption may be too simplistic, we can constrain their
values from the fitted straight line slopes. Results from this analysis are shown in
Fig. 16. The bluer colours show no increase in the
colour variance with dust column density, whereas i − z
show a slight increase in the variance indicating a possible dispersion of
σAV/AV
at the 30% level. This said, there are a few points that should be remembered:
(12)In
Fig. 15, we plot the variance
σ [E(X − Y)] 2
as a function of
Ed(X − Y)2 for
each standard colour of the QSO sample, expecting the variance at zero
Ed(X − Y)2 to
give the intrinsic colour variance
σ [Ei(X − Y)] 2
and the slope to be related to the scatter in
RV and
AV through the function
g [X,Y,RV,σ(RV),σ(AV)]
(using the CCM dust extinction parametrisation). As can be seen, there are no obvious
correlations between
σ [E(X − Y)] 2
and Ed(X − Y)2
(or
σ [E(X − Y)] 2
and the dust column density DT). Assuming
σRV/RV
and
σAV/AV
to be constant, although the results depicted in Fig. 15 indicate that this assumption may be too simplistic, we can constrain their
values from the fitted straight line slopes. Results from this analysis are shown in
Fig. 16. The bluer colours show no increase in the
colour variance with dust column density, whereas i − z
show a slight increase in the variance indicating a possible dispersion of
σAV/AV
at the 30% level. This said, there are a few points that should be remembered:
 |
Fig. 14 Constraints on p and RV when dividing data into regions with low (DT < 3 MJy sr-1) and high (DT > 3 MJy sr-1) dust column density. There is no evidence for any correlation between the dust column density and dust properties. Upper left: results for CCM dust for all regions with DT < 3 MJy sr-1 corresponding to 95.4% CL for one parameter of p = 0.020 ± 0.0016 and RV = 3.06 ± 0.56. Upper right: results for CCM dust at DT > 3 MJy sr-1 giving p = 0.019 ± 0.0019 and RV = 3.09 ± 0.65. Lower left: results for Fitzpatrick dust at DT < 3 MJy sr-1 giving p = 0.019 ± 0.0016 and RV = 3.28 ± 0.37. Lower right: results for Fitzpatrick dust at DT > 3 MJy sr-1 giving p = 0.018 ± 0.0018 and RV = 3.23 ± 0.41. |
 |
Fig. 15 Variance σ [E(X − Y)] 2 as a function of Ed(X − Y)2 for each standard colour of the QSO sample. The total variance at zero Ed(X − Y)2 is the intrinsic colour variance σ [Ei(X − Y)] 2 and the slope is related to the scatter in RV and AV. |
 |
Fig. 16 Constraints on constant σRV/RV and σAV/AV derived from the linear fits depicted in Fig. 15. The coloured regions correspond to 95.4% CL (red) and 68.3% CL (yellow) for two parameters. |
First, this is under the assumption that the relation between the variance and the colour is indeed linear, and that the data points are not correlated. Second, results for i − z are not consistent with the bluer colours that show no signs of a scatter in the dust properties, although it is possible that the scatter only manifests itself at longer wavelengths. Third, there is a weak binning dependence when calculating the dispersion as a function of Ed(X − Y)2. To summarize, there is no evidence in the QSO data for any additional scatter in the observed colours in regions with high column density, which indicates that dust properties are relatively homogeneous averaged over the size of spatial regions probed in this paper, except perhaps for a hint of slightly increased scatter at the reddest optical wavelengths probed by the QSO data.
9. Summary
By investigating the correlations between dust column density as inferred from infrared data and the observed colours of celestial objects at cosmological distances with low levels of colour dispersion, we constrain the properties of Milky Way dust. We expect analyses of the reddening of extragalactic sources to complement analyses of Galactic sources very well since they will have different systematic uncertainties, and in principle may also probe dust at different distances. Results from QSOs, BCGs, and LRGs colours are broadly consistent, indicating a proportionality constant between the reddening E(B − V) ≡ AB − AV and the dust column density DT (given in units of MJy/sr) of p = E(B − V)/DT ~ 0.02 and a reddening parameter RV ≡ AV/E(B − V) ~ 3 with relative uncertainties of approximately 10%. In spite of the increased statistics, the fractional error of p is similar to that of Schlegel et al. (1998), the reason being that we simultaneously fit for RV and that the uncertainty is dominated by the possibility of systematic shifts in the effective filter wavelengths.
We note that, in accordance with the analyses in Schlafly et al. (2010) and Schlafly & Finkbeiner (2011), the FTZ extinction curve may be argued to be preferred before the CCM parametrisation, since it is able to fit QSO, BCG, and LRG data with similar normalisations and reddening parameters. However, as argued in Sect. 7, such differences may also be traced to uncertainties in the spectral template functions.
The data does not provide evidence for any dependence of the dust properties as a function of dust column density, nor for any sizable scatter in the dust properties on the scales probed by the data, except for a hint of scatter σAV/AV ≳ 0.3 in the extinction properties of dust at the longest wavelengths probed by the data (corresponding to i − z). We have also checked that within the uncertainties there is no evidence of any systematic difference between the dust extinction properties in the northern and southern hemisphere. Assuming the dust maps of Schlegel et al. (1998) to be correct, it is fair to assume that we can correct for Milky Way dust by applying a proportionality constant p = E(B − V)/DT ~ 0.02 with reddening parameter RV ~ 3 to the dust maps.
Acknowledgments
E.M. acknowledges support for this study by the Swedish Research Council. E.M. also acknowledges discussions with Brice Menard and Ariel Goobar. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, Cambridge University, Case Western Reserve University, University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max Planck Institute for Astronomy (MPIA), the Max Planck Institute for Astrophysics (MPA), New Mexico State University, The Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Berry, M., Ivezić, Ž., Sesar, B., et al. 2011, ApJ, submitted [arXiv:1111.4985] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Doi, M., Tanaka, M., Fukugita, M., et al. 2010, AJ, 139, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Koester, B. P., McKay, T. A., Annis, J., et al. 2007, ApJ, 660, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Kohyama, T., Shibai, H., Fukagawa, M., & Hibi, Y. 2010, ApJ, 719, 873 [NASA ADS] [CrossRef] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Östman, L., & Mörtsell, E. 2005, J. Cosmology Astropart. Phys., 2, 5 [Google Scholar]
- Östman, L., Goobar, A., & Mörtsell, E. 2006, A&A, 450, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Östman, L., Goobar, A., & Mörtsell, E. 2008, A&A, 485, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peek, J. E. G., & Graves, G. J. 2010, ApJ, 719, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Fan, X., Newberg, H. J., et al. 2002, AJ, 123, 2945 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., Finkbeiner, D. P., Schlegel, D. J., et al. 2010, ApJ, 725, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Hall, P. B., Richards, G. T., et al. 2007, AJ, 134, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Telfer, R. C., Zheng, W., Kriss, G. A., & Davidsen, A. F. 2002, ApJ, 565, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Van den Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Yahata, K., Yonehara, A., Suto, Y., et al. 2007, PASJ, 59, 205 [NASA ADS] [Google Scholar]
All Figures
 |
Fig. 1 Galactic dust extinction represented as E(B − V) and plotted with degree resolution for Galactic latitudes |b| > 20°, together with the corresponding probability distribution function. This dust map peaks at E(B − V) ~ 0.016 mag, with a mean value of 0.048 mag and a median value of 0.028 mag. Data taken from Schlegel et al. (1998). |
| In the text | |
 |
Fig. 2 Dust extinction curves for different values of RV shown together with the (arbitrary normalised) SDSS filter transmission curves. Top: extinction curve for the CCM parametrisation. Bottom: extinction curve for the Fitzpatrick parametrisation. |
| In the text | |
 |
Fig. 3 Degeneracy between parameters p and RV for SDSS colours u − g (dark red), g − r (red), r − i (orange) and i − z (yellow). The degeneracy lines correspond to a reddening equivalent to p = 0.02 and RV = 3.0. It is evident that multiple colours allow the degeneracy to be broken. |
| In the text | |
 |
Fig. 4 Top: angular positions of the SDSS QSOs used in this analysis with darker colours corresponding to higher observed surface densities of QSOs, reflecting the given survey strategy. Bottom: restframe QSO template spectrum shown with arbitrary normalised SDSS filter transmission curves. |
| In the text | |
 |
Fig. 5 Observed g − r colour as a function of Galactic dust column density for SDSS QSOs at three different redshifts. Note the almost perfect linear relationship between the observed colour and the dust density. |
| In the text | |
 |
Fig. 6 Constraints on p and RV as derived from the observed colours of SDSS QSOs and the measured dust column density at the angular position of each QSO. Solid colours correspond to 95.4% CL for two parameters. Top: results for CCM dust corresponding to 95.4% CL for one parameter of p = 0.0205 ± 0.0015 and RV = 3.10 ± 0.43. Bottom: results for Fitzpatrick dust corresponding to 95.4% CL for one parameter of p = 0.0190 ± 0.0015 and RV = 3.25 ± 0.37. |
| In the text | |
 |
Fig. 7 Empirical dust law as derived from QSO colours (diamonds) compared to the extinction curves of CCM dust with p = 0.01,RV = 5.0 (dotted curve), p = 0.02,RV = 3.0 (dashed curve), and p = 0.03,RV = 1.0 (dash-dotted curve). |
| In the text | |
 |
Fig. 8 Top: angular positions of the SDSS BCGs used in this analysis with darker colours corresponding to higher observed surface densities of BCGs. Bottom: rest-frame BCG template spectrum shown together with arbitrarily normalised SDSS filter transmission curves. Note that the same template is used for the LRG analysis. |
| In the text | |
 |
Fig. 9 Constraints on p and RV as derived from the observed colours of SDSS BCGs and the measured dust column density at the angular position of each BCG. Solid colours correspond to 95.4% CL for two parameters. Top: results for CCM dust corresponding to 95.4% CL for one parameter of p = 0.0205 ± 0.0030 and RV = 2.89 ± 0.88. Bottom: results for Fitzpatrick dust corresponding to 95.4% CL for one parameter of p = 0.0177 ± 0.0020 and RV = 3.42 ± 0.48. |
| In the text | |
 |
Fig. 10 Empirical dust law as derived from BCG colours (diamonds) compared to the extinction curves of CCM dust with p = 0.01,RV = 5.0 (dotted curve), p = 0.02,RV = 3.0 (dashed curve), and p = 0.03,RV = 1.0 (dash-dotted curve). |
| In the text | |
 |
Fig. 11 Constraints on p and RV as derived from the observed colours of SDSS LRGs and the measured dust column density at the angular position of each LRG. Solid colours correspond to 95.4% CL for two parameters. Top: results for CCM dust corresponding to 95.4% CL for one parameter of p = 0.026 ± 0.004 and RV = 1.95 ± 0.35. Bottom: results for Fitzpatrick dust corresponding to 95.4% CL for one parameter of p = 0.019 ± 0.0025 and RV = 3.16 ± 0.36. |
| In the text | |
 |
Fig. 12 Empirical dust law as derived from LRG colours (diamonds) compared to the extinction curves of CCM dust with p = 0.01,RV = 5.0 (dotted curve), p = 0.02,RV = 3.0 (dashed curve), and p = 0.03,RV = 1.0 (dash-dotted curve). |
| In the text | |
 |
Fig. 13 Differences between the CCM and FTZ dust extinction curves. |
| In the text | |
 |
Fig. 14 Constraints on p and RV when dividing data into regions with low (DT < 3 MJy sr-1) and high (DT > 3 MJy sr-1) dust column density. There is no evidence for any correlation between the dust column density and dust properties. Upper left: results for CCM dust for all regions with DT < 3 MJy sr-1 corresponding to 95.4% CL for one parameter of p = 0.020 ± 0.0016 and RV = 3.06 ± 0.56. Upper right: results for CCM dust at DT > 3 MJy sr-1 giving p = 0.019 ± 0.0019 and RV = 3.09 ± 0.65. Lower left: results for Fitzpatrick dust at DT < 3 MJy sr-1 giving p = 0.019 ± 0.0016 and RV = 3.28 ± 0.37. Lower right: results for Fitzpatrick dust at DT > 3 MJy sr-1 giving p = 0.018 ± 0.0018 and RV = 3.23 ± 0.41. |
| In the text | |
 |
Fig. 15 Variance σ [E(X − Y)] 2 as a function of Ed(X − Y)2 for each standard colour of the QSO sample. The total variance at zero Ed(X − Y)2 is the intrinsic colour variance σ [Ei(X − Y)] 2 and the slope is related to the scatter in RV and AV. |
| In the text | |
 |
Fig. 16 Constraints on constant σRV/RV and σAV/AV derived from the linear fits depicted in Fig. 15. The coloured regions correspond to 95.4% CL (red) and 68.3% CL (yellow) for two parameters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


