| Issue |
A&A
Volume 550, February 2013
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201219973 | |
| Published online | 21 January 2013 | |
Determination of atmospheric velocity of bright meteors on the basis of high-resolution light curves
Astronomical Institute, Academy of Sciences, Ondřejov, Czech Republic
e-mail: shrbeny@asu.cas.cz
Received: 9 July 2012
Accepted: 28 November 2012
We introduce a new method for the determination of the atmospheric velocity of bright meteors (fireballs). The method uses high-time-resolution light curves of fireballs and photographic or digital records of the fireballs where dynamics data are not available, i.e. a rotating shutter was not used. Simultaneous identification of flares or other unambiguous events is needed on both the light curve and the photographic or digital record. These events, flares for instance, serve as time-marks and substitute the artificial rotating shutter time-marks. We studied the method on nine selected fireballs that fulfill the above conditions, occupy a wide interval of possible initial velocities (from 14.5 to 50 km s-1), and are of a different orbital origin (cometary and asteroidal). The method provides correct velocities with scatter of a few km s-1 around the average value that corresponds to the rotating shutter velocity.
Key words: meteorites, meteors, meteoroids / techniques: photometric
© ESO, 2013
1. Introduction
A meteor event is caused by the penetration of the atmosphere by an interplanetary body. If the meteor brightness is higher than the brightness of the planet Venus, the meteor is called a fireball. The flight of the fireball through the Earth’s atmosphere generally lasts a few seconds and using multi-station observation it is then possible to determine its precise position in the atmosphere, trajectory and velocity, intensity and changes of light production (light curve), and heliocentric orbit before its encounter with the Earth. If the precise velocity of the meteor and its changes (deceleration) are known, various methods can be applied to determine the physical properties of the meteoroid such as ablation abilities, tensile strength, weight, and bulk density. Meteor observation provides the properties of the meteoroid without analysing it in a laboratory.
The method of determination of meteor velocity depends on the method of observation: photographic, television and video, radar, acoustic, infrasonic, seismic, visual, or a combination of them. The most precise and accurate velocity is determined from photographic observation where a rotating shutter produces occultations of the meteor image which serve as time-marks in accurate time intervals. Various interpolation formulae, analytic or numeric models, or simply differences among distances along a meteor trajectory are used to determine the temporal dependence of velocity (Pecina & Ceplecha 1983; Ceplecha et al. 1998). A frequently used interpolation formula 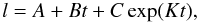 (1)where l is length, t time, and A, B, C, K are constants to be determined (Jacchia & Whipple 1961), is not suitable for very long fireballs with significant deceleration.
(1)where l is length, t time, and A, B, C, K are constants to be determined (Jacchia & Whipple 1961), is not suitable for very long fireballs with significant deceleration.
The same procedure can also be implemented for fainter television and video meteors. Radar observations use the ionized trails of meteors, first recognized by Skellett (1931) and Schafer & Goodall (1932). The velocity of a meteor from radar observation was first determined by Hey et al. (1947) on the basis of head-echoes. A detailed analysis of the production and propagation of sonic waves during the atmospheric flight of a fireball, which includes cylindrical blast waves (hypersonic flight) and quasi-spherical shock waves (fragmentations), may enable the determination of its trajectory and velocity. The acoustic energy can be detected by infrasonic microphones and seismographs (Brown et al. 2003; Pujol et al. 2006). The least accurate velocity comes from visual observation. If the length of the atmospheric trajectory and its duration are known, average velocity can be determined.
2. Description of the method
As briefly mentioned above, several methods are used to determine meteor velocities, so it might appear senseless to invent a new method. However, our motivation to do so is a recent increase in amateur digital observations (casual photography or scheduled night-time photographic observation using digital single-lens reflex (DSLR) cameras or digital compacts) and scientific digital observations (weather observation, observation of noctilucent clouds, or astronomy and meteor cameras like SBIG or SPOSH) where rotating shutters are not used. Such data provide only trajectories of meteors without dynamics. Other reasons for the absence of the velocity data can be attributed to a fault in rotating shutter, unfavourable angular velocity of the meteor, bad weather conditions, or short duration of the meteor.
The new method is based on light curves with high-time-resolution. The Czech part of the European fireball network (EN) is equipped with a new generation of photographic cameras: Autonomous Fireball Observatories (AFO; Spurný et al. 2007). We also operate long-focus cameras equipped with 360 mm Tessar lenses at the Ondřejov Observatory. The AFO imaging system consists of a Zeiss Distagon fish-eye lens (f/3.5, f = 30 mm) and large-format sheet film. Each AFO is equipped with a rotating shutter close to the focal plane to determine fireball velocity and also includes an all-sky brightness sensor (radiometer) with a sampling rate of 500 or 5000 measurements per second; therefore, along with an accurate time of the fireball passage and its duration, we also obtain a very detailed light curve.
If a detailed light curve is available and identification of flares or other unambiguous events on the luminous trajectory is possible (example in Fig. 1), the lengths of the fireball trajectories can be determined simultaneously with corresponding times (length is determined as a function of time). Various procedures can then be implemented for velocity determination. These velocities are then called light curve (LC) velocities. We compared LC velocities determined from different sources of records (DSLR cameras, all-sky, and long-focus photographic cameras) with precise velocities from all-sky photographic records based on rotating shutters (RS velocities) and we present the results in the following sections. An example of a light curve and identification of LC points and corresponding positions on the image is presented in Fig. 2 on the case of EN080111.
3. Verification of the method
 |
Fig. 1 High-time-resolution light curve of the EN040710 fireball with measured flares (gray arrows). |
 |
Fig. 2 Light curve of the fireball EN080111 as recorded by the radiometer at EN Station 11 Přimda. Details of the fireball’s luminous trajectories are shown below the light curve with all the points used for LC velocity determination. The upper image of the fireball was captured by digital DSLR camera at Fornach, Austria, the bottom one by 360 mm long-focus photographic camera at Ondrejov Observatory, Czech Republic, where the fireball end was hidden by clouds. |
Light curve (LC) and rotating shutter (RS) initial velocities.
Several fireballs with known dynamics were used to test and confirm the validity of the method. We chose both the most precisely determined fireballs and the less well-determined ones (cases with short atmospheric trajectory or high initial velocity). The most important criterion, however, was the presence of flares or other unambiguous events on luminous trajectory, i.e. at least two time-marks on the fireball trail. We measured and calculated nine fireballs (Table 1) that fulfill the above conditions, fit in a wide interval of possible initial velocities (from 14.5 to 50 km s-1), and are of a different orbital origin (cometary and asteroidal). The atmospheric trajectories and heliocentric data are presented in Tables 2 and 3. Note that all the atmospheric values in Table 2 (except for EN080111) are based on photographic records, even if, in a few cases, the atmospheric trajectories recorded by the more sensitive digital cameras are longer than those recorded by film photography. Digital records shift beginning heights a few km upwards and terminal heights downwards.
The comparison of LC and RS velocities, both measured directly from differences in time and length, is presented in Fig. 3. Open circles represent RS velocities; crosses and triangles LC velocities. The comparison of LC and RS initial velocities and the description of individual fireballs, source records, and the LC initial velocity extrapolation method are summarized in Table 1. Where possible, the LC initial velocities were determined using Eq. (1). In the other cases, the exponential term in Eq. (1) was neglected and if deceleration was clearly visible, only the first half of the LC points were used. Let us now briefly describe each fireball in chronological order.
The first case is the fireball EN040710. Besides fixed all-sky EN cameras, one pointed all-sky camera also recorded the fireball. The pointed camera is placed on equatorial mounting and follows the daily motion of the stars, and serves for the determination of the time of the meteor passage from the navigational triangle. The camera is not equipped with a rotating shutter thus the entire fireball trail is captured. We chose several applicable unambiguous points on the light curve and successfully identified seven of them with corresponding points on the fireball image. All the points of LC velocities were measured in the second half of the atmospheric flight of EN040710. Significant extrapolation of velocity is apparently the reason for the discrepancy (about 1.3 km s-1) among LC and RS initial velocities. This, without question, is one of the biggest disadvantages of the LC initial velocity determination. On the other hand, the internal accuracy of the LC velocity is comparable to the RS velocity as is clearly visible in the upper-left plot of Fig. 3 and authentically and correctly describes the progress of real (observed as RS) velocity. Since LC velocities cover a part of the fireball trajectory where strong deceleration is present, an extrapolation formula with an exponential term was successfully used.
The second fireball is labelled EN140710 and a long-focus photographic record (360 mm lens) was used to measure the LC velocity points on the meteor trail. The long-focus photographic camera is also not equipped with a rotating shutter thus the entire fireball trail is visible. We identified and measured 14 points on the fireball trail. Eleven of them fall into 0.2 s-long interval in the middle of the atmospheric trajectory, and thus the average LC velocity had to be used as the LC initial velocity (only the first seven points were used because of deceleration in the last part of the trajectory). Dispersion of these seven points is about 4 km s-1 and the difference between LC and RS initial velocities is about 1.5 km s-1. This spread is probably due to the shape of the light curve flares and their corresponding images in photographic emulsion. It was necessary to measure the centres of the flares on the photographic image of the meteor, as the best approximation, even if the maximum intensities do not match their centres (which is clearly seen in the light curve). This is one of the limitations of the LC velocity method.
The next case is fireball EN070211. A long-focus photographic record was used to measure the LC velocity points on the meteor trail. Equation (1) was applied and provides the LC initial velocity of 30.6 km s-1 which corresponds to an RS value of 31 km s-1, which was determined as an average velocity. This case is also interesting because the LC velocity is measured closer to the terminal point of the fireball than the RS velocity. The terminal part of the trajectory was too faint to be captured by the all-sky camera, except the terminal flare, which could not be used to determine the RS velocity. However, long-focus photographic records are able to detect fainter meteors, and four LC velocity points were successfully identified in two terminal flares on both the light curve and the photographic record. These four points provide enough deceleration data to apply Eq. (1). The LC velocity indicated deceleration at the very end of the EN070211 trajectory invisible in the RS data.
The next case is fireball EN280211A. A long-focus photographic record was used for LC velocity determination and the points were measured in the second part of the trajectory. Nevertheless, Eq. (1) was used and the values of LC and RS initial velocities differ by about 1 km s-1. The LC velocity corresponds, where it was measured, to the RS velocity.
The next case is fireball EN280211B. A long-focus photographic record was used to measure the LC velocity points on the meteor trail. The length of the trajectory, where dynamics data were available and the RS velocities were determined, is only 7 km and an average velocity of 20.2 km s-1 was determined from six RS points. On the other hand, five LC points provided the average LC velocity of 20.7 km s-1, which agrees closely. This case proves that the method is not limited by the length of the atmospheric trajectory but by the number of available flares or other unambiguous events on the luminous trajectory.
Fireball EN290611 is the next case and illustrates the disadvantages and limitations of the LC velocity method: the number of available unambiguous events on a luminous trajectory. Even if the RS velocity is determined with high accuracy (70 points), and the RS initial velocity with an error of only 0.003 km s-1, the LC velocity was determined from five points measured on the long-focus photographic record. Equation (1) could not be applied meaningfully, and because of evident deceleration, only the first two LC points were used for LC initial velocity determination. Despite these unfavourable conditions, the LC and RS velocities correspond.
Atmospheric trajectories of the studied fireballs.
Radiants and orbital elements (J2000.0) of the studied fireballs.
Fireball EN020811 is the fastest fireball among the ones studied, which is why it was possible to determine the LC initial velocity from only three points (on the basis of the pointed all-sky camera record), even if the points were measured in the very end of the trajectory. Since no deceleration was observed, the mean RS initial velocity of about 48 km s-1 was determined. The average LC velocity was also approximately 48 km s-1.
Fireball EN250911 is the first case where digital DSLR records were used for LC velocity determination and classic RS data are also available for comparison. This fireball was captured by DSLR cameras from two different stations, thus comparison between the two LC velocities is also possible. The comparison is shown in the right-hand plot in the fourth row of Fig. 3. The LC initial velocity was determined from Eq. (1) at Station 02 and the average LC velocity was determined from the first four points at Station 20. Both the LC initial velocities are equal and correspond with the RS velocity. The LC velocity points have the typical property at both stations, which is a slightly wider range of values than the RS velocities.
The last fireball used to compare LC and RS velocities is EN021211. This case provided us with the opportunity to compare digital and photographic LC velocities for one fireball, because long-focus photographic and digital DSLR records are available. Six LC points were measured on the digital record and ten on the photographic record. In both cases Eq. (1) was used for LC initial velocity determination and the values differ by about 0.5 km s-1. The LC points were measured in the second half and around the middle of the trajectory so the LC initial velocities are again a bit smaller (by about 1 km s-1) than the RS velocities.
 |
Fig. 3 Comparison of light curve (LC) and rotating shutter (RS) velocities. Open circles stand for RS velocities, crosses and triangles for LC velocities. Horizontal axes show height in km, vertical axes velocity in km s-1. Meteor names in EN format indicate dd, mm, yy. Source of LC velocity consists of Station number (20 – Ondřejov, 02 – Kunžak) and abbreviation describing nature of the record (a – all-sky photographic camera, h – 360 mm long-focus photographic camera, d – digital DSLR camera with all-sky lens). |
4. Application of the method
A bright fireball illuminated the sky above Central Europe for about six seconds on the evening of 8 January 2011. Most of the EN cameras were not in operation due to bad weather conditions. Fortunately, the fireball was recorded by a long-focus photographic camera (only the beginning), by two all-sky photographic cameras (only the brightest part), and fortuitously by one digital DSLR camera in Fornach, Austria (in clouds, but the entire trajectory). The RS velocity data are available only from three inaccurate points measured on one all-sky image, where the fireball is covered by clouds and is very close to the horizon (a rough average value of 20 km s-1 was determined). This dynamic information can describe neither pre-atmospheric velocity nor terminal velocity at the observed terminal height of 29.6 km. This dynamic information is crucial for heliocentric orbit determination and dark flight calculation (in the case of a surviving mass).
The dynamics data would remain an enigma forever without the LC velocity method. Fortunately, the fireball was recorded by several high-time-resolution radiometers (one is sufficient) and, moreover, seven unambiguous events on the light curve were identified and measured on the digital record and 13 events on the photographic record. The LC velocity values are shown in the bottom right-hand plot of Fig. 3. The LC initial velocities were determined as the average velocities at both stations. All the points were used at Station 20 because no deceleration was visible in the data. On the other hand, only first three points were used at the Fornach Station because of apparent deceleration. The velocity points from Station 20 are determined with less accuracy and fall, approximately, between 13 and 17 km s-1 with the average value of 14.4 km s-1. The velocity from Fornach decreases from an initial value of 16 ± 1 km s-1 to 11 ± 1 km s-1 at the height of 32 km. The possibility of a meteorite fall (more than few grams) from this fireball can be excluded on the basis of these results. The atmospheric trajectory and heliocentric data on this fireball are presented in Tables 2 and 3.
5. Accuracy of the method
The accuracy depends on the measurement of the flares on the meteor trail. Since the flare profiles differ from meteor to meteor, and also from flare to flare for one particular meteor, the errors of the measurement were not determined absolutely for each flare. This measurement is very similar to a measurement of the edges of the RS time-marks so we estimate that the accuracy is the same or less (especially for wide flares). The accuracy of an arbitrary point on the meteor trail, ε, ranges (for the nine meteors used in this work) from 43 m (EN070211) to 5 m (EN250911) with the mean value of about 20 m. This produces an error of measurement of a single velocity point of the RS velocity, εRS, measured directly from differences in time, △ t, and length, △ L, of εRS = 2ε/ △ t = 0.6 km s-1 (for 15 time-marks per second). We estimate that the error of measurement of the flares, εf, is, in the worst cases, about two times larger than the error of measurement of the edges of the RS time-marks (ε ≤ εf ≤ 2ε). The error of the LC velocity, εLC, can than be determined as 2εf/ △ t, but we have to use this equation with caution. Fireball EN070211, for instance, has a minimum value of △ t of 0.0012 s. This gives an error of 70 km s-1, which is unreal because the last two LC velocity points were measured with significantly higher accuracy than the edges of the RS time-marks. Since the comparison of RS and LC velocities measured directly from differences in time and length (Fig. 3) shows that the error εLC is not significantly higher than εRS, we estimate that εLC is about 1 km s-1 (in general εLC ≤ 2εRS).
We also point out that the initial velocities and fitted actual velocities (both RS and LC) are determined with a significantly higher accuracy than single velocity points. This accuracy cannot be estimated for all meteors in general because it depends on the number of velocity points, among other things, which varies from meteor to meteor.
6. Conclusions
The new method of determination of fireball velocity from light curves was proposed, tested, verified, and successfully applied. At least one high-time-resolution light curve, multi-station solution of atmospheric trajectory without dynamics data, and at least two flares or other unambiguous events on the light curve identifiable on at least one photographic record, is required for meaningful application. The advantages, disadvantages, and limitations of the method are summarized as follows:
The main advantages:
-
the method is independent of the fireball velocity and duration,which is a crucial limitation of the RS method;
-
the LC velocity method provides the correct velocities of fireballs;
-
the internal accuracy of the LC velocity is comparable to the RS velocity and authentically and correctly describes velocity change during the atmospheric flight of a meteoroid, i.e. deceleration;
-
long-focus, wide-angle, and all-sky photographic and digital records can be used for identification of unambiguous events on the luminous trajectory.
The main disadvantages:
-
the method is based on natural time-marks, thus only fireballswith parts of an atmospheric trajectory with flares or otherunambiguous events can be processed;
-
our radiometers measure intensity of the entire sky and nights when the Moon is full are unfavourable due to lower sensitivity and signal-to-noise ratio.
The main limitations and sources of errors:
-
suitable flares which can be used in this method are observedmostly in the second part of fireball atmospheric trajectories sothe initial velocity often must be significantly extrapolated; inthese cases this value is often slightly smaller than the real value(RS initial velocity);
-
in some cases it is necessary to measure centres of the flares on the photographic image of the meteor as the best approximation, even if the maximum intensities do not match their centres, as is clearly seen in light curves with 500 or 5000 sampling rate.
Since the disadvantages and limitations of the LC velocity method are caused by meteor properties and actual phases of the Moon, which are circumstances beyond our control, and the derived LC velocities are either of the same accuracy as corresponding RS velocities, or show a few km s-1 scatter around the RS velocity, we conclude that the LC velocity method is able to provide sufficiently accurate dynamics data to determine important physical and orbital parameters.
Acknowledgments
The authors are very much indebted to Hermann Koberger who operated his digital camera at Fornach, Austria, and kindly provided us with his record of the EN080111 fireball for measurements. This work was supported by the project RVO:67985815 and by GA ČR grants P209/11/P651, and 205/08/0411.
References
- Brown, P. G., Kalenda, P., Revelle, D. O., & Borovička, J. 2003, Meteor. Planet. Sci., 38, 989 [NASA ADS] [CrossRef] [Google Scholar]
- Ceplecha, Z., Borovička, J., Elford, W. G., et al. 1998, Space Sci. Rev., 84, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Hey, J. S., Parsons, S. J., & Stewart, G. S. 1947, MNRAS, 107, 176 [NASA ADS] [Google Scholar]
- Jacchia, L. G., & Whipple, F. L. 1961, Smithsonian Contributions to Astrophysics, 4, 97 [Google Scholar]
- Pecina, P., & Ceplecha, Z. 1987, Bull. Astron. Inst. Czechosl., 34, 102 [Google Scholar]
- Pujol, J., Rydelek, P., & Ishihara, Y. 2006, Planet. Space Sci., 54, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Schafer, J. P., & Goodall, W. M. 1932, Observations of Kennelly-Heaviside Layer Heights during the Leonid Meteor Shower of November, 1931, Proc. IRE 20, 1941 [Google Scholar]
- Skellett, A. M. 1931, Phys. Rev., 37, 1668 [NASA ADS] [CrossRef] [Google Scholar]
- Spurný, P., Borovička, J., & Shrbený, L. 2007, Automation of the Czech Part of the European Fireball Network: Equipment, methods and first results, Proc. IAU Symp., 236, 121 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 High-time-resolution light curve of the EN040710 fireball with measured flares (gray arrows). |
| In the text | |
 |
Fig. 2 Light curve of the fireball EN080111 as recorded by the radiometer at EN Station 11 Přimda. Details of the fireball’s luminous trajectories are shown below the light curve with all the points used for LC velocity determination. The upper image of the fireball was captured by digital DSLR camera at Fornach, Austria, the bottom one by 360 mm long-focus photographic camera at Ondrejov Observatory, Czech Republic, where the fireball end was hidden by clouds. |
| In the text | |
 |
Fig. 3 Comparison of light curve (LC) and rotating shutter (RS) velocities. Open circles stand for RS velocities, crosses and triangles for LC velocities. Horizontal axes show height in km, vertical axes velocity in km s-1. Meteor names in EN format indicate dd, mm, yy. Source of LC velocity consists of Station number (20 – Ondřejov, 02 – Kunžak) and abbreviation describing nature of the record (a – all-sky photographic camera, h – 360 mm long-focus photographic camera, d – digital DSLR camera with all-sky lens). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


