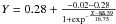| Issue |
A&A
Volume 549, January 2013
|
|
|---|---|---|
| Article Number | A127 | |
| Number of page(s) | 6 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219742 | |
| Published online | 10 January 2013 | |
Improving the performance of solar flare prediction using active longitudes information
1 Key Laboratory of Solar Activity, National Astronomical Observatories of Chinese Academy of Sciences, Beijing, PR China
e-mail: xhuang@bao.ac.cn
2 Physics Department, University of Oulu, Finland
Received: 4 June 2012
Accepted: 24 November 2012
Context. Solar flare prediction models normally depend on properties of active regions, such as sunspot area, McIntosh classifications, Mount Wilson classifications, and various measures of the magnetic field. Nevertheless, the positional information of active regions has not been used.
Aims. We define a metric, DARAL (distance between active regions and predicted active longitudes), to depict the positional relationship between active regions and predicted active longitudes and add DARAL to our solar flare prediction model to improve its performance.
Methods. Combining DARAL with other solar magnetic field parameters, we build a solar flare prediction model with the instance-based learning method, which is a simple and effective algorithm in machine learning. We extracted 70 078 active region instances from the Solar and Heliospheric Observatory (SOHO)/Michelson Doppler Imager (MDI) magnetograms containing 1055 National Oceanic and Atmospheric Administration (NOAA) active regions within 30° of the solar disk center from 1996 to 2007 and used them to train and test the solar flare prediction model.
Results. Using four performance measures (true positive rate, true negative rate, true skill statistic, and Heidke skill score), we compare performances of the solar flare prediction model with and without DARAL. True positive rate, true negative rate, true skill statistic, and Heidke skill score increase by 6.7% ± 1.3%, 4.2% ± 0.5%, 10.8% ± 1.4% and 8.7% ± 1.0%, respectively.
Conclusions. The comparison indicates that the metric DARAL is beneficial to performances of the solar flare prediction model.
Key words: Sun: flares / Sun: activity / Sun: magnetic topology
© ESO, 2013
1. Introduction
Solar flares are known as a kind of solar eruption. Generally, the energy storage and release mechanism of solar flares is explored from properties of their corresponding active regions. McIntosh (1990) defined a set of classifications to describe the magnetic field state of sunspot groups (Bornmann & Shaw 1994). Using McIntosh’s classifications, Gallagher et al. (2002) developed a solar flare prediction system supported with Poisson statistics, and Li et al. (2007) combined the support vector machine and the K-nearest neighbors method to construct a solar flare prediction model. Based on automatic McIntosh classification technology (Colak & Qahwaji 2008) and the machine learning method (Qahwaji & Colak 2007), Colak & Qahwaji (2009) developed a solar flare prediction platform, the Automated Solar Activity Prediction Tool (ASAP), to analyze solar images and provide solar flare forecasting products.
In order to avoid the subjectivity of McIntosh classifications, some magnetic field parameters have been proposed to characterize properties of active regions. Leka & Barnes (2003a) calculated numerous parameters from magnetic fields of active regions, while Leka & Barnes (2003b) set up a solar flare forecasting model in which these parameters are taken as inputs of linear discriminant analysis. Finally, Leka & Barnes (2007) tested the performance of this model, finding that these parameters are correlated with each other and combinations among them have limited predictive power for solar flares. Furthermore, comparing the four parameters (total flux, total excess energy (Leka & Barnes 2003a), total unsigned flux near the polarity separation line (Schrijver 2007), and effective connected magnetic field (Georgoulis & Rust 2007), Barnes & Leka (2008) found that there exists no clear distinction in their performances for solar flare prediction. In order to better quantify magnetic complexity, fractal (McAteer et al. 2005), multifractal (Abramenko 2005; Conlon et al. 2008; 2010), and multiscale (Ireland et al. 2008; Hewett et al. 2008) analysis are used to parameterize the magnetic structure of active regions. With a large dataset, Cui et al. (2006) analyzed the relationship between the solar flare productivity and three photospheric magnetic field parameters (maximum horizontal gradient, length of neutral lines, and number of singular points). Based on these parameters, the influence of active region evolution on solar flares (Yu et al. 2009; 2010a) and the optimized combinations of parameters (Huang et al. 2010; Yu et al. 2010b) are studied. Higgins et al. (2011) developed the Solar Monitor Active Region Tracking (SMART) algorithm to detect active regions and extract their parameters. Based on the magnetic field parameters generated by SMART, a solar flare prediction model is built (Ahmed et al. 2011), and its performance is more accurate than that of ASAP. Recently, Bloomfield et al. (2012) compared performances of several solar flare prediction models and analyzed the limitations of these methods. In addition to the above-mentioned photospheric properties, some parameters under or over the photosphere (Barnes & Leka 2006; Komm et al. 2011; Colak et al. 2011; Verbeeck et al. 2011) are extracted for the solar flare forecast.
Previous solar flare prediction models mainly focus on properties of active regions, such as McIntosh classifications and various magnetic measures, while locations of active longitudes have not been included. The distribution of solar activities is not uniform in longitude, and active longitudes exist on the surface of the Sun (Usoskin et al. 2005; Zhang et al. 2007; 2011a; 2011b; Li 2011). Active longitudes indicate the place where solar activities are more likely to occur. According to the statistics of Zhang et al. (2008), active longitudes with half width of 20° − 30° contain 80% of C-flares during the solar minimum and X-flares during the solar maximum. Based on the surface differential rotation law of the Sun (Usoskin et al. 2005), Zhang et al. (2008) proposed a method to predict the centers of solar active longitudes. This method provides the forecasting capability for the potentially active longitudes, and active regions near active longitudes are consider to be prone to erupt. Therefore, we define a metric, DARAL, to depict the distance between active regions and predicted active longitudes. Combining DARAL with the other magnetic field parameters of active regions, we set up a solar flare prediction model with the instance-based learning method and test the performance of this model with a large number of instances.
This paper is organized as follows. The data is described in Sect. 2. The instance-based learning algorithm is introduced in Sect. 3, and the performances of prediction models are analyzed in Sect. 4. Finally, conclusions and discussions are presented in Sect. 5.
2. Data
2.1. Flare data
The solar flare records are obtained from the National Geophysical Data Center (NGDC)1. According to the peak flux of X-rays observed by Geostationary Operational Environment Satellites (GOES), solar flares are generally classified as C-, M- or X-class. In order to consider the influence of all the flares within a certain time period, the total importance of these flares is defined (Cui et al. 2006): 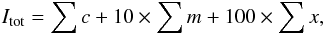 (1)where c,m, and x stand for linear scales after solar flare classifications of C, M, and X, respectively.
(1)where c,m, and x stand for linear scales after solar flare classifications of C, M, and X, respectively.
Active regions whose Itot exceeds 10 (M1.0 equivalent) within 48 h after the observation of these active regions are considered to be flaring instances. Otherwise, they are considered to be non-flaring instances.
2.2. Magnetic field data
In order to set up a solar flare prediction model with a machine learning method, a long-duration and consistent dataset is required. Long-term observations of the Michelson Doppler Imager (MDI, Scherrer et al. 1995) on the Solar and Heliospheric Observatory (SOHO) make it possible. SOHO/MDI full-disk magnetograms2 with a 96-min cadence are used to extract the photospheric magnetic field parameters of active regions. Mason & Hoeksema (2010) selected the National Oceanic and Atmospheric Administration (NOAA) active regions appearing in at least three magnetograms within 30° of the solar disk center, where projection effects can be negligible, from 1996 May 10 to 2007 June 93. The same active regions are selected to release the restriction in the work of Cui et al. (2006), who selected active regions producing at least one C1.0 flare. There are 70 078 magnetograms containing 1055 NOAA active regions in the dataset. The following three parameters are calculated to quantitatively describe the non-potentiality and complexity of active regions:
-
1.
The maximum horizontal gradient of the longitudinal magnetic field along neutral lines (|∇hBz|mL). The horizontal gradient of the longitudinal magnetic field can be calculated using
![\hbox{$\left| {\nabla_{\rm h} B_z }\right|=[(\frac{\partial B_{z}}{\partial x})^{2}+(\frac{\partial B_{z}}{\partial y})^{2}]^{1/2}$}](/articles/aa/full_html/2013/01/aa19742-12/aa19742-12-eq14.png) . In order to estimate maximum squeezing among flux systems in an active region, we calculate the maximum horizontal gradient of the longitudinal magnetic field along neutral lines rather than calculate the maximum horizontal gradient of the longitudinal magnetic field in the whole active region. Taking active region NOAA 10488 for example (Fig. 1a), Fig. 1b shows that the large magnetic field gradient usually appears in areas of opposite polarity. Figure 1c shows the magnetic field gradient distribution along neutral lines.
. In order to estimate maximum squeezing among flux systems in an active region, we calculate the maximum horizontal gradient of the longitudinal magnetic field along neutral lines rather than calculate the maximum horizontal gradient of the longitudinal magnetic field in the whole active region. Taking active region NOAA 10488 for example (Fig. 1a), Fig. 1b shows that the large magnetic field gradient usually appears in areas of opposite polarity. Figure 1c shows the magnetic field gradient distribution along neutral lines. -
2.
The length of neutral lines (L). The neutral lines separate opposite polarities of the longitudinal magnetic field. Falconer et al. (2003) first calculate the length of neutral lines using the line-of-sight magnetgram. The following steps are required in their algorithm. The first step is to compute the transverse component of the magnetic field inferred by the potential field model with the boundary condition of the line-of-sight magnetic field. The next step is to select pixels on which the strength of the inferred transverse component of the magnetic field is larger than 150 G. The third step is to choose pixels whose horizontal gradient of the longitudinal magnetic field is greater than 50 G/Mm. Finally, the number of pixels along neutral lines is used to measure their length. Using a similar algorithm, Cui et al. (2006) calculate from a large number of MDI magnetograms the length of neutral lines on which the potential transverse component of the magnetic field is larger than 200 G and the gradient of the longitudinal magnetic field is greater than 40 G/Mm. We adopt the algorithm used in Cui et al. (2006) in the present paper. An example of extracted neutral lines is shown in Fig. 1c.
-
3.
The number of singular points (η), which is the number of nodes in the network formed by magnetic separatrices (Cui et al. 2006). The singular point in a closed curve (C) can be detected by
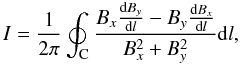 (2)where Bx and By are transverse components extrapolated from a potential model with the boundary condition of longitudinal magnetograms (Wang & Wang 1996). The magnetic topological complexity of active regions is characterized by η.
(2)where Bx and By are transverse components extrapolated from a potential model with the boundary condition of longitudinal magnetograms (Wang & Wang 1996). The magnetic topological complexity of active regions is characterized by η.
2.3. Active longitude data
Active longitudes are the central positions of heliographic longitude bands in which solar activities are more frequent than in other places over a long period of time. The active longitude data used in this study comes from the active longitude prediction model built by Zhang et al. (2008). The main process of the active longitude prediction is shown in Fig. 2.
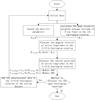 |
Fig. 2 Flow chart for prediction of active longitude. |
The central positions of the kth day in the ith Carrington rotation (Λik1 and Λik2) can be calculated as 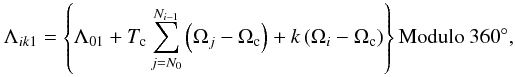 (3)and
(3)and 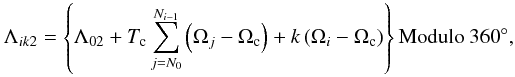 (4)where N0 and Ni − 1 are the numbers of the beginning Carrington rotation and the (i − 1)th rotation, respectively; Tc is the Carrington rotation period 27.27 days, Ωc is the angular velocity of Carrington frame (14.1844 deg/day), Ωi = Ω0 − Bsin2 ⟨ φi ⟩ is the differential rotation revised angular velocity in the ith Carrington rotation at the peak intensity weighted average latitude of X-ray flares during the ith Carrington rotation ( ⟨ φi ⟩ ). Here, Ω0 is the equatorial angular velocity, and B is the differential rotation rate. We assume that two active longitudes are separated by 180 degrees (Zhang et al. 2007), hence the central positions of active longitudes at the beginning of the dataset (Λ01 and Λ02) satisfy | Λ01 − Λ02 | = 180°.
(4)where N0 and Ni − 1 are the numbers of the beginning Carrington rotation and the (i − 1)th rotation, respectively; Tc is the Carrington rotation period 27.27 days, Ωc is the angular velocity of Carrington frame (14.1844 deg/day), Ωi = Ω0 − Bsin2 ⟨ φi ⟩ is the differential rotation revised angular velocity in the ith Carrington rotation at the peak intensity weighted average latitude of X-ray flares during the ith Carrington rotation ( ⟨ φi ⟩ ). Here, Ω0 is the equatorial angular velocity, and B is the differential rotation rate. We assume that two active longitudes are separated by 180 degrees (Zhang et al. 2007), hence the central positions of active longitudes at the beginning of the dataset (Λ01 and Λ02) satisfy | Λ01 − Λ02 | = 180°.
Taking the deviation between the center of active longitudes and the position of solar flares as the optimization target, we obtained the best-fit parameters of Ω0 and B. The forecasting angular velocity of active longitudes for the (i + 1)th Carrington rotation is 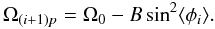 (5)The forecasting central positions of active longitudes for the (i + 1)th Carrington rotation are
(5)The forecasting central positions of active longitudes for the (i + 1)th Carrington rotation are 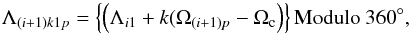 (6)and
(6)and 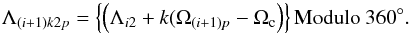 (7)At the end of the (i + 1)th Carrington rotation, we added the observational data in this Carrington rotation into the previous dataset. Using the updated dataset, we calculated the best-fit parameters of Ω0 and B again. Recursively implementing this method from 1996 to 2007, we could obtain the central positions of predicted active longitudes in this period.
(7)At the end of the (i + 1)th Carrington rotation, we added the observational data in this Carrington rotation into the previous dataset. Using the updated dataset, we calculated the best-fit parameters of Ω0 and B again. Recursively implementing this method from 1996 to 2007, we could obtain the central positions of predicted active longitudes in this period.
 |
Fig. 3 Ratio between number of flaring NOAA active regions and total number of NOAA active regions. The DARAL is divided into five parts (0−20°, 20−40°, 40−60°, 60−80° and >80°), and the ratio is calculated in each part. The horizontal dotted line stands for the ratio calculated by all the data, and the fitted curve is a sigmoid function |
Based on predicted active longitudes, we define a metric DARAL (degree) to depict the relationship between active regions and predicted active longitudes: 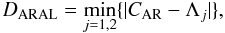 (8)where CAR (degree) is the center of an active region, Λj(j = 1,2) (degree) are predicted active longitudes which appear 180° apart in longitude. Because of the south-north asymmetry of active longitudes, DARAL is separately calculated in each hemisphere.
(8)where CAR (degree) is the center of an active region, Λj(j = 1,2) (degree) are predicted active longitudes which appear 180° apart in longitude. Because of the south-north asymmetry of active longitudes, DARAL is separately calculated in each hemisphere.
We divided the DARAL into five parts (0−20°, 20−40°, 40−60°, 60−80°, >80°) and calculated the ratio between the number of flaring NOAA active regions and the total number of NOAA active regions in each part. As shown in Fig. 3, we found that the ratio calculated by the data within 40−60° is equal to the ratio calculated by all the data. Furthermore, the small DARAL yields the high ratio and the large DARAL gives the low ratio. This means that the active region that is near the active longitude is prone to erupt and the active region that is far away from the active longitude produces solar flares with little probability. This indicates that the parameter DARAL can be used to improve the performance of the solar flare prediction.
3. Instance-based learning method
In machine learning algorithms, there are two types of modeling methods, the instance-based approach and the model-based one. The model-based approach summarizes laws from the dataset to generate a model. The prediction for the unseen instance is determined by the generated model, for example, the neutral network model (Qahwaji & Colak 2007), the decision tree model (Yu et al. 2009), and so on. The instance-based approach (Aha et al. 1991) assumes that the prediction information can directly obtain from the existing instances. Therefore, the prediction for the unseen instance is determined by its similar instances.
Generally, an instance is represented as an attribute-decision pair. For example, the mth instance (Im) can be represented by am1,am2,...,amk,dm, where amk is the kth attribute for the mth instance and dm is the decision for the mth instance. In the example of solar flare predictions, attributes stand for properties of active regions, and the decision is whether solar flares occur within the forward-looking period. The nearest neighbor algorithm is the most basic instance-based learning method (Mitchell 1997). In this algorithm, the training instances are stored. For a new instance, we retrieve its nearest instance in the stored dataset. The decision of the new instance is assigned to the class of its nearest neighbor. The similarity between two instances (Im and In) is defined as 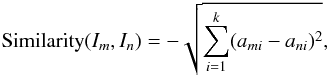 (9)where Im stands for the mth instance, k is the number of attributes for the instance, ami stands for the ith attribute for the mth instance.
(9)where Im stands for the mth instance, k is the number of attributes for the instance, ami stands for the ith attribute for the mth instance.
Instance-based learning has been successfully utilized on the astronomical dataset (Ball et al. 2007). The advantages of the instance-based approach are:
-
1.
Simplicity. The instance-based approach assumes that similarinstances require similar decisions.
-
2.
The ability of local approximation. The instance-based approach learns the complex concept by local sub-concepts provided by selected instances.
Because our main aim is to test the role of DARAL for solar flare predictions, we try to choose a simple modeling method. Furthermore, taking into account the complexity of the solar activity, an instance-based learning approach, which has the capacity of local approximation, is used to build the solar flare prediction model.
4. Performance of the solar flare prediction model
4.1. Performance measures
For a binary forecast, there are four possible combinations, which are shown in Table 1 (known as a contingency table). The instance that is correctly predicted as positive or negative is defined as true positive (TP) or true negative (TN), while the instance that is wrongly predicted as positive or negative is defined as false positive (FP) or false negative (FN).
Different combinations for binary forecast.
Our solar flare prediction model provides a flaring or non-flaring forecast, and we consider the flaring instance to be a positive class and the non-flaring instance to be a negative class. Based on the four combinations in Table 1, two basic measures (TP rate and TN rate) are defined to evaluate the performances of flaring prediction and non-flaring prediction, respectively. 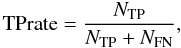 (10)where NTP is the number of true positive instances and NFN is the number of false negative instances.
(10)where NTP is the number of true positive instances and NFN is the number of false negative instances. 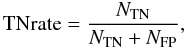 (11)where NTN is the number of true negative instances and NFP is the number of false positive instances.
(11)where NTN is the number of true negative instances and NFP is the number of false positive instances.
In order to use all the elements in the contingency table, the true skill statistic (TSS), which is not sensitive to the ratio between the number of flaring instances and the number of non-flaring instances (Bloomfield et al. 2012), and the Heidke skill score (HSS), which is commonly adopted in solar flare prediction (Barnes & Leka 2008), are defined. 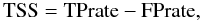 (12)where FPrate = 1 − TNrate.
(12)where FPrate = 1 − TNrate. 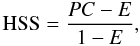 (13)where N = NTP + NTN + NFP + NFN,
(13)where N = NTP + NTN + NFP + NFN, 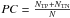 , and
, and 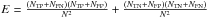 . Here, E is PC for random forecast. This version of HSS hence shows the increase in predictive power over that of random chance.
. Here, E is PC for random forecast. This version of HSS hence shows the increase in predictive power over that of random chance.
4.2. Experimental results and analyses
The dataset consists of 1055 NOAA active regions containing in 70 078 SOHO/MDI magnetograms. Excluding 5180 magnetograms with dead pixels, there are 64 898 instances in the dataset, including 9394 flaring instances and 55 504 non-flaring instances.
We adopted the instance-based learning method to build the solar flare prediction model and used ten-fold cross-validation technology to estimate the performance of this prediction model. The dataset was partitioned into ten subsets, nine of which were used as the training set and the remaining one subset as the testing set. We built the model from the training set and evaluated its performance by the testing set. This process was repeated ten times until each of the ten subsets was used once as the testing set. Hence, we obtained ten results during the process of the ten-fold cross-validation. The experimental result was estimated by the mean (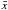 ) and standard deviation (s) of the ten results.
) and standard deviation (s) of the ten results. 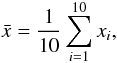 (14)where xi is one of the ten testing results.
(14)where xi is one of the ten testing results. 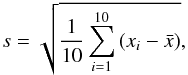 (15)where xi is one of the ten testing results and
(15)where xi is one of the ten testing results and 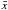 is the mean value of the ten results.
is the mean value of the ten results.
In order to test the influence of DARAL on the solar flare prediction, we used the simple modeling method (instance based learning algorithm) to build the solar flare prediction model, employing the same testing data to test the performance of the prediction model with and without DARAL. The contingency table of these solar flare prediction models is shown in Table 2. In this Table, the experimental result is represented by 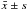 . Based on the same testing data, NTP and NTN for the prediction model with DARAL are more than those for the prediction model without DARAL. Meanwhile, NFP and NFN for the prediction model with DARAL are less than those for the prediction model without DARAL.
. Based on the same testing data, NTP and NTN for the prediction model with DARAL are more than those for the prediction model without DARAL. Meanwhile, NFP and NFN for the prediction model with DARAL are less than those for the prediction model without DARAL.
 |
Fig. 4 Performances of solar flare prediction with and without DARAL. The bar graph displays the mean of the ten-fold cross-validation, and the corresponding error bars show the standard deviations in the ten-fold cross-validation. |
Contingency table for solar flare prediction models with and without DARAL.
Using the proposed performance measures, we quantitatively compared the performances of solar flare prediction with and without DARAL. As shown in Fig. 4, TP rate, TN rate, TSS, and HSS increase by 6.7% ± 1.3%, 4.2% ± 0.5%, 10.8% ± 1.4% and 8.7% ± 1.0%, respectively. The magnetic field parameters characterize the non-potentiality and complexity of active regions, and DARAL reflects the closeness between active regions and predicted active longitudes. The performance improvement for adding DARAL indicates that DARAL can provide information in addition to the magnetic field parameters, and the predicted active longitude information is valuable for the solar flare prediction. In short, solar flare prediction is a complicated problem, so we need to take other information available into account besides the non-potentiality and complexity of active regions to improve the performance of the prediction model.
5. Conclusions
The predicted active longitude indicates the place where solar activities more frequently occur, and DARAL reflects the distance between active regions and predicted active longitudes. Dividing DARAL into five parts (0−20°, 20−40°, 40−60°, 60−80°, and >80°), we find that the ratio of the number of flaring NOAA active regions to the total number of NOAA active regions within 40−60° is equal to the average ratio calculated by all the data. The smaller distance yields the larger ratio, while the larger distance results in the smaller ratio. These results provide us the opportunity to add location information of active regions to the prediction model. By applying the instance-based learning method to the combination of the magnetic field parameters and DARAL, we built the solar flare prediction model to distinguish between flaring and non-flaring samples. By using various forecast verification measures, we compared the performances of the solar flare prediction model with and without DARAL. It is evident that the performance of the solar flare prediction model is improved by considering the active longitude information.
In the future, more information, e.g., under, over, or near the active regions on the surface of the photosphere (Komm et al. 2011; Barnes & Leka 2006) and the information about the previous solar eruptions (Wheatland 2005), should be combined with the parameters used in our prediction model to generate more accurate prediction models. Furthermore, the triggering mechanisms of solar flares should be analyzed in more detail.
Acknowledgments
We thank the SOHO consortium for the data. SOHO is a project of international cooperation between ESA and NASA. This work is supported by the Young Researcher Grant of National Astronomical Observatories, Chinese Academy of Sciences, the National Basic Research Program of China (973 Program, Grant No. 2011CB811406), and the National Natural Science Foundation of China (Grant Nos. 11273031, 10733020, 10921303, 11003026, and 11078010). Xin Huang especially thanks Prof. Daren Yu and Qinghua Hu for the helpful discussions. This paper has benefited from comments of the anonymous reviewer.
References
- Abramenko, V. I. 2005, Sol. Phys., 228, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Aha, D. W., Kibler, D., & Albert, M. K. 1991, Mach. Learn., 6, 37 [Google Scholar]
- Ahmed, O. W., Qahwaji, R., Colak, T., et al. 2011, Sol. Phys., DOI: 10.1007/s11207-011-9896-1 [Google Scholar]
- Ball, N. M., Brunner, R. J., Myers, A. D., et al. 2007, ApJ, 663, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, G., & Leka, K. D. 2006, ApJ, 646, 1303 [Google Scholar]
- Barnes, G., & Leka, K. D. 2008, ApJ, 688, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Bloomfield, D. S., Higgins, P. A., McAteer, R. T., & Gallagher, P. T. 2012, ApJ, 747, L41 [Google Scholar]
- Bornmann, P. L., & Shaw, D. 1994, Sol. Phys., 150, 127 [Google Scholar]
- Colak, T., & Qahwaji, R. 2008, Sol. Phys., 248, 277 [Google Scholar]
- Colak, T., & Qahwaji, R. 2009, Space Weather, 7, S06001 [NASA ADS] [CrossRef] [Google Scholar]
- Colak, T., Qahwaji, R., Ipson, S., & Ugail, H. 2011, Adv. Space Res., 47, 2092 [NASA ADS] [CrossRef] [Google Scholar]
- Conlon, P. A., Gallagher, P. T., McAteer, R. T. J., et al. 2008, Sol. Phys., 248, 297 [Google Scholar]
- Conlon, P. A., McAteer, R. T. J., Gallagher, P. T., & Fennell, L. 2010, ApJ, 722, 577 [Google Scholar]
- Cui, Y., Li, R., Zhang, L., He, Y., & Wang, H. 2006, Sol. Phys., 237, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Falconer, D. A., Moore, R. L., & Gary, G. A. 2003, J. Geophys. Res., 108, 1380 [Google Scholar]
- Gallagher, P. T., Moon, Y. J., & Wang, H. 2002, Sol. Phys., 209, 171 [Google Scholar]
- Georgoulis, M. K., & Rust, D. M. 2007, ApJ, 661, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, R. J., Gallagher, P. T., McAteer, R. T. J., et al. 2008, Sol. Phys., 248, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Higgins, P. A., Gallagher, P. T., McAteer, R. T. J., & Bloomfield, D. S. 2011, Adv. Space Res., 47, 2105 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, X., Yu, D., Hu, Q., Wang, H., & Cui, Y. 2010, Sol. Phys., 263, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Ireland, J., Young, C. A., McAteer, R. T. J., et al. 2008, Sol. Phys., 252, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Komm, R., Ferguson, R., Hill, F., Barnes, G., & Leka, K. D. 2011, Sol. Phys., 268, 389 [Google Scholar]
- Leka, K. D., & Barnes, G. 2003a, ApJ, 595, 1277 [CrossRef] [Google Scholar]
- Leka, K. D., & Barnes, G. 2003b, ApJ, 595, 1296 [CrossRef] [Google Scholar]
- Leka, K. D., & Barnes, G. 2007, ApJ, 656, 1173 [NASA ADS] [CrossRef] [Google Scholar]
- Li, J. 2011, ApJ, 735, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Li, R., Wang, H. N., He, H., Cui, Y. M., & Du, Z. L. 2007, Chin. J. Astron. Astrophys., 7, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, J. P., & Hoeksema, J. T. 2010, ApJ, 723, 634 [NASA ADS] [CrossRef] [Google Scholar]
- McAteer, R. T. J., Gallagher, P. T., & Ireland, J. 2005, ApJ, 631, 628 [Google Scholar]
- McIntosh, P. S. 1990, Sol. Phys., 125, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Mitchell, T. M. 1997, Machine Learning (New York: McGraw-Hill Company) [Google Scholar]
- Qahwaji, R., & Colak, T. 2007, Sol. Phys., 241, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Scherrer, P. H., Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [Google Scholar]
- Schrijver, C. J. 2007, ApJ, 655, L117 [Google Scholar]
- Usoskin, I. G., Berdyugina, S. V., & Poutanen, J. 2005, A&A, 441, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verbeeck, C., Higgins, P. A., Colak, T., et al. 2011, Sol. Phys., DOI: 10.1007/s11207-011-9859-6 [Google Scholar]
- Wang, H. N., & Wang, J. X. 1996, A&A, 313, 285 [NASA ADS] [Google Scholar]
- Wheatland, M. S. 2005, Space Weather, 3, S07003 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, D., Huang, X., Wang, H., & Cui, Y. 2009, Sol. Phys., 255, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, D., Huang, X., Hu, Q., Zhou, R., Wang, H., & Cui, Y. 2010a, ApJ, 709, 321 [Google Scholar]
- Yu, D., Huang, X., Wang, H., Cui, Y., Hu, Q., & Zhou, R. 2010b, ApJ, 710, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, L., Wang, H., Du, Z., & He, H. 2007, A&A, 471, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, L., Wang, H., & Du, Z. 2008, A&A, 484, 523 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, L., Mursula, K., Usoskin, I., & Wang, H. 2011a, A&A, 529, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, L., Mursula, K., Usoskin, I., & Wang, H. 2011b, J. Atmos. Sol. Terr. Phys., 73, 258 [Google Scholar]
All Tables
All Figures
 |
Fig. 2 Flow chart for prediction of active longitude. |
| In the text | |
 |
Fig. 3 Ratio between number of flaring NOAA active regions and total number of NOAA active regions. The DARAL is divided into five parts (0−20°, 20−40°, 40−60°, 60−80° and >80°), and the ratio is calculated in each part. The horizontal dotted line stands for the ratio calculated by all the data, and the fitted curve is a sigmoid function |
| In the text | |
 |
Fig. 4 Performances of solar flare prediction with and without DARAL. The bar graph displays the mean of the ten-fold cross-validation, and the corresponding error bars show the standard deviations in the ten-fold cross-validation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.