EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 548 (December 2012) A&A, 548 (2012) A3 Full HTML
Free Access
Issue
A&A
Volume 548, December 2012
Article Number A3
Number of page(s) 3
Section Astrophysical processes
DOI https://doi.org/10.1051/0004-6361/201220254
Published online 13 November 2012

© ESO, 2012

The Swift source Sw 164449+57 at redshift z = 0.3543 is believed to be a super-massive dormant black hole at the center of an inactive galaxy. During a recent X-ray outburst (probably activated by a tidal disruption of a star), the source was in many respects similar to a small-scale blazar; see e.g. Bloom et al. (2011). In particular, it displayed a relativistic jet (Burrows et al. 2011; Zauderer et al. 2011). If one accepts (as we do) theoretical and observational arguments that link relativistic jets with a high black hole spin (discussed by Narayan & McClintock 2012, and many other authors), then the presence of a jet suggests that the black hole in Sw 164449+57 is rotating rather rapidly (a > 0.6, say). However, one should also note that this evidence of jets being powered by the black hole rotation is not unanimously accepted. Using much of the same data, Fender et al. (2010) came to very different conclusions – that even the relatively simple radio-loud versus radio-quiet dichotomy in AGN may be due to the AGN states rather than to spins. In this context it is also relevant to note that McKinney et al. (2012) discuss the possibility of exciting QPOs through a disk-jet coupling.

During the outburst, Reis et al. (2012) detected a firm (statistically significant) QPO1 with the centroid frequency fobs = 4.8(1 + z) mHz. In this short article we examine the possibility that this frequency may correspond to a lower (or upper) frequency of the “twin peak” QPOs in which the two frequencies are in the 3:2 ratio. Such twin peaks are observed in several microquasars and other black hole sources (see e.g. Török et al. 2005).

It has been argued by Kluźniak & Abramowicz (2001) that the phenomenon of the 3:2 twin peak QPOs in the black hole sources is due to a nonlinear parametric resonance in two eigenmodes of accretion disk oscillations. According to the simplest version of the 3:2 resonance model, the observed QPO twin peak frequencies should be identified with the vertical epicyclic and radial epicyclic frequencies, which in the Kerr geometry are given by fver=ΩK2π[1−4ax−3/2+3a2x-2]1/2,frad=ΩK2π[1−6x-1+8ax−3/2−3a2x-2]1/2,ΩK=(GMr3)1/2[1+x−3/2a]-1,\begin{eqnarray} \label{epicyclic} \label{vertical} f_{\rm ver} &=& \frac{\Omega_{\rm K}}{2\pi} \left[ 1 - 4a x^{-3/2} + 3 a^2 x^{-2} \right]^{1/2}, \\ \label{radial} f_{\rm rad} &=& \frac{\Omega_{\rm K}}{2\pi} \left[ 1 - 6x^{-1} + 8a x^{-3/2} - 3 a ^2 x^{-2} \right]^{1/2}, \\ \label{keplerian} \Omega_{\rm K} &=& \left( \frac{GM}{r^3}\right)^{1/2} \left[ 1 +x^{-3/2} a \right]^{-1}, \end{eqnarray}where M is the black hole mass, a its dimensionless spin (0 ≤ |a| ≤ 1), and the dimensionless radial coordinate is defined by 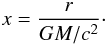x=rGM/c2·\begin{equation} \label{radius-dimensionless} x = \frac{r}{GM/c^2}\cdot \end{equation}(4)Here G is the Newtonian gravitational constant and c the speed of light. The 3:2 epicyclic resonance occurs at the “resonance radius” x3:2 = x3:2(a), defined by the condition 32=[1−4a(x3:2)−3/2+3a2(x3:2)-21−6(x3:2)-1+8a(x3:2)−3/2−3a2(x3:2)-2]1/2·\begin{equation} \label{radius-resonance} \frac{3}{2} = \left[ \frac{1 - 4a (x_{3:2})^{-3/2} + 3 a^2 (x_{3:2})^{-2}}{1 - 6(x_{3:2})^{-1} + 8a (x_{3:2})^{-3/2} - 3 a ^2 (x_{3:2})^{-2}} \right]^{1/2}\cdot \end{equation}(5)For a nonrotating black hole (a = 0), this implies x3:2(0) = 54/5, which is approximately twice the radius of ISCO.

The epicyclic resonance hypothesis allows for an accurate estimate of the black hole mass and spin, as first discussed by Abramowicz & Kluźniak (2001) for the microquasar GRO J1655-40. Applying this idea to Sw 164449+57, we first assume that fobs = 4.8(1 + z) mHz corresponds to the lower of the twin peak frequencies, i.e. to the radial epicyclic frequency in the Kluźniak & Abramowicz resonance model2. After a few lines of simple algebra we may write, in this case, MM⊙=A[1−6(x3:2)-1+8a(x3:2)−3/2−3a2(x3:2)-2]1/2(x3:2)3/2+aA=c32πGfobsM⊙=4.97×106,\begin{eqnarray} \label{hypothesis-radial} \frac{M}{M_\odot} &=& A \frac{\left[1 - 6(x_{3:2})^{-1} + 8a (x_{3:2})^{-3/2} - 3 a ^2 (x_{3:2})^{-2}\right]^{1/2}}{ (x_{3:2})^{3/2} + a } \nonumber \\[1mm] A &=& \frac{c^3}{2\pi G f_{\rm obs} M_{\odot}} = 4.97 \times 10^6 , \end{eqnarray}(6)where M⊙ is the solar mass. Similarly, if we assume the other possibility, i.e. that fobs = 4.8(1 + z) mHz corresponds to the upper of the twin peak frequencies, i.e. to the vertical epicyclic frequency, we may write MM⊙=A[1−4a(x3:2)−3/2+3a2(x3:2)-2]1/2(x3:2)3/2+a·\begin{equation} \label{hypothesis-vertical} \frac{M}{M_\odot} = A \frac{\left[1 - 4a (x_{3:2})^{-3/2} + 3 a^2 (x_{3:2})^{-2}\right]^{1/2}}{ (x_{3:2})^{3/2} + a }\cdot \end{equation}(7)Because for a non rotating black hole it is x3:2(0) = 54/5, in this case from Eqs. (6) and (7) it follows that MM⊙={iffobs=frad,iffobs=fver,  for  a=0.\begin{equation} \label{mass-non-rotating} \frac{M}{M_\odot} = \begin{cases} 9.34 \times 10^4 &\mbox{if } f_{\rm obs} = f_{\rm rad}, \\[2mm] 1.40\times 10^5 & \mbox{if } f_{\rm obs} = f_{\rm ver}, \end{cases} ~~ {\rm for}~~ a = 0. \end{equation}(8)Similarly, one may calculate that in the two extreme cases, corresponding to a = ± 1. We consider both the corotating (a ≥ 0) and counter-rotating (a ≤ 0) cases, because the star may come to the vicinity of Sw 164449+57 from a random direction before being tidally disrupted, and the stellar debris can form either a corotating or a counter-rotating accretion disk. We have 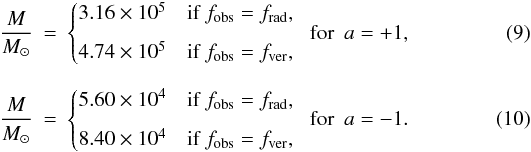MM⊙=  for  a=+1,MM⊙=  for  a=−1.\begin{eqnarray} \label{mass-max-rotating-plus} \frac{M}{M_\odot} &=& \begin{array}{ll} 3.16 \times 10^5 &\mbox{if } f_{\rm obs} = f_{\rm rad}, \\ 4.74 \times 10^5 & \mbox{if } f_{\rm obs} = f_{\rm ver}, \end{array} ~~ {\rm for}~~ a = +1,\\ \frac{M}{M_\odot} &=& \begin{array}{ll} 5.60 \times 10^4 &\mbox{if } f_{\rm obs} = f_{\rm rad}, \\ 8.40 \times 10^4 & \mbox{if } f_{\rm obs} = f_{\rm ver}, \end{array} ~~ {\rm for}~~ a = -1. \end{eqnarray}Mass estimates for the case of a rotating black hole for any value of the spin in Sw 164449+57 are given in Fig. 1. Figure 1 suggests that if the black hole in Sw 164449+57 is rapidly co-rotating with a > 0.6, the mass should be in the range 1.6×105 < M/M⊙ < 3.2×105 if fobs = frad or 2.3×105 < M/M⊙ < 4.7×105 if fobs = fver. While, if the black hole is counter-rotating with a < −0.6, the mass would be in the range 5.6×104 < M/M⊙ < 6.7×104 if fobs = frad or 8.4×104 < M/M⊙ < 1.0×105 if fobs = fver.

thumbnail Fig. 1

Mass estimate for the supermassive black hole in the Swift source Sw 164449+57, based on the assumption that the observed QPO frequency fobs = 4.8(1 + z) mHz corresponds either to the radial epicyclic (solid line), fobs = frad, or to the vertical epicyclic (dashed line), fobs = fver, frequency, in accordance with the twin peak QPO 3:2 resonance model. For a comparison, we also show the mass estimate based on an assumption that fobs = ΩK/2π is the Keplerian frequency at ISCO (dash-dotted line).

No direct measurement of the mass of the black hole in Sw 164449+57 has been reported. If the outburst was powered by a tidal disruption of a solar-type main sequence star, the black hole mass must be M ≲ 108 M⊙ (Rees 1988). If a white dwarf was disrupted, as suggested by Krolik & Piran (2011a), the black hole mass would correspond to the intermediate mass range, M ≲ 105 M⊙ (but see also Krolik & Piran 2012b). Because the host galaxy of Sw 164449+57 is not resolved and the host morphology is unknown, the bulge luminosity cannot be determined. Therefore, the empirical relation (black hole mass – bulge luminosity) (Magorrian et al. 1998) cannot be used directly to estimate the black hole mass. By employing the relation of black hole mass and bulge luminosity to the total luminosity of host galaxy, an upper limit of black hole mass M ≲ 107 M⊙ has been given in the literature; see Bloom et al. (2011); Burrows et al. (2011); Zauderer et al. (2011); Levan et al. (2011). The “fundamental plane” of the black hole accretion, described by a relation between radio luminosity, X-ray luminosity, and black hole mass may be used to determine mass from the observed radio and X-ray luminosities. This way, Miller & Gültekin (2011) estimate the black hole mass of Sw 164449+57: to be log (M/M⊙) = 5.5 ± 1.1.

Reis et al. (2012) noticed that Sw 164449+57 is a beamed source and therefore its accretion disk must be viewed at very low inclination (nearly face-on). This excludes the possibility that the disk oscillations are modulated directly by the relativistic Doppler effect and by the light trajectory bending, as these effects work only for highly inclined disks (Bursa et al. 2004). It is not obvious what the modulation mechanism is in the case of the black hole disks that are seen nearly face-on, in particular whether the disk oscillations may modulate (with the same frequencies) the properties of the disk. This is an interesting issue for further theoretical studies. In this context we would like to note that McKinney et al. (2012) discuss the possibility of exciting QPOs through a disk-jet coupling (see also Krolik & Piran 2012b, who discuss the jet issue specifically for Sw 164449+57).

We conclude that the hypothesis that the QPO frequency observed in Sw 164449+57 is one of the twin peak 3:2 frequencies, and the hypothesis of the high spin in this source, are together consistent with the above-mentioned low mass estimates (M ~ 105 M⊙), implying an intermediate-mass black hole in Sw 164449+57.

1

It should be mentioned that Miller & Strohmayer (2011) note the possibility of a QPO in Sw 164449+57.

2

Reis et al. (2012) also report a less certain QPO with the centroid frequency about mHz. They give no estimate of error in the determination of this value, but if it is about 16%, then it could be that , which would strengthen the case for .

Acknowledgments

We are grateful to the referee who quickly wrote a very helpful report and who pointed out a few issues connected with the low inclination of the disk in Sw 164449+57. This work was done during a visit of M.A.A. to Kavli Institute of Astronomy and Astrophysics and Astronomy Department at Peking University, and was supported by the National Natural Science Foundation of China (NSFC11073002) and China Scholarship Council (2009601137) as well as by M.A.A. grants: IAU travel grant, Polish NCN UMO-2011/01/B/ST9/05439 grant, and Swedish VR grant.

References

  1. Abramowicz, M. A., & Kluźniak, W. 2001, A&A, 374, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bloom, E., Giannios, D., Metzger, B. D., et al. 2011, Science, 333, 203 [CrossRef] [PubMed] [Google Scholar]
  3. Burrows, D. N., Kennea, J. A., Ghisellini, G., et al. 2011, Nature, 476, 421 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  4. Bursa, M., Abramowicz, M. A., Karas, V., & Kluźniak, W. 2004, ApJ, 617, L45 [NASA ADS] [CrossRef] [Google Scholar]
  5. Fender, R. P., Gallo, E., & Russell, D. 2010, MNRAS, 406, 1425 [NASA ADS] [Google Scholar]
  6. Kluźniak, W., & Abramowicz, M. A. 2001 [arXiv:astro-ph/0105057] [Google Scholar]
  7. Krolik, J. H., & Piran, T. 2011a, ApJ, 743, 134 [NASA ADS] [CrossRef] [Google Scholar]
  8. Krolik, J. H., & Piran, T. 2011b, ApJ, 749, 92 [Google Scholar]
  9. Levan, A. J., Tanvir, N. R., Cenko, S. B., et al. 2011, Science, 333, 199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  10. Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
  11. McKinney, J. C., Tchekhovskoy, A., & Blandford, R. D. 2012, MNRAS, 423, 3083 [NASA ADS] [CrossRef] [Google Scholar]
  12. Miller, J. M., & Gültekin 2011, ApJ, 738, L13 [NASA ADS] [CrossRef] [Google Scholar]
  13. Miller, J. M., & Strohmayer, T. E. 2011, The Astronomer’s Telegram, 3447 [Google Scholar]
  14. Narayan, R., & McClintock, J. E. 2012, MNRAS, 419, L69 [NASA ADS] [CrossRef] [Google Scholar]
  15. Rees, M. J. 1988, Nature, 333, 523 [NASA ADS] [CrossRef] [Google Scholar]
  16. Reis, R. C., Miller, J. M., Reynolds, M. T., et al. 2012, Science, 337, 949 [NASA ADS] [CrossRef] [Google Scholar]
  17. Török, G., Abramowicz, M. A., Kluźniak, W., & Stuchlík, Z. 2005, A&A, 436, 18 [Google Scholar]
  18. Zauderer, B. A., Berger, E., Soderberg, A. M., et al. 2011, Nature, 476, 425 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

All Figures

thumbnail Fig. 1

Mass estimate for the supermassive black hole in the Swift source Sw 164449+57, based on the assumption that the observed QPO frequency fobs = 4.8(1 + z) mHz corresponds either to the radial epicyclic (solid line), fobs = frad, or to the vertical epicyclic (dashed line), fobs = fver, frequency, in accordance with the twin peak QPO 3:2 resonance model. For a comparison, we also show the mass estimate based on an assumption that fobs = ΩK/2π is the Keplerian frequency at ISCO (dash-dotted line).

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.