| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 9 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201220066 | |
| Published online | 15 November 2012 | |
Physical properties of OSIRIS-REx target asteroid (101955) 1999 RQ36
Derived from Herschel, VLT/ VISIR, and Spitzer observations⋆,⋆⋆
1
Max-Planck-Institut für extraterrestrische Physik (MPE),
Giessenbachstrasse,
85748
Garching,
Germany
e-mail: tmueller@mpe.mpg.de
2
European Space Astronomy Centre (ESAC), European Space Agency,
Apartado de Correos 78, 28691 Villanueva de la Cañada, Madrid, Spain
3
Observatoire de Paris, Laboratoire d’Études Spatiales et
d’Instrumentation en Astrophysique (LESIA), 5 place Jules Janssen, 92195
Meudon Cedex,
France
4
Konkoly Observatory, Research Center for Astronomy and Earth
Sciences, Hungarian Academy of Sciences; Konkoly Thege 15–17,
1121
Budapest,
Hungary
5
Ludwig-Maximilians-Universität München,
Fakultät für Physik, Schellingstraße
4, 80799
München,
Germany
6
INSA at European Space Astronomy Centre (ESAC), European Space
Agency, Apartado de Correos 78, 28691 Villanueva de la Cañada,
Madrid,
Spain
Received: 20 July 2012
Accepted: 8 October 2012
In September 2011, the Herschel Space Observatory performed an observation campaign with the PACS photometer observing the asteroid (101955) 1999 RQ36 in the far infrared. The Herschel observations were analysed, together with ESO VLT/VISIR and Spitzer/IRS data, by means of a thermophysical model in order to derive the physical properties of 1999 RQ36. We find the asteroid has an effective diameter in the range 480 to 511 m, a slightly elongated shape with a semi-major axis ratio of a/b = 1.04, a geometric albedo of 0.045+0.015-0.012, and a retrograde rotation with a spin vector between –70 and –90° ecliptic latitude. The thermal emission at wavelengths below 12 μm-originating in the hot sub-solar region- shows that there may be large variations in roughness on the surface along the equatorial zone of 1999 RQ36, but further measurements are required for final proof. We determine that the asteroid has a disk-averaged thermal inertia of Γ = 650 Jm-2 s-0.5 K-1 with a 3-σ confidence range of 350 to 950 Jm-2 s-0.5 K-1, equivalent to what is observed for 25143 Itokawa and suggestive that 1999 RQ36 has a similar surface texture and may also be a rubble-pile in nature. The low albedo indicates that 1999 RQ36 very likely contains primitive volatile-rich material, consistent with its spectral type, and that it is an ideal target for the OSIRIS-REx sample return mission.
Key words: minor planets, asteroids: individual: (10955) 1999 RQ36 / radiation mechanisms: thermal / techniques: photometric / infrared: planetary systems
© ESO, 2012
1. Introduction
On May 25, 2011, NASA announced the selection of OSIRIS-REx as the third selected mission of its New Frontiers Program. The OSIRIS-REx mission will be launched in September 2016, fly by the Earth for a gravity assist in September 2017, and encounter the near-Earth asteroid (NEA) (101955) 1999 RQ36 (Lauretta et al. 2010) in November 2019. Proximity operations at the asteroid last through March 2021, when it will acquire up to 2 kg sample of its surface material. The sample return capsule will return to the Earth’s surface in September 2023.
Based on its visible spectrum, 1999 RQ36 is classified as a B-type and CM chondrite meteorites are considered to be the corresponding spectral analog (Clark et al. 2011). B-class asteroids are found mostly in the middle and outer regions of the main belt and are believed to be primitive and volatile-rich. However, the Polana family in the inner belt contains B-types, and dynamical studies have shown that 1999 RQ36 might be a liberated member of this family, considered as an important inner-belt source of low-albedo NEAs (Campins et al. 2010; Cellino et al. 2001). Additionally, since its orbit makes it especially accessible to spacecraft and it has been identified as a potentially hazardous asteroid (Milani et al. 2009), it was considered an ideal choice for NASA’s OSIRIS-REx sample return mission (Lauretta et al. 2012).
Radar images, taken during its previous two closest approaches in 1999 and in 2005 (and the next occurred in September 2011 when our observations were performed) found 1999 RQ36 to be an irregular spheroid about 580 m in diameter (Nolan et al. 2007). The nearly spheroidal shape suggests that it might be a strengthless rubble pile, formed by mechanisms similar to near-Earth binary systems (Walsh et al. 2008). The latest analysis, where all available radar data was combined with visible lightcurves (Nolan et al. 2012), derived a mean diameter of 493 ± 20 m (mean equatorial diameter of 545 ± 15 m) and a “spinning top” shape similar to 1999 KW4 (Ostro et al. 2006), but with a less well-defined equatorial ridge.
The object’s rotation period is 4.297812 ± 0.000001 h (Nolan et al. 2012), which was derived from combined radar and lightcurve measurements. This period is very similar to the 4.288 h found by Nolan et al. (2007) from radar measurements alone and to the 4.2968 ± 0.0017 h based on the analysis of lightcurves (Hergenrother et al. 2012) and about twice the value given in Krugly et al. (2002) derived from incomplete R-band lightcurve observations during the 1999 opposition. The rotation period suggests that it has not been greatly spun up by tidal or radiation forces. However, the radar-derived pole orientation (βpole = −90° ± 15°) is the equilibrium state for the YORP effect (Vokrouhlický et al. 2003). The negative pole orientation indicates a retrograde rotation.
Observation summary.
Emery et al. (2010) find a size of 610 m and estimate its thermal inertia to be around 600 Jm-2 s-0.5 K-1, assuming a moderate surface roughness (rms-slopes ~20°). Their results are based on Spitzer/IRS spectra and a dual-band thermal lightcurve, taken on May 3/4, 2007 at a phase angle of about 63°.
In this paper, we first present our PACS and VLT/VISIR Director discretionary awarded time (DDT) observations taken of 1999 RQ36 and their data reduction. We follow this with the description of the Spitzer/IRS measurements and the corresponding data reduction. We analyse the derived flux densities by means of our thermal model. We proceed to present our radiometrically derived properties (Sect. 3). In Sect. 4 we discuss the object’s size, shape, and albedo in a wider context and study the influences of surface roughness and thermal inertia in detail. We finally conclude the paper with a summary of all derived properties and with the implications of our results for the preparations for the OSIRIS-REx mission.
2. Observations of 1999 RQ36
2.1. Herschel/PACS observations and data processing
The European Space Agency’s (ESA) Herschel Space Observatory (Pilbratt et al. 2010), launched in 2009, performs observations from the 2nd Lagrangian point (L2) at 1.5 × 106 km from Earth. It has three science instruments on board covering the far-infrared part of the spectrum, of which the PACS photometer (covering the wavelength range of 60–210 μm) has been used to observe 1999 RQ36.
The PACS photometer (Poglitsch et al. 2010) imaged the asteroid on September 9, 2011 (between 19:00 and 21:00 UT) at a heliocentric distance of 1.0146–1.0144 AU and a Herschel-centric distance of 0.1742 AU, and the phase angle was 85.3–85.4°. The time used for the observation was DDT-awarded specifically due to this optimum closest approach to Earth. The 70/160 μm scan-map observation was repeated ten times (5 times at scanangle 70° and 5 times at 110°), the 100/160 μm observation was repeated 14 times (7 times in each scanangle).
The PACS scan-map measurements were processed using HIPE 7.0 (Ott et al. 2009). The reduction steps were very similar to those used for trans-Neptunian objects (Santos-Sanz et al. 2012; Mommert et al. 2012; Vilenius et al. 2012), including corrections for moving targets. The final, single-repetition PACS maps (10 at 70 μm, 14 at 100 μm, and 24 at 160 μm) have been median-averaged to remove (or at least decrease) the otherwise large instrumental noise. The background confusion noise has been eliminated as much as possible via techniques that have been developed for other moving sources (see detailed description in the electronic appendix in Santos-Sanz et al. 2012). The derived fluxes were aperture- and colour-corrected to obtain monochromatic flux densities at the PACS reference wavelengths. The colour correction values for 1999 RQ36 of 1.01, 1.02, 1.07 in blue (70 μm), green (100 μm) and red (160 μm) bands are based on a thermophysical model SED (spectral energy distribution), corresponding roughly to a 250 K black-body curve (PACS photometer passbands and colour correction factors, 2011). The flux calibration was verified by a set of five high-quality fiducial stars (β And, α Cet, α Tau, α Boo, and γ Dra), which were observed multiple times in the same PACS observing mode (PACS photometer – point source flux calibration, 2011).
The final values obtained for the PACS instrument datasets were deemed to be accurate within 5% based upon existing calibrations. The absolute flux calibration uncertainty is included in the values given in Table 1 (added quadratically to observational errors and errors related to aperture photometry). The fluxes given in Table 1 are colour-corrected, monochromatic flux densities at 70.0, 100.0, and 160.0 μm, the three PACS reference wavelengths for the blue, green, and red bands, respectively. Figure 1 shows the combined PACS images aligned with the output from our thermal model of what PACS has observed during its observation campaign.
2.2. VLT/ VISIR observations and data processing
Besides the DDT awarded for Herschel, we also were awarded DDT to observe 1999 RQ36 in September 2011 via ground-based N- and Q-band observations with the VLT/VISIR instrument (Lagage et al. 2004) mounted on the 8.2 m VLT telescope MELIPAL (UT 3) on Paranal.
The service-mode observers attempted twice to execute our four observing blocks in imaging mode, including each time the PAH1 (8.59 μm), NeII (12.81 μm), and the Q2 (18.72 μm) filters. The 1999 RQ36 observations were done in parallel nod-chop mode with a throw of 8′′. Owing to poor observing conditions and difficulties during the target acquisition phase, combined with end-of-night constraints, the science observations were never executed. Nevertheless, we found 1999 RQ36, with both the positive and two negative nod-chop beams on-chip, in the PAH1 target acquisition images taken on September 17, 2011 at an airmass of 1.79.
 |
Fig. 1 The combined PACS images (top), at 70 (blue), 100 (green), and 160 μm (red), along with the output from our thermal model (bottom) of 1999 RQ36, at the geometry of Herschel’s viewpoint. The shorter wavelengths effectively sampled the warmer facets of 1999 RQ36’s surface, located in the subsolar region. Note that Herschel cannot spatially resolve the target. |
We processed the four useful raw images using the VLT/VISIR pipeline Gasgano1 to produce a combined image suitable for aperture photometry. It was possible to calibrate those data using the standard star HD 217902 (9.923 Jy at 8.59 μm, taken at airmass 1.30) that was observed before the acquisition of 1999 RQ36 and another one, HD 16815 (11.679 Jy at 8.59 μm, taken at airmass 1.40), which was observed the day after in the same filter and observing mode. Based on the derived count-to-Jy conversion factors and the experience from large calibration programmes (Schütz & Sterzik 2005), we were also able to correct for the airmass difference between the calibration stars and our science target. The counts decrease by about 10% for an airmass increase of 0.5. The fluxes of the standard stars and our target were extracted in an identical way to standard aperture photometry techniques. In the case of 1999 RQ36 we checked that the first nod-chop pair was consistent with the second (i.e. that all three beams were in all the acquisition images) by also reducing them separately. The derived fluxes from each pair were consistent with those produced by combining both pairs together. We applied a colour correction of 1.004 (for 150–250 K blackbodies, considering the full atmosphere and bandpass transmission profiles) to the measured 1999 RQ36 flux to obtain a mono-chromatic flux density at the PAH1 reference wavelength (see Table 1). For the error calculation (Pantin et al., priv. comm.), we quadratically added the following error sources: error in count-to-Jy conversion factor (2%), error of stellar model (2%), photometry error (10%), error of colour correction (2%), estimated additional uncertainty for measurements at airmass larger than 1.5 (5%), and flat-field error for an off-centre position in the acquisition images (10%), summing up to a total of 15% error in the derived flux density.
2.3. Observations of 1999 RQ36 with the Spitzer Space Telescope
To complete the dataset, we also analysed and utilised data from the Spitzer Space Telescope (Werner et al. 2004). Emery et al. (2010) present part of these observations, but the results were based on a preliminary data reduction alone.
Spitzer observed 1999 RQ36 in different modes. Thermal IR spectra from 5.2 to 38 μm were taken with the Infrared Spectrograph (IRS) of opposite hemispheres of the body on 3/4 May 2007 21:42:03–22:46:57 (ID 21412352) and 23:48:51–00:53:40 UT (ID 21412608). Photometry at 16 and 22 μm was obtained with the IRS peak-up imaging (PUI) mode (IDs 21412864/4400/4912/3120/5168/8240/3632/4144/4656/3888/3376), taken at regular intervals between 3 May 2007 00:00:15 UT and 4 May 2007 11:11:37 UT. The 11 measurements cover the full rotation period uniformly. The phase angles, the heliocentric, and Spitzer-centric distances are given in Table 1.
The Spitzer/IRS observations were reduced with SPICE2 in the recommended way following the data analysis cookbook for moving targets3. We used the PBCD-products4 from the Spitzer Heritage Archive SHA5, subtracted the background measurements from the on-source measurements, and produced two spectra for each order in the short-low (SL) and long-low (LL) modules6, using the appropriate uncertainty and mask files. We averaged the resulting A-B and B-A spectra. The low flux in the SL2 range (5.2 to 7.5 μm) was averaged using a boxcar filter; in addition, we resampled the data in bins of uniform resolution R = λ/Δλ, with R = 40 (SL1: 7.6 to 14.3 μm) and R = 30 (SL2) to better measure the continuum signal of 1999 RQ36 and to reduce the number of data points for the thermophysical model (TPM) analysis. For each bin we determined the weighted averaged wavelength, the median flux, and the root-sum-square of the propagated errors, including a 5% absolute flux calibration error as specified by the Spitzer/IRS team. Our derived fluxes and errors agreed within the given errorbars with the published figures in Emery et al. (2010) and are shown in Fig. 2.
 |
Fig. 2 Both Spitzer IRS spectra (SL-part only) are shown together with 2 PUI measurements taken close in time at similar rotational phases. Our best TPM solution is shown as a solid line. |
2.4. Observation summary
In total, including the Herschel, VLT/VISIR and Spitzer dataset (see Table 1), we were able to place into our model a set of observations covering the wavelengths from 6 to 160 μm, phase angles of –63°, +85°, and +89° (positive before opposition, negative after opposition), and covering nicely all rotational phases. For the TPM analysis (Sect. 3) we use the true observing and illumination geometries (Spitzer-, Herschel-, VLT-centric) for each measurement individually as given in Table 1. The importance of this dataset becomes clear in the coming section where it can be seen that our comprehensive coverage of wavelength and phase angle is key to extracting the main thermal parameters output from our thermal model.
3. Thermophysical analysis of the observational data
We started the thermophysical model (TPM) analysis of the complete dataset by using a simple spherical shape model. For the object’s rotation period we used 4.297812 ± 0.000001 h (Nolan et al. 2012). Thermal data are very sensitive to the orientation of the spin axis (see e.g., Müller et al. 2011) and we used it as a free parameter in our analysis. Due to computing speed limitations we restricted this exercise to 60 different orientations for the rotation axis distributed over the entire sphere. The ecliptic latitude and longitude pairs to describe the spin vector orientation correspond to the 60 vertices of a mathematical description of a truncated icosahedron7 with 12 regular pentagonal faces and 20 regular hexagonal faces. To complete the picture, we added a few key spin axis orientations: pro- and retrograde rotations with the spin vector perpendicular to the ecliptic plane (βpole = ± 90°), pole-on viewing geometries as seen during the Spitzer, the Herschel, and the VISIR observations, and another four orientations (with βpole < −70°) to explore the YORP spin-up equilibrium state (Vokrouhlický et al. 2003), which corresponds to the latest value derived by Nolan et al. (2012): The obliquity 180° case for the spin vector (βpole = −83.98°, λpole = 92.17°) is very well covered by by this set of different spin axis orientations, which included values of –78°, –80°, and –90° for βpole (each time for a range of λpole values).
The spherical shape model with the almost 70 different spin axis orientations were imported into our TPM code (Lagerros 1996, 1997, 1998). Details about the techniques have recently been described in Müller et al. (2011) and O’Rourke et al. (2012). The TPM produces accurate thermal IR spectra and thermal lightcurves, taking a number of physical and thermal processes into account. In the TPM, the object is described by a given size, shape, spin-state, and albedo, placed at the true observing and illumination geometry. The TPM considers a 1-d heat conduction into the surface and allows surface roughness to be included, described by “f”, the fraction of the surface covered by spherical crater segments and “ρ”, the rms of the surface slopes, connected to the crater width-to-depth ratio (Lagerros 1998). A default setting (Müller et al. 1999) with ρ = 0.7 and f = 0.6 has been used as baseline.
The contributions of the subsurface emission at longer wavelength is accounted for by a wavelength-dependent emissivity decreasing from 0.9 at mid/far-IR (5 to 100 μm) to about 0.8 in the submillimetre/millimetre range of the spectrum, derived from a combined set of large main-belt asteroids (Müller & Lagerros 1998, 2002). Here, all radiometrically critical measurements are taken at wavelength below 100 μm, and there is no difference in using a constant emissivity of 0.9 or the wavelength-dependent emissivity model presented in Müller & Lagerros (2002).
For the full treatment of the energy balance on each surface facet within the model, we need to describe the amount of reflected light, described by the commonly used H-G-system (Bowell et al. 1989). The value for the absolute V-band magnitude HV was determined by Krugly et al. (2002) and recently refined by Hergenrother et al. (2012). The best value of HV = 20.65 mag was obtained by a linear phase function fit (phase slope β = 0.039 ± 0.005 mag) to V-band photometry covering the phase angle range from 15° to 100°. Hergenrother et al. (2012) discuss the issue of a shallow opposition effect for low-albedo asteroids and conclude that a more realistic HV-value for 1999 RQ36 would be 20.5 ± 0.3 mag. For G (slope parameter) we used the Krugly et al. (2002) value of 0.12.
Based on all available thermal data we searched for the best size and albedo solutions via well-established radiometric techniques (e.g., Harris & Lagerros 2002 and references therein) by using the above described settings. For each of the above spin vector orientations we calculated the reduced χ2-value for a wide range of typical thermal inertias (Delbo et al. 2007). We calculated the the reduced χ2-values in the following way: 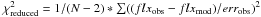 , with N the number of degrees of freedom. Figure 3 shows the result of the analysis. The lowest χ2 values are found for retrograde rotations (βpole < −70°) and thermal inertias around 600 Jm-2 s-0.5 K-1. The thermal inertia 3-σ confidence interval is from 400 to just above 1000 Jm-2 s-0.5 K-1. The 3-σ confidence interval
, with N the number of degrees of freedom. Figure 3 shows the result of the analysis. The lowest χ2 values are found for retrograde rotations (βpole < −70°) and thermal inertias around 600 Jm-2 s-0.5 K-1. The thermal inertia 3-σ confidence interval is from 400 to just above 1000 Jm-2 s-0.5 K-1. The 3-σ confidence interval  ) is based on actual χ2 = ∑ ((obs−mod)/err)2 calculations (not the reduced χ2 as shown in Fig. 3).
) is based on actual χ2 = ∑ ((obs−mod)/err)2 calculations (not the reduced χ2 as shown in Fig. 3).
 |
Fig. 3 χ2 test for the full set of spin vector orientations and the full range of thermal inertias. The retrograde solutions with βpole < −45° are given as solid lines, the prograde ones with βpole > +45° as dashed lines, the ones where the latitude of the rotation pole is in the range −45° < βpole < +45° are shown in dotted lines. The thicker solid and dashed lines represent the βpole = ± 90° solutions, the thick dashed-dotted line the Herschel pole-on geometry. |
Considering this possible Γ-range in combination with a spherical shape model and a pole axis pointing to the ecliptic south pole (βpole = −90°, retrograde rotation) leads to a size in the range 498 to 513 m and a geometric albedo pV in the range 0.043 to 0.046. The true errors are larger: (i) the TPM fit to the observations is not perfect (mainly due to the spherical shape model), and the rms of all observation/model ratios (see Figs. 4 and 5) has to be included (dominating error contribution for the diameter); (ii) the solution also depends slightly on the selected spin vector orientation within the possible range βpole < −70°; (iii) the H-magnitude is given with an error of ± 0.3 mag (dominating error contribution for the albedo). Combining all errors quadratically led to an effective size of 503 m for a spherical shape and a geometric albedo of
m for a spherical shape and a geometric albedo of  . These numbers are based on the assumption that 1999 RQ36 has a “default roughness” that is typical of large main-belt asteroids (see also discussion in Sect. 4 below).
. These numbers are based on the assumption that 1999 RQ36 has a “default roughness” that is typical of large main-belt asteroids (see also discussion in Sect. 4 below).
4. Discussions
4.1. Spin-axis orientation, sense of rotation
The before/after opposition data are the key element for extracting the sense of rotation. Our Herschel observations are all taken before opposition, i.e. leading the Sun (here positive phase angles). This means that Herschel has observed the target, while the unilluminated part of the surface was cold (see Fig. 1) corresponding to the pre-dawn part of the surface (for a retrograde sense of rotation). Spitzer has seen 1999 RQ36 after opposition when the unilluminated part was still warm after it had rotated out of the Sun (see Fig. 7). The importance of the sense of rotation can clearly be seen in Fig. 3. The prograde rotation options produced very high values for the reduced χ2 and can therefore be excluded with high confidence. The models with spin axes close to the ecliptic plane (including pole-on geometries) constrain the thermal inertia only very little; nevertheless, the reduced χ2-values are very high so these solutions can be ruled out. The TPM analysis clearly favours an axis orientation with βpole < −70° in the ecliptic coordinate system. This agrees with the findings by Nolan et al. (2012) that the pole is close to the equilibrium state for the YORP effect (Vokrouhlický et al. 2003). 1999 RQ36 has an orbit inclination of 6.02°, and Ω, the argument of ascending node, is 2.17°. The YORP predicted asymptotic zone with obliquity ϵ of 180° would therefore correspond to βpole = −83.98° and λpole = 92.17° in our convention, very close to the south ecliptic pole.
 |
Fig. 4 Ratio between the observed fluxes and the corresponding TPM predictions as a function of phase angle (negative: after opposition; positive: before opposition). The model calculations are based on a thermal inertia of 600 Jm-2 s-0.5 K-1 and ρ = 0.2 for the surface roughness. The VISIR data point can only be matched by assuming a higher surface roughness (see also Sect. 4.2 for further discussions). |
4.2. Surface roughness
Due to the lack of observations close to opposition, our dataset does not constrain very well the surface roughness that plays a more dominant role at phase angles close to opposition (Müller 2002). In Sect. 3 we used the “default roughness” that was derived for large main-belt asteroids that are covered with a low thermal conductivity regolith (Müller et al. 1999). To study the influence of roughness on the final size and albedo solutions, we analysed all thermal data, but this time for different levels of roughness. For simplicity, we assumed that 100% of the surface is covered by craters (f = 1.0), which is a reasonable assumption considering that the model crater definition also includes micro-craters down to very small scales where the geometric optics approximation is still valid (Müller & Lagerros 1998). We varied the rms of the surface slopes ρ in steps of 0.1 from a perfectly smooth surface (ρ = 0.0) to a very rough surface (ρ = 1.0) and repeated our radiometric analysis. The reduced χ2-minima indeed reach acceptable values for almost all levels of roughness: a very low surface roughness with ρ < 0.1 would lead to a thermal inertia of 450 Jm-2 s-0.5 K-1 which corresponds to an effective size of 490 m and a geometric albedo of pV = 0.047. A surface roughness with ρ > 0.9 would point to a thermal inertia of 850 Jm-2 s-0.5 K-1 with Deff = 508 m and pV = 0.044. This size range is entirely consistent with the possible range given by radar (Nolan et al. 2012), but it confirms that our dataset suffers from the degeneracy between surface roughness and thermal inertia. Figures 4 and 5 show the comparison between observations and model predictions assuming a roughness of ρ = 0.2 (with f = 1.0), similar to the moderate surface roughness (rms-slopes ~20°) used by Emery et al. (2010) to fit the IRS data.
The only data that do contain some information about roughness are the data at short wavelengths below 12 μm (IRS-spectrum and VISIR data point). The Wien part of the SED is strongly influenced by the hottest temperatures in the sub-solar region, while data at longer wavelengths beyond the thermal emission peak are more connected to the disk-averaged temperatures. This can be seen in Fig. 6: the low-roughness case fits the IRS-data very well (top of Fig. 6), but the model prediction for the VISIR data-point is overestimated by about 30%. If we use a high-roughness solution, then it is the other way round, where the VISIR data-point is well matched by the model prediction, but the IRS-spectrum divided by the corresponding model prediction shows a slight, wavelength-dependent mismatch (bottom of Fig. 6). The effects are small, and the VISIR data point has been taken in marginal conditions and as an acquisition frame. Also, modelling aspects like the implementation of surface roughness might play a role. The VISIR and IRS dataset are taken at very large and very different phase angles where the roughness effects on the IR beaming have not been studied very well. Nevertheless, the VISIR data point might indicate that we see variations in surface properties while the object is rotating. Based on the above specified rotation period, the two IRS spectra and the VISIR data are indeed taken at different rotational phases and correspond to different regions on the surface. A look at the reduced χ2-values seems to confirm this idea. The low-roughness model (top of Fig. 6) matches our thermal dataset very well (reduced χ2-values below 0.75), while the high roughness model (bottom of Fig. 6) clearly has problems with many of our data points (reduced χ2-values above 1.25), although it produces a perfect fit to the VISIR data point, which was taken at a unique rotational phase. But this aspect of surface roughness variations is clearly on vague grounds and should be confirmed via radar measurements or short-wavelength thermal lightcurves.
 |
Fig. 5 Ratio between the observed fluxes and the corresponding TPM predictions as a function of wavelength. |
 |
Fig. 6 Ratio between the observed fluxes and the corresponding TPM predictions as a function of wavelength. Top: assuming moderate surface roughness with a rms-slope of 0.2 gives a nice match to the 2 Spitzer/IRS spectra taken at opposite hemispheres (reduced χ2 < 0.75). Bottom: assuming a high surface roughness with a rms-slope >0.8 gives a nice match to the VLT/VISIR data point, but there remains a slight trend with wavelengths for the IRS data which are taken at different rotation phases (reduced χ2 > 1.25). |
We should note here that the thermal emission at wavelengths shorter than 12 μm originates mainly in the hottest sub-solar region, which is equatorial in the case of 1999 RQ36. Our speculation about possible surface roughness heterogeneity is therefore only related to a broad equatorial zone. Our dataset is not sensitive to roughness variations in the polar regions.
Roughness can in principle be present on any scale. Radar observations from Goldstone and Arecibo in 1999 and 2005 revealed a featureless surface down to the radar resolution limit of 7.5 m (Hudson et al. 2000; Nolan et al. 2007), but so far the radar team(s) have not investigated whether there are also variations in surface roughness seen in the radar echoes (Mike Nolan, priv. comm.).
4.3. Thermal inertia Γ
Pre- and post-opposition observations are the key to constraining the thermal inertia Γ, even more when the observations are taken at large phase angles (see Fig. 4). But, as described above, uncertainty remains because of the degeneracy between surface roughness effects and thermal inertia. From the exercise with different levels of roughness we find thermal inertias ranging from 450 to 850 Jm-2 s-0.5 K-1. If we also include variations for the spin pole (βpole = −90° ± 20°), the possible confidence range lies between 350 to 950 Jm-2 s-0.5 K-1, with the most likely value at 650 Jm-2 s-0.5 K-1.
A closer inspection of possible thermal inertias confirms that thermal inertias outside this range cause a very obvious mismatch between the data taken before opposition (positive phase angles in our convention) and the ones taken after opposition(negative phase angles): a figure similar to Fig. 4, but with thermal inertias less than 350 or greater than 950 Jm-2 s-0.5 K-1 would show a large imbalance between data taken before opposition and data taken after opposition. The determined Γ-range is close to the 600 Jm-2 s-0.5 K-1 derived by Emery et al. (2010) for 1999 RQ36 and also close to to Γ = 750 Jm-2 s-0.5 K-1 derived for (25143) Itokawa (Müller et al. 2005). Such a thermal inertia value indicates regions with high conductivity, i.e. coherent boulders. It can therefore be expected that the surface of 1999 RQ36 might show a similar texture to Itokawa’s: with zones with different surface rock size distributions, though possibly with fewer large boulders that would have shown up as surface features in the radar measurements (Nolan et al. 2012). But, as discussed before, our results are only connected to the warm region where the measured thermal flux originates. Other parts of the surface – at very large and very low latitudes – could have very different thermal properties. Seismic vibrations or YORP-introduced regolith turn-over (see Binzel et al. 2010, and references therein) could have influenced these “invisible” parts by moving material towards the equatorial region that we “see” in our thermal dataset. This means that our analysis does not preclude some regions with small grains.
4.4. Spheroidal or ellipsoidal shape
The visual lightcurves presented by Hergenrother et al. (2012) were taken at large phase angles between 60° and 70° and showed a low amplitude of 0.17 mag and a trimodal shape. It is not possible to reproduce the observed lightcurve shape with a simple ellipsoidal shape model of uniform albedo, but small shape deviations in combination with high phase angles could explain the trimodal lightcurve. The lightcurve amplitude (at a phase angle of 65°) can be reproduced by a slightly deformed body with an axis ratio of a/b = 1.04 and rotating around a c-axis that points at the ecliptic south pole. We tested if such a rotating ellipsoid in combination with our derived mean thermal inertia of 600 Jm-2 s-0.5 K-1 could also explain the two-band Spitzer/PUI thermal lightcurve (see also Fig. 2 presented in Emery et al. 2010). Axis ratios a/b above about 1.1 (for the given spin vector and thermal inertia) can be excluded on basis of these 16 and 22 μm lightcurves.
 |
Fig. 7 Top: Spitzer/PUI data with the TPM prediction overplotted. Bottom: the corresponding output from our thermal model of 1999 RQ36 as seen by Spitzer during its observation campaign. Spitzer cannot resolve the target spatially. |
Figure 7 shows the result as a function of rotational phase. The zero rotational phase was determined in 10° steps via a χ2-test against the observational Spitzer/PUI data. The thermal lightcurve of a slightly elongated shape model with a 180° obliquity of the spin vector (combined with the derived low surface roughness and a thermal inertia of 600 Jm-2 s-0.5 K-1) explains the different absolute flux levels at 16 and 22 μm very well and, at the same time, matches the two-band PUI thermal lightcurve and amplitude better than a simple spherical shape model. A lower thermal inertia would (for the given PUI observing geometry) increase the thermal lightcurve amplitude, a larger inertia would lower the amplitude. But the uncertainties of the individual PUI measurements and the remaining degeneracy with roughness do not allow constraining the thermal inertia even more. Unfortunately, the application of our PUI-derived rotating ellipsoidal model directly to the PACS dataset was not successful. The PACS data cover about 1.5 h of the rotation period, but the quality of the PACS dataset with respect to S/N and time resolution is not sufficient to repeat the thermal lightcurve exercise as we did for the PUI data. The predicted 70.0 μm lightcurve amplitude is about 1 mJy peak-to-peak, while the flux error of the best 70.0 μm data point is already 1.5 mJy.
4.5. Size
The unknowns in surface roughness influenced the optimum thermal inertia slightly (see above), but the size and albedo values did not change significantly. We repeated the exercise shown in Fig. 3 with a the low surface roughness (rms-slope ρ = 0.2), which produced the best match to the Spitzer/IRS data using a spherical and the ellipsoidal shape model specified above. The χ2 values are now a few percent lower due to the better fit to the shortest wavelength data and, in the case of the ellipsoidal shape model, also a better match to the PUI data. The χ2-minimum is pointing towards a thermal inertia of Γ = 650 Jm-2 s-0.5 K-1, resulting in an equivalent diameter of an equal volume sphere of 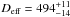 m when we consider the full 3-σ confidence level for the thermal inertia. The VISIR data are better matched by a relatively high roughness. The derived corresponding values are then
m when we consider the full 3-σ confidence level for the thermal inertia. The VISIR data are better matched by a relatively high roughness. The derived corresponding values are then 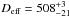 m (at ρ = 1.0, Γoptimum = 850 Jm-2 s-0.5 K-1). The equivalent size of 1999 RQ36 (of an equal volume sphere) is therefore in the range between 480 to 511 m. The true size error is probably a bit larger because the equator-on observing geometry does not allow us to “see” the pole regions in the mid-to-far-IR thermal emission.
m (at ρ = 1.0, Γoptimum = 850 Jm-2 s-0.5 K-1). The equivalent size of 1999 RQ36 (of an equal volume sphere) is therefore in the range between 480 to 511 m. The true size error is probably a bit larger because the equator-on observing geometry does not allow us to “see” the pole regions in the mid-to-far-IR thermal emission.
The derived diameter is significantly smaller than the 610 m derived from Spitzer measurements alone (Emery et al. 2010). Such a large size is clearly not compatible with the full set of thermal measurements. Emery (priv. comm.) confirms that the published size was produced by a simple thermal model (NEATM, Harris 1998), which is known to overestimate the diameters of asteroids by 15–20% especially when the thermal dataset is limited to only large phase angles (Harris 2006).
It is interesting to note that Hudson et al. (2000) used the first Goldstone radar images – taken in 1999 – to derive a diameter estimate of ~500 m, very close to our value. Their preliminary results indicate a remarkably featureless surface (down to the resolution limit of 19 m) and an almost spherical object, but they derived a wrong spin period of ~2 h. Later on, Nolan et al. (2007) used multiple radar data from 1999 and 2005, some of them taken with unusually good aspect coverage, and conclude from the combined dataset that 1999 RQ36 must be an irregular spheroid with about 580 m in diameter, more than 15% larger than our value. Only the recent work by Nolan et al. (2012) has brought the size back to the 500 m value.
4.6. Geometric albedo
The derived albedo is in the mid-range of values suggested for B-type asteroids (Tholen & Barucci 1989). But, as noted before, the albedo value depends directly on the H-magnitude. Our solution of  already includes the error of ± 0.3 in H-magnitude. If it turns out that the opposition effect of 1999 RQ36 is steeper or shallower than assumed for calculating of the H-magnitude, then the derived geometric albedo would also change. Hergenrother et al. (2012) provide, in addition to the above H-magnitude, HV and G by strictly following the IAU H−G photometric system for airless bodies (Bowell et al. 1989) and find HV = 19.90 ± 0.10 mag and G = −0.14 ± 0.02. The corresponding radiometric size would not change, but the geometric albedo could then be as high as pV = 0.085. The low albedos for near-Earth objects are believed to be connected to a primitive volatile-rich surface composition (Fernandez et al. 2005). But a dedicated orbital evolution and thermal history study by Delbo & Michel (2011) has shown that 1999 RQ36 has approached the Sun in the past to regions of q ≤ 0.8 (corresponding to about 400 K at the sub-solar point) with an 80% probability and with a lower probability even to q ≤ 0.6 (480 K at the sub-solar point). Such high temperatures alter the pristine properties of the surface material, because some of the expected primitive compounds already break up at moderate temperatures above 300 K, and the surface volatiles might be completely lost (e.g., Marchi et al. 2009). But the temperature maxima at 3–5 cm below the surface are already lower by 100 K, and organics have very likely been protected from thermal break-up (Delbo & Michel 2011).
already includes the error of ± 0.3 in H-magnitude. If it turns out that the opposition effect of 1999 RQ36 is steeper or shallower than assumed for calculating of the H-magnitude, then the derived geometric albedo would also change. Hergenrother et al. (2012) provide, in addition to the above H-magnitude, HV and G by strictly following the IAU H−G photometric system for airless bodies (Bowell et al. 1989) and find HV = 19.90 ± 0.10 mag and G = −0.14 ± 0.02. The corresponding radiometric size would not change, but the geometric albedo could then be as high as pV = 0.085. The low albedos for near-Earth objects are believed to be connected to a primitive volatile-rich surface composition (Fernandez et al. 2005). But a dedicated orbital evolution and thermal history study by Delbo & Michel (2011) has shown that 1999 RQ36 has approached the Sun in the past to regions of q ≤ 0.8 (corresponding to about 400 K at the sub-solar point) with an 80% probability and with a lower probability even to q ≤ 0.6 (480 K at the sub-solar point). Such high temperatures alter the pristine properties of the surface material, because some of the expected primitive compounds already break up at moderate temperatures above 300 K, and the surface volatiles might be completely lost (e.g., Marchi et al. 2009). But the temperature maxima at 3–5 cm below the surface are already lower by 100 K, and organics have very likely been protected from thermal break-up (Delbo & Michel 2011).
4.7. TPM concept
The calculations for the TPM beaming function for a rough surface are, strictly speaking, only applicable to the sunlit part of the asteroid (Lagerros 1998). A change in roughness changes the radiation field. A rougher surface has the tendency to emit or “beam” more in the solar direction at the expense of emission into larger phase angles. And this calculation is only done for the sunlit part of the surface. But even at large phase angles, the observed mid- and far-IR thermal emission is still dominated by the emission from the sunlit part of the object (~T4), the emission from the dark and cold part beyond the terminator is negligible with or without roughness. Only for sub-millimetre/millimetre/centimetre wavelengths observations at very large phase angles above 90° are the night side contributions not negligible anymore, and these assumptions might turn out to be problematic and might result in wrong predictions. Müller et al. (2005) used observations up to 110° phase angle to derive highly accurate size and albedo values for 25143 Itokawa. The corresponding roughness and thermal inertia settings (similar to the values found here) explain the observations taken at 27° and 54° with a similar accuracy to the observations taken at 108–110°, giving us confidence that our TPM setup is appropriate also for the 1999 RQ36 observations.
5. Conclusions
The Herschel DDT measurements of 1999 RQ36, combined with VLT/VISIR DDT measurements and data from the Spitzer Space, have allowed us to conclude that this asteroid has a diameter of an equal volume sphere in the range 480 to 511 m, considerably smaller than previously estimated radar and radiometric values (Emery et al. 2010; Nolan et al. 2007), but in good agreement with the recent mean diameter given by Nolan et al. (2012) of 493 ± 20 m. The thermal lightcurve variations are best-fit by an ellipsoidal shape model with a best fit a/b-ratio of of 1.04, corresponding to an ellipsoidal body with 509 × 489 × 489 m (±about 10 m in a- and b- and an unknown error in c-dimension). 1999 RQ36 has a geometric albedo 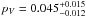 , in the nominal range for primitive volatile-rich NEAs of this type, and has a thermal inertia Γ = 650 ± 300 Jm-2 s-0.5 K-1, similar to Itokawa, a rubble pile asteroid. Our results further serve to confirm that the asteroid has a retrograde rotation with a spin vector between –70 to –90°. The inconsistency between the flux value derived from VISIR observations and the Spitzer/IRS dataset, taken at very different observing geometries, suggests there may be large variations in roughness on the surface. If the motion of surface material or regolith turnover processes are responsible for different terrains, then one can expect to find regions on the surface with very fresh material, at least at subsurface layers at several centimetres depth. The results of this work on the hypothesis that two different types of terrains exist with different levels of roughness and the possibility of having part of the surface with fine dust and pebbles is very important for the OSIRIS-REx mission sample mechanism strategy. A global mapping during the presampling phase will then allow the OSIRIS-REx team to select the most optimal area for collecting pristine and organic-rich material.
, in the nominal range for primitive volatile-rich NEAs of this type, and has a thermal inertia Γ = 650 ± 300 Jm-2 s-0.5 K-1, similar to Itokawa, a rubble pile asteroid. Our results further serve to confirm that the asteroid has a retrograde rotation with a spin vector between –70 to –90°. The inconsistency between the flux value derived from VISIR observations and the Spitzer/IRS dataset, taken at very different observing geometries, suggests there may be large variations in roughness on the surface. If the motion of surface material or regolith turnover processes are responsible for different terrains, then one can expect to find regions on the surface with very fresh material, at least at subsurface layers at several centimetres depth. The results of this work on the hypothesis that two different types of terrains exist with different levels of roughness and the possibility of having part of the surface with fine dust and pebbles is very important for the OSIRIS-REx mission sample mechanism strategy. A global mapping during the presampling phase will then allow the OSIRIS-REx team to select the most optimal area for collecting pristine and organic-rich material.
With this project we explore possibilities for thermophysical model techniques for an individual target that will soon be seen and characterised in detail. It will allow us to verify our findings on physical and thermal properties, as well as the proposed different surface terrains that are needed to explain the derived roughness and thermal inertia. Radiometric techniques are very powerful for deriving highly reliable size and albedo information, but signatures of surface texture, shape, spin-state, and thermal properties are also included in the object’s thermal emission. In fact, because thermal data is (or will soon be) available for many thousands of asteroids (IRAS, MSX, ISO, Akari, Spitzer, WISE, ground-based mid-IR/submm/mm programmes, etc.), the results from 1999 RQ36 can be considered to be the key to allowing us to transfer our model techniques to many other targets that will not be visited by spacecraft in the near future, but for which similar important questions can now be answered.
http://sha.ipac.caltech.edu/applications/Spitzer/SHA/ [May 7, 2012].
Acknowledgments
HSpot and HIPE are joint developments by the Herschel Science Ground Segment Consortium, consisting of ESA,the NASA Herschel Science Center, and the HIFI, PACS, and SPIRE consortia. We gratefully acknowledge the awarding of director discretionary time from the Herschel Space Observatory and ESO to support the work published here. We would also like to acknowledge the generous support by Mario van den Ancker (ESO) for installating and running of the VISIR pipeline and the support by Eric Pantin (CEA) and Ralf Siebenmorgen (ESO) for VISIR calibration and error calculation issues. Support for the Spitzer data reduction was provided by Sonia Fornasier, Josh Emery, and Jeffrey Van Cleve. It is also our pleasure to thank the Herschel Science Centre Mission Planning Team for their efforts in the optimal scheduling of these observations. Cs.K. and A.P. are supported by the ESA Grant PECS-98073 and by the Bolyai Research Fellowship of the Hungarian Acedemy of Sciences. We would also like to thank the anonymous referee for a very thorough and very constructive review of the manuscript.
References
- Binzel, R. P., Morbidelli, A., Merouane, S., et al. 2010, Nature, 463, 331 [Google Scholar]
- Bowell, E. 1989, Asteroids II; Proceedings of the Conference, Tucson, AZ, Mar. 8−11, 1988 (University of Arizona Press), 524 [Google Scholar]
- Campins, H., Morbidelli, A., Tsiganis, K., et al. 2010, ApJ, 721, 53 [Google Scholar]
- Cellino, A., Zappalá, V., Doressoundiram, A., et al. 2001, Icarus, 152, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, B. E., Binzel, R. P., Howell, E., et al. 2011, Icarus, 216, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Delbo, M., & Michel, P. 2011, ApJ, 728, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Delbó, M., Dell’Oro, A., Harris, A. W., et al. 2007, Icarus, 190, 236 [NASA ADS] [CrossRef] [Google Scholar]
- Dombard, A. J., Barnouin, O. S., Prockter, L. M., & Thomas, P. C. 2010, Icarus, 210, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Emery, J. P., Fernández, Y. R., Kelley, M. S., et al. 2010, 41st LPSC, LPI contribution No. 1533, 2282 [Google Scholar]
- Fernández, Y. R., Jewitt, D. C., & Sheppard, S. S. 2005, AJ, 130, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W. 1998, Icarus 131, 291 [Google Scholar]
- Harris, A. W. 2006, in Asteroids, Comets, Meteors, eds. D. Lazzaro, S. Ferraz-Mello, & J. A. Fernández, Proc. IAU Symp., 229, 2005 [Google Scholar]
- Harris, A. W., & Lagerros. J. S. V. 2002, Asteroids III, eds. W. F. Bottke Jr., A. Cellino, P. Paolicchi, & R. P. Binzel (Tucson: University of Arizona Press), 205 [Google Scholar]
- Hergenrother, C. W., Nolan, M., d’Aubigny, C., et al. 2012, LPS XXXXIII, Abstract #2219 [Google Scholar]
- Hudson, R. S., Ostro, S. J., Benner, L. A. M., et al. 2000, AAS DPS # 32, #07.10, BAAS 32, 1001 [Google Scholar]
- Krugly, Y. N., Belskaya, I. N., Shevchenko, V. G., et al. 2002, Icarus, 158, 293 [Google Scholar]
- Lagage, P. O., Pel, J. W., Authier, M., et al. 2004, The Messenger 117, 12 [Google Scholar]
- Lagerros, J. S. V. 1996, A&A, 310, 1011 [NASA ADS] [Google Scholar]
- Lagerros, J. S. V. 1997, A&A, 325, 1226 [NASA ADS] [Google Scholar]
- Lagerros, J. S. V. 1998, A&A, 332, 1123 [NASA ADS] [Google Scholar]
- Lauretta, D. S., Drake, M. J., Binzel, R. P., et al. 2010, M&PSA, 73, 5153 [Google Scholar]
- Lauretta, D. S., & The OSIRIS-REx Team 2012, LPS XXXXIII, Abstract #2491 [Google Scholar]
- Marchi, S., Delbó, M., Morbidelli, A., et al. 2009, MNRAS 400, 147 [Google Scholar]
- Milani, A., Chesley, S. R., Sansaturio, M. E., et al. 2009, Icarus, 203, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Mommert, M., Harris, A. W., Kiss, C., et al. 2012, A&A, 541, 93 [Google Scholar]
- Müller, T. G. 2002, M&PS, 37, 1919 [Google Scholar]
- Müller, T. G., & Lagerros, J. S. V. 1998, A&A, 338, 340 [NASA ADS] [Google Scholar]
- Müller, T. G., & Lagerros, J. S. V. 2002, A&A, 381, 324 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., Lagerros, J. S. V., Burgdorf, M., et al. 1999, in The Universe as Seen by ISO, eds. P. Cox, & M. F. Kessler, ESA-SP 427, 141 [Google Scholar]
- Müller, T. G., Sekiguchi, T., Kaasalainen, M., et al. 2005, A&A, 443, 347 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. G., Durech, J., Hasegawa, S., et al. 2011, A&A, 525, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolan, M. C., Magri, C., Ostro, S. J., et al. 2007, BAAS, 39, 433 [NASA ADS] [Google Scholar]
- Nolan, M. C., Magri, C., Benner, L. A. M., et al. 2012, ACM 2012 abstract # 6345, http://www.lpi.usra.edu/meetings/acm2012/pdf/6345.pdf [Google Scholar]
- O’Rourke, L., Müller, T. G., Valtchanov, I., et al. 2012, P&SS, 66, 192 [Google Scholar]
- Ostro, S. J., Margot, J.-L., Benner, L. A. M., et al. 2006, Science, 314, 1276 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, S. 2009, Herschel Interactive Processing Environment, HIPE, Proc. Astronomical Data Analysis Software and Systems XIX Conference, 434, 139 [Google Scholar]
- PACS photometerPoint Source Flux Calibration, Müller et al. 2011, PICC-ME-TN-037, Version 1.0, retrieved 29/Feb/2012; technical report available via URL: http://herschel.esac.esa.int/twiki/bin/view/Public/PacsCalibrationWeb/pacs_bolo_fluxcal_report_v1.pdf [Google Scholar]
- PACS Photometer Passbands and Colour Correction Factors for Various Source SEDs, Müller, T., Okumura, K., Klaas, U. 2011, PICC-ME-TN-038, Version 1.0, retrieved 29/Feb/2012; technical report available via URL: http://herschel.esac.esa.int/twiki/pub/Public/PacsCalibrationWeb/cc_report_v1.pdf [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos-Sanz, P., Lellouch, E., Fornasier, S., et al. 2012, A&A, 541, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schütz, O., & Sterzik, M. 2005, in High Resolution Infrared Spectroscopy in Astronomy, Proc. ESO Workshop held at Garching, Germany, 18–21 November 2003, eds. H. U. Käufl, R. Siebenmorgen, & A. Moorwood, 104 [Google Scholar]
- Tholen, D. J., & Barucci, A. M. 1989, Asteroids II, Proc. Conference, Tucson, AZ, Mar. 8–11, 1988 (University of Arizona Press), 298 [Google Scholar]
- Vilenius, E., Kiss, C., Mommert, M., et al. 2012, A&A, 541, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vokrouhlický, D., Nesvorný, D., & Bottke, W. F. 2003, Nature, 425, 147 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Walsh, K. J., Richardson, D. C., & Michel, P. 2008, Nature 454, 188 [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 The combined PACS images (top), at 70 (blue), 100 (green), and 160 μm (red), along with the output from our thermal model (bottom) of 1999 RQ36, at the geometry of Herschel’s viewpoint. The shorter wavelengths effectively sampled the warmer facets of 1999 RQ36’s surface, located in the subsolar region. Note that Herschel cannot spatially resolve the target. |
| In the text | |
 |
Fig. 2 Both Spitzer IRS spectra (SL-part only) are shown together with 2 PUI measurements taken close in time at similar rotational phases. Our best TPM solution is shown as a solid line. |
| In the text | |
 |
Fig. 3 χ2 test for the full set of spin vector orientations and the full range of thermal inertias. The retrograde solutions with βpole < −45° are given as solid lines, the prograde ones with βpole > +45° as dashed lines, the ones where the latitude of the rotation pole is in the range −45° < βpole < +45° are shown in dotted lines. The thicker solid and dashed lines represent the βpole = ± 90° solutions, the thick dashed-dotted line the Herschel pole-on geometry. |
| In the text | |
 |
Fig. 4 Ratio between the observed fluxes and the corresponding TPM predictions as a function of phase angle (negative: after opposition; positive: before opposition). The model calculations are based on a thermal inertia of 600 Jm-2 s-0.5 K-1 and ρ = 0.2 for the surface roughness. The VISIR data point can only be matched by assuming a higher surface roughness (see also Sect. 4.2 for further discussions). |
| In the text | |
 |
Fig. 5 Ratio between the observed fluxes and the corresponding TPM predictions as a function of wavelength. |
| In the text | |
 |
Fig. 6 Ratio between the observed fluxes and the corresponding TPM predictions as a function of wavelength. Top: assuming moderate surface roughness with a rms-slope of 0.2 gives a nice match to the 2 Spitzer/IRS spectra taken at opposite hemispheres (reduced χ2 < 0.75). Bottom: assuming a high surface roughness with a rms-slope >0.8 gives a nice match to the VLT/VISIR data point, but there remains a slight trend with wavelengths for the IRS data which are taken at different rotation phases (reduced χ2 > 1.25). |
| In the text | |
 |
Fig. 7 Top: Spitzer/PUI data with the TPM prediction overplotted. Bottom: the corresponding output from our thermal model of 1999 RQ36 as seen by Spitzer during its observation campaign. Spitzer cannot resolve the target spatially. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


