| Issue |
A&A
Volume 548, December 2012
|
|
|---|---|---|
| Article Number | L5 | |
| Number of page(s) | 4 | |
| Section | Letters | |
| DOI | https://doi.org/10.1051/0004-6361/201219813 | |
| Published online | 26 November 2012 | |
GRB 090618: a candidate for a neutron star gravitational collapse onto a black hole induced by a type Ib/c supernova
Dipartimento di Fisica and ICRASapienza Università di Roma,
P.le Aldo Moro 5, 00185 Rome, Italy ICRANet, P.zza
della Repubblica 10,
65122
Pescara,
Italy
e-mail: luca.izzo@icra.it; jorge.rueda@icra.it; ruffini@icra.it
Received:
13
June
2012
Accepted:
16
October
2012
A novel concept has recently been proposed for explaining the temporal coincidence of some gamma ray bursts (GRBs) with an associated supernova (SN) in terms of the gravitational collapse of a neutron star (NS) onto a black hole (BH), induced by a type Ib/c SN explosion. We applied these considerations to the exceptional case of GRB 090618, for which there is evidence of an SN ~ 10 days after the GRB occurrence. We calculated the accretion rate and total accreted mass onto an NS from an SN Ib/c that originated from a companion evolved star. These calculations show that the NS reaches the critical mass in a few seconds and undergoes gravitational collapse onto a BH, leading to the emission of a GRB. We find for the mass of the NS companion, MNS, and for the SN core progenitor, Mcore, the following mass ranges: 1.8 ≲ MNS/M⊙ ≲ 2.1 and 3 ≤ Mcore/M⊙ ≤ 8. Finally, we discuss the complementarity of these considerations to alternative processes explaining long and short GRBs.
Key words: accretion, accretion disks / binaries: general / gamma-ray burst: general / stars: neutron / supernovae: general
© ESO, 2012
The temporal coincidence of some gamma ray bursts (GRBs) and their associated supernovae (SNe) represent one of the most outstanding and hottest topic in relativistic physics and astrophysics. We recall that the optical emission of an SN reaches its maximum about 15 days after the SN explosion (see e.g. Arnett 1996). This implies that the onset of SNe and the occurrence of the GRB can be almost simultaneous (see e.g. Della Valle 2011; Hjorth & Bloom 2011, for a recent review on GRB-SN systems). For these reasons the concept of the induced gravitational collapse (IGC) was initially proposed (Ruffini et al. 2001) and further developed in Ruffini et al. (2008). Recently we have theoretically developed the basic equations describing this concept (Rueda & Ruffini 2012). In Rueda & Ruffini (2012) the GRB-SN connection has been explained in terms of the final stage of the evolution of a close binary system composed of an evolved star (likely a C+O star in the case of SN Ic) with a neutron star (NS) companion. The explosion of the SN Ib/c in this system leads to an accretion process onto the NS companion. The NS reaches the critical mass value in a few seconds, undergoing gravitational collapse onto a black hole (BH). The process of gravitational collapse onto a BH leads to the emission of the GRB. We have evaluated the accretion rate onto the NS and have given the explicit expression of the accreted mass as a function of the nature of the components and the binary parameters.
We turn now to an explicit quantitative description of the IGC process and compare the results with the observational data of GRB-SN. We apply these considerations in this Letter to the specific case of GRB 090618 and its associated SN. We recall that GRB 090618 is one of the nearest (z = 0.54) and at the same time more energetic GRBs (Eiso = 3 × 1053 erg) ever observed. Indeed, no beaming appears to be present from the data. These two important properties of GRB 090618 have produced an exceptional set of data from the very fortunate joint observations of the major satellites observing in X and γ rays: Fermi, Swift-BAT and XRT, AGILE, Suzaku-WAM, Konus-WIND, and Coronas PHOTON RT-2. This has allowed studying GRB 090618 in a very wide electromagnetic energy range, from 0.3 keV to 40 MeV. There have also been observations from the optical telescopes: from the Hubble Space Telescope, the Shane Telescope at the Lick Observatory, and from the Palomar 60-inch Telescope, which led to the clear identification of a late ~10 days optical bump in the afterglow light curve of GRB 090618 that is associated to the SN emission (Cano et al. 2011).
We have recently shown that GRB 090618 (Izzo et al.
2012) is composed of two sharply different emission episodes (see Fig. 1). A time-resolved spectral analysis showed that the first
episode, which lasts ~32 s in the rest frame, is characterized by a black-body emission that
evolves due to a decreasing temperature with time (see Fig. 17 in Izzo et al. 2012). Associated to the decreasing black-body temperature, the
radius of the emitter has been found to increase with time (see Figs. 2 and 18 in Izzo et al. 2012). From
radius evolution of the black-body emitter, we find that it expands at nonrelativistic
velocities (see Eq. (1), below). Consequently,
the first episode cannot be associated to a GRB. Because it happens prior to the GRB and
therefore to the BH formation, this first episode emission has been temporally called
proto-BH, 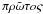 , from the ancient Greek, that
means, anteriority in space and time.
, from the ancient Greek, that
means, anteriority in space and time.
 |
Fig. 1 Fermi GRB (NaI 8-1000 keV) light curve of GRB 090618. We explicitly indicate the two episodes of GRB 090618, identified by Izzo et al. (2012). The first episode lasting 50 s in the observed frame corresponds to ~32 s in the rest frame of this source. |
We here identify the proto-BH of the first episode as the first stages of the SN expansion.
The black-body-emitting surface in the first episode evolves during the first ~32 s, as
observed in the rest frame, following a power-law behavior 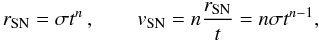 (1)where
σ = 8.048 × 108 cm s−n,
n ≈ 3/5 as shown in Fig. 2,
and vSN = drSN/dt
is the corresponding early SN velocity of the SN, so ~4 × 108 cm s-1
at the beginning of the expansion.
(1)where
σ = 8.048 × 108 cm s−n,
n ≈ 3/5 as shown in Fig. 2,
and vSN = drSN/dt
is the corresponding early SN velocity of the SN, so ~4 × 108 cm s-1
at the beginning of the expansion.
 |
Fig. 2 Radius evolution of the black-body emitter given by Eq. (1) in the first episode of GRB 090618 (Izzo et al. 2012), here assumed as the radius of the SN. The time is here measured in the rest frame, i.e. divided by a factor 1 + z, where z = 0.54, compared that one of the first episode given in Fig. 1. |
When the accreted mass onto the NS triggers the gravitational collapse of the NS onto a BH,
the authentic GRB emission is observed in the subsequent episode
at t − t0 ≳ 50 s (observer frame). The
characteristics of GRB 090618 are shown in Table 3 of Izzo
et al. (2012) and we refer to that reference for more details on the GRB light curve
and spectrum simulation. We find that the optically thick e+e− plasma
expands, reaching a bulk Lorentz factor Γ ~ 500 at a radius
of rtr = 1.4 × 1014 cm. At the transparency of
the e+e− plasma the proper GRB emission has been observed at a
temperature of 29 keV and the corresponding baryon load,
B ~ 2 × 10-3, has been obtained (see Sect. 5.2 in Izzo et al. 2012). The baryon load is defined
as 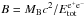 ,
where MB is the engulfed baryon mass from the progenitor remnant
and
,
where MB is the engulfed baryon mass from the progenitor remnant
and 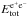 is the total energy of the e+e− plasma, which is assumed in the fit as
the total observed GRB isotropic energy. We obtained an average density of the circumburst
medium (CBM) of 0.6 particles cm-3, and each spike of the light curve corresponds
to an interaction of the expanding plasma with clouds of radius ≈ 1015 cm and
densities ≈ 2 particles cm-3 (see Fig. 10 in Izzo et al. 2012, for details).
is the total energy of the e+e− plasma, which is assumed in the fit as
the total observed GRB isotropic energy. We obtained an average density of the circumburst
medium (CBM) of 0.6 particles cm-3, and each spike of the light curve corresponds
to an interaction of the expanding plasma with clouds of radius ≈ 1015 cm and
densities ≈ 2 particles cm-3 (see Fig. 10 in Izzo et al. 2012, for details).
We now turn to the details of the accretion process of the SN material onto the NS. The NS of
initial mass MNS accretes mass from the SN ejecta at a rate given
by (see Rueda & Ruffini 2012, for details)
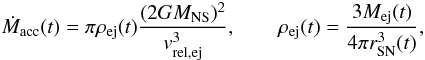 (2)where
(2)where
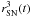 given by Eq. (1),
Mej(t) = Mej,0 − Macc(t)
is the available mass to be accreted by the NS as a function of time, with
Mej,0 the mass ejected in the SN.
given by Eq. (1),
Mej(t) = Mej,0 − Macc(t)
is the available mass to be accreted by the NS as a function of time, with
Mej,0 the mass ejected in the SN.
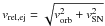 is the velocity of the ejecta relative to the NS, where vSN is the
SN ejecta velocity given by Eq. (1)
and
is the velocity of the ejecta relative to the NS, where vSN is the
SN ejecta velocity given by Eq. (1)
and 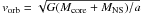 is the orbital velocity of the NS. Here Mcore is the mass of the
SN core progenitor and a the binary separation. Hereafter we
assume a = 9 × 109 cm, a value higher than the maximum distance
traveled by the SN material during the total time interval of Episode 1,
Δt ≃ 32 s, Δr ~ 7 × 109 cm (see Fig. 2).
is the orbital velocity of the NS. Here Mcore is the mass of the
SN core progenitor and a the binary separation. Hereafter we
assume a = 9 × 109 cm, a value higher than the maximum distance
traveled by the SN material during the total time interval of Episode 1,
Δt ≃ 32 s, Δr ~ 7 × 109 cm (see Fig. 2).
If the accreted mass onto the NS is much smaller than the initial mass of the ejecta, i.e.,
Macc/Mej,0 ≪ 1,
the total accreted mass can be obtained from the analytic expression given by Eq. (8) of Rueda & Ruffini (2012), which for GRB 090618 leads
to 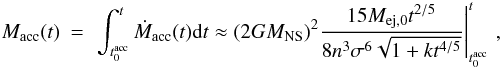 (3)where
(3)where
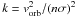 and
and 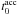 is the time at which
the accretion process starts, namely the time at which the SN ejecta reaches the NS capture
region,
is the time at which
the accretion process starts, namely the time at which the SN ejecta reaches the NS capture
region, 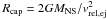 , so
for
, so
for 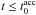 we
have Macc(t) = 0. The accretion process leads
to the gravitational collapse of the NS onto a BH when it reaches the critical mass value.
Here we adopt the critical
mass Mcrit = 2.67 M⊙ computed
recently by Belvedere et al. (2012). Eq. (3) is more accurate for massive NSs since the
amount of mass needed to reach the critical mass by accretion is much smaller
than Mej,0. In general, the total accreted mass
must be computed from the numerical integration of Eq. (2), which we present below for GRB 090618.
we
have Macc(t) = 0. The accretion process leads
to the gravitational collapse of the NS onto a BH when it reaches the critical mass value.
Here we adopt the critical
mass Mcrit = 2.67 M⊙ computed
recently by Belvedere et al. (2012). Eq. (3) is more accurate for massive NSs since the
amount of mass needed to reach the critical mass by accretion is much smaller
than Mej,0. In general, the total accreted mass
must be computed from the numerical integration of Eq. (2), which we present below for GRB 090618.
The occurrence of a GRB-SN event in the accretion induced collapse scenario is subjected to
some specific conditions of the binary progenitor system such as a short binary separation and
orbital period. The orbital period in the present case is 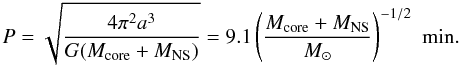 (4)We denote as
Δtacc the total time interval since the beginning of the SN
ejecta expansion all the way up to the instant where the NS reaches the critical mass. In
Fig. 4 we have plotted
Δtacc as a function of the initial NS mass, and for different
masses of the SN core progenitor mass. The mass of the SN ejecta assumed to
be Mej,0 = Mcore − Mrem,
where Mrem is the mass of the central compact remnant (NS) left
by the SN explosion. Here we
assumed Mcore = (3–8) M⊙ at the
epoch of the SN explosion,
and Mrem = 1.3 M⊙, following
some of the type Ic SN progenitors studied in Nomoto &
Hashimoto (1988); Nomoto et al. (1994); Iwamoto et al. (1994).
(4)We denote as
Δtacc the total time interval since the beginning of the SN
ejecta expansion all the way up to the instant where the NS reaches the critical mass. In
Fig. 4 we have plotted
Δtacc as a function of the initial NS mass, and for different
masses of the SN core progenitor mass. The mass of the SN ejecta assumed to
be Mej,0 = Mcore − Mrem,
where Mrem is the mass of the central compact remnant (NS) left
by the SN explosion. Here we
assumed Mcore = (3–8) M⊙ at the
epoch of the SN explosion,
and Mrem = 1.3 M⊙, following
some of the type Ic SN progenitors studied in Nomoto &
Hashimoto (1988); Nomoto et al. (1994); Iwamoto et al. (1994).
We can see from Fig. 4 that, for GRB 090618, the mass of the NS companion that collapses onto a BH should be in the range 1.8 ≲ MNS/M⊙ ≲ 2.1 corresponding to the SN Ic progenitors 3 ≤ Mcore/M⊙ ≤ 8.
The massive NS companion of the evolved star is in line with the binary scenario proposed by Ruffini et al. (2008). It is appropriate to illustrate a more accurate evolutionary scenario that leads to the occurrence of a GRB-SN event following the works of Nomoto & Hashimoto (1988); Nomoto et al. (1994); Iwamoto et al. (1994). The binary system is expected to evolve as follows: the initial binary system is composed of main-sequence stars 1 and 2 with a mass ratio M2/M1 ≳ 0.4. The initial mass of star 1 is expected to be M1 ≳ 11 M⊙, evolving through an SN event that leaves an NS. Star 2, now with M2 ≳ 11 M⊙ after some almost conservative mass transfer, evolves filling its Roche lobe. It then starts a spiral-in of the NS into the envelope of the star 2. Consequently, it will be composed of a helium star and an NS in close orbit. The helium star expands, filling its Roche lobe and a nonconservative mass transfer onto the NS takes place. This scenario naturally leads to a binary system composed of a C + O star and a massive NS, which can originate the process of IGC that we have proposed (Ruffini et al. 2008; Rueda & Ruffini 2012).
These results also agree with the well-understood Ib/c nature of the SN associated with GRBs. The most likely explanation for SN Ib/c, which lack H and He in their spectra, is that the SN progenitor star is in a binary system with an NS, see also Nomoto & Hashimoto (1988); Nomoto et al. (1994); Iwamoto et al. (1994) and also Tutukov & Fedorova (2007); Chevalier (2012)
In the current literature, the GRB-SN connection has at time been assumed to originate from a particularly violent SN process called hypernova or a collapsar (see e.g. Woosley & Bloom 2006, and references therein). Both of these possibilities imply a very dense and strong wind-like CBM structure. This dense medium is in contrast with the CBM density found in most GRBs (see e.g. Ruffini 2011). Specifically, for GRB 090618 the average CBM density, ⟨ n ⟩ , inferred from the analysis of the afterglow has been shown to be of ~1 particle cm-3 (see e.g. Fig. 10 and Table 3 in Izzo et al. 2012).The Lorentz gamma factor of the electron-positron plasma has been estimated to be Γ = 495 ± 40, corresponding to a baryon load B = (1.98 ± 0.15) × 10-3, (see Table 3 in Izzo et al. 2012). Such an ultra-relativistic expansion can only occur if the amount of engulfed baryon matter, quantifiable through the baryon load parameter B, does not exceed the critical value B ~ 10-2 (Ruffini et al. 2000). In view of the spherical symmetry of GRB 090618 this limit would be largely violated in the collapsar model.
It is also interesting to compare the results on the IGC of an NS to a BH by a type Ib/c supernova Rueda & Ruffini (2012) with the results of Chevalier (Chevalier 1989) on the accretion of a supernova material by the central NS generated by the supernova. A total accreted mass of up to 0.1 M⊙ in a time of a few hours was obtained there for normal type II SN. Thus, a similar amount of mass can be accreted in the two cases, but in the latter the accretion occurs over a longer time. To reach a high accretion rate of the inner SN material onto the central NS, a mechanism is needed that helps to increase the density of the NS surrounding layers, which is decreasing due to the expansion after being unbound by the SN explosion. Chevalier (1989) analyzed the possibility of having a reverse shock wave as this mechanism while it moves back through the SN core. The reverse shock is formed in the interaction of the mantle gas with the low-density envelope. The time scale of the accretion process is thus determined by the time it takes the reverse shock to reach the vicinity of the central newly born NS, which is a few hours in the case of SN II progenitors. However, the existence of a low-density outer envelope, e.g., H and He outer layers, is essential for the strength of the reverse shock. Fall-back accretion onto the central NS is expected to be relevant only in SN II but not in SN Ic like those associated to GRBs, where H and He are absent.
 |
Fig. 3 Time |
 |
Fig. 4 Time interval Δtacc of the accretion process onto the NS as a function of initial NS mass MNS for selected values of the SN core progenitor mass Mcore. The horizontal dashed line is the duration of the first episode of GRB 090618, Δt = 32.5 s, which constrains the duration of the time needed by the NS to reach the critical mass. The crossing points between the dashed horizontal line and the solid curves give the NSs with MNS that reach the critical mass in the time Δt. |
The argument presented in this Letter naturally explains the sequence of events: SN explosion
– IGC- BH formation – GRB emission. Correspondingly, the accretion of the material ejected by
the SN into the nearby NS of the IGC model presented here occurs almost instantaneously.
Indeed, for the SN expansion parameters obtained from the observations of Episode 1 in
GRB 090618 (see Eq. (1) and Fig. 2), the accretion of the SN material onto the nearby NS
occurs in a few seconds (see Figs. 3 and 4). The binary parameters are such that the ejecta density
does not decrease too much (from 106 to ~104 g cm-3) before
reaching the capture region of the NS, leading to a high accretion rate. As pointed out by
Chevalier (1989), radiative diffusion will lower the
accretion rate up to the Eddington limit (and then to even lower rates) when the trapping
radius of the radiation in the
flow rtr = κṀacc/(4πc)
(see Eq. (3.24) in Chevalier 1989),
where κ is the opacity, is equal to the Bondi
radius 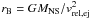 , the gravitational
capture radius. The radius rtr is located where the outward
diffusion luminosity is equal to the inward convective luminosity. It can be checked that for
the parameters of our system given by Eqs. (1)–(3), the
equality rtr = rB occurs in a
characteristic time ~200 days, where we
used κ = 0.2 cm2 g-1. Thus, this regime is not
reached in the present case since the NS is brought to its critical mass just in a few
seconds. In the case analyzed by Chevalier (1989), it
happens in a time ~8 days.
, the gravitational
capture radius. The radius rtr is located where the outward
diffusion luminosity is equal to the inward convective luminosity. It can be checked that for
the parameters of our system given by Eqs. (1)–(3), the
equality rtr = rB occurs in a
characteristic time ~200 days, where we
used κ = 0.2 cm2 g-1. Thus, this regime is not
reached in the present case since the NS is brought to its critical mass just in a few
seconds. In the case analyzed by Chevalier (1989), it
happens in a time ~8 days.
It is also appropriate, before concluding, to consider possible astrophysical systems that might have been the precursor of the GRB 090618 and its associated SN, as well as their possible final outcome.
As for the precursor, a natural candidate are binary X-ray sources formed by an NS in a binary system with a main-sequence companion, where the masses of the NS are observed to be close to the canonical value 1.4 M⊙, e.g. Cen X-3 and Her X-1 (Schreier et al. 1972; Wilson 1972; Tananbaum et al. 1972; Leach & Ruffini 1973; Davidson & Ostriker 1973; Gursky & Ruffini 1975); see also Rawls et al. (2011), for up-to-date estimates of the mass of the NSs in the X-ray binaries Vela X-1, 4U 1538-52, SMC X-1, LMC X-4, Cen X-3, and Her X-1.
As for the possible final outcome, we consider the final state after the explosion of the SN and the trigger of the GRB. There is still a possibility of forming an NS-BH binary system. The outcome of the SN explosion leads necessarily to the formation of an NS: evidence can be acquired by the observation of a characteristic late-time X-ray emission (called URCA sources, see Ruffini et al. 2005). This emission has been interpreted as originating from the young (t ~ 1 min–(10–100) years), hot (T ~ 107–108 K) NS, which we have called neo-NS (see Negreiros et al. 2012, for details). This emission can indeed be observed in the afterglow light curves of GRB 090618 (see e.g. Izzo et al. 2012) and GRB 101023 (see e.g. Penacchioni et al. 2012). If the neo-NS and the BH are gravitationally bound after the GRB-SN emission, this new binary system might lead itself to a new merging process to a single BH. In this case the system could originate yet another GRB with a possibly predominant emission in gravitational waves.
In conclusion, the IGC binary scenario applied here to the specific case of GRB 090618 naturally leads to understanding the energetics and the temporal coincidence of SN and GRBs, as well as their astrophysical scenario and makes. It also provides new predictions on the final outcomes. It originates from a binary system composed of an evolved core and an NS. It is clear, however, that these GRBs and their associated SNe form a special class of long GRBs and of SNe Ib/c. There are in fact SNe Ib/c that are not associated to a GRB, e.g., SN 1994I (Immler et al. 2002) and SN 2002ap (Soria et al. 2004). Their observations refer to late phases of the SN evolution typically ~15–20 days after the original collapse process. The existing descriptions of these late phases after 15–20 days from the original explosion make use of a Sedov-type behavior r ∝ t2/5 (Sedov 1946, 1959). In the present case of the IGC we are presenting here for the first time, the first ~30 s of the very early evolution of an SN Ib/c associated to a GRB (see Eq. (1) and Fig. 2). The energetic of this SN Ib/c, as shown from Episode 1, appears to be much higher than the ones of the usual SNe Ib/c not associated to GRBs, Eiso,Epi1 ∝ 1052 erg (Izzo et al. 2012). The reason for this marked difference is certainly due to the accretion process during an SN explosion into the companion NS and consequent gravitational collapse of the NS onto a BH. The description of this challenging process, although clear from a general energetic point of view, has still to be theoretically explored in detail and certainly does not present any relation to the Sedov-type solution.
From the point of view of the long GRBs, it is clear that the IGC concept leads to the formation of a BH of typical mass just larger than the critical mass of NS.
There are of course GRBs originating in binary-NS systems clearly do not have an associated SN, e.g. GRB 090227B
(Muccino et al. 2012). These binary systems clearly depart from the one studied in Rueda & Ruffini (2012) and in this Letter. For selected masses of the NS, such binary system leads to a short GRB with very low value of the baryon load, corresponding to genuine short GRBs. There are also systems such as GRB 060614 that do not show an SN (Della Valle et al. 2006; Gal-Yam et al. 2006) and that are expected to be originating possibly from yet a different binary system formed by a white dwarf and an NS (Caito et al. 2009).
Finally, it is appropriate to recall a selection effect in the study of the IGC scenario. Only for systems with cosmological redshift z ≲ 1 the current optical instrumentation allows the observation of the related SN Ib/c. A particularly challenging analysis is that of the system GRB 101023 (Penacchioni et al. 2012) in which the SN is not detectable but the IGC nature of the source is clearly recognized by the two different episodes in the GRB sources and the spectral features of the first episode.
Acknowledgments
We thank Massimo Della Valle for many years of discussions. We are grateful to the anonymous referee for important remarks that have improved the presentation of our results.
References
- Arnett, D. 1996, Supernovae and nucleosynthesis. an investigation of the history of matter, from the Big Bang to the present (Princeton University Press) [Google Scholar]
- Belvedere, R., Pugliese, D., Rueda, J. A., Ruffini, R., & Xue, S.-S. 2012, Nucl. Phys. A, 883, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Caito, L., Bernardini, M. G., Bianco, C. L., et al. 2009, A&A, 498, 501 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cano, Z., Bersier, D., Guidorzi, C., et al. 2011, MNRAS, 413, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 1989, ApJ, 346, 847 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A. 2012, ApJ, 752, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., & Ostriker, J. P. 1973, ApJ, 179, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Della Valle, M. 2011, Int. J. Mod. Phys. D, 20, 1745 [Google Scholar]
- Della Valle, M., Chincarini, G., Panagia, N., et al. 2006, Nature, 444, 1050 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gal-Yam, A., Fox, D. B., Price, P. A., et al. 2006, Nature, 444, 1053 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gursky, H., & Ruffini, R. 1975, Neutron stars, black holes and binary X-ray sources; Proc. of the Annual Meeting, San Francisco, Calif., February 28, 1974, Astrophys. Space Sci. Libr., 48 [Google Scholar]
- Hjorth, J., & Bloom, J. S. 2011, in Gamma-Ray Bursts, eds. C. Kouveliotou, R. A. M. J. Wijers, & S. E. Woosley (Cambridge University Press) [Google Scholar]
- Immler, S., Wilson, A. S., & Terashima, Y. 2002, 573, L27 [Google Scholar]
- Iwamoto, K., Nomoto, K., Hoflich, P., et al. 1994, ApJ, 437, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Izzo, L., Ruffini, R., Penacchioni, A. V., et al. 2012, A&A, 543, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leach, R. W., & Ruffini, R. 1973, ApJ, 180, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Muccino, M., Ruffini, R., Bianco, C. L., Izzo, L., & Penacchioni, A. V. 2012, ApJ, submitted [arXiv:1205.6600] [Google Scholar]
- Negreiros, R., Ruffini, R., Bianco, C. L., & Rueda, J. A. 2012, A&A, 540, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nomoto, K., & Hashimoto, M. 1988, Phys. Rep., 163, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Nomoto, K., Yamaoka, H., Pols, O. R., et al. 1994, Nature, 371, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Penacchioni, A. V., Ruffini, R., Izzo, L., et al. 2012, A&A, 538, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rawls, M. L., Orosz, J. A., McClintock, J. E., et al. 2011, ApJ, 730, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Rueda, J. A., & Ruffini, R. 2012, ApJ, 758, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffini, R. 2011, Int. J. Mod. Phys. D, 20, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffini, R., Salmonson, J. D., Wilson, J. R., & Xue, S.-S. 2000, A&A, 359, 855 [NASA ADS] [Google Scholar]
- Ruffini, R., Bianco, C. L., Fraschetti, F., Xue, S.-S., & Chardonnet, P. 2001, ApJ, 555, L117 [Google Scholar]
- Ruffini, R., Bernardini, M. G., Bianco, C. L., et al. 2005, in The Tenth Marcel Grossmann Meeting. On recent developments in theoretical and experimental general relativity, gravitation and relativistic field theories, eds. M. Novello, S. Perez Bergliaffa, & R. Ruffini (Singapore: World Scientific), 369 [Google Scholar]
- Ruffini, R., Bernardini, M. G., Bianco, C. L., et al. 2008, in The Eleventh Marcel Grossmann Meeting, eds. H. Kleinert, R. T. Jantzen, & R. Ruffini, 368 [Google Scholar]
- Schreier, E., Levinson, R., Gursky, H., et al. 1972, ApJ, 172, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Sedov, L. I. 1946, Compt. Rend. (Doklady) Acad. Sci. URSS, 52, 17 [Google Scholar]
- Sedov, L. I. 1959, Similarity and Dimensional Methods in Mechanics (New York: Academic Press) [Google Scholar]
- Soria, R., Pian, E., & Mazzali, P. A. 2004, 413, 107 [Google Scholar]
- Tananbaum, H., Gursky, H., Kellogg, E. M., et al. 1972, ApJ, 174, L143 [NASA ADS] [CrossRef] [Google Scholar]
- Tutukov, A. V., & Fedorova, A. V. 2007, Astron. Rep., 51, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E. 1972, ApJ, 174, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Woosley, S. E., & Bloom, J. S. 2006, ARA&A, 44, 507 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Fermi GRB (NaI 8-1000 keV) light curve of GRB 090618. We explicitly indicate the two episodes of GRB 090618, identified by Izzo et al. (2012). The first episode lasting 50 s in the observed frame corresponds to ~32 s in the rest frame of this source. |
| In the text | |
 |
Fig. 2 Radius evolution of the black-body emitter given by Eq. (1) in the first episode of GRB 090618 (Izzo et al. 2012), here assumed as the radius of the SN. The time is here measured in the rest frame, i.e. divided by a factor 1 + z, where z = 0.54, compared that one of the first episode given in Fig. 1. |
| In the text | |
 |
Fig. 3 Time |
| In the text | |
 |
Fig. 4 Time interval Δtacc of the accretion process onto the NS as a function of initial NS mass MNS for selected values of the SN core progenitor mass Mcore. The horizontal dashed line is the duration of the first episode of GRB 090618, Δt = 32.5 s, which constrains the duration of the time needed by the NS to reach the critical mass. The crossing points between the dashed horizontal line and the solid curves give the NSs with MNS that reach the critical mass in the time Δt. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


