| Issue |
A&A
Volume 547, November 2012
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 11 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201219512 | |
| Published online | 19 October 2012 | |
Kelvin-Helmholtz instability of kink waves in photospheric twisted flux tubes
1
Faculty of Physics, Sofia University,
5 James Bourchier Blvd.,
1164
Sofia,
Bulgaria
e-mail: izh@phys.uni-sofia.bg
2
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstrasse 6,
8042
Graz,
Austria
e-mail: teimuraz.zaqarashvili@oeaw.ac.at
3
Abastumani Astrophysical Observatory at Ilia State University, 2
University Street, 0160
Tbilisi,
Georgia
Received:
30
April
2012
Accepted:
11
September
2012
Aims. We investigate conditions under which kink magnetohydrodynamic waves propagating along photospheric uniformly twisted flux tubes with axial mass flows become unstable as a consequence of the Kelvin-Helmholtz instability.
Methods. We employed the dispersion relations of kink waves derived from the linearised magnetohydrodynamic equations. We assumed real wave numbers and complex angular wave frequencies, namely complex wave phase velocities. The dispersion relations were solved numerically at fixed input parameters and several mass flow velocities.
Results. We show that the stability of the waves depends upon four parameters, the density contrast between the flux tube and its environment, the ratio of the background magnetic fields in the two media, the twist of the magnetic field lines inside the tube, and the value of the Alfvén-Mach number (the ratio of the jet velocity to Alfvén speed inside the flux tube). We assume that the azimuthal component of the magnetic field in the tube is proportional to the distance from the tube axis and that the tube is only weakly twisted (i.e., the ratio of the azimuthal and axial components of the magnetic field is low). At certain densities and magnetic field twists, an instability of the Kelvin-Helmholtz type of kink (m = 1) mode can arise if the Alfvén-Mach number exceeds a critical value. In particular, for an isolated twisted magnetic flux tube (magnetically free environment) at a density contrast (the ratio of the mass density of the environment to that of the tube itself) equal to 2 and a magnetic field twist (defined as the ratio of azimuthal magnetic field component at the inner surface of the tube to the background magnetic field strength) equal to 0.4, the threshold Alfvén-Mach number has a magnitude of 1.250075, which means that for an Alfvén speed inside the tube of 10 km s-1 the jet velocity should be higher than 12.5 km s-1 to ensure the onset of the Kelvin-Helmholtz instability of the kink (m = 1) mode. Speeds of that order can be detected in photospheric tubes.
Conclusions. The observed mass flows may trigger the Kelvin-Helmholtz instability of the kink (m = 1) mode in weakly twisted photospheric magnetic flux tubes at critical Alfvén-Mach numbers lower that those in untwisted tubes if the magnetic field twist lies in the range 0.36−0.4 and the flow speed exceeds a critical value. A weak external magnetic field (with a ratio to the magnetic field inside the tube in the range 0.1−0.5) slightly increases that critical value.
Key words: magnetohydrodynamics (MHD) / waves / plasmas / magnetic fields / methods: numerical
© ESO, 2012
1. Introduction
With the wealth of recent high-resolution observations from SDO, Hinode, Stereo, TRACE, SOHO, and RHESSI as well as from ground-based observations, the concepts of the magnetic flux tube and coronal loops have become increasingly important for understanding explosive phenomena such as solar flares and eruptive prominences and also for the problem of the solar corona heating mechanism. The observations reveal a wide range of shapes and sizes, ranging from the small-size magnetic flux tubes found in the granular network, sunspots, coronal loops, and arcades with many loops to huge loops such as prominences. The registered mass flows speeds in these magnetic tubes range from a few tens of kilometers per second in the photosphere/chromosphere (Shibata et al. 2007; Katsukawa et al. 2007; De Pontieu et al. 2007) up to hundreds or thousands of kilometers per second in coronal holes and X-ray jets (Shimojo & Shibata 2000; Cirtain et al. 2007; Ofman & Wang 2008; Wallace et al. 2010; Madjarska 2011; Kamio et al. 2011; Tian et al. 2011; Srivastava & Murawski 2011).
An additional feature of the flux tube is its twist. There is observational evidence for a twist in the solar atmosphere. Aschwanden et al. (1999) confirmed the existence of twisted loops in the corona by detecting a post-flare loop system in extreme ultraviolet wavelengths (171 Å) with the Coronal Explorer (TRACE). Rotational movement along a loop as observed in the active region NOAA 8668 of the photosphere by Chae et al. (2001) indicates that there is a twist in the magnetic field lines. More recently, Srivastava et al. (2010), using multi-wavelength observations of SOHO/MDI, SOT-Hinode/blue-continuum (4504 Å), G band (4305 Å), Ca ii H (3968 Å), and TRACE 171 Å, presented the observational signature of a strongly twisted magnetic loop in AR 10960 during the period 04:43−04:52 UT on June 4, 2007.
It is well-known that the hydromagnetic flows are generally unstable against the Kelvin-Helmholtz instability when the flow speed exceeds a certain threshold/critical value (Chandrasekhar 1961). Recent observations of Kelvin-Helmholtz vortices (Foullon et al. 2011; Ofman & Thompson 2011) increased the interest in flow instability in the solar corona. On the other hand, the twisted magnetic field itself can cause the so-called kink instability even when there is no flow. The stability of static twisted magnetic flux tubes has also been studied extensively in the context of laboratory plasma (e.g., Shafranov 1957; Kruskal et al. 1958). Magnetic tubes are subject to the kink instability when the twist exceeds a critical value (Lundquist 1951; Hood & Priest 1979). Oscillations and waves and their stability in twisted magnetic flux tubes without flow have been studied in the framework of the normal mode analysis in earlier works (see Dungey & Loughhead 1954; Roberts 1956; Trehan 1958; Bogdan 1984; Linton et al. 1996; Bennett et al. 1999; Erdélyi & Carter 2006; Erdélyi & Fedun 2006; 2007; 2010; Ruderman 2007; Carter & Erdélyi 2008; Ruderman & Erdélyi 2009; Karami & Barin 2009; and Karami & Bahari 2010). Most of these papers deal with relatively simple twisted magnetic configurations: incompressible plasma cylinders/slabs surrounded by perfectly conducting unmagnetised plasma or a medium with an untwisted homogeneous magnetic field. Erdélyi & Fedun (2006) were the first to study the wave propagation in a twisted cylindrical magnetic flux tube embedded in an incompressible but also magnetically twisted plasma. A more complex magnetic field configuration has been studied by Erdélyi & Carter (2006), who investigated the propagation of magnetohydrodynamic (MHD) waves in a fully magnetically twisted flux tube consisting of a core, an annulus, and an external region. These authors considered magnetic twist just in the annulus, while the internal and external regions retained a straight magnetic field. Two modes of sausage oscillations occur in this configuration, notably pure surface (i.e., evanescent) and hybrid (spatially oscillatory in the twisted annulus, otherwise evanescent) waves. The propagation characteristics of the kink mode in the same magnetically twisted annulus have been studied by Carter & Erdélyi (2008). The influence of compressibility on the dispersion characteristics of the sausage mode (m = 0) propagating in a magnetically twisted flux tube embedded in a compressible uniformly magnetised plasma environment in cylindrical geometry has been investigated by Erdélyi & Fedun (2007). That analysis has been generalised by the authors (see Erdélyi & Fedun 2010) for the kink mode (m = 1), as well as for the fluting modes (m > 1); m being the azimuthal order of a given mode. The last work by Erdélyi & Fedun (2010) – the most elaborate study to date – deals with the MHD wave propagation along twisted magnetic tubes of compressible ideal plasma surrounded by also compressible but uniformly magnetised fully ionized medium. The effect of a twisted magnetic field on the spectra and the resonant absorption of kink and fluting surface modes in resistive incompressible cylindrical plasmas have been studied by Karami & Barin (2009) and Karami & Bahari (2010). It was found that a magnetic twist will increase the frequencies, damping rates, and the ratio of the oscillation frequency to the damping rate of these modes. The period ratio P1/P2 of the fundamental and its first-overtone surface waves for kink (m = 1) and fluting (m = 2,3) modes is lower than two (the value for an untwisted loop) in the presence of a twisted magnetic field. In particular, for the kink modes, the magnetic twists Bφ/Bz = 0.0065 and 0.0255 can achieve deviations from two of the same order of magnitude as in the observations. The only work studying the wave propagation in a twisted magnetic tube with a mass density variation along the tube is that of Ruderman (2007). He investigated non-axisymmetric oscillations of thin (tube radius a much smaller than the finite tube length L) twisted magnetic tubes in a zero-beta plasma. With an asymptotic analysis, Ruderman (2007) showed that the eigenmodes and the eigenfrequencies of the kink and fluting oscillations are described by a classical Sturm-Liouville problem for a second-order ordinary differential equation. He also concluded that the results concerning non-axisymmetric waves in twisted magnetic tubes obtained by Bennett et al. (1999) for incompressible plasmas can be applied to global non-axisymmetric modes, i.e., kink and fluting modes, in coronal loop even though the coronal plasma is a low-beta plasma. This conclusion also agrees well with the results obtained by Erdélyi & Fedun (2007).
An open question is how a flow along a twisted magnetic flux tube will change the dispersion properties of the propagating modes and their stability. It turns out that the flow may decrease the threshold for the kink instability, as was tested experimentally in a laboratory twisted plasma column (Furno et al. 2007). This observation was theoretically confirmed by Zaqarashvili et al. (2010). The authors studied the influence of axial mass flows on the stability of an isolated twisted magnetic tube of incompressible plasma embedded in a perfectly conducting unmagnetised plasma. Two main results were found. First, the axial mass flow reduces the threshold of the kink instability in twisted magnetic tubes. Second, the twist of the magnetic field leads to the Kelvin-Helmholtz instability of sub-Alfvénic flows for the harmonics with a sufficiently large azimuthal mode number m. The effect is more significant for photospheric magnetic flux tubes than for coronal ones. In a recent paper, Díaz et al. (2011) also studied the equilibrium and stability of twisted magnetic flux tubes with mass flows, but for flows along the field lines. The authors focused on the stability and oscillatory modes of magnetic tubes with a uniform twist in a zero-beta plasma surrounded by a uniform cold plasma embedded in a purely longitudinal magnetic filed. Regarding the equilibrium, the authors claimed that the only value of the flow that satisfies the equations for their magnetic field configuration is a super-Alfvénic one. The main conclusion is that the twisted tube is subject to the kink instability unless the magnetic field pitch is very high, since the Lundquist criterion is significantly lowered. This is caused by the requirement of having an Alfvén-Mach number greater than 1, so the magnetic pressure balances the magnetic field tension and fluid inertia. The authors suggest that this type of instability might be observed in some solar atmospheric structures, such as surges.
Kink waves are frequently observed in the chromospheric spectral lines as a periodic Doppler shift and/or periodic spatial displacement of the tube axis (Kukhianidze et al. 2006; Zaqarashvili et al. 2007; Zaqarashvili & Erdélyi 2009; He et al. 2009; Pietarila et al. 2011; Tavabi et al. 2011; Ebadi et al. 2012). Most of the observations have been associated to spicules, which are chromospheric plasma jets. It is well known that a simple hydrodynamic jet is unstable against the antisymmetric (kink) mode (Drazin 2002; Zaqarashvili 2011), therefore the observed periodic displacements can be connected to the unstable kink mode of a plasma jet in spicules. However, the magnetic field of spicules may significantly influence the stability of the kink mode in the plasma jet, therefore studying the instability of m = 1 mode of the jet in a magnetic cylinder is of vital importance.
In the present work, our aim is to investigate the effect of a twisted magnetic field on the stability of kink (m = 1) waves propagating on a cylindrical incompressible radially homogeneous tube with axial mass flow, assuming that the waves are subject, under certain conditions, to the Kelvin-Helmholtz instability. To evaluate that effect, we compare the critical flow speeds at which the instability occurs with those in the untwisted magnetic tubes. It is necessary to point out that our simplified model of radially homogeneous plasma density inside the tube rules out the resonant absorption of MHD modes that can modify both the wave frequency spectrum and conditions under which the Kelvin-Helmholtz instability occurs. The radial density inhomogeneity is usually introduced as a nonuniform transition layer that continuously connects the internal density to the external one. Owing to this transverse inhomogeneous transitional layer, wave modes with m ≠ 1 are spatially damped by resonant absorption. In particular, the effect of longitudinal flow on the resonantly damped propagating kink waves has been studied by Terradas et al. (2010a; 2010b) and by Soler et al. (2010a). We note that a Kelvin-Helmholtz instability of kink oscillations in flux tubes with both a sharp and smooth transition layer can also occur as a result of shear motions (Terradas et al. 2008). But as Terradas et al. (2008) claim, a magnetic twist, not included in their model, might decrease or even suppress the instability because a magnetic field component along the flow stabilises the Kelvin-Helmholtz instability. The same conclusion for the stabilising role of a small azimuthal component of the magnetic field has been drawn in the paper by Soler et al. (2010b). The influence of a twisted magnetic field on the stability status of kink waves propagating along radially inhomogeneous solar cylindrical photospheric/chromospheric jets is beyond the scope of this study, and as was mentioned above, we limit ourselves to considering radially homogeneous flowing plasmas only.
This paper is organized as follows. In Sect. 2 we specify the geometry of the problem, governing equations, and the derivation of the wave dispersion relation. Section 3 deals with the numerical solutions to the dispersion relation for various values of the input parameters and compares derived dispersion curves and growth rates of the unstable kink waves with those in untwisted magnetic tubes. The last Sect. 4 summarises our results.
2. Geometry, the basic MHD equations, and the wave dispersion relation
We consider a magnetic flux tube with radius a and density ρi embedded in a uniform field environment with density ρe. Both media (inside and outside the tube) are supposed to be incompressible. The magnetic field inside the tube is helicoidal, Bi = (0,Biφ(r),Biz(r)), while outside the magnetic field is uniform and directed along the z-axis, Be = (0,0,Be). Both ρi and ρe are assumed to be homogeneous. We consider the mass flow v0 = (0,0,v0) directed along the z-axis; thus the equilibrium mass flow is not field-aligned. No mass flow is present outside the tube, therefore the surrounding photospheric medium is considered to be uniformly magnetised (Beẑ is constant), uniform (ρe constant), and lacking mass flow at equilibrium.
In cylindrical equilibrium the magnetic field and plasma pressure satisfy the equilibrium
condition in the radial direction 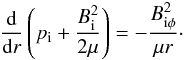 (1)Here,
(1)Here,
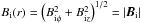 denotes the strength of the equilibrium magnetic field, and μ is the
magnetic permeability. We note that in Eq. (1) the total (plasma plus magnetic) pressure gradient is balanced by the tension
force (the right-hand side of Eq. (1)) in the
twisted field. We consider the special case of an equilibrium with uniform twist, i.e., the
one for
which Biφ(r)/rBiz(r)
is a constant. Accordingly, the background magnetic field is assumed to be
denotes the strength of the equilibrium magnetic field, and μ is the
magnetic permeability. We note that in Eq. (1) the total (plasma plus magnetic) pressure gradient is balanced by the tension
force (the right-hand side of Eq. (1)) in the
twisted field. We consider the special case of an equilibrium with uniform twist, i.e., the
one for
which Biφ(r)/rBiz(r)
is a constant. Accordingly, the background magnetic field is assumed to be 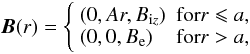 (2)where
A, Biz, and
Be are constant. Then the equilibrium condition (1) gives the equilibrium plasma
pressure pi(r) as
(2)where
A, Biz, and
Be are constant. Then the equilibrium condition (1) gives the equilibrium plasma
pressure pi(r) as
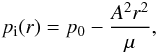 where
p0 is the plasma pressure at the centre of the tube. We note
that the jump in the value
of Bφ(r) across
r = a implies a surface current there.
where
p0 is the plasma pressure at the centre of the tube. We note
that the jump in the value
of Bφ(r) across
r = a implies a surface current there.
The plasma motion is governed by the set of linearised MHD equations for an ideal
incompressible plasma: 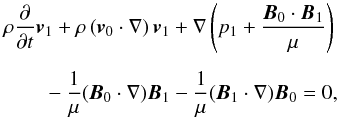 (3)
(3)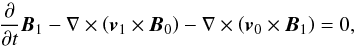 (4)
(4)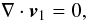 (5)
(5)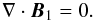 (6)Here, the index “0”
denotes equilibrium values of the fluid velocity and the medium magnetic field, and the
index “1” their perturbations. Below, the
sum p1 + B0·B1/μ
in Eq. (3) will be replaced
by p1tot, which represents the total pressure perturbation.
(6)Here, the index “0”
denotes equilibrium values of the fluid velocity and the medium magnetic field, and the
index “1” their perturbations. Below, the
sum p1 + B0·B1/μ
in Eq. (3) will be replaced
by p1tot, which represents the total pressure perturbation.
Assuming that all perturbations are proportional to
g(r)exp[i(−ωt + mφ + kzz)]
with g(r) being just a function of r,
and that in cylindrical coordinates the nabla operator has the form
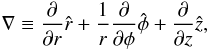 from
the above set of equations one can obtain a second-order differential equation for the total
pressure perturbation p1tot
from
the above set of equations one can obtain a second-order differential equation for the total
pressure perturbation p1tot![\begin{equation} \left[ \frac{{\rm d}^2}{{\rm d}r^2} + \frac{1}{r} \frac{{\rm d}}{{\rm d} r} - \left( \kappa^2 + \frac{m^2}{r^2} \right) \right] p_{\rm 1 tot} = 0, \label{eq:diffeq} \end{equation}](/articles/aa/full_html/2012/11/aa19512-12/aa19512-12-eq57.png) (7)as well as an
expression for the radial component v1r of the
fluid velocity perturbation v1 in terms
of p1tot and its first derivative
(7)as well as an
expression for the radial component v1r of the
fluid velocity perturbation v1 in terms
of p1tot and its first derivative 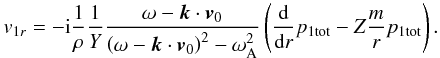 (8)In Eq. (7), κ is the so-called
wave attenuation coefficient, which characterises the space structure of
the wave and whose squared magnitude is given by the expression
(8)In Eq. (7), κ is the so-called
wave attenuation coefficient, which characterises the space structure of
the wave and whose squared magnitude is given by the expression ![\begin{equation} \kappa^2 = k_z^2 \left( 1 - \frac{4 A^2 \omega_{\rm A}^2} {\mu \rho \left[ \left( \omega - \vec{k} \cdot \vec{v}_0 \right)^2 - \omega_{\rm A}^2\right]^2} \right), \label{eq:kappa} \end{equation}](/articles/aa/full_html/2012/11/aa19512-12/aa19512-12-eq62.png) (9)where
(9)where 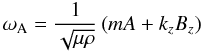 (10)is
the so-called local Alfvén frequency (Bennett et al. 1999). The numerical coefficients Z
and Y in the expression
of v1r (see Eq. (8)) are respectively
(10)is
the so-called local Alfvén frequency (Bennett et al. 1999). The numerical coefficients Z
and Y in the expression
of v1r (see Eq. (8)) are respectively
![\begin{eqnarray*} Z = \frac{2A \omega_{\rm A}}{\sqrt{\mu \rho}\left[ \left( \omega - \vec{k} \cdot \vec{v}_0 \right)^2 - \omega_{\rm A}^2\right]} \qquad \mbox{and} \qquad Y = 1 - Z^2. \end{eqnarray*}](/articles/aa/full_html/2012/11/aa19512-12/aa19512-12-eq66.png) As
seen from the expressions for the wave attenuation coefficient and the radial fluid velocity
component perturbation, the two quantities have different values inside and outside the
twisted flux tube owing to the different spatial structure of the magnetic field in both
media, and to the different mass densities (ρi
and ρe, respectively). It is important to note that the
attenuation coefficient κe outside the tube is simply equal
to kz, whilst that inside the tube can become
a purely imaginary quantity, thus allowing the propagation of pseudosurface (body) waves
along the tube. Notably the twisted magnetic field inside the tube enables the existence of
these waves, which otherwise are pure surface modes (Bennett et al. 1999).
As
seen from the expressions for the wave attenuation coefficient and the radial fluid velocity
component perturbation, the two quantities have different values inside and outside the
twisted flux tube owing to the different spatial structure of the magnetic field in both
media, and to the different mass densities (ρi
and ρe, respectively). It is important to note that the
attenuation coefficient κe outside the tube is simply equal
to kz, whilst that inside the tube can become
a purely imaginary quantity, thus allowing the propagation of pseudosurface (body) waves
along the tube. Notably the twisted magnetic field inside the tube enables the existence of
these waves, which otherwise are pure surface modes (Bennett et al. 1999).
Equation (7) has two different solutions
inside and outside the jet 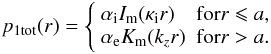 Here
Im and Km are the modified Bessel
functions of the first and second kind, and αi
and αe are arbitrary constants.
Here
Im and Km are the modified Bessel
functions of the first and second kind, and αi
and αe are arbitrary constants.
The boundary conditions have to ensure that the normal component of the interface
perturbation 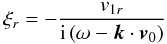 remains
continuous across the unperturbed tube boundary r = a, and
also that the total Lagrangian pressure is conserved across the perturbed boundary. This
leads to the conditions (Bennett et al. 1999)
remains
continuous across the unperturbed tube boundary r = a, and
also that the total Lagrangian pressure is conserved across the perturbed boundary. This
leads to the conditions (Bennett et al. 1999)
![\begin{equation} \left[ \xi_r \right]^{\rm inner} = \left[ \xi_r \right]^{\rm outer}, \label{eq:contxi} \end{equation}](/articles/aa/full_html/2012/11/aa19512-12/aa19512-12-eq75.png) (11)
(11)![\begin{equation} \left[ p_{\rm 1 tot} - \frac{B_{\phi}^2}{\mu a}\xi_r \right]^{\rm inner} = \left[ p_{\rm 1 tot} - \frac{B_{\phi}^2}{\mu a}\xi_r \right]^{\rm outer}\cdot \label{eq:contp1tot} \end{equation}](/articles/aa/full_html/2012/11/aa19512-12/aa19512-12-eq76.png) (12)Applying boundary
conditions (11) and (12) to our solutions
of p1tot and v1r
(and respectively ξr), we obtain after some
algebra the dispersion relation of the normal modes propagating along a twisted magnetic
tube with axial mass flow v0
(12)Applying boundary
conditions (11) and (12) to our solutions
of p1tot and v1r
(and respectively ξr), we obtain after some
algebra the dispersion relation of the normal modes propagating along a twisted magnetic
tube with axial mass flow v0![\begin{eqnarray} \frac{\left[ \left( \omega - \vec{k} \cdot \vec{v}_0 \right)^2 - \omega_{\rm Ai}^2 \right]{\displaystyle \frac{\kappa_{\rm i}a I_{\rm m}^{\prime}(\kappa_{\rm i}a)}{I_{\rm m}(\kappa_{\rm i}a)}} - 2m \omega_{\rm Ai} {\displaystyle \frac{A}{\sqrt{\mu \rho_{\rm i}}}}} {\left[ \left( \omega - \vec{k} \cdot \vec{v}_0 \right)^2 - \omega_{\rm Ai}^2 \right]^2 - 4\omega_{\rm Ai}^2 {\displaystyle \frac{A^2}{\mu \rho_{\rm i}}} } \nonumber \\ \nonumber \\ {}= \frac{{\displaystyle \frac{k_z a K_{\rm m}^{\prime}(k_z a)}{K_{\rm m}(k_z a)}}} {{\displaystyle \frac{\rho_{\rm e}}{\rho_{\rm i}}} \left( \omega^2 - \omega_{\rm Ae}^2 \right) + {\displaystyle \frac{A^2}{\mu \rho_{\rm i}} \frac{k_z a K_{\rm m}^{\prime}(k_z a)}{K_{\rm m}(k_z a)}}}\cdot \label{eq:dispeq} \end{eqnarray}](/articles/aa/full_html/2012/11/aa19512-12/aa19512-12-eq79.png) (13)This
dispersion relation is a generalisation of Eq. (23) in the work by Bennett et al. (1999) that is applicable to a twisted magnetic flux tube
without flow and of Eq. (13) in the work by Zaqarashvili et al. (2010) that is applicable to a twisted magnetic flux tube with a flow
embedded in a non-magnetic environment. As we have already seen, the wave
frequency ω is Doppler-shifted inside the jet. In the above equation a
prime (′) denotes the derivative of a Bessel function to its dimensionless argument, and the
local Alfvén frequencies inside and outside the tube are correspondingly
(13)This
dispersion relation is a generalisation of Eq. (23) in the work by Bennett et al. (1999) that is applicable to a twisted magnetic flux tube
without flow and of Eq. (13) in the work by Zaqarashvili et al. (2010) that is applicable to a twisted magnetic flux tube with a flow
embedded in a non-magnetic environment. As we have already seen, the wave
frequency ω is Doppler-shifted inside the jet. In the above equation a
prime (′) denotes the derivative of a Bessel function to its dimensionless argument, and the
local Alfvén frequencies inside and outside the tube are correspondingly
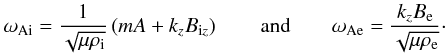 The
wave attenuation coefficient inside the tube, according to Eq. (9), is given by
The
wave attenuation coefficient inside the tube, according to Eq. (9), is given by
![\begin{eqnarray*} \kappa_{\rm i} = k_z \left( 1 - \frac{4 A^2 \omega_{\rm Ai}^2} {\mu \rho_{\rm i} \left[ \left( \omega - \vec{k} \cdot \vec{v}_0 \right)^2 - \omega_{\rm Ai}^2\right]^2} \right)^{1/2}\cdot \end{eqnarray*}](/articles/aa/full_html/2012/11/aa19512-12/aa19512-12-eq83.png) Assuming
no twist, when Biφ = 0, the dispersion
relation (13) reduces to
Assuming
no twist, when Biφ = 0, the dispersion
relation (13) reduces to ![\begin{eqnarray} && \frac{\rho_{\rm e}}{\rho_{\rm i}}\left( \omega^2 - k_z^2 v_{\rm Ae}^2 \right) \frac{I_{\rm m}^{\prime}(k_z a)}{I_{\rm m}(k_z a)} \nonumber \\ \nonumber \\ &&\qquad\qquad {-} \left[ \left( \omega - \vec{k} \cdot \vec{v}_0 \right)^2 - k_z^2 v_{\rm Ai}^2 \right] \frac{K_{\rm m}^{\prime}(k_z a)}{K_{\rm m}(k_z a)} = 0. \label{eq:edwineq} \end{eqnarray}](/articles/aa/full_html/2012/11/aa19512-12/aa19512-12-eq85.png) (14)\arraycolsep1.75ptThe
Alfvén speeds in this equation are expressed in terms of the background magnetic fields in
both media and the corresponding mass densities via the well-known definitions
(14)\arraycolsep1.75ptThe
Alfvén speeds in this equation are expressed in terms of the background magnetic fields in
both media and the corresponding mass densities via the well-known definitions
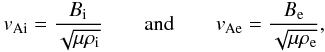 respectively.
Equation (14) is akin to a dispersion
relation in the same form as was previously obtained by Edwin & Roberts (1983) for untwisted magnetic tubes without flow. We also
recall that for the kink mode (m = 1) one defines the so-called
kink speed (Edwin & Roberts 1983)
respectively.
Equation (14) is akin to a dispersion
relation in the same form as was previously obtained by Edwin & Roberts (1983) for untwisted magnetic tubes without flow. We also
recall that for the kink mode (m = 1) one defines the so-called
kink speed (Edwin & Roberts 1983) 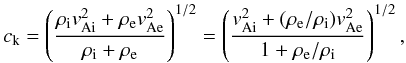 (15)which characterises the
propagation of transverse perturbations.
(15)which characterises the
propagation of transverse perturbations.
3. Numerical solutions and wave dispersion diagrams
We focus our study on the propagation of the kink mode, i.e., for m = 1.
It is obvious that Eqs. (13) and (14) can be solved only numerically. The first
step is to define the input parameters that characterise the twisted magnetic tube and the
axial flow, and to normalise all variables in the dispersion equations. The density contrast
between the tube and its environment is characterised by the parameter
η = ρe/ρi.
In investigating the kink instability in twisted magnetic tubes with axial and field-aligned
flows with their equilibrium magnetic fields in the form
B(r) = (0,Ar,B0),
Zaqarashvili et al. (2010) and Díaz et al. (2011) chose as twist characteristics the so-called
“dimensionless pitch” kzp,
in which the specific length p is defined (in their notation) as
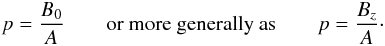 That
dimensionless pitch can be presented in the form
kzp = 2πp/λ,
where 2πp is the magnetic field pitch in its common sense. As we showed,
this parameter is associated with a fixed wavelength λ. To study the
Kelvin-Helmholtz instability in these tubes we prefer to specify the twist by the ratio of
the two magnetic field components, Bφ
and Bz, evaluated at the inner boundary of
the tube, r = a,
i.e., via Bφ/Bz,
where Bφ = Aa. This choice is
symbolically equivalent to the replacement of the wavelength λ by the tube
radius a. Following Aschwanden (2005), the magnetic twist
parameter Bφ/Bz
can be estimated as
Bφ/Bz = tanθ,
where θ is the shear angle between the untwisted and twisted field line.
The geometric shear angle, θ, can observationally be measured in twisted
photospheric magnetic tubes and in twisted coronal loops. We note that our choice of the
twist parameter allows us to immediately compare the dispersion curves of kink waves and the
growth rates when the waves become unstable in twisted magnetic tubes with those in
untwisted ones.
That
dimensionless pitch can be presented in the form
kzp = 2πp/λ,
where 2πp is the magnetic field pitch in its common sense. As we showed,
this parameter is associated with a fixed wavelength λ. To study the
Kelvin-Helmholtz instability in these tubes we prefer to specify the twist by the ratio of
the two magnetic field components, Bφ
and Bz, evaluated at the inner boundary of
the tube, r = a,
i.e., via Bφ/Bz,
where Bφ = Aa. This choice is
symbolically equivalent to the replacement of the wavelength λ by the tube
radius a. Following Aschwanden (2005), the magnetic twist
parameter Bφ/Bz
can be estimated as
Bφ/Bz = tanθ,
where θ is the shear angle between the untwisted and twisted field line.
The geometric shear angle, θ, can observationally be measured in twisted
photospheric magnetic tubes and in twisted coronal loops. We note that our choice of the
twist parameter allows us to immediately compare the dispersion curves of kink waves and the
growth rates when the waves become unstable in twisted magnetic tubes with those in
untwisted ones.
As usual, we normalise the velocities to the Alfvén speed
vAi = Bi/(μρi)1/2,
where 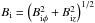 is evaluated
at the inner boundary of the tube, r = a. Thus, we
introduce the dimensionless wave phase velocity
Vph = vph/vAi
and the Alfvén-Mach number
MA = v0/vAi,
the latter characterising the axial mass flow. The wavelength is normalised to the tube
radius a, which means that the dimensionless wave number is
K = kza.
It is worth to discuss the normalisation of the local
Alfvén frequency ωAi. After multiplying both sides of
Eq. (10) by the tube
radius a and extracting a Bi from the
brackets, we derive that
is evaluated
at the inner boundary of the tube, r = a. Thus, we
introduce the dimensionless wave phase velocity
Vph = vph/vAi
and the Alfvén-Mach number
MA = v0/vAi,
the latter characterising the axial mass flow. The wavelength is normalised to the tube
radius a, which means that the dimensionless wave number is
K = kza.
It is worth to discuss the normalisation of the local
Alfvén frequency ωAi. After multiplying both sides of
Eq. (10) by the tube
radius a and extracting a Bi from the
brackets, we derive that 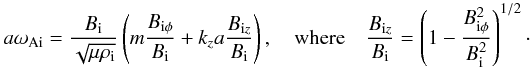 To
simplify the numerical code, and largely for clarity, we can redefine our twist parameter as
Biφ/Bi ≡ ε,
and consequently the normalised local Alfvén frequency is expressed in terms of the
Alfvén speed vAi, the dimensionless wave
number K, and ε:
To
simplify the numerical code, and largely for clarity, we can redefine our twist parameter as
Biφ/Bi ≡ ε,
and consequently the normalised local Alfvén frequency is expressed in terms of the
Alfvén speed vAi, the dimensionless wave
number K, and ε: 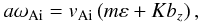 where
the dimensionless axial magnetic field component
bz = (1 − ε2)1/2.
The new twist parameter, ε, is related to the real
twist Bφ/Bz
via the simple relation
where
the dimensionless axial magnetic field component
bz = (1 − ε2)1/2.
The new twist parameter, ε, is related to the real
twist Bφ/Bz
via the simple relation 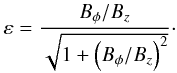 (16)Thus, if we have an
observationally measured shear angle θ of some solar twisted magnetic tube,
then
Bφ/Bz = tanθ
can be inserted into expression (16) to
obtain the adopted twist ε of that specific magnetic tube.
(16)Thus, if we have an
observationally measured shear angle θ of some solar twisted magnetic tube,
then
Bφ/Bz = tanθ
can be inserted into expression (16) to
obtain the adopted twist ε of that specific magnetic tube.
Before starting the numerical calculation, we have to specify the values of the input parameters. First we will examine, as in the work of Zaqarashvili et al. (2010), the case of an isolated twisted magnetic tube with axial mass flow, i.e., with Be = 0, and hence for parameter b ≡ Be/Bi = 0. Then, we will study the influence of the external magnetic field on the instability onset by choosing b equal to 0.1 and 0.5, respectively. Concerning the density contrast, η, we consider two cases, namely η = 2 and η = 0.1. Following Ruderman (2007), to satisfy the Shafranov-Kruskal stability criterion for a kink instability, we assume that the azimuthal component of the magnetic field is smaller than its axial component, i.e., we will choose our twist parameter ε to be always less than 1. In particular, we will study the dispersion diagrams of kink waves and their growth rates (when the waves are unstable) for three fixed values of ε: 0 (untwisted magnetic tube), 0.1, and 0.4. The Alfvén-Mach number MA will take values from zero (no flow) to any reasonable number.
3.1. Kink waves in twisted magnetic tubes with a density contrast η = 2
We start by calculating the dispersion curves of kink waves assuming that the twist parameter ε = 0.1, and that the angular wave frequency ω is real. As a reference, we first assume that the plasma in the flux tube is static, i.e., MA = 0. The dispersion curves, which present the dependence of the normalised wave phase velocity, vph/vAi, on the normalised wave number, kza, are in this case shown in Fig. 1. One can recognise two types of waves: a sub-Alfvénic wave labelled ck (the green curve), and a family of super-Alfvénic waves accommodated in a narrow band depicted by the two purple dispersion curves. The green dispersion curve is related to the kink speed defined by Eq. (15). For a weakly twisted magnetic tube (ε = 0.1) with a density contrast η = 2 the kink speed is equal to 0.5774vAi – our numerical code yields in the long wavelength limit, ck = 0.5738vAi, which agrees well with the value calculated from Eq. (15). If we assume that the Alfvén speed inside the tube is typically 10 km s-1, then the kink speed in the twisted magnetic tube is equal to 5.7 km s-1, or approximately to 6 km s-1. We recall that the expression of ck was defined for untwisted magnetic tubes and there is no guarantee that it will be valid for twisted tubes as well.
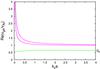 |
Fig. 1 Dispersion curves of kink waves propagating along a twisted magnetic flux tube at η = 2, Be/Bi = 0, Biφ/Bi = 0.1, and MA = 0. The green curve is the dispersion curve of the wave associated with the kink speed ck. The two purple curves depict a band that contains nine dispersion curves of similar form, not plotted here. |
 |
Fig. 2 (Left panel) Dispersion curves of forward propagating stable and unstable kink waves in a twisted magnetic flux tube with the same input parameters as in Fig. 1 for various values of the Alfvén-Mach number MA. The non-labelled green closed curve corresponds to MA = 1.325, and the black one – to MA = 1.328. (Right panel) Growth rates of the unstable kink waves for MA = 1.32205,1.347,1.372, and 1.397. |
 |
Fig. 3 (Left panel) Dispersion curves of forward propagating stable and unstable kink waves in an untwisted magnetic flux tube at η = 2 and Be/Bi = 0 for various values of the Alfvén-Mach number MA. (Right panel) Growth rates of the unstable kink waves for MA = 1.30825,1.325,1.35, and 1.375. |
Bennett et al. (1999), in studying the kink wave propagation in a twisted magnetic tube with parameters similar to ours, had discovered a band that contains an infinite number of pseudosurface (body) wave harmonics (Fig. 5a in their paper). Among those, generally super-Alfvénic, waves we were able to easily calculate only 11 dispersion curves from Eq. (13) with search steps (in decreasing order) from 0.00025 to 0.000000025. They are not plotted in Fig. 1 because there is no room for all of them in that narrow band, but they will be shown shortly in a similar plot for a tube with ε = 0.4. With diminishing search step, taking it equal to 0.0000000025 or smaller, one can extract a few (3) additional curves, but finding them is an extremely hard numerical task – for such small search steps the data are very noisy. However, these high-harmonics pseudosurface kink waves are not too important to us since we are primarily interested in the evolution of the kink mode associated with the kink speed ck when the plasma starts to flow. It is worth noticing that the ck-labelled dispersion curve for small dimensionless wave numbers, till kza = 0.1228, describes a pseudosurface (body) wave, while behind that value the wave is a pure surface mode. These types of waves are sometimes called hybrid waves (Bennett et al. 1999).
It is essential to emphasise that the dispersion Eq. (13) also yields solutions for negative values of the wave phase velocity (i.e., for backward-propagating waves), which are a mirror image of the solutions in the positive semi-space. Including the flow, the whole pattern shifts en bloc upwards, changing of course both the ck-labelled dispersion curve and the wave harmonics dispersion curves. For each MA we have two ck-dispersion curves that initially, for small Alfvén-Mach numbers, are independent, but at certain magnitudes of MA begin to interact; for example, they form semi-closed or closed dispersion curves by merging. These dispersion curves are an indication that we are in a region in which the kink wave may become unstable (see Zhelyazkov 2010).
To study the stability/instability status of the ck-kink
wave, we have to assume that the wave frequency is complex,
i.e., ω → ω + iγ,
where γ is the expected instability growth rate. Thus, the dispersion
equation becomes complex (complex wave phase velocity and real wave number) and deriving
the solutions to a transcendental complex equation is generally a hard task (see Acton
1990). We numerically solve Eq. (13) using the Muller method (Muller 1956) to find the complex roots at fixed input
parameters η = 2, b = 0, and ε = 0.1,
and varying Alfvén-Mach numbers MA from zero to generally
reasonable values. The evolution of the two kink waves with increasing flow velocity
(or equivalently MA) is shown in Fig. 2. We note that while for rest plasma or small Alfvén-Mach numbers the
lower kink wave (i.e., the one that is a mirror image of the green curve in Fig. 1) is a backward one, for
MA = 1 it becomes a forward wave. At the next increase of the
Alfvén-Mach number the two dispersion curves change their form and structure – initially
being hybrid modes, for MA > 1.23 they
are pure surface waves. The most interesting observation is that for
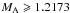 both curves begin to merge and for
both curves begin to merge and for 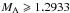 they form a closed dispersion curve. The ever increasing
MA yields yet smaller closed dispersion curves – the smallest
one depicted in the left panel of Fig. 2 corresponds
to MA = 1.328. All these dispersion curves present a stable
propagation of the kink waves. However, for
they form a closed dispersion curve. The ever increasing
MA yields yet smaller closed dispersion curves – the smallest
one depicted in the left panel of Fig. 2 corresponds
to MA = 1.328. All these dispersion curves present a stable
propagation of the kink waves. However, for 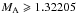 we obtain a new family of wave dispersion curves that correspond to an unstable wave
propagation. We plot in Fig. 2 four curves of that
kind that were calculated for MA = 1.32205, 1.347, 1.372,
and 1.397, respectively. The growth rates of the unstable waves are shown in the right
panel of the same figure. The instability that arises is of the Kelvin-Helmholtz type.
Note the shape of red curve labelled 1.32205: the growth rate has relatively high values
for small normalised wave numbers, then passes through a minimum (its relative value there
is ~0.003) after which it starts to grow. That specific curve is to some extent a
marginal curve – for values of MA lower than 1.32205 the kink
wave is stable whilst at
we obtain a new family of wave dispersion curves that correspond to an unstable wave
propagation. We plot in Fig. 2 four curves of that
kind that were calculated for MA = 1.32205, 1.347, 1.372,
and 1.397, respectively. The growth rates of the unstable waves are shown in the right
panel of the same figure. The instability that arises is of the Kelvin-Helmholtz type.
Note the shape of red curve labelled 1.32205: the growth rate has relatively high values
for small normalised wave numbers, then passes through a minimum (its relative value there
is ~0.003) after which it starts to grow. That specific curve is to some extent a
marginal curve – for values of MA lower than 1.32205 the kink
wave is stable whilst at 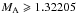 the wave is definitely unstable. This means that the instability onset at the
critical MA will prevent the occurrence of the neutral
dispersion curve with MA = 1.328.
the wave is definitely unstable. This means that the instability onset at the
critical MA will prevent the occurrence of the neutral
dispersion curve with MA = 1.328.
It is interesting to see how the twist of the magnetic field has changed the dispersion curves and growth rates of unstable kink waves calculated for an untwisted magnetic tube. In that case the dispersion curves and growth rates can be obtained through the exact numerical solutions of Eq. (14) (see Zhelyazkov 2010). The results are shown in Fig. 3. Comparing Figs. 2 and 3, we immediately see that the dispersion diagrams and growth rates of the unstable kink waves are very similar. There are differences, of course; firstly the magnetic field twist visibly extends the closed dispersion curves in the horizontal direction, and secondly, it slightly increases the threshold Alfvén-Mach number for the onset of the Kelvin-Helmholtz instability – for the untwisted magnetic tube it is equal to 1.30825, whilst for the twisted one it is slightly higher – the corresponding value is 1.32205. The similarities between the dispersion diagrams and the growth rates are important to us – they indirectly confirm the correctness of our numerical solutions derived by solving the complex dispersion Eq. (13).
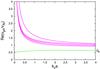 |
Fig. 4 Dispersion curves of kink waves propagating along a twisted magnetic flux tube at η = 2, Be/Bi = 0, Biφ/Bi = 0.4, and MA = 0. The green curve is the dispersion curve of the wave associated with the kink speed ck. The purple curves depict all 11 dispersion curves; 9 of them are divided into two sub-groups. The “evolution” of those curves when increasing kza can be seen in the next figure, which shows them near the left top and right bottom corners of the plot. |
 |
Fig. 5 Zoomed-in parts of the 11 dispersion curves near the left top (top panel) and right bottom (bottom panel) corners of the plot in Fig. 4. |
Figure 4 shows the dispersion curves of kink waves when the twist parameter ε = 0.4 and there is no flow. Now one can see all 11 easily derived dispersion curves of the wave harmonics. They have similar shapes, and as seen in Figs. 4 and 5, one can distinguish two sub-groups of four and five curves, respectively. We note that the eleventh (the highest) dispersion curve is not visible in the top panel of Fig. 5 because it simply begins at about kza = 0.23, which is far beyond the right side of the plot. Another important observation is that the kink speed is markedly lower than expected from the Eq. (15) value – here its normalised magnitude is equal to 0.5167, which corresponds to a kink speed of 5 km s-1. The kink wave itself is a hybrid mode – till kza = 0.5623 it is a pseudosurface (body) wave, becoming a pure surface wave for the next values of the normalised wave number. When plasma in the tube is flowing, the kink waves are pure surface mode for MA > 1.197.
The dispersion curves and growth rates of kink waves for this higher value of the magnetic field twist are given in Fig. 6. At the left panel of this figure we see dramatic changes in the shape and position of the closed dispersion curves. The most striking changes, however, are the circumstances that the onset of unstable kink waves, like in Fig. 2, starts at a value of the Alfvén-Mach number lower than that of the narrowest closed dispersion curve – 1.250075 vs. 1.29! In untwisted flux tubes the kink mode appears at Alfvén-Mach numbers higher than those of the smallest closed dispersion curves, as seen in Fig. 3 (cf. also Fig. 4 in Zhelyazkov (2012a)). In reality, of course, the onset of a Kelvin-Helmholtz instability in a twisted tube will “reject” the co-existence of stable kink waves like those labelled 1.267, 1.28, 1.287, and 1.29 in Fig. 6.
 |
Fig. 6 (Left panel) Dispersion curves of forward-propagating stable and unstable kink waves in a twisted magnetic flux tube with the same input parameters as in Fig. 4 for various values of the Alfvén-Mach number MA. (Right panel) Growth rates of the unstable kink waves for MA = 1.250075,1.275,1.3, and 1.325. |
Similar calculations were performed for the two external magnetic fields specified by b = 0.1 and 0.5. As expected, the environment’s magnetic field stabilises the kink wave propagation (Bennett et al. 1999) – the instability onset occurs at slightly higher threshold Alvfén-Mach numbers, but the shapes of the dispersion and growth rate curves are similar to those of an isolated twisted flux tube as depicted in Figs. 2, 3, and 6. The influence of the magnetic field twist, ε, at a fixed external magnetic field, b, and that of the environment’s magnetic field at a fixed tube twist on the specific growth rate curves are illustrated in Figs. 7 and 8. As seen in Fig. 7, at a fixed magnetic field configuration, the tube twist shifts to the right the minimum of the specific growth rate curve. This is most pronounced at b = 0.5. A twist of 0.4 notably decreases the wave growth rate for each b and yields the lowest threshold Alfvén-Mach number for a given b. Thus, for a photospheric twisted magnetic tube with ε = 0.4 flow speeds in the range 12.5−13.6 km s-1 can ensure the occurrence of a Kelvin-Helmholtz instability of the kink waves propagating along that tube. These flow speeds can be observed/detected in the solar photosphere. It becomes clear from Fig. 8 that an external magnetic field visibly increases the threshold Alfvén-Mach number and diminishes the wave growth rate – the latter effect is strongest for a magnetic tube with twist parameter ε = 0.4.
 |
Fig. 7 Specific growth rates of kink waves propagating along an untwisted/twisted magnetic flux tube at η = 2, Be/Bi = 0 (left panel), Be/Bi = 0.1 (middle panel), and Be/Bi = 0.5 (right panel) for various values of the twist parameter Biφ/Bi, equal to 0 (red curve), 0.1 (green curve), and 0.4 (blue curve), respectively. The curve labels denote the threshold Alfvén-Mach number. |
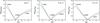 |
Fig. 8 Specific growth rates of kink waves propagating along an untwisted/twisted magnetic flux tube at η = 2, Biφ/Bi = 0 (left panel), Biφ/Bi = 0.1 (middle panel), and Biφ/Bi = 0.4 (right panel) for various values of the environment’s magnetic field Be/Bi, equal to 0 (red curve), 0.1 (green curve), and 0.5 (blue curve), respectively. The curve labels denote the threshold Alfvén-Mach number. |
3.2. Kink waves in twisted magnetic tubes with a density contrast η = 0.1
 |
Fig. 9 (Left panel) Dispersion curves of forward-propagating stable and unstable kink waves in a twisted magnetic flux tube with η = 0.1, Be/Bi = 0, and Biφ/Bi = 0.4 for various values of the Alfvén-Mach number MA. (Right panel) Growth rates of the unstable kink waves for MA = 3.778422,3.81,3.835, and 3.86. |
 |
Fig. 10 Specific growth rates of kink waves propagating along an untwisted/twisted magnetic flux tube at η = 0.1, Be/Bi = 0 (left panel), Be/Bi = 0.1 (middle panel), and Be/Bi = 0.5 (right panel) for various values of the twist parameter Biφ/Bi, equal to 0 (red curve), 0.1 (green curve), and 0.4 (blue curve), respectively. The curve labels denote the threshold Alfvén-Mach number. |
A density contrast η = 0.1 is perhaps more suitable for a coronal and upper chromospheric magnetic flux tube than to a photospheric one, but nevertheless, studying this case is important for us to see how the density contrast affects the threshold/critical Alfvén-Mach numbers for the onset of the Kelvin-Helmholtz instability of kink waves propagating along twisted magnetic tubes. The procedure for performing calculations and plotting dispersion diagrams is the same as in the previous subsection. This lower value of η yields markedly higher threshold Alfvén-Mach numbers as well as higher growth rates compared to η = 2. Here, in Fig. 9, we show only one set of plots – namely that for an isolated flux tube (b = 0) with a twist of 0.4. At these values of the input parameters we obtain the smallest threshold MA. In Fig. 10, like in Fig. 7, we present the specific growth rate curves at fixed external magnetic fields for the three different values of the magnetic twist. As seen from this figure, for that value of the density contrast (η = 0.1) the influence of the magnetic twist, ε, on the shapes and positions of the specific growth rate curves, irrespective of the magnitude of the environment’s magnetic field, is negligibly small. That is why a figure, similar to Fig. 8, is useless – in each subfigure for given ε the three curves would practically coincide because the differences are only in the second/third places behind the decimal point. As for a photospheric twisted tube, one obtains the lowest threshold MA at b = 0 and ε = 0.4 – the corresponding value is 3.778422. If we accept that such a twisted magnetic tube can model a coronal loop, to estimate the Alfvén speed inside the tube, we assume a typical particle number density ni ≈ 109 cm-3 (see Ugarte-Urra et al. 2005) and a magnetic field strength Bi = 11 G (see Verwichte et al. 2009); then vAi ≈ 900 km s-1. With this high Alfvén speed one would need a flow speed of about 3400 km s-1 for the onset of an instability of the Kelvin-Helmholtz type. Since the detected flow velocities in the coronal loops are of the order of a few tens of kilometers per second, we can conclude that the kink waves in coronal loops with axial mass flows are stable against the Kelvin-Helmholtz instability.
4. Conclusion
We have studied the dispersion properties and the stability of the MHD kink modes running along the length of photospheric/chromospheric uniformly twisted magnetic tubes with axial mass flows. These were modelled as straight cylindrical jets of ideal incompressible plasma surrounded by a rest unmagnetised/magnetised also incompressible fully ionized medium. The wave propagation was investigated in the context of standard ideal magnetohydrodynamics by using linearised equations for the perturbations of the basic quantities: pressure, fluid velocity, and wave magnetic field. The derived dispersion equation describes the propagation of the kink mode influenced by the twist of the equilibrium magnetic field Bi and the presence of moving plasma. The twist itself is characterised by the ratio of the azimuthal, Biφ, to the axial, Biz, background magnetic field components both evaluated at the inner surface of the twisted magnetic tube. To avoid competition from the so-called kink instability, which is largely caused by the twist of the equilibrium magnetic field, we chose the ratio Biφ/Biz to be less than 1. For simplicity and clarity of the numerical code used for solving the wave dispersion relation (in complex variables) we used a safer twist parameter ε defined as Biφ/Bi. Our ε and the real twist Biφ/Biz have generally rather close magnitudes, because they are related by a simple expression. The streaming plasma is characterised by its velocity v0, which is directed along the axis of the twisted magnetic tube. An alternative and more convenient way of specifying the mass flow is by defining the Alfvén-Mach number: the ratio of the jet speed to the Alfvén speed inside the jet, MA = v0/vAi. The key parameters controlling the dispersion properties of the kink waves are the so-called density contrast, η = ρe/ρi, defined as the ratio of the density of the environment to that of the twisted tube, the ratio of the two background magnetic fields, b = Be/Bi, the twist of the magnetic field, ε, and, naturally, the mass flow characterised by the Alfvén-Mach number MA.
To study the influence of the mass flow, the twist of the equilibrium magnetic field inside the tube, as well as the environment’s magnetic field on the dispersion properties and stability of the kink waves, we considered two cases with fixed density contrasts η = 2 and 0.1, respectively. For a given η and a specified external magnetic field via the parameter b, we investigated the kink wave dispersion curves and the instability growth rate when the wave becomes unstable for two different magnetic field twist parameters, namely ε = 0.1 and 0.4, respectively, by gradually changing the normalised mass flow velocity, i.e., the Alfvén-Mach number MA, from zero (rest plasma) to some reasonable values. The flow shifts both the kink-speed curves and the dispersion curves of the wave harmonics upwards. We focused our study on the kink-speed wave only since it is the mode that plays an important role in the dynamics of photospheric and chromospheric/coronal flows.
To evaluate the effect of the adopted magnetic field twist, ε, on the
kink-speed wave dispersion curves and chiefly on the value of the critical Alfvén-Mach
number that determines that flow speed that ensures the onset of an instability of the
Kelvin-Helmholtz type, we compared the wave dispersion diagrams in twisted tubes with those
in untwisted magnetic tubes. It is well established that in untwisted magnetic tubes the
kink waves are subject to the Kelvin-Helmholtz instability
when MA exceeds a certain critical value, depending upon the
density contrast, η, and on the ratio of the background magnetic
fields, b, in both media (see Vasheghani Farahani et al. 2009; Zhelyazkov 2010; 2012a). For an isolated magnetic
tube, b = 0, and, hence, the threshold value of the Alfvén-Mach number
depends only on the density contrast, η. Relatively high values
of η yield lower threshold Alfvén-Mach numbers while the lower values
of η do just the opposite – for our chosen two ηs the
corresponding critical normalised flow speeds are 1.30825 and 3.902503. The effect of the
magnetic field twist critically depends on the value of the twist
parameter ε. This effect is strongest when ε = 0.4 –
then one observes a noticeable decrease in the threshold Alfvén-Mach number: for a tube with
η = 2 and b = 0, 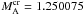 ,
while at η = 0.1 it is equal to 3.778422. This substantial finding that the
twisted magnetic field lowers the threshold MA for the
occurrence of the Kelvin-Helmholtz instability of m = 1 mode agrees with
the same statement declared in the works by Bennett et al. (1999) and Zaqarashvili et al. (2010).
In particular, in twisted photospheric magnetic tubes with a density contrast
η = 2, magnetic field twist ε = 0.4, and Alfvén speed
vA = 10 km s-1, a reliable mass flow
of 12.5 km s-1 can cause the onset of an instability of the Kelvin-Helmholtz
type of m = 1 mode. Any none-zero environment magnetic
field, Be, increases
,
while at η = 0.1 it is equal to 3.778422. This substantial finding that the
twisted magnetic field lowers the threshold MA for the
occurrence of the Kelvin-Helmholtz instability of m = 1 mode agrees with
the same statement declared in the works by Bennett et al. (1999) and Zaqarashvili et al. (2010).
In particular, in twisted photospheric magnetic tubes with a density contrast
η = 2, magnetic field twist ε = 0.4, and Alfvén speed
vA = 10 km s-1, a reliable mass flow
of 12.5 km s-1 can cause the onset of an instability of the Kelvin-Helmholtz
type of m = 1 mode. Any none-zero environment magnetic
field, Be, increases 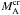 , slightly for
b = 0.1, and more noticeable at b = 0.5. The
observation/detection of the Kelvin-Helmholtz instability of m = 1 mode in
a coronal twisted magnetic tube (at η = 0.1) is generally problematic, but
a twist of 0.4 might help starting this instability in coronal X-ray flows, for which the
parameter η is slightly bigger (of the order of 0.14), and the observed
flow speeds can be much higher, a few thousand kilometers per second (see Madjarska 2011; also Zhelyazkov 2012b, and the discussion therein).
, slightly for
b = 0.1, and more noticeable at b = 0.5. The
observation/detection of the Kelvin-Helmholtz instability of m = 1 mode in
a coronal twisted magnetic tube (at η = 0.1) is generally problematic, but
a twist of 0.4 might help starting this instability in coronal X-ray flows, for which the
parameter η is slightly bigger (of the order of 0.14), and the observed
flow speeds can be much higher, a few thousand kilometers per second (see Madjarska 2011; also Zhelyazkov 2012b, and the discussion therein).
A criterion for the appearance of the Kelvin-Helmholtz instability of kink waves in
untwisted magnetic tubes is the satisfaction of an inequality suggested by Andries &
Goossens (2001), which in our notation reads
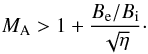 For
twisted magnetic tubes, and in particular for isolated ones (with
Be = 0), this criterion provides a fairly rough prediction,
just MA > 1. In other words, the mass
flows must be super-Alfvénic to trigger an instability – this seems to be a norm for twisted
magnetic tubes with field-aligned flows (see Díaz et al. 2011). Our numerical findings of the critical Alfvén-Mach numbers also agree with
that rough criterion – in both cases (η = 2 and 0.1) the Kelvin-Helmholtz
instability occurs when the axial mass flows are super-Alfvénic.
For
twisted magnetic tubes, and in particular for isolated ones (with
Be = 0), this criterion provides a fairly rough prediction,
just MA > 1. In other words, the mass
flows must be super-Alfvénic to trigger an instability – this seems to be a norm for twisted
magnetic tubes with field-aligned flows (see Díaz et al. 2011). Our numerical findings of the critical Alfvén-Mach numbers also agree with
that rough criterion – in both cases (η = 2 and 0.1) the Kelvin-Helmholtz
instability occurs when the axial mass flows are super-Alfvénic.
On the other hand, a criterion for the appearance of the Kelvin-Helmholtz instability in
isolated twisted magnetic tubes is the satisfaction of an inequality suggested by
Zaqarashvili et al. (2010), which in our notation is
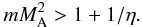 For
the kink mode, i.e., m = 1, this inequality gives
MA > 1.2247 for η = 2
and MA > 3.3166 for
η = 0.1. Our numerical findings of the critical Alfvén-Mach numbers agree
with this criterion in both cases.
For
the kink mode, i.e., m = 1, this inequality gives
MA > 1.2247 for η = 2
and MA > 3.3166 for
η = 0.1. Our numerical findings of the critical Alfvén-Mach numbers agree
with this criterion in both cases.
The next steps in studying the Kelvin-Helmholtz instability of kink waves in twisted magnetic tubes are obviously (i) to investigate the role of the transverse density inhomogeneity inside the tube and associated with it, resonant wave absorption on the kink waves propagation and their stability/instability status; and (ii) to consider a field-aligned mass flow instead of an axial one.
Acknowledgments
I.Zh. thanks the Sofia University Scientific Fund for support under grant No. 147-2012. The work of T.V.Z. was supported by the Austrian Fonds zur Förderung der wissenschaftlichen Forschung (project P21197-N16) and by the European FP7-PEOPLE-2010-IRSES-269299 project-SOLSPANET. The authors thank the anonymous referee for his/her constructive comments and suggestions, which led to significant improvements in the paper.
References
- Acton, F. S. 1990, Numerical Methods That (Usually) Work (Washington, D.C.: Mathematical Association of America), Chap. 14 [Google Scholar]
- Andries, J., & Goossens, M. 2001, A&A, 368, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aschwanden, M. J. 2005, Physics of the Solar Corona (Berlin: Springer), Chap. 6 [Google Scholar]
- Aschwanden, M. J., Fletcher, L., Schrijver, C. J., & Alexander, D. 1999, ApJ, 520, 880 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, K., Roberts, B., & Narain, U. 1999, Sol. Phys., 185, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Bogdan, T. J. 1984, ApJ, 282, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, B. K., & Erdélyi, R. 2008, A&A, 481, 239 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chae, J., Wang, H., Qiu, J., et al. 2001, ApJ, 560, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Chandrasekhar, S. 1961, Hydrodynamic and Hydromagnetic Stability (Oxford: Clarendon Press), Chap. 11 [Google Scholar]
- Cirtain, J. W., Golub, L., Lundquist, L., et al. 2007, Science, 318, 1580 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- de Pontieu, B., McIntosh, S., Hansteen, V. H., et al. 2007, PASJ, 59, S655 [Google Scholar]
- Díaz, A. J., Oliver, R., Ballester, J. L., & Soler, R. 2011, A&A, 533, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drazin, P. G. 2002, Introduction to Hydrodynamic Stability (Cambridge: Cambridge University Press), Chap. 8 [Google Scholar]
- Dungey, J. W., & Loughhead, R. E. 1954, Aust. J. Phys., 7, 5 [Google Scholar]
- Ebadi, H., Zaqarashvili, T. V., & Zhelyazkov, I. 2012, Astrophys. Space Sci., 337, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Edwin, P. M., & Roberts, B. 1983, Sol. Phys., 88, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Erdélyi, R., & Carter, B. K. 2006, A&A, 455, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erdélyi, R., & Fedun, V. 2006, Sol. Phys., 238, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Erdélyi, R., & Fedun, V. 2007, Sol. Phys., 246, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Erdélyi, R., & Fedun, V. 2010, Sol. Phys., 263, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Foullon, C., Verwichte, E., Nakariakov, V. M., Nykyri, K., & Farrugia, C. J. 2011, ApJ, 729, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Furno, I., Intrator, T. P., Lapenta, G., et al. 2007, Phys. Plasmas, 14, 022103 [NASA ADS] [CrossRef] [Google Scholar]
- He, J., Marsch, E., Tu, C., & Tian, H. 2009, ApJ, 705, L217 [NASA ADS] [CrossRef] [Google Scholar]
- Hood, A. W., & Priest, E. R. 1979, Sol. Phys., 64, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Kamio, S., Peter, H., Curdt, W., & Solanki, S. K. 2011, A&A, 532, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karami, K., & Bahari, K. 2010, Sol. Phys., 263, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Karami, K., & Barin, M. 2009, MNRAS, 394, 521 [NASA ADS] [CrossRef] [Google Scholar]
- Katsukawa, Y., Berger, T. E., Ichimoto, K., et al. 2007, Science, 318, 1594 [NASA ADS] [CrossRef] [Google Scholar]
- Kruskal, M. D., Johnson, J. L., Gottlieb, M. B., & Goldman, L. M. 1958, Phys. Fluids, 1, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Kukhianidze, V., Zaqarashvili, T. V., & Khutsishvili, E. 2006, A&A, 449, L35 [Google Scholar]
- Linton, M. G., Longcope, D. W., & Fisher, G. H. 1996, ApJ, 469, 954 [NASA ADS] [CrossRef] [Google Scholar]
- Lundquist, S. 1951, Phys. Rev., 83, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Madjarska, M. S. 2011, A&A, 526, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muller, D. E. 1956, Math. Tables Other Aids Comput., 10, 208 [Google Scholar]
- Ofman, L., & Wang, T. J. 2008, A&A, 482, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ofman, L., & Thompson, B. J. 2011, ApJ, 734, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Pietarila, A., Aznar Cuadrado, R., Hirzberger, J., & Solanki, S. K. 2011, ApJ, 739, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, P. H. 1956, ApJ, 124, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S. 2007, Sol. Phys., 246, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Ruderman, M. S., & Erdélyi, R. 2009, Space Sci. Rev., 149, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Shafranov, V. D. 1957, J. Nuclear Energy II, 5, 86 [Google Scholar]
- Shibata, K., Nakamura, T., Matsumoto, T., et al. 2007, Science, 318, 1591 [Google Scholar]
- Shimojo, M., & Shibata, K. 2000, ApJ, 542, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Soler, R., Terradas, J., & Goossens, M. 2010a, ApJ, 734, 80 [Google Scholar]
- Soler, R., Terradas, J., Verth, G., & Goossens, M. 2010b, ApJ, 736, 10 [Google Scholar]
- Srivastava, A. K., & Murawski, K. 2011, A&A, 534, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Srivastava, A. K., Zaqarashvili, T. V., Kumar, P., & Khodachenko, M. L. 2010, ApJ, 715, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Tavabi, E., Koutchmy, S., & Ajabshirizadeh, A. 2011, New Astron., 16, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Terradas, J., Andries, J., Goossens, M., et al. 2008, ApJ, 687, L115 [Google Scholar]
- Terradas, J., Goossens, M., & Ballai, I. 2010a, A&A, 515, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Terradas, J., Goossens, M., & Verth, G. 2010b, A&A, 524, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tian, H., McIntosh, S. W., Rifal Habbal, S., & He, J. 2011, ApJ, 736, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Trehan, S. K. 1958, ApJ, 127, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Ugarte-Urra, I., Doyle, J. G., Walsh, R. W., & Madjarska, M. S. 2005, A&A, 439, 351 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- VasheghaniFarahani, S., Van Doorsselaere, T., Verwichte, E., & Nakariakov, V. M. 2009, A&A, 498, L29 [Google Scholar]
- Verwichte, E., Aschwanden, M. J., Van Doorsselaere, T., Foullon, C., & Nakariakov, V. M. 2009, ApJ, 698, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Wallace, A. J., Harra, L. K., van Driel-Gesztelyi, L., Green, L. M., & Matthews, S. A. 2010, Sol. Phys., 267, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V. 2011, in 3rd School and Workshop on Space Plasma Physics, eds. I. Zhelyazkov, & T. Mishonov, AIP Conf. Proc., 1356, 106 [Google Scholar]
- Zaqarashvili, T. V., & Erdélyi, R. 2009, Space Sci. Rev., 149, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Zaqarashvili, T. V., Khutsishvili, E., Kukhianidze, V., & Ramishvili, G. 2007, A&A, 474, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zaqarashvili, T. V., Díaz, A. J., Oliver, R., & Ballester, J. L. 2010, A&A, 516, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhelyazkov, I. 2010, Plasma Phys. Control. Fusion, 52, 065008 [NASA ADS] [CrossRef] [Google Scholar]
- Zhelyazkov, I. 2012a, A&A, 537, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhelyazkov, I. 2012b, in Topics in Magnetohydrodynamics, ed. L. Zheng, InTech – Open Access Company, Chap. 6 [Google Scholar]
All Figures
 |
Fig. 1 Dispersion curves of kink waves propagating along a twisted magnetic flux tube at η = 2, Be/Bi = 0, Biφ/Bi = 0.1, and MA = 0. The green curve is the dispersion curve of the wave associated with the kink speed ck. The two purple curves depict a band that contains nine dispersion curves of similar form, not plotted here. |
| In the text | |
 |
Fig. 2 (Left panel) Dispersion curves of forward propagating stable and unstable kink waves in a twisted magnetic flux tube with the same input parameters as in Fig. 1 for various values of the Alfvén-Mach number MA. The non-labelled green closed curve corresponds to MA = 1.325, and the black one – to MA = 1.328. (Right panel) Growth rates of the unstable kink waves for MA = 1.32205,1.347,1.372, and 1.397. |
| In the text | |
 |
Fig. 3 (Left panel) Dispersion curves of forward propagating stable and unstable kink waves in an untwisted magnetic flux tube at η = 2 and Be/Bi = 0 for various values of the Alfvén-Mach number MA. (Right panel) Growth rates of the unstable kink waves for MA = 1.30825,1.325,1.35, and 1.375. |
| In the text | |
 |
Fig. 4 Dispersion curves of kink waves propagating along a twisted magnetic flux tube at η = 2, Be/Bi = 0, Biφ/Bi = 0.4, and MA = 0. The green curve is the dispersion curve of the wave associated with the kink speed ck. The purple curves depict all 11 dispersion curves; 9 of them are divided into two sub-groups. The “evolution” of those curves when increasing kza can be seen in the next figure, which shows them near the left top and right bottom corners of the plot. |
| In the text | |
 |
Fig. 5 Zoomed-in parts of the 11 dispersion curves near the left top (top panel) and right bottom (bottom panel) corners of the plot in Fig. 4. |
| In the text | |
 |
Fig. 6 (Left panel) Dispersion curves of forward-propagating stable and unstable kink waves in a twisted magnetic flux tube with the same input parameters as in Fig. 4 for various values of the Alfvén-Mach number MA. (Right panel) Growth rates of the unstable kink waves for MA = 1.250075,1.275,1.3, and 1.325. |
| In the text | |
 |
Fig. 7 Specific growth rates of kink waves propagating along an untwisted/twisted magnetic flux tube at η = 2, Be/Bi = 0 (left panel), Be/Bi = 0.1 (middle panel), and Be/Bi = 0.5 (right panel) for various values of the twist parameter Biφ/Bi, equal to 0 (red curve), 0.1 (green curve), and 0.4 (blue curve), respectively. The curve labels denote the threshold Alfvén-Mach number. |
| In the text | |
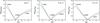 |
Fig. 8 Specific growth rates of kink waves propagating along an untwisted/twisted magnetic flux tube at η = 2, Biφ/Bi = 0 (left panel), Biφ/Bi = 0.1 (middle panel), and Biφ/Bi = 0.4 (right panel) for various values of the environment’s magnetic field Be/Bi, equal to 0 (red curve), 0.1 (green curve), and 0.5 (blue curve), respectively. The curve labels denote the threshold Alfvén-Mach number. |
| In the text | |
 |
Fig. 9 (Left panel) Dispersion curves of forward-propagating stable and unstable kink waves in a twisted magnetic flux tube with η = 0.1, Be/Bi = 0, and Biφ/Bi = 0.4 for various values of the Alfvén-Mach number MA. (Right panel) Growth rates of the unstable kink waves for MA = 3.778422,3.81,3.835, and 3.86. |
| In the text | |
 |
Fig. 10 Specific growth rates of kink waves propagating along an untwisted/twisted magnetic flux tube at η = 0.1, Be/Bi = 0 (left panel), Be/Bi = 0.1 (middle panel), and Be/Bi = 0.5 (right panel) for various values of the twist parameter Biφ/Bi, equal to 0 (red curve), 0.1 (green curve), and 0.4 (blue curve), respectively. The curve labels denote the threshold Alfvén-Mach number. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


