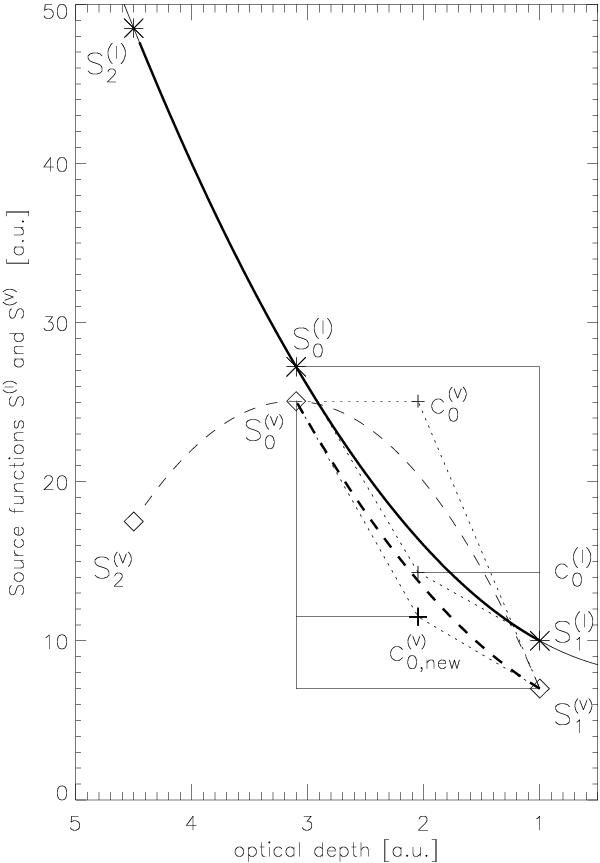
Interpolation method for the full Stokes vector problem. Even with monotonic Bézier interpolation, the source function of a Stokes component, e.g. S_V (dashed thin) may become larger than S_I (solid thick) in the range from S₀ to S₁. The standard control point 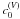 lies far above  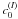(thin plus signs, both defined by two tangents given by thin dotted lines) owing to the different curvatures of the source function parabolas. To prevent these situations, we chose the control point for the Stokes V component (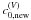, thick plus sign), according to 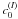. Our 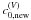 is defined by the ratio  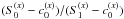(with x equal to I or V), which has to be constant. This choice prevents the source function integrals of the Stokes components from becoming larger than those of Stokes I.