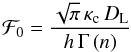| Issue |
A&A
Volume 546, October 2012
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 13 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201219539 | |
| Published online | 01 October 2012 | |
Analytical shear and flexion of Einasto dark matter haloes
1 Escuela de Física, Universidad de Costa Rica, San Pedro 11501, Costa Rica
e-mail: edwin@fisica.ucr.ac.cr
2 Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281-S9, 9000 Gent, Belgium
e-mail: maarten.baes@ugent.be
Received: 4 May 2012
Accepted: 5 July 2012
N-body simulations predict that dark matter haloes are described by specific density profiles on both galactic- and cluster-sized scales. Weak gravitational lensing through the measurements of their first and second order properties, shear and flexion, is a powerful observational tool for investigating the true shape of these profiles. One of the three-parameter density profiles recently favoured in the description of dark matter haloes is the Einasto profile. We present exact expressions for the shear and the first and second flexions of Einasto dark matter haloes derived using a Mellin-transform formalism in terms of the Fox H and Meijer G functions, that are valid for general values of the Einasto index. The resulting expressions can be written as series expansions that permit us to investigate the asymptotic behaviour of these quantities. Moreover, we compare the shear and flexion of the Einasto profile with those of different mass profiles including the singular isothermal sphere, the Navarro-Frenk-White profile, and the Sérsic profile. We investigate the concentration and index dependences of the Einasto profile, finding that the shear and second flexion could be used to determine the halo concentration, whilst for the Einasto index the shear and first and second flexions may be employed. We also provide simplified expressions for the weak lensing properties and other lensing quantities in terms of the generalized hypergeometric function.
Key words: methods: analytical / gravitational lensing: weak / galaxies: clusters: general / galaxies: halos / dark matter
© ESO, 2012
1. Introduction
A more accurate description of the elements that constitute our universe, such as the dark matter haloes that are believed to exist around galaxies and clusters, is of crucial importance for our understanding of cosmological structural formation. Recent results from N-body simulations of cold dark matter (CDM; Navarro et al. 2004; Merritt et al. 2006; Gao et al. 2008; Hayashi & White 2008; Stadel et al. 2009; Navarro et al. 2010; Reed et al. 2011; Vera-Ciro et al. 2012) indicate that nonsingular three-parameter models such as the Einasto (1965) profile, fit a wide range of dark matter haloes better than singular two-parameter models, e.g. the Navarro et al. (NFW) profile (Navarro et al. 1996, 1997).
The Einasto profile is given by ![\begin{equation} \rho(r)=\rho_{\text{s}}\exp\left\{ -d_{n}\left[\left(\frac{r}{{r_{{\text{s}}}}}\right)^{1/n}-1\right]\,\right\} ,\label{eq:einasto_generic} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq4.png) (1)where r is the spatial radius, the shape parameter n is called the Einasto index, rs represents the radius of the sphere that contains half of the total mass, ρs is the mass density at r = rs, and dn is a function that ensures that rs is indeed the half-mass radius. An analytical expansion for the function
(1)where r is the spatial radius, the shape parameter n is called the Einasto index, rs represents the radius of the sphere that contains half of the total mass, ρs is the mass density at r = rs, and dn is a function that ensures that rs is indeed the half-mass radius. An analytical expansion for the function 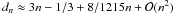 is provided by Retana-Montenegro et al. (Retana-Montenegro et al. 2012, hereafter RM12). One important characteristic of this profile is that its power-law logarithmic slope,
is provided by Retana-Montenegro et al. (Retana-Montenegro et al. 2012, hereafter RM12). One important characteristic of this profile is that its power-law logarithmic slope, 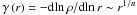 , depends on the Einasto index, which provides a profile that more accurately fits in the inner regions of simulated dark matter haloes than other profiles such as the NFW profile. In the study of real galaxies, several authors have used multi-component Einasto models, consisting generally of two or more Einasto components for each galaxy, where each component represents a homogeneous stellar population with its own set of parameters. For example, some of the first galaxies to be modelled using multi-component Einasto models were M 31 by Einasto (1969a) with values of 0.25 ≤ n ≤ 1, and other nearby galaxies such as Milky Way, M 87, M 32, Fornax, and Sculptor, and M 31 by Einasto (1974) with 0.5 ≤ n ≤ 4. Later, in a series of papers multi-component Einasto models were employed to model the luminous components of several galaxies such as the Milky Way (Einasto & Haud 1989), M 87 (Tenjes et al. 1991), M 31 (Tenjes et al. 1994), and M 81 (Tenjes et al. 1998); in these papers, the Einasto index is characterised by values of 0.36 ≤ n ≤ 7.1. The seven distant spiral galaxies GSS 074-2237, GSS 064-4412, GSS 094-2210, GSS 104-4024, GSS 064-4442, MDS uem0-043, and HDFS J223247.66-603335.9 were studied by Tamm & Tenjes (2003) and Tamm & Tenjes (2005), respectively. As in the earlier works mentioned, they modelled each visual component with a Einasto profile, the authors found values of 0.25 ≤ n ≤ 0.91 and noted that the Einasto indices for the disk component of the galaxies at high redshift follow a trend of having smaller values than the ones at lower redshift. Tempel & Tenjes (2006) fitted a multi-component Einasto model to the Sombrero galaxy, with 0.78 ≤ n ≤ 3 for the visual components. Tamm et al. (2007) and Tempel et al. (2007) presented a multi-component Einasto law study of M 31: using photometric data and metallicity measurements, they obtained the matter distribution of luminous components with 0.70 ≤ n ≤ 4.20, then tried to fit several models for the dark matter halo using kinematical data from the literature to construct a dynamical model and derive the dark matter density of the galaxy, they concluded that Einasto and NFW profiles give the best fits. Dhar & Williams (2011) fitted the surface brightness density of a sample of elliptical galaxies using a multi-component Einasto profile, finding values of 1 ≤ n ≤ 3 for the central components, and 5 ≤ n ≤ 8 for the outer components. Chemin et al. (2011), who studied the rotation curves of low mass spiral galaxies, modelled the dark matter halo with a Einasto profile, and obtained smaller values of n than predicted by computational simulations. On the other hand, according to N-body numerical calculations the Einasto index depends on both the halo mass and redshift (Hayashi & White 2008; Gao et al. 2008). Typical values of the Einasto index are in the range 5 ≤ n ≤ 8 according to the results of N-body simulations (Navarro et al. 2004; Gao et al. 2008; Hayashi & White 2008; Navarro et al. 2010). Vera-Ciro et al. (2012) analysed dark matter haloes of Milky Way-like systems and concluded that the Einasto model with values of 2 ≤ n ≤ 5 is preferred over the NFW profile.
, depends on the Einasto index, which provides a profile that more accurately fits in the inner regions of simulated dark matter haloes than other profiles such as the NFW profile. In the study of real galaxies, several authors have used multi-component Einasto models, consisting generally of two or more Einasto components for each galaxy, where each component represents a homogeneous stellar population with its own set of parameters. For example, some of the first galaxies to be modelled using multi-component Einasto models were M 31 by Einasto (1969a) with values of 0.25 ≤ n ≤ 1, and other nearby galaxies such as Milky Way, M 87, M 32, Fornax, and Sculptor, and M 31 by Einasto (1974) with 0.5 ≤ n ≤ 4. Later, in a series of papers multi-component Einasto models were employed to model the luminous components of several galaxies such as the Milky Way (Einasto & Haud 1989), M 87 (Tenjes et al. 1991), M 31 (Tenjes et al. 1994), and M 81 (Tenjes et al. 1998); in these papers, the Einasto index is characterised by values of 0.36 ≤ n ≤ 7.1. The seven distant spiral galaxies GSS 074-2237, GSS 064-4412, GSS 094-2210, GSS 104-4024, GSS 064-4442, MDS uem0-043, and HDFS J223247.66-603335.9 were studied by Tamm & Tenjes (2003) and Tamm & Tenjes (2005), respectively. As in the earlier works mentioned, they modelled each visual component with a Einasto profile, the authors found values of 0.25 ≤ n ≤ 0.91 and noted that the Einasto indices for the disk component of the galaxies at high redshift follow a trend of having smaller values than the ones at lower redshift. Tempel & Tenjes (2006) fitted a multi-component Einasto model to the Sombrero galaxy, with 0.78 ≤ n ≤ 3 for the visual components. Tamm et al. (2007) and Tempel et al. (2007) presented a multi-component Einasto law study of M 31: using photometric data and metallicity measurements, they obtained the matter distribution of luminous components with 0.70 ≤ n ≤ 4.20, then tried to fit several models for the dark matter halo using kinematical data from the literature to construct a dynamical model and derive the dark matter density of the galaxy, they concluded that Einasto and NFW profiles give the best fits. Dhar & Williams (2011) fitted the surface brightness density of a sample of elliptical galaxies using a multi-component Einasto profile, finding values of 1 ≤ n ≤ 3 for the central components, and 5 ≤ n ≤ 8 for the outer components. Chemin et al. (2011), who studied the rotation curves of low mass spiral galaxies, modelled the dark matter halo with a Einasto profile, and obtained smaller values of n than predicted by computational simulations. On the other hand, according to N-body numerical calculations the Einasto index depends on both the halo mass and redshift (Hayashi & White 2008; Gao et al. 2008). Typical values of the Einasto index are in the range 5 ≤ n ≤ 8 according to the results of N-body simulations (Navarro et al. 2004; Gao et al. 2008; Hayashi & White 2008; Navarro et al. 2010). Vera-Ciro et al. (2012) analysed dark matter haloes of Milky Way-like systems and concluded that the Einasto model with values of 2 ≤ n ≤ 5 is preferred over the NFW profile.
An alternative form of the density often used in dark matter halo studies is ![\begin{equation} \rho\left(r\right)=\rho_{-2}\,\exp\left\{ -2n\left[\left(\frac{r}{r_{-2}}\right)^{1/n}-1\right]\,\right\} ,\label{eq:einasto_halo_vers} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq22.png) (2)where r-2 is the radius at which the logarithmic slope of the density distribution has a value of − 2 and
(2)where r-2 is the radius at which the logarithmic slope of the density distribution has a value of − 2 and 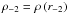 . A useful quantity to define is the concentration cE = r200/r-2, where r200 is the virial radius of a halo of mass M200, whose density is 200 times the critical density of the Universe at the halo redshift. One of the advantages of the Einasto profile over other profiles is that it has excellent agreement with the conditions outlined by Einasto (1969b) for constructing real galactic models, specifically, some moments must be finite. In particular, for this profile some moments, such as the total mass, central gravitational potential, and effective radius, are finite. In contrast, other profiles have logarithmic moments that must be truncated at some radius to ensure that the profile remains finite.
. A useful quantity to define is the concentration cE = r200/r-2, where r200 is the virial radius of a halo of mass M200, whose density is 200 times the critical density of the Universe at the halo redshift. One of the advantages of the Einasto profile over other profiles is that it has excellent agreement with the conditions outlined by Einasto (1969b) for constructing real galactic models, specifically, some moments must be finite. In particular, for this profile some moments, such as the total mass, central gravitational potential, and effective radius, are finite. In contrast, other profiles have logarithmic moments that must be truncated at some radius to ensure that the profile remains finite.
Gravitational lensing provides a direct way to study the mass distribution of large structures in the universe, such as galaxies and clusters, without making any assumptions about their dynamical state or composition. Lensing studies taking advantage of high-quality imaging have proven to be successful in mapping the distribution of dark matter in clusters and galaxies (Kneib et al. 2003; Clowe et al. 2006; Bradač et al. 2008; Abate et al. 2009; Okabe et al. 2010; Oguri et al. 2010; Okabe et al. 2011; Huang et al. 2011; Ragozzine et al. 2012; Jee et al. 2012; Oguri et al. 2012). There are two lensing regimes: the strong regime, where multiple images or strong distortions of a galaxy can be produced by an intervening distribution of matter, and the weak regime, where the lensed galaxy image is only slightly distorted, causing the intrinsic elliptical galaxy to appear as a distorted elliptical image. Weak lensing is a valuable and accurate tool for determining the shapes of dark-matter-halo density profiles, such as ellipticity (Hoekstra et al. 2004; Mandelbaum et al. 2006; Parker et al. 2007; Evans & Bridle 2009; Deb et al. 2010; Oguri et al. 2010) and triaxiality (Oguri et al. 2005; Gavazzi 2005; Corless & King 2007; Corless et al. 2009; Feroz & Hobson 2012). Until now, most weak lensing studies have considered only linear-order effects such as the weak shear, the quantity responsible for the induced ellipticity in the galaxy (see e.g. Kaiser et al. 1995; Bartelmann & Schneider 2001; Schneider et al. 2006; Hoekstra & Jain 2008, for reviews).
In the past few years, the study of high-order lensing properties has grown in importance (Goldberg & Natarajan 2002; Goldberg & Bacon 2005; Bacon et al. 2006, hereafter B06). These properties written as high-order derivatives of the deflection potential can be recognized as convergence and shear gradients. The convergence gradient, called the first flexion ℱ, induces a centroid shift in the lensed image with respect to the source or “skewness”. The shear gradient, called second flexion 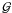 , generates an arc-like shape in the lensed image or “arcness”. Weak flexion provides useful information about dark matter haloes on galactic- and cluster-sized scales, particularly when probing substructure on smaller-scales where flexion is more sensitive to shear-only studies (Leonard et al. 2009; Bacon et al. 2010; Er et al. 2010).
, generates an arc-like shape in the lensed image or “arcness”. Weak flexion provides useful information about dark matter haloes on galactic- and cluster-sized scales, particularly when probing substructure on smaller-scales where flexion is more sensitive to shear-only studies (Leonard et al. 2009; Bacon et al. 2010; Er et al. 2010).
Several methods have been developed to measure the flexion of a lensed image, e.g. shapelets (B06; Massey et al. 2007; Fluke et al. 2012) and surface brightness moments (Irwin & Shmakova 2006; Irwin & Shmakova 2005; Irwin et al. 2007; Goldberg & Leonard 2007; Okura et al. 2007, 2008; Okura & Futamase 2009; Schneider & Er 2008). Cain et al. (2011) introduced a new method, called the analytic image model (AIM), to study flexion in astronomical images. Observational measurements of flexion include the detection of mass substructure in the Abell 1689 cluster by Leonard et al. (2007) and Cain et al. (2011) using observations of the Hubble Space Telescope (HST), as well as Okura et al. (2008) employing Subaru images; galaxy-galaxy flexion detection in the ground-based survey Deep Lens Survey (Goldberg & Bacon 2005) and the space-based HST COSMOS survey (Velander et al. 2011).
In addition, flexion has been proposed as a powerful cosmological tool: Munshi et al. (2011) suggested the use of convergence shear and flexion maps to decrease errors in the measuring standard candles distances, Camera & Diaferio (2011) studied how the flexion signal-to-noise ratio could be used to discern between cosmological models, Munshi et al. (2011) and Schäfer et al. (2012) proposed the use of cosmic flexion to probe large-scale structure. Hawken & Bridle (2009) studied the halo ellipticity on galactic scales, and found that the inclusion of flexion yields tighter constraints on ellipticity than shear-only studies. Er & Schneider (2011) and Er et al. (2011) proposed a new way to determine the halo ellipticity using the ratio of tangential-to-radial flexion and studied its behaviour as a radius function. Er et al. (2012) concluded that flexion is more sensitive to ellipticity than shear by performing a likehood analysis of mock flexion and shear data. Additionally, Viola et al. (2012) considered the case in which cross-terms between both shear and flexion and between intrinsic galaxy ellipticities and flexion are not ignored, concluding that these terms can cause a considerable bias in the flexion estimations.
In view of the increased use of the Einasto profile in cosmological studies (e.g. see Catena & Ullio 2010; Reed et al. 2011; Chemin et al. 2011; Dhar & Williams 2011; Catena & Ullio 2012; Narikawa & Yamamoto 2012), it is natural to extend its applications to weak shear and flexion lensing studies. Previously, several authors had performed weak lensing studies using the Einasto profile. For example, Hayashi & White (2008) measured the cross-correlations between halo centres and mass, and between galaxies and mass, in the Millennium Run (Springel et al. 2005), and found that the Einasto profile provides a close fit in the inner regions of their two-part model of the halo-mass cross-correlation function. Mandelbaum et al. (2008) analysed, using a weak statistical approach, a sample of galactic- and cluster-sized dark matter haloes from the Sloan Digital Sky Survey, and obtained very similar concentration-mass relations for the NFW and Einasto profiles. Mamon et al. (2010) used analytical approximations of the shear of the Einasto profile to compare it with the NFW shear.
Parametric models such as the singular isothermal sphere, the NFW, and Sérsic profiles have been used to model the dark matter distribution in weak lensing analyses (e.g. Hawken & Bridle 2009; Umetsu et al. 2011; van Uitert et al. 2011; Er et al. 2011; Viola et al. 2012; Soucail 2012), the properties of these models having been studied by several authors (Wright & Brainerd 2000; B06; Lasky & Fluke 2009). In the case of the Einasto profile, RM12 studied the analytical properties of the Einasto profile by applying a Mellin-transform formalism. In terms of Fox H and Meijer G functions, they derived analytical expressions of lensing properties for all values of the Einasto index, concentrating on the surface mass density, cumulative mass, deflection angle, and deflection potential. However, by means of the Mellin-transform formalism it is possible to extensively study the weak-lensing analytical properties of the Einasto profile. This study provides analytical expressions that can used to model realistic Einasto dark matter haloes in weak lensing modelling studies.
In this work, we apply Mellin-transform formalism to obtain and study in detail the analytical expressions for the weak lensing properties of the Einasto profile: the shear, and first, and second flexions. This paper is organized as follows. We summarize the weak lensing formalism in Sect. 2.1, and present the Mellin-transform technique in Sect. 2.2. In Sect. 3 we derive closed expressions for the shear and first and second flexions in terms of the Fox H and Meijer G functions. We then use the series expansions of these expressions to investigate their asymptotic behaviour. In Sect. 4, we compare our results with those for the SIS, NFW, and Sérsic profiles. In Sect. 5, we summarise and discuss our main results. Finally, in the Appendices A and B we provide series expansions of the lensing properties, and explicit expressions in terms of the generalized hypergeometric function, respectively. Throughout the paper, we adopt a cosmological model with the matter density ΩM = 0.26, the cosmological constant ΩΛ = 0.74, and the Hubble constant H0 = 72 km s-1 Mpc-1.
2. Theory
We provide a brief description of the two main theoretical aspects employed throughout this paper.
2.1. Weak lensing formalism
The weak lensing formalism using complex notation was introduced by B06. In the thin lens approximation, the lens equation is given by (Schneider et al. 1992) 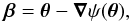 (3)where β and θ denote the positions on the source plane, and on the image plane, respectively, and ψ(θ) is the deflection potential defined by a two-dimensional Poisson, ∇2ψ(θ) = 2κ(θ), with the convergence κ(θ). Moreover, the convergence can be written as
(3)where β and θ denote the positions on the source plane, and on the image plane, respectively, and ψ(θ) is the deflection potential defined by a two-dimensional Poisson, ∇2ψ(θ) = 2κ(θ), with the convergence κ(θ). Moreover, the convergence can be written as 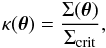 (4)where Σ(θ) is the surface mass density,
(4)where Σ(θ) is the surface mass density, 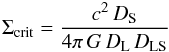 (5)is the critical surface mass density, and DL, DS, and DLS are the angular distances from observer to lens, from observer to source, and from lens to source, respectively. In addition, it is convenient to define the complex gradient operator (B06)
(5)is the critical surface mass density, and DL, DS, and DLS are the angular distances from observer to lens, from observer to source, and from lens to source, respectively. In addition, it is convenient to define the complex gradient operator (B06) 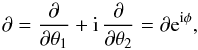 (6)where φ is the rotation angle, relative to the basis. The ∂ operator is simply a spin-s1 raising operator and its complex conjugate ∂ ⋆ a spin-s lowering operator.
(6)where φ is the rotation angle, relative to the basis. The ∂ operator is simply a spin-s1 raising operator and its complex conjugate ∂ ⋆ a spin-s lowering operator.
When we study gravitational lensing on scales where the deflection potential changes are larger than the scale of the lensed image, we can expand up to second order the lens equation in Eq. (3) around the neighbourhood of the lensed image2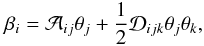 (7)where
(7)where 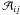 is the Jacobian matrix defined by
is the Jacobian matrix defined by 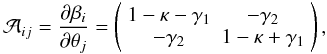 (8)with the convergence,
(8)with the convergence, 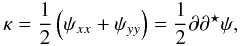 (9)which is a spin-0 field, and with
(9)which is a spin-0 field, and with 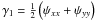 ,
, 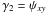 , the components of the complex shear
, the components of the complex shear 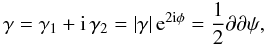 (10)which is a spin-2 field. The matrix
(10)which is a spin-2 field. The matrix 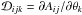 describes the behaviour of the convergence and shear across the lensed image by introducing two new lensing properties
describes the behaviour of the convergence and shear across the lensed image by introducing two new lensing properties 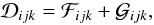 (11)namely the first flexion field or spin-1 first flexion ℱijk and the second flexion field or spin-3 second flexion
(11)namely the first flexion field or spin-1 first flexion ℱijk and the second flexion field or spin-3 second flexion 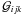 . Both field components can be expressed as third-order derivatives of the deflexion potential (Hawken & Bridle 2009)
. Both field components can be expressed as third-order derivatives of the deflexion potential (Hawken & Bridle 2009) 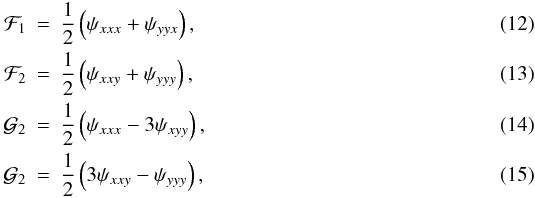 and taking advantage of the complex formalism, we can compactly write the first and second flexions as
and taking advantage of the complex formalism, we can compactly write the first and second flexions as  From Eqs. (16) and (17), one can clearly see the rotation symmetry for both flexions. Applying the complex conjugate operator to Eqs. (9), and (10) and comparing with Eqs. (16), and (17), we find a compact and elegant definition of the second-order properties as gradients of the first-order lensing properties
From Eqs. (16) and (17), one can clearly see the rotation symmetry for both flexions. Applying the complex conjugate operator to Eqs. (9), and (10) and comparing with Eqs. (16), and (17), we find a compact and elegant definition of the second-order properties as gradients of the first-order lensing properties 
2.2. Mellin-transform technique
The Mellin transform technique (Marichev 1983; Adamchick 1996; Fikioris 2007) consists in that one-dimensional definite integrals 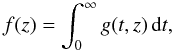 (20)can be expressed as the Mellin convolution of the functions f1 and f2
(20)can be expressed as the Mellin convolution of the functions f1 and f2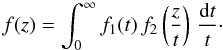 (21)The Mellin convolution theorem, which states that the Mellin transform of a Mellin convolution of two functions is the pointwise product of their Mellin transforms, can be applied to Eq. (21) inverting the Mellin transform of the Mellin convolution,
(21)The Mellin convolution theorem, which states that the Mellin transform of a Mellin convolution of two functions is the pointwise product of their Mellin transforms, can be applied to Eq. (21) inverting the Mellin transform of the Mellin convolution, 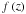 can be expressed as the inverse Mellin transform of the pointwise product of the f1 and f2 Mellin transforms. The Mellin transform is defined by
can be expressed as the inverse Mellin transform of the pointwise product of the f1 and f2 Mellin transforms. The Mellin transform is defined by 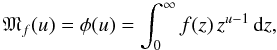 (22)and the inverse Mellin transform by
(22)and the inverse Mellin transform by 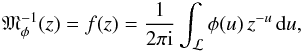 (23)where the integration path is a vertical line in the complex plane.
(23)where the integration path is a vertical line in the complex plane.
The integral in Eq. (20) may then be written as 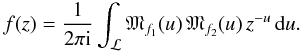 (24)With the requirement that f1 and f2 are of hypergeometric type, their Mellin transforms can be written as products of the form Γ(a + Au) or
(24)With the requirement that f1 and f2 are of hypergeometric type, their Mellin transforms can be written as products of the form Γ(a + Au) or ![\hbox{$\left[\Gamma\left(a+Au\right)\right]^{-1}$}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq74.png) , with
, with 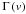 the gamma function and A real. The resulting integral in Eq. (24) is of the Mellin-Barnes type and it then can be evaluated as either a Fox H function for A ≠ 1 or as a Meijer G function for A = 1.
the gamma function and A real. The resulting integral in Eq. (24) is of the Mellin-Barnes type and it then can be evaluated as either a Fox H function for A ≠ 1 or as a Meijer G function for A = 1.
3. Weak lensing
We derive closed expressions for the weak-lensing first- and second-order properties of the Einasto profile: the shear γ, and the first ℱ and second 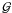 flexions in terms of Fox H, Meijer G functions, and the generalized hypergeometric function. Using these expressions, we calculate the expansion series and investigate its asymptotic behaviour. The results of this section provide a useful and straightforward way to study weak lensing, where the matter distribution is believed to be described by an Einasto profile.
flexions in terms of Fox H, Meijer G functions, and the generalized hypergeometric function. Using these expressions, we calculate the expansion series and investigate its asymptotic behaviour. The results of this section provide a useful and straightforward way to study weak lensing, where the matter distribution is believed to be described by an Einasto profile.
3.1. Convergence and shear
In the weak lensing regime up to first order, the lensed galaxy image has two distortions: the convergence κ causes an isotropic stretching in the lensed image, which magnifies the image by increasing its size, and the shear γ also causes an anisotropic stretching in the lensed image, that is responsible for the induced ellipticity in the lensed galaxy.
Foremost, to calculate the convergence, we must project the density profile on the lens plane using an Abel transform 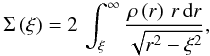 (25)where ξ is the radius from the lens centre, and r is the spatial radius. We follow here the notation of RM12 for the Einasto profile
(25)where ξ is the radius from the lens centre, and r is the spatial radius. We follow here the notation of RM12 for the Einasto profile ![\begin{equation} \rho(r)=\rho_{0}\exp\left[-\left(\frac{r}{h}\right)^{1/n}\right],\label{eq:einasto_gen_vers} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq83.png) (26)where we define the central density ρ0 = ρs edn = ρ-2 e2n and scale length
(26)where we define the central density ρ0 = ρs edn = ρ-2 e2n and scale length 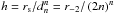 . Additionally, we define another quantity, the central convergence
. Additionally, we define another quantity, the central convergence 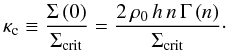 (27)Combining Eqs. (4), (25), (26) and (27), we get
(27)Combining Eqs. (4), (25), (26) and (27), we get 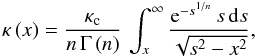 (28)where x = θ DL/h = ξ/h and s = r/h are the dimensionless radii.
(28)where x = θ DL/h = ξ/h and s = r/h are the dimensionless radii.
The integral in Eq. (28) cannot be expressed in terms of elementary or special functions for general values of n. However, using the Mellin transform technique explained in Sect. (2.2), we can write this integral as a Mellin-Barnes integral ![\begin{equation} \kappa\left(x\right)=\frac{\kappa_{\text{c}}\,\sqrt{\pi}\, x\,}{\Gamma\left(n\right)}\,\frac{1}{2\pi {\rm i}}\int_{\mathcal{L}}\frac{\Gamma\left(2ny\right)\Gamma\left(-\frac{1}{2}+y\right)}{\Gamma\left(y\right)}\left[\, x^{2}\right]^{-y}{\text{d}}y.\label{eq:Convergence-MellinBarnes} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq90.png) (29)The Fox H function (Fox 1961) is denoted as a Mellin-Barnes integral,
(29)The Fox H function (Fox 1961) is denoted as a Mellin-Barnes integral, ![\begin{eqnarray} &&H_{p,q}^{m,n}\left[\left.\begin{matrix}({\boldsymbol{a}},{\boldsymbol{A}})\\ ({\boldsymbol{b}},{\boldsymbol{B}}) \end{matrix}\,\right|\, z\right]=\nonumber\\ &&\frac{1}{2\pi i}\int_{{\cal L}}\frac{\prod_{j=1}^{m}\Gamma(b_{j}+B_{j}s)\prod_{j=1}^{n}\Gamma(1-a_{j}-A_{j}s)}{\prod_{j=m+1}^{q}\Gamma(1-b_{j}-B_{j}s)\prod_{j=n+1}^{p}\Gamma(a_{j}+A_{j}s)}\, z^{-s}\,{\text{d}}s.\label{eq:defH} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq91.png) (30)Comparing the integral in Eq. (29) with the above definition, we obtain a close expression for the convergence in terms of the Fox H function (RM12)
(30)Comparing the integral in Eq. (29) with the above definition, we obtain a close expression for the convergence in terms of the Fox H function (RM12) ![\begin{equation} \kappa\left(x\right)=\frac{\kappa_{\text{c}}\,\sqrt{\pi}}{\Gamma\left(n\right)}\, x\, H_{1,2}^{2,0}\left[\begin{array}{c} (0,\,1)\\ (0,\,2n),(-\frac{1}{2},\,1) \end{array}\biggr|\, x^{2}\right].\label{eq:convergence-Fox} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq92.png) (31)The shear for an circularly symmetric lens is (Miralda-Escude 1991)
(31)The shear for an circularly symmetric lens is (Miralda-Escude 1991) 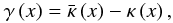 (32)where
(32)where 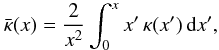 (33)is the average convergence within the dimensionless radius x.
(33)is the average convergence within the dimensionless radius x.
Inserting Eq. (31) into Eq. (33) and substituting this result along with Eq. (31) into Eq. (32), we can re-express the resulting integral as a Fox H function and obtain the shear for the Einasto profile ![\begin{equation} \gamma\left(x\right)=\left\{ \frac{\kappa_{\text{c}}\,\sqrt{\pi}}{\Gamma\left(n\right)}\, x\, H_{2,3}^{2,1}\left[\begin{array}{c} (-\frac{1}{2},\,1),(0,\,1)\\ (0,\,2n),(\frac{1}{2},\,1),(-\frac{3}{2},\,1) \end{array}\biggr|\, x^{2}\right]\right\} {\rm e}^{2{\rm i}\phi}.\label{eq:shear-Fox} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq96.png) (34)Equation (34) provides an expression for the shear in terms of one Fox H function, instead of two Fox H functions as found by RM12. Writing Eq. (34) in terms of one instead of two Fox H functions makes it easier to manipulate for analytical and numerical purposes.
(34)Equation (34) provides an expression for the shear in terms of one Fox H function, instead of two Fox H functions as found by RM12. Writing Eq. (34) in terms of one instead of two Fox H functions makes it easier to manipulate for analytical and numerical purposes.
The Fox H function is a very general function and reduces to most of the elementary and special functions. Despite not being a common special function, it has great potential as an analytical tool in theoretical astrophysics, in particular to study the analytical properties of density models such as the Sérsic profile (Baes & Gentile 2011; Baes & van Hese 2011) and Einasto profile (RM12). This function will be included in future versions of the software Mathematica. Additionally, several authors such as Yilmaz & Alouini (2009) and Shafique Ansari et al. (2012) have made available accurate and fast numerical routines to compute the Fox H function. Details about the many properties of this function can be found in Mathai (1978), Srivastava et al. (1982), Kilbas & Saigo (2004), and Mathai et al. (2009).
We remark that the shear 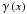 is not a directly measurable property owing to the mass-sheet degeneracy, but that the measurable property is the reduced shear (Falco et al. 1985; Gorenstein et al. 1988; Schneider & Seitz 1995; Narayan & Bartelmann 1996)
is not a directly measurable property owing to the mass-sheet degeneracy, but that the measurable property is the reduced shear (Falco et al. 1985; Gorenstein et al. 1988; Schneider & Seitz 1995; Narayan & Bartelmann 1996) 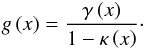 (35)
(35)
3.2. First and second flexions
Considering the weak lensing regime up to second order, two new lensing properties can be recognized: the first flexion ℱ, which describes the behaviour of the convergence gradient across the lensed image and the second flexion 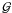 , which describes the behaviour of the shear gradient across the lensed image. These flexions produce centre-shift and arc-like distortions that, with the addition of the shear, cause the lensed image of the elliptical galactic source appear to have a “banana-like” shape.
, which describes the behaviour of the shear gradient across the lensed image. These flexions produce centre-shift and arc-like distortions that, with the addition of the shear, cause the lensed image of the elliptical galactic source appear to have a “banana-like” shape.
The first flexion can be found by simply calculating the convergence gradient, using Eqs. (31) and (18) ![\begin{equation} \mathcal{F}\left(x\right)=\mathcal{F}_{0}\,\left\{ H_{2,3}^{2,1}\left[\begin{array}{c} (-1,\,2),(0,\,1)\\ (0,\,2n),(-\frac{1}{2},\,1),(0,\,2) \end{array}\biggr|\, x^{2}\right]\right\} {\rm e}^{{\rm i}\phi},\label{eq:flexion01-Fox} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq99.png) (36)with
(36)with
Combining Eqs. (19) and (34), plus some algebra, the second flexion may be obtained 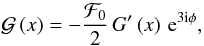 (37)with
(37)with ![\begin{equation} G^{\prime}\left(x\right)=H_{4,5}^{3,2}\left[\begin{array}{c} (-1,\,2),(-\frac{1}{2},\,1),(0,\,1),(1,\,2)\\ (0,\,2n),(-\frac{1}{2},\,1),(2,\,2),(0,\,2),(-\frac{3}{2},\,1) \end{array}\biggr|\, x^{2}\right]. \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq102.png) (38)We have obtained analytical expressions for both flexions expressed as Fox H functions, where the flexions are circularly symmetric as expected for the Einasto profile. The second flexion with nine gamma functions in the integrand is a more complicated function than the first flexion with only five gamma functions.
(38)We have obtained analytical expressions for both flexions expressed as Fox H functions, where the flexions are circularly symmetric as expected for the Einasto profile. The second flexion with nine gamma functions in the integrand is a more complicated function than the first flexion with only five gamma functions.
As indicated before, the shear is affected by the so-called mass-sheet degeneracy, and the same measurement difficulty arises with the first and second flexion. Schneider & Er (2008) demonstrated that the observable properties are the reduced flexions 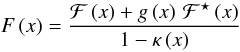 (39)and
(39)and 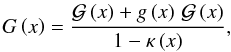 (40)where
(40)where 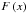 is a spin-0 field,
is a spin-0 field, 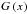 is a spin-3 field, and
is a spin-3 field, and 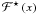 is the complex conjugate of the first flexion.
is the complex conjugate of the first flexion.
Given that the scope of this work is to present analytical expressions of different weak lensing properties and the quantitative comparison of these properties for several profiles, we focus on the lensing properties given in Eqs. (34), (36), and (37), instead of the reduced ones in Eqs. (35), (39), and (40).
3.3. Integer and half-integer values of n
We simplify the expressions for the shear in Eq. (34) and first, in Eq. (36), and second, in Eq. (37), flexions in terms of the Fox H function for rational values of n, to the case when n is an integer or half-integer number, where the resulting expressions can be written in terms of the Meijer G function.
The Meijer G function is defined by the Mellin-Barnes integral (Meijer 1936) ![\begin{eqnarray} &&G_{p,q}^{m,n}\left[\left.\begin{matrix}{\boldsymbol{a}}\\ {\boldsymbol{b}} \end{matrix}\,\right|\, z\right]=\nonumber\\ &&~~~~~~\frac{1}{2\pi i}\int_{{\cal \mathcal{L}}}\frac{\prod_{j=1}^{m}\Gamma(b_{j}+s)\prod_{j=1}^{n}\Gamma(1-a_{j}-s)}{\prod_{j=m+1}^{q}\Gamma(1-b_{j}-s)\prod_{j=n+1}^{p}\Gamma(a_{j}+s)}\, z^{-s}\,{\text{d}}s.\label{eq:defG} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq108.png) (41)There is extensive literature about the Meijer G function and its many useful properties (Bateman & Erdélyi 1953; Luke 1976; Andrews 1985; Prudnikov et al. 1990).
(41)There is extensive literature about the Meijer G function and its many useful properties (Bateman & Erdélyi 1953; Luke 1976; Andrews 1985; Prudnikov et al. 1990).
For the Fox H function, for there is not yet a numerical implementation contrarily, there are various software packages with Meijer G numerical routines, such as the commercial Maple, Mathematica, and the free open-source Sage and mpmath library.
By substituting the Gauss multiplication formula (Abramowitz & Stegun 1970) 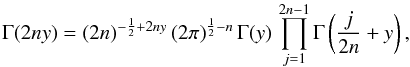 (42)into Eq. (29), and making use of Eq. (41) for the comparison, we have (RM12)
(42)into Eq. (29), and making use of Eq. (41) for the comparison, we have (RM12) ![% subequation 2180 0 \begin{equation} \kappa\left(x\right)=\frac{\kappa_{\text{c}}}{2\,(2\pi)^{n-1}\,\sqrt{n}\,\Gamma\left(n\right)}\, x\, G_{0,2n}^{2n,0}\left[\begin{array}{c} -\\ {\boldsymbol{b}} \end{array}\biggr|\,\frac{x^{2}}{\left(2n\right)^{2n}}\right], \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq110.png) (43a)where b is a vector of size 2n given by
(43a)where b is a vector of size 2n given by 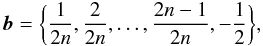 (43b)which is an expression for the convergence of the Einasto profile in terms of the Meijer G function.
(43b)which is an expression for the convergence of the Einasto profile in terms of the Meijer G function.
Now, substituting the convergence into Eq. (33) and performing the integration of Meijer G function (Eq. (07.34.21.0003.01) at the Wolfram Functions Site3), and inserting the integral product along with the convergence in Eq. (32), we may write the shear as ![% subequation 2252 0 \begin{eqnarray} \gamma\left(x\right)&=&\left\{ \frac{\kappa_{\text{c}}}{2\,(2\pi)^{n-1}\,\sqrt{n}\,\Gamma\left(n\right)}\, x\right.\nonumber\\ &&\times\left.G_{1,2n+1}^{2n,1}\left[\begin{array}{c} -\frac{1}{2}\\ {\boldsymbol{b}^{\prime}},-\frac{3}{2} \end{array}\biggr|\,\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right\} {\rm e}^{2{\rm i}\phi}, \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq114.png) (44a)where b′ is a vector of size 2n given by
(44a)where b′ is a vector of size 2n given by 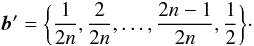 (44b)Calculating the gradient for convergence following Eq. (18) and using the differentiation properties of Meijer G function (Eq. (07.34.20.0005.01) on the Wolfram Functions Site), we find
(44b)Calculating the gradient for convergence following Eq. (18) and using the differentiation properties of Meijer G function (Eq. (07.34.20.0005.01) on the Wolfram Functions Site), we find ![\begin{equation} \mathcal{F}\left(x\right)=\left\{ \frac{\mathcal{F}_{0}}{(2\pi)^{n-1}\,\sqrt{n\,\pi}}\, G_{1,2n+1}^{2n,1}\left[\begin{array}{c} -\frac{1}{2}\\ {\boldsymbol{b}},\frac{1}{2} \end{array}\biggr|\,\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right\} {\rm e}^{{\rm i}\phi}.\label{eq:flexion01-Meijer} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq117.png) (45)Applying again the differentiation properties of Meijer G function to derive the gradient for shear according to Eq. (19), the result may be written as
(45)Applying again the differentiation properties of Meijer G function to derive the gradient for shear according to Eq. (19), the result may be written as ![\begin{eqnarray} &&\mathcal{G}\left(x\right)=\left\{ -\frac{\mathcal{F}_{0}}{(2\pi)^{n-1}\,\sqrt{n\,\pi}}\right.\nonumber\\ &&\qquad\quad\times\left.G_{3,2n+3}^{2n+1,2}\left[\begin{array}{c} {-\frac{1}{2},-\frac{1}{2},\frac{1}{2}}\\ {\boldsymbol{b},\frac{3}{2},\frac{1}{2},-\frac{3}{2}} \end{array}\biggr|\,\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right\} {\rm e}^{3{\rm i}\phi}.\label{flexion02-Meijer} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq118.png) (46)Additional simplifications in terms of generalized hypergeometric function for half-integer values of n can be found in Appendix A.
(46)Additional simplifications in terms of generalized hypergeometric function for half-integer values of n can be found in Appendix A.
3.4. Simple cases: n = 1 and n = 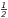
For n = 1, the density profile decreases exponentially from the system centre 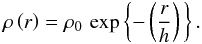 (47)For the exponential case, the resulting weak lensing expressions can be found by substituting n = 1 in Eqs. (38)–(46)
(47)For the exponential case, the resulting weak lensing expressions can be found by substituting n = 1 in Eqs. (38)–(46) ![\begin{eqnarray} &&\kappa(x)=\frac{\kappa_{\text{c}}}{2}\, x\, G_{0,2}^{2,0}\left[\begin{array}{c}- \\ \frac{1}{2},-\frac{1}{2} \end{array}\biggr|\,\frac{x^{2}}{4}\right], \\ &&\left|\gamma\left(x\right)\right|=\frac{\kappa_{\text{c}}}{2}\, x\, G_{1,3}^{2,1}\left[\begin{array}{c} -\frac{1}{2} \\\frac{1}{2},\frac{1}{2},-\frac{3}{2} \end{array}\biggr|\,\frac{x^{2}}{4}\right], \\ &&\left|\mathcal{F}\left(x\right)\right|=\frac{\mathcal{F}_{0}}{\sqrt{\pi}}\, G_{1,3}^{2,1}\left[\begin{array}{c} -\frac{1}{2}\\ \frac{1}{2},-\frac{1}{2},\frac{1}{2} \end{array}\biggr|\,\frac{x^{2}}{4}\right], \\ &&\left|\mathcal{G}\left(x\right)\right|=-\frac{\mathcal{F}_{0}}{\sqrt{\pi}}\, G_{3,5}^{3,2}\left[\begin{array}{c} -\frac{1}{2},-\frac{1}{2},\frac{1}{2} \\ \frac{1}{2},-\frac{1}{2},\frac{3}{2},\frac{1}{2},-\frac{3}{2} \end{array}\biggr|\,\frac{x^{2}}{4}\right]\cdot \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq122.png) We may write the above Meijer G functions in terms of Bessel functions
We may write the above Meijer G functions in terms of Bessel functions ![\begin{eqnarray} &&\kappa\left(x\right)=\kappa_{\text{c}}\, x\, K_{1}\left(x\right)\label{kappa-n1} \\ &&\left|\gamma\left(x\right)\right|=\frac{4\,\kappa_{\text{c}}}{x^{2}}\,\left[1-\frac{x^{2}}{2}\, K_{2}\left(x\right)-\frac{x^{3}}{4}\, K_{1}\left(x\right)\right],\label{eq:shear-n1} \\ &&\left|\mathcal{F}\left(x\right)\right|=-\frac{\mathcal{F}_{0}}{\sqrt{\pi}}\, x\, K_{0}\left(x\right),\label{flexion01-n1} \\ \label{eq:flexion02-n1} &&\left|\mathcal{G}\left(x\right)\right|=\frac{\mathcal{F}_{0}}{\sqrt{\pi}}\,\left[\frac{16}{x^{3}}\left(1-\frac{x^{2}}{2}\, K_{2}\left(x\right)\right)-x\, K_{0}\left(x\right)-4\, K_{1}\left(x\right)\right], \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq123.png) with Kν(z) the modified Bessel function of the second kind of order ν.
with Kν(z) the modified Bessel function of the second kind of order ν.
For 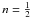 , the Einasto mass distribution presents a Gaussian fall-off
, the Einasto mass distribution presents a Gaussian fall-off 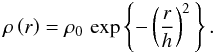 (56)Therefore, we set
(56)Therefore, we set 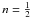 in Eqs. (38)–(46) to obtain
in Eqs. (38)–(46) to obtain ![\begin{eqnarray} &&\kappa(x)=\kappa_{\text{c}}\, x\, G_{0,1}^{1,0}\left[\begin{array}{c} -\\ -\frac{1}{2} \end{array}\biggr|\, x^{2}\right], \\ &&\left|\gamma\left(x\right)\right|=\kappa_{\text{c}}\, x\, G_{1,2}^{1,1}\left[\begin{array}{c} -\frac{1}{2}\\ \frac{1}{2},-\frac{3}{2} \end{array}\biggr|\, x^{2}\right], \\ &&\left|\mathcal{F}\left(x\right)\right|=2\,\mathcal{F}_{0}\, G_{1,2}^{1,1}\left[\begin{array}{c} -\frac{1}{2}\\ -\frac{1}{2},\frac{1}{2} \end{array}\biggr|\, x^{2}\right], \\ &&\left|\mathcal{G}\left(x\right)\right|=-2\,\mathcal{F}_{0}\, G_{3,4}^{2,2}\left[\begin{array}{c} -\frac{1}{2},-\frac{1}{2},\frac{1}{2}\\ -\frac{1}{2},\frac{3}{2},\frac{1}{2},-\frac{3}{2} \end{array}\biggr|\, x^{2}\right]. \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq128.png) We can equivalently express these Meijer G functions in terms of elementary functions
We can equivalently express these Meijer G functions in terms of elementary functions ![\begin{eqnarray} \label{kappa-n-1/2} &&\kappa\left(x\right)=\kappa_{\text{c}}\,{\text{e}}^{-x^{2}}, \\ \label{eq:shear-n-1/2} &&\left|\gamma\left(x\right)\right|=\frac{\kappa_{\text{c}}}{x^{2}}\,{\text{e}}^{-x^{2}}\,\left({\text{e}}^{x^{2}}-1-x^{2}\right), \\ \label{flexion01-n-1/2} &&\left|\mathcal{F}\left(x\right)\right|=-2\,\mathcal{F}_{0}\, x\,{\text{e}}^{-x^{2}}, \\ \label{flexion02-n-1/2} &&\left|\mathcal{G}\left(x\right)\right|=\frac{4\mathcal{\, F}_{0}}{x^{3}}\,{\text{e}}^{-x^{2}}\,\left[{\text{e}}^{x^{2}}-1-\frac{x^{2}}{2}\left(x^{2}+2\right)\right]. \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq129.png) The results for the exponential profile described in Eqs. (52) − (55), and for the Gaussian profile in Eqs. (61) − (64) can be checked separately by substituting the density profiles in Eqs. (47) and (56) into Eq. (28) and performing the relevant derivations for the shear and flexions.
The results for the exponential profile described in Eqs. (52) − (55), and for the Gaussian profile in Eqs. (61) − (64) can be checked separately by substituting the density profiles in Eqs. (47) and (56) into Eq. (28) and performing the relevant derivations for the shear and flexions.
3.5. Asymptotic behaviour
The behaviour of the weak lensing properties of the Einasto profile at small radii (x ≪ 1) can be studied by using the series expansions of Appendix B. We easily arrive at appropriate expressions, which depend on the value of n for the shear ![\begin{eqnarray} \left|\mathcal{\gamma}\left(x\right)\right| & \sim&\frac{\kappa_{\text{c}}}{4}\,\frac{\Gamma\left(1-n\right)}{\Gamma\left(1+n\right)}\, x^{2}\qquad \text{for \ensuremath{n<1}},\\[3mm] \left|\mathcal{\gamma}\left(x\right)\right| & \sim&\frac{\kappa_{\text{c}}}{4}\, x^{2}\,\left[-\ln\left(\frac{x}{2}\right)+\frac{1}{4}-\gamma\right]\qquad \text{for \ensuremath{n=1}},\\ \left|\mathcal{\gamma}\left(x\right)\right| & \sim&\frac{\kappa_{\text{c}}\,\sqrt{\pi}}{2n\,\left(3n+1\right)}\,\left[\frac{\Gamma\left(\frac{n-1}{2n}\right)}{\Gamma\left(n\right)\,\Gamma\left(\frac{2n-1}{2n}\right)}\right]\, x^{1+1/n} \text{for \ensuremath{n>1.}} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq132.png) The first flexion near zero behaves as
The first flexion near zero behaves as ![\begin{eqnarray} \left|\mathcal{F}\left(x\right)\right| & \sim&-\frac{\mathcal{F}_{0}}{n\,\sqrt{\pi}}\,\Gamma\left(1-n\right)\, x\qquad \text{for \ensuremath{n<1}},\\ \left|\mathcal{F}\left(x\right)\right| & \sim&\frac{\mathcal{F}_{0}}{n\,\sqrt{\pi}}\, x\,\left[\ln\left(\frac{x}{2}\right)+1+\gamma\right]\qquad \text{for \ensuremath{n=1}},\\ \left|\mathcal{F}\left(x\right)\right| & \sim&-\frac{\mathcal{F}_{0}}{2n^{2}}\,\left[\frac{\Gamma\left(\frac{n-1}{2n}\right)}{\Gamma\left(\frac{2n-1}{2n}\right)}\right]\, x^{1/n}\qquad \text{for \ensuremath{n>1.}} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq133.png) For the second flexion, the asymptotic behaviour in the neighbourhood of the lensed image origin is described by
For the second flexion, the asymptotic behaviour in the neighbourhood of the lensed image origin is described by ![\begin{eqnarray} \left|\mathcal{G}\left(x\right)\right| & \sim&-\frac{\mathcal{F}_{0}}{6n\,\sqrt{\pi}}\,\Gamma\left(1-3n\right)\, x^{3}\qquad \text{\text{for \ensuremath{n<\frac{1}{3}}\ or \ensuremath{n=\frac{1}{2}}}}, \\ \left|\mathcal{G}\left(x\right)\right| & \sim&-\frac{9\,\mathcal{F}_{0}}{32\,\sqrt{\pi}}\,\Gamma\left(\frac{1}{15}\right)\, x^{5}\quad\qquad\qquad\qquad\nonumber \\ && +\frac{\mathcal{F}_{0}}{\sqrt{\pi}}\, x^{3}\,\left[\frac{1}{3}\ln\left(\frac{x}{2}\right)+\frac{5}{2}+\gamma\right] \qquad \qquad\text{for \ensuremath{n=\frac{1}{3}}}, \\ \left|\mathcal{G}\left(x\right)\right|&\sim&-\frac{3\mathcal{F}_{0}}{32n\,\sqrt{\pi}}\,\Gamma\left(1-5n\right)\, x^{5}\qquad\nonumber \quad\qquad\quad \\ &&\quad+\frac{\mathcal{F}_{0}}{2n^{2}}\,\left(\frac{n^{2}-1}{3n+1}\right)\,\left[\frac{\Gamma\left(-\frac{n+1}{2n}\right)}{\Gamma\left(-\frac{1}{2n}\right)}\right]\, x^{1/n} \quad \text{ for \ensuremath{n>\frac{1}{3}}}, \\ \left|\mathcal{G}\left(x\right)\right| & \sim&\frac{\mathcal{F}_{0}}{\sqrt{\pi}}\,\frac{x^{3}}{12}\,\left[\ln\left(\frac{x}{2}\right)-\frac{2}{3}+\gamma\right]~\qquad \qquad \text{for \ensuremath{n=1}},\\ \left|\mathcal{G}\left(x\right)\right| & \sim&\frac{\mathcal{F}_{0}}{2n^{2}}\left(\frac{n^{2}-1}{3n+1}\right)\,\left[\frac{\Gamma\left(-\frac{n+1}{2n}\right)}{\Gamma\left(-\frac{1}{2n}\right)}\right]\, x^{1/n}~\qquad \text{for \ensuremath{n>1.}} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq134.png) The power-law and logarithmic series converge very slowly at large radii (x ≫ 1). Hence, we cannot use them to investigate the behaviour of the shear and flexions at large radii. However, following Kilbas & Saigo (1999), we derive asymptotic expansions at large radii for these properties. For the shear, we have
The power-law and logarithmic series converge very slowly at large radii (x ≫ 1). Hence, we cannot use them to investigate the behaviour of the shear and flexions at large radii. However, following Kilbas & Saigo (1999), we derive asymptotic expansions at large radii for these properties. For the shear, we have 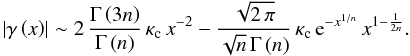 (76)When x → ∞, the first flexion behaves as
(76)When x → ∞, the first flexion behaves as 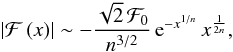 (77)and the second flexion is characterised by the behaviour
(77)and the second flexion is characterised by the behaviour 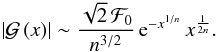 (78)
(78)
4. Profile comparisons
We compare the weak lensing properties for the Einasto profile obtained in the Sect. 3 with the properties of the singular isothermal sphere, the Navarro-Frenk-White profile, and Sérsic model. The properties for these models can be found in Bartelmann (1996), Wright & Brainerd (2000, B06, and Lasky & Fluke (2009). We follow the same approach that was used by Wright & Brainerd (2000) and Lasky & Fluke (2009), which consists in fixing the halo mass M200 and permits the calculation of the virial radius. We use M200 = 1 × 1012 h-1 M⊙ and zl = 0.4, which are the approximate average galactic-sized halo mass and lens redshift, respectively, found by Parker et al. (2007) in their galaxy-galaxy weak lensing analysis of the Canada-France-Hawaii Telescope Legacy Survey (CFHTLS). We choose to place the source at zs = 0.92, which implies DLS/DS ≃ 0.5. We assume that the concentration-mass varies with the halo redshift in the range 0 ≤ z ≤ 2 as (Duffy et al. 2008) 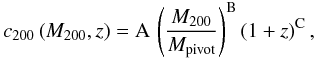 (79)where Mpivot = 2 × 1012 h-1 M⊙ and { A, B, C } = { 6.40, −0.108, −0.62 } for the Einasto profile. Using the above relation, we find a concentration of cE = 5.80. In the case of the Einasto halo, we alse choose to use a value of n ≃ 6 that corresponds to the halo mass that is used according to Gao et al. (2008). For the NFW halo, the concentration can be determined using Eq. (79) with { A, B, C } = { 5.71, −0.048, −0.47 } (Duffy et al. 2008), we obtain cNFW = 5.31. The calculation of the parameters model is explicit, except in the case of the Sérsic profile, for which we construct the model using the procedure outlined in Appendix B of Lasky & Fluke (2009). This procedure requires employing the Prugniel & Simien (1997) model, which is an analytical approximation of the Sérsic deprojection; we use a Sérsic index of m ≃ 8.6.
(79)where Mpivot = 2 × 1012 h-1 M⊙ and { A, B, C } = { 6.40, −0.108, −0.62 } for the Einasto profile. Using the above relation, we find a concentration of cE = 5.80. In the case of the Einasto halo, we alse choose to use a value of n ≃ 6 that corresponds to the halo mass that is used according to Gao et al. (2008). For the NFW halo, the concentration can be determined using Eq. (79) with { A, B, C } = { 5.71, −0.048, −0.47 } (Duffy et al. 2008), we obtain cNFW = 5.31. The calculation of the parameters model is explicit, except in the case of the Sérsic profile, for which we construct the model using the procedure outlined in Appendix B of Lasky & Fluke (2009). This procedure requires employing the Prugniel & Simien (1997) model, which is an analytical approximation of the Sérsic deprojection; we use a Sérsic index of m ≃ 8.6.
Figure 1 shows the convergence, shear, and both first and second flexion expected for a galatic-sized halo, assuming that the mass distribution is given by the Einasto, SIS, NFW, and Sérsic profiles as a function of the angular separation from the lens centre. An indicator of where the weak lensing effects are relevant is the Einstein radius of the SIS profile, which is θE = 0.216″ for the halo that is being studied. As can be seen, the overall behaviours of the profiles are comparable, the differences between the magnitudes of the lensing quantities being stronger at smaller angular separations, with the shear and second flexion showing a greater dissimilarity than the convergence and first flexion. These dissimilarities in the central region indicate that the Einasto profile may be differentiable from the other profiles in observational weak lensing studies. Our result agrees with Mamon et al. (2010), who compared the shear for the Einasto and NFW profiles finding that the major differences between the profiles are at small distances. As can be seen, the magnitudes of all properties at small distances are stronger for the SIS than the NFW profile and large distances the relation is inverted. In addition, the magnitudes are stronger for the NFW profile than that of SIS, which is consistent with the slope for the SIS being − 2, and for the NFW profile the inner slope being − 1 and the outer being − 3. Interestingly, we also note that the lensing properties of the Einasto profile tend to be very similar to those of the NFW profile for increasing angular separation.
 |
Fig. 1 Comparison of the magnitude of convergence, shear, first and second flexion due to a dark matter halo of mass M200 = 1 × 1012 h-1 M⊙, assuming that the mass distribution is described by Einasto, NFW, and SIS profiles and the Sérsic model. The lens and source planes are located at redshifts zL = 0.4 and zS = 0.92, respectively. The Einsten radius for the SIS is θE = 0.216″, indicating the angular distance when the weak lensing effects are relevant. |
In Fig. 2, we plot dependence of the weak lensing properties on the concentration for the Einasto profile. We use the same mass as in the previous comparison, and values of c = 4, 8, 12, 16, 20, 24 for the concentration. The concentration dependence of these properties is clearly non-linear, and very similar to that of the NFW profile investigated by Lasky & Fluke (2009). As with the NFW profile, the concentration dependence is far stronger at small separations. With increasing angular distance from the lensed image the dependence gets less pronounced and the curves become almost identical, except the convergence, which curves seem to be distinguishable at both small and large angular distances. The shear and second flexion seem to be more sensitive to the concentration variation than the convergence and first flexion, making the first two lensing properties useful tools for breaking the degeneracy between mass and concentration, if this occurs, as discussed by Lasky & Fluke (2009) for the NFW profile.
 |
Fig. 2 Comparison of the magnitude of convergence, shear, first and second flexion due to an Einasto dark matter halo of mass M200 = 1 × 1012 h-1 M⊙, for different values of the concentration c = 4, 8, 12, 16, 20, 24. |
We illustrate the index dependence of the Einasto profile in Fig. 3. We again use the same halo mass M200 = 1 × 1012 h-1 M⊙, and vary the Einasto index, n, across the range 1 ≤ n ≤ 9. It is evident, that the index dependence is greater at smaller angular separations for the lensing properties, becoming marginally distinguishable at increasing θ, with the only two exceptions being the exponential profile (n = 1), which can be clearly identified, and with a little bit more work the n = 2 profile can be distinguished as well. The convergence is the less dependent on n of all the lensing quantities; the shear and the first and second flexions depend more strongly on n than the convergence, near the lensed halo centre; this feature is very important, because it is near the lensed image that the lensing signal is stronger, making the first flexion, shear, and second flexion excellent tools for constraining n, whilst the convergence may be used to derive the halo mass. In contrast to the concentration dependence of the Einasto profile, which is similar to that of the NFW profile, the index dependence of the Einasto profile differs from the corresponding dependence of the Sérsic profile. Lasky & Fluke (2009) found that for the Sérsic profile the index dependence is stronger in κ and ℱ, and very weak in γ and  , whenever this dependence is present for the Sérsic profile, its effect decreases with boosted angular separations, where the lensing signal is weaker, making it difficult to constraint the Sérsic index. Thereby, we conclude that may be easier to constrain the index for an Einasto halo rather that for a Sérsic halo.
, whenever this dependence is present for the Sérsic profile, its effect decreases with boosted angular separations, where the lensing signal is weaker, making it difficult to constraint the Sérsic index. Thereby, we conclude that may be easier to constrain the index for an Einasto halo rather that for a Sérsic halo.
 |
Fig. 3 Comparison of the magnitude of convergence, shear, first and second flexion due to an Einasto dark matter halo of mass M200 = 1 × 1012 h-1 M⊙, for different values of the Einasto index, n, between 1 ≤ n ≤ 9. |
5. Summary and conclusions
We have applied the Mellin transform technique to obtain closed-form expressions for the weak lensing properties of the Einasto profile. The expressions for the shear 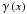 , first flexion
, first flexion 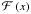 , and second flexion
, and second flexion 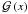 can be written in terms of the Fox H function for general values of the Einasto index n, and can simplified in terms of the Meijer G function for integer or half-integer values of n. We utilized the residue theorem to calculate specific power and logarithmic-power expansions for these expressions. The expansions permit us to study the asymptotic behaviour of the weak lensing properties at small and large radii. Furthermore, we employed the Slater’s theorem (Marichev 1983) to derive an expression for the convergence
can be written in terms of the Fox H function for general values of the Einasto index n, and can simplified in terms of the Meijer G function for integer or half-integer values of n. We utilized the residue theorem to calculate specific power and logarithmic-power expansions for these expressions. The expansions permit us to study the asymptotic behaviour of the weak lensing properties at small and large radii. Furthermore, we employed the Slater’s theorem (Marichev 1983) to derive an expression for the convergence 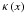 in terms of the generalized hypergeometric function, which is valid for half-integer values of n. This enables the other expressions for the lensing properties to be written in terms of the hypergeometric function.
in terms of the generalized hypergeometric function, which is valid for half-integer values of n. This enables the other expressions for the lensing properties to be written in terms of the hypergeometric function.
We have examined in detail the convergence, shear, and first and second flexions for an Einasto profile and other profiles including the singular isothermal sphere, the NFW, and Sérsic profiles. We found that the Einasto profile overall has a similar behaviour to these profiles. Nonetheless, this profile is clearly different from the others, particularly at small angular separations from the lens centre, where the lensing signal is stronger. At large angular separations, the Einasto profile behaves far very similarly to the NFW profile than the other profiles. We explored the dependence of the Einasto profile on the concentration parameter, our results indicating that it has a non-linear concentration dependence and that the shear and second flexion are more effective indicators of the dependence than the convergence and the first flexion. In addition, we studied the Einasto index dependence. For this parameter, the dependence seems to be weaker than for the concentration, for which the shear, second, and first flexions seem to be more sensitive to the index dependence that the convergence. We note that the magnitude of the lensing properties of a Sérsic model are stronger than for the other profiles, this indicates that the profile selected to model the halo must be chosen with caution as discussed by Lasky & Fluke (2009). We note that the index dependence of an Einasto halo is stronger at small angular distances from the lens centre, which is the opposite of the case for a Sérsic halo for which at large angular distances the dependence is stronger. This means that observationally it is easier to constrain the value of the index for the Einasto profile rather than the Sérsic model, because the lensing signal is stronger near the lensed image.
The availability of analytical expressions for the Einasto-profile weak-lensing properties is of foremost importance, and constitutes an effort to foster the inclusion of this density profile in weak lensing modelling studies. There are several possible applications of our results for modelling studies. For example, one of them is the generation of the shear signal in weak lensing analyses, which can provide valuable information about the description of the mass density profiles. This, in turn, places constraints on the model parameters such as mass, concentration, and particularly the Einasto index, which is known to scale with mass and redshift according to N-body simulations (Gao et al. 2008; Hayashi & White 2008), and for which our results could be used to verify this variation observationally. Likewise, weak flexion might be generated using our expressions and used to constrain the model parameters, particularly when halo substructure has to be proven, providing another scale within the haloes, where the behaviour of n can be studied.
Here, we considered spherically symmetrical haloes, but haloes are far from ideal symmetric objects (see e.g. Shaw et al. 2006; Bett et al. 2007; Howell & Brainerd 2010). Nevertheless, weak shear has proven successfully in studying deviations in the halo shape from spherical symmetry, such as the halo ellipticity (Hoekstra et al. 2004; Mandelbaum et al. 2006; Parker et al. 2007; Evans & Bridle 2009; Oguri et al. 2010). Similarly, weak flexion has been proposed as a tool to investigate the halo ellipticity (Hawken & Bridle 2009; Er & Schneider 2011; Er et al. 2011). Triaxiality is another aspect of the halo shape that has been explored using weak lensing (Oguri et al. 2005; Gavazzi 2005; Sereno & Umetsu 2011; Feroz & Hobson 2012); ignoring the halo triaxiality can affect the parameter estimation in lens-rich clusters (Corless & King 2007; Corless et al. 2009), leading to the cluster appearing to be more massive and concentrated, particularly, if its major axis is aligned with the line of sight (Hennawi et al. 2007; Oguri & Blandford 2009; Meneghetti et al. 2010). Some cluster studies where there are apparently lensing biases in the estimated concentration and mass include that of Broadhurst et al. (2008), who analysed the mass and concentration of four nearly relaxed clusters, that of the gravitational lens with the largest Einstein radius detected so far MACS J0717.5+3745 (Zitrin et al. 2009), and Oguri et al. (2009), who obtained the radial profile of four clusters combining lensing data from the Subaru telescope. The inclusion of our results in weak lensing ellipticity and triaxiality studies is straightforward, therefore it enables the possibility of investigating the halo ellipticity and triaxiality with the Einasto profile.
Our current knowledge of the structure of the Universe on large scales will be improved by new gravitational lensing surveys such as the Dark Energy Survey4 (DES), Euclid5, the Large Synoptic Survey Telescope (LSST)6, the James Webb Space Telescope7, KiDS8, Pan-STARRS9, and WFIRST10. These surveys will provide more accurate measurements of weak lensing that could be modelled using the analytical expressions presented in this work.
This paper constitutes a further step in studying the properties of the Einasto profile using analytical means. In addition, it extends and complements the work of RM12, providing additional simplified expressions for their results. With this work, we hope to encourage the use of special functions such as the Fox H function, the Meijer G function, and the generalized hypergeometric function in astronomy and astrophysics.
Acknowledgments
E.R.M. and F.F.A. wish to thank H. Morales, R. Carboni, J. Gutirrez, R. Magaña, and M. Chaves for their critical reading of the manuscript. Moreover, we wish to thank the referee for valuable comments and suggestions. This research has made use of NASA’s Astrophysics Data System Bibliographic Services.
References
- Abate, A., Wittman, D., Margoniner, V. E., et al. 2009, ApJ, 702, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Abramowitz, M., & Stegun, I. A. 1970, Handbook of mathematical functions (Dover) [Google Scholar]
- Adamchick, V. 1996, Mathematica in Education and Research, 5, 16 [Google Scholar]
- Andrews, L. 1985, Special functions for engineers and applied mathematicians (Macmillan) [Google Scholar]
- Bacon, D. J., Goldberg, D. M., Rowe, B. T. P., & Taylor, A. N. 2006, MNRAS, 365, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, D. J., Amara, A., & Read, J. I. 2010, MNRAS, 409, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., & Gentile, G. 2011, A&A, 525, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baes, M., & van Hese, E. 2011, A&A, 534, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bartelmann, M. 1996, A&A, 313, 697 [NASA ADS] [Google Scholar]
- Bartelmann, M., & Schneider, P. 2001, Phys. Rep., 340, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Bateman, H., & Erdélyi, A. 1953, Higher transcendental functions No. v. 1 (McGraw-Hill) [Google Scholar]
- Bett, P., Eke, V., Frenk, C. S., et al. 2007, MNRAS, 376, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Bradač, M., Allen, S. W., Treu, T., et al. 2008, ApJ, 687, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T., Umetsu, K., Medezinski, E., Oguri, M., & Rephaeli, Y. 2008, ApJ, 685, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Cain, B., Schechter, P. L., & Bautz, M. W. 2011, ApJ, 736, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Camera, S., & Diaferio, A. 2011 [arXiv:1104.3955] [Google Scholar]
- Catena, R., & Ullio, P. 2010, JCAP, 8, 4 [Google Scholar]
- Catena, R., & Ullio, P. 2012, JCAP, 5, 005 [NASA ADS] [CrossRef] [Google Scholar]
- Chemin, L., de Blok, W. J. G., & Mamon, G. A. 2011, AJ, 142, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Clowe, D., Bradač, M., Gonzalez, A. H., et al. 2006, ApJ, 648, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Corless, V. L., & King, L. J. 2007, MNRAS, 380, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Corless, V. L., King, L. J., & Clowe, D. 2009, MNRAS, 393, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Deb, S., Goldberg, D. M., Heymans, C., & Morandi, A. 2010, ApJ, 721, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Dhar, B. K., & Williams, L. L. R. 2011 [arXiv:1112.3120] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dalla Vecchia, C. 2008, MNRAS, 390, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J. 1965, Trudy Inst. Astroz. Alma-Ata (Tartu. Astr. Obs. Teated No. 17), 5, 87 [Google Scholar]
- Einasto, J. 1969a, Astrofizika, 5, 137 [NASA ADS] [Google Scholar]
- Einasto, J. 1969b, Astron. Nachr., 291, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J. 1974, in Stars and the Milky Way System, ed. L. N. Mavridis, 291 [Google Scholar]
- Einasto, J., & Haud, U. 1989, A&A, 223, 89 [NASA ADS] [Google Scholar]
- Er, X., & Schneider, P. 2011, A&A, 528, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Er, X., Li, G., & Schneider, P. 2010, A&A, submitted [arXiv:1008.3088] [Google Scholar]
- Er, X., Mao, S., Xu, D., & Cao, Y. 2011, MNRAS, 417, 2197 [NASA ADS] [CrossRef] [Google Scholar]
- Er, X., Tereno, I., & Mao, S. 2012, MNRAS, 421, 1443 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, A. K. D., & Bridle, S. 2009, ApJ, 695, 1446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falco, E. E., Gorenstein, M. V., & Shapiro, I. I. 1985, ApJ, 289, L1 [Google Scholar]
- Feroz, F., & Hobson, M. P. 2012, MNRAS, 420, 596 [NASA ADS] [CrossRef] [Google Scholar]
- Fikioris, G. 2007, Mellin Transform Method for Integral Evaluation: Introduction and Applications to Electromagnetics (Morgan & Claypool) [Google Scholar]
- Fluke, C. J., Malec, A. L., Lasky, P. D., & Barsdell, B. R. 2012, MNRAS, 2376 [Google Scholar]
- Fox, C. 1961, Trans. Am. Math. Soc., 98, 395 [Google Scholar]
- Gao, L., Navarro, J. F., Cole, S., et al. 2008, MNRAS, 387, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, R. 2005, A&A, 443, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldberg, D. M., & Bacon, D. J. 2005, ApJ, 619, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, D. M., & Leonard, A. 2007, ApJ, 660, 1003 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, D. M., & Natarajan, P. 2002, ApJ, 564, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Gorenstein, M. V., Shapiro, I. I., & Falco, E. E. 1988, ApJ, 327, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Hankin, R. K. S., & Lee, A. 2006, Aust. New Zealand J. Stat., 48, 67 [CrossRef] [Google Scholar]
- Hawken, A. J., & Bridle, S. L. 2009, MNRAS, 400, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Hayashi, E., & White, S. D. M. 2008, MNRAS, 388, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Hennawi, J. F., Dalal, N., Bode, P., & Ostriker, J. P. 2007, ApJ, 654, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Hoekstra, H., & Jain, B. 2008, Ann. Rev. Nucl. Part. Sci., 58, 99 [Google Scholar]
- Hoekstra, H., Yee, H. K. C., & Gladders, M. D. 2004, ApJ, 606, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, P. J., & Brainerd, T. G. 2010, MNRAS, 407, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Z., Radovich, M., Grado, A., et al. 2011, A&A, 529, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Irwin, J., & Shmakova, M. 2005, New Astron. Rev., 49, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., & Shmakova, M. 2006, ApJ, 645, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Shmakova, M., & Anderson, J. 2007, ApJ, 671, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Jee, M. J., Mahdavi, A., Hoekstra, H., et al. 2012, ApJ, 747, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser, N., Squires, G., & Broadhurst, T. 1995, ApJ, 449, 460 [NASA ADS] [CrossRef] [Google Scholar]
- Kilbas, A. A., & Saigo, M. 1999, J. Appl. Math. Stochast. Anal., 12, 191 [Google Scholar]
- Kilbas, A. A., & Saigo, M. 2004, H-Transforms: Theory and Applications (CRC Press) [Google Scholar]
- Kneib, J.-P., Hudelot, P., Ellis, R. S., et al. 2003, ApJ, 598, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Lasky, P. D., & Fluke, C. J. 2009, MNRAS, 396, 2257 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, A., Goldberg, D. M., Haaga, J. L., & Massey, R. 2007, ApJ, 666, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Leonard, A., King, L. J., & Wilkins, S. M. 2009, MNRAS, 395, 1438 [NASA ADS] [CrossRef] [Google Scholar]
- Luke, Y. L. 1969, The Special Functions and Their Approximations: v. 1 (Mathematics in Science and Engineering) (Academic Press), A53 [Google Scholar]
- Luke, Y. L. 1976, Mathematical Functions and Their Approximations (Academic Press) [Google Scholar]
- Mamon, G. A., Biviano, A., & Murante, G. 2010, A&A, 520, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Broderick, T., Seljak, U., & Brinkmann, J. 2006, MNRAS, 370, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Seljak, U., & Hirata, C. M. 2008, J. Cosmol. Astropart. Phys., 2008, 006 [CrossRef] [Google Scholar]
- Marichev, O. 1983, Handbook of integral transforms of higher transcendental functions: theory and algorithmic tables (E. Horwood) [Google Scholar]
- Massey, R., Rowe, B., Refregier, A., Bacon, D. J., & Bergé, J. 2007, MNRAS, 380, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Mathai, A. M. 1978, The H-function with applications in statistics and other disciplines (Wiley) [Google Scholar]
- Mathai, A., Saxena, R., & Haubold, H. 2009, The H-Function: Theory and Applications (Springer) [Google Scholar]
- Meijer, C. S. 1936, Nieuw Archief voor Wiskunde, 18, 10 [Google Scholar]
- Meneghetti, M., Fedeli, C., Pace, F., Gottlöber, S., & Yepes, G. 2010, A&A, 519, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Merritt, D., Graham, A. W., Moore, B., Diemand, J., & Terzić, B. 2006, AJ, 132, 2685 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda-Escude, J. 1991, ApJ, 370, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Munshi, D., Smidt, J., Heavens, A., Coles, P., & Cooray, A. 2011, MNRAS, 411, 2241 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Bartelmann, M. 1996, unpublished [arXiv:astroph/9606001] [Google Scholar]
- Narikawa, T., & Yamamoto, K. 2012, J. Cosmology Astropart. Phys., 5, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Hayashi, E., Power, C., et al. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Ludlow, A., Springel, V., et al. 2010, MNRAS, 402, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., & Blandford, R. D. 2009, MNRAS, 392, 930 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Takada, M., Umetsu, K., & Broadhurst, T. 2005, ApJ, 632, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Hennawi, J. F., Gladders, M. D., et al. 2009, ApJ, 699, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Oguri, M., Takada, M., Okabe, N., & Smith, G. P. 2010, MNRAS, 405, 2215 [NASA ADS] [Google Scholar]
- Oguri, M., Bayliss, M. B., Dahle, H., et al. 2012, MNRAS, 420, 3213 [NASA ADS] [CrossRef] [Google Scholar]
- Okura, Y., & Futamase, T. 2009, ApJ, 699, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Okura, Y., Umetsu, K., & Futamase, T. 2007, ApJ, 660, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Okura, Y., Umetsu, K., & Futamase, T. 2008, ApJ, 680, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, N., Takada, M., Umetsu, K., Futamase, T., & Smith, G. P. 2010, PASJ, 62, 811 [NASA ADS] [Google Scholar]
- Okabe, N., Bourdin, H., Mazzotta, P., & Maurogordato, S. 2011, ApJ, 741, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, L. C., Hoekstra, H., Hudson, M. J., van Waerbeke, L., & Mellier, Y. 2007, ApJ, 669, 21 [Google Scholar]
- Prudnikov, A., Brychkov, Y., & Marichev, O. 1990, Integrals and Series: More special functions, Integrals and Series (Gordon and Breach Science Publishers) [Google Scholar]
- Prugniel, P., & Simien, F. 1997, A&A, 321, 111 [NASA ADS] [Google Scholar]
- Ragozzine, B., Clowe, D., Markevitch, M., Gonzalez, A. H., & Bradač, M. 2012, ApJ, 744, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, D. S., Koushiappas, S. M., & Gao, L. 2011, MNRAS, 415, 3177 [NASA ADS] [CrossRef] [Google Scholar]
- Retana-Montenegro, E., Van Hese, E., Gentile, G., Baes, M., & Frutos-Alfaro, F. 2012, A&A, 540, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schäfer, B. M., Heisenberg, L., Kalovidouris, A. F., & Bacon, D. J. 2012, MNRAS, 420, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P., & Er, X. 2008, A&A, 485, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P., & Seitz, C. 1995, A&A, 294, 411 [NASA ADS] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses [Google Scholar]
- Schneider, P., Kochanek, C., & Wambsganss, J. 2006, Gravitational Lensing: Strong, Weak and Micro: Saas-Fee Advanced Course 33 (Saas-Fee Advanced Courses) (Springer) [Google Scholar]
- Sereno, M., & Umetsu, K. 2011, MNRAS, 416, 3187 [NASA ADS] [CrossRef] [Google Scholar]
- Shafique Ansari, I., Yilmaz, F., Alouini, M.-S., & Kucur, O. 2012, SPAWC, accepted [arXiv:1202.2576] [Google Scholar]
- Shaw, L. D., Weller, J., Ostriker, J. P., & Bode, P. 2006, ApJ, 646, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Soucail, G. 2012, A&A, 540, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Srivastava, H., Gupta, K., & Goyal, S. 1982, The H-functions of one and two variables, with applications (South Asian Publishers) [Google Scholar]
- Stadel, J., Potter, D., Moore, B., et al. 2009, MNRAS, 398, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Tamm, A., & Tenjes, P. 2003, A&A, 403, 529 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tamm, A., & Tenjes, P. 2005, A&A, 433, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Tamm, A., & Tenjes, P. 2007, unpublished [arXiv:0707.4374] [Google Scholar]
- Tamm, A., Tempel, E., & Tenjes, P. 2007, unpublished [arXiv:0707.4375] [Google Scholar]
- Tempel, E., & Tenjes, P. 2006, MNRAS, 371, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Tenjes, P., Einasto, J., & Haud, U. 1991, A&A, 248, 395 [NASA ADS] [Google Scholar]
- Tenjes, P., Haud, U., & Einasto, J. 1994, A&A, 286, 753 [NASA ADS] [Google Scholar]
- Tenjes, P., Haud, U., & Einasto, J. 1998, A&A, 335, 449 [NASA ADS] [Google Scholar]
- Umetsu, K., Broadhurst, T., Zitrin, A., Medezinski, E., & Hsu, L.-Y. 2011, ApJ, 729, 127 [NASA ADS] [CrossRef] [Google Scholar]
- van Uitert, E., Hoekstra, H., Velander, M., et al. 2011, A&A, 534, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Velander, M., Kuijken, K., & Schrabback, T. 2011, MNRAS, 412, 2665 [NASA ADS] [CrossRef] [Google Scholar]
- Vera-Ciro, C. A., Helmi, A., Starkenburg, E., & Breddels, M. A. 2012, MNRAS, submitted [arXiv:1202.6061] [Google Scholar]
- Viola, M., Melchior, P., & Bartelmann, M. 2012, MNRAS, 419, 2215 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, C. O., & Brainerd, T. G. 2000, ApJ, 534, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Yilmaz, F., & Alouini, M.-S. 2009, in Global Telecommunications Conference, 2009, GLOBECOM 2009. IEEE, 1 [Google Scholar]
- Zitrin, A., Broadhurst, T., Rephaeli, Y., & Sadeh, S. 2009, ApJ, 707, L102 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Simplified half-integer expressions of the Einasto profile lensing properties
The Eqs. (38)–(46) written in terms of Meijer G function can be reduced to expressions in terms of the generalized hypergeometric function (Luke 1969; Abramowitz & Stegun 1970) 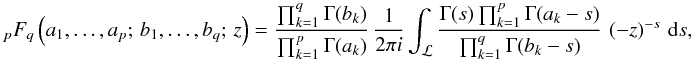 (A.1)for half-integer values of n, for which the poles are simple, using the Slater’s theorem (Marichev 1983)
(A.1)for half-integer values of n, for which the poles are simple, using the Slater’s theorem (Marichev 1983) ![\appendix \setcounter{section}{1} \begin{equation} G_{p,q}^{m,n}\left[\left.\begin{matrix}{\boldsymbol{a}}\\ {\boldsymbol{b}} \end{matrix}\,\right|\, z\right]=\sum_{k=1}^{m}\frac{\prod_{j=1}^{m}\Gamma(b_{j}-b_{k})^{*}\prod_{j=1}^{n}\Gamma(1+b_{k}-a_{j})\, z^{b_{k}}}{\prod_{j=m+1}^{q}\Gamma(1+b_{k}-b_{j})\prod_{j=n+1}^{p}\Gamma(a_{j}-b_{k})}\,{}_{p}F_{q-1}\left[\left.\begin{matrix}{1+b_{k}-\boldsymbol{a}}\\ {\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\, (-1)^{p-m-n} \; z\right],\label{eq:slater-theorem} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq171.png) (A.2)where the asterisk in the gamma function indicates that the term k = j, which corresponds to
(A.2)where the asterisk in the gamma function indicates that the term k = j, which corresponds to 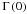 , must be replaced by 1; and in the hypergeometric function that the vector 1 + bk − b must be reduced in size from q to q − 1.
, must be replaced by 1; and in the hypergeometric function that the vector 1 + bk − b must be reduced in size from q to q − 1.
It is evident from Eqs. (38) and (A.2) that the convergence may be written as ![\appendix \setcounter{section}{1} \begin{equation} \kappa\left(x\right)=\frac{\kappa_{\text{c}}}{2\,(2\pi)^{n-1}\,\sqrt{n}\,\Gamma\left(n\right)}\, x\,\left\{ \sum_{k=1}^{2n}\,\prod_{j=1}^{2n}\Gamma(b_{j}-b_{k})^{*}\,\left(\frac{x^{2}}{\left(2n\right)^{2n}}\right)^{b_{k}}\,{}_{0}F_{\,2n-1}\left[\left.\begin{matrix}-\\ {\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\left(-1\right)^{-2n}\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right\} ,\label{eq:convergence-hyperg} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq178.png) (A.3)with bk the components of b given by Eq. (43b).
(A.3)with bk the components of b given by Eq. (43b).
Inserting Eq. (A.3) into Eqs. (32), (18) and (19), we obtain the expressions ![\appendix \setcounter{section}{1} \begin{eqnarray} &&\left|\gamma\left(x\right)\right|=\frac{-\kappa_{\text{c}}}{2\,(2\pi)^{n-1}\,\sqrt{n}\,\Gamma\left(n\right)}\, x\,\left\{\sum_{k=1}^{2n}\,\prod_{j=1}^{2n}\Gamma(b_{j}-b_{k})^{*}\,\left(\frac{\frac{1}{2}+b_{k}}{\frac{3}{2}+b_{k}}\right)\,\left(\frac{x^{2}}{\left(2n\right)^{2n}}\right)^{b_{k}}\right.\notag \\ &&\hspace{5.5cm}\left.\phantom{sum_{k=1}^{2n}\,\prod_{j=1}^{2n}\Gamma(b_{j}-b_{k})^{*}}\times\,_{2}F_{\,2n+1}\left[\left.\begin{matrix}{\frac{3}{2}+b_{k},\frac{3}{2}+b_{k}}\\ {\frac{1}{2}+b_{k},\frac{5}{2}+b_{k},\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\left(-1\right)^{-2n}\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right\},\label{eq:shear-hyperg} \\ &&\left|\mathcal{F}\left(x\right)\right|=\frac{\mathcal{F}_{0}}{(2\pi)^{n-1}\,\sqrt{n\,\pi}}\,\left\{ \sum_{k=1}^{2n}\,\prod_{j=1}^{2n}\Gamma(b_{j}-b_{k})^{*}\,\left(\frac{1}{2}+b_{k}\,\right)\,\left(\frac{x^{2}}{\left(2n\right)^{2n}}\right)^{b_{k}}{}_{1}F_{\,2n}\left[\left.\begin{matrix}{\frac{3}{2}+b_{k}}\\ {\frac{1}{2}+b_{k},\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\left(-1\right)^{-2n}\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right\} ,\label{eq:flexion01-hyperg} \\ &&\left|\mathcal{G}\left(x\right)\right|=\frac{\mathcal{F}_{0}}{(2\pi)^{n-1}\,\sqrt{n\,\pi}}\,\left\{ \sum_{k=1}^{2n}\,\prod_{j=1}^{2n}\Gamma(b_{j}-b_{k})^{*}\,\left(\frac{1}{2}+b_{k}\right)\,\left(\frac{x^{2}}{\left(2n\right)^{2n}}\right)^{b_{k}}\Biggl\{\,{}_{1}F_{\,2n}\left[\left.\begin{matrix}{\frac{3}{2}+b_{k}} \notag \\ &&{\frac{1}{2}+b_{k},\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\left(-1\right)^{-2n}\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right.\\ &&\hspace{8cm}\left.-\frac{2}{\frac{3}{2}+b_{k}}\,{}_{2}F_{\,2n+1}\left[\left.\begin{matrix}{\frac{3}{2}+b_{k},\frac{3}{2}+b_{k}}\\ {\frac{1}{2}+b_{k},\frac{5}{2}+b_{k},\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\left(-1\right)^{-2n}\frac{x^{2}}{\left(2n\right)^{2n}}\right]\Biggr\}\right\} .\label{eq:flexion02-hyperg} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq180.png) Other important lensing quantities such as the cumulative surface mass density
Other important lensing quantities such as the cumulative surface mass density  , deflection angle
, deflection angle  , and deflection potential
, and deflection potential 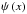 also can be written in terms of the generalized hypergeometric function
also can be written in terms of the generalized hypergeometric function ![\appendix \setcounter{section}{1} \begin{eqnarray} M\left(x\right)&=&\frac{\sqrt{n}\,\rho_{0}\, h^{3}}{2(2\pi)^{n-2}}\, x^{3}\,\left\{ \sum_{k=1}^{2n}\,\frac{\prod_{j=1}^{2n}\Gamma(b_{j}-b_{k})^{*}}{\left(\frac{3}{2}+b_{k}\right)}\,\left(\frac{x^{2}}{\left(2n\right)^{2n}}\right)^{b_{k}}\,_{1}F_{\,2n}\left[\left.\begin{matrix}{\frac{3}{2}+b_{k}}\\ {\frac{5}{2}+b_{k},\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\left(-1\right)^{-2n}\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right\} , \\ \alpha\left(x\right)&=&\frac{\kappa_{\text{c}}}{2\,(2\pi)^{n-1}\,\sqrt{n}\,\Gamma\left(n\right)}\, x^{2}\,\left\{ \sum_{k=1}^{2n}\,\frac{\prod_{j=1}^{2n}\Gamma(b_{j}-b_{k})^{*}}{\left(\frac{3}{2}+b_{k}\right)}\,\left(\frac{x^{2}}{\left(2n\right)^{2n}}\right)^{b_{k}}\,{}_{1}F_{\,2n}\left[\left.\begin{matrix}{\frac{3}{2}+b_{k}}\\ {\frac{5}{2}+b_{k},\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\left(-1\right)^{-2n}\frac{x^{2}}{\left(2n\right)^{2n}}\right]\right\} , \\ \psi\left(x\right)&=&\frac{\kappa_{\text{c}}}{4\,(2\pi)^{n-1}\,\sqrt{n}\,\Gamma\left(n\right)}\, x^{3}\,\Biggl\{\sum_{k=1}^{2n}\,\frac{\prod_{j=1}^{2n}\Gamma(b_{j}-b_{k})^{*}}{\left(\frac{3}{2}+b_{k}\right)^{2}}\,\left(\frac{x^{2}}{\left(2n\right)^{2n}}\right)^{b_{k}}\,_{2}F_{\,2n+1}\left[\left.\begin{matrix}{\frac{3}{2}+b_{k},\frac{3}{2}+b_{k}}\\ {\frac{5}{2}+b_{k},\frac{5}{2}+b_{k},\left(1+b_{k}-\boldsymbol{b}\right){}^{*}} \end{matrix}\,\right|\left(-1\right)^{-2n}\frac{x^{2}}{\left(2n\right)^{2n}}\right]\Biggr\}\cdot~~~~~~~~~~~~~\label{eq:deflection-hyperg} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq184.png) The Eqs. (A.3)–(A.9) are ready for being use in numerical calculations because there are already several available numerical implementations of the generalized hypergeometric function. Some software that includes an implementation of this function are the proprietary Maple, Mathematica, and Matlab, and freely available Sage, mpmath library, and the package hypergeo (Hankin & Lee 2006) of the R language.
The Eqs. (A.3)–(A.9) are ready for being use in numerical calculations because there are already several available numerical implementations of the generalized hypergeometric function. Some software that includes an implementation of this function are the proprietary Maple, Mathematica, and Matlab, and freely available Sage, mpmath library, and the package hypergeo (Hankin & Lee 2006) of the R language.
Appendix B: Series expansions of the shear and first and second flexions
The expressions for the shear 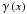 and first ℱ(x) and second
and first ℱ(x) and second 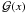 flexions can be written as series expansions to study its asymptotic behaviour near zero. We apply the residue theorem to the contour integral in Eq. (30) and obtain the explicit power or power-logarithmic series expansions depending on the multiplicity of the poles of the gamma functions Γ(bj + Bjs). Examples of specific applications of the residue theorem can be found in Baes & van Hese (2011), for the deprojected Sérsic profile, and in RM12 for the projected Einasto profile. The general theorem for the Fox H function can be found in Kilbas & Saigo (1999). We encounter two cases:
flexions can be written as series expansions to study its asymptotic behaviour near zero. We apply the residue theorem to the contour integral in Eq. (30) and obtain the explicit power or power-logarithmic series expansions depending on the multiplicity of the poles of the gamma functions Γ(bj + Bjs). Examples of specific applications of the residue theorem can be found in Baes & van Hese (2011), for the deprojected Sérsic profile, and in RM12 for the projected Einasto profile. The general theorem for the Fox H function can be found in Kilbas & Saigo (1999). We encounter two cases:
Case 1: if n is either non-rational or rational number p/q with an even denominator (and p,q are coprime), all poles are simple, so that the expansion takes the form of a power series ![\appendix \setcounter{section}{2} \begin{eqnarray} \left|\gamma(x)\right|&=&\frac{\kappa_{\text{c}}\,\sqrt{\pi}}{\Gamma\left(n\right)}\,\left\{ \,\sum_{k=1}^{\infty}\left[\left(\tfrac{1}{2}+\tfrac{k}{2n}\right)\,\frac{\Gamma\left(-\tfrac{3}{2}-\tfrac{k}{2n}\right)}{\Gamma\left(-\tfrac{k}{2n}\right)}\,\frac{(-1)^{k}}{k!}\,\frac{x^{k/n+1}}{2n}\right]\ -\sum_{k=0}^{\infty}\frac{\Gamma(n-2nk)}{\Gamma\left(\tfrac{1}{2}-k\right)}\,\frac{(-1)^{k}}{\left(k+1\right)\left(k-1\right)!}\, x^{2k}\,\right\} ,\label{eq:shear-gen-series}~~~~~~~~~~~~~~~ \\ \left|\mathcal{F}(x)\right|&=&\mathcal{F}_{0}\,\left[\,-\sum_{k=1}^{\infty}\frac{\Gamma\left(\tfrac{1}{2}-\tfrac{k}{2n}\right)}{\Gamma\left(-\tfrac{k}{2n}\right)}\,\frac{(-1)^{k}}{k!}\,\frac{x^{k/n}}{n}\,+\,2\,\sum_{k=0}^{\infty}\frac{\Gamma(n-2nk)}{\Gamma\left(\tfrac{1}{2}-k\right)}\,\frac{(-1)^{k}}{\left(k-1\right)!}\, x^{2k-1}\,\right],\label{flexion01-gen-series-1} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq190.png) and
and ![\appendix \setcounter{section}{2} \begin{equation} \left|\mathcal{G}(x)\right|=\mathcal{F}_{0}\,\left[\,\sum_{k=1}^{\infty}\frac{\Gamma\left(-\tfrac{1}{2}-\tfrac{k}{2n}\right)}{\Gamma\left(-\tfrac{k}{2n}\right)}\,\frac{k^{2}-n^{2}}{3n+k}\,\frac{(-1)^{k}}{k!}\,\frac{x^{k/n}}{2n^{2}}\,+\,2\,\sum_{k=0}^{\infty}\frac{\Gamma(n-2nk)}{\Gamma\left(\tfrac{1}{2}-k\right)}\,\frac{k-1}{k+1}\,\frac{(-1)^{k}}{\left(k-1\right)!}\, x^{2k-1}\,\right].\label{flexion02-gen-series} \end{equation}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq191.png) (B.3)Case 2: if n is either an integer or rational number p/q with an odd denominator, some poles are of second order, then the expansion takes the form of a logarithmic-power series
(B.3)Case 2: if n is either an integer or rational number p/q with an odd denominator, some poles are of second order, then the expansion takes the form of a logarithmic-power series ![\appendix \setcounter{section}{2} \begin{eqnarray} \left|\gamma(x)\right|&=&\frac{\kappa_{\text{c}}\,\sqrt{\pi}}{\Gamma\left(n\right)}\,\left\{ \sum_{\substack{k=1\\ k\,{\text{mod}}\, p\ne0 } }^{\infty}\biggl[\left(\tfrac{1}{2}+\tfrac{k}{2n}\right)\,\frac{\Gamma\left(-\tfrac{3}{2}-\tfrac{k}{2n}\right)}{\Gamma\left(-\tfrac{k}{2n}\right)}\,\frac{(-1)^{k}}{k!}\,\frac{x^{k/n+1}}{2n}\biggr]\ -\ \hspace{-3ex}\sum_{\substack{k=1\\ (k+k_{0})\,{\text{mod}}\, q\ne0 } }^{\infty}\hspace{-3ex}\frac{\Gamma(n-2nk)}{\Gamma\left(\tfrac{1}{2}-k\right)}\,\frac{(-1)^{k}}{\left(k+1\right)(k-1)!}\, x^{2k}\,\right\} \nonumber\\ &&\qquad-\ \frac{\kappa_{\text{c}}}{n\,\Gamma\left(n\right)}\hspace{-3ex}\sum_{\substack{k=1\\ (k+k_{0})\,{\text{mod}}\, q=0 } }^{\infty}\hspace{-3ex}\frac{(-1)^{p}\,(2k)!}{(2nk-n)!\,\left(k+1\right)!\,(k-1)!}\left(\frac{x}{2}\right)^{2k}\,\left[-\ln\left(\frac{x}{2}\right)-\frac{1}{2k}-\frac{1}{2k\left(k+1\right)}+\psi(k+1)+n\,\psi(2nk-n)-\psi(2k-1)\right],\label{shear-rat-series} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq193.png) (B.4)
(B.4)
![\appendix \setcounter{section}{2} \begin{eqnarray} \left|\mathcal{F}(x)\right|&=&\mathcal{F}_{0}\,\left[\ \ -\hspace{-1.5ex}\sum_{\substack{k=1\\ k\,{\text{mod}}\, p\ne0 } }^{\infty}\hspace{-1.5ex}\frac{\Gamma\left(\tfrac{1}{2}-\tfrac{k}{2n}\right)}{\Gamma\left(-\tfrac{k}{2n}\right)}\,\frac{(-1)^{k}}{k!}\,\frac{x^{k/n}}{n}\ +\ 2\ \hspace{-3ex}\sum_{\substack{k=1\\ (k+k_{0})\,{\text{mod}}\, q\ne0 } }^{\infty}\hspace{-3ex}\frac{\Gamma(n-2nk)}{\Gamma\left(\tfrac{1}{2}-k\right)}\,\frac{(-1)^{k}}{\left(k-1\right)!}\, x^{2k-1}\ \right]\nonumber\\ &&\qquad+\ \frac{\mathcal{F}_{0}}{n\,\sqrt{\pi}}\hspace{-3ex}\sum_{\substack{k=1\\ (k+k_{0})\,{\text{mod}}\, q=0 } }^{\infty}\hspace{-3ex}\frac{(-1)^{p}\,(2k)!}{(2nk-n)!\, k!\,(k-1)!}\left(\frac{x}{2}\right)^{2k-1}\,\left[-\ln\left(\frac{x}{2}\right)-\frac{1}{k}+\psi(k+1)+n\,\psi(2nk-n)-\psi(2k-1)\right],\label{flexion01-rat-series} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq194.png) (B.5)and
(B.5)and ![\appendix \setcounter{section}{2} \begin{eqnarray} \left|\mathcal{G}(x)\right|&=&\mathcal{F}_{0}\,\left\{ \sum_{\substack{k=1\\ k\,{\text{mod}}\, p\ne0 } }^{\infty}\,\left[\frac{\Gamma\left(-\tfrac{1}{2}-\tfrac{k}{2n}\right)}{\Gamma\left(-\tfrac{k}{2n}\right)}\,\frac{k^{2}-n^{2}}{3n+k}\,\frac{(-1)^{k}}{k!}\,\frac{x^{k/n}}{2n^{2}}\right]\ +\ 2\ \hspace{-3ex}\sum_{\substack{k=1\\ (k+k_{0})\,{\text{mod}}\, q\ne0 } }^{\infty}\hspace{-3ex}\frac{\Gamma(n-2nk)}{\Gamma\left(\tfrac{1}{2}-k\right)}\,\frac{k-1}{k+1}\,\frac{(-1)^{k}}{(k-1)!}\, x^{2k-1}\,\right\} \nonumber\\ &&\qquad \qquad +\ \frac{\mathcal{F}_{0}}{n\,\sqrt{\pi}}\hspace{-3ex}\sum_{\substack{k=1\\ (k+k_{0})\,{\text{mod}}\, q=0 } }^{\infty}\hspace{-3ex}\frac{(-1)^{p}\,(2k)!}{(2nk-n)!\,\left(k+1\right)!\,(k-2)!}\left(\frac{x}{2}\right)^{2k-1}\,\Bigl[-\ln\left(\frac{x}{2}\right)-\frac{1}{k-1}+\frac{1}{k\left(k+1\right)\left(k-1\right)}+\psi(k+1)+n\,\psi(2nk-n), \nonumber\\ &&\qquad \qquad \qquad \qquad -\psi(2k-1)\Bigr],\label{flexion02-rat-series} \end{eqnarray}](/articles/aa/full_html/2012/10/aa19539-12/aa19539-12-eq195.png) (B.6)with ψ(k) the digamma function and
(B.6)with ψ(k) the digamma function and 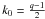 .
.
All Figures
 |
Fig. 1 Comparison of the magnitude of convergence, shear, first and second flexion due to a dark matter halo of mass M200 = 1 × 1012 h-1 M⊙, assuming that the mass distribution is described by Einasto, NFW, and SIS profiles and the Sérsic model. The lens and source planes are located at redshifts zL = 0.4 and zS = 0.92, respectively. The Einsten radius for the SIS is θE = 0.216″, indicating the angular distance when the weak lensing effects are relevant. |
| In the text | |
 |
Fig. 2 Comparison of the magnitude of convergence, shear, first and second flexion due to an Einasto dark matter halo of mass M200 = 1 × 1012 h-1 M⊙, for different values of the concentration c = 4, 8, 12, 16, 20, 24. |
| In the text | |
 |
Fig. 3 Comparison of the magnitude of convergence, shear, first and second flexion due to an Einasto dark matter halo of mass M200 = 1 × 1012 h-1 M⊙, for different values of the Einasto index, n, between 1 ≤ n ≤ 9. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.