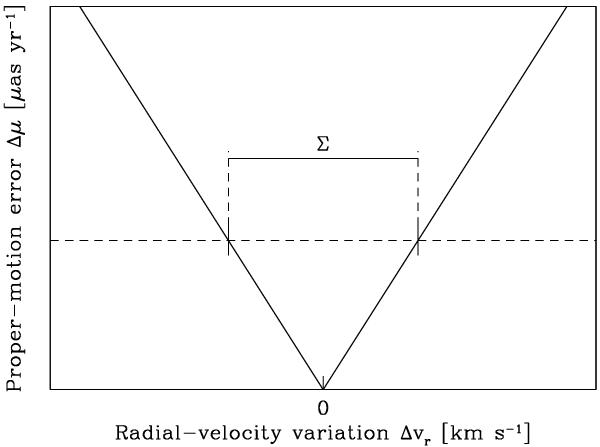
Schematic diagram showing how to quantify the sensitivity of the proper motion to a change in (read: measurement error of) radial velocity. A change in the radial velocity Δv_r introduced before the backward solution leads to a certain (HTPM) proper-motion error Δμ. The linear dependence is commented on in Sect. 4.3. Since the magnitude of the proper-motion error does not depend on the sign but only on the magnitude of the radial-velocity variation, the sensitivity curve is symmetric with respect to the true radial velocity. The dashed horizontal line denotes the maximum perspective-acceleration-induced proper-motion error we are willing to accept in the HTPM proper motion. The distance Σ between the intersection points of the dashed horizontal line and the solid sensitivity curves determines the tolerance on the radial-velocity error.