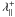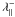| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A149 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219636 | |
| Published online | 24 September 2012 | |
Simulating cosmic-ray transport with adiabatic focusing
1 Zentrum für Astronomie und Astrophysik, Technische Universität Berlin, Hardenbergstraße 36, 10623 Berlin, Germany
e-mail: rct@gmx.eu
2 Center for Space Plasmas and Aeronomic Research, University of Alabama in Huntsville, 320 Sparkman Drive, Huntsville, AL 35805, USA
e-mail: alexanderm.dosch@gmail.com
3 Institut für Geowissenschaften, Naturwissenschaftliche Fakultät III, Martin-Luther-Universität Halle, 06099 Halle, Germany
e-mail: lercheian@yahoo.com
Received: 21 May 2012
Accepted: 8 August 2012
Context. Magnetized space plasmas such as the heliosphere contain a spatially variable guide magnetic field that is superposed by turbulence. Understanding the transport of energetic particles in such an environment is important for many applications.
Aims. The modifications of the scattering mean free path caused by the effect of adiabatic focusing have so far been studied only analytically. Here, the exact analytical conditions are reproduced in a numerical simulation to allow for a detailed comparison.
Methods. A Monte-Carlo simulation code was modified to include a guide magnetic field with a constant focusing length. The turbulence strength was kept constant either throughout the simulation space or relative to the variable background field strength.
Results. In contrast to both quasi-linear and nonlinear analytical predictions, an increased parallel mean free path is found for almost all cases. Particle diffusion is found to be asymmetric depending on the initial particle velocity relative to the guide field.
Conclusions. The increased parallel mean free path can be explained by a coherent particle motion toward lower magnetic field strengths. The possible reduction of the diffusion parameter is consequently obscured.
Key words: plasmas / magnetic fields / turbulence / solar wind / cosmic rays
© ESO, 2012
1. Introduction
Understanding magnetic turbulence and the transport behavior of charged particles in turbulent magnetic fields is a problem of major importance in space physics and astrophysics with implications for space probes and other technological installations. Usually, the particle motion in turbulent magnetic fields is described by assuming a diffusive behavior, even though there are cases when the particle motion is sub- or superdiffusive (Tautz & Shalchi 2010). For a long time, the standard theory to describe such processes has been the quasi-linear theory (QLT) of Jokipii (1966, see also Schlickeiser 2002 with numerous nonlinear extensions and modifications both for parallel (Shalchi 2005; Tautz et al. 2008) and perpendicular (Matthaeus et al. 2003; Shalchi 2010, see also Shalchi 2009b).
In general, nonuniform magnetic fields lead to drift motions (Burger & Visser 2010; Schlickeiser & Jenko 2010; Tautz & Shalchi 2012). These naturally influence the scattering and diffusion parameters of charged particles even if the dominant contribution comes from turbulent fields that vary on much shorter scales than the mean magnetic field. Therefore, it is important to model the large-scale structure of the mean magnetic field (Tautz et al. 2011). For the solar system, the magnetic field can be described in terms of the Parker (1958) or Fisk-Parker (Burger et al. 2008) spiral structure. Strictly speaking, a nonuniform magnetic field violates the conditions for the applicability of a diffusive description (Kóta 2000). Furthermore, including the details into a transport theory is complicated; hence, concentration is often focused on single aspects such as the diverging or converging of the mean magnetic field lines (Roelof 1969; Kunstmann 1979). The usual way has been to modify the derivation of the diffusion parameters by including the large-scale geometry of the magnetic field – instead of finding a completely new description.
Applications of adiabatic focusing are manifold and include (i) modeling of solar flares such as the Bastille-Day event (Bieber et al. 2002); (ii) using the angular distribution of observed particle events to infer the scattering mean-free path (Bieber et al. 1986); (iii) space weather prediction by tracing solar energetic particle events (He & Wan 2012); (iv) particle trapping in the Earth’s magnetosphere (Duggal 1979; Zhang 2006); (v) modeling of ion acceleration at the termination shock (le Roux et al. 2007; le Roux & Webb 2009); (vi) energetic electron transport in extragalactic radio sources, which has been used to model observed radio spectra (Spangler & Basart 1981).
When electric fields are to be neglected, the particle energy is always conserved. Often, however, the turbulent fields are modeled as plasma waves with random directions of propagation such as Alfvén (Michałek & Ostrowski 1996; Schlickeiser 2002; Tautz et al. 2006b), magnetosonic (Schlickeiser & Miller 1998; Michałek & Ostrowski 1998; Michałek 2001), or Whistler waves. This leads to momentum diffusion (Ostrowski & Siemieniec-Ozi¸ebło 1997; Michałek et al. 1999; Tautz 2010b) because of the turbulent electric field component of each plasma wave, which usually accelerates the particles. The influence of time-dependent turbulence by means of magnetohydrodynamic plasma waves such as Alfvén waves (Schlickeiser & Shalchi 2008) on the particles leads to a Fermi-I like acceleration mechanism (Schlickeiser 2009), which has been named “focused acceleration” (Litvinenko & Schlickeiser 2011) or “adiabatic deceleration” (Jokipii & Parker 1970; Ruffolo 1995).
However, despite the numerous analytical work, where various transport theories have been modified to include the effects of adiabatic focusing, there appear to be no systematic numerical investigation to test the analytical framework and either put it on solid ground or falsify the various assumptions and approximations used to derive as simple as possible formulae. It therefore seems appropriate to remedy this defect by employing a numerical Monte-Carlo simulation code, which was designed to operate under the exact same conditions as the analytical test-particle theories (Tautz 2010a).
It should be noted that the physics behind combining a nonconstant focusing length (leading to position-dependent scattering) with diffusion (which requires position-independent scattering over a relatively large area) is not entirely clear. One can of course employ a focusing length that is long compared to the mean free path. But then the differences to the homogeneous case are very small. Accordingly the natural choice is to implement a constant focusing length, which leads to the magnetic field structure investigated here (with the additional constraint that, in a strict sense, the focusing length is only constant for low x and y values).
The paper is organized as follows: Sect. 2 introduces the basic theory of adiabatic focusing in diffusion theories and its application to energetic particle scattering. In Sects. 3 and 4, the numerical simulation scheme is described and the resulting diffusion parameters are compared to analytical calculations, respectively. Sections 5 and 6 provide a discussion of the results and a short summary and conclusion.
2. Technical problems of adiabatic focusing
For an ensemble of collisionless energetically charged particles that are scattered solely under the influence of turbulent electromagnetic fields, the phase-space distribution function, f, evolves according to the transport equation (Parker 1965; Luhmann 1976; Earl 1976) ![\begin{equation} \label{eq:tra} \pd[f]t+v\mu\,\pd[f]z+\frac{v}{2L}\left(1-\mu^2\right)\pd[f]\mu=\pd\mu\left(\dm\,\pd[f]\mu\right), \end{equation}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq4.png) (1)where the mean magnetic field, B, is assumed to be (approximately) aligned with the z axis and where μ = cos∠(v,B). Mathematically, the transport equation can be derived from the Vlasov-Maxwell equations (Schlickeiser 2002) under the assumptions of stationary, homogeneous, and weak magnetic turbulence. Note that Eq. (1)neglects all terms due to momentum diffusion (cf. Litvinenko & Schlickeiser 2011) and catastrophic loss processes.
(1)where the mean magnetic field, B, is assumed to be (approximately) aligned with the z axis and where μ = cos∠(v,B). Mathematically, the transport equation can be derived from the Vlasov-Maxwell equations (Schlickeiser 2002) under the assumptions of stationary, homogeneous, and weak magnetic turbulence. Note that Eq. (1)neglects all terms due to momentum diffusion (cf. Litvinenko & Schlickeiser 2011) and catastrophic loss processes.
2.1. Focusing length
To describe the variation in the mean magnetic field strength – and, according to ∇·B = 0, a spatial variation – a characteristic length scale L is introduced in Eq. (1)according to the theory of adiabatic focusing as (Roelof 1969) ![\begin{equation} \label{eq:L} L^{-1}=-\frac{1}{B}\,\pd[B]z\cdot \end{equation}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq10.png) (2)Strictly speaking, here z denotes the direction along the magnetic field lines and not the Cartesian coordinate. For the purpose of a simple investigation, a constant length scale is chosen, which immediately gives rise to an exponential variation in the mean magnetic field as
(2)Strictly speaking, here z denotes the direction along the magnetic field lines and not the Cartesian coordinate. For the purpose of a simple investigation, a constant length scale is chosen, which immediately gives rise to an exponential variation in the mean magnetic field as 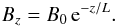 (3)This agrees with analytical investigations of Litvinenko & Schlickeiser (2011), who assumed L = const. on spatial scales that are large compared to the parallel mean free path of the particles.
(3)This agrees with analytical investigations of Litvinenko & Schlickeiser (2011), who assumed L = const. on spatial scales that are large compared to the parallel mean free path of the particles.
If one requires a similar behavior of Bx and By so that axisymmetry is retained, the condition that the divergence of the magnetic field be zero immediately yields  Accordingly, the mean magnetic field is no longer aligned with the z axis as it is in most analytical and numerical investigations. However, the approach described here should remain valid as long as the spatial scales of the x and y components of the magnetic field are large compared with that of the z component of the field (cf. Litvinenko & Schlickeiser 2011). This is ensured by the exponential z dependence as opposed to the linear dependence on x and y. The general case is briefly discussed in Appendix A.
Accordingly, the mean magnetic field is no longer aligned with the z axis as it is in most analytical and numerical investigations. However, the approach described here should remain valid as long as the spatial scales of the x and y components of the magnetic field are large compared with that of the z component of the field (cf. Litvinenko & Schlickeiser 2011). This is ensured by the exponential z dependence as opposed to the linear dependence on x and y. The general case is briefly discussed in Appendix A.
Therefore, both the magnetic field strength and the orientation vary with z. With 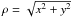 , the first is given by
, the first is given by 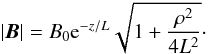 (5)The orientation, i.e., the angle between the magnetic field vector and the z axis, is determined in Appendix B.
(5)The orientation, i.e., the angle between the magnetic field vector and the z axis, is determined in Appendix B.
2.2. Analytical parallel mean free path
The parallel scattering length or mean free path is calculated from the weighted pitch-angle average of the inverse Fokker-Planck coefficient of pitch-angle scattering, Dμμ, as (Hasselmann & Wibberenz 1968; Earl 1974) 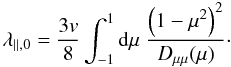 (6)For the turbulent magnetic field energy entering the Fokker-Planck coefficient, a spectral distribution of the form
(6)For the turbulent magnetic field energy entering the Fokker-Planck coefficient, a spectral distribution of the form ![\begin{equation} \label{eq:spect} G(k)\propto\delta B^2\ell_0\left[1+\left(\ell_0k\right)^2\right]^{-s/2} \end{equation}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq19.png) (7)is assumed with ℓ0 = ℓslab = 0.03 a.u. as the turbulence bend-over scale and s = 5/3 as the Kolmogorov inertial range spectral index. The normalization function is determined from the condition that the integral of the magnetic correlation tensor over the whole wavenumber range be equal to the squared turbulence strength (Batchelor 1982; Schlickeiser 2002; Shalchi 2009b), yielding
(7)is assumed with ℓ0 = ℓslab = 0.03 a.u. as the turbulence bend-over scale and s = 5/3 as the Kolmogorov inertial range spectral index. The normalization function is determined from the condition that the integral of the magnetic correlation tensor over the whole wavenumber range be equal to the squared turbulence strength (Batchelor 1982; Schlickeiser 2002; Shalchi 2009b), yielding 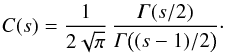 (8)Analytical investigations of the modifications to the parallel mean free path due to adiabatic focusing were performed using standard QLT (Earl 1976; Schlickeiser & Shalchi 2008; Shalchi 2009a) and, recently, the nonlinear second-order version (Shalchi 2005; Tautz et al. 2008) of QLT (Shalchi 2011). For slab turbulence, where the turbulent magnetic fields depend solely on the spatial coordinate along the mean magnetic field, i.e., δB = δB(z), the application of QLT allowed one to analytically evaluate the modification of the parallel mean free path. The result reads (Shalchi 2009a)
(8)Analytical investigations of the modifications to the parallel mean free path due to adiabatic focusing were performed using standard QLT (Earl 1976; Schlickeiser & Shalchi 2008; Shalchi 2009a) and, recently, the nonlinear second-order version (Shalchi 2005; Tautz et al. 2008) of QLT (Shalchi 2011). For slab turbulence, where the turbulent magnetic fields depend solely on the spatial coordinate along the mean magnetic field, i.e., δB = δB(z), the application of QLT allowed one to analytically evaluate the modification of the parallel mean free path. The result reads (Shalchi 2009a) 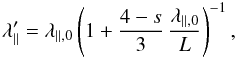 (9)where λ ∥ ,0 is the mean free path obtained for a homogeneous mean magnetic field according to Eq. (6). It is important to note that Eq. (9)was derived using QLT so that the usual assumptions of QLT apply, such as that the turbulent magnetic field is weak compared to the background field strength. That condition may indeed be violated for the case of an absolute constant turbulence strength if z ≫ ℓ0.
(9)where λ ∥ ,0 is the mean free path obtained for a homogeneous mean magnetic field according to Eq. (6). It is important to note that Eq. (9)was derived using QLT so that the usual assumptions of QLT apply, such as that the turbulent magnetic field is weak compared to the background field strength. That condition may indeed be violated for the case of an absolute constant turbulence strength if z ≫ ℓ0.
Clearly, Eq. (9)predicts a reduced mean free path1. The nonlinear calculation, in contrast, gave the result (Shalchi 2011) 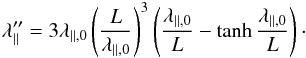 (10)In contrast to the QLT result, Eq. (10)only requires that particle energies be “not too high” (Shalchi 2011), which has been specified by Shalchi et al. (2009) through R = RL/l0 ≪ B0/δB, which assumption can be seen as fulfilled except perhaps for the highest energy value.
(10)In contrast to the QLT result, Eq. (10)only requires that particle energies be “not too high” (Shalchi 2011), which has been specified by Shalchi et al. (2009) through R = RL/l0 ≪ B0/δB, which assumption can be seen as fulfilled except perhaps for the highest energy value.
In Sect. 4, the two results from Eqs. (9)and (10)are compared to numerical results, showing that neither formula provides qualitative or quantitative agreement with the simulation results.
2.3. Numerical parallel mean free path
The determination of the parallel mean free path in a Monte-Carlo simulation requires the particle displacement Δs|| along the magnetic field line (see Sect. 3). Without loss of generality, consider the magnetic field line equation in the ρ-z plane, ![\begin{equation} -\dd[\rho]z=\frac{\sqrt{B_x^2+B_y^2}}{B_z}=\frac{\rho}{2L}, \end{equation}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq31.png) (11)which has the solution ρ(z) = ρ0e − (z − z0)/2L with ρ(z0) = ρ0. The general arc-length function along the magnetic field line is then given by
(11)which has the solution ρ(z) = ρ0e − (z − z0)/2L with ρ(z0) = ρ0. The general arc-length function along the magnetic field line is then given by ![% subequation 1202 0 \begin{eqnarray} \mathcal L(z)&=&\int\df s=\int\df z\sqrt{1+\left(\dd[\rho]z\right)^2}\\ &=& 2L\ln\left(2L+\sqrt{4L^2+\rho_0^2{\rm e}^{-\left(z-z_0\right)/L}}\right)\nonumber\\[1mm] &\quad+ & \left(z-z_0\right)-\sqrt{4L^2+\rho_0^2{\rm e}^{-\left(z-z_0\right)/L}}. \end{eqnarray}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq34.png) Accordingly, the parallel displacement can be expressed through
Accordingly, the parallel displacement can be expressed through 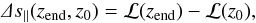 (13)with the second summand being simplified because of z = z0, which removes the exponential function.
(13)with the second summand being simplified because of z = z0, which removes the exponential function.
3. Monte-Carlo simulations
In the Padian code (Tautz 2010a), the trajectories of a large number of test particles are integrated numerically using the Dorman-Prince 853 (Hairer et al. 1993; Press et al. 2007) method with an adaptive step size. The time-dependent (i.e., “running”), parallel mean free path is then obtained from the standard prescription 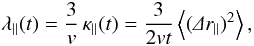 (14)with r|| the distance traveled along the mean magnetic field line. The angular brackets denote the average first over all N particle trajectories starting at different positions (but on a line of equal turbulent magnetic field strength) and second over M such ensembles in different turbulent realizations. This allows calculating an estimated mean error, which is shown in subsequent figures and which can be used to judge the reliability of the simulation results (see Tautz 2010a, for more details). Here, N = M = 100 is used.
(14)with r|| the distance traveled along the mean magnetic field line. The angular brackets denote the average first over all N particle trajectories starting at different positions (but on a line of equal turbulent magnetic field strength) and second over M such ensembles in different turbulent realizations. This allows calculating an estimated mean error, which is shown in subsequent figures and which can be used to judge the reliability of the simulation results (see Tautz 2010a, for more details). Here, N = M = 100 is used.
3.1. Turbulence generation
Turbulent magnetic fields can be generated through the superposition of many (usually N ~ 102–103) plane waves (Giacalone & Jokipii 1999; Michałek 2001; Tautz 2010a) with random directions of propagation and random polarizations. It can be shown analytically that, in the limit of N → ∞, a fully developed turbulent field is obtained (Batchelor 1982). The homogeneous (cf. Batchelor 1982) turbulent magnetic field can be written in the form 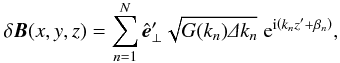 (15)where βn is the random phase angle. The primed coordinates are calculated from a rotation matrix with random angles, and
(15)where βn is the random phase angle. The primed coordinates are calculated from a rotation matrix with random angles, and 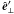 is the unit polarization vector in the x′ − y′ plane. For each simulation set, typically 100 different turbulence realizations are used, i.e., different sets of random numbers in Eq. (15).
is the unit polarization vector in the x′ − y′ plane. For each simulation set, typically 100 different turbulence realizations are used, i.e., different sets of random numbers in Eq. (15).
For the turbulence power spectrum, Eq. (7)is used. Furthermore, the turbulence geometry, which specifies the orientation of the Fourier modes of the magnetic field components, is chosen according to the two most prominent models, which are (i) the slab model, for which by definition one has δB(r) = δB⊥ (z) for the turbulent fields and δB∥ = 0. In Fourier space, the spectrum depends solely on the parallel wavenumber k∥ in this special case; (ii) the isotropic model, in which it is assumed that the turbulence has no preferred direction. In addition, in the case of a curved background field, the orientation (but not the field strength or the structure itself) of the slab turbulent magnetic field becomes position-dependent, as detailed in Appendix B.
 |
Fig. 1 Sample trajectories for the magnetic field geometry described by Eqs. (3) and (4) with an additional turbulent component δB, which is generated according to the Fourier superposition of Eq. (15). In the upper panel, the magnitude of the turbulent field is (δB/B0)2 = 0.1. In the lower panel, the turbulence strength is varied together with the background magnetic field strength so that (δB/|B|)2 = 0.1 = const. also along the z direction. |
3.2. Initial particle distribution
For a Monte-Carlo simulation with randomly chosen initial particle positions, one has to ensure that each particle experiences – on average – the same initial conditions. Consequently, the lines of constant magnetic field strength have to be determined, which, from the solution of Eq. (5), read ![\begin{equation} \label{eq:rho0} z(\rho,\abs{\f B})=L\left[\frac{1}{2}\ln\left(1+\frac{\rho^2}{4L^2}\right)-\ln\,\frac{\abs{\f B}}{B_0}\right]\cdot \end{equation}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq55.png) (16)For the initial particle position, a reasonable choice is ρ ∈ [0,L] corresponding to
(16)For the initial particle position, a reasonable choice is ρ ∈ [0,L] corresponding to 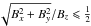 . From Eq. (16)one then has z ∈ [z0,z ⋆ ] , where
. From Eq. (16)one then has z ∈ [z0,z ⋆ ] , where ![\begin{eqnarray*} z_0&=&-L\ln\left(\frac{\abs{\f B}}{B_0}\right),\\ z_\star&=&-\frac{1}{2}L\ln\left[\frac{4}{5}\left(\frac{\abs{\f B}}{B_0}\right)^2\right]\cdot \end{eqnarray*}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq59.png) Note that the particles experience comparable conditions, although they start at different positions. The underlying reason is of course that the turbulence generated by means of Eq. (15)is homogeneous (see previous subsection).
Note that the particles experience comparable conditions, although they start at different positions. The underlying reason is of course that the turbulence generated by means of Eq. (15)is homogeneous (see previous subsection).
In Fig. 1, a few sample particle trajectories are shown for a magnetic field that has two components: (i) the curved mean magnetic field in agreement with a constant focusing length that leads to Eqs. (3) and (4); (ii) a turbulent component that results from the superposition of 1024 Fourier modes according to Eq. (15). The relative strength is (δB/B0)2 = 0.1.
 |
Fig. 2 Parallel scattering mean free path as a function of the normalized simulation time vt/ℓslab for a slab turbulence with (δB/B0)2 = 0.1. In the upper panel, the case of slab turbulence is shown, while the lower panel shows the case of isotropic turbulence. Both panels show the homogeneous case, i.e., L → ∞. For vt/ℓslab ≳ 102, the diffusive regime has been reached where λ∥ ≈ const. In both panels, the various curves show different particle rigidities R = RL/ℓslab as indicated. |
The difference between the two panels of Fig. 1 is that while in the upper panel the turbulent magnetic field strength is kept constant with respect to the parameter B0, the turbulence strength is varied in the lower panel together with the background magnetic field strength so that (δB/|B|)2 = 0.1. This is motivated by the fact that magnetic turbulence is not a property of space itself but is generated for example by anisotropic particle streams. For the solar system, for instance, a radial dependence of the turbulent field strength with r−3/2 can be derived using a WKB approach (see, e.g., Zank et al. 1996, Sect. 3.1; Tautz et al. 2011). This indicates that a variation of the turbulent field strength similar to that of the mean field might be an appropriate case to consider. On the other hand, there are plasma instabilities that are independent of a mean magnetic field (e.g., Schlickeiser 2005), which could cause the turbulent field strength to be independent of the mean magnetic field. Now because both cases give rise to different particle diffusion coefficients as shown in Sect. 4, both cases represent scenarios that are applicable to astrophysical plasmas such as (i) the heliosphere; (ii) galactic halo; but also to (iii) planetary magnetic fields; or (iv) interstellar magnetic fields.
4. Simulation results
First, Fig. 2 shows the parallel mean free path in a homogeneous background magnetic field without adiabatic focusing as a function of the simulation time for various particle energies. The particles are scattered in a slab turbulence geometry with (δB/B0)2 = 0.1. The figure illustrates that well-defined, diffusive values for the mean free paths are obtained if vt/ℓslab ≳ 102. These values serve as reference values λ∥,0 for the evaluation of Eqs. (9)and (10). The particle energy is contained in the parameter R = v/(Ωℓ0), which is frequently used in particle transport theories and can be described as the particle rigidity divided by magnetic field strength or as a normalized Larmor radius.
In what follows, two cases are to be distinguished, which keep the turbulence strength constant with respect to (i) the normalization field strength B0 in Eqs. (3)and (4); (ii) the spatially varying background magnetic field strength that results from the magnitude |B|. Consider both cases in turn, each for slab and for isotropic turbulence. Furthermore, note that for the case of isotropic turbulence, analytical results are apparently not available.
 |
Fig. 3 Simulation results (black diamonds) for the parallel scattering mean free path in slab turbulence with adiabatic focusing as described by Eqs. (3)and (4). The focusing length is chosen as L/ℓslab = 10 (upper panel) and L/ℓslab = 1 (lower panel). Furthermore, the two analytical results are shown as open diamonds for the quasi-linear result from Eq. (9)and as gray triangles for the nonlinear result from Eq. (10). For comparison, the parallel mean free path is shown also for a homogeneous background magnetic field (gray circles). The magnitude of the turbulence is (δB/B0)2 = 0.1. |
-
Slab model with
δB/B0 = const.:
the values shown in Fig. 2 for theparallel mean free path, λ∥,0, serve as an input parameter to evaluate Eqs. (9)and (10). The result is shown in Fig. 3 for focusing lengths of L/ℓslab = 10 and L/ℓslab = 1 together with the corresponding simulation results with and without adiabatic focusing. The comparison reveals that no agreement is found – neither qualitatively nor quantitatively (with the exception of rigidities R ≈ 0.2).
-
Slab model with
δB/|B| = const.:
the results are shown in Fig. 4. For large L, the behavior is qualitatively similar to the previous case. In addition, for small R ≪ 0.1 some degree of agreement between analytical theory and simulation can be found. However, the situation is entirely different for small L, which case can be associated with a strongly curved magnetic field. There, the simulated mean free path is (i) almost rigidity-independent; and (ii) between one and two orders of magnitude larger than the analytical prediction.
-
Isotropic model with
δB/B0 = const.:
the results shown in Fig. 5 indicate that owing to the effects of adiabatic focusing, the parallel mean free path is significantly reduced for the entire range of rigidity values and for both short and long focusing lengths. This is in contrast to the behavior exhibited for slab turbulence.
-
Isotropic model with
δB/|B| = const.:
for a short focusing length, the parallel mean free path is almost rigidity-independent, as is clearly shown in the lower panel of Fig. 5. Together with the fact that the values are roughly two orders of magnitude higher than the mean free path in the homogeneous case, this agrees with the results found for slab turbulence. Likewise, there is a limited agreement found for long focusing lengths together with low rigidities.
A general result is that for relatively high rigidity values, the mean free path exceeds the theoretical predictions by at least one order of magnitude. Accordingly, neither of the analytical formulae gives an accurate description of the simulation results. Furthermore, for a long focusing length – corresponding to a weakly curved magnetic field – there is a strong difference between low and high rigidities. For a short focusing length, in contrast, the mean free path values are relatively high at all rigidities.
5. Discussion
It is remarkable that analytical theories predict a reduced parallel mean free path, λ∥, at all (positive) values of the focusing length, L. This is obviously in contrast to the results obtained from the simulation. However, the following estimate provides an insight as to what happens when the magnetic background field is curved according to Eqs. (3) and (4).
5.1. Coherent streaming
 |
Fig. 4 Simulation results (black squares) for a relative turbulence strength, on average, kept constant throughout the simulation space so that (δB/|B|)2 = 0.1. Same as Fig. 3 for other points. Additionally, here results are considered also for L = 50ℓ0. |
 |
Fig. 5 Simulation results for the parallel scattering mean free path in isotropic turbulence with adiabatic focusing. The focusing length is chosen as L/ℓ0 = 10 (upper panel) and L/ℓ0 = 1 (lower panel). The black diamonds show the case of an absolutely constant turbulence strength as (δB/B0)2 = 0.1 (cf. Fig. 3), whereas the black squares show the case of turbulence strength that varies with the background field strength as (δB/|B|)2 = 0.1 (cf. Fig. 4). For comparison, the parallel mean free path is shown also for a homogeneous background magnetic field (gray circles). |
First, it is well known that in a weakly variable field, the magnetic momentum is adiabatically conserved, i.e., 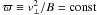 . Now for pure magnetic fields the energy E of each particle is also conserved so that
. Now for pure magnetic fields the energy E of each particle is also conserved so that 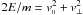 . Thus
. Thus 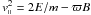 . As B increases, v∥ decreases and reaches a turning point (i.e., where v∥ = 0) when B approaches a critical value, Bcrit = 2E/(mϖ) so that all the energy is in the perpendicular motion. Conversely, as B decreases, v∥ increases and all the energy moves to parallel motion. Thus an initially isotropic distribution develops anisotropy in the sense of a stream parallel to B in the weak direction and a stagnation in the strong direction, leading to high transverse pressure in the strong B regime – hence the diffusion cannot be symmetric.
. As B increases, v∥ decreases and reaches a turning point (i.e., where v∥ = 0) when B approaches a critical value, Bcrit = 2E/(mϖ) so that all the energy is in the perpendicular motion. Conversely, as B decreases, v∥ increases and all the energy moves to parallel motion. Thus an initially isotropic distribution develops anisotropy in the sense of a stream parallel to B in the weak direction and a stagnation in the strong direction, leading to high transverse pressure in the strong B regime – hence the diffusion cannot be symmetric.
This is confirmed by two additional simulation runs, in which all particles initially move toward stronger field strengths (vz > 0) and weaker field strengths (vz < 0), respectively. Figure 6 shows the difference in the resulting parallel mean free paths, illustrating that particles stream toward higher z, corresponding to regions of weaker magnetic field. Furthermore, the effect is also known from analytical treatments, where it was found that in the presence of adiabatic focusing, “particle transport can be approximately represented as a combination of coherent streaming and diffusion” (Litvinenko 2012).
Furthermore, Roelof (1969) already considered the competition between scattering and a coherent motion, which he expressed through a parameter α = vT/(2L) with α ≪ 1 indicating the predominance of diffusion, whereas for α ≫ 1 one has a “deterministic motion”. Here, T is the relaxation time, which is connected to the turbulence power spectrum at a wavenumber ℓ0kc = 1/R as 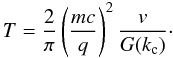 (17)With Eq. (7)and the remaining normalization factors for example for isotropic turbulence, the critical parameter α can be expressed as
(17)With Eq. (7)and the remaining normalization factors for example for isotropic turbulence, the critical parameter α can be expressed as ![\begin{equation} \alpha=\frac{\left(\Om T\right)R}{2L/\ell_0}=\frac{R^2}{4\pi}\left(\frac{\delta B}{B_0}\right)^{-2}\frac{\left[1+\left(\ell_0k_{\rm c} \right)^2\right]^{s/2}}{2C(s)L/\ell_0}\cdot \end{equation}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq97.png) (18)For the rigidity values considered, α has values of the order of 1, which again confirms the presence of coherent particle motion. In contrast, for scattering to dominate, lower values of α can be obtained for longer focusing lengths. But, according to λ/λ0 ≈ 1 − (λ0/L)2/15, the resulting correction to the mean free path would then be very small2 (see Litvinenko 2012, and references therein).
(18)For the rigidity values considered, α has values of the order of 1, which again confirms the presence of coherent particle motion. In contrast, for scattering to dominate, lower values of α can be obtained for longer focusing lengths. But, according to λ/λ0 ≈ 1 − (λ0/L)2/15, the resulting correction to the mean free path would then be very small2 (see Litvinenko 2012, and references therein).
 |
Fig. 6 Comparison of the parallel mean free path for particles moving initially with vz > 0 (denoted by |
5.2. Mean free path scaling relations
Now with v⊥ = vsinθ one has B ∝ sin2θ = (1 − μ2), where μ is the pitch-angle cosine. Next, assume an isotropic Fokker-Planck coefficient for pitch-angle scattering (Shalchi 2009b, 2010; Tautz & Lerche 2010), i.e., Dμμ ∝ (1 − μ2), and note that the parallel mean free path is proportional to the inverse of Dμμ. One then obtains the scaling relation 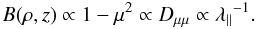 (19)Furthermore, the preferred particle motion will always be toward weaker field strengths so that Eq. (19)predicts an increased mean free path. Quantitative results can be obtained from a histogram of the particle displacement as illustrated in Fig. 7.
(19)Furthermore, the preferred particle motion will always be toward weaker field strengths so that Eq. (19)predicts an increased mean free path. Quantitative results can be obtained from a histogram of the particle displacement as illustrated in Fig. 7.
 |
Fig. 7 Histogram of the particle displacement in z direction, Δz ≡ z(tmax) − z(t0) for the case of slab turbulence with a focusing length L = 10ℓslab. The upper panel shows the case of δB/B0 = const., whereas the lower panel shows the case of δB/|B| = const. Clearly, most particles move toward weaker field strengths. |
Of course, the above relation does not take into account any turbulence effects. Therefore, note that as a simple estimate, the mean free path scales with the particle rigidity as (Shalchi et al. 2004) λ∥ ∝ R1/3 for R ≪ 1 and λ∥ ∝ R2 for R ≫ 1. The crucial point is that the rigidity is related to the field strength via R ∝ B-1 so that one obtains 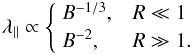 (20)By averaging over the particle positions (cf. Fig. 7), the mean magnetic field encountered by the particles can be obtained, which allows for a rough estimate of the factor by which the mean free path is scaled. For the highest rigidity values considered, the maximum of the resulting factor is 8 × 109 and 3 × 108 for the cases of absolute and relative constant turbulence strengths, respectively. This indicates that for sufficiently high initial rigidity values, the mean free path is strongly increased. Superimposed to this relation is the additional requirement that λ∥ ∝ (δB/B0)2, which, however, has only been verified for weak turbulence δB ≲ B (see Isichenko 1991; Zimbardo et al. 2009) and hence is not necessarily applicable if z ≫ L, for the case where δB/B0 is held constant.
(20)By averaging over the particle positions (cf. Fig. 7), the mean magnetic field encountered by the particles can be obtained, which allows for a rough estimate of the factor by which the mean free path is scaled. For the highest rigidity values considered, the maximum of the resulting factor is 8 × 109 and 3 × 108 for the cases of absolute and relative constant turbulence strengths, respectively. This indicates that for sufficiently high initial rigidity values, the mean free path is strongly increased. Superimposed to this relation is the additional requirement that λ∥ ∝ (δB/B0)2, which, however, has only been verified for weak turbulence δB ≲ B (see Isichenko 1991; Zimbardo et al. 2009) and hence is not necessarily applicable if z ≫ L, for the case where δB/B0 is held constant.
In conclusion, there are two scaling relations that govern the parallel mean free path, both of which have been confirmed by previous simulations (e.g., Tautz et al. 2006a, 2008): (i) the mean free path scales with the particle gyroradius as for example expressed by the Bohm limit for which λ∥ = RL; (ii) the mean free path scales with the ratio of turbulent and averaged magnetic field strength. While in the presence of adiabatic focusing, the analytical calculations predict a reduced parallel mean free path, the dominating effect is that of particles streaming toward weaker field strengths so that the mean free path is strongly increased. One notable exception is found for the case of isotropic turbulence with a variable ratio of turbulence and background field strength, where the mean free path was found to be reduced. It is therefore expected that for slightly anisotropic turbulence, there must be a limiting anisotropy for which the mean free path reduces almost to the isotropic case and above which the mean free path is increased.
6. Summary and conclusion
We investigated the scattering properties of charged particles in the presence of a smoothly curved magnetic field superposed by a turbulent component. This configuration is commonly known as the adiabatic focusing case and has been thoroughly investigated analytically. A numerical implementation of the exact same situation, however, seemed to be lacking so far, presumably because analytical investigations usually do not specify all the conditions necessary for a straightforward implementation in a numerical setting. Therefore, two different scenarios were presented.
The simulation results show that in contrast to analytical predictions, the scattering mean free path along the background magnetic field lines is strongly increased. This can be understood by taking into account that the usual, direction-independent diffusion now has a superposed coherent motion of the particles toward weaker magnetic fields. A rough estimate confirmed that the resulting factor is high. This qualitatively agrees with investigations of convective galactic outflow, where it was found that advection along the expanding magnetic field lines has to be taken into account to obtain agreement with gamma-ray observations (see Zirakashvili et al. 1996, and references therein). Future work should therefore separate the coherent particle motion from the diffusion process within the framework of test particles.
Furthermore, additional effects might have to be taken into account. First, at the turning points where v⊥ ≫ v∥, particles are prone to excite additional turbulent magnetic fields via the Weibel (1959) instability. Conversely, in the low-magnetic field region where v⊥ ≪ v∥, the two-stream instability (Buneman 1959; Fried 1959) is likely to occur. However, to include the turbulent fields generated by the unstable particle distribution, the test-particle approach would need to be replaced by a self-consistent description. While including these effects is beyond the scope of the current investigation, it may be worthwhile to do so in a future paper.
 |
Fig. 8 “True” focusing length L as obtained from Eq. (A.4)for the magnetic field given by Eqs. (3) and (4) for L = 10ℓ0. Additionally, the deviation of the true focusing length from the parameter L is depicted at ρ = L and ρ = 2L. |
Note that, according to Eq. (2), L can be positive or negative (cf. Bieber & Burger 1990). Accordingly, we presume that Eq. (9)should contain the absolute value of L, because Shalchi (2009a) made no statement about an assumed asymmetry in the initial particle velocity distribution.
For the same reason, a plot such as Fig. 1 in Shalchi (2011) would not be meaningful to discuss the obtained simulation results.
Acknowledgments
The work of A. D. is supported by the Deutsche Forschungsgemeinschaft (DFG) under grant DO 1505/1-1.
References
- Batchelor, G. K. 1982, The Theory of Homogeneous Turbulence (Cambridge: University Press) [Google Scholar]
- Bieber, J. W., & Burger, R. A. 1990, ApJ, 348, 597 [NASA ADS] [CrossRef] [Google Scholar]
- Bieber, J. W., Evenson, P. A., & Pomerantz, M. A. 1986, J. Geophys. Res., 91, 8713 [NASA ADS] [CrossRef] [Google Scholar]
- Bieber, J. W., Dröge, W., Evenson, P. A., et al. 2002, ApJ, 567, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Buneman, O. 1959, Phys. Rev. Lett., 115, 503 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Burger, R. A., & Visser, D. J. 2010, ApJ, 725, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Burger, R. A., Krüger, T. P. J., Hitge, M., & Engelbrecht, N. E. 2008, ApJ, 674, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Duggal, S. P. 1979, Rev. Geophys., 17, 1021 [Google Scholar]
- Earl, J. A. 1974, ApJ, 193, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Earl, J. A. 1976, ApJ, 205, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Fried, B. D. 1959, Phys. Fluids, 2, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Giacalone, J., & Jokipii, J. R. 1999, ApJ, 520, 204 [Google Scholar]
- Hairer, E., Nørsett, S. P., & Wanner, G. 1993, Solving Ordinary Differential Equations I. Nonstiff Problems, 2nd edn. (New York: Springer) [Google Scholar]
- Hasselmann, K., & Wibberenz, G. 1968, Z. Geophys., 34, 353 [Google Scholar]
- He, H.-Q., & Wan, W. 2012, ApJ, 747, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Isichenko, M. B. 1991, Plasma Phys. Contr. Fusion, 33, 809 [Google Scholar]
- Jokipii, J. R. 1966, ApJ, 146, 480 [Google Scholar]
- Jokipii, J. R., & Parker, E. N. 1970, ApJ, 160, 735 [Google Scholar]
- Kóta, J. 2000, J. Geophys. Res., 105, 2403 [CrossRef] [Google Scholar]
- Kunstmann, J. E. 1979, ApJ, 229, 812 [NASA ADS] [CrossRef] [Google Scholar]
- le Roux, J. A., & Webb, G. M. 2009, ApJ, 693, 534 [NASA ADS] [CrossRef] [Google Scholar]
- le Roux, J. A., Webb, G. M., Florinski, V., & Zank, G. P. 2007, ApJ, 662, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E. 2012, ApJ, 745, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Litvinenko, Y. E., & Schlickeiser, R. 2011, ApJ, 732, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Luhmann, J. G. 1976, J. Geophys. Res., 81, 2089 [NASA ADS] [CrossRef] [Google Scholar]
- Matthaeus, W. H., Qin, G., Bieber, J. W., & Zank, G. P. 2003, ApJ, 590, L53 [Google Scholar]
- Michałek, G. 2001, A&A, 376, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałek, G., & Ostrowski, M. 1996, Nonlin. Processes Geophys., 3, 66 [Google Scholar]
- Michałek, G., & Ostrowski, M. 1998, A&A, 337, 558 [NASA ADS] [Google Scholar]
- Michałek, G., Ostrowski, M., & Schlickeiser, R. 1999, Sol. Phys., 184, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Ostrowski, M., & Siemieniec-Ozįebło, G. 1997, Astropart. Phys., 6, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Parker, E. N. 1965, Planet. Space Sci., 13, 9 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 2007, Numerical Recipes (Cambridge: University Press) [Google Scholar]
- Roelof, E. C. 1969, in Lectures in high energy astrophysics, eds. H. B. Ögelmann, & J. R. Wayland Jr. (Washington, DC: NASA SP-199), 111 [Google Scholar]
- Ruffolo, D. 1995, ApJ, 442, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 2002, Cosmic Ray Astrophysics (Berlin: Springer) [Google Scholar]
- Schlickeiser, R. 2005, Plasma Phys. Contr. Fusion, 47, A205 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 2009, Mod. Phys. Lett. A, 24, 1461 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R., & Jenko, F. 2010, J. Plasma Phys., 76, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R., & Miller, J. A. 1998, ApJ, 499, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R., & Shalchi, A. 2008, ApJ, 686, 292 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2005, Phys. Plasmas, 12, 052905 [Google Scholar]
- Shalchi, A. 2009a, J. Phys. G: Nucl. Part. Phys., 36, 025202 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A. 2009b, Nonlinear Cosmic Ray Diffusion Theories (Berlin: Springer) [Google Scholar]
- Shalchi, A. 2010, ApJ, 720, L127 [Google Scholar]
- Shalchi, A. 2011, ApJ, 728, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Shalchi, A., Bieber, J. W., & Matthaeus, W. H. 2004, ApJ, 604, 675 [Google Scholar]
- Shalchi, A., Škoda, T., Tautz, R. C., & Schlickeiser, R. 2009, A&A, 507, 589 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spangler, S. R., & Basart, J. P. 1981, ApJ, 243, 1103 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C. 2010a, Computer Phys. Commun., 81, 71 [Google Scholar]
- Tautz, R. C. 2010b, Plasma Phys. Contr. Fusion, 52, 045016 [Google Scholar]
- Tautz, R. C., & Lerche, I. 2010, Phys. Lett. A, 374, 4573 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., & Shalchi, A. 2010, J. Geophys. Res., 115, A03104 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., & Shalchi, A. 2012, ApJ, 744, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., Shalchi, A., & Schlickeiser, R. 2006a, J. Phys. G: Nucl. Part. Phys., 32, 809 [Google Scholar]
- Tautz, R. C., Shalchi, A., & Schlickeiser, R. 2006b, J. Phys. G: Nucl. Part. Phys., 32, 1045 [Google Scholar]
- Tautz, R. C., Shalchi, A., & Schlickeiser, R. 2008, ApJ, 685, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Tautz, R. C., Dosch, A., & Shalchi, A. 2011, J. Geophys. Res., 116, A02102 [NASA ADS] [CrossRef] [Google Scholar]
- Weibel, E. S. 1959, Phys. Rev. Lett., 2, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G. P., Matthaeus, W. H., & Smith, C. W. 1996, J. Geophys. Res., 101, 17093 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, M. 2006, J. Geophys. Res., 111, A04208 [NASA ADS] [CrossRef] [Google Scholar]
- Zimbardo, G., Bitane, R., Pommois, P., & Veltri, P. 2009, Plasma Phys. Contr. Fusion, 51, 015005 [Google Scholar]
- Zirakashvili, V. N., Breitschwerdt, D., Ptuskin, V. S., & Völk, H. J. 1996, A&A, 311, 113 [NASA ADS] [Google Scholar]
Appendix A: General focusing
In his seminal article, Roelof (1969) defined the focusing length as L = −B/(∂B/∂z). However, z is the coordinate along the magnetic field, B, so that in cartesian coordinates, the focusing length is connected to the gradient of the absolute magnetic field strength as 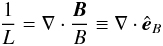 (A.1)with B = |B| and where
(A.1)with B = |B| and where 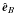 is the unit vector in the direction of the magnetic field. By making use of ∇·B = 0, the above definition can be rewritten as
is the unit vector in the direction of the magnetic field. By making use of ∇·B = 0, the above definition can be rewritten as 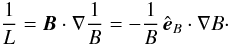 (A.2)With the magnetic field line equation,
(A.2)With the magnetic field line equation, 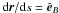 , the latter expression can be transformed according to
, the latter expression can be transformed according to ![\appendix \setcounter{section}{1} \begin{equation} \eb\cdot\nabla=(\eb)_i\,\pd{x_i}=\dd[x_i]s\,\pd{x_i}=\dd s, \end{equation}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq133.png) (A.3)yielding an expression that involves the derivative along the field lines as
(A.3)yielding an expression that involves the derivative along the field lines as ![\appendix \setcounter{section}{1} \begin{equation} \label{eq:Ltrue} \frac{1}{L}=-\frac{1}{B}\,\left(\eb\right)_i\,\pd[B]{x_i}=-\frac{1}{B}\,\dd[B]s\cdot \end{equation}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq134.png) (A.4)This illustrates that Eq. (2)is only an approximation that is valid – in the sense that L is constant – so long as the magnetic field is more or less aligned with the z direction. In particular, one requires
(A.4)This illustrates that Eq. (2)is only an approximation that is valid – in the sense that L is constant – so long as the magnetic field is more or less aligned with the z direction. In particular, one requires 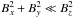 . For the specific choice of the magnetic field components in Eqs. (3) and (4), one has
. For the specific choice of the magnetic field components in Eqs. (3) and (4), one has 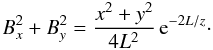 (A.5)Strictly speaking, therefore, the model used here has a constant focusing length only inside a cylinder with the radius
(A.5)Strictly speaking, therefore, the model used here has a constant focusing length only inside a cylinder with the radius 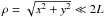 , as illustrated by Fig. 8.
, as illustrated by Fig. 8.
If one were to find a magnetic field geometry that complies with the requirement that L = const., one would need to find a solution that obeys Eq. (A.4), which, together with the condition ∇·B = 0 can be rewritten as ![\appendix \setcounter{section}{1} % subequation 2612 0 \begin{eqnarray} \frac{1}{L}&=&-\frac{1}{B^3}\,B_iB_j\,\pd[B_i]{x_j}\\ 0&=&\pd[B_i]{x_i}, \end{eqnarray}](/articles/aa/full_html/2012/09/aa19636-12/aa19636-12-eq138.png) where i,j ∈ { x,y,z } or, under the assumption of axisymmetry, i,j ∈ { ρ,z } . Possible solutions to Eqs. (A.6) and their properties will be discussed elsewhere.
where i,j ∈ { x,y,z } or, under the assumption of axisymmetry, i,j ∈ { ρ,z } . Possible solutions to Eqs. (A.6) and their properties will be discussed elsewhere.
Appendix B: Curved slab geometry
In addition to the modified parallel displacement expressed by Eq. (13), the curved magnetic field lines also affect the geometry of the turbulent magnetic fields – unless said geometry is isotropic and the orientation does not matter.
Because the turbulence generator implemented in Padian requires the background magnetic field to be in z direction, the reference frame has to be rotated so that the actual field vector now represents the new 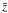 direction. With B given by
direction. With B given by 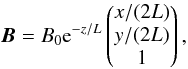 (B.1)the axis of rotation can be chosen as
(B.1)the axis of rotation can be chosen as 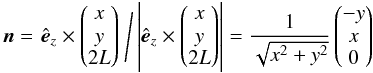 (B.2)as illustrated in Fig. B.1. Accordingly, the rotation angle can be determined from
(B.2)as illustrated in Fig. B.1. Accordingly, the rotation angle can be determined from 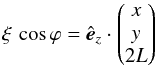 (B.3)with
(B.3)with 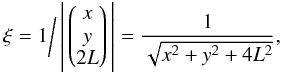 (B.4)yielding
(B.4)yielding 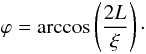 (B.5)The general matrix for a rotation in the x-y plane is given through
(B.5)The general matrix for a rotation in the x-y plane is given through 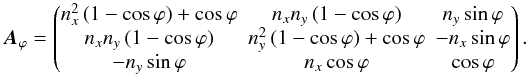 (B.6)To ensure that the resulting turbulent magnetic field depends only on the direction parallel to the background magnetic field, first the position vector has to be rotated according to
(B.6)To ensure that the resulting turbulent magnetic field depends only on the direction parallel to the background magnetic field, first the position vector has to be rotated according to 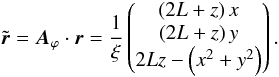 (B.7)For x = y = 0, one has
(B.7)For x = y = 0, one has 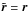 as expected because
as expected because 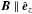 .
.
 |
Fig. B.1 (Color online) Illustration of the rotation axis (blue), by which the z axis is rotated to be aligned with the background magnetic field vector B (red) as given by Eq. (B.1). This is necessary because the turbulent slab magnetic field obeys δB = δB(s) and δB ⊥ B, where s is the direction along the magnetic background field B. |
As a second step, the generated turbulent magnetic field vector 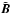 needs to be rotated by an angle − ϕ, yielding
needs to be rotated by an angle − ϕ, yielding 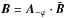 with
with 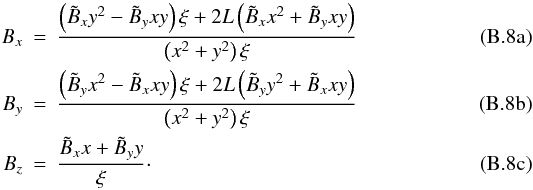 Again, for x = y = 0, one has
Again, for x = y = 0, one has 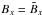 ,
, 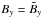 , and Bz = 0 with the latter being a general constraint for slab geometry. Hence, Eqs. (B.8) are valid only for
, and Bz = 0 with the latter being a general constraint for slab geometry. Hence, Eqs. (B.8) are valid only for 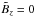 , as is the case for example for the slab and the composite models, with the latter defined as the superposition of slab and two-dimensional modes.
, as is the case for example for the slab and the composite models, with the latter defined as the superposition of slab and two-dimensional modes.
The two rotations described above are required for every particle at every time step. The exact choice of the step size is made by the adaptive integration method so that the error in the particle energy accumulates to no more than one-tenth of a percent for the whole simulation time (cf. Tautz 2010a; Giacalone & Jokipii 1999).
All Figures
 |
Fig. 1 Sample trajectories for the magnetic field geometry described by Eqs. (3) and (4) with an additional turbulent component δB, which is generated according to the Fourier superposition of Eq. (15). In the upper panel, the magnitude of the turbulent field is (δB/B0)2 = 0.1. In the lower panel, the turbulence strength is varied together with the background magnetic field strength so that (δB/|B|)2 = 0.1 = const. also along the z direction. |
| In the text | |
 |
Fig. 2 Parallel scattering mean free path as a function of the normalized simulation time vt/ℓslab for a slab turbulence with (δB/B0)2 = 0.1. In the upper panel, the case of slab turbulence is shown, while the lower panel shows the case of isotropic turbulence. Both panels show the homogeneous case, i.e., L → ∞. For vt/ℓslab ≳ 102, the diffusive regime has been reached where λ∥ ≈ const. In both panels, the various curves show different particle rigidities R = RL/ℓslab as indicated. |
| In the text | |
 |
Fig. 3 Simulation results (black diamonds) for the parallel scattering mean free path in slab turbulence with adiabatic focusing as described by Eqs. (3)and (4). The focusing length is chosen as L/ℓslab = 10 (upper panel) and L/ℓslab = 1 (lower panel). Furthermore, the two analytical results are shown as open diamonds for the quasi-linear result from Eq. (9)and as gray triangles for the nonlinear result from Eq. (10). For comparison, the parallel mean free path is shown also for a homogeneous background magnetic field (gray circles). The magnitude of the turbulence is (δB/B0)2 = 0.1. |
| In the text | |
 |
Fig. 4 Simulation results (black squares) for a relative turbulence strength, on average, kept constant throughout the simulation space so that (δB/|B|)2 = 0.1. Same as Fig. 3 for other points. Additionally, here results are considered also for L = 50ℓ0. |
| In the text | |
 |
Fig. 5 Simulation results for the parallel scattering mean free path in isotropic turbulence with adiabatic focusing. The focusing length is chosen as L/ℓ0 = 10 (upper panel) and L/ℓ0 = 1 (lower panel). The black diamonds show the case of an absolutely constant turbulence strength as (δB/B0)2 = 0.1 (cf. Fig. 3), whereas the black squares show the case of turbulence strength that varies with the background field strength as (δB/|B|)2 = 0.1 (cf. Fig. 4). For comparison, the parallel mean free path is shown also for a homogeneous background magnetic field (gray circles). |
| In the text | |
 |
Fig. 6 Comparison of the parallel mean free path for particles moving initially with vz > 0 (denoted by |
| In the text | |
 |
Fig. 7 Histogram of the particle displacement in z direction, Δz ≡ z(tmax) − z(t0) for the case of slab turbulence with a focusing length L = 10ℓslab. The upper panel shows the case of δB/B0 = const., whereas the lower panel shows the case of δB/|B| = const. Clearly, most particles move toward weaker field strengths. |
| In the text | |
 |
Fig. 8 “True” focusing length L as obtained from Eq. (A.4)for the magnetic field given by Eqs. (3) and (4) for L = 10ℓ0. Additionally, the deviation of the true focusing length from the parameter L is depicted at ρ = L and ρ = 2L. |
| In the text | |
 |
Fig. B.1 (Color online) Illustration of the rotation axis (blue), by which the z axis is rotated to be aligned with the background magnetic field vector B (red) as given by Eq. (B.1). This is necessary because the turbulent slab magnetic field obeys δB = δB(s) and δB ⊥ B, where s is the direction along the magnetic background field B. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.