| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A150 | |
| Number of page(s) | 6 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201219613 | |
| Published online | 24 September 2012 | |
Nijboer-Zernike phase retrieval for high contrast imaging
Principle, on-sky demonstration with NACO, and perspectives in vector vortex coronagraphy
1 60 rue des bergers, 75015 Paris, France
e-mail: riaud.pierre@gmail.com
2 Université de Liège, 17 Allée du 6 Août, 4000 Sart Tilman, Belgium
3 European Southern Observatory, Alonso de Cordóva 3107, Vitacura, Santiago, Chile
e-mail: dmawet@eso.org
4 NASA-Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, CA 91109, USA
5 Techspace-Aero, route de Liers 121, 4041 Milmort, Belgium
e-mail: arnaud.magette@techspace-aero.be
Received: 16 May 2012
Accepted: 19 July 2012
We introduce a novel phase retrieval method for astronomical applications based on the Nijboer-Zernike (NZ) theory of diffraction. We present a generalized NZ phase retrieval process that is not limited to small and symmetric aberrations and can therefore be directly applied to astronomical imaging instruments. We describe a practical demonstration of this novel method that was recently performed using data taken on-sky with NAOS-CONICA, the adaptive optics system of the Very Large Telescope. This demonstration presents the first online on-sky phase retrieval results ever obtained, and allows us to plan subsequent refinements on a well-tested basis. Among the potential refinements, and within the framework of high-contrast imaging of extra-solar planetary systems (which requires exquisite wavefront quality), we introduce an extension of the generalized NZ to the high-dynamic range case, and particularly to its use with the vector vortex coronagraph. This induces conjugated phase ramps applied to the orthogonal circular polarizations, which can be used to instantaneously retrieve the complex amplitude of the field, yielding a real-time calibration of the wavefront that does not need any other modulation such as focus or other deformable mirror probe patterns. Paper II (Riaud et al. 2012, A&A, 545, A151) presents the mathematical and practical details of the new method.
Key words: instrumentation: high angular resolution / instrumentation: adaptive optics / methods: numerical / techniques: polarimetric
© ESO, 2012
1. Introduction
We present a phase retrieval method derived from the Nijboer-Zernike (NZ) theory of diffraction (i.e. the polar theory of diffraction) to sense optical aberrations in an imaging system. Sensing and subsequent correction, which is out of the scope of this paper, is crucial for optimizing the efficiency of imaging instruments. Within the framework of high-contrast imaging of extra-solar planetary systems, high-accuracy measurement and correction of wavefront is absolutely necessary for space-based or ground-based instruments. The current most popular phase diversity approach uses as its iterative-transform error-reduction method the Gerchberg-Saxton algorithm (Gerchberg & Saxton 1972; Feinup 1982). Examples of application of this phase retrieval method are numerous: NAOS-CONICA (NACO), the adaptive optics system of the Very Large Telescope, the phasing of the James Webb Space Telescope (JWST), Palomar and Keck image-sharpening procedures, pre-correction of the NASA JPL High Contrast Imaging Testbed (HCIT), etc. Despite its success and widespread use, this technique has fundamental flaws:
-
The error-reduction method heavily relies on Fourier transform,and in particular on its fast Fourier transform (FFT)implementation, which is fundamentally limited by numericalerrors (sampling, wrap-arounds, round-off, etc.).The NZ theory is fully analyticaland relies on rigorous modal decomposition of aberrations.
-
High-order aberration retrieval is generally noisy. Dean & Bowers (2003), Sect. 9, presented the limitations of the classical error-reduction method, which heavily depends on the diversity nature and amplitude. The NZ theory overcomes this problem because it uses a modal description of the aberration directly at the focal plane.
-
For a coupled amplitude and phase aberrations, the true wavefront is not retrieved by the iterative-transform method. Indeed, this generally does not take the amplitude error into account in the process. The NZ polar theory of diffraction uses complex
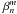 coefficients that include both amplitude and phase aberrations.
coefficients that include both amplitude and phase aberrations.
In summary, the NZ phase retrieval approach, while generally using a focus modulation for diversity similar as the aforementioned method, allows us to retrieve the true input wavefront within a rigorous mathematical and analytical framework.
The first part of this first introductory paper presents the NZ-based phase retrieval technique and applies it to estimate non-common path aberrations of the adaptive optics NACO on the VLT. Note that this live demonstration is to our knowledge the first successful attempt at retrieving the phase online and on-sky, using real starlight instead of static and close-to-perfect calibration fibers.
We use this successful demonstration as a firm foundation to qualitatively introduce a novel instantaneous phase retrieval method finely and rigorously adapted from the NZ-based method to the vector vortex coronagraph (VVC). In this two-part presentation, we use the analogy between the focus modulation and the new photon orbital angular momentum (POAM) modulation provided by the novel coronagraphic device.
In Sect. 2, a description of the phase diversity concept using the NZ theory is given along with the specific algorithm. In Sect. 3, a presentation of the experimental validation of the NZ phase diversity is proposed with the NACO instrument on the VLT. Finally, in Sect. 4, we present a new concept of phase retrieval derived from the previous one, but using the VVC. Detailed explanations of the full theoretical and optical implementation with the VVC are presented in (Riaud et al. 2012, hereafter Paper II).
2. Phase diversity using the NZ theory
2.1. The Nijboer-Zernike theory of diffraction
The expression of the complex amplitude in the image plane U(r,φ) as a function of the pupil complex amplitude P(ρ,θ) can be calculated by the Fraunhofer diffraction integral in polar coordinates: 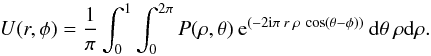 The integration limits are defined by the pupil function r ∈ [0,1] , θ ∈ [0,2π] . We chose the diffraction integral independent of the wavelength, because our proposed modal decomposition will be adjusted with respect to the image sampling. The pupil complex amplitude P(ρ,θ) can be expressed in terms of a sum of Zernike polynomials
The integration limits are defined by the pupil function r ∈ [0,1] , θ ∈ [0,2π] . We chose the diffraction integral independent of the wavelength, because our proposed modal decomposition will be adjusted with respect to the image sampling. The pupil complex amplitude P(ρ,θ) can be expressed in terms of a sum of Zernike polynomials 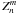 (Magette 2010):
(Magette 2010): 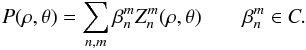 (1)The
(1)The 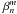 are complex weighting coefficients, and the Zernike polynomials
are complex weighting coefficients, and the Zernike polynomials 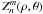 are defined as usual.
are defined as usual.
This polar diffraction theory, which expresses optical aberrations directly in the form of Zernike polynomials, is called Nijboer-Zernike (NZ) theory (Nijboer 1943, 1947). It is completely described in Magette (2010). Using explicit Bessel series to represent the diffraction integral (Janssen 2002), the NZ theory allows us to compute the final expression of the image intensity I(r,φ) thanks to a modal set of functions Vn,m, defined as follows: ![\begin{eqnarray} \label{eq:vnm} && V_{n,m}(r) = (-1)^{(n+m)/2} \frac{J_{n+1}(2\pi r)} {2\pi r} \qquad \{n,m\}\in [0,+\infty]\\[1.5mm] && I(r,\phi) \propto \left|\sum_{n,m} V_{n,m}(r)\left(\beta_{cn}^m \cos(m\phi) + \beta_{sn}^m \sin(m\phi)\right)\right|^2, \end{eqnarray}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq12.png) where
where 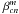 ,
, 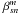 are coefficients for cos and sin functions respectively. In conclusion, the generalized NZ diffraction theory analytically computes the point spread function (PSF) of any optical system from its known pupil-plane aberrations, described by Zernike coefficients.
are coefficients for cos and sin functions respectively. In conclusion, the generalized NZ diffraction theory analytically computes the point spread function (PSF) of any optical system from its known pupil-plane aberrations, described by Zernike coefficients.
2.2. The NZ theory with defocus
Estimating aberrations from the focused image alone does not ensure the uniqueness of the solution. This indetermination is due to the Fourier relationship between the PSF and the aberrated input phase: an infinite number of phase solutions exists in the pupil plane, which results in the same PSF. The classical phase diversity method (Blanc et al. 2003) introduces a known aberration (generally a defocus) to remove this indetermination (see Fig. 1).
Here we present a modified version of the NZ diffraction theory that allows taking into account a defocus term f in the final image intensity. During the phase diversity process, the input Zernike polynomials are defocused and the polar transform becomes ![\begin{eqnarray} \label{pd1} && U(r,\phi,f) = \frac{1}{\pi} \int_{0}^{1} \int_{0}^{2\pi} {\rm e}^{{\rm i} f \rho^2}Z_n^m \: {\rm e}^{\left(-2 {\rm i} \pi \: r \: \rho \: \cos \left(\theta - \phi\right)\right)} \: {\rm d} \theta \: \rho {\rm d}\rho \nonumber \\[1.5mm] && I(r,\phi,f) \propto \left|\sum_{n,m} V^f_{n,m}(r)\left(\beta_{cn}^m \cos(m\phi) + \beta_{sn}^m \sin(m\phi)\right)\right|^2. \end{eqnarray}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq16.png) (4)The amplitude is the same as in the classical NZ theory, but using a new set of modal functions
(4)The amplitude is the same as in the classical NZ theory, but using a new set of modal functions 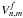 that take into account the focus amplitude f:
that take into account the focus amplitude f: ![\begin{eqnarray} \label{vnm2} &&V_{n,m}^f(r) = (-1)^m {\rm e}^{{\rm i}f} \sum_{l=1}^{\infty} v_f(l,j) \frac{J_{m+l+2j}(2 \pi r)}{l (2 \pi r)^l} \nonumber\\[1.5mm] && v_f(l,j) = (-2{\rm i}f)^{l-1} \sum_{j=0}^{(n-m)/2} (-1)^{(n-m)/2} B(n,m,j,l)\nonumber\\[1.5mm] && B(n,m,j,l) = (m+l+2j) \frac{\binom{m+j+l-1}{l-1} \binom{j+l-1}{l-1} \binom{l-1}{{(n-m)/2}-j}}{\binom{{(n+m)/2}+l+j}{l}}\cdot \end{eqnarray}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq18.png) (5)Physically, using the focus term f induces a radial modulation of images with f/2π nodes. The image intensity becomes
(5)Physically, using the focus term f induces a radial modulation of images with f/2π nodes. The image intensity becomes ![\begin{eqnarray} \label{high_d2} I(r,\phi) &=& 4\left(\beta_0^0\right)^2 \left|V_{0,0} \right|^2 + f^{(1)}\left[\beta_{cn}^m,\beta_{sn}^m \right] \nonumber\\[1.5mm] &&\quad + f^{(2)}\left[\left(\beta_{cn}^m\right)^2, \left(\beta_{sn}^m\right)^2, \left(\beta_{cn}^m \beta_{sn}^m\right) \right]. \end{eqnarray}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq20.png) (6)The intensity is composed of three different terms:
(6)The intensity is composed of three different terms:
-
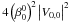 : a constant term
: a constant term -
![\hbox{$f^{(1)}\left[\beta_{cn}^m,\beta_{sn}^m \right] $}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq22.png) : a linear function of
: a linear function of 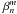 coefficients
coefficients -
![\hbox{$f^{(2)}\left[(\beta_{cn}^m)^2,(\beta_{sn}^m)^2,(\beta_{cn}^m\cdot\beta_{sn}^m) \right]$}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq23.png) : a term quadratic in the
: a term quadratic in the 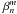 coefficients and cos/sin cross terms.
coefficients and cos/sin cross terms.
In the two functions f(1)/f(2), the summation over n,m values except n = 0, m = 0 are included. The complete mathematical development of I(r,φ) is presented in Paper II (Riaud et al. 2012).
 |
Fig. 1 Phase diversity principle. An entrance-aberrated pupil P(ρ,θ) is propagated through an optical system. For a circular pupil, the Fourier propagation between the pupil and the image plane is related to the polar Fourier transform equation PFT[P(ρ,θ)]. If there is a focus aberration, this propagation must be developed as a function of the focus f coefficient: the new optical propagation function becomes PFTf[P(ρ,θ)]. This mathematical development allows us to express the three image planes by a complete set of modal functions |
2.3. The NZ phase retrieval process
The NZ theory gives us tools for a straightforward and rigorous retrieval procedure. The first step of the retrieval process, which can be considered as a linearization, assumes that images can be described as linear combinations of the entrance pupil aberrations (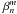 coefficients). This is equivalent to omitting f(2) terms. Equation (6) thus becomes
coefficients). This is equivalent to omitting f(2) terms. Equation (6) thus becomes ![\begin{equation} \label{high_d3} I_L(r,\phi) \approx 4\left(\beta_0^{'0}\right)^2 \left|V_{0,0} \right|^2 + f^{(1)} \left[\beta_{cn}^m,\beta_{sn}^m\right]. \end{equation}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq31.png) (7)The phase retrieval process based on the NZ theory then proceeds as a two-step procedure, filling both sides of an equality to subsequently identify them using the
(7)The phase retrieval process based on the NZ theory then proceeds as a two-step procedure, filling both sides of an equality to subsequently identify them using the 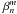 coefficient as free parameters. On one hand, we use the linearized modal expression the intensity PSF that we derived above, where a radial modal analysis was performed to analytically decompose the PSF into radial modes. On the other hand, we project the measured defocused PSFs on the basis of the same decoupled radial modes by means of a polar Fourier transform. The equalization of both sides of this newly formed equation (on one side we have an analytical model and on the other side the data) leads to the formations of decoupled systems of linear equations. Resolving these systems yields the aberration coefficients that we are looking for, and hence a first linear estimate of the wavefront.
coefficient as free parameters. On one hand, we use the linearized modal expression the intensity PSF that we derived above, where a radial modal analysis was performed to analytically decompose the PSF into radial modes. On the other hand, we project the measured defocused PSFs on the basis of the same decoupled radial modes by means of a polar Fourier transform. The equalization of both sides of this newly formed equation (on one side we have an analytical model and on the other side the data) leads to the formations of decoupled systems of linear equations. Resolving these systems yields the aberration coefficients that we are looking for, and hence a first linear estimate of the wavefront.
In other words, analyzing the measured and model PSF with different foci on the basis of template modes 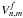 leads indeed to a system of decoupled linear equations (Magette 2010), which after solving through classical matrix algebra calculation yields an estimate (an upper limit) of the aberrated coefficients
leads indeed to a system of decoupled linear equations (Magette 2010), which after solving through classical matrix algebra calculation yields an estimate (an upper limit) of the aberrated coefficients 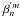 .
.
The quadratic term f(2) can then be directly calculated using the retrieved coefficients obtained in the first linearized step, using a recursive corrector approach defined by the following equations: ![\begin{eqnarray*} I(r,\phi) - f^{(2)} \left[\left(\beta_{cn}^{'m}\right)^2, \left(\beta_{sn}^{'m}\right)^2, \left(\beta_{cn}^{'m}\beta_{sn}^{'m}\right)\right] = I_L(r,\phi)\\[1.5mm] f^{(2)}\left[\left(\beta_{cn}^{'m}\right)^2,\left(\beta_{sn}^{'m}\right)^2,\left(\beta_{cn}^{'m}\beta_{sn}^{'m}\right)\right] = I(r,\phi)-I_L(r,\phi). \end{eqnarray*}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq33.png) After iterating,
After iterating, 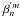 will tend to
will tend to 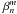 if and only if f(2) < f(1).
if and only if f(2) < f(1).
 |
Fig. 2 Top: input PSFs used for the retrieval. Middle: output PSFs computed from the NZ phase retrieval. They are very similar to the input images in spite of the exposure time difference between the three defocused images. Bottom: differences between the input and retrieved PSFs. The low residuals (<10%) are due to a blurring effect related to the tip/tilt during exposure time. The intensities are represented to the power 1/4 to improve the contrast of the images. |
3. Application of classical NZ phase retrieval on NACO
To illustrate the phase diversity retrieval using the NZ theory, we present an experiment recently conducted on-sky with NAOS-CONICA, the adaptive optics camera of the Very Large Telescope. Using CONICA, three focus images (i.e. images intra, in, and extra focus) of the star HD 25026 were taken on September 26, 2009 (prog. ID 383.C-0550(A)). We note that the images were taken in closed loop, using NAOS’s visible wavefront sensor (Fig. 2). All images consist of a co-addition of 160 frames of 0.35 s exposure. Their observational characteristics and the setup are summarized in Table 1.
We then applied the classical NZ phase retrieval method presented above using these temporally averaged images of HD 25026. Our goal was to derive the complex amplitude of the NACO pupil online, in quasi real-time.
3.1. Practical considerations
The pixel sampling has to be adjusted at the beginning of the NZ retrieval process to take into account the tip-tilt blurring caused by the long exposure time (56 s). Indeed, with a camera sampling of 13.27 mas/pixel and an undersized Lyot stop inside the CONICA camera, the image sampling would be ≈ 4.67 pixels/(λ/D). The best sampling retrieved as a free parameter by the NZ analysis is 5.3 pixels/(λ/D) (see Table 2). The difference of 0.62 pixel on the PSF width corresponds to 8.3 mas of PSF blurring, which is close to the estimated value of the tip-tilt residuals. In other words, during a long exposure image, the turbulence increases the PSF width (blurring) and the NZ phase retrieval allows us to retrieve the long-term residual aberrations on the NACO instrument under sky operation.
One of the input parameters required by the NZ phase retrieval is a first estimate of the maximum number of Zernike polynomials that can be retrieved from the input sky images, which are indeed affected by the photon and the readout noises. Several retrieval runs with different numbers of complete Zernike coefficient sets (21, 28, 36, 45, 55, 66) empirically showed that using an optimal number of Zernike polynomials equal to 45 leads to a smaller 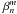 coefficient variation. Indeed, if the number of Zernike coefficients is lower than the optimal value, fewer high frequencies can be retrieved. If the number of the Zernike aberrations is greater than the maximum limited by the input image’s signal-to-noise ratio, the variance of the
coefficient variation. Indeed, if the number of Zernike coefficients is lower than the optimal value, fewer high frequencies can be retrieved. If the number of the Zernike aberrations is greater than the maximum limited by the input image’s signal-to-noise ratio, the variance of the 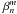 coefficients increases. The variance minimum of
coefficients increases. The variance minimum of 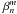 as a function of the number of Zernike coefficients indicates the highest spatial frequencies retrievable.
as a function of the number of Zernike coefficients indicates the highest spatial frequencies retrievable.
3.2. Online phase retrieval results
Figure 3 shows the retrieved aberrated pupil of NACO after our NZ phase retrieval while Fig. 4 gives the 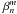 coefficient values. We note that the amplitude (top left in Fig. 3) is larger than 1, which is an artifact related to a global energy normalization in the PSF. We also note that amplitude variations are small, which indicates that very small amplitude aberrations (reflection or transmission problems) are present in the system.
coefficient values. We note that the amplitude (top left in Fig. 3) is larger than 1, which is an artifact related to a global energy normalization in the PSF. We also note that amplitude variations are small, which indicates that very small amplitude aberrations (reflection or transmission problems) are present in the system.
Characteristics of the images that were used to perform the phase retrieval.
Resuts of the NZ retrieval process.
 |
Fig. 3 Top: amplitude and phase calculated from the retrieved NZ aberrations. Bottom: real and imaginary parts of NACO’s complex pupil. All images present border effects due to the “Undersized” diaphragm of the NACO coronagraph (the two dashed black circles in each image). The effect of the central obscuration is also visible, especially in the imaginary part of the pupil (bottom right). |
Hartung et al. (2003) presented results of classical phase diversity on NACO using a fibered calibration source. Here, we used instead the direct on-sky image of a real star in closed-loop (in the Bγ filter, centered at 2.166 μm). The stellar averaged PSF is blurred due to tip-tilt and other high-order turbulence-induced aberrations uncorrected by the AO system, but it also presents clear underlying static residual phase and amplitude aberrations of about 0.105 wave rms ( ≈ 60% Strehl ratio) for the phase and ≈ 10% error on the amplitude, respectively. The level of static amplitude aberrations measured on-sky could be the direct hint of an important item in the error budget that accounts for the actual Strehl limitation of NACO when observing on-sky. With the nominal calibration procedure of static aberrations described in Hartung et al. (2003), the unique DM will be driven to compensate for the phase but not the amplitude error of the wavefront.
 |
Fig. 4
|
4. Perspectives: NZ phase diversity with the VVC
In this section, we present a promising evolution of the NZ phase retrieval method using the modulation properties of the VVC, which potentially would allow one to retrieve the phase instantaneously on-sky, requiring no offline (nor online) scanning in focus or any other kind of temporal wavefront modulation. The VVC indeed provides a natural instantaneous phase diversity that can be substituted for the classical focus variation. Using POAM modulation provided naturally by the VVC yields two significant advantages over the classical phase diversity: high dynamic range because the Airy pattern is naturally removed by the coronagraph, and instantaneity, because no scanning in focus or any other kind of temporal wavefront modulation is necessary.
4.1. The vector vortex coronagraph
The VVC is a transparent phase-mask that applies two conjugated phase ramps ei ± lpφ to the orthogonal circular polarization components of the incoming starlight, with lp the topological charge or the POAM. When the VVC is centered on the PSF, it redirects the light outside the downstream pupil where it can be blocked by a Lyot stop (Mawet et al. 2005). Because of optical aberrations in the input pupil P(ρ,θ), the coronagraphic rejection (the stellar flux attenuation coefficient) is not perfect and a small amount of the starlight remains in the coronagraphic pupil plane Pc(ρ,θ) after the diaphragm filtering by the Lyot stop (see Fig. 4). This residual light in turn focuses into aberrated PSFs, carrying the information about the aberrations modulated by the conjugated phase ramps.
4.2. New modal decomposition for the NZ theory
Here we establish the fundamental equation of the new enhanced NZ theory applied to the VVC-modulated PSFs. Note that the complete theoretical demonstration of VVC function properties under polar diffraction analysis (Fraunhofer and Fresnel propagation) is given in the more detailed Paper II (Riaud et al. 2012). We showed that going from the pupil to the first focal plane with a polar Fourier transform is PFT[P(ρ,θ)], yielding the classical modal decomposition basis Vn,m. Multiplying by the VVC phase function, and performing the inverse polar transform to propagate to the downstream pupil yields PFTlp, − 1[U(r,φ)]. Note that the remaining light in the coronagraphic pupil Pc(ρ,θ) possesses a POAM ± lp added by the phase-mask. The final polar transform PFTlp[Pc(ρ,θ)] to the final focal plane leads to a new modal decomposition using 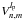 functions defined as
functions defined as ![\begin{eqnarray} \label{pd2b} && U\left(r,\phi,l_{\rm p}\right) = \frac{1}{\pi} \int_{0}^{d_{\rm c}} \int_{0}^{2\pi} {\rm e}^{{\rm i} l_{\rm p} \theta}Z_n^m \: {\rm e}^{\left(-2 {\rm i} \pi \: r \: \rho \: \cos \left(\theta - \phi\right)\right)} \: {\rm d} \theta \: \rho {\rm d}\rho \nonumber\\[1.5mm] && I\left(r,\phi,l_{\rm p}\right) \propto \left|\sum_{n,m} V_{n,m}^{l_{\rm p}} (r,\phi) \left(\beta_{cn}^m \cos(m\phi) + \beta_{sn}^m \sin(m\phi)\right)\right|^2 \\[1.5mm] && V_{n,m}^{l_{\rm p}}(r,\phi) = \epsilon_{l_{\rm p}} (-1)^{(n+m)/2} \: {\rm e}^{{\rm i} l_{\rm p}\phi} \frac{J_{n+1}(2\pi r)} {2\pi r} \\[1.5mm] && \epsilon_{l_{\rm p}} = -i, \: l_{\rm p}\neq0 \qquad \epsilon_{l_{\rm p}}=1, \: l_{\rm p}=0 \qquad d_{\rm c}<1,\nonumber \end{eqnarray}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq63.png) where dc is the size in pupil unit of the Lyot stop in the coronagraphic pupil.
where dc is the size in pupil unit of the Lyot stop in the coronagraphic pupil.
4.3. The phase retrieval process with VVC
The VVC naturally simultaneously adds two conjugated multiplicative Exp [ ± ilpφ] terms on the Vn,m modal function at the first focal plane on the orthogonal circular polarizations (left- and right-hand). The direct modified polar transform ![\hbox{$\textit{PFT}^{l_{\rm p}}_m\left[P_{\rm c}(\rho,\theta)\right]$}](/articles/aa/full_html/2012/09/aa19613-12/aa19613-12-eq66.png) then yields two overlapping final attenuated coronagraphic image functions of the lp or POAM parameter.
then yields two overlapping final attenuated coronagraphic image functions of the lp or POAM parameter.
If the orthogonal circular polarizations are split (with a polarizing beamsplitter, see Fig. 5), we can directly and simultaneously have access to the opposite POAM modulations. Similarly to the classical NZ phase retrieval theory, but this time using the POAM instead of the focus as the modulator, the coronagraphic attenuated images can be projected onto the modified 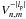 and
and 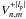 modal functions.
modal functions.
The POAM phase retrieval process is the same as the classical focus phase diversity (with new modal functions, resolution of the linearized system, and iterative correction of the non-linear term), except that the lp parameter is now fixed by the phase-mask. We note that the modulation that was radial with the focus diverstiy now becomes azimuthal with the VVC-POAM, but with 2lp nodes.
In contrast to previous systems of phase retrieval using a purely recursive process, this novel technique is rigorous (analytical), and not limited to small aberrations. The simultaneous POAM modulation provided by the VVC allows us to extend the NZ theory to high dynamic coronagraphic images. The expected dynamical gain is twofold:
-
1 -
reduced photon noise due to the coronagraphic attenuation ofthe Airy pattern;
-
2 -
no radial modulation in the
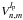 functions that spread the final images when the focus is applied.
functions that spread the final images when the focus is applied.
To additionally consolidate the validity of this new approach by analogy, we summarize in Table 3 the two phase retrieval modal decompositions in the NZ theory of diffraction, presented in this work, while emphasizing the equivalent role of focus and topological (or POAM).
 |
Fig. 5 POAM diversity principle. The optical propagation is more complicated for a coronagraphic phase-mask. Indeed, this scheme presents three different polar propagations with the same entrance aberrated pupil, which is presented in the classical phase diversity system. The first polar Fourier transform is the same as for classical imaging (PFT[P(ρ,θ)]), but after the phase-mask coronagraph, the inverse polar Fourier transform including the VVC POAM properties becomes PFTlp, − 1[U(r,φ)]. In the coronagraphic pupil plane Pc(ρ,θ), the main part of stellar photons are rejected at the edge of the pupil and some of the remaining photons inside the pupil possess an added POAM ± lp. The final polar propagation PFTlp[Pc(ρ,θ)] gives the final attenuated coronagraphic image. An optical polarizing system (quarter waveplates and Wollaston) located after the Lyot stop (the circular dashed circle in the coronagraphic pupil) allows us to separate the two circular polarizations and then the two POAMs. This mathematical development gives a complete set of modal functions |
Different phase retrieval.
A double modulation with f and lp is possible but more mathematically complicated. The focus modulation has to be introduced into the coronagraphic pupil (not in the entrance pupil) for the two lp images. Theoretically, this process would allow an easy separation of the common and non-common path aberrations.
5. Conclusion
We presented the NZ phase retrieval approach to sense and calibrate wavefront aberrations (amplitude and phase). On-sky results under low Strehl ratio (≈36−38%) conditions on the adaptive optics NAOS-CONICA were also presented as a proof of concept, showing great flexibility and ease of use for an online wavefront sensing methodology.
In the second part of this first paper, we introduced the extension of the NZ theory of diffraction to the high dynamic range case, and in particular to the VVC, which enables instantaneity of the phase retrieval process. Indeed, the VVC provides a natural instantaneous phase diversity that can be substituted for the classical focus variation. Using the POAM modulation provided naturally by the VVC yields two significant advantages over the classical phase diversity: high dynamic range because the Airy pattern is naturally removed by the coronagraph, and instantaneity, because no scanning in focus or any other kind of temporal
wavefront modulation is necessary. For additional details and the thorough mathematical development of the new method, the interested reader is referred to our companion Paper II.
Acknowledgments
This work received the support of the University of Liège. The authors are grateful to C. Hanot (IAGL), and J. Surdej (IAGL) for the manuscript corrections. The authors wish to thank the referee Wesley Traub for useful comments and corrections. The authors also acknowledge support from the Communauté française de Belgique – Actions de recherche concertées – Académie universitaire Wallonie-Europe. This idea dates back to 2005 − 2006 and the first author is grateful to Sect. 17 and the CNAP French commissions for their outstanding recruitment work.
References
- Blanc, A., Fusco, T., Hartung, M., Mugnier, L. M., & Rousset, G. 2003, A&A, 399, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dean, B., & Bowers, C. 2003, JOSA A, 20, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Feinup, J. 1982, Appl. Opt., 21, 2758 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gerchberg, R., & Saxton, W. 1972, Optik, 35, 237 [Google Scholar]
- Hartung, M., Blanc, A., Fusco, T., et al. 2003, A&A, 399, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janssen, A. 2002, JOSA A, 19, 849 [NASA ADS] [CrossRef] [Google Scholar]
- Magette, A. 2010, Ph.D. Thesis: The International Liquid Mirror Telescope: optical testing and alignment using a Nijboer-Zernike aberration retrieval approch (IAGL, University of Liège), 1 [Google Scholar]
- Mawet, D., Riaud, P., Absil, O., & Surdej, J. 2005, ApJ, 633, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Nijboer, B. 1943, Physica, 10, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Nijboer, B. 1947, Physica, 13, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Riaud, P., Mawet, D., & Magette, A. 2012, A&A, 545, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Phase diversity principle. An entrance-aberrated pupil P(ρ,θ) is propagated through an optical system. For a circular pupil, the Fourier propagation between the pupil and the image plane is related to the polar Fourier transform equation PFT[P(ρ,θ)]. If there is a focus aberration, this propagation must be developed as a function of the focus f coefficient: the new optical propagation function becomes PFTf[P(ρ,θ)]. This mathematical development allows us to express the three image planes by a complete set of modal functions |
| In the text | |
 |
Fig. 2 Top: input PSFs used for the retrieval. Middle: output PSFs computed from the NZ phase retrieval. They are very similar to the input images in spite of the exposure time difference between the three defocused images. Bottom: differences between the input and retrieved PSFs. The low residuals (<10%) are due to a blurring effect related to the tip/tilt during exposure time. The intensities are represented to the power 1/4 to improve the contrast of the images. |
| In the text | |
 |
Fig. 3 Top: amplitude and phase calculated from the retrieved NZ aberrations. Bottom: real and imaginary parts of NACO’s complex pupil. All images present border effects due to the “Undersized” diaphragm of the NACO coronagraph (the two dashed black circles in each image). The effect of the central obscuration is also visible, especially in the imaginary part of the pupil (bottom right). |
| In the text | |
 |
Fig. 4
|
| In the text | |
 |
Fig. 5 POAM diversity principle. The optical propagation is more complicated for a coronagraphic phase-mask. Indeed, this scheme presents three different polar propagations with the same entrance aberrated pupil, which is presented in the classical phase diversity system. The first polar Fourier transform is the same as for classical imaging (PFT[P(ρ,θ)]), but after the phase-mask coronagraph, the inverse polar Fourier transform including the VVC POAM properties becomes PFTlp, − 1[U(r,φ)]. In the coronagraphic pupil plane Pc(ρ,θ), the main part of stellar photons are rejected at the edge of the pupil and some of the remaining photons inside the pupil possess an added POAM ± lp. The final polar propagation PFTlp[Pc(ρ,θ)] gives the final attenuated coronagraphic image. An optical polarizing system (quarter waveplates and Wollaston) located after the Lyot stop (the circular dashed circle in the coronagraphic pupil) allows us to separate the two circular polarizations and then the two POAMs. This mathematical development gives a complete set of modal functions |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



