| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A131 | |
| Number of page(s) | 31 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201219542 | |
| Published online | 19 September 2012 | |
Photometry and models of selected main belt asteroids
IX. Introducing interactive service for asteroid models (ISAM)⋆,⋆⋆
1 Astronomical Observatory Institute, Faculty of Physics, A. Mickiewicz University, Słoneczna 36, 60-286 Poznań, Poland
e-mail: aniab@lab.astro.amu.edu.pl
2 Observatoire de Bédoin, 47 rue Guillaume Puy, 84000 Avignon, France
3 Geneva Observatory, 1290 Sauverny, Switzerland
4 Bathurst, NSW, Australia
5 Les Engarouines Observatory, 84570 Mallemort-du-Comtat, France
6 IMCCE, Paris Observatory, UMR 8028, CNRS, 77 av. Denfert-Rochereau, 75014 Paris, France
7 Agrupación Astronómica de Sabadell, Apartado de Correos 50, PO Box 50, 08200 Sabadell, Barcelona, Spain
8 Stazione Astronomica di Sozzago, 28060 Sozzago, Italy
9 Association AstroQueyras, 05350 Saint-Véran, France
10 Observatoire du Bois de Bardon, 16110 Taponnat, France
11 DTU Space, Technical University of Denmark, Juliane Maries Vej 30, 2200 Copenhagen, Denmak
12 Kapteyn Astronomical Institute, University of Groningen, PO box 800, 9700 AV Groningen, The Netherlands
13 Canberra, ACT, Australia
14 Astronomy Division, Department of Physics, PO Box 3000, 90014 University of Oulu, Finland
15 Forte Software, Os. Jagiełły 28/28, 60-694 Poznań, Poland
16 SUPA (Scottish Universities Physics Alliance), Institute for Astronomy, University of Edinburgh, Royal Observatory, Edinburgh, EH9 3HJ, UK
17 Groupe européen d’observation stellaire (GEOS), 23 Parc de Levesville, 28300 Bailleau l’Evêque, France
18 2 rue des Ecoles, 34920 Le Crès, France
19 Blauvac Observatory, 84570 St-Estève, France
20 N. Copernicus Astronomical Centre, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
21 Institute of Astronomy, Karazin Kharkiv National University, Sums’ka 35, 61022 Kharkiv, Ukraine
22 Laboratoire d’Astrophysique de Marseille, OAMP, Universite Aix-Marseille & CNRS, 38 rue Frederic Joliot Curie, 13388 Cedex 13, France
Received: 4 May 2012
Accepted: 12 July 2012
Context. The shapes and spin states of asteroids observed with photometric techniques can be reconstructed using the lightcurve inversion method. The resultant models can then be confirmed or exploited further by other techniques, such as adaptive optics, radar, thermal infrared, stellar occultations, or space probe imaging.
Aims. During our ongoing work to increase the set of asteroids with known spin and shape parameters, there appeared a need for displaying the model plane-of-sky orientations for specific epochs to compare models from different techniques. It would also be instructive to be able to track how the complex lightcurves are produced by various asteroid shapes.
Methods. Basing our analysis on an extensive photometric observational dataset, we obtained eight asteroid models with the convex lightcurve inversion method. To enable comparison of the photometric models with those from other observing/modelling techniques, we created an on-line service where we allow the inversion models to be orientated interactively.
Results. Our sample of objects is quite representative, containing both relatively fast and slow rotators with highly and lowly inclined spin axes. With this work, we increase the sample of asteroid spin and shape models based on disk-integrated photometry to over 200. Three of the shape models obtained here are confirmed by the stellar occultation data; this also allowed independent determinations of their sizes to be made.
Conclusions. The ISAM service can be widely exploited for past and future asteroid observations with various, complementary techniques and for asteroid dimension determination.
Key words: techniques: photometric / minor planets, asteroids: general
Photometric data are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/545/A131
© ESO, 2012
1. Introduction
Asteroids observed at various viewing and illumination geometries can be uniquely modelled with the lightcurve inversion method (Kaasalainen et al. 2001). The observed light variations can be in the form of both traditional dense lightcurves and calibrated datapoints distributed sparsely in time. The resulting model consists of the convex shape representation and the spin parameters of the sidereal period and spin axis orientation. Other observing techniques such as stellar occultations by asteroids, adaptive optics imaging, radar echo, or thermal infrared technique can yield or exploit detailed shape models. To obtain as much shape details as possible, we decided to focus on asteroid modelling based on low-scatter dense lightcurves.
A comparison of the inversion models with the adaptive optics technique was succesfully made in, e.g., Marchis et al. (2006). In most cases, this allowed the rejection of the mirror pole solution, and the shape outline was confirmed. We performed another comparison in Marciniak et al. (2011), that confirmed one of the pole and shape solutions for asteroid (679) Pax.
Since stellar occultations by asteroids are being observed nowadays more extensively and accurately than ever before (see Dunham et al. 2011)1, it has become possible to overlay the occultation shadow chords and the photometric asteroid model (see Timerson et al. 2009; or Ďurech et al. 2011). This can confirm the shape model and distinguish which of the pole solutions is correct. However, there has been no interactive tool that could be used to perform a straightforward orientation of the asteroid models in the plane of sky for a given moment (though the physical ephemeris can be obtained with the Virtual Observatory service2, Berthier et al. 2008). Spin and shape models obtained from photometric techniques are being gathered in the DAMIT database3 (Ďurech et al. 2010).
To enable comparison of the photometric models with those from other observing or modelling techniques, we created an online service where we allow the orientation of these models to be determined interactively. Moreover, we present new photometric observations and physical models of asteroids (76) Freia, (127) Johanna, (355) Gabriella, (386) Siegena, (417) Suevia, (435) Ella, (505) Cava, and (699) Hela. In cases when data from stellar occultations are available, we compare our shape models to the occultation profiles. This allows us to calibrate the asteroid size, and provides the pole and shape confirmation.
2. Observations
We gathered data from our continuing main-belt asteroid observations at the Borowiec station of the Poznań Astronomical Observatory (see Michałowski et al. 2004), and from other observatories, both amateur and professional. This joint effort allowed us to obtain a larger than usual sample of asteroid spin and shape models based exclusively on dense lightcurves. This sample of eight asteroids should crucially be free of common biases, containing both relatively fast and slow rotators (P = 3 to 12 h) and high and low spin-axis inclinations with respect to the ecliptic plane (|βp| from 10 to 88 degrees). There are also large (200 km in diameter) and relatively small (13 km) objects in our sample of main-belt asteroids.
The total number of lightcurves used in our modelling was 248, 199 of which were new lightcurves and the remaining ones taken from SAPC4, ALCDEF5, or provided by the authors themselves.
The data are presented in a form of composite lighturves (Figs. 21−67, see Appendix). They can be obtained from both the CDS and DAMIT databases. Table 1 (see Appendix) contains the aspect data for all the observing runs. The mid-time of the observing run and the distances to the Earth and Sun in astronomical units are indicated in the first three columns. The table also shows the corresponding Sun-object-Earth phase angle and the J2000 ecliptic latitude and longitude of an asteroid in the sky. The next two columns give the number of points in each lightcurve and an estimate of the observational quality, which we estimated using the dispersion in the corresponding magnitude difference between two comparison stars, where such information was available. The last column provides the observatory code.
Table 2 contains the physical characteristics of these asteroids, including their effective diameters, geometric albedoes, taxonomic types, and orbital parameters67.
Asteroid parameters.
3. Photometry and models
We briefly describe earlier results on the selected targets, summarise the general character of their light variations, and describe our models with an outline of the modelling process. The lightcurve inversion method used here is described in Kaasalainen & Torppa (2001) and Kaasalainen et al. (2001). Table 3 contains the obtained spin parameters, their error values estimated from the parameter space, and a comparison to previous results. After the sidereal period value, there are λp,βp J2000 ecliptic coordinates of the spin-axis pole solutions, usually with an inevitable mirror pair of values. Since the error values were similar for both solutions, we cannot point at any of two poles as preferred. The next few columns of Table 3 give the overall number of apparitions (Napp) when an asteroid was observed, the number of separate lightcurves (Nlc) used for modelling, the method used (“A” stands for amplitude, “M” – magnitude, “E” – epoch, and “L” – lightcurve inversion methods), and the reference. The shape models and their example lightcurves compared to data are shown in Figs. 1 to 16.
Parameters of the models with their estimated error values.
 |
Fig. 1 Observed lightcurves (points) superimposed on the model lightcurves (lines) at the same epochs for (76) Freia. The overall root mean square (rms) residual of the fit was 0.0120 mag. |
 |
Fig. 2 Convex shape model “2” of (76) Freia, shown at equatorial viewing and illumination geometry, with rotational phases 90° apart (two pictures on the left), and the pole-on view at the right. The reflectivity law is artificial, to reveal the shape details. |
 |
Fig. 3 Observed vs. modelled lightcurves for (127) Johanna. The rms residual of the fit was 0.0127 mag. |
 |
Fig. 4 Shape model “2” of (127) Johanna. |
 |
Fig. 5 Observed vs. modelled lightcurves for (355) Gabriella. The rms residual of the fit was 0.0226 mag. |
 |
Fig. 6 Shape model “2” of (355) Gabriella. |
 |
Fig. 7 Observed vs. modelled lightcurves for (386) Siegena. The rms residual of the fit was 0.0083 mag. |
 |
Fig. 8 Shape model “2” of (386) Siegena. |
 |
Fig. 9 Observed vs. modelled lightcurves for (417) Suevia. The rms residual of the fit was 0.0165 mag. |
 |
Fig. 10 Shape model “2” of (417) Suevia. |
 |
Fig. 11 Observed vs. modelled lightcurves for (435) Ella. The rms residual of the fit was 0.0153 mag. |
 |
Fig. 12 Shape model “1” of (435) Ella. |
 |
Fig. 13 Observed vs. modelled lightcurves for (505) Cava. The rms residual of the fit was 0.0122 mag. |
 |
Fig. 14 Shape model “1” of (505) Cava. |
 |
Fig. 15 Observed vs. modelled lightcurves for (699) Hela. The rms residual of the fit was 0.0287 mag. |
 |
Fig. 16 Shape model “2” of (699) Hela. |
3.1. (76) Freia
The first photometric observations of (76) Freia were performed by Harris & Young (1983) in 1979, yielding a synodic period value of 9.79 h. Further observations were obtained in 1981 by Lagerkvist et al. (1987) and Harris et al. (1992). The latter work reported a synodic period of 9.972 h. In 1984, (76) Freia was obseved again, with a determined period of 9.98 h (Lagerkvist et al. 1986).
Publications that also contain data on this asteroid include Armstrong et al. (1996), Kryszczyńska et al. (1996), and Shevchenko et al. (2005, 2008), where synodic periods from 9.97 to 9.994 h are reported. All these results show that this rather long-period and low-amplitude asteroid exhibits regular, bimodal lightcurves.
Stephens & Warner (2008) obtained a preliminary model of (76) Freia using the lightcurve inversion method, for a dataset of 13 separate lightcurves from four apparitions (see Table 3).
We observed Freia during five apparitions (see Table 1 for dates and other information about the observing runs). The synodic period that fitted all of the apparitions was 9.974 h, which is identical to the Shevchenko et al. (2005) determination. Figures 21 to 25 (see Appendix) show our observations in the form of composite lighcturves with the model orientation at the zero time. The amplitudes were smallest in the 2002 apparition (0.06 mag), and greatest in 2010 (0.20 mag). Characteristic flat minima could be seen in some of the apparitions.
Obtaining a unique solution for the spin/shape model of Freia was surprisingly difficult. We could not find a unique sidereal period, even with our large dataset. Only by modifying the initial period-scanning procedure and enlarging the number of 6 initial poles to 12, did we find the best-fit model for both spin-axis orientation and period. We created the final model for 38 lightcurves from 8 apparitions (see Table 3 for the best-fit model parameters and their error values). The spin pole position is defined with very small uncertainty, but the z-axis dimension of the shape model is poorly constrained. Figures 2 and 1 display one of two shape models and its fit to the observed lightcurves. Our model differs substantially from that of Stephens & Warner (2008) in terms of the sidereal period value, but agrees with one of their pole solutions. A much larger dataset and improved modelling method would ensure that the model presented here was more reliable. The same applies to the remaining models differing from the previous solutions presented Table 3. In addition, the error values, which here usually do not exceed ± 5° indicate that the lightcurve inversion method on dense lightcurves is superior to the classical E, A, and M methods, where the spin poles were usually only accurate to ± 20°.
3.2. (127) Johanna
There are only two previous papers with observations of this asteroid’s light variations. The first one, by Harris et al. (1999), contains data from 1982 and a suggestion of a period of around 11 h, based on one fragmentary lightcurve. The other one, by Toth (1997), reports on observations of (127) Johanna taken in 1991. Many short fragments of the lightcurve were folded with a period of 6.94 h, which is much shorter than the previous determination.
We have been gathering data on Johanna since 1997, which resulted in 37 individual lightcurves coming from eight apparitions and a precise synodic period value of 12.7976 h. Composite lightcurves shown in Figs. 26 to 32 (see Appendix) have asymmetric maxima and a steady amplitude of around 0.20 mag. Our observing runs were long and extensive enough to pinpoint the right synodic period value, thus resolving previous ambiguities.
During the modelling with the lightcurve inversion, we were unable to obtain a model fitting of all the available lightcurves simultaneously. After rejecting all the data from 1991 and 1997, the model fit immediately improved, while the final model parameters remained almost the same, only now they were much tighter in the parameter space than before. This effect is usually seen when adding more data, while here it happened after discarding discrepant data. The final model was created on 33 lightcurves from 8 apparitions (see Table 3). The second solution for the pole, being much “higher” implies that there is larger uncertainty in a pole longitude than the first one. Figures 4 and 3 present one of two obtained shape models and its fit to three example lightcurves.
3.3. (355) Gabriella
Di Martino et al. (1994) observed (355) Gabriella in 1992, obtaining 0.35 mag amplitude lightcurves, and a 4.830 h period. There are three available spin and shape solutions based on combined sparse + dense datasets by Ďurech (2006), Ďurech et al. (2009), and Hanuš et al. (2011) (see Table 3), all placing the pole far from the ecliptic plane.
Beginning in the year 2005, both professional and amateur observations enlarged the dataset to 16 lightcurves from five apparitions, enabling us to obtain a unique model based on dense lightcurves. In these observations, Gabriella displayed high amplitude lightcurves (up to 0.60 mag, depending on a phase angle) with asymmetric minima (Figs. 33 to 36, see Appendix).
Interestingly, even though apparitions were placed in only four distinct places on the asteroid’s orbit, a unique model was found without a problem. Owing to the high albedo of this object, a Lambertian part of the light scattering by the model had to be increased in order to obtain realistic shape models (Fig. 6). Figure 5 shows some of the lightcurve fits. Our model is close to the previous determinations in the sidereal period and, to a lesser extent, in the spin axis position (Table 3). The pole presented here is closer to the pole of the ecliptic, and two obtained solutions may actually be one, which is almost perpendicular to the ecliptic plane.
3.4. (386) Siegena
The first photometric observations of (386) Siegena come from 1979 (Harris & Young 1983) and 1980 (Zappala et al. 1982). The latter paper determined the period to be 9.763 h. Stephens (2005) gives a period of 15.98 h based on new data gathered in 2004, but corrects the value to 9.760 h in 2007 (Stephens 2007), thus confirming the period derived by Zappala et al. Blanco & Riccioli (1998) made a preliminary pole determination using the amplitude-magnitude method (see Table 3), which was not confirmed by our results.
We observed Siegena during 8 apparitions. Unfortunately, some of them happened in the same places in its orbit (see Table 1, in Appendix). The composite lightcurves in Figs. 37 to 44 (Appendix) display rather small amplitudes of from 0.08 mag to 0.19 mag, and the minima at different levels. The synodic period fitting all the apparitions was 9.765 h, which is close to two of the previous determinations.
The best-fit sidereal period could only be found during a higher spatial-resolution scan of the initial poles (as in the case of (76) Freia). The modelling was also complicated by noisy lightcurves from the 1999 and 2004 apparitions. After excluding the most noisy lightcurves from these years, a unique model was found for 60 lightcurves from 10 apparitions, placed at six distinct positions along the ecliptic longitude. There are two strong, but narrow solutions for the pole in the parameter space (Table 3). The preferred shape model and its lightcurve fits are presented in Figs. 8 and 7.
3.5. (417) Suevia
The only published Suevia lightcurve observations are those of Barucci et al. (1992). They were performed in 1989 and the authors determined a period of 7.034 h.
Our data span six apparitions and are displayed in Figs. 45 − 50. The lightcurves show changes that are typical of an asteroid that has a low-lying pole with respect to the ecliptic. We detected both relatively large (0.37 mag) and small (0.07 mag) amplitudes, and the synodic period was 7.019 h, which is close to the determination of Barucci et al. (1992).
Our lightcurve inversion model of Suevia was based on 37 lightcurves from 7 apparitions. Although scanning possible sidereal period values gives a few possibilities in addition to the best-fitting one, only this period solution (see Table 3) provides physical shape models (Fig. 10) and good lightcurve fits (Fig. 9).
3.6. (435) Ella
Observed previously by Barucci et al. (1992) and Piironen et al. (1998), Ella showed rather regular lightcurves with periods of 4.623 h and 4.624 h, respectively.
Our observations confirmed this behaviour and synodic period values (Figs. 51 − 56). Interesting features can be noticed in the shape of the minima. The amplitudes did not change much between the apparitions, always reaching 0.4 − 0.5 mag.
Although all of the seven apparitions were unevenly distributed along Ella’s orbit and clumped into groups, a unique spin and shape model was easily found using 18 lightcurves (see Table 3 for the model parameters). The resulting shape model and lightcurve fits can be found in Figs. 12 and 11.
 |
Fig. 17 Occultation chords with both scaled shape models for asteroid (76) Freia. Two occultation events. |
3.7. (505) Cava
Photometric observations of Cava started in 1975 with the work of Lagerkvist et al. (1978) and continued in Harris & Young (1980), Young & Harris (1985), Harris et al. (1999), and Chiorny et al. (2003, 2007). Most of these papers agreed in the synodic period value being close to 8.178 h.
We observed this asteroid during five apparitions, starting in 1997. Our data confirmed the period value and the irregularity of the lightcurve shapes (see Figs. 57 − 61 for composite lightcurves). It displayed amplitudes in the range of 0.13 − 0.28 mag. In the apparition at the turn of 2004 and 2005, the phase angle (α) span was especially large, reaching an unprecedented 29°. Such data are good indicators of the shadowing properties of the surface and of great value in shape modelling.
During our modelling, we found three short but noisy lightcurves, which prevented us from finding a best-fit solution. After excluding them, a final dataset contained 40 lightcurves from 8 apparitions (counting both our and literature data), and a unique spin and shape model was found (see Table 3). Our model is similar to the one found by Michałowski (1996), even though only in the pole longitude values, but disagrees with the early model of Young & Harris (1985). The shape model visualisations and example lightcurve fits are given in Figs. 14 and 13.
3.8. (699) Hela
The first lightcurve studies of this asteroid were those of started by Pilcher (1983) and Binzel (1987). Subsequent data were gathered by Harris & Young (1999), Pilcher et al. (2000), and Szabo et al. (2001). These authors determined its rotational period at different values, for example 3.396 h given by Pilcher (2000).
Data gathered by us spanned six apparitions (Figs. 62 − 67). Hela exhibited minima of different depths and strongly variable amplitudes (from 0.15 mag to 0.5 mag). The synodic period that fitted all the composite lightcurves was 3.3961 h.
The model with parameters displayed in Table 3 was the only plausible one, though in some of the lightcurves the fit was unsatisfactory (Fig. 15) and the shape model vertical dimension (Fig. 16) was poorly constrained, because most of the possible shape models were unnaturally flat. Models with more extrema per period were checked, but were found to be implausible. This model was based on 21 lightcurves from 7 apparitions.
4. Comparison with occultation chords
We implemented the method described by Ďurech et al. (2011) to compare newly created photometric models with available data on stellar occultations by these asteroids. Only three of the asteroids modelled here had occultation data with a sufficient number of chords. Comparison of the photometric models with occultation chords provides invaluable information in at least two ways: it gives a confirmation of the shape models, sometimes allowing for the rejection of the mirror pole solution, and the comparison also gives an independent size determination.
 |
Fig. 18 Occultation chords with both scaled shape models for asteroid (386) Siegena. Two occultation events. |
 |
Fig. 19 Occultation chords with both scaled shape models for asteroid (127) Johanna. |
In Figs. 17–19, silhouettes were produced when the shape models’ orientations were displayed for the given moment of occultation, and were overlayed on the occultation chords (timing data came from the pds (Planetary Data System) occultation database, Dunham et al. 2011). The models were scaled to minimise the χ2 measure from the occultation chords. The frame in the figures is scaled in km on the Earth fundamental plane (ξ, η) defined in Ďurech et al. (2011). Unfortunately, in these specific cases, none of the mirror models can be rejected with certainty. We applied no mutual shifting to the visually acquired chords, because there were not enough electronically measured chords for reference. Nevertheless, the main outlines of the model shapes are confirmed. The sizes of the equivalent volume spheres, with 1-σ standard deviation, are given in Table 4, where they are compared to the IRAS (Tedesco et al. 2004) and AKARI infrared results (Usui et al. 2011). Our results are consistent with these sources within the error values. In the case of (76) Freia, our results are closer to AKARI measurements than to previously available IRAS data (Tedesco et al. 2004), while for (386) Siegena our value is exactly between the two. The diameters derived from stellar occultation data are less model-dependent than from other techniques (such as the instantaneous infrared flux observations), provided there is more than one event observed. In that case, the derived diameters do not depend strongly on the momentary model orientation at the time of occultation, because we register the asteroid’s shape cross-section in more than one rotational phase. It would even be possible to incorporate the occultation data into the modelling process itself, thus more tightly constraining the resulting spin and shape parameters. However, in these particular cases, both the quality of the available data and a posteriori fits are imperfect, so our diameter estimates can only be treated as approximate.
Equivalent sphere diameters based on fitting to occultation chords (D), compared to their IRAS (DIRAS) and AKARI (DAKARI) values.
5. Interactive service for asteroid models (ISAM)
The field of asteroid modelling from disk-integrated photometry has started to draw on research advances in the previously separate fields of adaptive optics imaging, observations made at infrared wavelengths, or stellar occultations. There is now quite a large number of asteroids for which it is possible to cross-check or modify models based on photometric data using models from different techniques. Howewer, a common tool was needed to allow for a comparison of both models in the plane of sky at a given epoch.
We thus created an interactive service where this can be done. On the ISAM webpage8, one can choose a polyhedral asteroid model and display its orientation for any requested date and in different modes, including stereoscopic views. One can also generate animations, both for the rotating model and the resulting lightcurve. Making predictions for the future light variations and object orientations is also possible. Our orientating codes were cross-checked against adaptive optics (Marciniak et al. 2011) and occultation observations (George et al. 2011). All of the model snapshots shown next to the composite lightcurves (Figs. 21−67, see Appendix) were created with this service.
5.1. Service description
The transformations necessary to fit the data from other techniques utilise the asteroid model with its spin axis defined in an ecliptic coordinate frame, to perform a sky-plane projection where the celestial north is up and east is left, as in the conventional displays of either occultation results or adaptive optics images.
We start from the body model defined by triangular facets in its own reference frame, with the “z” axis coinciding with the axis of rotation and the “x” axis usually orientated according to the epoch of its first photometric observation. We then apply a series of rotations to the model using the orientating algorith, which first rotates the body by three angles defined by the model’s spin axis ecliptic coordinates and a rotation angle at a specific epoch. The algorithm then takes into account the target’s position with respect to the Earth and the Sun, resulting from its orbital parameters, and projects the body onto the plane perpendicular to the observer-asteroid vector. Finally, this 2D image is rotated so that north is at the top and east is to the left.
The service was developed in LAMP (Linux, Apache, MySQL, PHP) technology and works on a Debian GNU/ Linux 6.0 operating system. The management of the www sites is done with Apache ver.2, while the site is based on the PHP 5.0 language and HTML forms with the addition of JavaScript. The PHP code works with the programmes written in C++ language. The C++ codes use the “z-buffer” algorithm to plot the asteroid orientation and return “png” type images. In both modifying the images and creating animations and the three-dimensional (3D) effects, the functions “convert” and “composite” from the Image Magick package are used. Data on the asteroid models and their orbital parameters are stored in the MySQL database. This approach allows for an efficient application run. In the near future, the applications will be installed on the computer cluster and managed with the CORBA (Common Object Request Broker Architecture) and CUDA (Compute Unified Device Architecture) technologies, using GPU.
 |
Fig. 20 Example view of the “orientation” mode of the ISAM service. One of our earlier models is displayed. |
5.2. Model
In the “model” mode of the ISAM service, one can see the basic, equatorial view of the model. The viewing and lighting geometries can be changed here by selecting different ellipsoidal coordinates of an observer and the Sun over an asteroid’s surface, with an adjustable step. The coorditate system is similar to a geographic longitude λ and latitude φ, which here are an asterocentric longitude L and latitude B. If the model is nonconvex, as in the case of (25 143) Itokawa from Hayabusa spacecraft, the shadowing effects can clearly be seen. A 3D stereoscopic view, in the form of an anaglyph, can also be generated here and observed with the usage of special colour glasses.
5.3. Orientation
A short description is provided at the webpage of how to use the “orientation” mode. This is the place where one can generate the model plane-of-sky views for any requested date and time (restricted to the calendar years 1700 − 3000). Both Julian and Gregorian date formats are possible. A display of a legend can be adjusted and additional options can be chosen. If parameters remain unchanged, the model orientation for the present moment is displayed. To generate the lightcurve that the model would produce at a given orientation, one needs to choose the “Generate lightcurve” option. The plotted lightcurve takes a few seconds to be generated and can be downloaded, both as a plot or in the form of data file.
In Fig. 20, the outcome of the “orientation” mode is shown. The displayed model is described by the Julian date, coordinates of the north pole, an aspect angle, and the period of rotation bound to a specific model solution. The north and east directions in the plane-of-sky are also shown. Images with their legends can be displayed in black and white and downloaded for the use in publication, provided that a proper reference is given.
One of the novelties of the displaying tool is the visibility of the rotation axis, which is marked by a straight line piercing the poles and has a length that depends on the viewing angle. To help one visualise the axis in space, a small circle is shown over the north pole, which changes its shape with changing viewing angle. It also shows the sense of rotation and moves when the animation mode is used.
For research purposes, views corrected for light-travel time are possible. Choosing this option does not affect the JD epoch, but changes the model orientation to the rotation phase later compared to the default one (seen from the Earth). For some applications, e.g., the occultation observations, the full silhouette of the shape model can be displayed. Normally, only the visible and illuminated parts of the model are shown against a black background (as in our example in Fig. 20). Three different 3D effect options are also possible, provided that the lightcurve is not requested. These are an anaglyph, cross-eye, and parallel views. They allow for a spatial view of a model.
5.4. Video
The “video” mode is probably the most interesting for illustrative purposes. It allows one to create an animated model rotation, with the addition of a lightcurve generated live. Possible options in this mode are similar to those in the “orientation” mode, with the addition of an adjustable number of frames per period. The movie takes a few minutes to be fully generated, but the intermediate stages are displayed. For detailed analysis, we recommend generating a slower running movie by choosing more frames per period. The date typed in the “orientation” mode and the chosen options are transferred here, to allow for an investigation of how various lightcurve features are created by a rotating model.
Any generated views or movies can be saved to the gallery by a user. The galleries are divided into four categories: movie, picture, lightcurve, and plot gallery. The static and animated model views created by other users can be viewed here, where images in the picture and plot galleries are static, while in the movie and lightcurve galleries they are animated.
6. Summary and future plans
The eight models obtained in this work have enlarged the statistical sample of asteroid spin and shape models, partly in an attempt to overcome the observational bias against long periods and low pole latitudes. In three cases, we obtained their size values by comparing with stellar occultation chords, which are independent of both absolute magnitudes and albedo determinations.
Our ISAM web-based service was created to allow a visual comparison of shape models with occultations and for a variety of other applications. It has been designed to aid both researchers and tutors in the community studying asteroids. It allows the direct comparison of photometric asteroid models to those obtained with different techniques, and can be used without any limitations to conduct further research. After the service upgrade, it will be possible to directly derive the model absolute dimensions from the comparison with occultation data. Moreover, as the tool will provide a monochromatic flux for a model’s temporary cross-section, it will be possible to recalibrate asteroid diameter determinations based on infrared data gathered by satellites in the past.
In the near future, we plan to move the service to a computer cluster, which will improve its functionality. The models in the database, which are now mostly from the DAMIT database, can come from various sources and techniques, and we plan to include models based on, e.g., radar ranging or space probe imaging (such as already available model of (25 143) Itokawa). We also plan to add an option to allow users to temporarily upload their own models and check both their lightcurves and/or orientations.
Appendix: Lightcurve data
Aspect data.
continued.
continued.
 |
Fig. 21 Composite lightcurve of (76) Freia in 2002 with the orientation of model 2 for the zero phase. |
 |
Fig. 22 Composite lightcurve of (76) Freia in 2006 with the orientation of model 2 for the zero phase. |
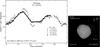 |
Fig. 23 Composite lightcurve of (76) Freia in 2007/2008 with the orientation of model 2 for the zero phase. |
 |
Fig. 24 Composite lightcurve of (76) Freia in 2009 with the orientation of model 2 for the zero phase. |
 |
Fig. 25 Composite lightcurve of (76) Freia in 2010 with the orientation of model 2 for the zero phase. |
 |
Fig. 26 Composite lightcurve of (127) Johanna in 2000 with the orientation of model 2 for the zero phase. |
 |
Fig. 27 Composite lightcurve of (127) Johanna in 2002 with the orientation of model 2 for the zero phase. |
 |
Fig. 28 Composite lightcurve of (127) Johanna in 2005/2006 with the orientation of model 2 for the zero phase. |
 |
Fig. 29 Composite lightcurve of (127) Johanna in 2007 with the orientation of model 2 for the zero phase. |
 |
Fig. 30 Composite lightcurve of (127) Johanna in 2008 with the orientation of model 2 for the zero phase. |
 |
Fig. 31 Composite lightcurve of (127) Johanna in 2009 with the orientation of model 2 for the zero phase. |
 |
Fig. 32 Composite lightcurve of (127) Johanna in 2011 with the orientation of model 2 for the zero phase. |
 |
Fig. 33 Composite lightcurve of (355) Gabriella in 2005/2006 with the orientation of model 2 for the zero phase. |
 |
Fig. 34 Composite lightcurve of (355) Gabriella in 2007 with the orientation of model 2 for the zero phase. |
 |
Fig. 35 Composite lightcurve of (355) Gabriella in 2008 with the orientation of model 2 for the zero phase. |
 |
Fig. 36 Composite lightcurve of (355) Gabriella in 2009/2010 with the orientation of model 2 for the zero phase. |
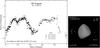 |
Fig. 37 Composite lightcurve of (386) Siegena in 1998 with the orientation of model 2 for the zero phase. |
 |
Fig. 38 Composite lightcurve of (386) Siegena in 1999 with the orientation of model 2 for the zero phase. |
 |
Fig. 39 Composite lightcurve of (386) Siegena in 2002 with the orientation of model 2 for the zero phase. |
 |
Fig. 40 Composite lightcurve of (386) Siegena in 2004 with the orientation of model 2 for the zero phase. |
 |
Fig. 41 Composite lightcurve of (386) Siegena in 2007 with the orientation of model 2 for the zero phase. |
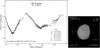 |
Fig. 42 Composite lightcurve of (386) Siegena in 2008 with the orientation of model 2 for the zero phase. |
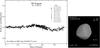 |
Fig. 43 Composite lightcurve of (386) Siegena in 2009 with the orientation of model 2 for the zero phase. |
 |
Fig. 44 Composite lightcurve of (386) Siegena in 2010 with the orientation of model 2 for the zero phase. |
 |
Fig. 45 Composite lightcurve of (417) Suevia in 2001 with the orientation of model 2 for the zero phase. |
 |
Fig. 46 Composite lightcurve of (417) Suevia in 2005 with the orientation of model 2 for the zero phase. |
 |
Fig. 47 Composite lightcurve of (417) Suevia in 2006 with the orientation of model 2 for the zero phase. |
 |
Fig. 48 Composite lightcurve of (417) Suevia in 2008 with the orientation of model 2 for the zero phase. |
 |
Fig. 49 Composite lightcurve of (417) Suevia in 2009 with the orientation of model 2 for the zero phase. |
 |
Fig. 50 Composite lightcurve of (417) Suevia in 2010 with the orientation of model 2 for the zero phase. |
 |
Fig. 51 Composite lightcurve of (435) Ella in 2003 with the orientation of model 1 for the zero phase. |
 |
Fig. 52 Composite lightcurve of (435) Ella in 2004 with the orientation of model 1 for the zero phase. |
 |
Fig. 53 Composite lightcurve of (435) Ella in 2006 with the orientation of model 1 for the zero phase. |
 |
Fig. 54 Composite lightcurve of (435) Ella in 2008 with the orientation of model 1 for the zero phase. |
 |
Fig. 55 Composite lightcurve of (435) Ella in 2009 with the orientation of model 1 for the zero phase. |
 |
Fig. 56 Composite lightcurve of (435) Ella in 2011 with the orientation of model 1 for the zero phase. |
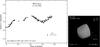 |
Fig. 57 Composite lightcurve of (505) Cava in 1997 with the orientation of model 1 for the zero phase. |
 |
Fig. 58 Composite lightcurve of (505) Cava in 2004/2005 with the orientation of model 1 for the zero phase. |
 |
Fig. 59 Composite lightcurve of (505) Cava in 2006 with the orientation of model 1 for the zero phase. |
 |
Fig. 60 Composite lightcurve of (505) Cava in 2008 with the orientation of model 1 for the zero phase. |
 |
Fig. 61 Composite lightcurve of (505) Cava in 2010 with the orientation of model 1 for the zero phase. |
 |
Fig. 62 Composite lightcurve of (699) Hela in 1999 with the orientation of model 2 for the zero phase. |
 |
Fig. 63 Composite lightcurve of (699) Hela in 2003 with the orientation of model 2 for the zero phase. |
 |
Fig. 64 Composite lightcurve of (699) Hela in 2005 with the orientation of model 2 for the zero phase. |
 |
Fig. 65 Composite lightcurve of (699) Hela in 2007 with the orientation of model 2 for the zero phase. |
 |
Fig. 66 Composite lightcurve of (699) Hela in 2009 with the orientation of model 2 for the zero phase. |
 |
Fig. 67 Composite lightcurve of (699) Hela in 2009/2010 with the orientation of model 2 for the zero phase. |
Data for these properties come from The Small Bodies Node of the NASA Planetary Data System http://pdssbn.astro.umd.edu/), where the diameters and albedoes are mainly from the asteroid catalogue using AKARI Ver. 1.0 (Usui et al. 2011), and the taxonomic classifications are given after Bus & Binzel (2002).
Acknowledgments
We thank Josef Ďurech for useful comments that led to substantial improvement of our service. This work was supported by grant N N203 404139 from the Polish Ministry of Science and Higher Education. The work of TSR was carried out through the Gaia Research for European Astronomy Training (GREAT-ITN) network. He received funding from the European Union Seventh Framework Programme (FP7/2007-2013) under grant agreement No. 264895. This work is partially based on observations made at the South African Astronomical Observatory (SAAO). Part of the data presented here were taken during a summer school organised by the Niels Bohr Institute at the Nordic Optical Telescope in 2008. We use the convex version of the lightcurve inversion code, designed by M. Kaasalainen and modified by J. Ďurech, which is available at http://astro.troja.mff.cuni.cz/projects/asteroids3D.
References
- Armstrong, J. C., Nellermoe, B. L., & Reitzler, L. E. 1996, I.A.P.P.P. Comm., 63, 59 [NASA ADS] [Google Scholar]
- Barucci, M. A., Di Martino, M., & Fulchignoni, M. 1992, AJ, 103, 1679 [NASA ADS] [CrossRef] [Google Scholar]
- Berthier, J., Hestroffer, D., Carry, B., et al. 2008, Asteroids, Comets, Meteors 2008 held July 14 − 18, in Baltimore, Maryland, LPI Contribution No. 1405, id. 8374 [Google Scholar]
- Binzel, R. P. 1987, Icarus, 72, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, C., & Riccioli, D. 1998, A&AS, 131, 385 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bus, S. J., & Binzel, R. P. 2002, Icarus, 158, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Chiorny, V. G., Shevchenko, V. G., Krugly, Yu. N., Velichko, F. P., & Gaftonyuk, N. M. 2003, in Abstracts of Photometry and Polarimetry of Asteroids: Impact on Collaboration, Kharkiv, 9 [Google Scholar]
- Chiorny, V. G., Shevchenko, V. G., Krugly, Yu. N., Velichko, F. P., & Gaftonyuk, N. M. 2007, Planet. Space Sci., 55, 986 [NASA ADS] [CrossRef] [Google Scholar]
- Di Martino, M., Dotto, E., Barucci, M. A., Fulchignoni, M., & Rotundi, A. 1994, Icarus, 109, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, D., Herald, D., Frappa, et al. 2011, Asteroid Occultations V9.0. EAR-A-3-RDR-OCCULTATIONS-V9.0, NASA Planetary Data System, 2011 [Google Scholar]
- Ďurech, J. 2006, IAU 2006, poster paper [Google Scholar]
- Ďurech, J., Kaasalainen, M., Warner, B. D., et al. 2009, A&A, 493, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ďurech, J., Sidorin, V., & Kaasalainen, M. 2010, A&A, 465, 331 [Google Scholar]
- Ďurech, J., Kaasalainen, M., Herald, D., et al. 2011, Icarus, 214, 652 [NASA ADS] [CrossRef] [Google Scholar]
- George, T., Timerson, B., Beard, T., et al. 2011, J. Double Star Obs., 7, 175 [Google Scholar]
- Hanuš, J., Ďurech, J., Brož, M., et al. 2011, A&A, 530, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harris, A. W., & Young, J. W. 1980, Icarus, 43, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., & Young, J. W. 1983, Icarus, 54, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Dockweiler, T., et al. 1992, Icarus, 95, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, A. W., Young, J. W., Bowell, E., & Tholen, D. J. 1999, Icarus, 142, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., & Torppa, J. 2001, Icarus, 153, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Kaasalainen, M., Torppa, J., & Muinonen, K. 2001, Icarus, 153, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kryszczyńska, A., Colas, F., Berthier, J., Michałowski, T., & Pych, W. 1996, Icarus, 124, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Lagerkvist, C.-I. 1978, A&AS, 31, 361 [NASA ADS] [Google Scholar]
- Lagerkvist, C.-I., Hahn, G., Magnusson, P., Rickman, H., & Hammarback, G. 1986, in Asteroids, Comets, Meteors II, eds. C.-I. Lagerkvist, B. A. Lindblad, M. Lundstedt, & H. Rickman, Uppsala, 67 [Google Scholar]
- Lagerkvist, C.-I., Hahn, G., Magnusson, P., & Rickman, H. 1987, A&AS, 70, 21 [NASA ADS] [Google Scholar]
- Marchis, F., Kaasalainen, M., Hom, E. F. Y., et al. 2006, Icarus, 185, 39 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Marciniak, A., Michałowski, T., Polińska, M., et al. 2011, A&A, 529, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, T. 1996, Icarus, 123, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, T., Kwiatkowski, T., Kaasalainen, M., et al. 2004, A&A, 416, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piironen, J., Lagerkvist, C.-I., Erikson, A., et al. 1998, A&AS, 128, 525 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilcher, F. 1983, Minor Planet Bull., 10, 18 [NASA ADS] [Google Scholar]
- Pilcher, F., Warner, B. D., & Goretti, V. 2000, Minor Planet Bull., 27, 56 [NASA ADS] [Google Scholar]
- Shevchenko, V. G., Chiorny, V. G., Gaftonyuk, N. M., et al. 2005, Abstr. IAU Symp., 229, 133 [Google Scholar]
- Shevchenko, V. G., Chiorny, V. G., Gaftonyuk, M., et al. 2008, Icarus, 196, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, R. D. 2005, Minor Planet Bull., 32, 2 [Google Scholar]
- Stephens, R. D. 2007, Minor Planet Bull., 34, 64 [Google Scholar]
- Stephens, R. D., & Warner, B. D. 2008, Minor Planet Bull., 35, 84 [Google Scholar]
- Szabo, Gy. M., Csak, B., Sarneczky, K., & Kiss, L. L. 2001, A&A, 375, 285 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tedesco, E. F., Noah, P. V., Noah, M., & Price, S. D. 2004, IRAS Minor Planet Survey, IRAS-A-FPA-3-RDR-IMPS-V6.0, NASA Planetary Data System, 2004 [Google Scholar]
- Timerson, B., Ďurech, J., Aguirre, S., et al. 2009, Minor Planet Bull., 36, 98 [Google Scholar]
- Toth, I. 1997, Planet. Space Sci., 45, 1625 [NASA ADS] [CrossRef] [Google Scholar]
- Usui, F., Kuroda, D., Mueller, T., et al. 2011, Pub. Astron. Soc. Japan, 63, 1117 [CrossRef] [Google Scholar]
- Warner, B. D., Harris, A. W., & Pravec, P. 2009, Icarus, 202, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Young, J., & Harris, A. W. 1985, Icarus, 64, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Zappala, V., Scaltriti, F., Lagerkvist, C.-I., Rickman, H., & Harris, A. W. 1982, Icarus, 52, 196 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Equivalent sphere diameters based on fitting to occultation chords (D), compared to their IRAS (DIRAS) and AKARI (DAKARI) values.
All Figures
 |
Fig. 1 Observed lightcurves (points) superimposed on the model lightcurves (lines) at the same epochs for (76) Freia. The overall root mean square (rms) residual of the fit was 0.0120 mag. |
| In the text | |
 |
Fig. 2 Convex shape model “2” of (76) Freia, shown at equatorial viewing and illumination geometry, with rotational phases 90° apart (two pictures on the left), and the pole-on view at the right. The reflectivity law is artificial, to reveal the shape details. |
| In the text | |
 |
Fig. 3 Observed vs. modelled lightcurves for (127) Johanna. The rms residual of the fit was 0.0127 mag. |
| In the text | |
 |
Fig. 4 Shape model “2” of (127) Johanna. |
| In the text | |
 |
Fig. 5 Observed vs. modelled lightcurves for (355) Gabriella. The rms residual of the fit was 0.0226 mag. |
| In the text | |
 |
Fig. 6 Shape model “2” of (355) Gabriella. |
| In the text | |
 |
Fig. 7 Observed vs. modelled lightcurves for (386) Siegena. The rms residual of the fit was 0.0083 mag. |
| In the text | |
 |
Fig. 8 Shape model “2” of (386) Siegena. |
| In the text | |
 |
Fig. 9 Observed vs. modelled lightcurves for (417) Suevia. The rms residual of the fit was 0.0165 mag. |
| In the text | |
 |
Fig. 10 Shape model “2” of (417) Suevia. |
| In the text | |
 |
Fig. 11 Observed vs. modelled lightcurves for (435) Ella. The rms residual of the fit was 0.0153 mag. |
| In the text | |
 |
Fig. 12 Shape model “1” of (435) Ella. |
| In the text | |
 |
Fig. 13 Observed vs. modelled lightcurves for (505) Cava. The rms residual of the fit was 0.0122 mag. |
| In the text | |
 |
Fig. 14 Shape model “1” of (505) Cava. |
| In the text | |
 |
Fig. 15 Observed vs. modelled lightcurves for (699) Hela. The rms residual of the fit was 0.0287 mag. |
| In the text | |
 |
Fig. 16 Shape model “2” of (699) Hela. |
| In the text | |
 |
Fig. 17 Occultation chords with both scaled shape models for asteroid (76) Freia. Two occultation events. |
| In the text | |
 |
Fig. 18 Occultation chords with both scaled shape models for asteroid (386) Siegena. Two occultation events. |
| In the text | |
 |
Fig. 19 Occultation chords with both scaled shape models for asteroid (127) Johanna. |
| In the text | |
 |
Fig. 20 Example view of the “orientation” mode of the ISAM service. One of our earlier models is displayed. |
| In the text | |
 |
Fig. 21 Composite lightcurve of (76) Freia in 2002 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 22 Composite lightcurve of (76) Freia in 2006 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 23 Composite lightcurve of (76) Freia in 2007/2008 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 24 Composite lightcurve of (76) Freia in 2009 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 25 Composite lightcurve of (76) Freia in 2010 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 26 Composite lightcurve of (127) Johanna in 2000 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 27 Composite lightcurve of (127) Johanna in 2002 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 28 Composite lightcurve of (127) Johanna in 2005/2006 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 29 Composite lightcurve of (127) Johanna in 2007 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 30 Composite lightcurve of (127) Johanna in 2008 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 31 Composite lightcurve of (127) Johanna in 2009 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 32 Composite lightcurve of (127) Johanna in 2011 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 33 Composite lightcurve of (355) Gabriella in 2005/2006 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 34 Composite lightcurve of (355) Gabriella in 2007 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 35 Composite lightcurve of (355) Gabriella in 2008 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 36 Composite lightcurve of (355) Gabriella in 2009/2010 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 37 Composite lightcurve of (386) Siegena in 1998 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 38 Composite lightcurve of (386) Siegena in 1999 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 39 Composite lightcurve of (386) Siegena in 2002 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 40 Composite lightcurve of (386) Siegena in 2004 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 41 Composite lightcurve of (386) Siegena in 2007 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 42 Composite lightcurve of (386) Siegena in 2008 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 43 Composite lightcurve of (386) Siegena in 2009 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 44 Composite lightcurve of (386) Siegena in 2010 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 45 Composite lightcurve of (417) Suevia in 2001 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 46 Composite lightcurve of (417) Suevia in 2005 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 47 Composite lightcurve of (417) Suevia in 2006 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 48 Composite lightcurve of (417) Suevia in 2008 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 49 Composite lightcurve of (417) Suevia in 2009 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 50 Composite lightcurve of (417) Suevia in 2010 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 51 Composite lightcurve of (435) Ella in 2003 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 52 Composite lightcurve of (435) Ella in 2004 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 53 Composite lightcurve of (435) Ella in 2006 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 54 Composite lightcurve of (435) Ella in 2008 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 55 Composite lightcurve of (435) Ella in 2009 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 56 Composite lightcurve of (435) Ella in 2011 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 57 Composite lightcurve of (505) Cava in 1997 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 58 Composite lightcurve of (505) Cava in 2004/2005 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 59 Composite lightcurve of (505) Cava in 2006 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 60 Composite lightcurve of (505) Cava in 2008 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 61 Composite lightcurve of (505) Cava in 2010 with the orientation of model 1 for the zero phase. |
| In the text | |
 |
Fig. 62 Composite lightcurve of (699) Hela in 1999 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 63 Composite lightcurve of (699) Hela in 2003 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 64 Composite lightcurve of (699) Hela in 2005 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 65 Composite lightcurve of (699) Hela in 2007 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 66 Composite lightcurve of (699) Hela in 2009 with the orientation of model 2 for the zero phase. |
| In the text | |
 |
Fig. 67 Composite lightcurve of (699) Hela in 2009/2010 with the orientation of model 2 for the zero phase. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


