EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 545 (September 2012) A&A, 545 (2012) A52 Full HTML
Free Access
Issue
A&A
Volume 545, September 2012
Article Number A52
Number of page(s) 7
Section The Sun
DOI https://doi.org/10.1051/0004-6361/201219404
Published online 05 September 2012

© ESO, 2012

1. Introduction

Ever since Hyder (1965) advocated the use of the Hanle effect as a magnetic field diagnostic in astrophysics, it has proven to be invaluable especially in the study of solar prominences (Bommier et al. 1994, and references therein). Owing to its sensitivity to even relatively weak fields of a few G for various optically thin coronal UV lines, it could become very important for coronal magnetic-field diagnostics.

This paper is the fourth in a series devoted to the investigation of the diagnostic content of optically thin resonantly scattered coronal UV lines after a line-of-sight (LOS) integration. In the first paper, Khan et al. (2011, Paper 1), we investigated the consequences of three polarimetrically active agents on the linear polarisation parameters for the first three lines of the Lyman series, i.e., magnetic fields, non-radial outflow velocities, and active regions on the solar surface, using a self-consistent, 2.5-dimensional, magnetohydrodynamics (MHD), global coronal model with a solar minimum-like magnetic-field topology, i.e. a global dipole field directed along the Sun’s polar regions with a current-sheet-like structure in the equatorial plane, and strengths that lie in the realistic range of a few G. In the second paper, Khan & Landi Degl’Innocenti (2011, Paper 2), we focussed on the symmetry aspects inherent to the linear polarisation parameters due to active regions of the Lα line, using a spherically symmetric coronal thermodynamic model. In the third paper, Khan & Landi Degl’Innocenti (2012, Paper 3), we investigated the signatures of anisotropic velocity-distribution functions for the same coronal model used in paper 1, for the two most promising coronal UV lines, i.e., the Lα and the O vi lines.

There is, unfortunately, only one single linear polarisation measurement for UV coronal lines that one can compare forward modelling results to, namely the 1032 Å O vi line detected by the Solar Ultraviolet Measurements of Emitted Radiation (SUMER) instrument operating aboard the SOlar and Heliospheric Observatory (SOHO) spacecraft (Wilhelm et al. 1995, 1997; Lemaire et al. 1997). Hassler et al. (1997) provide a description of the pre-launch calibration of the polarimetric sensitivity. For a point located on the southern solar polar axis at 0.29 R⊙ above the photosphere, the measured degree of linear polarisation was 9 ± 2% and the rotation angle of the direction of linear polarisation with respect to the tangent to the closest solar limb was found to be 9° ± 6°, (Raouafi et al. 1999; Raouafi et al. 2002a). In Raouafi et al. (2002a) and Raouafi et al. (2002b), the authors interpreted the measurements in terms of either the Hanle effect or non-radial outflows, or both, and in Raouafi & Solanki (2003) the authors even included anisotropic velocity-distribution functions. In their interesting preliminary investigations, however, the effect of the LOS integration was not taken into account, which is one of the goals of the present paper, i.e., to use the self-consistent 2.5-D, MHD global coronal model from Paper 1 for the O vi line to see whether it is possible to reproduce the results obtained by SUMER/SOHO.

It is well-known, and amply demonstrated in our previous papers that vertical fields in the plane of the sky, magnetic or velocity, do not have any effect on the polarisation parameters1. How is it then that one can measure a rotation of the plane of linear polarisation right above the solar pole where both magnetic and velocity fields are thought to be vertical at solar minimum conditions? At the time of the SUMER measurements (March 1996), it was known that the Sun’s polar axis was tilted by  ~7° as seen from the earth. To accommodate the measured values, we add this “new” agent capable of altering the polarimetric landscape to those previously studied, i.e., the rotation of the solar axis. This creates non-vertical fields right above the Sun in the plane of the sky, and the present investigation is dedicated to the exploration of subsets of parameter space to infer the possible values of the plasma parameters. In this study, we assume the incident radiation field to be cylindrically symmetric about the vertical axis from the centre of the Sun through the scattering point. An additional way of introducing asymmetries into the profiles could be by considering the angular dependences of the incoming radiation field, i.e., the limb-brightening function, as done in Raouafi et al. (2002a).

It must be stressed, however, that the spectropolarimetric forward modelling procedure presented here, i.e., the realistic synthesis of the Stokes parameters of the emergent coronal emission in the O vi line and subsequent comparison with the observed values, is obstructed by there only being one measurement for one LOS. In Paper 3, we showed how important it is to have measurements from as extensive a portion of the sky as possible to be able to infer the plasma parameters correctly, and must therefore conclude preliminarily that one measurement only constitutes an aid in understanding their possible ranges.

In spite of only having this one measurement, it is indeed very interesting to note how the measured value to some extent points us towards the conditions of the physical environment in which it originated. The tilt of the solar polar axis is virtually compulsory owing to the measured rotation of the plane of linear polarisation, and is a positive finding for the advent of inversion algorithms in that one can hope that future observations will assist the forward modeller in choosing where and how to search parameter spaces’ complicated maze of ambiguity.

2. Results

In Sects. 2 and 3 of Paper 3, we presented the coronal and atomic models, and showed the most important formulae for the resonance scattering of O5+ ions in the presence of the Sun’s pumping anisotropic radiation field with and without anisotropic velocity-distribution functions, and isotropic electronic collisions. To give the reader an idea of what life is like for a typical O5+ ion in the plane of the sky at 1.29 R⊙, we made Table 1, in which we display the most important plasma parameters after the solar axis had been tilted 7°.

Our coordinate system (x,y,z) has its origin at the centre of the Sun. The y axis is directed in the observer-Sun direction, while the z axis lies in the plane of the sky, and is directed such that the (y,z) plane contains the Sun’s rotation axis and points towards the solar north pole. The x axis is also in the plane of the sky and directed in a manner that (x,y,z) forms a right-handed coordinate system. The coordinates are expressed in units of solar radii, R⊙ = 6.9626 × 105 km. The “observations” are made around the Sun in an equidistant rectangular grid ranging from ±2 R⊙ in the plane of the sky and ± ~7   R⊙ along the LOS. Through trial and error, we found that there were no changes up to the fourth significant figure in the four Stokes emission coefficients if the step size of the numerical integration was 0.03 R⊙ along the LOS.

Table 1

Plasma parameters in the plane of the sky at 1.29 R⊙ along the vertical axis as given by the model of Wang et al. (1993).

2.1. The Hanle effect with and without tilting the solar polar axis by 7°

thumbnail Fig. 1

The rotation angle for the Hanle effect in a static atmosphere (upper left graph, 1a), the Hanle effect with the solar outflow (upper right graph, 1b), and the same two cases repeated after a tilt of the solar rotation axis by 7°, lower left, 1c), and lower right, 1d).

thumbnail Fig. 2

The rotation angle and fractional linear polarisation as a function of the tilt-angle, δ.

It has been known for almost a century that a magnetic field in resonance scattering simultaneously both modifies the degree of linear polarisation and rotates the plane of linear polarisation in a way that depends non-linearly on its strength and orientation (Hanle 1924; Mitchell & Zemanski 1934). These effects are best analysed by defining the rotation angle, Dα, as the difference, measured counter-clockwise in degrees, of the polarisation angle, α, given by tan(2α) = U/Q, with respect to the parallel to the solar limb2. In Fig. 1a, we show the results of resonance scattering in the sole presence of the magnetic field as given by the coronal model of Wang et al. (1993) for a static atmosphere. The rotations are left/right antisymmetric with respect to the (y,z) plane and are found in close proximity to the photosphere to the right and left of the poles, and amount to roughly a tenth of a degree. We note also that the Hanle effect vanishes along the poles. In Fig. 1b, we add the effect of the solar outflow, and see the emergence of the “arm” structure delineating the region where magnetic field lines go from being open to closed. The rotations are an order of magnitude more pronounced than for the Hanle effect, and effectively eclipse the rotations of the latter. In Figs. 1c–d, we show the same results after a tilt of the rotation axis by 7° towards the observer. Since we are only interested in the region above the pole, we chose to show only a restricted part of the plane of the sky3.

As can be seen in Table 1, the tilting of the solar rotation axis has the interesting effect of creating slightly non-radial fields, of both the magnetic field and velocity, that scatter electromagnetic radiation differently from radial ones. In the lower left figure, the appearance of a component of the magnetic field along the y axis has the effect of breaking the left/right antisymmetry, which can be understood along the lines of the symmetry operations defined in Sect. 3 of Paper 2. The rotations range from  ~–1° to 0°4. In Fig. 1d, we add the effect of the solar outflow, which restores some of the left/right antisymmetry and changes the rotations from −1.55° to 0°. At 1.29 R⊙ along the z axis, the rotation amounts to −0.66°. These are interesting findings in that they point us towards the measured values, although there still is an order of magnitude difference.

In an attempt to come closer to the observed values, in Figs. 2 we investigate how the tilt affects the rotation of the plane of both linear polarisation and fractional linear polarisation exclusively at 1.29 R⊙ along the z axis. We display the rotation and the fractional linear polarisation defined as 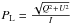, where I = (I,Q,U,V)T is the usual Stokes vector, after a LOS integration, as a function of the tilt angle, δ.

The rotation angle is approximately a linear function of the tilt angle, with Dα ~−2° for δ = 25°. The fractional linear polarisation goes from  ~0.44% to  ~0.47% for the same range of angles, meaning that neither observable can be explained by realistic variations in the tilt around 7°. We note that tilt angles much beyond δ ~ 7° are highly hypothetical, and are shown only to indicate the trend in the polarimetric response. For δ > 7°, the plasma parameters most probably do not reflect actual conditions at solar minimum.

In summary, by tilting the solar rotation axis, we have taken a step in the right direction towards reproducing the observed rotation angle and fractional linear polarisation. We are, however, still roughly an order of magnitude off in both observables. In our quest for alignment between our forward modelling efforts and observation, in the following we continue to use the MHD model by Wang et al. (1993), but increase the magnetic field intensity and the solar outflow at will, i.e., in a non-self-consistent fashion, while leaving the basic structure of the corona unaltered, i.e., all the angles, magnetic and velocity, are the same as before.

thumbnail Fig. 3

The rotation angle and fractional linear polarisation as a function of the solar outflow for an isotropic velocity-distribution function of the O5+ ions (solid lines), for anisotropic velocity-distribution functions (w⊥/w∥ = 2, dotted lines), (w⊥/w∥ = 1/2, broken lines). The perpendicular and parallel velocity-distribution functions are proportional to the local thermal velocity of the O5+ ions, i.e., .

2.2. The O5+ preferential heating, preferential acceleration, and anisotropic velocity-distribution functions

In all the following subsections, we leave the tilt of the solar axis at its measured value of 7°, and deal exclusively only with the LOS for which we have observations, that is, at 1.29 R⊙ along the z axis.

Our Paper 3 on the spectropolarimetric signatures of anisotropic velocity-distribution functions was inspired by the analyses of the Ultraviolet Coronagraph Spectrometer (UVCS) data, which concluded that there must be both intense preferential heating and preferential acceleration of O5+ ions, in comparison to hydrogen atoms, and a strong field-aligned anisotropy, possibly with a higher kinetic temperature in the direction perpendicular to the magnetic field than in the parallel direction, above  ~2.1 R⊙. Below  ~2 R⊙, the observations are consistent with an isotropic velocity distribution (Kohl et al. 1997; Li et al. 1998; Cranmer et al. 1999; Antonucci et al. 2000; Cranmer et al. 2008). We are well aware that the “extrapolation” of the UVCS data to heights as low as 1.29 R⊙ is almost rude, and certainly motivated more by our curiosity to see how preferential heating, preferential acceleration, and anisotropic velocity distributions all affect the polarisation parameters, than hard scientific fact. It must not be forgotten, however, that we do integrate along the LOS, and that these effects should be felt by the scattering atoms as we move along the LOS.

In Fig. 3, we show the rotation angle and fractional linear polarisation as a function of the solar outflow (preferential acceleration) for an isotropic velocity-distribution function of the O5+ ions (solid lines), and anisotropic velocity-distribution functions (w⊥/w∥ = 2, dotted lines), (w⊥/w∥ = 1/2, broken lines). The perpendicular and parallel velocity-distribution functions are proportional to the local thermal velocity of the O5+ ions, i.e., . We did not try to select “realistic” values for the anisotropy, but simply a “prudential” factor of 2, and tested the effects of both senses of anisotropy, even though the UVCS data favours w⊥ over w∥, i.e., w⊥ > w∥.

In terms of the rotation angle, both the isotropic and anisotropic (w⊥ = 2w, and w∥ = w, with ) cases give values that correspond to the upper boundary of the measurement plus an uncertainty of  ~–3° at roughly six to seven times the nominal value of the solar outflow as given by the Wang et al. (1993) model. For the reversed anisotropy, i.e. w⊥ = w, and w∥ = 2w, with , this value is reached at about thirteen times the nominal outflow values, which could mean that the field aligned anisotropy with the higher kinetic temperature in the direction perpendicular to the magnetic field is to be favoured over the one parallel to the field, as most analyses of the UVCS data have suggested. The rotation angle saturates at −5°, meaning that preferential heating with what we believe are realistic anisotropies (w⊥, w∥ ≤ 2w) in 1.29 R⊙ along the z axis are not enough to explain the observed values plus uncertainties. The fractional linear polarisation decreases drastically as we increase the solar outflow owing to the Doppler dimming effect. The collisional component is not Doppler dimmed and this quenches the linear polarisation. Judging by the trend shown in Fig. 3b, it would seem that outflow velocities of more than five times the nominal velocity, corresponding to roughly 100 km s-1, should be ruled out.

2.3. The O5+ preferential heating, preferential acceleration, anisotropic velocity-distribution functions, and increased magnetic-field intensity

thumbnail Fig. 4

The rotation angle and fractional linear polarisation as a function of the magnetic field in the presence of preferential acceleration. The higher the solar outflow, the more the plane of linear polarisation rotates. The upper curves (full lines) are reference cases for the normal solar outflows given by the model of Wang et al. (1993), the ones below (dotted curves) have their outflow velocity multiplied by two, the broken lines have their outflow velocities multiplied by three, the dot-line-dot curves have their outflow multiplied by four, and the lowest curves (three dots and one line) have the nominal value of the solar outflow multiplied by a factor of five.

thumbnail Fig. 5

The rotation angle and fractional linear polarisation as a function of the magnetic field in the presence of anisotropic velocity-distribution functions with and without preferential acceleration. The full lines are the reference cases (solar outflow as given by the model by Wang et al. (1993), and an isotropic velocity-distribution function). The dotted curves have w⊥/w∥ = 2, while the broken lines have w⊥/w∥ = 1/2 with the usual outflow velocities. The curves with dots and lines have w⊥/w∥ = 2, while the ones with three dots and one line have w⊥/w∥ = 1/2 in the presence of slight preferential acceleration, i.e., twice as high a solar-outflow velocity of  ~43 km s-1.

In this subsection, we investigate whether the full range of measurements plus uncertainties can be modelled by increasing the magnetic field intensity. We first add preferential acceleration and then anisotropic velocity-distribution functions, and in the end combine the two effects. The magnetic field intensity used in Wang et al. (1993) is prudentially low, amounting to roughly 3 G at 1.29 R⊙ along the z axis. In Fig. 4, we analyse the linear polarisation parameters as a function of the magnetic field intensity for five different higher values of the solar outflow. The basic structure of the corona remains the same, i.e., all angles maintain their previous values, and we merely increase the intensity of the fields. The chosen ranges are from one to twenty-five times the nominal magnetic field, whereas the range of the velocity field is from one to five times the nominal values. The general trend is as expected, i.e., the greatest absolute rotations for a given magnetic-field intensity are achieved by the highest outflow velocities. All curves, however, saturate at roughly fifteen times the nominal value of the magnetic field strength, which is  ~45 G. The linear polarisation on the other hand decreases as a function of the solar outflow (Doppler dimming), while showing little sensitivity to the magnetic field intensity, since the component of the magnetic field along the LOS remains relatively small for the range of magnetic field intensities used here. To reach the lower limit of the observed rotation plus uncertainty (− 15°), we had to increase the magnetic field intensity by a factor of at least fifteen, and the solar outflow by a factor of roughly five, while the upper limit was reached at all the parametrised velocities for magnetic field increases by factors of 2–6.

There is no empirical data for the magnetic flux intensity at 1.29 R⊙ in a polar coronal hole at solar minimum conditions. This circumstance makes it difficult to assess what a “realistic” range of field strengths could be. A spectropolarimetric measurement using Zeeman magnetometry by Lin et al. (2004) found a LOS coronal magnetic field at 1.1 R⊙ above an active region to have a flux density of about 4 G. This value is very much in line with many other estimates shown in Fig. 5 of Peter et al. (2012), and we therefore do not expect the flux density to be more than at most two or three times the nominal values given by our coronal model, i.e.,  ≲ 10 G. We note, however, that the only way of reproducing the full range of measurements plus uncertainties found by SUMER/SOHO, is by increasing the flux to the values cited in the previous paragraph.

In Fig. 5, we show the combined effect of weak preferential acceleration in the presence of anisotropic velocity-distribution functions as a function of the magnetic field intensity. The solid curve is the reference case, where the solar outflow is given by the model of Wang et al. (1993), and an isotropic velocity-distribution function. The dotted curves have w⊥/w∥ = 2, while the broken lines have w⊥/w∥ = 1/2 with the usual outflow velocities. In this case of higher magnetic field strength, we have an inversion of the trend compared to the case of no increase in the field, i.e., the w⊥/w∥ = 1/2 anisotropy is more likely than the w⊥/w∥ = 2 case to create greater absolute rotations. This trend is maintained even in the presence of slight preferential acceleration. The curves with dots and lines have w⊥/w∥ = 2, while those with three dots and one line have w⊥/w∥ = 1/2 in the presence of slight preferential acceleration, i.e., twice as high a solar outflow velocity of  ~43 km s-1.

The degree of linear polarisation remains an order of magnitude below the observed values, and depends as expected more on the amount of preferential acceleration through Doppler dimming than on the sense of the anisotropy.

2.4. The incident chromospheric intensity, the electronic temperature, the collision rate, the number density of O5+ ions, and the electronic density

Inspection of the equations of resonance scattering in the presence of collisions leads us to examine an additional four parameters that can influence the linear polarisation parameters, namely (1) the incident chromospheric intensity in the O vi line; (2) the electronic temperature entering the expressions of both the local thermal velocity, w, and the collision rate, αc; (3) the number density of O5+ ions in the lower level; and finally (4) the electronic density, ne.

From the definition of the rotation angle, we can see that it is independent of realistic changes in any one of the four aforementioned parameters. Atomic polarisation, hence the ability of the ions to emit polarised radiation, strongly depends on both the intensity and the anisotropy of the incoming radiation field, as well as the electronic density. It is, however, almost independent of realistic changes in both the temperature, the collision rate, and the number density of O5+ ions.

To test how sensitive PL is to differences in the chromospheric intensity, we increased it by 50%, which increased PL from 0.43% to 0.64%, while an increase in the intensity by 100% increases PL to 0.85%. The trend is very clear, i.e., the more intense the incoming radiation, the higher the value of PL. Realistic changes in the incoming intensity are, however, hardly more than ±10%, and are thus unable to bring the modelled PL into accord with the observed one.

The most sensitive parameter for PL is the electronic density. In Table 2, we display the electron densities found from various models in 1.29 R⊙ above the photosphere along the solar axis. It is striking that the values used by Raouafi et al. (2002a) are an order of magnitude smaller than those due to any of the other models. In Fig. 6, we show PL as a function of the electronic density, in units of the density given by the model of Wang et al. (1993). To stay within the uncertainty limits of the observed values, i.e., 9 ± 2%, the density must lie in the narrow range from 0.01 to 0.03 times its actual value.

The electronic density in the solar corona is determined by measuring the linear polarisation due to Thomson-scattered white light from the photosphere (Minnaert 1930, van de Hulst 1950). Cranmer et al. (1999) discusses three possible explanations of the seemingly high UVCS coronal-hole densities at low heights, i.e., non-K-corona polarisation, LOS contamination, and epochal variations. One cannot help but wonder how it is that there can be such a large discrepancy between the inferred electronic density and the range of densities that one needs to achieve agreement with the observed PL. This remains an unresolved problem that will probably only be settled when one can determine both PL and ne from measurements done at the same time and for the same region of the sky.

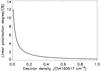thumbnail Fig. 6

PL as a function of the electronic density in units of the density given by the model of Wang et al. (1993) at 1.29 R⊙ above the solar pole.

Table 2

Electronic densities at 1.29 R⊙.

3. Conclusions

The objective of this paper has been to test to what extent spectropolarimetry could be used to provide more stringent bounds on vital coronal plasma parameters. We performed a forward modelling of the coronal emission coefficients in the four Stokes parameters of the optically thin 1032 Å O vi line for varying subsets of the ten parameters, (ne, nO5+, αc, Ichr, T, B, v, w⊥, w∥, δ) i.e., the number density of electrons and O5+ ions, respectively, the electronic collision rate, the chromospheric intensity in the O vi line, the electronic temperature, the magnetic and solar outflow velocity vectors, the perpendicular and parallel (with respect to the magnetic field) parameters of the anisotropic velocity-distribution functions, and finally the tilt of the solar rotation axis. We searched parameter space in a non-rigorous fashion to determine whether it was possible to reach agreement between the modelled and the observed values, i.e., the rotation angle, Dα, defined as the difference, measured counter-clockwise in degrees, of the polarisation angle, α, given by tan(2α) = U/Q, with respect to the parallel to the solar limb, and the fractional linear polarisation, PL, defined as 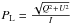, where I = (I,Q,U,V)T is the usual Stokes vector after a LOS integration. The coronal model used is a self-consistent, 2.5-D, MHD, global coronal model with a solar minimum-like magnetic-field topology, i.e. a global dipole field directed along the Sun’s polar regions with a current-sheet-like structure in the equatorial plane, and strengths that lie in the realistic range of a few Gauss.

From the definition of α, we see that it is independent, or almost independent of (ne, nO5+, αc, Ichr,T), while it is heavily dependent on (B, v, w⊥, w∥,δ). On the other hand, PL shows little dependence on realistic variations in (nO5+, αc, Ichr,T,B), but does strongly depend on (ne, v) along the only LOS for which we have measurements, i.e., at 1.29 R⊙ along the z axis.

At the time of the measurements (March 1996), the solar rotation axis tilt, δ, was 7°. In Fig. 1, we show graphs of the rotation angle for the Hanle effect with and without the solar outflow for δ = 0° and δ = 7°. The velocity distribution functions for the electrons and the O5+ ions were assumed to be isotropic. The tilting of the solar rotation axis creates non-radial fields in the plane of the sky above the Sun and rotates the linear polarisation in a way that differs drastically form the non-tilted case. At 1.29 R⊙ along the z axis, Dα = −0.66°, and thus far from the measured value of −9° ± 6°. The fractional linear polarisation is  ~0.43%, and therefore differs by more than an order of magnitude from the measured value of 9%  ±  2%.

In Fig. 2, we showed how the two linear polarisation parameters behave as a function of the tilt-angle, δ. Even for δ = 25°, Dα is only roughly -2°, while PL goes from 0.43% to 0.47%.

In Fig. 3, we investigated the effect of the preferential acceleration of the O5+ ions in the presence of isotropic and anisotropic velocity-distribution functions. On the basis of PL, the Doppler dimming effect seems to set some limits on the amount of preferential acceleration that is permitted. We found that values of more than five times the nominal solar outflow gave too low values of PL, and should be excluded. The rotation angles for both the isotropic and the anisotropic cases with w⊥ = 2w, and w∥ = w, where , barely coincide with the upper uncertainty limit to the measured rotation. The inverse anisotropy, i.e., w⊥ = w, and w∥ = 2w, needs much greater outflows to reach same rotations which could mean that the field aligned anisotropy with a higher kinetic temperature in the direction perpendicular to the magnetic field is more likely than the one parallel to the field, as most analyses of the UVCS data have suggested.

In Figs. 4 and 5, we showed the rotation angle and the fractional linear polarisation as a function of increasing magnetic field strength in the case of preferential acceleration with and without anisotropic velocity-distribution functions. The higher the solar outflow velocities and magnetic field strengths, the more compatible the rotations are with the measured values. If we increase the solar outflow by a factor of five, and the nominal magnetic-field strength by factors of 3–15, we recover the measured values to within the uncertainties. Increasing the nominal magnetic field from three to fifteen times corresponds to field strength ranges of roughly 9–45 G. Most realistic estimates of the flux intensity at 1.29 R⊙ do not exceed  ~10 G, and the sober conclusion is therefore that the rotations measured by SUMER/SOHO are to be found in the lower absolute limit to possible values of roughly 3°. In contrast, PL remains an order of magnitude below the observed value, and is very sensitive to the solar outflow owing to the Doppler dimming effect, but almost insensitive to the magnetic field coordinates5.

Finally, in Fig. 6 we explored the acceptable electronic density range in units of the value found at 1.29 R⊙ in the plane of the sky above the Sun based on the Wang et al. (1993) model. One needs density ranges that are 1–2 orders of magnitude below the actual value in order to reproduce the measured PL. The explanation for this discrepancy remains unclear, and will probably only be solved by new simultaneous measurements of both ne and PL.

With this paper, we have introduced another polarimetrically active agent capable of modifying the linear polarisation parameters that we have studied, thus enlarging the parameter space by one dimension. We note that after tilting the solar rotation axis by 7°, the previously rather uninteresting area above the Sun’s poles from the polarimetric point of view has now become

highly “active” owing to the non-radial fields of both magnetic and velocity, preferential acceleration, and isotropic/anisotropic velocity-distribution functions, and that now rotation angles of 9° ± 6° seem less intractable than before.

It is likewise very interesting to see how the measurement of in particular the rotation angle almost compels the solar tilt to occur. Without it, we are simply otherwise unable to create non-radial fields and thus modifications to the linear polarisation. This bodes well for spectropolarimetry because it shows that the very observations that one hopes to be able to forward model could contain in them information about how and where to start searching the possibly terribly complicated maze of parameter space.

1

As one moves away from the plane of the sky along a given LOS, the fields become non-vertical, yet due to the symmetry in the coronal fore and background of the MHD model, this effect is not seen.

2

In absence of symmetry breaking agents such as magnetic fields, non-radial outflows etc., the polarisation angle is always parallel to the nearest solar limb, i.e. Dα = 0.

3

The solar south pole is identical to the figure shown except for the sense of rotation, which is inverted.

4

Owing to the definition of our coordinate system and the sense of rotation of δ, the measured values of the rotation angle to be emulated are −9° ± 6°.

5

PL is in general strongly dependent on the magnetic coordinates, yet due to the particular location of the LOS for which we have observations, the predominantly radial field neither de- nor hyperpolarises.

Acknowledgments

The author wishes to thank E. Landi Degl’Innocenti, S. Fineschi, and M. Romoli for many helpful discussions. This work was possible thanks to a grant from the Italian Space Agency (ASI).

References

  1. Antonucci, E., Dodero, M. A., & Giordano, S. 2000, Sol. Phys., 197, 115 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bommier, V., Landi Degl’Innocenti, E., Leroy, J. C., & Sahal-Bréchot, S. 1994, Sol. Phys., 154, 231 [NASA ADS] [CrossRef] [Google Scholar]
  3. Cranmer, S. R., Kohl, J. L., & Noci, G., et al. 1999, ApJ, 511, 481 [NASA ADS] [CrossRef] [Google Scholar]
  4. Cranmer, S. R., Panasyuk, A. V., & Kohl, J. L. 2008, ApJ, 678, 1480 [NASA ADS] [CrossRef] [Google Scholar]
  5. Fineschi, S. 2001, ASP Conf. Ser., 248, 597 [NASA ADS] [Google Scholar]
  6. Hanle, W. 1924, Z. Phys., 30, 93 [Google Scholar]
  7. Hassler, D. M., Lemaire, L., & Longval, Y. 1997, Appl. Opt., 36, 353 [NASA ADS] [CrossRef] [Google Scholar]
  8. Hyder, C. L. 1965, ApJ, 141, 1374 [NASA ADS] [CrossRef] [Google Scholar]
  9. Khan, A., & Landi Degl’Innocenti, E. 2011, A&A, 532, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Khan, A., & Landi Degl’Innocenti, 2012, A&A, 543, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Khan, A., Belluzzi, L., Landi Degl’ Innocenti, E., Fineschi, S., & Romoli, M. 2011, A&A, 529, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Kohl, J. L., Noci, G., Antonucci, E., et al. 1997, Sol. Phys., 175, 613 [NASA ADS] [CrossRef] [Google Scholar]
  13. Kohl, J. L., Noci, G., Antonucci, E., et al. 1998, ApJ, 501, 127 [Google Scholar]
  14. Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in Spectral Lines (Dordrecht: Kluwer) (LL04) [Google Scholar]
  15. Lemaire, P., Wilhelm, K., Curdt, W., et al. 1997, Sol. Phys., 170, 105 [NASA ADS] [CrossRef] [Google Scholar]
  16. Lemaire, P., Emerich, C., Vial, J. C., et al. 2005, Adv. Space Res., 35, 384 [NASA ADS] [CrossRef] [Google Scholar]
  17. Li, X., Habbal, S. R., Kohl, J. L., & Noci, G. 1998, ApJ, 501, 133 [Google Scholar]
  18. Lin, H., Kuhn, J. R., & Coulter, R. 2004, ApJ, 613, 177 [Google Scholar]
  19. Minnaert, M. 1930, Z. Astrophys., 1, 209 [NASA ADS] [Google Scholar]
  20. Mitchell, A. C. G., & Zemanski, M. W. 1934, Resonance Radiation and Exited Atoms (Cambridge Univ. Press) [Google Scholar]
  21. Peter, H., Abbo, L., Andretta, V., et al. 2012, Exp. Astron., 33, 271 [Google Scholar]
  22. Raouafi, N. E., & Solanki, S. K. 2003, A&A, 412, 271 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Raouafi, N. E., Lemaire, P., & Sahal-Bréchot, S. 1999, A&A, 345, 999 [NASA ADS] [Google Scholar]
  24. Raouafi, N. E., Sahal-Bréchot, L. P., & Bommier, V. 2002a, A&A, 390, 691 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Raouafi, N. E., Sahal-Bréchot, P., & Lemaire, P. 2002b, A&A, 396, 1019 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Raymond, J. C., Kohl, J. L., Noci, G., et al. 1997, Sol. Phys., 175, 645 [NASA ADS] [CrossRef] [Google Scholar]
  27. Sahal-Bréchot, S., Malinovski, M., & Bommier, V. 1986, A&A, 168, 284 [NASA ADS] [Google Scholar]
  28. Sahal-Bréchot, S., Bommier, V., & Feautrier, N. 1998, A&A, 340, 579 [NASA ADS] [Google Scholar]
  29. van de Hulst, H. C. 1950, Bull. Astron. Inst. Netherlands, 11, 135 [Google Scholar]
  30. Wang, A. H., Wu, T. S., Suess, S. T., & Poletto, G. 1993, Sol. Phys., 147, 55 [NASA ADS] [CrossRef] [Google Scholar]
  31. Wilhelm, K., Curdt, W., Marsch, E., et al. 1995, Sol. Phys., 162, 189 [NASA ADS] [CrossRef] [Google Scholar]
  32. Wilhelm, K., Lemaire, P., Curdt, W., et al. 1997, Sol. Phys., 170, 75 [NASA ADS] [CrossRef] [Google Scholar]
  33. Withbroe, G. L., Kohl, J. L., Weiser, H., Noci, G., & Munro, R. H. 1982, ApJ, 254, 361 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Plasma parameters in the plane of the sky at 1.29 R⊙ along the vertical axis as given by the model of Wang et al. (1993).

In the text
Table 2

Electronic densities at 1.29 R⊙.

In the text

All Figures

thumbnail Fig. 1

The rotation angle for the Hanle effect in a static atmosphere (upper left graph, 1a), the Hanle effect with the solar outflow (upper right graph, 1b), and the same two cases repeated after a tilt of the solar rotation axis by 7°, lower left, 1c), and lower right, 1d).
In the text
thumbnail Fig. 2

The rotation angle and fractional linear polarisation as a function of the tilt-angle, δ.
In the text
thumbnail Fig. 3

The rotation angle and fractional linear polarisation as a function of the solar outflow for an isotropic velocity-distribution function of the O5+ ions (solid lines), for anisotropic velocity-distribution functions (w⊥/w∥ = 2, dotted lines), (w⊥/w∥ = 1/2, broken lines). The perpendicular and parallel velocity-distribution functions are proportional to the local thermal velocity of the O5+ ions, i.e., .
In the text
thumbnail Fig. 4

The rotation angle and fractional linear polarisation as a function of the magnetic field in the presence of preferential acceleration. The higher the solar outflow, the more the plane of linear polarisation rotates. The upper curves (full lines) are reference cases for the normal solar outflows given by the model of Wang et al. (1993), the ones below (dotted curves) have their outflow velocity multiplied by two, the broken lines have their outflow velocities multiplied by three, the dot-line-dot curves have their outflow multiplied by four, and the lowest curves (three dots and one line) have the nominal value of the solar outflow multiplied by a factor of five.
In the text
thumbnail Fig. 5

The rotation angle and fractional linear polarisation as a function of the magnetic field in the presence of anisotropic velocity-distribution functions with and without preferential acceleration. The full lines are the reference cases (solar outflow as given by the model by Wang et al. (1993), and an isotropic velocity-distribution function). The dotted curves have w⊥/w∥ = 2, while the broken lines have w⊥/w∥ = 1/2 with the usual outflow velocities. The curves with dots and lines have w⊥/w∥ = 2, while the ones with three dots and one line have w⊥/w∥ = 1/2 in the presence of slight preferential acceleration, i.e., twice as high a solar-outflow velocity of  ~43 km s-1.
In the text
thumbnail Fig. 6

PL as a function of the electronic density in units of the density given by the model of Wang et al. (1993) at 1.29 R⊙ above the solar pole.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.