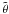Bayesian analysis of exoplanet and binary orbits - Demonstrated using astrometric and radial-velocity data of Mizar A

T. Schulze-Hartung; R. Launhardt; T. Henning

doi:10.1051/0004-6361/201219074

Home

All issues

Volume 545 (September 2012)

A&A, 545 (2012) A79

Full HTML

Free Access

Issue		A&A Volume 545, September 2012


Article Number		A79
Number of page(s)		19
Section		Numerical methods and codes
DOI		https://doi.org/10.1051/0004-6361/201219074
Published online		11 September 2012

A&A 545, A79 (2012)

Bayesian analysis of exoplanet and binary orbits^⋆

Demonstrated using astrometric and radial-velocity data of Mizar A

T. Schulze-Hartung, R. Launhardt and T. Henning

Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: schulze@mpia.de

Received: 20 February 2012
Accepted: 12 July 2012

Abstract

Aims. We introduce BASE (Bayesian astrometric and spectroscopic exoplanet detection and characterisation tool), a novel program for the combined or separate Bayesian analysis of astrometric and radial-velocity measurements of potential exoplanet hosts and binary stars. The capabilities of BASE are demonstrated using all publicly available data of the binary Mizar A.

Methods. With the Bayesian approach to data analysis we can incorporate prior knowledge and draw extensive posterior inferences about model parameters and derived quantities. This was implemented in BASE by Markov chain Monte Carlo (MCMC) sampling, using a combination of the Metropolis-Hastings, hit-and-run, and parallel-tempering algorithms to explore the whole parameter space. Nonconvergence to the posterior was tested by means of the Gelman-Rubin statistic (potential scale reduction). The samples were used directly and transformed into marginal densities by means of kernel density estimation, a “smooth” alternative to histograms. We derived the relevant observable models from Newton’s law of gravitation, showing that the motion of Earth and the target can be neglected.

Results. With our methods we can provide more detailed information about the parameters than a frequentist analysis does. Still, a comparison with the Mizar A literature shows that both approaches are compatible within the uncertainties.

Conclusions. We show that the Bayesian approach to inference has been implemented successfully in BASE, a flexible tool for analysing astrometric and radial-velocity data.

Key words: astrometry / celestial mechanics / methods: data analysis / methods: statistical / techniques: interferometric / techniques: radial velocities

^⋆

BASE, the computer program introduced in this article, can be downloaded at http://www.mpia.de/homes/schulze/base.html.

© ESO, 2012

1. Introduction

The search for extrasolar planets – places where one day humankind might find other forms of life in the Universe – has been a subject of scientific investigation since the nineteenth century, but only became successful in 1992 with the first confirmed discovery of an exoplanet orbiting the pulsar PSR B1257+12 (Wolszczan & Frail 1992). Still, because it is situated in an environment hostile to life as we know it, this case has been of less relevance to the public than the first detection of a Sun-like planet-host star, 51 Pegasi (Mayor & Queloz 1995). Since that time, more than 700 extrasolar planet candidates have been unveiled in more than 500 systems, more than 90 of which show signs of multiplicity (Schneider 2012).

Closely related to the detection of extrasolar planets is the characterisation of their orbits. Both these tasks now profit from the existence of a variety of observational techniques, which we briefly sketch in the following. Comprehensive reviews can be found in Perryman (2000) and Deeg et al. (2007).

Direct observational methods refer to the imaging of exoplanets (e.g. Levine et al. 2009), which reflect the light of their host stars but also emit their own thermal radiation. To overcome the major obstacle of the high brightness contrast between planet and star, techniques such as coronagraphy (Lyot 1932; Levine et al. 2009), angular differential imaging (Marois et al. 2006; Vigan et al. 2010), spectral differential imaging (Smith 1987; Vigan et al. 2010), and polarimetric differential imaging (Kuhn et al. 2001; Adamson et al. 2005) have been invented. Still, imaging has only revealed few detections and orbit determinations so far.

The most productive methods in terms of the number of detected and characterised exoplanets are of an indirect nature, observing the effects of the planet on other objects or their radiation.

Of these, transit photometry (e.g. Charbonneau et al. 2000; Seager 2008) is noteworthy because it has helped uncover more than 200 exoplanet candidates, plus over 2000 still unconfirmed candidates from the Kepler space mission (Koch et al. 2010): small decreases in the apparent visual brightness of a star during the primary or secondary eclipse point to the existence of a transiting companion. These data allow one to determine the planet’s radius and orbital inclination and may also yield information on the planet’s own radiation.

Timing methods include measurements of transit timing variations (TTV) and transit duration variations (TDV) (e.g. Holman & Murray 2005; Nascimbeni et al. 2011) of either binaries or stars known to harbour a transiting planet. The method used in the first exoplanet detection (Wolszczan & Frail 1992) is pulsar timing, which relies on slight anomalies in the exact timing of the radio emission of a pulsar and is sensitive to planets in the Earth-mass regime.

Microlensing (Mao & Paczynski 1991; Gould 2009), which accounted for about 15 exoplanet candidates, uses the relativistic curvature of spacetime due to the masses of both a lens star and its potential companion, with the latter causing a change in the apparent magnification and thus the observed brightness of a background source.

Perhaps the most well-known technique, and one of those on which this article is based, is known as Doppler spectroscopy or radial-velocity (RV) measurements (e.g. Mayor & Queloz 1995; Lovis & Fischer 2010). With more than 500 exoplanet candidates, it has been most successful in detecting new exoplanets and determining their orbits to date. From a set of high-resolution spectra of the target star, a time series of the line-of-sight velocity component of the star is deduced. These data allow one to determine the orbit in terms of its geometry and kinematics in the orbital plane as well as the minimum planet mass m_p,min ≈ m_psini. To derive the actual planet mass m_p, the inclination i of the orbit plane with respect to the sky plane needs to be derived with a different method, e.g. astrometry. The RV technique is distance-independent by principle, but signal-to-noise requirements do pose constraints on the maximum distance to a star. Stellar variability sometimes makes this approach difficult because it alters the line shapes and thus mimicks RV variations. The signal in stellar RVs caused by a planet in a circular orbit has a semi-amplitude of approximately 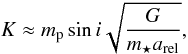$K \approx m_{p} \sin i \sqrt{\frac{G}{m_{⋆} a_{rel}}},$ $\begin{equation} \PMK \approx \PMmP\sin\PMi\sqrt{\frac{G}{\PMmS \PMaRel}},\label{eq_RV_semiamp_general} \end{equation}$ (1)where m_p,m_⋆,i,G, and a_rel are the masses of planet and host star, the orbital inclination, Newton’s gravitational constant, and the semi-major axis of the planet’s orbit relative to the star, respectively. This approximation holds for m_p ≪ m_⋆, which is true in most cases. It should be noted that the sensitivity of the RV method decreases towards less inclined (more face-on) orbits, which is an example for the selection effects inherent to any planet-detection method.

Finally, astrometry (AM; e.g. Gatewood et al. 1980; Sozzetti 2005; Reffert 2009) – on which this work is also based – is the oldest observational technique known in astronomy: a stellar position is measured with reference to a given point and direction on sky. Astrometry can thus be considered as complementary to Doppler spectroscopy, which measures the kinematics perpendicular to the sky plane. In contrast to the latter, AM allows one to determine the orientation of the orbital plane relative to the sky in terms of its inclination i and the position angle Ω of the line of nodes with respect to the meridian of the target. A planet in circular orbit around its host star displaces the latter on sky with an approximate angular semi-amplitude of 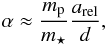$α \approx \frac{m_{p}}{m_{⋆}} \frac{a_{rel}}{d},$ $\begin{equation} \alpha \approx \frac{\PMmP}{\PMmS}\frac{\PMaRel}{\PMd},\label{eq_AM_semiamp_general} \end{equation}$ (2)where d is the distance between the star and the observer. Again, this approximation holds for m_p ≪ m_⋆.

Imaging astrometry, in its attempt to reach sufficient presicion, still faces problems due to various distortion effects. By contrast, interferometric astrometry has been used to determine the orbits of previously known exoplanets, mainly with the help of space-borne telescopes such as Hipparcos or the Hubble Space Telescope (HST), which presently still excel their Earth-bound competitors (e.g. McArthur et al. 2010). However, instruments like PRIMA (Delplancke et al. 2000; Delplancke 2008; Launhardt et al. 2008) or GRAVITY (Gillessen et al. 2010) at the ESO Very Large Telescope Interferometer are promising to advance ground-based AM even more in the near future.

While planet-induced signals in AM and RVs are both approximately linear in planetary mass m_p, they differ in their dependence on the orbital semi-major axis a_rel (Eqs. (1) and (2)). Doppler spectroscopy is more sensitive to smaller orbits (or higher orbital frequencies, Eq. (45)), while AM favours larger orbital separations, viz. longer periods.

In this article we introduce BASE, a Bayesian astrometric and spectroscopic exoplanet detection and characterisation tool. Its goals are to fulfil two major tasks of exoplanet science, namely the detection of exoplanets and the characterisation of their orbits. BASE has been developed to provide for the first time the possibility of an integrated Bayesian analysis of stellar astrometric and Doppler-spectroscopic measurements with respect to their companions’ signals¹, correctly treating the measurement uncertainties and allowing one to explore the whole parameter space without the need for informative prior constraints. Still, users may readily incorporate prior knowledge, e.g. from previous analyses with other tools, by means of priors on the model parameters. The tool automatically diagnoses convergence of its Markov chain Monte Carlo (MCMC) sampler to the posterior and regularly outputs status information. For orbit characterisation, BASE delivers important results such as the probability densities and correlations of model parameters and derived quantities.

Because published high-precision AM observations of potential exoplanet host stars are still sparse, we used data of the well-known binary Mizar A to demonstrate the capabilities of BASE. It is also planned to gain astrophysical insights into exoplanet systems using BASE in the near future.

This article is organised as follows. Section 2 provides an overview of the most often-used methods of data analysis, including Bayes’ theorem and MCMC as theoretical and implementational foundations of this work, as well as a derivation of the necessary observable models. BASE is described in Sect. 3. In Sect. 4, the target Mizar A and the data used in this article are discussed. Section 5 presents and discusses our analysis of Mizar A. Conclusions are drawn in Sect. 6.

2. Methods and models

Data analysis is a type of inductive reasoning in that it infers general rules from specific observational data (e.g. Gregory 2005b). These general rules are described by observable models, simply called models in the following, which produce theoretical values of the observables as a function of parameters. The primary tasks of data analysis are listed in the following.

1.
In model selection, the relative probabilities of a set ofconcurrent models {ℳ_i}, chosen a priori, are assessed. Specifically, exoplanet detection tries to decide the question of whether a certain star is accompanied by a planet or not, based on available data. Additionally, model-assessment techniques can be used to determine whether the most probable model describes the data accurately enough.
2.
Parameter estimation aims to determine the parameters θ of a chosen model. This is specifically referred to as exoplanet characterisation (or orbit determination) in the present context.
3.
The purpose of uncertainty estimation is to provide a measure of the parameters’ uncertainties.

Although model selection is equally important, in what follows we focus entirely on the second and third tasks, viz. parameter and uncertainty estimation. This is because for a known binary system, only one model is appropriate, viz. two bodies orbiting each other. Accordingly, BASE can only perform model selection when it analyses data from stars for which it is a-priori unknown whether a companion exists.

2.1. Likelihoods and frequentist inference

The well-established, conventional frequentist approach to inference is touched upon only briefly here. Its name stems from the fact that it defines probability as the relative frequency of an event. Measurements are regarded as values of random variables drawn from an underlying population that is characterised by population parameters, e.g. mean and standard deviation in the case of a normal (Gaussian) population. In the following, we derive the joint probability density of the values of AM and RV data, known as the likelihood ℒ, which plays a central role in frequentist inference.

When combining data of different types, one should generally be aware that potential systematic errors may differ between the data sets, e.g. due to a calibration error in one instrument that renders the data inconsistent with each other. In this case, each data set analysed separately would imply a different result. In other instances, systematic errors in one set do not affect the other data: for example, any constant offset in radial velocity is absorbed into parameter V, which is irrelevant to the analysis of astrometric data. In the following derivation, we assumed that no systematic effects are present that led to inconsistent data.

In the following, we assumed that the error ϵ_i of any datum y_i is statistically independent of those of all other data and consists of two components, each distributed according to a (uni- or bivariate) normal distribution with zero mean:

a component ϵ_0,i corresponding to a nominal measurement error, whose distribution is characterised by the covariance matrix E_0,i or standard deviation σ_0,i given with the datum, for AM and RV data respectively, and
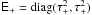a component ϵ_+ ,i representing e.g. instrumental, atmospheric or stellar effects not modelled otherwise, whose distribution is characterised by scalar covariance matrix $E_{+} = diag (τ_{+}^{2}, τ_{+}^{2})$ $\hbox{$\dataCovMAdd = \mathrm{diag}(\PMtauP^2,\PMtauP^2)$}$ – assuming no correlation between the noise in the two AM components – or variance $σ_{+}^{2}$ $\hbox{$\PMsgmP^2$}$ , respectively, where τ₊ and σ₊ are free noise-model parameters.

The AM data covariance matrix E_0,i of datum i, representing the uncertainty of and correlation between the two components measured, can be written using singular-value decomposition as 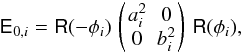$E_{0,i} = R (- φ_{i}) (\begin{matrix} a_{i}^{2} & 0 \\ 0 & b_{i}^{2} \end{matrix}) R (φ_{i}),$ $\begin{equation} \dataCovMNomi{i} = \rotmi{-\UNCERTELLphi_i}\,\pmatrxii{ a_i^2 & 0\\ 0 & b_i^2 }\,\rotmi{\UNCERTELLphi_i},\label{eq_data_cov_matrix} \end{equation}$ (3)where R(·),a_i,b_i and φ_i are the 2 × 2 passive rotation matrix, the nominal semi-major and -minor axes of the uncertainty ellipse and the position angle of its major axis, respectively.

Using characteristic functions, it is readily shown that the sum ϵ_i = ϵ_0,i + ϵ_+ ,i of the two independent error components is again normally distributed, with zero mean and covariance matrix E_i = E_0,i + E₊ or standard deviation , respectively.

The probability density² of the values of N_AM two-dimensional AM data 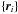${r i}$ $\hbox{$\seti{\vr_i}$}$ and N_RV RV data {v_i}, known as the likelihood ℒ, is then given by $ℒ = ℒ_{AM} ℒ_{RV},$ $\begin{equation} \likhood = \likhood\iAM\,\likhood\iRV, \end{equation}$ (4)where ℒ_AM and ℒ_RV are the likelihoods pertaining to the individual data types, $\begin{matrix} ℒ_{AM} & = & {((2 π)^{N_{AM}} 􏽙_{i = 1}^{N_{AM}} \sqrt{\begin{matrix} \det \end{matrix} E_{i}})}^{-1} \exp (- \frac{1}{2} χ_{AM}^{2}), \\ ℒ_{RV} & = & {((2 π)^{\frac{N_{RV}}{2}} 􏽙_{i = 1}^{N_{RV}} σ_{i})}^{-1} \exp (- \frac{1}{2} χ_{RV}^{2}) . 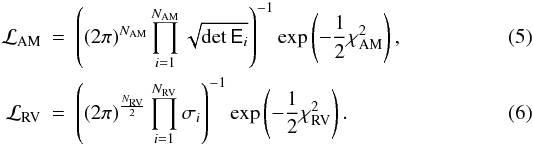\end{matrix}$ $\begin{eqnarray} \likhood\iAM &=& \left((2\pi)^{N\iAM}\prod_{i=1}^{N\iAM}\sqrt{\det \dataCovM_i}\right)\inv \exp\left(-\oneHalf\chi^2\iAM\right),\\ \likhood\iRV &=& \left((2\pi)^{\frac{N\iRV}{2}}\prod_{i=1}^{N\iRV}\measUncToti{i}\right)\inv \exp\left(-\oneHalf\chi^2\iRV\right). 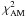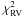\end{eqnarray}$ Furthermore, the sums of squares $χ_{AM}^{2}$ $\hbox{$\chi^2\iAM$}$ and $χ_{RV}^{2}$ $\hbox{$\chi^2\iRV$}$ are defined by 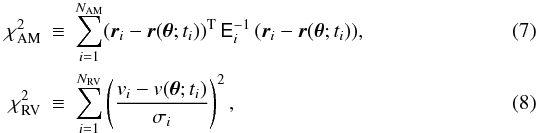$\begin{matrix} χ_{AM}^{2} & \equiv & \sum_{i = 1}^{N_{AM}} (r i - r (θ; t_{i}))^{T} E_{i}^{-1} (r i - r (θ; t_{i})), \\ χ_{RV}^{2} & \equiv & \sum_{i = 1}^{N_{RV}} {(\frac{v_{i} - v (θ; t_{i})}{σ_{i}})}^{2}, \end{matrix}$ $\begin{eqnarray} \label{eqchisqAM} \chi^2\iAM &\defby& \sum_{i=1}^{N\iAM} (\vr_i-\mdlFctAM{\vPar}{\tm_i})\transp\,\dataCovM_i\inv\,(\vr_i-\mdlFctAM{\vPar}{\tm_i}),\\ \label{eqchisqRV} \chi^2\iRV &\defby& \sum_{i=1}^{N\iRV} \left(\frac{\RV_i-\mdlFctRV{\vPar}{\tm_i}}{\measUncToti{i}}\right)^2, \end{eqnarray}$ where r_i,v_i are the ith AM and RV datum, r(·;·),v(·;·) the AM and RV model functions and θ is the vector of model parameters. The relevant models are derived in Sect. 2.3.

Parameter estimation.

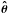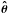Frequentist parameter estimation is generally equivalent to maximising ℒ or minimising χ² as functions of θ. The resulting best estimates of the parameters $\hbox{$\vHPar$}$ are therefore often called maximum-likelihood or least-squares estimates. For linear models, χ²(θ) is a quadratic function and consequently $\hbox{$\vHPar$}$ can be found unambiguously by matrix inversion. In the more realistic cases of nonlinear models, however, χ² may have many local minima, therefore care needs to be taken not to mistake a local minimum for the global one. Several methods exist to this end, including evaluation of χ²(θ) on a finite grid, simulated annealing or genetic algorithms (e.g. Gregory 2005b).

Uncertainty estimation.

Frequentist parameter uncertainties are usually quoted as confidence intervals. Procedures to derive these are designed such that when repeated many times based on different data, a certain fraction of the resulting intervals will contain the true parameters. Popular methods use bootstrapping (Efron & Tibshirani 1993) or the Fischer information matrix, which is based on a local linearisation of the model (e.g. Ford 2004). However, these methods suffer from specific caveats: the Fischer matrix is only appropriate for a quadratic-shaped χ² in the vicinity of the minimum, and bootstrapping, which relies on modified data, may lead to severe misestimation of the parameter uncertainties, especially when these are large (Vogt et al. 2005).

2.2. Bayesian inference

Bayesian inference (e.g. Sivia 2006), which has gained popularity in various scientific disciplines during the past few decades, defines probability as the degree of belief in a certain hypothesis ℋ. While this is sometimes criticised as leading to subjective assignments of probabilities, Bayesian probabilities are not subjective if they are based on all relevant knowledge 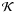$\hbox{$\I$}$ , hence different people having the same knowledge will assign them the same value (e.g. Sivia 2006). Thus, Bayesian probabilities are conditional on the knowledge 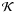$\hbox{$\I$}$ , and this conditionality should be stated explicitly, as in the following equations.

2.2.1. Bayes’ theorem

In the eighteenth century, Thomas Bayes laid the foundation of a new approach to inference with what is now known as Bayes’ theorem (Bayes & Price 1763). For the purpose of parameter and uncertainty estimation, the hypothesis ℋ refers to the values of model parameters θ, and Bayes’ theorem can be expressed as 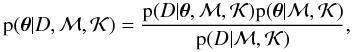$p (θ | D, ℳ, 𝒦) = \frac{p (D | θ, ℳ, 𝒦) p (θ | ℳ, 𝒦)}{p (D | ℳ, 𝒦)},$ $\begin{equation} \pPostr{\vPar} = \frac{\pLikh{\Data}{\vPar}\pPri{\vPar}}{\pEv{\Data}},\label{eq_bayes_theorem_param_est} \end{equation}$ (9)where p(·) is a probability (density). Furthermore, D ≡ {(t_i,y_i)} is the set of pairs of observational times³ and corresponding data values, and ℳ denotes the particular model assumed. 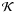As mentioned above, all probabilities are also conditional on the knowledge $\hbox{$\I$}$ , including statements on the types of parameters and the parameter space Θ (which we assume to be a subset of R^k with k ∈ N) as well as the noise model.

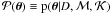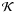Using Bayes’ theorem, the aim is to determine the posterior $\hbox{$\postr(\vPar) \defby \pPostr{\vPar}$}$ , i.e. the probability distribution of the parameters θ in light of the data D, given the model ℳ and prior knowledge $\hbox{$\I$}$ . The other terms, located on the right-hand side of the theorem, are explained below.

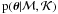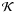The term prior refers to the probability distribution $\hbox{$\pPri{\vPar}$}$ of the parameters θ given only the model and prior knowledge $\hbox{$\I$}$ ; it characterises the knowledge about the parameters present before considering the data. For objective choices of priors, based on classes of parameters, see Sect. A.
The likelihood 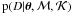$\hbox{$\pLikh{\Data}{\vPar}$}$ is the probability distribution of the data values D, given the times of observation, the model and the parameters. It is introduced in the context of frequentist inference in Sect. 2.1.
The evidence is the probability distribution of the data values D, given the times of observation and the model but neglecting the parameter values, 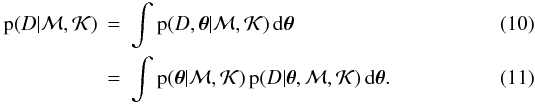$\begin{matrix} p (D | ℳ, 𝒦) & = & \int p (D, θ | ℳ, 𝒦) d θ \\ = & \int p (θ | ℳ, 𝒦) p (D | θ, ℳ, 𝒦) d θ . \end{matrix}$ $\begin{eqnarray} \label{eq_evidence} \pEv{\Data} &= &\int\p(\Data,\vPar|\mdl,\I)\ddd\vPar\\ &=& \int\pPri{\vPar}\,\pLikh{\Data}{\vPar}\ddd\vPar. \end{eqnarray}$ It equals the integral of the product of prior and likelihood over the parameter space Θ and plays the role of a normalising constant, which is hard to calculate in practice, however.

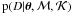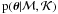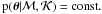It may be instructive here to note that the frequentist approach of maximising the likelihood $\hbox{$\pLikh{\Data}{\vPar}$}$ is equivalent to maximising the posterior when assuming uniform priors $\hbox{$\pPri{\vPar}$}$ . This can be seen by inserting $\hbox{$\pPri{\vPar} = \const$}$ into Eq. (9), which leads to 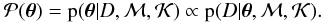$𝒫 (θ) = p (θ | D, ℳ, 𝒦) \propto p (D | θ, ℳ, 𝒦) .$ $\begin{equation} \postr(\vPar) = \pPostr{\vPar} \propto \pLikh{\Data}{\vPar}. \end{equation}$ (12)However, this maximum-likelihood approach ignores the fact that uniform priors are not always the most objective choice (see Appendix A) and the posterior cannot be fully characterised just by the position of its maximum. Still, the latter can be used as a posterior summary in the Bayesian framework (Sect. 2.2.2).

2.2.2. Posterior inference

Sampling from the posterior.

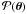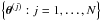To estimate the normalised posterior $\hbox{$\postr(\vPar)$}$ , i.e. the probability distribution of the parameters θ in light of the data, N samples of the parameter vector ${θ (j) : j = 1, ..., N^{}}$ $\hbox{$\left\{\vPar\samp:\iSamp=1,\ldots,\nSamp\right\}$}$ are collected using the Markov chain Monte Carlo method (MCMC; e.g. Gilks et al. 1996) in the variant described by the Metropolis-Hastings algorithm (MH; Metropolis et al. 1953; Hastings 1970), which performs a random walk through parameter space. 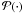The distribution of these samples – excluding the first M < N burn-in samples, which are still strongly correlated with the starting state θ⁽⁰⁾ – converges to the posterior $\hbox{$\postr(\cdot)$}$ in the limit of many samples if the chain obeys certain regularity conditions (e.g. Roberts 1996). Methods for setting the starting state θ⁽⁰⁾ and detecting convergence are described in Sect. 3.4.

Starting from the current chain link θ^(j + 1) ∈ Θ, the following steps lead to the next link, according to the MH algorithm and the hit-and-run sampler (step 1; Boneh & Golan 1979; Smith 1980):

1.
Set up a candidate C:
- (a)
  sample a direction, viz. a random unit vector d ∈ R^k from an isotropic density over the k-dimensional unit sphere;
- (b)
  sample a (signed) distance r from a uniform distribution over the interval { r′ ∈ R:θ^(j) + r′d ∈ Θ } ;
- (c)
  set candidate C ≡ θ^(j) + rd;
2.
calculate the acceptance probability $α (θ (j), C) \equiv \begin{matrix} \min \end{matrix} (1, \frac{𝒫 (C)}{𝒫 (θ (j))});$ $\begin{equation} \accProb{\vPar\samp}{\vect C} \defby \min\left(1,\frac{\postr(\vect C)}{\postr(\vPar\samp)}\right); \end{equation}$ (13)
3.
draw a random number β from a uniform distribution over the interval [0,1] ;
4.
if β ≤ α, accept the candidate, i.e. set the next link θ^(j + 1) ≡ C; otherwise, θ^(j + 1) ≡ θ^(j).

The hit-and-run sampler, compared to alternatives like the Gibbs sampler (Geman & Geman 1984), favours exploring of the whole parameter space Θ without becoming “trapped” in the vicinity of a local posterior maximum (Gilks et al. 1996).

Because only the ratio of two posterior values is used (step 2), the normalising evidence 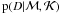$\hbox{$\pEv{\Data}$}$ – a constant that is difficult to determine, as mentioned above – is irrelevant in the MH algorithm.

Marginalisation and density estimation.

Obviously, the posterior mode alone reveals only one particular aspect of the posterior. However, as a density over k > 2 dimensions, the posterior cannot be displayed unambiguously in a figure.

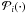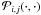To obtain a plottable summary of the posterior, a set of marginal posteriors $\hbox{$\mapo{i}{\cdot}$}$ , i.e. probability densities over each of the parameters θ_i, and joint marginal posteriors $\hbox{$\jointmapo{i}{j}{\cdot}{\cdot}$}$ over two parameters, can be estimated. Theoretically, these densities are derived from the posterior density by marginalisation, viz. 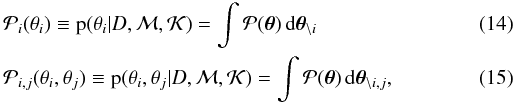integration over all other parameters, $\begin{matrix} 𝒫_{i} (θ_{i}) \equiv p (θ_{i} | D, ℳ, 𝒦) = \int 𝒫 (θ) d θ \ i \\ 𝒫_{i,j} (θ_{i}, θ_{j}) \equiv p (θ_{i}, θ_{j} | D, ℳ, 𝒦) = \int 𝒫 (θ) d θ \ i,j, \end{matrix}$ $\begin{eqnarray} \label{eq_def_mapo} &&\mapo{i}{\param_i} \defby \pPostr{\param_i} = \int\postr(\vPar)\ddd\vPar_{\backslash i} \\ \label{eq_def_JMP} &&\jointmapo{i}{j}{\param_i}{\param_j} \defby \pPostr{\param_i,\param_j} = \int\postr(\vPar)\ddd\vPar_{\backslash i,j}, \end{eqnarray}$ where $\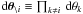hbox{$\ddd\vPar_{\backslash i} \defby \prod_{k\neq i}\ddd\param_k$}$ and $\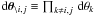hbox{$\ddd\vPar_{\backslash i,j} \defby \prod_{k\neq i,j}\ddd\param_k$}$ . 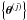Practically, marginal posteriors are estimated by only considering component i of the collected samples ${θ {(j)}^{}}$ $\hbox{$\seti{\vPar\samp}$}$ and performing a density estimation based on them. Joint marginal posteriors are derived analogously, based on components i and j.

Several density estimators exist for deriving a density from a set of samples. One of them – the oldest and probably most popular type, known as the histogram – has several drawbacks: its shape depends on the choice of origin and bin width, and when used with two-dimensional data, a contour diagram cannot easily be derived from it. Generalising the histogram to kernel density estimation over one or two dimensions, the samples can be represented more accurately and unequivocally (Silverman 1986).

Below, we refer only to the simpler one-dimensional case. There, the kernel estimator can be written as 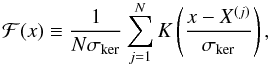$ℱ (x) \equiv \frac{1}{N σ_{\ker}} \sum_{j = 1}^{N} K (\frac{x - X^{(j)}}{σ_{\ker}}),$ $\begin{equation} \kerEst(x) \defby \frac{1}{\nSamp\winWidth}\sum_{\iSamp=1}^{\nSamp}\kr\left(\frac{x-X\samp}{\winWidth}\right), \end{equation}$ (16)where x is a scalar variable, K(·) the kernel, σ_ker the window width and X^(j) are the underlying samples. As detailed by Silverman (1986), the efficiency of various kernels in terms of the achievable mean integrated square error is very similar, and therefore the choice of kernel can be based on other requirements. 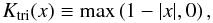Since no differentiability is required for the estimated densities and computational effort plays an important practical role, a triangular kernel, $K_{tri} (x) \equiv \begin{matrix} \max \end{matrix} (1 - | x |, 0),$ $\begin{equation} \kr_{\mathrm{tri}}(x) \defby \max\left(1-|x|,0\right), \end{equation}$ (17)was selected for estimating the marginal posteriors. 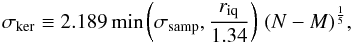The window width is chosen following the recommendations of Silverman (1986), $σ_{\ker} \equiv 2.189 \begin{matrix} \min \end{matrix} (σ_{samp}, \frac{r_{iq}}{1.34}) (N - M)^{\frac{1}{5}},$ $\begin{equation} \winWidth \defby 2.189\min\left(\sampStdDev,\frac{\interQuartRge}{1.34}\right)\,(\nSamp-\nSampBurn)^{\frac{1}{5}},\label{eq_def_KDE_win_width} \end{equation}$ (18)where σ_samp,r_iq,N and M are the sample standard deviation, the interquartile range of the samples, number of samples and burn-in length, respectively.

Periodogram mode.

By default, the window width for marginal posteriors is based on the MCMC sample standard deviation σ_samp (Eq. (18)). If there are multiple maxima, however, this can lead to artificially broad peaks, which can be particularly problematic for the orbital frequency f (see Sect. 2.3), which plays an important role in distinguishing different solutions in orbit-related parameter estimation. Therefore, BASE includes a periodogram mode, in which the window width of the marginal posterior of f (a Bayesian analogon to the frequentist periodogram) is reduced according the following procedure.

1.
Initially assume a default window width as given byEq. (18);
2.
estimate the marginal posterior of f and find its local maximum f_max nearest to posterior mode 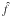$\hbox{$\md\PMf$}$ , as well as the local minimum f_min nearest to f_max;
3.
calculate the marginal-posterior standard deviation σ′ over the half-peak between f_max and f_min;
4.
re-calculate the window width using Eq. (18), with 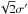$\sqrt{2} σ^{'}$ $\hbox{$\sqrt{2}\sampStdDevPer$}$ replacing σ_samp;
5.
repeat step 2, but only consider local minima with ordinates 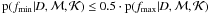$\hbox{$\pPostr{\PMf_\TMin} \leq 0.5\cdot\pPostr{\PMf_\TMax}$}$ in order not to be misled by weak marginal-posterior fluctuations;
6.
repeat steps 3 and 4.

Table 1

Model parameters used by BASE.

Table 2

Quantities derived from model parameters.

Parameter estimation.

To obtain a single most probable estimate of the parameters, the posterior density 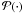$\hbox{$\postr(\cdot)$}$ can be summarised by the posterior mode 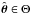$\hat{θ} \in Θ$ $\hbox{$\md\vPar\in\parSpace$}$ , i.e. the point where the posterior assumes its maximum value, 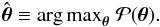$\hat{θ} \equiv {\arg \begin{matrix} \max \end{matrix}}_{θ} 𝒫 (θ) .$ $\begin{equation} \md\vPar \defby {\arg\max}_{\vPar}\;\postr(\vPar). 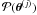\end{equation}$ (19)This point, also known as the maximum a-posteriori (MAP) parameter estimate, can be approximated by the MCMC sample with highest posterior density, based on the values of $\hbox{$\postr(\vPar\samp)$}$ already calculated during sampling. This approximation neglects the finite spacing between samples.

Alternatively, the following scalar summaries can be inferred from the samples or, for the marginal mode, from the marginal posteriors 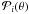$\hbox{$\mapo{i}{\param}$}$ :

mean or expectation $\hbox{$\mn\param$}$ , $θ̅ \equiv \int_{- \infty}^{\infty} θ 𝒫_{i} (θ) d θ,$ $\begin{equation} \mn\param \defby \int_{-\infty}^{\infty} \param\,\postr_i(\param)\ddd\param, \end{equation}$ (20)
median $\begin{matrix} ˜ \\ θ \end{matrix}$ $\hbox{$\med\param$}$ , $\int_{- \infty}^{\begin{matrix} ˜ \\ θ \end{matrix}} 𝒫_{i} (θ) d θ \equiv 0.5,$ $\begin{equation} \int_{-\infty}^{\med\param} \postr_i(\param)\ddd\param \defby 0.5, \end{equation}$ (21)
marginal mode $\begin{matrix} ˇ \\ θ \end{matrix}$ $\hbox{$\margMd\param$}$ , $\begin{matrix} ˇ \\ θ \end{matrix} \equiv {\arg \begin{matrix} \max \end{matrix}}_{θ} 𝒫_{i} (θ) .$ $\begin{equation} \margMd\param \defby {\arg\max}_\param\;\postr_i(\param). \end{equation}$ (22)

Uncertainty estimation.

For uncertainty estimation, highest posterior-density intervals (HPDIs) can be derived from the posterior samples. For any given C ∈ R with 0 < C < 1, a HPDI I_HPD ≡ [a,b] is defined as the smallest interval over which the posterior contains a probability C, 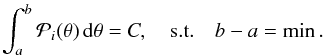$\int_{a}^{b} 𝒫_{i} (θ) d θ = C, s . t . b - a = \begin{matrix} \min \end{matrix} .$ $\begin{equation} \int_a^b\postr_i(\param)\ddd\param = \probCont, \quad\mathrm{s.t.}\quad b-a=\min. \end{equation}$ (23)BASE automatically calculates HPDIs of probability contents 50%, 68.27%, 95%, 95.45%, 99%, and 99.73%; others may be added on user request.

In contrast to frequentist confidence intervals, HPDIs are generally not symmetric, meaning that their midpoint does not correspond to the best estimate. This is because the marginal posteriors may be asymmetric, including any amount of skew.

It should also be noted that HPDIs are not useful with multimodal posteriors because several modes cannot be meaningfully summarised by one interval per dimension, nor by a single best estimate.

To quantify linear dependencies between parameters, the a posteriori Pearson correlation coefficient, 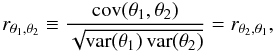$r_{θ_{1}, θ_{2}} \equiv \frac{cov (θ_{1}, θ_{2})}{\sqrt{var (θ_{1}) var (θ_{2})}} = r_{θ_{2}, θ_{1}},$ $\begin{equation} \corrCoeff{\param_1}{\param_2} \defby \frac{\cov(\param_1,\param_2)}{\sqrt{\var(\param_1)\,\var(\param_2)}} = \corrCoeff{\param_2}{\param_1}, \end{equation}$ (24)can be inferred from the samples. There may also be nonlinear correlations between parameters that are not described by the correlation coefficients. One should also be aware that for strong linear or non-linear relationships between parameters, uncertainties of single parameters as characterised by HPDIs may not be meaningful.

We stress that the (joint) marginal posteriors can – and should – always be referred to, especially when best estimates and/or HPDIs do not adequately characterise the posterior. The availability of these more informative densities is one of the advantages of a Bayesian approach with posterior sampling.

2.3. Observable models

Independent of the chosen approach to inference – frequentist or Bayesian –, theoretical values of the observables need to be calculated and compared to the data by means of the likelihood. To this end, an observable model is set up for each relevant type of data, i.e. a function f(θ;t) of the model parameters θ and time t. An overview of all model parameters used in this work is given in Table 1, while Table 2 lists quantities that can be derived from them.

In this section, we only sketch the derivation of the observable models, beginning with a single-planet system. For an in-depth treatment of celestial mechanics, the interested reader is referred e.g. to Moulton (1984).

2.3.1. Stellar motion in the orbital plane

Newton’s Law of Gravity governs the motion of a non-relativistic two-body system of star and planet, whose centre of mass (CM) rests in some inertial reference frame. A solution to it is given by both the star and the planet moving in elliptical Keplerian orbits with a fixed common orbital plane and each with one focus coinciding with the CM.

To describe the stellar position, whose variation is observable with astrometry and Doppler spectroscopy, we set up a coordinate system S₁ whose origin is identical to the CM, z-axis perpendicular to the orbital plane and the vector from the CM to the periapsis orientated in positive x-direction. In S₁, the stellar barycentric position is given by 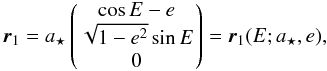$r 1 = a_{⋆} (\begin{matrix} \cos E - e \\ \sqrt{1 - e^{2}} \sin E \\ 0 \end{matrix}) = r 1 (E; a_{⋆},e),$ $\begin{equation} \label{eq_pos_star_S_one} \vr_1 = \PMaS \pmatrxi{ \cos\EA-\PMe\\ \sqrt{1-\PMe^2}\sin\EA\\ 0 } = \vr_1(\EA;\PMaS,\PMe), \end{equation}$ (25)where a_⋆ is the semi-major axis, e the eccentricity and E the eccentric anomaly.

The time-dependent eccentric anomaly is determined implicitly by Kepler’s equation, 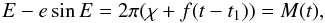$E - e \sin E = 2 π (χ + f (t - t_{1})) = M (t),$ $\begin{equation} \EA-\PMe\sin\EA = 2\pi(\PMchi+\PMf(\tm-\tmOne)) = \MA(\tm),\\\label{eq_Keplers_eq_chi} \end{equation}$ (26)where f = P^-1 is the orbital frequency, P the orbital period, t₁ the time of first measurement and M(·) the mean anomaly, which varies uniformly over the course of an orbit. 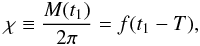Furthermore, following Gregory (2005a), we use $χ \equiv \frac{M (t_{1})}{2 π} = f (t_{1} - T),$ $\begin{equation} \PMchi \defby \frac{\MA(\tmOne)}{2\pi} = \PMf(\tmOne-\PMT),\label{eq_def_chi} \end{equation}$ (27)with T standing for the last time the periapsis was passed prior to t₁ (time of periapsis). Kepler’s equation is transcendental and needs to be solved numerically to obtain E for every relevant combination of e and M.

BASE performs a one-time pre-calculation of E over an (e,M)-grid, which, because of the monotonicity of E as an (implicit) function of e and M, allows one to reduce the effort of numerically solving Eq. (26) by providing lower and upper bounds on E.

By reference to Eqs. (25) and (26), it is readily shown that the stellar coordinates are periodic functions of χ with period 1. We therefore call χ a cyclic parameter and treat it as lying in the range [0,1).

2.3.2. Transformation into the reference system

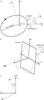Fig. 1

Definition of the angles ω_⋆,i,Ω. a) From S₁ to S₂, the star and its sense of rotation about the CM are indicated; the dotted line marks the major axis of the orbital ellipse. b) From S₂ to S₃, the observer and line of sight are indicated. c) From S₃ to S₄, the positive x₄-axis points northward along the meridian of the CM.

To derive the stellar barycentric position as seen from the perspective of an observer, we transform S₁ into a new coordinate system S₄ by three successive rotations. These are described by three Euler angles, termed in our case argument of the periapsis ω_⋆, inclination i and position angle of the ascending node Ω, and are carried out as follows (Fig. 1):

1.
Rotate S₁ about its z₁-axis by (−ω_⋆) such that the ascending node ⁴ of thestellar orbit lies on the positive x₂-axis.
2.
Rotate S₂ about its x₂-axis by (+ i) such that the new z₃-axis passes through the observer.
3.
Rotate S₃ about its z₃-axis by (− Ω) such that the new x₄-axis is parallel to the meridian of the CM and points in a northern direction.

Thus, the stellar barycentric position has new coordinates 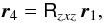$r 4 = R_{zxz} r 1,$ $\begin{equation} \vr_4 = \rotmzxz\,\vr_1,\label{eq_pos_star_S_four} \end{equation}$ (28)with matrix 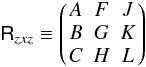$R_{zxz} \equiv (\begin{matrix} A & F & J \\ B & G & K \\ C & H & L \end{matrix})$ $\begin{equation} \label{eq_rot_matrix_comp} \rotmzxz \defby \pmatrxiii{ A & F & J\\ B & G & K\\ C & H & L } \end{equation}$ (29)defining the rotations; its components are 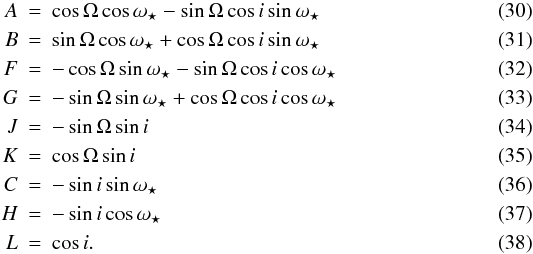$\begin{matrix} A & = & \cos Ω \cos ω_{⋆} - \sin Ω \cos i \sin ω_{⋆} \\ B & = & \sin Ω \cos ω_{⋆} + \cos Ω \cos i \sin ω_{⋆} \\ F & = & - \cos Ω \sin ω_{⋆} - \sin Ω \cos i \cos ω_{⋆} \\ G & = & - \sin Ω \sin ω_{⋆} + \cos Ω \cos i \cos ω_{⋆} \\ J & = & - \sin Ω \sin i \\ K & = & \cos Ω \sin i \\ C & = & - \sin i \sin ω_{⋆} \\ H & = & - \sin i \cos ω_{⋆} \\ L & = & \cos i . \end{matrix}$ $\begin{eqnarray} \label{eq_rot_matrix_A} A &=& \cos\PMOmega\cos\PMomegaS-\sin\PMOmega\cos\PMi\sin\PMomegaS\\ B &=& \sin\PMOmega\cos\PMomegaS+\cos\PMOmega\cos\PMi\sin\PMomegaS\\ F &=& -\cos\PMOmega\sin\PMomegaS-\sin\PMOmega\cos\PMi\cos\PMomegaS\\ \label{eq_rot_matrix_G} G &=& -\sin\PMOmega\sin\PMomegaS+\cos\PMOmega\cos\PMi\cos\PMomegaS\\ J &=& -\sin\PMOmega\sin\PMi\\ \label{eq_rot_matrix_K} K &=& \cos\Omega\sin\PMi\\ C &=& -\sin\PMi\sin\PMomegaS\\ H &=& -\sin\PMi\cos\PMomegaS\\ L &=& \cos\PMi. \end{eqnarray}$ A,B,F,and G are known as the Thiele-Innes constants, first introduced by Thiele (1883).

By taking the time derivative of Eq. (28), we obtain the stellar velocity in S₄, 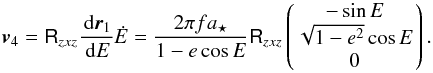$v 4 = R_{zxz} \frac{d r 1}{d E} Ė = \frac{2 πf a_{⋆}}{1 - e \cos E} R_{zxz} (\begin{matrix} - \sin E \\ \sqrt{1 - e^{2}} \cos E \\ 0 \end{matrix}) .$ $\begin{equation} \vv_4 = \rotmzxz\frac{\ddd\vr_1}{\ddd\EA}\tmDeriv{\EA} = \frac{2\pi\PMf\PMaS}{1-\PMe\cos\EA}\rotmzxz\pmatrxi{ -\sin\EA\\ \sqrt{1-e^2}\cos\EA\\ 0 }.\label{eq_RV_S_four} \end{equation}$ (39)

2.3.3. Relation to the planetary orbit

By reference to the above results, the observables of AM and RV are easily derived (Sect. 2.3.4). Based on the following simple relation, they can be parameterised by quantities pertaining to the planetary instead of the stellar orbit.

According to the definition of the CM, the line connecting star and planet contains the CM and the ratio of their respective distances from the CM equals the inverse mass ratio, 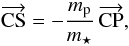$\begin{matrix} - 0 \to \\ CS \end{matrix} = - \frac{m_{p}}{m_{⋆}} \begin{matrix} - 0 \to \\ CP \end{matrix},$ $\begin{equation} \overrightarrow{\mathrm{CS}} = -\frac{\PMmP}{\PMmS}\,\overrightarrow{\mathrm{CP}},\label{eq_def_CM} \end{equation}$ (40)where C, S and P stand for CM, star and planet, respectively. This implies a simple relation between the orbits of the star and the planet as follows. The two bodies orbit the CM with a common orbital frequency f and time of periapsis T. With regard to the corresponding periapsis, they always have the same eccentric anomaly E. Their orbital shapes, viz. eccentricities e, are identical as well.

Furthermore, the two bodies share the same sense of orbital revolution, hence those nodes of both orbits which lie on the positive x₂-axis are ascending. Consequently, the only Euler angle that differs between stellar and planetary orbit is the argument of periapsis, which differs by π because star and planet are in opposite directions from the CM.

2.3.4. Observables

To express the stellar barycentric position as a two-dimensional angular position, we performed a final transformation of S₄ into a spherical coordinate system S₅ with radial, elevation and azimuthal coordinates (r,δ,α). Its origin is identical with the observer, its reference plane coincides with the (y₄,z₄)-plane and its fixed direction is −z₄. In S₅, the radial coordinate of the CM equals a distance d = 1AU ϖ^-1, with ϖ being the parallax. Stellar coordinates r₄ therefore correspond to a two-dimensional angular position 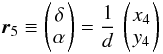$r 5 \equiv (\begin{matrix} δ \\ α \end{matrix}) = \frac{1}{d} (\begin{matrix} x_{4} \\ y_{4} \end{matrix})$ $\begin{equation} \AMAngPosNum{5} \defby \pmatrxi{ \POSdel\\ \POSal } = \frac{1}{\PMd}\,\pmatrxi{ x_4\\ y_4 } \end{equation}$ (41)in S₅, where δ and α are called the declination and right ascension, respectively. Using Eqs. 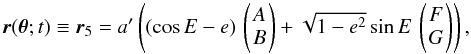(25), (28) and (29), the model function for the angular position of the star with respect to the CM becomes $r (θ; t) \equiv r 5 = a^{'} ((\cos E - e) (\begin{matrix} A \\ B \end{matrix}) + \sqrt{1 - e^{2}} \sin E (\begin{matrix} F \\ G \end{matrix})),$ $\begin{equation} \label{eq_pos_star_S_five} \mdlFctAM{\vPar}{\tm} \defby \AMPosNum{5} = \PMaApp\left((\cos\EA-\PMe)\, \pmatrxi{ A\\ B }+\sqrt{1-\PMe^2}\sin\EA\, \pmatrxi{ F\\ G }\right), \end{equation}$ (42)with a′ ≡ ϖa_⋆(1AU)^-1. In practice, complications arise because the stellar position is often measured relative to a physically unattached reference star, whose distance and motion differ, and not relative to the unobservable CM. By contrast, for a visual binary, the companion can be used as a reference, yielding the simple model described below.

Other astrometric effects may be caused by the accelerated motion of Earth-bound observers around the solar system barycentre (SSB). This is discussed for the case of the binary Mizar A in Sect. 2.3.5.

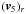In contrast to astrometry, RV data are usually automatically transformed into an inertial frame resting with respect to the SSB (e.g. Lindegren & Dravins 2003), which allows the Earth’s motion to be neglected in this model and treats the observer’s rest frame as being inertial. 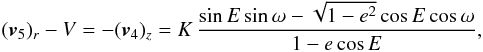The model function for the stellar radial velocity measured by an observer is thus given by $(v {}_{5})_{r}$ $\hbox{$(\vv_5)_r$}$ , with $(v 5)_{r} - V = - (v 4)_{z} = K \frac{\sin E \sin ω - \sqrt{1 - e^{2}} \cos E \cos ω}{1 - e \cos E},$ $\begin{equation} (\vv_5)_r-\PMV = -(\vv_4)_z = \PMK\,\frac{\sin\EA\sin\PMomegaP-\sqrt{1-e^2}\cos\EA\cos\PMomegaP}{1-\PMe\cos\EA},\label{eq_RV_S_five} \end{equation}$ (43)where V is the RV offset, consisting of the radial velocity of the CM plus an offset due to the specific calibration of the instrument – which therefore differ, in general, between RV data sets – and K is the RV semi-amplitude, which can be expressed as $K = 2 πf a_{⋆} \sin i = 3 \sqrt{2 πGf} m_{p} (m_{p} + m_{⋆})^{- \frac{2}{3}} \sin i .$ $\begin{equation} K = 2\pi\PMf\PMaS\sin\PMi = \sqrt[3]{2\pi\gravConst\PMf}\,\PMmP(\PMmP+\PMmS)^{-\frac{2}{3}}\sin\PMi.\label{eq_RV_amplitude_II} \end{equation}$ (44)The last equality holds because of Kepler’s third law, $(a_{p} + a_{⋆})^{3} f^{2} = \frac{G}{4 π^{2}} (m_{p} + m_{⋆})$ $\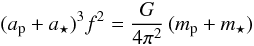begin{equation} (\PMaP+\PMaS)^3\PMf^2 = \frac{\gravConst}{4\pi^2}\,(\PMmP+\PMmS)\label{eq_Kepler_III} \end{equation}$ (45)and the definition of the CM (Eq. (40)). Owing to Eq. (44), only one of a_⋆,K needs to be employed in the AM and RV models; for BASE, K was adopted.

As an aside, in the literature (e.g. Gregory 2005a) often a different version of Eq. (43) is employed that involves ν instead of E and the alternative definition 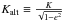$K_{alt} \equiv \frac{K}{\sqrt{1 - e^{2}}}$ $\hbox{$\PMKLit \defby \frac{\PMK}{\sqrt{1-\PMe^2}}$}$ (see Table 2).

Binary system.

If the primary and secondary binary components assume the roles of star and planet, respectively, the above reasoning also yields the observables of a binary system.

For visual binaries, AM measurements often refer to the position of the secondary with respect to the primary. 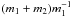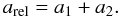From the definition of the CM, it follows that the orbit of the secondary with respect to the primary is identical with its barycentric orbit but scaled by a factor $(m_{1} + m_{2}) m_{1}^{-1}$ $\hbox{$(\PMmC{1}+\PMmC{2})\PMmC{1}\inv$}$ , or with the semi-major axis equaling the sum of the two components’ barycentric semi-major axes, $a_{rel} = a_{1} + a_{2} .$ $\begin{equation} \PMaRel = \PMaC{1}+\PMaC{2}.\label{eq_rel_semimaj_ax_binary} \end{equation}$ (46)Thus, the AM model of Eq. 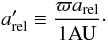(42) can be used for a binary with a_rel replacing a_⋆, ω₂ + π replacing ω_⋆ and $a_{rel}^{'} \equiv \frac{ϖ a_{rel}}{1 AU} \cdot$ $\begin{equation} \PMaRelApp \defby \frac{\PMpi\PMaRel}{1\UNITAU} \cdot \label{eq_def_a_rel_app} \end{equation}$ (47)Equation (43) yields the RV of component i if K is replaced by (− 1)^i + 1K_i and ω by ω₂. If AM and RV data are combined, BASE uses K_1,2 instead of a_1,2 and calculates a_rel using the equivalent of Eq. (44) in combination with Eq. (46).

2.3.5. Effects of the motion of observer and CM

If we consider the observer, whose position relative to the CM defines the orientation of S_{2......11...5}, to be located on Earth and therefore to be subject to Earth’s accelerated motion around the SSB, the angles Ω,i,ω as defined above are not constant but rather functions of time; an additional source of their variation is the (assumedly linear) proper motion of the CM. Consequently, these angles are not appropriate constant model parameters even within a timespan of a few months. Furthermore, the systems S_{2......11...5} defined above are not strictly inertial, which renders the simple coordinate transformations invalid. However, we argue below that the variation in these angles is so weak that these effects are indeed negligible in the context of this work.

Because AM determines instantaneous positions, it is directly influenced by changes in the positions of the observer and the CM. In the following, we assess for Mizar A the greatest possible magnitude of a change in the AM position Δr ≡ |Δr| due to angular changes ΔΩ,Δi,Δω > 0, which are in turn caused by the varying relative position of observer and CM. Finally, we compare Δr to the AM measurement uncertainties.

An upper limit on each of the angular changes ΔΩ,Δi,Δω can be derived from the proper motion of the CM and the annual parallax from the Earth’s motion, as 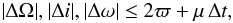$| ΔΩ |, | Δ i |, | Δ ω | \leq 2 ϖ + μ Δ t,$ $\begin{equation} |\DELOmega|,|\DELi|,|\DELomega| \le 2\PMpi+\propMotOrth\,\tmSpan,\label{eq_max_ang_chg} \end{equation}$ (48)where the first term corresponds to the annual parallax and μ is the magnitude of the CM’s proper motion. 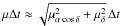For the second term, we have $μ Δ t \approx \sqrt{μ_{α \cos δ}^{2} + μ_{δ}^{2}} Δ t$ $\hbox{$\propMotOrth\tmSpan \approx \sqrt{\propMotAl^2+\propMotDel^2}\,\tmSpan$}$ .

Using sin(x + ξ) ≈ sinx + ξcosx, for ξ ≪ 1, along with Eqs. (30)–(35) and (48) as well as the final results for Ω,i,ω and ϖ (using the values 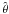$\hbox{$\md\param$}$ from Table B.1) and the proper motion from Table 3 yields the following maximum changes of the Thiele-Innes constants: $\begin{matrix} | Δ A | & ⪅ & 8.30 \times 10^{-6} \\ | Δ B | & ⪅ & 8.00 \times 10^{-6} \\ | Δ F | & ⪅ & 7.99 \times 10^{-6} \\ | Δ G | & ⪅ & 4.34 \times 10^{-6} . \end{matrix}$ $\begin{eqnarray} |\Delta A| &\lessapprox& \EE{8.30}{-6}\\ |\Delta B| &\lessapprox& \EE{8.00}{-6}\\ |\Delta F| &\lessapprox& \EE{7.99}{-6}\\ |\Delta G| &\lessapprox& \EE{4.34}{-6}. 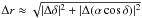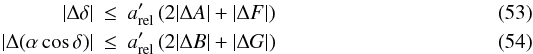\end{eqnarray}$ Hence, with $Δ r \approx \sqrt{| Δ δ |^{2} + | Δ (α \cos δ) |^{2}}$ $\hbox{$\DELangPos \approx \sqrt{|\Delta\POSdel|^2+|\Delta(\POSalCosDel)|^2}$}$ , $\begin{matrix} | Δ δ | & \leq & a_{rel}^{'} (2 | Δ A | + | Δ F |) \\ | Δ (α \cos δ) | & \leq & a_{rel}^{'} (2 | Δ B | + | Δ G |) \end{matrix}$ $\begin{eqnarray} |\Delta\POSdel| &\le& \PMaRelApp\,(2|\Delta A|+|\Delta F|)\\ |\Delta(\POSalCosDel)| &\le& \PMaRelApp\,(2|\Delta B|+|\Delta G|) \end{eqnarray}$ and the final posterior median $\begin{matrix} ˜ \\ a_{rel} \end{matrix}$ $\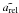hbox{$\med\PMaRel$}$ (Table B.2), we obtain the maximum change in relative angular position of the two components, $Δ r ⪅ 0.311 μ as .$ $\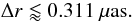begin{equation} \DELangPos \lessapprox 0.311~\UNITmuas. \end{equation}$ (55)Comparison with Table 4 reveals that this is more than two orders of magnitude smaller than the median AM measurement uncertainty, proving that the motions of the Earth and the CM of Mizar A can indeed be neglected.

Table 3

Basic physical properties of Mizar A.

Table 4

Published data for Mizar A used in this work.

3. BASE – Bayesian astrometric and spectroscopic exoplanet detection and characterisation tool

We have developed BASE, a computer program for the combined Bayesian analysis of AM and RV data according to Sect. 2, for the following main reasons.

A statistically well-founded, reliable tool was needed that was able to perform a complete Bayesian parameter and uncertainty estimation, along with model selection (only for planetary systems, not detailed in this article).
We aimed to combine astrometry and Doppler-spectroscopy analyses.
A possibility to include knowledge from earlier analyses was needed.
Finding all relevant solutions across a multidimensional, high-volume parameter space Θ was required. A more detailed knowledge of the parameters than a best estimate and a confidence interval can provide is especially important when the data do not constrain the parameters well, e.g. when only few data have been recorded or the signal-to-noise ratio is low (as can be the case for lightweight planets or young host stars).

BASE is a highly configurable command-line tool developed in Fortran 2008 and compiled with GFortran (Free Software Foundation 2011a). Options can be used to control the program’s behaviour and supply information such as the stellar mass or prior knowledge (see Sect. 3.1). Any option can be supplied in a configuration file and/or on the command line.

3.1. Prior knowledge

Any model parameter can be assigned a prior probability density in one of three forms:

a fixed value;
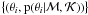a user-defined shape, i.e. a set $\hbox{$\seti{(\param_i,\pPri{\param_i})}$}$ ;
a range (either in combination with a specific shape, which is then clipped to the given range, or else using one of the standard prior shapes detailed in Sect. A).

Any parameter for which no such option is present is assigned a default prior shape and range to pose the weakest possible restraints justified by the data, the model, and mathematical/ physical considerations.

3.2. Physical systems and modes of operation

As mentioned above, BASE is capable of analysing data for two similar types of systems, whose physics have been described in Sect. 2.3. These are systems with

1.
one observable component that may be accompanied by one ormore unobserved bodies (generally referred to as planetarysystems here for simplicity); in this normal mode, the number ofcompanions can be set to a value ranging from zero to nine, or a listof such values, in which case several runs are conducted and theoutcome is compared in terms of model selection;
2.
two observable, gravitationally bound components (referred to as binary stars); this mode of operation is called binary mode.

3.3. Types of data

Observational data of the following types can be treated by BASE:

AM data, whose observable, in the case of binary targets, is therelative angular position of the two binary components. Each datarecord consists of a date, the angular position(αcosδ,δ) or (ρ,θ) in a cartesian or polar coordinate system, and its standard uncertainty ellipse, given by (a,b,φ);
RV data, where each data record consists of a date and the observed stellar radial velocity as well as its uncertainty.

3.4. Computational techniques

In the following, we describe some computational techniques implemented in BASE that are relevant to the present work.

Improved exploration of parameter space.

To enhance the mixing, i.e. rapidness of exploration of the parameter space, of Markov chains produced by the Metropolis-Hastings (MH) algorithm (Sect. 2.2.2) and decrease their attraction by local posterior modes, the parallel tempering (PT) algorithm (e.g. Gregory 2005b) is employed one level above MH. 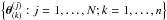Its function is to create in parallel n chains of length N, ${θ \begin{matrix} (j) \\ (k) \end{matrix} : j = 1, ...,N; k = 1, ..., n^{}}$ $\hbox{$\left\{\vPar\indexCh\samp:\iSamp=1,\ldots,\nSamp;\iCh=1,\ldots,\nCh\right\}$}$ each sampled by an independent MH procedure, where the cold chain k = 1 uses an unmodified likelihood ℒ(·), while the others, the heated chains, use as replacement ℒ(·)^γ_(k) with the positive tempering parameter γ_(k) < 1. 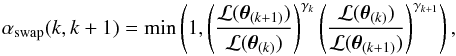After n_swap samples of each chain, two chains k ≥ 1 and k + 1 ≤ n are randomly selected and their last links, denoted here by θ_(k) and θ_(k + 1), are swapped with probability $α_{swap} (k,k + 1) = \begin{matrix} \min \end{matrix} (1, {(\frac{ℒ (θ (k + 1))}{ℒ (θ (k))})}^{γ_{k}} {(\frac{ℒ (θ (k))}{ℒ (θ (k + 1))})}^{γ_{k + 1}}),$ $\begin{equation} \alpha_{\mathrm{swap}}(k,k+1) = \min\left(1,\left(\frac{\likhood(\vPar\indxCh{k+1})}{\likhood(\vPar\indxCh{k})}\right)^{\tPar_{k}}\left(\frac{\likhood(\vPar\indxCh{k})}{\likhood(\vPar\indxCh{k+1})}\right)^{\tPar_{k+1}}\right),\label{eq_swap_prob} \end{equation}$ (56)which ensures that the distributions of both chains remain unchanged.

This procedure allows states from the “hotter” chains, which explore parameter space more freely, to “seep through” to the cold chain without compromising its distribution. Conclusions are only drawn from the samples of the cold chain.

In contrast to MCMC sampling, which is sequential in nature, the structure of PT allows one to exploit the multiprocessing facilities provided by many modern computing architectures. For this purpose, BASE uses the OpenMP API (OpenMP Architecture Review Board 2008) as implemented for GFortran by the GOMP project (Free Software Foundation 2011b).

Assessing convergence.

As a matter of principle, it cannot be proven that a given Markov chain has converged to the posterior. However, convergence may be meaningfully defined as the degree to which the chain does not depend on its initial state θ⁽⁰⁾ any more. This can be determined on the basis of a set of independent chains – in our case, the cold chains of m independent PT procedures – started at different points in parameter space. These starting states should be defined such that for each of their components, they are overdispersed with respect to the corresponding marginal posteriors.

Since the marginal posteriors are difficult to obtain before the actual sampling, BASE determines the starting states by repeatedly drawing, for each parameter, a set of m samples from the prior using rejection sampling; the repetition is stopped as soon as the sample variance exceeds the corresponding prior variance, which yields a set of starting states overdispersed with respect to the prior. Assuming that the prior variance exceeds the marginal-posterior variance, the overdispersion requirement is met.

Such a test, using the potential scale reduction (PSR) or Gelman-Rubin statistic, was proposed by Gelman & Rubin (1992) and was later refined and corrected by Brooks & Gelman (1998). It is repeatedly carried out during sampling and, in the case of a positive result, sampling is stopped before the user-defined maximum runtime and/or number of samples have been reached. It may also sometimes be useful to abort sampling manually, which can be done at any time.

The statistic is calculated with respect to each parameter θ separately, using the post-burn-in samples⁵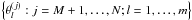 ${}^{{}θ_{l}^{(j)} : j = M + 1, ...,N; l = 1, ..., m^{}}$ $\hbox{$\left\{\param\indexPT\samp:\iSamp=\nSampBurn+1,\ldots,\nSamp;\iPT=1,\ldots,\nPT\right\}$}$ of θ provided by the m independent chains. It compares the actual variances of θ within the chains built up thus far to an estimate of the marginal-posterior (i.e. target) variance of θ, thus estimating how closely the chains have approached convergence.

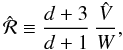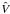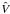The PSR is defined as $ℛ̂ \equiv \frac{d + 3}{d + 1} \frac{V̂}{W},$ $\begin{equation} \PSRSq \defby \frac{\PSRDOF+3}{\PSRDOF+1}\,\frac{\PSRV}{\PSRW}, \end{equation}$ (57)where $\hbox{$\PSRV$}$ is an estimate of the marginal-posterior variance, d the estimated number of degrees of freedom underlying the calculation of $\hbox{$\PSRV$}$ , and W the mean within-sequence variance. 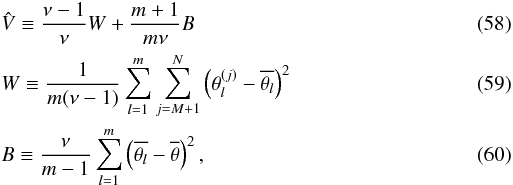The quantities are defined as $\begin{matrix} V̂ \equiv \frac{ν - 1}{ν} W + \frac{m + 1}{mν} B \\ W \equiv \frac{1}{m (ν - 1)} \sum_{l = 1}^{m} \sum_{j = M + 1}^{N} {(θ_{l}^{(j)} - {θ_{l}}^{)}}^{2} \\ B \equiv \frac{ν}{m - 1} \sum_{l = 1}^{m} {(θ_{l} - θ^{)}}^{2}, \end{matrix}$ $\begin{eqnarray} && \PSRV \defby \frac{\nu-1}{\nu}\PSRW+\frac{\nPT+1}{\nPT\nu}\PSRB\\ && \PSRW \defby \frac{1}{\nPT(\nu-1)}\sum_{\iPT=1}^\nPT \sum_{\iSamp=\nSampBurn+1}^\nSamp \left(\param\indexPT\samp-\overline{\param\indexPT}\right)^2\\ && \PSRB \defby \frac{\nu}{\nPT-1} \sum_{\iPT=1}^\nPT \left(\overline{\param\indexPT}-\overline{\param}\right)^2, \end{eqnarray}$ \arraycolsep1.75ptwhere B is the between-sequence variance and ν ≡ N − M; a horizontal bar denotes the mean taken over the set of samples obtained by varying the omitted indexes.

Owing to the initial overdispersion of starting states, 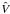$\hbox{$\PSRV$}$ overestimates the marginal-posterior variance in the beginning and subsequently decreases. Furthermore, while the chains are still exploring new areas of parameter space, W underestimates the marginal-posterior variance and increases. Thus, as convergence to the posterior is accomplished, . Therefore, we can assume convergence as soon as the PSR has fallen below a threshold . If BASE is run with ℛ_∗ ≡ 1, sampling is continued up to the user-defined length or duration, respectively.

For cyclic parameters (Sect. 2.3), the default lower and upper prior bounds are equivalent, which needs to be taken into account when calculating the PSR. Thus, BASE uses the modified definition of the PSR by Ford (2006) for these parameters.

4. Target and data

Mizar A (ζ¹ Ursae Majoris, HD 116656, HR 5054), the first spectroscopic binary discovered, is of double-lined type (SB II; Pickering 1890). Its basic physical properties are summarised in Table 3. Together with the spectroscopic binary Mizar B, it forms the Mizar quadruple system, seen from Earth as a visual binary with the components separated by about $14 \overset{″}{.} 4$ $\hbox{$14\farcs4$}$ . Mizar is the first double star discovered by a telescope and also the first one to be imaged photographically (Bond 1857).

At an apparent angular separation of about $11 \overset{'}{.} 8$ $\hbox{$11\farcm8$}$ , or 74 ± 39 kAU spatial distance, Mizar is accompanied by Alcor, which has recently turned out to be a spectroscopic binary itself (Mamajek et al. 2010). Mizar and Alcor, also known as the “Horse and Rider”, form an easy naked-eye double star, while it is still a matter of debate whether or not they constitute a physically bound sextuplet.

Published data used in this article are displayed in Figs. 7, 8 along with the model functions determined by BASE and their properties are summarised in Table 4. Using a Coudé spectrograph at the 1.93-m telescope at Observatoire Haute Provence, Prevot (1961) obtained 17 optical photographic spectra of the light of Mizar A combined with that of electric arcs or sparks between iron electrodes. For each of the 13 individual stellar lines identified in the spectra, one intermediate radial-velocity value per binary component was obtained by comparison with a set of reference lines of iron. Finally, a set of 17 pairs of RVs for the two components was calculated as arithmetic means of the corresponding intermediate values. The RV measurement uncertainty is not given by Prevot (1961) and was therefore estimated in the course of the present work, as described in Sect. 5.

High-precision AM data of Mizar A were first obtained by Hummel et al. (1995) using the Mark III optical interferometer on Mount Wilson, California (Shao et al. 1988), with baseline lengths between 3 and 31 m. It measured the squared visibilities and their uncertainties at positions sampled over the aperture plane due to Earth’s rotation. The visibilities can be modelled as a function of the diameters, magnitude differences, and relative angular positions (ρ,θ) of the binary components, Armstrong et al. (1992). These authors also describe a procedure to derive one angular position for each night of observation from a corresponding set of visibilities, which was adopted by Hummel et al. (1995) to obtain initial estimates of the orbital parameters. These positional data are also relevant for the present work. Hummel et al. (1995) also performed a direct fit to the squared visibilities to derive final estimates of the component diameters and orbital parameters.

Later, a descendant instrument, the Navy Prototype Optical Interferometer (NPOI) at Lowell observatory, Arizona (Armstrong et al. 1998), was used by Hummel et al. (1998) to obtain more accurate results using three siderostats, viz. three baselines at a time. This allowed a better calibration using the closure phase⁶, which is independent of atmospheric turbulence. Similarly as before, Hummel et al. (1998) separately fitted binary orbits directly to the visibility data and also to the positional angles derived for each night, concluding that the respective results agree well with each other and that those parameters in common with spectroscopic analyses are compatible with Prevot (1961); they also performed a fit to both AM and RV data to obtain their final parameter estimates.

While Hummel et al. (1998) did not include the older, less accurate Mark III data in their analysis, we present a combined treatment of all published data, i.e. the AM positions of Hummel et al. (1995) and Hummel et al. (1998) along with the RV data of Prevot (1961).

5. Analysis and results

Table 5

Analysis passes carried out sequentially.

To illustrate the features of BASE and demonstrate its validity, we used the tool to analyse all published data of Mizar A. This section details the steps taken in and the results of our analysis. Its general goal was, given uninformative prior knowledge, to search the parameter space as comprehensively as possible to find and characterise the a posteriori most probable solution together with its uncertainty and other characteristics. For reasons detailed below, once the RV data had been prepared, several runs of BASE (Table 5) were manually conducted, each using priors derived from the previous pass, with relatively uninformative priors in the first step.

In this analysis, our approach was to regard all nominal measurement uncertainties as accurate by setting parameters characterising additional noise in AM (τ₊) as well as RV (σ₊) data to zero.

Astrometric data alone allow one to constrain neither the RV offset V nor the amplitudes K₁,K₂ but only the sum K₁ + K₂ (Sect. 2.3.4). By contrast, these parameters can be constrained using spectroscopic data alone, or AM and RV data both. However, the AM data reduce the relative weight of the spectroscopic data and thus make the determination of these parameters harder. We found in the course of this work that by an iterative approach, starting with a first pass using only RV data, this difficulty could be resolved.

In all passes, BASE was configured to build up eight parallel chains, including the cold chain, using the parallel-tempering technique (detailed in Sect. 3.4). 10⁸ posterior samples were collected, the first 10% of which were assumed to be burn-in samples. In the final pass, two PT procedures were employed to enable a test of convergence to the posterior, which reduced the number of samples collected with unchanged memory requirements to 5 × 10⁷. Convergence was not assessed in earlier passes, because convergence was difficult to reach as long as several distinct solutions existed within the prior support.

5.1. Preparation of RV data

Assuming appropriate measurement uncertainties is a prerequisite for the proper relative weighting of the different data types when combining them. Because these uncertainties are not quoted by Prevot (1961) for the spectroscopic data, we estimated them according to the following method.

First, we assumed that each RV datum v_i is the sum of the model value v(θ_true;t_i) and an error e_i, where θ_true are the true parameter values and the errors are independent and identically Gaussian-distributed with an unknown standard deviation σ. Furthermore, we assumed that the model parameters found in a particular analysis are identical with θ_true. It follows that the uncertainty σ can be estimated as the sample standard deviation of the set of residuals 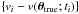${v_{i} - v (θ true; t_{i})}$ $\hbox{$\seti{\RV_i-\mdlFctRV{\vParTrue}{\tm_i}}$}$ .

Thus, based on the sample standard deviation of the best-fit residuals of Prevot (1961), viz. 2.13 km s^-1, we initially assumed a conservative value of 2.50 km s^-1 for all data. To quantify the measurement uncertainties based on our own inference, we then conducted a preliminary analysis similar to pass A described in the next subsection, from which we finally inferred σ = 2.05 km s^-1. In addition, we took a more correct alternative approach to estimating the RV uncertainties by assuming a relatively low value of σ = 2.00 km s^-1 and allowing for higher noise via σ₊, which led to an estimate 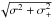$\sqrt{σ^{2} + σ_{+}^{2}}$ $\hbox{$\sqrt{\measUnc^2+\PMsgmP^2}$}$ deviating by less than 1.7% from our previous estimate.

5.2. Pass A: first constraints on RV parameters

Table 6

Pass A: initial prior ranges.

Fig. 2

Pass A: marginal posteriors of RV amplitudes K₁ (top, solid line), K₂ (top, dashed line) and offset V (bottom), all plotted over the approximate range of the corresponding 99% HPDI.

To facilitate the determination of the RV parameters K₁,K₂ and V, a first pass using only RV data was carried out, as mentioned above. It used uninformative priors (Sect. A and Table 1), with bounds listed in Table 6.

Figure 2 shows the resulting marginal posteriors (see Sect. 2.2.2) of the RV offset V and the amplitudes K₁,K₂, with the abscissae approximately corresponding to the 99% HPDIs. These marginal posteriors represent much tighter constraints on the parameters than the corresponding priors do.

5.3. Pass B: combining all data

Providing as new priors the marginal posteriors of all RV parameters e,f,χ,ω₂,V,K₁ and K₂ from pass A, constrained to the corresponding 99% HPDIs I_HPD,99%, and again using uninformative priors on the additional parameters (Table 7), the AM data were added and BASE was run again. Using the resulting posterior samples, BASE was additionally invoked in periodogram mode to refine the kernel window width for the marginal posterior of f as described in Sect. 2.2.2. (This refinement was not used in pass A in order not to constrain the frequency too tightly before adding the AM data, because the combined data are expected to correspond to a marginally differing frequency.)

The resulting marginal posterior (Fig. 3) exhibits a very strong mode around 0.04869 d^-1, whose height is 8.1 times that of the next lower peak. Over the range of its mode, the marginal posterior contains a total probability of 45.0%. Most other parameters in this stage have very broad and/or multimodal marginal posteriors, hinting at different solutions still probable within the prior support.

Table 7

Pass B: prior ranges for additional AM parameters.

Fig. 3

Pass B: marginal posterior of orbital frequency f, plotted over the range of the corresponding 99% HPDI. This is a Bayesian analogon to the frequentist periodogram.

5.4. Pass C: selecting the frequency f

For the next pass, the prior of f was provided by the marginal posterior of pass B (Fig. 3), constrained to the range of the marginal mode. For all other parameters, priors were identical with the previous marginal posteriors, constrained to I_HPD,99%.

With the frequency thus restrained, the pass produced unimodal marginal posteriors in all parameters except for ω₂ and Ω.

The marginal posteriors of the argument of periapsis ω₂ and the position angle of the ascending node Ω exhibited small local maxima located at a distance of −1.02π and + 1.03π from their marginal modes, respectively (indicated by triangles in Fig. 4). This can be explained by the fact that the Thiele-Innes constants (Eqs. (30)–(33)), which appear in the AM model, contain products of sin(·) and/or cos(·) functions with ω₂ and Ω as arguments. These products retain their values when ω₂ and Ω are both shifted by π – with opposite signs, since the marginal modes of these angles lie in different halves of the interval [0,2π). Consequently, the AM model function is invariant with respect to such shifts. (Thus, when analysing only AM data, it cannot be determined which node is ascending, hence Ω is defined only over the interval [0,π) and refers to the first node.) Owing to the combination with RV data, which independently constrain ω₂ (Eq. (43)), the ambiguity is strongly reduced, as illustrated by the very small subpeaks in Fig. 4 – though it is not completely resolved.

As another result from this pass, the high correlation coefficient of the two angles, r_ω₂,Ω = −0.62, expresses the strong negative linear relationship between them introduced by the possibility of a contrarious change.

Fig. 4

Pass C: marginal posteriors of the argument of periapsis ω₂ (solid line) and position angle of the ascending node Ω (dashed line), plotted over the approximate range of the corresponding 99% HPDIs. Triangles indicate the positions of small local maxima located approximately ± π from the corresponding marginal modes.

5.5. Passes D and E: selecting ω₂ and Ω and refining results

In pass D, the ambiguity in ω₂ and Ω was resolved by selecting the range around their marginal modes via the new priors. For all other parameters, priors were again identical to the previous marginal posteriors, constrained to I_HPD,99%. All resulting marginal posteriors turned out to be unimodal, corresponding to a single solution as opposed to several clearly distinct orbital solutions.

As a final step, pass E was conducted to refine the results by using all previous marginal posteriors, constrained to I_HPD,99%, as new priors, thus confining the parameter space a priori to the most probable solution.

Fig. 5

Marginal posteriors of parameters e,f,χ,ω₂,i,Ω,ϖ,V,K₁,K₂ (see also Table 1) and derived quantities P,T,d,ρ,K_alt,1,K_alt,2,m₁,m₂,a₁,a₂,a_rel (Table 2) with marginal-posterior medians (dotted line) and 68.27% HPDIs (dashed lines), from the final pass. Abscissae ranges are identical with the corresponding 95% HPDIs. Ordinate values were omitted but follow from normalisation. Open triangles on the upper abscissae indicate the MAP estimates. Open circles on the lower abscissae bound the confidence intervals given by or derived from Prevot (1961), while open triangles refer to the intervals of Hummel et al. (1998). Some of these literature estimates are not plotted because they are outside the abscissa range; for f and χ, no literature uncertainty estimate is available. For derivations and numerical values, see Tables B.1 and B.2.

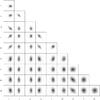Fig. 6

Two-parameter joint marginal posterior densities $\hbox{$\jointmapo{i}{j}{\cdot}{\cdot}$}$ from pass E. The figure consists of 45 sub-plots, one for each combination of two parameters. Black denotes highest density. The inner and outer contours contain 50% and 64.86% probability, respectively. All plots aligned in one column share the same abscissa, denoted on the bottom; all plots aligned in one row share the same ordinate, denoted on the left. All abscissae and ordinates are displayed over the corresponding 95% HPDIs (Table B.1), such that the total probability content of each plot is between 90% and 95%.

Fig. 7

AM and RV data and models calculated with the MAP parameter estimates (Table B.1). a) AM data (uncertainty ellipses, solid lines), model (large ellipse, solid line) and residual vectors (dashed lines). b) Residual AM error ellipses. c) RV data and model for primary (normal error bars, solid line) and secondary (hourglass-shaped error bars, dotted line). The horizontal dashed line indicates the RV offset V. RV residuals are presented in Fig. 8.

Fig. 8

All data types: from top to bottom: AM data and model (δ coordinate); AM residuals Δδ; AM data and model (αcosδ coordinate); AM residuals Δ(αcosδ); RV data and model v (primary: solid line, secondary: dotted line, RV offset V: horizontal dashed line); RV residuals Δv (primary: normal error bars, secondary: dashed error bars, model: dashed line). AM error bars are defined as the sides of the smallest rectangle orientated along the coordinate axes and containing the respective error ellipse. Abscissa values are mean anomalies M (Eq. (26)), i.e. times folded with respect to the MAP estimates of the time of periapsis T and period P.

Fig. 9

Distribution of normalised residuals of AM data (long-dashed line), RV data (short-dashed) and all data (solid), along with the standard normal distribution $\hbox{$\stdNormDistr$}$ (dotted). For definitions of the normalised residuals (see Eqs. (61)–(65)).

(Joint) marginal posteriors and correlations.

The final marginal posteriors of all model parameters, plotted over the corresponding 95% HPDIs, are shown in Fig. 5, along with the medians, 68.27% HPDIs (corresponding in probability content to the frequentist 1-σ confidence intervals) and MAP estimates. For comparison, literature estimates and confidence intervals are also included, where permitted by the abscissa range.

Linear and nonlinear dependencies between a pair of parameters may be qualitatively judged by means of the joint marginal posteriors (Sect. 2.2.2) shown in Fig. 6. The inclinations of their equiprobability contours with respect to the coordinate axes are related to the corresponding correlation coefficients. Some joint marginal posteriors exhibit clear deviations from bivariate normal distributions, illustrating that a Gaussian approximation of the likelihood by use of the Fischer matrix (Sect. 2.1) would be inappropriate.

Table B.3 lists the final posterior correlation coefficients. When these attain high absolute values, model-related equations can sometimes serve as an explanation.

For example, the highly negative correlation between f and χ is related to Eq. (26) in the following way. Given data and estimated model parameters, let t_m be the time midway between the first and last observations, and E_m the eccentric anomaly at t_m. Now increase f by a small amount. This can be balanced by a small decrease of χ (or, equivalently, by increasing the time of periapsis T) such that the eccentric anomaly at t_m again equals E_m. This contrarious change of f and χ, as opposed to leaving only one of them altered, will make E deviate less, on average, over the total timespan; i.e. the model will fit the data better. The relation between f and χ so introduced is indicated by their negative correlation coefficient.

As another example, the highly negative correlation coefficient ω₂ and Ω can be understood by reference to Eqs. (30)–(33), which describes the Thiele-Innes constants of the AM model as follows. In the case of edge-on orbits (inclination i = 0), these expressions simplify to sums or differences of cos(·) and sin(·) functions, the arguments being ω₂ + Ω or ω₂ − Ω, with both arguments appearing equally often. An additional simplification is observed for face-on orbits (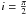 $i = \frac{π}{2}$ $\hbox{$\PMi = \frac{\pi}{2}$}$ ), where the Thiele-Innes constants are A = G = −cos(Ω + ω₂) and B = −F = −sin(Ω + ω₂). Thus, for orbits nearly face-on, the strong appearance of the sum Ω + ω₂ introduces a negative correlation between the two angles, because their contrarious change can lead to the same value of the model function. For Doppler-spectroscopic data, this is counteracted by the fact that the RV model function does not contain Ω.

Models and residuals.

Figure 7 presents all data with the models calculated from the MAP estimates listed in Table B.1, as well as residual vectors and error ellipses for astrometry. While this analysis used both the older (Hummel et al. 1995) and newer (Hummel et al. 1998) AM in combination with RV data (Prevot 1961), the AM model is very similar to the one calculated by Hummel et al. (1998, Fig. 11) using only the newer AM data because of the overall agreement in parameters.

Figure 8 shows all data, models and residuals, separately by coordinate for AM. The abscissa corresponds to the mean anomaly M (Eq. (26)), i.e. the plots are folded with respect to a time of periapsis T and period P corresponding to the posterior mode. Again, due to the similarity in parameters, the folded RV plot in Fig. 8 is very similar to the corresponding figure in Prevot (1961).

To assess the distribution of the residuals and compare it to a normal distribution, thus checking the validity of our noise model, we normalised the residuals of both data types as follows. For AM, we defined the normalised residual as a signed version of the Mahalanobis distance (Mahalanobis 1936) between the observed and the modelled values, $ϱ_{AM, i} \equiv s_{i} \sqrt{(r i - r (θ; t_{i}))^{T} E_{i}^{-1} (r i - r (θ; t_{i}))},$ $\begin{equation} \RESIDnorm_{\mathrm{AM,i}} \defby s_i\sqrt{(\vr_i-\mdlFctAM{\vPar}{\tm_i})\transp\,\dataCovM_i\inv\,(\vr_i-\mdlFctAM{\vPar}{\tm_i})},\label{eq_def_norm_resid_AM} \end{equation}$ (61)with sign $s_{i} \equiv sgn ((φ_{i} - ϕ_{i}) (π - [φ_{i} - ϕ_{i}])),$ $\begin{equation} s_i \defby \sgn\left((\UNCERTELLphi_i-\RESIDphi_i)(\pi-[\UNCERTELLphi_i-\RESIDphi_i])\right), \end{equation}$ (62)where ϕ_i and φ_i are the position angles of the residual and of the uncertainty ellipse (see Sect. 2.1), respectively. This definition allows us to write, according to Eq. 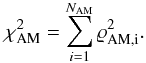(7), $χ_{AM}^{2} = \sum_{i = 1}^{N_{AM}} ϱ_{AM, i}^{2} .$ $\begin{equation} \chi^2\iAM = \sum_{i=1}^{N\iAM} \RESIDnorm_{\mathrm{AM,i}}^2 . \end{equation}$ (63)For RV data, we define 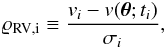$ϱ_{RV, i} \equiv \frac{v_{i} - v (θ; t_{i})}{σ_{i}},$ $\begin{equation} \RESIDnorm_{\mathrm{RV,i}} \defby \frac{\RV_i-\mdlFctRV{\vPar}{\tm_i}}{\measUncToti{i}}, \end{equation}$ (64)which analogously yields 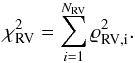$χ_{RV}^{2} = \sum_{i = 1}^{N_{RV}} ϱ_{RV, i}^{2} .$ $\begin{equation} \chi^2\iRV = \sum_{i=1}^{N\iRV} \RESIDnorm_{\mathrm{RV,i}}^2.\label{eq_chi_sq_RV_simple} \end{equation}$ (65)The distributions of normalised residuals of both data types individually as well as of all data, estimated using kernel density estimation (Sect. 3.4), are shown in Fig. 9. Table 8 lists the p-values of the Kolmogorov-Smirnov statistic, which relates each distribution to the standard normal distribution 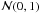$\hbox{$\stdNormDistr$}$ .

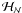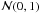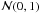The p-value equals the probability, under the hypothesis $\hbox{$\hy_{\mathcal N}$}$ that the normalised residuals are randomly drawn from $\hbox{$\stdNormDistr$}$ , to observe a distribution of normalised residuals that differs at least as much from $\hbox{$\stdNormDistr$}$ as is actually the case. This difference is quantified here by the Kolmogorov-Smirnov statistic. 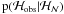Denoting the hypothesis of such an observation by ℋ_obs, the p-value can be expressed as $\hbox{$\p(\hy_{\mathrm{obs}}|\hy_{\mathcal N})$}$ . 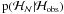We note that according to the Bayes theorem, this is not equal to the “inverse” probability $\hbox{$\p(\hy_{\mathcal N}|\hy_{\mathrm{obs}})$}$ of the residuals coming from the normal distribution, given the observation.

For the AM residuals, as well as for all residuals, a heavy-tailed distribution (Fig. 9) is observed and the low p-value indicates a minute probability of such an observation under 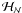$\hbox{$\hy_{\mathcal N}$}$ , i.e. the normalised residuals comply poorly with the standard normal distribution 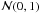$\hbox{$\stdNormDistr$}$ . This reflects the fact that several AM data points are outliers with respect to the observable and noise model (Fig. 7). We interpret this in terms of systematic effects in the measurements that are not contained in our noise model. In contrast, the normalised RV residuals are more normally-distributed, and there are no such severe outliers (Figs. 7 and 8).

According to the principle of maximum entropy, given only the mean and variance of a distribution, the normal distribution has maximum information-theoretic entropy, equivalent to minimum bias or prejudice with respect to the missing information (e.g. Kapur 1989). Still, it is well-known that this widely used noise model is relatively prone to outliers; Lange et al. (1989) have suggested to replace it by a non-standardised t-distribution, resulting in the down-weighting of outliers. This distribution can be derived from the normal distribution under the assumption that the noise variance is unknown with a certain probability distribution. The t-distribution has an additional unknown degrees-of-freedom parameter ν ∈ R; for ν = 1, it resembles the Cauchy-distribution.

In contrast, our approach has been to regard every datum with its standard deviation as accurate, which also implies that we have not discarded any data as outliers. Under this assumption, deviating from the maximum-entropy principle by selecting a different distribution introduces prior “knowledge” that we may not actually have and thus potentially biases the results.

6. Conclusions

We have presented BASE, a novel and highly configurable tool for Bayesian parameter and uncertainty estimation with respect to model parameters and additional derived quantities, which can be applied to AM as well as RV data of both exoplanet systems and binary stars. With user-specified or uninformative prior knowledge, it employs a combination of Markov chain Monte Carlo (MCMC) and several other techniques to explore the whole parameter space and collect samples distributed according to the posterior distribution. We presented a new, simple method of refining the window width of one-dimensional kernel density estimation, which is used to derive marginal posterior densities.

We derived the observable models from Newton’s law of gravitation, neglecting the motion of the observer and the target system, which we showed is justified in the case of Mizar A. After sketching how we estimated the RV uncertainties that are missing in the original publication (Prevot 1961), we detailed our analysis of all publicly available AM and RV data of Mizar A. It consists of five consecutive stages and has produced estimates of the values, uncertainties, and correlations of all model parameters and derived quantities, as well as marginal posterior densities over one and two dimensions.

As illustrated in Fig. 5 and Table B.1, our new results exhibit overall compatibility with previous literature values; this is also the case for the models in Fig. 7, whose plots differ only slightly from those published earlier. Several outliers in the AM data are visible in the distribution of the corresponding normalised residuals, which deviates significantly more from a standard normal distribution than that of the RV residuals. Nevertheless, it is not necessary to remove outliers for our program to finish successfully.

In the near future, we plan to apply BASE to a potential exoplanet host star. In this study one of the aims will be to determine the existence probability of a planetary companion.

Table 8

p-values of the Kolmogorov-Smirnov statistic^a.

Table B.1

Model parameters: new and previous results.

Table B.2

Derived quantities: new and previous results.

¹

Although most methods described in this introduction apply to any kind of companion to a star, we refer here to companions as “exoplanets”, irrespective of whether they are able to sustain hydrogen or deuterium burning.

²

Throughout, we use the term probability density wherever it refers to a continuous quantity, as opposed to probability for discrete quantities. Probability distribution, denoted by p(·), is a generic term used for both cases.

³

In general, t_i is the value of an independent variable, which may e.g. be temporal or spatial. We assumed the measurement durations to be short in comparison with the characteristic time of orbital motion, given by the orbital period, and thus the observations to take place at points in time t_i which are known exactly.

⁴

The ascending node is the point of intersection of the orbit and the sky plane where the moving object passes away from the observer. In step 2, a positive rotation angle is used to ensure that the node is indeed ascending (Fig. 1b).

⁵

Because the burn-in length M cannot be determined in advance, BASE considers a fixed but configurable fraction of samples to belong to the burn-in phase at any time.

⁶

The closure phase φ_cl is the phase of the product of three visibilities, each pertaining to a different baseline.

Acknowledgments

We wish to thank David W. Hogg, Sabine Reffert, René Andrae, and Mathias Zechmeister for fruitful discussions, and an anonymous referee for comments that have improved the quality and clarity of this article. This research has made use of the SIMBAD database and VizieR catalogue access tool, operated at CDS, Strasbourg, France, as well as NASA’s Astrophysics Data System.

References

Adamson, A., Aspin, C., Davis, C., et al. 2005, Astronomical Polarimetry: Current Status and Future Directions, ASP Conf. Ser., 343 [Google Scholar]
Armstrong, J. T., Mozurkewich, D., Vivekanand, M., et al. 1992, AJ, 104, 241 [NASA ADS] [CrossRef] [Google Scholar]
Armstrong, J. T., Mozurkewich, D., Rickard, L. J., et al. 1998, ApJ, 496, 550 [NASA ADS] [CrossRef] [Google Scholar]
Bayes, M., & Price, M. 1763, Philosoph. Trans., 53, 370 [Google Scholar]
Bond, G. 1857, MNRAS, 17, 230 [NASA ADS] [Google Scholar]
Boneh, A., & Golan, A. 1979, in Third European Congress on Operations Research, EURO III, Amsterdam [Google Scholar]
Brooks, S. P., & Gelman, A. 1998, J. Computat. Graphic. Statist., 7, 434 [Google Scholar]
Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Deeg, H. J., Belmonte, J. A., & Aparicio, A. 2007, Extrasolar Planets (Cambridge University Press) [Google Scholar]
Delplancke, F. 2008, New Astron. Rev., 52, 199 [NASA ADS] [CrossRef] [Google Scholar]
Delplancke, F., Leveque, S. A., Kervella, P., Glindemann, A., & D’Arcio, L. 2000, in SPIE Conf. Ser. 4006, eds. P. Léna, & A. Quirrenbach, 365 [Google Scholar]
Efron, B., & Tibshirani, R. 1993, An introduction to the bootstrap, Monographs on statistics and applied probability (Chapman & Hall) [Google Scholar]
Ford, E. B. 2004, in The Search for Other Worlds, eds. S. S. Holt, & D. Deming, ASP Conf. Ser., 713, 27 [Google Scholar]
Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]
Free Software Foundation. 2011a, GFortran, http://gcc.gnu.org/fortran/ [Google Scholar]
Free Software Foundation. 2011b, GOMP, http://gcc.gnu.org/projects/gomp/ [Google Scholar]
Gatewood, G., Breakiron, L., Goebel, R., et al. 1980, Icarus, 41, 205 [NASA ADS] [CrossRef] [Google Scholar]
Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
Geman, S., & Geman, D. 1984, Pattern Analysis and Machine Intelligence, IEEE Transactions on, PAMI-6, 721 [Google Scholar]
Gilks, W. R., Richardson, S., & Spiegelhalter, D. J. 1996, Markov Chain Monte Carlo in Practice, 1st edn. (London: Chapman & Hall) [Google Scholar]
Gillessen, S., Eisenhauer, F., Perrin, G., et al. 2010, in SPIE Conf. Ser., 7734 [Google Scholar]
Gould, A. 2009, in ASP Conf. Ser. 403, ed. K. Z. Stanek, 86 [Google Scholar]
Gregory, P. C. 2005a, ApJ, 631, 1198 [NASA ADS] [CrossRef] [Google Scholar]
Gregory, P. C. 2005b, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with Mathematica Support (Cambridge: Cambridge University Press) [Google Scholar]
Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
Hoffleit, D., & Jaschek, C. 1982, The Bright Star Catalogue (Yale University Observatory) [Google Scholar]
Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
Hummel, C. A., Armstrong, J. T., Buscher, D. F., et al. 1995, AJ, 110, 376 [NASA ADS] [CrossRef] [Google Scholar]
Hummel, C. A., Mozurkewich, D., Armstrong, J. T., et al. 1998, AJ, 116, 2536 [NASA ADS] [CrossRef] [Google Scholar]
Kapur, J. 1989, Maximum-Entropy Models in Science and Engineering (Wiley) [Google Scholar]
Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]
Kuhn, J. R., Potter, D., & Parise, B. 2001, ApJ, 553, L189 [NASA ADS] [CrossRef] [Google Scholar]
Lange, K. L., Little, R. J. A., & Taylor, J. M. G. 1989, J. Am. Statist. Assoc., 84, 881 [Google Scholar]
Launhardt, R., Queloz, D., Henning, T., et al. 2008, in SPIE Conf. Ser., 7013 [Google Scholar]
Levine, M., Soummer, R., Arenberg, J., et al. 2009, in The Astronomy and Astrophysics Decadal Survey, 2010, 37 [Google Scholar]
Lindegren, L., & Dravins, D. 2003, A&A, 401, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Lovis, C., & Fischer, D. 2010, Radial Velocity Techniques for Exoplanets (University of Arizona Press), 27 [Google Scholar]
Lyot, B. 1932, ZAp, 5, 73 [Google Scholar]
Mahalanobis, P. C. 1936, in Proc. National Institute of Science, India, 2, 49 [Google Scholar]
Mamajek, E. E., Kenworthy, M. A., Hinz, P. M., & Meyer, M. R. 2010, AJ, 139, 919 [NASA ADS] [CrossRef] [Google Scholar]
Mao, S., & Paczynski, B. 1991, ApJ, 374, L37 [NASA ADS] [CrossRef] [Google Scholar]
Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]
Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]
McArthur, B. E., Benedict, G. F., Barnes, R., et al. 2010, ApJ, 715, 1203 [NASA ADS] [CrossRef] [Google Scholar]
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
Moulton, F. 1984, An Introduction to Celestial Mechanics, Dover Books on Astronomy (Dover Publications) [Google Scholar]
Nascimbeni, V., Piotto, G., Bedin, L. R., & Damasso, M. 2011, A&A, 527, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
OpenMP Architecture Review Board. 2008, OpenMP, http://openmp.org/ [Google Scholar]
Perryman, M. A. C. 2000, Rep. Progr. Phys., 63, 1209 [NASA ADS] [CrossRef] [Google Scholar]
Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
Pickering, E. C. 1890, The Observatory, 13, 80 [NASA ADS] [Google Scholar]
Prevot, L. 1961, J. Observateurs, 44, 83 [NASA ADS] [Google Scholar]
Reffert, S. 2009, New Astron. Rev., 53, 329 [NASA ADS] [CrossRef] [Google Scholar]
Roberts, G. O. 1996, in Markov Chain Monte Carlo in Practice, 1st edn., eds. W. R. Gilks, S. Richardson, & D. J. Spiegelhalter (London: Chapman & Hall), 45 [Google Scholar]
Schneider, J. 2012, The Extrasolar Planets Encyclopædia, http://exoplanet.eu/catalog.php [Google Scholar]
Seager, S. 2008, Space Sci. Rev., 135, 345 [NASA ADS] [CrossRef] [Google Scholar]
Shao, M., Colavita, M. M., Hines, B. E., Staelin, D. H., & Hutter, D. J. 1988, A&A, 193, 357 [NASA ADS] [Google Scholar]
Silverman, B. 1986, Density estimation for statistics and data analysis, Monographs on statistics and applied probability (Chapman and Hall) [Google Scholar]
Sivia, D. S. 2006, Data Analysis – A Bayesian Tutorial, 2nd edn. (Oxford: Oxford University Press) [Google Scholar]
Smith, R. L. 1980, in Bulletin of the TIMS/ORSA Joint National Meeting, Washington, DC, 101 [Google Scholar]
Smith, W. H. 1987, PASP, 99, 1344 [NASA ADS] [CrossRef] [Google Scholar]
Sozzetti, A. 2005, PASP, 117, 1021 [NASA ADS] [CrossRef] [Google Scholar]
Thiele, T. N. 1883, Astron. Nachr., 104, 245 [NASA ADS] [CrossRef] [Google Scholar]
Tolbert, C. R. 1964, ApJ, 139, 1105 [NASA ADS] [CrossRef] [Google Scholar]
van Leeuwen, F. 2007, Astrophys. Space Sci. Library 350, Hipparcos, the New Reduction of the Raw Data (Springer Verlag) [Google Scholar]
Vigan, A., Moutou, C., Langlois, M., et al. 2010, MNRAS, 407, 71 [NASA ADS] [CrossRef] [Google Scholar]
Vogt, S. S., Butler, R. P., Marcy, G. W., et al. 2005, ApJ, 632, 638 [NASA ADS] [CrossRef] [Google Scholar]
Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Encoding prior knowledge

By means of the prior, Bayesian analysis allows one to incorporate knowledge obtained earlier, e.g. using different data. When no prior knowledge is available for some model parameter, except for its allowed range, maximum prior ignorance about the parameter can be encoded by a prior of one of the following functional forms for the most common classes of location and scale parameters (Gregory 2005b; Sivia 2006).

For a location parameter, we demand that the prior be invariantagainst a shift Δ in the parameter, i.e. 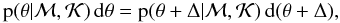$p (θ | ℳ, 𝒦) d θ = p (θ + Δ | ℳ, 𝒦) d (θ + Δ),$ $\appendix \setcounter{section}{1} \begin{equation} \pPri{\param}\ddd\param = \pPri{\param+\Delta}\ddd(\param+\Delta), \end{equation}$ (A.1)which leads to the uniform prior 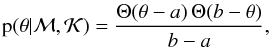$p (θ | ℳ, 𝒦) = \frac{Θ (θ - a) Θ (b - θ)}{b - a},$ $\appendix \setcounter{section}{1} \begin{equation} \pPri{\param} = \uniformPrior{\param}{a}{b}, \end{equation}$ (A.2)where Θ(·),a, and b are the Heaviside step function, the lower and the upper prior bounds. Here, we note that the frequentist approach, lacking an explicit definition of the prior, corresponds to the implicit assumption of a uniform prior for all parameters.
A positive scale parameter, which often spans several decades, is characterised by its invariance against a stretch of the coordinate axis by a factor ϕ, i.e. 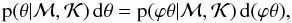$p (θ | ℳ, 𝒦) d θ = p (ϕθ | ℳ, 𝒦) d (ϕθ),$ $\appendix \setcounter{section}{1} \begin{equation} \pPri{\param}\ddd\param = \pPri{\varphi\param}\ddd(\varphi\param), \end{equation}$ (A.3)which is solved by the Jeffreys prior, 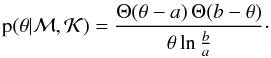$p (θ | ℳ, 𝒦) = \frac{Θ (θ - a) Θ (b - θ)}{θ \ln \frac{b}{a}} \cdot$ $\appendix \setcounter{section}{1} \begin{equation} \pPri{\param} = \jeffreysPrior{\param}{a}{b} \cdot \end{equation}$ (A.4)That a uniform prior would be inappropriate for this parameter is also illustrated by the fact that it would assign higher probabilities to θ lying in a higher decade of [a,b] than in a lower.
If the lower prior bound of a scale parameter is zero, e.g. for the RV semi-amplitude K, a modified Jeffreys prior is used. It has the form 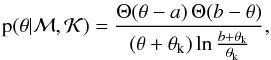$p (θ | ℳ, 𝒦) = \frac{Θ (θ - a) Θ (b - θ)}{(θ + θ_{k}) \ln \frac{b + θ_{k}}{θ_{k}}},$ $\appendix \setcounter{section}{1} \begin{equation} \pPri{\param} = \modJeffreysPrior{\param}{\knee{\param}}{a}{b}, \end{equation}$ (A.5)where θ_k is the knee of the prior. For θ ≪ θ_k, this prior is approximately uniform, while it approaches a Jeffreys prior for θ ≫ θ_k.

Appendix B: Numerical posterior summaries

The following tables list the numerical values of several posterior summaries. Those in Tables B.1 and B.2 are derived from the marginal posteriors (Fig. 5), while the correlation coefficients in Table B.3 reflect linear relations between parameters and, in this respect, can be regarded as summaries of the joint marginal posteriors (Fig. 6).

Compared to the underlying densities, all of these summaries are incomplete. Still, they are useful e.g. for the calculation of model functions or comparison with literature results.

Table B.3

Pearson correlation coefficients of pairs of parameters.

All Tables

Table 1

Model parameters used by BASE.

In the text

Table 2

Quantities derived from model parameters.

In the text

Table 3

Basic physical properties of Mizar A.

In the text

Table 4

Published data for Mizar A used in this work.

In the text

Table 5

Analysis passes carried out sequentially.

In the text

Table 6

Pass A: initial prior ranges.

In the text

Table 7

Pass B: prior ranges for additional AM parameters.

In the text

Table 8

p-values of the Kolmogorov-Smirnov statistic^a.

In the text

Table B.1

Model parameters: new and previous results.

In the text

Table B.2

Derived quantities: new and previous results.

In the text

Table B.3

Pearson correlation coefficients of pairs of parameters.

In the text

All Figures

	Fig. 1 Definition of the angles ω_⋆,i,Ω. a) From S₁ to S₂, the star and its sense of rotation about the CM are indicated; the dotted line marks the major axis of the orbital ellipse. b) From S₂ to S₃, the observer and line of sight are indicated. c) From S₃ to S₄, the positive x₄-axis points northward along the meridian of the CM.
In the text

	Fig. 2 Pass A: marginal posteriors of RV amplitudes K₁ (top, solid line), K₂ (top, dashed line) and offset V (bottom), all plotted over the approximate range of the corresponding 99% HPDI.
In the text

	Fig. 3 Pass B: marginal posterior of orbital frequency f, plotted over the range of the corresponding 99% HPDI. This is a Bayesian analogon to the frequentist periodogram.
In the text

	Fig. 4 Pass C: marginal posteriors of the argument of periapsis ω₂ (solid line) and position angle of the ascending node Ω (dashed line), plotted over the approximate range of the corresponding 99% HPDIs. Triangles indicate the positions of small local maxima located approximately ± π from the corresponding marginal modes.
In the text

Fig. 5

Marginal posteriors of parameters e,f,χ,ω₂,i,Ω,ϖ,V,K₁,K₂ (see also Table 1) and derived quantities P,T,d,ρ,K_alt,1,K_alt,2,m₁,m₂,a₁,a₂,a_rel (Table 2) with marginal-posterior medians (dotted line) and 68.27% HPDIs (dashed lines), from the final pass. Abscissae ranges are identical with the corresponding 95% HPDIs. Ordinate values were omitted but follow from normalisation. Open triangles on the upper abscissae indicate the MAP estimates. Open circles on the lower abscissae bound the confidence intervals given by or derived from Prevot (1961), while open triangles refer to the intervals of Hummel et al. (1998). Some of these literature estimates are not plotted because they are outside the abscissa range; for f and χ, no literature uncertainty estimate is available. For derivations and numerical values, see Tables B.1 and B.2.

In the text

Fig. 6

Two-parameter joint marginal posterior densities $\hbox{$\jointmapo{i}{j}{\cdot}{\cdot}$}$ from pass E. The figure consists of 45 sub-plots, one for each combination of two parameters. Black denotes highest density. The inner and outer contours contain 50% and 64.86% probability, respectively. All plots aligned in one column share the same abscissa, denoted on the bottom; all plots aligned in one row share the same ordinate, denoted on the left. All abscissae and ordinates are displayed over the corresponding 95% HPDIs (Table B.1), such that the total probability content of each plot is between 90% and 95%.

In the text

Fig. 7

AM and RV data and models calculated with the MAP parameter estimates (Table B.1). a) AM data (uncertainty ellipses, solid lines), model (large ellipse, solid line) and residual vectors (dashed lines). b) Residual AM error ellipses. c) RV data and model for primary (normal error bars, solid line) and secondary (hourglass-shaped error bars, dotted line). The horizontal dashed line indicates the RV offset V. RV residuals are presented in Fig. 8.

In the text

Fig. 8

All data types: from top to bottom: AM data and model (δ coordinate); AM residuals Δδ; AM data and model (αcosδ coordinate); AM residuals Δ(αcosδ); RV data and model v (primary: solid line, secondary: dotted line, RV offset V: horizontal dashed line); RV residuals Δv (primary: normal error bars, secondary: dashed error bars, model: dashed line). AM error bars are defined as the sides of the smallest rectangle orientated along the coordinate axes and containing the respective error ellipse. Abscissa values are mean anomalies M (Eq. (26)), i.e. times folded with respect to the MAP estimates of the time of periapsis T and period P.

In the text

	Fig. 9 Distribution of normalised residuals of AM data (long-dashed line), RV data (short-dashed) and all data (solid), along with the standard normal distribution $\hbox{$\stdNormDistr$}$ (dotted). For definitions of the normalised residuals (see Eqs. (61)–(65)).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Adamson, A., Aspin, C., Davis, C., et al. 2005, Astronomical Polarimetry: Current Status and Future Directions, ASP Conf. Ser., 343 [Google Scholar]

[2] Armstrong, J. T., Mozurkewich, D., Vivekanand, M., et al. 1992, AJ, 104, 241 [NASA ADS] [CrossRef] [Google Scholar]

[3] Armstrong, J. T., Mozurkewich, D., Rickard, L. J., et al. 1998, ApJ, 496, 550 [NASA ADS] [CrossRef] [Google Scholar]

[4] Bayes, M., & Price, M. 1763, Philosoph. Trans., 53, 370 [Google Scholar]

[5] Bond, G. 1857, MNRAS, 17, 230 [NASA ADS] [Google Scholar]

[6] Boneh, A., & Golan, A. 1979, in Third European Congress on Operations Research, EURO III, Amsterdam [Google Scholar]

[7] Brooks, S. P., & Gelman, A. 1998, J. Computat. Graphic. Statist., 7, 434 [Google Scholar]

[8] Charbonneau, D., Brown, T. M., Latham, D. W., & Mayor, M. 2000, ApJ, 529, L45 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[9] Deeg, H. J., Belmonte, J. A., & Aparicio, A. 2007, Extrasolar Planets (Cambridge University Press) [Google Scholar]

[10] Delplancke, F. 2008, New Astron. Rev., 52, 199 [NASA ADS] [CrossRef] [Google Scholar]

[11] Delplancke, F., Leveque, S. A., Kervella, P., Glindemann, A., & D’Arcio, L. 2000, in SPIE Conf. Ser. 4006, eds. P. Léna, & A. Quirrenbach, 365 [Google Scholar]

[12] Efron, B., & Tibshirani, R. 1993, An introduction to the bootstrap, Monographs on statistics and applied probability (Chapman & Hall) [Google Scholar]

[13] Ford, E. B. 2004, in The Search for Other Worlds, eds. S. S. Holt, & D. Deming, ASP Conf. Ser., 713, 27 [Google Scholar]

[14] Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]

[15] Free Software Foundation. 2011a, GFortran, http://gcc.gnu.org/fortran/ [Google Scholar]

[16] Free Software Foundation. 2011b, GOMP, http://gcc.gnu.org/projects/gomp/ [Google Scholar]

[17] Gatewood, G., Breakiron, L., Goebel, R., et al. 1980, Icarus, 41, 205 [NASA ADS] [CrossRef] [Google Scholar]

[18] Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]

[19] Geman, S., & Geman, D. 1984, Pattern Analysis and Machine Intelligence, IEEE Transactions on, PAMI-6, 721 [Google Scholar]

[20] Gilks, W. R., Richardson, S., & Spiegelhalter, D. J. 1996, Markov Chain Monte Carlo in Practice, 1st edn. (London: Chapman & Hall) [Google Scholar]

[21] Gillessen, S., Eisenhauer, F., Perrin, G., et al. 2010, in SPIE Conf. Ser., 7734 [Google Scholar]

[22] Gould, A. 2009, in ASP Conf. Ser. 403, ed. K. Z. Stanek, 86 [Google Scholar]

[23] Gregory, P. C. 2005a, ApJ, 631, 1198 [NASA ADS] [CrossRef] [Google Scholar]

[24] Gregory, P. C. 2005b, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with Mathematica Support (Cambridge: Cambridge University Press) [Google Scholar]

[25] Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]

[26] Hoffleit, D., & Jaschek, C. 1982, The Bright Star Catalogue (Yale University Observatory) [Google Scholar]

[27] Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]

[28] Hummel, C. A., Armstrong, J. T., Buscher, D. F., et al. 1995, AJ, 110, 376 [NASA ADS] [CrossRef] [Google Scholar]

[29] Hummel, C. A., Mozurkewich, D., Armstrong, J. T., et al. 1998, AJ, 116, 2536 [NASA ADS] [CrossRef] [Google Scholar]

[30] Kapur, J. 1989, Maximum-Entropy Models in Science and Engineering (Wiley) [Google Scholar]

[31] Koch, D. G., Borucki, W. J., Basri, G., et al. 2010, ApJ, 713, L79 [NASA ADS] [CrossRef] [Google Scholar]

[32] Kuhn, J. R., Potter, D., & Parise, B. 2001, ApJ, 553, L189 [NASA ADS] [CrossRef] [Google Scholar]

[33] Lange, K. L., Little, R. J. A., & Taylor, J. M. G. 1989, J. Am. Statist. Assoc., 84, 881 [Google Scholar]

[34] Launhardt, R., Queloz, D., Henning, T., et al. 2008, in SPIE Conf. Ser., 7013 [Google Scholar]

[35] Levine, M., Soummer, R., Arenberg, J., et al. 2009, in The Astronomy and Astrophysics Decadal Survey, 2010, 37 [Google Scholar]

[36] Lindegren, L., & Dravins, D. 2003, A&A, 401, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[37] Lovis, C., & Fischer, D. 2010, Radial Velocity Techniques for Exoplanets (University of Arizona Press), 27 [Google Scholar]

[38] Lyot, B. 1932, ZAp, 5, 73 [Google Scholar]

[39] Mahalanobis, P. C. 1936, in Proc. National Institute of Science, India, 2, 49 [Google Scholar]

[40] Mamajek, E. E., Kenworthy, M. A., Hinz, P. M., & Meyer, M. R. 2010, AJ, 139, 919 [NASA ADS] [CrossRef] [Google Scholar]

[41] Mao, S., & Paczynski, B. 1991, ApJ, 374, L37 [NASA ADS] [CrossRef] [Google Scholar]

[42] Marois, C., Lafrenière, D., Doyon, R., Macintosh, B., & Nadeau, D. 2006, ApJ, 641, 556 [Google Scholar]

[43] Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [NASA ADS] [CrossRef] [Google Scholar]

[44] McArthur, B. E., Benedict, G. F., Barnes, R., et al. 2010, ApJ, 715, 1203 [NASA ADS] [CrossRef] [Google Scholar]

[45] Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]

[46] Moulton, F. 1984, An Introduction to Celestial Mechanics, Dover Books on Astronomy (Dover Publications) [Google Scholar]

[47] Nascimbeni, V., Piotto, G., Bedin, L. R., & Damasso, M. 2011, A&A, 527, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[48] OpenMP Architecture Review Board. 2008, OpenMP, http://openmp.org/ [Google Scholar]

[49] Perryman, M. A. C. 2000, Rep. Progr. Phys., 63, 1209 [NASA ADS] [CrossRef] [Google Scholar]

[50] Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]

[51] Pickering, E. C. 1890, The Observatory, 13, 80 [NASA ADS] [Google Scholar]

[52] Prevot, L. 1961, J. Observateurs, 44, 83 [NASA ADS] [Google Scholar]

[53] Reffert, S. 2009, New Astron. Rev., 53, 329 [NASA ADS] [CrossRef] [Google Scholar]

[54] Roberts, G. O. 1996, in Markov Chain Monte Carlo in Practice, 1st edn., eds. W. R. Gilks, S. Richardson, & D. J. Spiegelhalter (London: Chapman & Hall), 45 [Google Scholar]

[55] Schneider, J. 2012, The Extrasolar Planets Encyclopædia, http://exoplanet.eu/catalog.php [Google Scholar]

[56] Seager, S. 2008, Space Sci. Rev., 135, 345 [NASA ADS] [CrossRef] [Google Scholar]

[57] Shao, M., Colavita, M. M., Hines, B. E., Staelin, D. H., & Hutter, D. J. 1988, A&A, 193, 357 [NASA ADS] [Google Scholar]

[58] Silverman, B. 1986, Density estimation for statistics and data analysis, Monographs on statistics and applied probability (Chapman and Hall) [Google Scholar]

[59] Sivia, D. S. 2006, Data Analysis – A Bayesian Tutorial, 2nd edn. (Oxford: Oxford University Press) [Google Scholar]

[60] Smith, R. L. 1980, in Bulletin of the TIMS/ORSA Joint National Meeting, Washington, DC, 101 [Google Scholar]

[61] Smith, W. H. 1987, PASP, 99, 1344 [NASA ADS] [CrossRef] [Google Scholar]

[62] Sozzetti, A. 2005, PASP, 117, 1021 [NASA ADS] [CrossRef] [Google Scholar]

[63] Thiele, T. N. 1883, Astron. Nachr., 104, 245 [NASA ADS] [CrossRef] [Google Scholar]

[64] Tolbert, C. R. 1964, ApJ, 139, 1105 [NASA ADS] [CrossRef] [Google Scholar]

[65] van Leeuwen, F. 2007, Astrophys. Space Sci. Library 350, Hipparcos, the New Reduction of the Raw Data (Springer Verlag) [Google Scholar]

[66] Vigan, A., Moutou, C., Langlois, M., et al. 2010, MNRAS, 407, 71 [NASA ADS] [CrossRef] [Google Scholar]

[67] Vogt, S. S., Butler, R. P., Marcy, G. W., et al. 2005, ApJ, 632, 638 [NASA ADS] [CrossRef] [Google Scholar]

[68] Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]

Bayesian analysis of exoplanet and binary orbits⋆

Demonstrated using astrometric and radial-velocity data of Mizar A

1. Introduction

2. Methods and models

2.1. Likelihoods and frequentist inference

Parameter estimation.

Uncertainty estimation.

2.2. Bayesian inference

2.2.1. Bayes’ theorem

2.2.2. Posterior inference

Sampling from the posterior.

Marginalisation and density estimation.

Periodogram mode.

Parameter estimation.

Uncertainty estimation.

2.3. Observable models

2.3.1. Stellar motion in the orbital plane

2.3.2. Transformation into the reference system

2.3.3. Relation to the planetary orbit

2.3.4. Observables

Binary system.

2.3.5. Effects of the motion of observer and CM

3. BASE – Bayesian astrometric and spectroscopic exoplanet detection and characterisation tool

3.1. Prior knowledge

3.2. Physical systems and modes of operation

3.3. Types of data

3.4. Computational techniques

Improved exploration of parameter space.

Assessing convergence.

4. Target and data

5. Analysis and results

5.1. Preparation of RV data

5.2. Pass A: first constraints on RV parameters

5.3. Pass B: combining all data

5.4. Pass C: selecting the frequency f

5.5. Passes D and E: selecting ω2 and Ω and refining results

(Joint) marginal posteriors and correlations.

Models and residuals.

6. Conclusions

Acknowledgments

References

Appendix A: Encoding prior knowledge

Appendix B: Numerical posterior summaries

All Tables

All Figures

Bayesian analysis of exoplanet and binary orbits^⋆

5.5. Passes D and E: selecting ω₂ and Ω and refining results