| Issue |
A&A
Volume 545, September 2012
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 4 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201118603 | |
| Published online | 24 September 2012 | |
New astrometric observations of Deimos with the SRC on Mars Express⋆
1 German Aerospace Center, Institute of Planetary Research, Planetary Geodesy, Rutherfordstrasse 2, 12489 Berlin, Germany
e-mail: andreas.pasewaldt@dlr.de
2 Technische Universität Berlin, Institute for Geodesy and Geoinformation Science, Planetary Geodesy, Strasse des 17. Juni 135, 10623 Berlin, Germany
3 Moscow State University for Geodesy and Cartography, Extraterrestrial Laboratory, 4, Gorokchovsky pereulok, 105064, Moscow, Russia
Received: 7 December 2011
Accepted: 22 June 2012
Between July 2005 and July 2011 Mars Express performed 50 Deimos approaches. 136 super resolution channel (SRC) images were acquired and used for astrometric (positional) measurements of the small Martian satellite. For this study, we have developed a new technique, in which the center-of-figure of the odd-shaped Deimos is determined by fitting the predicted to the observed satellite limb. The prediction of the limb was made based on the moon’s known shape model. The camera pointing was verified and corrected for by means of background star observations. We obtained a set of spacecraft-centered Deimos coordinates with accuracies between 0.6 and 3.6 km (1σ). Comparisons with current orbit models indicate that Deimos is ahead of or falling behind its predicted position along its track by as much as +3.4 km or −4.7 km, respectively, depending on the chosen model. Our data may be used to improve the orbit models of the satellite.
Key words: astrometry / ephemerides / planets and satellites: individual: Deimos
Table 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/545/A144
© ESO, 2012
1. Introduction
Deimos, the outer of the two Martian satellites, revolves at a mean Mars-centered distance of 23 458 km in a near-circular, near-equatorial orbit. Its rotation is tidally locked to the parent planet.
There is great interest in the orbital tracking of Deimos, in particular when it is combined with tracking of its satellite companion Phobos (Lainey et al. 2007; Jacobson 2010). Phobos, moving deep in the gravity field of Mars, is strongly affected by tidal interaction with the planet, and is expected to disrupt on short time scales (Burns 1977). In contrast, Deimos moves beyond the synchronous orbit and is rather believed to escape from Mars in the distant future (Burns 1977). The simultaneous modeling of the Deimos and Phobos orbits may provide strong constraints on the origin and evolution of the Martian satellite system. Further on, precise orbit data may also help in planning future Deimos exploration missions.
Previous astrometric data have been obtained from ground-based (Morley 1989; Colas 1992) and spacecraft-based observations (Duxbury & Callahan 1988, 1989; Kolyuka et al. 1991). More recent measurements include those by the Panoramic Cameras on Mars Exploration Rovers (Bell et al. 2005; Berthier et al. 2006) and the optical navigation camera on the Mars Reconnaissance Orbiter1. Comprehensive lists on astrometric observations of the Martian moons have been compiled by Arlot & Emelyanov (2009) and Jacobson (2010).
This article is the third in a series (Oberst et al. 2006; Willner et al. 2008), reporting on astrometric observations of the Martian satellites by the super resolution channel (SRC) on Mars Express. In this paper, we exclusively discuss Deimos observations, and we report on improved measurement and reduction schemes.
 |
Fig. 1 Deimos images obtained from different orbits. The SRC always points to Deimos’ sub-Mars hemisphere under slightly varying viewing angles. The surface of Deimos is rather bland. Image blurring and ghost features are discernible along the limb and near crater rims (see text for details). |
2. Mars Express mission and the SRC camera
The Mars Express spacecraft revolves in a highly elliptical and highly inclined orbit around Mars, well within the mean distance of Deimos. Good opportunities for imaging arise when Deimos is at an appropriate orbital phase and when the spacecraft is near the Mars equatorial plane (about ± 25° latitude). From 2005 to 2011, Mars Express has engaged in 50 such Deimos approaches. Images of Deimos are typically taken from distances of 14 000 km and shorter. The closest approach was in March 2011 when the spacecraft was at a range of about 9600 km. Because Deimos is in synchronous rotation, the SRC images show mostly its near side (see Fig. 1). The astrometric observations of Deimos are well distributed over its full orbit.
The Mars Express spacecraft carries seven science instruments, among them the HRSC/SRC camera. The High Resolution Stereo Camera (HRSC), a push-broom scanner with nine CCD line scanners mounted in one focal plane, has been developed for mapping Mars in three dimensions and color at medium scale (Neukum & Jaumann 2004; Jaumann et al. 2007). The SRC is a 1K × 1K CCD-framing camera featuring a Maksutov-Cassegrain optical design with a focal length of 988.6 mm. Its purpose is to show features of interest within the HRSC image strips with higher detail (Oberst et al. 2008). In comparison with the HRSC, it magnifies features in the image by a factor of about four.
3. Measurement of star positions: Pointing verification and improvement
Classical astrometric observations from the ground and ad hoc observations from spacecraft in the context of deep space missions differ in some details. Any positional measurement requires good knowledge of the observer’s position and pointing. In ground-based astrometry campaigns the coordinates of the observatory and the pointing of the telescope are typically known. Parameters enabling the transformation from image to celestial coordinates – so-called plate constants – are determined by careful astrometric calibration on the basis of reference stars. Positions of the target are then measured with respect to these stars.
 |
Fig. 2 Limb-fit procedure in five steps: a) Predicted limb (red) and terminator (yellow), b) manual fit of predicted limb to observed limb, c) computed limb (green), d) computed limb after blunder removal, e) best fit of predicted limb to computed limb. |
For astrometric observations from Mars Express the position of the spacecraft and the pointing of the camera are taken from nominal navigation data that are provided by the mission project at ESOC (European space operations center). Star observations are only used to verify and improve the pointing data. In-flight calibrated misalignment angles of the SRC with respect to the HRSC base frame and focal length have been obtained previously by using dedicated image sequences of star fields (Oberst et al. 2008). The attitude of the spacecraft (and therefore the pointing of the body-mounted camera) is measured by using two star trackers and three laser gyroscopes. According to Pischel & Zegers (2009), the spacecraft attitude is known with an accuracy of 0.01°, which corresponds to 19 SRC pixels.
Hence, a verification and improvement of the camera pointing is desirable. The pointing data are verified by measuring differences in position between observed and predicted background stars. Following our previous astrometric measurement efforts (Willner et al. 2008), star positions are predicted based on the current star catalogs Hipparcos and Tycho-2. In general, measurements relative to Hipparcos stars are preferred because of the catalog’s higher accuracy. However, even the quality of the less accurate Tycho-2 catalog is at least seven times higher than the field of view of one SRC pixel. The predicted star positions are projected onto the SRC image and compared to the observed star locations in the image. As a result, the positional differences between observed and predicted stars can be determined as pointing offsets in terms of sample and line for each image.
In 2006 the image acquisition planning was specifically modified to allow for targeting of background stars with a magnitude of 8.0 or lower during Phobos and Deimos approaches. Owing to the SRC’s narrow field of view, usually one or two faint stars per image can be observed. Stars with magnitudes of 8.5 and higher can hardly be discerned, because of the high level of background noise in the images.
Generally, at least two background stars would be required to determine the pointing of the camera. In our case only pointing shift errors were determined. Any rotation about the boresight axis of the camera was neglected, because any such error was expected to become apparent and correctable during the fitting of the irregularly shaped limb. In our previous analysis of Phobos data, Willner et al. (2008) did not find any significant errors in the boresight angle predictions.
During a Deimos approach, the spacecraft is in inertial pointing mode, i.e. the SRC camera is pointing to a fixed point on the celestial sphere. Within 1.5 to 3.5 min, a sequence of seven or eight images is acquired with Deimos moving across the field of view. In all cases, the first and the last image are taken with long-time exposures (about 500 ms) to capture faint background stars (magnitudes ranging from 3.4 to 8.8). From the five or six short-time exposure images, usually two to four images show Deimos.
Typically, star positions were found to differ slightly (up to 39 pixels in line and 51 pixels in sample direction) from image to image. To estimate the pointing correction for individual Deimos images, a linear pointing drift between the first and the last star image of the sequence was assumed. Corresponding error estimates were assigned to each measurement (Willner et al. 2008). From 50 orbits we fortuitously had nine where stars were sufficiently bright to be seen in all images. Here, a pointing correction could be applied directly without prior interpolations.
Because of the possibility of uncontrolled pointing drift during the acquisition of an image sequence, measurements without the possibility of pointing verification before and after the Deimos encounter (e.g., Deimos approaches with no or only one star observation) are not reported in this paper.
Owing to thermal distortion effects within the camera’s optical system, SRC images are observed to suffer from blurring and ghost features (Oberst et al. 2008, Fig. 1). These effects may introduce random or even small ( ≤ 2 px) systematic errors to the star positional measurements and limb fitting (described below). However, we believe that these errors are small compared to the described uncertainties from image smear and pointing drift.
4. Measurement of Deimos’ position: Determining the center of figure
In the SRC images, Deimos is well-resolved and reveals its odd shape. In this study, we developed a new limb-fit technique for positional measurements of the satellite. While we previously used ellipsoidal models for Phobos and Deimos to predict their limb positions (Oberst et al. 2006), in this paper our method uses explicit 3D shape models.
The Deimos shape model is based on observations by the Viking Orbiters (Thomas et al. 2000) made available through the National Space Science Data Center (NSSDC) as part of the PDS Small Body Shape Models V2.1 dataset. The original shape data are converted into a triangular mesh network and conveniently stored in NAIF’s digital shape kernel (DSK) format2. The SPICE software allows us to carry out various coordinate transformations and perform various samplings of these data.
Using nominal data on Deimos’ position, rotational state, and shape, its limb is predicted as observed from the spacecraft position. The limb is projected onto the SRC image by means of the camera’s nominal pointing and known geometric parameters. Then, the predicted limb is fitted to the observed limb in several steps: First, the predicted limb is fitted manually to the observed limb. Then, automatic limb detection is applied by searching for a typical pixel pattern along the transition between target object and surrounding space. The algorithm uses the predicted limb points as starting values and searches inside and outside of these limb points by a certain amount of pixels. Blunders are eliminated in the process. The predicted limb is then fitted to the computed limb by minimizing the sum of radial distances from the Deimos center between corresponding limb points. These work steps are repeated up to three times to reach sub-pixel accuracy. As a result, we obtain the position of Deimos’ COF in terms of image line and sample (see Fig. 2). Following the correction of the pointing data, line and sample are transformed to SRC Cartesian camera coordinates and finally to spacecraft-centered equatorial J2000 coordinates. While orbital analysts are commonly interested in center of mass (COM), the coordinate origin of our shape model is center-of-figure (COF), with the relationship between center-of-mass and center-of-figure of Deimos being unknown. Unfortunately, because of the similar viewing geometry from the Mars direction for all images, it is not possible to obtain constraints on the offset between the two, should one exist.
5. Results
We measured the position of Deimos COF in 136 images obtained during 50 spacecraft approaches in the time between July 2005 and July 2011, covering a major part of the moon’s orbit (see Table 1).
The accuracies of the measurements were estimated on the basis of the statistical model introduced by Duxbury & Callahan (1988): 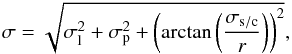 (1)where σl is the error in limb measurement, σp is the error in camera pointing, and σs/c is the error in spacecraft position in relation to r, the distance between spacecraft and Deimos.
(1)where σl is the error in limb measurement, σp is the error in camera pointing, and σs/c is the error in spacecraft position in relation to r, the distance between spacecraft and Deimos.
The error in limb measurement is estimated based on the fractional portion of the limb that is visible in the image and the average radial distance between computed and predicted limb points. The former error was assessed empirically. If about 75% of Deimos’ limb were visible in the image, a shift of the moon’s COF of one pixel was assumed. If only 25% of the natural satellite’s limb were observable, the assumed shift was about three pixels. The average radial distance between computed and predicted limb points describes the goodness of fit of the theoretical limb on the apparent part of the limb. Owing to the high quality of the shape model, this quantity varied between 0.5 to 1.5 pixels.
Pointing uncertainties are the greatest contributors to the total error budget. As described above, the image pointing data were corrected on the basis of star positional measurements. Differences in the measurements before and after an image sequence were used as an indication of the pointing error for all images of one sequence. The adopted 1-σ errors are half the difference between the two pointing measurements. To consider image blur and ghost effects, an error of 2 pixels was added to the pointing error.
In the early mission, estimates for the accuracy in spacecraft position suggested average errors of ±500 m (Oberst et al. 2006). More recently, improvements in radio tracking scheduling (shorter wheel offloadings, longer data arcs) have enabled the determination of the spacecraft position with mean accuracies of ±100−200 m (Pischel & Zegers 2009, T. Morley, priv. comm.), with the position being most accurate at periapsis, where the spacecraft speed is highest. Because our observations are taken around the spacecraft apoapsis and almost over the entire lifetime of the mission, the more conservative early estimate was used as a basis for our total error reporting.
By combining all error contributions, the accuracy of our astrometric observations is between 0.0025° and 0.0168°, which corresponds ± 0.6 km resp. ± 3.6 km in object space, considering the respective Deimos distances.
6. Discussion and outlook
To assess the quality of our astrometric observations, the measurements were compared with current Deimos orbit models from the Royal Observatory of Belgium (ROB) (Lainey et al. 2007) and the Jet Propulsion Laboratory (JPL) (Jacobson 2010). The two models differ regarding the observational data sets and model parameters that were used.
Owing to the similar viewing geometry in all Deimos approaches (with the camera being in the orbit plane of Deimos pointing at the satellite’s Mars-facing hemisphere; see Fig. 1), it is possible to separate our measured positional errors in the along-track (y-) and out-of-plane (z-) portions of the Deimos orbit. We cannot determine any offsets in the Mars (x-) direction. Our observations show average offsets in y-direction with respect to the JPL model of − 4.7 km i.e., suggesting that Deimos is lagging behind its predicted position (see Fig. 3), and with respect to the ROB model of +3.4 km i.e., suggesting that Deimos is ahead (see Fig. 3). The offsets are seen to vary with the orbital position of Deimos, i.e. with its orbital speed (see Fig. 4). Any offsets in the out-of-plane direction are smaller than 1 km for both orbit models. Our astrometric data will help improve the current Deimos orbit models.
Currently, new image calibration and restoration efforts are under way, which will eventually remove blurring and image ghosts, to improve the geometric quality of SRC imagery (Duxbury, in prep.). Improved images may allow us to derive more accurate limb positions, pointing corrections, and error estimates. While we anticipate a re-analysis of previous image data, recently obtained observations of Phobos are still awaiting data reduction and analysis. In August 2011 an error occurred while SRC was writing data into the spacecraft mass memory, with the consequence that Mars Express switched to safe mode. Since that incidence, the SRC was not put back into regular operation again. Therefore, we do not expect any new astrometric data for either Deimos or Phobos in the near future.
 |
Fig. 3 Offsets between astrometric observations and JPL resp. ROB orbit models in along-track direction, plotted with respect to time. |
 |
Fig. 4 Data as in Fig. 3, plotted with respect to mean anomaly. |
Acknowledgments
This research has received funding from the European Community’s Seventh Framework Programme ([FP7/2007-2013]) under grant agreement n° 263466. J. Oberst and V. Lupovka have been supported by a Grant from the Ministry of Education and Science of the Russian Federation.
References
- Arlot, J.-E., & Emelyanov, N. V. 2009, A&A, 503, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, J. F., Lemmon, M. T., Duxbury, T. C., et al. 2005, Nature, 436, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Berthier, J., Lainey, V., Bell, J., & Dehant, V. 2006, in SF2A-2006: Semaine de l’Astrophysique Française, eds. D. Barret, F. Casoli, G. Lagache, A. Lecavelier, & L. Pagani, 379 [Google Scholar]
- Burns, J. A. 1977, Orbital Evolution, ed. J. A. Burns (University of Arizona Press), 113 [Google Scholar]
- Colas, F. 1992, A&AS, 96, 485 [NASA ADS] [Google Scholar]
- Duxbury, T. C., & Callahan, J. D. 1988, A&A, 201, 169 [NASA ADS] [Google Scholar]
- Duxbury, T. C., & Callahan, J. D. 1989, A&A, 216, 284 [NASA ADS] [Google Scholar]
- Jacobson, R. A. 2010, AJ, 139, 668 [Google Scholar]
- Jaumann, R., Neukum, G., Behnke, T., et al. 2007, Planet. Space Sci., 55, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Kolyuka, Y., Tikhonov, V., Ivanov, N., et al. 1991, A&A, 244, 236 [NASA ADS] [Google Scholar]
- Lainey, V., Dehant, V., & Pätzold, M. 2007, A&A, 465, 1075 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morley, T. A. 1989, A&AS, 77, 209 [NASA ADS] [Google Scholar]
- Neukum, G., & Jaumann, R. 2004, in Mars Express: the Scientific Payload, eds. A. Wilson, & A. Chicarro, ESA SP, 1240, 17 [Google Scholar]
- Oberst, J., Matz, K. D., Roatsch, T., et al. 2006, A&A, 447, 1145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oberst, J., Schwarz, G., Behnke, T., et al. 2008, Planet. Space Sci., 56, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Pischel, R., & Zegers, T. 2009, in Mars Express – The Scientific Investigations, ed. A. Chicarro, ESA SP, 1291, 249 [Google Scholar]
- Thomas, P. C., Yoder, C. F., Synnott, S. P., et al. 2000, NASA Planetary Data System, 173 [Google Scholar]
- Willner, K., Oberst, J., Wählisch, M., et al. 2008, A&A, 488, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Deimos images obtained from different orbits. The SRC always points to Deimos’ sub-Mars hemisphere under slightly varying viewing angles. The surface of Deimos is rather bland. Image blurring and ghost features are discernible along the limb and near crater rims (see text for details). |
| In the text | |
 |
Fig. 2 Limb-fit procedure in five steps: a) Predicted limb (red) and terminator (yellow), b) manual fit of predicted limb to observed limb, c) computed limb (green), d) computed limb after blunder removal, e) best fit of predicted limb to computed limb. |
| In the text | |
 |
Fig. 3 Offsets between astrometric observations and JPL resp. ROB orbit models in along-track direction, plotted with respect to time. |
| In the text | |
 |
Fig. 4 Data as in Fig. 3, plotted with respect to mean anomaly. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


