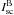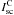| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A45 | |
| Number of page(s) | 5 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201219768 | |
| Published online | 25 July 2012 | |
Spectral line profiles changed by dust scattering in heavily obscured young stellar objects
1
Pulkovo Astronomical Observatory of the Russian Academy of
Sciences,
Pulkovskoe shosse 65,
196140
St. Petersburg,
Russia
e-mail: grinin@gao.spb.ru; lvtamb@mail.ru
2
The V.V. Sobolev Astronomical Institute of the St. Petersburg
University, Petrodvorets, 198904
St. Petersburg,
Russia
3
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
e-mail: weigelt@mpifr-bonn.mpg.de
Received: 6 June 2012
Accepted: 2 July 2012
It is known that scattering of radiation by circumstellar dust can strongly change the line profiles in stellar spectra. This hampers the analysis of spectral lines originating in the emitting regions of heavily obscured young stars. To calculate the line profile of the scattered radiation, we suggest to use the approximation of remote scattering particles. This approximation assumes that the scattering dust grains are at a distance from the star that is much larger than the characteristic size of the emitting region. Using this method, we calculated the line profiles of several simple models. They show the Hα line profiles of Herbig AeBe stars in the presence and absence of motionless or moving dust.
Key words: line: profiles / scattering / stars: winds, outflows / stars: pre-main sequence
© ESO, 2012
1. Introduction
Some amount of radiation scattered by circumstellar (CS) dust is present in the radiation of many young stars and is the main source of their linear polarization (Bastien & Landtsreet 1979). In most cases, the contribution of this radiation is very small and does not exceed a few percent. Exceptions are three groups of young stellar objects whose scattered radiation can substantially exceed the direct stellar radiation. First, these are young stellar objects (YSO) embedded in opaque gas and dust envelopes. According to the current classification, these are objects of Class I (White et al. 2007). The extinction toward some of them exceeds 20m (see, e.g., Beck et al. 1991). Young stars surrounded by circumstellar disks seen edge-on belong to the second group. In these stars, the direct radiation is strongly attenuated due to the extinction in the disk, and one can observe them only via scattered radiation (Padgett et al. 1999). The T Tauri star HH 30 is a prototype of these objects (Burrows et al. 1996). The third group consists of the UX Ori type stars. The photometric activity of these young stars is caused by the nonhomogeneous structure of their circumstellar disks and their small inclination to the line of sight (Grinin et al. 1991; Natta et al. 1999). Opaque fragments of the CS disk intersect the line of sight from time to time. During these events, the direct radiation of the star decreases while the contribution of the scattered radiation increases, which is testified by the growth of the linear polarization of the star (Grinin et al. 1991).
In all these cases, an observer obtains the information on the stellar spectrum by observing the radiation scattered by the circumstellar dust. It is well known that in the coordinate system of the dust particle, the photon frequency before and after scattering is the same. However, the resulting scattered-light spectrum is not the same as the spectrum in the absence of scattering.
As noted by Appenzeller et al. (2005), scattered light is not a precise source of information about obscured objects. These authors observed several T Tauri stars with edge-on disks. The analysis of their spectra showed that the disks are completely opaque at visible wavelengths and that light from the central objects reaches an observer only via scattering layers above and below the disk planes. According to these authors, light could be scattered either by matter located along the rotation axis or in the disk atmosphere. As a result, the spectrum of scattered radiation can differ from the spectrum of the CS emitting region. Grinin et al. (2006) considered the broadening of photospheric lines due to the scattering by the CS dust at the puffed-up inner rim of the accretion disks. This effect can be observed in UX Ori type stars during eclipses by opaque fragments of CS disks. The transformation of the spectral line profiles due to dust scattering in expanding dusty envelopes can also be observed in the spectra of evolved stars (see Lefevre 1992, and references therein).
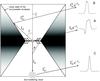 |
Fig. 1 Sketch of a deeply embedded young star with a rotating accreting disk, disk wind, and an envelope (cocoon) with low-density polar cavities. Dust particles are assumed to be near the polar axis and walls of the cavity. Possible profiles of emission lines are shown for several viewing conditions: direct (A) and scattered (B and C) radiation from the central object, which consists of the star, and its surrounding emitting region (e.g., disk and disk wind region). Here Ie is the emergent radiation from this central object, |
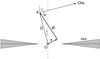 |
Fig. 2 Geometric parameters of the considered model (a central cross-section of the CS region). |
Below we consider several model situations typical for embedded YSOs (Fig. 1) and show how the profiles of spectral lines broadened by motion in the emitting gas (e.g., disk wind) can change after scattering by circumstellar dust particles.
2. Scattering by the motionless dust
The effect of scattering by dust particles depends on the geometry and kinematics of the line-formation region and the scattering region (see Fig. 1). If the spectral line arises, for example, in a flattened rotating envelope or accretion disk, the line profiles of the direct and scattered radiation can be very different: observer A, for example, would observe a wide double-peaked or P Cygni line profile from the accretion disk and/or disk wind. However, if the direct view to the emitting region is blocked, then observer B would observe a narrow single or double-peaked line. If there is scattering dust near the polar axis of the disk far away from the disk, then observer C would observe a very narrow line, since the radial motion seen at the position of the scattering dust is almost zero. These three simple examples show that the observed spectrum depends on both the geometry and kinematics of the emitting region itself and the distribution of the scattering particles in the neighborhood of the star.
In the general case when the spectral line originates in a moving gas with an arbitrary velocity field, the expression for the intensity Isc(ν) at the frequency ν of the radiation scattered at point A (Fig. 2) by a single motionless (in the coordinate system of the star) particle is 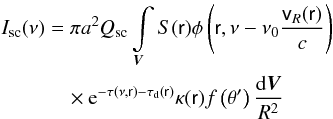 (1)here V is the volume occupied by the emitting gas, a is the radius of the particle, Qsc, f, and θ′ are the efficiency factor for scattering, phase function, and the scattering angle, respectively, S(r) is the source function for the transition considered at the point r of the emitting region, φ is the profile of the absorption coefficient normalized to the unity, vR(r) is the projection of the velocity of the emitting gas in the point r onto the vector R, which connects this point with the scattering particle at point A,
(1)here V is the volume occupied by the emitting gas, a is the radius of the particle, Qsc, f, and θ′ are the efficiency factor for scattering, phase function, and the scattering angle, respectively, S(r) is the source function for the transition considered at the point r of the emitting region, φ is the profile of the absorption coefficient normalized to the unity, vR(r) is the projection of the velocity of the emitting gas in the point r onto the vector R, which connects this point with the scattering particle at point A, 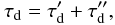 (2)where
(2)where 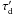 is the optical thickness between point r and point A caused by the CS extinction,
is the optical thickness between point r and point A caused by the CS extinction, 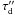 is the optical thickness between point A and the observer; κ is the integrated line opacity in the considered spectral line, and τ(ν,r) is the line optical depth at point r and for the frequency ν in the direction of point A
is the optical thickness between point A and the observer; κ is the integrated line opacity in the considered spectral line, and τ(ν,r) is the line optical depth at point r and for the frequency ν in the direction of point A 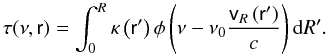 (3)Here the integration is performed along the vector R linking the scattering particles with the point r; r’ and R′ are the integration variables. We assume a complete redistribution in the line frequencies in the reference frame of the atom and use the Doppler profile φ in the calculations of τ and the line intensity.
(3)Here the integration is performed along the vector R linking the scattering particles with the point r; r’ and R′ are the integration variables. We assume a complete redistribution in the line frequencies in the reference frame of the atom and use the Doppler profile φ in the calculations of τ and the line intensity.
In order to take into account scattering by all particles, we have to integrate the expression (1) over the total volume occupied by the dust, as well as to consider all sizes and types of dust particles participating in scattering. The solution of this problem faces substantial difficulties. Therefore, below we consider the simplified model when scattering grains are at some fixed distance D = |D| from the star, and D is much larger than the characteristic size of the emitting region. This approximation is quite realistic in many cases since the region of the permitted line formation is usually much more compact than the region occupied by the CS dust.
2.1. Approximation of remote scattering particles
In this case, we can use the following simplifications: i) in integral (1), it is possible to replace R-2 by D-2 and thus to extract D-2 from the integral; ii) in the phase function f(θ′), it is possible to replace θ′ by ψ, where ψ is the angle between vector D and direction from the point A to the observer, and also extract it from the integral. We can do the same with the optical thickness τd if we use the optical thickness between the points O (location of the star) and A instead of 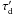 . After these simplifications we obtain the asymptotic equation for single scattering by the elementary volume at point A, which can be written in the following form:
. After these simplifications we obtain the asymptotic equation for single scattering by the elementary volume at point A, which can be written in the following form: 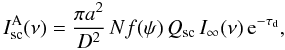 (4)where N is the number density of particles, I∞(ν) is the over the whole emitting region integrated intensity at frequency ν in the direction to the remote observer whose line of sight coincides with the vector D:
(4)where N is the number density of particles, I∞(ν) is the over the whole emitting region integrated intensity at frequency ν in the direction to the remote observer whose line of sight coincides with the vector D: 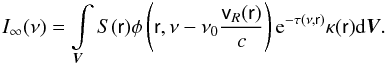 (5)Since the scattering particle is assumed to be motionless in the star coordinate system, the frequency of the scattered radiation in any direction will coincide with the frequency of the incident radiation, and since the values of f(ψ) and Qsc before the integral are practically constant within the profile of the spectral line, the value I∞(ν) will determine the line profile in the spectrum of the scattered radiation. It is important that this profile is the same for all scattering angles and depends only on the angle i′.
(5)Since the scattering particle is assumed to be motionless in the star coordinate system, the frequency of the scattered radiation in any direction will coincide with the frequency of the incident radiation, and since the values of f(ψ) and Qsc before the integral are practically constant within the profile of the spectral line, the value I∞(ν) will determine the line profile in the spectrum of the scattered radiation. It is important that this profile is the same for all scattering angles and depends only on the angle i′.
It should be stressed that the intensity of the radiation in the expression given above corresponds to the case of single scattering. Since we assume here that the dust particles are motionless in the star coordinate system, the photon frequency will be conserved in the next scattering. Thus, the first scattering plays a key role in the transformation of the line profile in the considered case. It should be noted, that in the optical region of the spectrum, albedo of scattering by CS dust is about 0.5 (see, e.g., Natta & Whitney 2000). Therefore, the first scattering gives the main contribution to the intensity of the scattered radiation.
2.2. The Hα line in the spectrum of the scattered radiation
As an example, let us consider the following model: the emission spectrum of the young star is formed in the axially symmetric disk wind, which starts from the surface of the accretion disk. The star and the emission region are surrounded by an optically thick axially symmetric envelope with cavity (see Fig. 1), whose polar region is transparent for the radiation. The spectrum of the radiation scattered by the dust on the surface of the cavity walls and by dust in the polar region is observed as the spectrum of the star.
For the calculations of 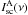 of the Hα line, we used the model of the magnetocentrifugal disk wind of Ae/Be Herbig stars reported by Grinin & Tambovtseva (2011). A description of this model is given in the cited paper and the Appendix.
of the Hα line, we used the model of the magnetocentrifugal disk wind of Ae/Be Herbig stars reported by Grinin & Tambovtseva (2011). A description of this model is given in the cited paper and the Appendix.
 |
Fig. 3 Profile of the Hα line in the spectrum of the radiation scattered at point A a–d) and the spectrum of direct radiation e). The parameters of the wind model are described in the text and the Appendix. The angle i′ between the symmetry axis of the disk and the vector D are 5° a), 20° b), 40° c), and 60° d). The angle between the line of sight and the symmetry axis of the disk is i = 80°e). |
The profiles of the Hα line in the spectrum of the scattered radiation are calculated for several cases where the angle i′ between the symmetry axis of the wind and the direction to the scattering particle ranged from 5 to 60 degrees (Figs. 3a−d), and the angle between the line of sight and the symmetry axis of the disk was i = 80°. Figure 3e shows the Hα line profile which the observer could see in the absence of scattering. We see that this profile (broadened by the motion of the emitting gas) has a P Cygni shape (instead of pure emission) and it is wider than the profiles observed after scattering at the point A. This example shows that even in the case of the motionless dust, the profile of the spectral line of the direct radiation and the radiation after scattering can strongly differ.
3. Scattering by the moving dust
In the reality, the dust particles are moving. The motion may be purely Keplerian rotation of the CS disk or purely radial (bi-conical) outflow, or their combination, like in the dusty disk wind (Safier 1993; Königl & Salmeron 2011). Scattering of photons by moving dust provides an additional Doppler shift of the photon frequency, which leads to an additional deformation of the line profiles. In this case, in Eq. (4) we have to replace ν by ν′, where ![\begin{equation} \label{5} \nu' = \nu + \left[v_s + u_s - v\cos{\left(\theta-i'\right)}\right]/c \end{equation}](/articles/aa/full_html/2012/08/aa19768-12/aa19768-12-eq56.png) (6)here vs and us are the projections of the radial (v) and rotation (u) velocity components at point A on the line of sight s:
(6)here vs and us are the projections of the radial (v) and rotation (u) velocity components at point A on the line of sight s: ![\begin{eqnarray} \label{6} v_s &= v\left(\cos{\theta}\cos{i} + \sin{\theta}\sin{i}\cos{\varphi}\right), \\[1.5mm] \label{7} u_s &= - u\sin{i}\sin{\varphi}, \end{eqnarray}](/articles/aa/full_html/2012/08/aa19768-12/aa19768-12-eq61.png) where ϕ is the azimuthal coordinate angle of point A (see Fig. 4).
where ϕ is the azimuthal coordinate angle of point A (see Fig. 4).
The term −vcos(θ − i′)/c in Eq. (6) takes into account the Doppler shift of the frequency ν due to the motion of the scattering particles relatively to the emitting region.
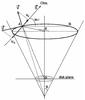 |
Fig. 4 Sketch of a dust particle at point A moving with the velocity components v and u and scattering the photons in the direction to an observer. |
 |
Fig. 5 Profile of the Hα line in the spectrum of the scattered radiation with (solid) and without (dots) assuming dust motion: a) line profile transformation due to a radial outflow with velocity v = 100 km s-1; b) line profile transformation due to rotation (u = 100 km s-1); c) line profile of direct radiation in the absence of dust scattering. The angle between the symmetry axis and the direction to the scattering particle is i′ = 40°, the angle between the symmetry axis of the disk and the line of sight is i = 80°. |
The intensity of the scattered radiation at the frequency ν in the direction to an observer is the integral over the whole volume V: 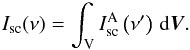 (9)Below we consider two limiting cases: a) radial motion of the dust particles with constant velocity v and tangential velocity u = 0, and b) tangential motion of the dust with the velocity u and radial velocity v = 0. The intensity of the scattered radiation from all elementary segments of the scattering volume with fixed coordinates θ, D is:
(9)Below we consider two limiting cases: a) radial motion of the dust particles with constant velocity v and tangential velocity u = 0, and b) tangential motion of the dust with the velocity u and radial velocity v = 0. The intensity of the scattered radiation from all elementary segments of the scattering volume with fixed coordinates θ, D is: 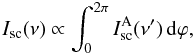 (10)where
(10)where 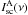 is determined from Eq. (4) but with changes described above (Eqs. (6)−(8)).
is determined from Eq. (4) but with changes described above (Eqs. (6)−(8)).
When calculating the line profile of the scattered radiation on the base of this formula, we assumed for simplicity that θ = i′, the optical thickness between the scattering particles and the observer τ′′ ≪ 1, and the scattering is isotropic.
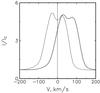 |
Fig. 6 Profile of the Hα line in the spectrum of the scattered radiation with (solid) and without (dots) radial outflow of the dust with v = 100 km s-1. The contribution of the back wall is only considered here. Therefore, the angle ϕ in Eq. (8) is varied from π/2 to 3π/2. The other parameters are the same as in Fig. 5. See text for more details. |
The results of the calculations for the limiting cases described above are presented in Figs. 5 and 6. According to Fig. 5, a radial motion of the dust from the star provides a red shift of the line profile. This shift will be larger if the main contribution to the scattered light is provided by the back wall of the conical cavity (Fig. 6), which is observed in some heavily obscured stars (see, e.g., Preibisch et al. 2003). The rotation does not shift the line profile, but smooths it and makes it broader (Fig. 5b).
These examples show that the effect of motion of the CS dust leads to more divers transformations of the line profiles compared to the case of motionless dust. In the both cases considered above, the line profile of the scattered radiation strongly deviates from the profile of the direct radiation in the absence of scattering presented in Fig. 5c.
4. Summary and concluding remarks
The presented calculations show that the profiles of spectral lines arising in moving CS gas can change when scattering by CS dust takes place. The distortion can appear even if the CS dust is not moving in the coordinate system of the star. The lines have more diverse forms in the case of the moving dust. This is important to keep in mind when analyzing emission spectra of heavily obscured young stars, and it is especially important for the comparison of spectral lines at different wavelength (e.g., Hα and Brγ), since the dust extinction depends on the wavelength. In heavily obscured young objects, the Hα line is observed via the scattering radiation in practically all cases. The contribution of the scattered light to the Brγ line is less important if AV ≤ 7−8m. However, in young objects with AV ≫ 8m, even the Brγ is predominatingly observed in the scattered light and its profile can also be distorted by scattering. In these cases, only observations of mid- and far-infrared spectral lines may avoid these scattering effects.
The changes of the spectral line profiles due to the scattering by the CS dust is also valid for the photospheric spectrum of the star itself since its radiation propagates in a similar same way to an observer as the radiation of the CS emitting region. As a result, the measured radial and rotational velocities of the heavily obscured star can differ from their real values.
It should be noted, that in the case when the spectral line is formed in a spherically symmetric stellar wind, the spectrum of radiation scattered by a single particle at an arbitrary remote point will be the same for any scattering angle and will coincide with the spectrum of the direct radiation of the star. This is the only kind of model where the profiles of the spectral lines do not change in the case of dust scattering.
Finally, we emphasize that highly obscured YSOs are, of course, not the only objects in which the scattered radiation can be an important component of the observed radiation. Similar conditions exist in active galaxy nuclei observed under certain inclinations (see Antonucci & Miller 1985; Antonucci 1993; Cohen et al. 1999; Smith et al. 2005, and references there). In these objects, the scattered radiation arises due to the Thomson scattering on free electrons and also due to scattering by dust particles in the dusty torus and the Narrow Line region. Spectropolarimetric observations have played an important role in studies of the physical properties of these objects. Similar spectropolarimetric observations would also be very useful in studies of heavily obscured YSOs.
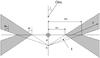 |
Fig. 7 Sketch of the geometry of the disk-wind model adopted. |
Appendix: The disk wind model
For the description of the disk wind, we use a coordinate system (l, θ, ω) centered at point S (see the sketch in Fig. 7). In MHD models of the disk wind, the inclination angle of the first streamline with respect to the disk plane is typically assumed to be around 60° (Blandford & Payne 1982). However, in the case of the hot Herbig Be stars, the strong stellar radiation pressure can bend down the streamlines and make the disk wind flatter. The kinematical model described below is typical for disk-wind models adopted for different astrophysical objects with accretion disks including young stars stars (see e.g., Kurosava et al. 2006, and references there). It is assumed that the tangential velocity of the wind changes along streamlines as: 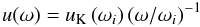 (11)where ω = l sinθ is the distance of the point (l,θ) from the rotation axis and ωi = li sinθ; uK (ωi) = (G M∗/ωi)1/2 at the point (ωi) at the base of streamline i.
(11)where ω = l sinθ is the distance of the point (l,θ) from the rotation axis and ωi = li sinθ; uK (ωi) = (G M∗/ωi)1/2 at the point (ωi) at the base of streamline i.
The radial velocity v increases along the streamlines as 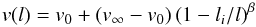 (12)where v0 and v∞ are the initial and terminal values of the radial velocity and β is a parameter. We adopt for simplicity v∞ = f uK(ωi), where uK(ωi) is the Keplerian velocity at distance ωi from the disk axis, and f is a parameter. As in the Kurosawa et al. (2006) paper we used f = 2.
(12)where v0 and v∞ are the initial and terminal values of the radial velocity and β is a parameter. We adopt for simplicity v∞ = f uK(ωi), where uK(ωi) is the Keplerian velocity at distance ωi from the disk axis, and f is a parameter. As in the Kurosawa et al. (2006) paper we used f = 2.
The local mass-loss rate per unit area of the disk, ṁw, is a function of the cylindric radius ω. For the description of ṁw, we use a simple power law 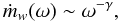 (13)where γ is the input parameter. The other input parameter is the total mass loss rate integrated over all the disk wind ejection region (from both sides of the disk) Ṁw.
(13)where γ is the input parameter. The other input parameter is the total mass loss rate integrated over all the disk wind ejection region (from both sides of the disk) Ṁw.
Using the continuity equation, we calculated the distribution of the number density in each point of the disk wind. The calculations of the ionization state and the number densities of the atomic levels were performed for the isothermal disk wind model with the account of both collision and radiative processes on the base of the Sobolev approximation (see Grinin & Tambovtseva 2011, for more details).
The radiation of the disk wind was calculated for the following model parameters: the mass loss rate Ṁw = 10-9 M⊙ yr-1; the electron temperature Te = 8000 K, M∗ = 2.5 M⊙, R∗ = 2.4 R⊙, γ = 1, the disk wind launching region is located between 0.1 and 1 AU. The half opening angle of the disk wind θ1 = 60° (see Fig. 7). The radiation of the star is described by the Kurucz model with the effective temperature Tef = 104 K and log g = 4.
Acknowledgments
This research has been supported in part by the program of the Presidium of RAS N 21 and grant N. Sh.- 1625.2012.2.
References
- Antonucci, R. R. J. 1993, ARA&A, 31, 473 [Google Scholar]
- Antonucci, R. R. J., & Miller, J. S. 1985, ApJ, 297, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., Bertout, C., & Stahl, O. 2005, A&A, 434, 1005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Bastien, P., & Landstreet, J. D. 1979, ApJ, 229, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Beck, S. C., Fischer, J., & Smith, H. A. 1991, ApJ, 383, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Burrows, C. J., Stapelfeldt, K. R., Watson, A. M., et al. 1996, ApJ, 473, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., Ogle, P. M., Tran, H. D., et al. 1999, AJ, 118, 1963 [NASA ADS] [CrossRef] [Google Scholar]
- Grinin, V. P., & Tambovtseva, L. V. 2011, Astron. Rep., 55, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Grinin, V. P., Kiselev, N. N., Chernova, G. P., et al. 1991, Ap. Sp. Sci., 186, 283 [Google Scholar]
- Grinin, V. P., Mitskevich, A. S., & Tambovtseva, L. V., 2006, Astron. Lett., 32, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Königl, A., & Salmeron, R. 2011, in Physical Processes in Circumstellar Disks around Young Stars, ed. P. J. V. Garcia (Chicago, IL: University of Chicago Press), 283 [Google Scholar]
- Kurosawa, R., Harries, T. J., & Symington, N. H. 2006, MNRAS, 370, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Lefevre, J. 1992, A&A, 254, 274 [NASA ADS] [Google Scholar]
- Malbet, F., Benisty, M., de Wit, W.-J., et al. 2007, A&A, 464, 43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Natta, A., & Whitney, B. 2000, A&A, 364, 633 [NASA ADS] [Google Scholar]
- Natta, A., Prusti, T., Neri, R., et al. 1999, A&A, 350, 541 [NASA ADS] [Google Scholar]
- Padgett, D. L., Brandner, W., Stapelfeldt, K. R., et al. 1999, AJ, 117, 1490 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., Balega, Y. Y., Schertl, D., & Weigelt, G. 2003, A&A, 412, 735 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Safier, P. 1993, ApJ, 408, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, J. E., Robinson, A., Young, S., et al. 2005, MNRAS, 359, 846 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. J., Greene, T. P., Doppmann, G. W., et al. 2007, in Protostars & Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil (Tucson: University of Arizona Press), 951 [Google Scholar]
- Weigelt, G., Grinin, V. P., Groh, J. H., et al. 2011, A&A, 527, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Sketch of a deeply embedded young star with a rotating accreting disk, disk wind, and an envelope (cocoon) with low-density polar cavities. Dust particles are assumed to be near the polar axis and walls of the cavity. Possible profiles of emission lines are shown for several viewing conditions: direct (A) and scattered (B and C) radiation from the central object, which consists of the star, and its surrounding emitting region (e.g., disk and disk wind region). Here Ie is the emergent radiation from this central object, |
| In the text | |
 |
Fig. 2 Geometric parameters of the considered model (a central cross-section of the CS region). |
| In the text | |
 |
Fig. 3 Profile of the Hα line in the spectrum of the radiation scattered at point A a–d) and the spectrum of direct radiation e). The parameters of the wind model are described in the text and the Appendix. The angle i′ between the symmetry axis of the disk and the vector D are 5° a), 20° b), 40° c), and 60° d). The angle between the line of sight and the symmetry axis of the disk is i = 80°e). |
| In the text | |
 |
Fig. 4 Sketch of a dust particle at point A moving with the velocity components v and u and scattering the photons in the direction to an observer. |
| In the text | |
 |
Fig. 5 Profile of the Hα line in the spectrum of the scattered radiation with (solid) and without (dots) assuming dust motion: a) line profile transformation due to a radial outflow with velocity v = 100 km s-1; b) line profile transformation due to rotation (u = 100 km s-1); c) line profile of direct radiation in the absence of dust scattering. The angle between the symmetry axis and the direction to the scattering particle is i′ = 40°, the angle between the symmetry axis of the disk and the line of sight is i = 80°. |
| In the text | |
 |
Fig. 6 Profile of the Hα line in the spectrum of the scattered radiation with (solid) and without (dots) radial outflow of the dust with v = 100 km s-1. The contribution of the back wall is only considered here. Therefore, the angle ϕ in Eq. (8) is varied from π/2 to 3π/2. The other parameters are the same as in Fig. 5. See text for more details. |
| In the text | |
 |
Fig. 7 Sketch of the geometry of the disk-wind model adopted. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.