© ESO, 2012

1. Introduction

Studies of planetary formation in binary stellar systems are an intriguing and challenging task. Although the majority of stars are members of such systems (Duquennoy & Mayor 1991), only a handful of exoplanets have so far been detected around compact binaries (i.e. stellar separation below  ~50 AU). Even so, their very existence appears to be inconsistent with models and theories that work for single stars, which pushes some crucial parameters to extreme values.

The case of the γ-Cephei binary is particularly interesting because it is one of the most extreme systems that harbors a giant planet. The stellar system is formed by a primary star with a mass of M_A = 1.6   M_⊙ and a secondary with a mass of M_B = 0.34   M_⊙. The M_B body orbits around M_A with a semimajor axis of a_AB = 18.5AU and an eccentricity of e_AB = 0.36 (Hatzes et al. 2003).

The giant planet that orbits M_A has been the object of many studies over the past decade (e.g. Marzari & Scholl 2002; Thébault 2004; 2006; Haghighipour & Raymond 2007; Paardekooper et al. 2008; Beaugé et al. 2010) and we have yet to find a suitable physical scenario to explain its existence. Artymowicz and Lubow (1994) showed that the circumplanetary disk is tidally truncated by its companion. This truncation occurs at a location close to the outer limit for dynamical stability of solid particles, and therefore safely lies beyond the position of all detected exoplanets. It nevertheless poses a problem, especially for giant planet formation, because it deprives the disk from a large fraction of its mass. Another consequence of disk truncation is that it shortens the lifetime of the disk, and in turn the timespan for gaseous planet formation (Cieza et al. 2009). To complicate the scenario even more, Nelson (2000) suggested that for an equal-mass binary of separation 50 AU, temperatures in the disk might stay too high to allow grains to condense.

Even if grains can condense, binary perturbations might impede their growth by increasing the impact velocities beyond the disruption limit (e.g. Marzari & Scholl 2000). Although gas drag helps to introduce a phase alignment in the pericenter and, thus, to decrease the relative velocities of nearby bodies, this appears to work only for equal-size planetesimals (e.g. Thébault et al. 2006) and circular gas disks. Eccentric and even precessing gas disks complicate the picture still more (Paardekooper et al. 2009; Marzari et al. 2009; 2012), although it may indeed work in our favor in the outer parts of the disk (Beaugé et al. 2010).

In recent years several studies have been performed on the role of mutual inclinations between the planetesimals, the gas disk, and the binary companion (Marzari et al. 2009b; Xie et al. 2010; Thébault et al. 2010; Müller & Kley 2012; Zhao et al. 2012). However, even this additional degree of freedom does not appear to be a solution and, in the particular case of γ-Cephei, does not seem to favor planetary formation for bodies at a > 2 AU, which is expected to be the breading ground for the planet detected in this system.

In a recent review of the state of the art in this problem, Thébault (2011) wondered whether the whole idea of core-instability planetary formation is feasible in such systems, or if we must resort to gas-instability models (Duchene 2010). However, as Thébault (2011) points out, “the disk instability scenario also encounters severe difficulties in the context of close binaries, and it is too early to know if it can be a viable alternative formation channel”.

So, the question remains: how did the planet manage to form around the star γ-Cephei-A? Here we revisit an alternative route, based on the concept of stellar scattering. We assume that planet m_p formed (by one of the accepted models of planetary formation) around M_A, but in a different dynamical configuration in which the star M_A is single or the companion M_B is sufficiently wide to allow the formation of the planetary system.

The scenario explained is not new. Pfahl (2005) and Portegies Zwart & McMillan (2005) discussed such a mechanism to explain the origin of a planet then believed to exist in the HD 188753 system (Konacki 2005), although the existence of this body was subsequently questioned and is so far unconfirmed.

A slightly different analysis was later presented by Marzari & Barbieri (2007a,b), were the authors studied the survival of circumstellar planets in dynamically unstable triple stellar systems or in binaries that suffered a close encounter with a third (background) star. These papers explored, for the first time the possibility that the current configuration of the γ-Cephei stellar components may not be primordial, and that the exoplanet may have been formed under different circumstances.

In this paper we again address the proposal of Marzari & Barbieri (2007a), and study the effects of hyperbolic fly-bys of background stars in a binary system similar to γ-Cephei. The idea is to see under which initial conditions and system parameters it is possible to transform a primordial accretion-friendly stellar system to the current (accretion-hostile) configuration. Since our work is dedicated to a single binary system, we are able to explore a larger set of parameters and situations, as well as different types of outcomes. We also include a statistical analysis of the results considering distribution probabilities for impacting velocities and stellar masses.

The work is organized as follows. In Sect. 2 we review the idea of gravitational scattering, with special emphasis on hierarchical three-body systems. Section 3 presents our N-body code and some test runs to analyze the importance of the free parameters in the scattering outcomes. Our main numerical simulations are discussed in Sect. 4, while a probability analysis of positive outcomes is presented in Sect. 5. Conclusions finally close the paper in Sect. 6.

2. Gravitational scattering in hierarchical three-body systems

The gravitational interaction between a star and a binary system is a classical problem in stellar dynamics (e.g. Heggie 1975; Hills 1975; Hut & Bahcall 1983; Heggie & Hut 1993; Portegies Zwart et al. 1997), although it is focused on the relationship between binaries and the dynamical evolution of open clusters. The same principles, however, may also be applied to other problems, such as the origin of exoplanets in multiple stellar systems (Pfahl 2005; Portegies Zwart & McMillan 2005) and the dynamical evolution of “cold” exoplanets with orbits very distant from the central star (e.g. Veras et al. 2009).

2.1. The hyperbolic two-body problem

We assume a compact stellar binary system with masses m_A and m_B, whose orbital separation is small compared with the initial distance of an incoming star m_C. In this scenario, and at least for the initial conditions of the hyperbolic encounter, we may approximate the two binary components by a unique body of mass m_A + m_B (see Hut & Bahcall 1983), and refer the orbit of the impactor with respect to the barycenter of the binary.

In classical scattering problems, the outcome of the fly-by may be defined by two fundamental parameters: the infall velocity of the incoming body at infinity 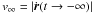${\mathit{v}}_{\mathrm{\infty }}\mathrm{=}\mathrm{\left|}\dot{{r}}\mathrm{\right(}\mathit{t}\mathrm{\to }\mathrm{-}\mathrm{\infty }\mathrm{\left)}\mathrm{\right|}$ and the impact parameter b, defined as the minimum distance between the two bodies if there were no deflection. Alternatively, it is possible to substitute b with the minimum distance r_min = a(1 − e) between the impactor and the center of mass of the pair m_A + m_B.

Following the approach developed by Hills (1975), we can approximate the total orbital energy of the three-star system, prior to the encounter, by 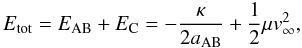${\mathit{E}}_{\mathrm{tot}}\mathrm{=}{\mathit{E}}_{\mathrm{AB}}\mathrm{+}{\mathit{E}}_{\mathrm{C}}\mathrm{=}\mathrm{-}\frac{\mathit{\kappa }}{\mathrm{2}{\mathit{a}}_{\mathrm{AB}}}\mathrm{+}\frac{\mathrm{1}}{\mathrm{2}}\mathit{\mu }{\mathit{v}}_{\mathrm{\infty }}^{\mathrm{2}}\mathit{,}$(1)where both κ and μ are two mass factors defined according to 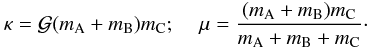$\mathit{\kappa }\mathrm{=}\mathrm{𝒢}\mathrm{(}{\mathit{m}}_{\mathrm{A}}\mathrm{+}{\mathit{m}}_{\mathrm{B}}\mathrm{)}{\mathit{m}}_{\mathrm{C}}\mathrm{;}\mathit{\mu }\mathrm{=}\frac{\mathrm{(}{\mathit{m}}_{\mathrm{A}}\mathrm{+}{\mathit{m}}_{\mathrm{B}}\mathrm{)}{\mathit{m}}_{\mathrm{C}}}{{\mathit{m}}_{\mathrm{A}}\mathrm{+}{\mathit{m}}_{\mathrm{B}}\mathrm{+}{\mathit{m}}_{\mathrm{C}}}\mathrm{·}$(2)In Eq. (1) E_AB is the binding energy of the binary and E_C is the kinetic energy of the impactor. a_AB is the semimajor axis of m_B with respect to m_A. We assume that initially m_C is sufficiently far from the other two that we can neglect its potential energy. The same calculation can also be made after the scattering event has taken place, now in terms of the new semimajor axis of the binary (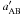${\mathit{a}}_{\mathrm{AB}}^{\mathrm{\prime }}$) and the outgoing velocity of m_C (which we will denote by ${\mathit{v}}_{\mathrm{\infty }}^{\mathrm{\prime }}$).

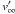We can then use the conservation of E_tot to write (see Heggie 1975) 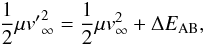$\frac{\mathrm{1}}{\mathrm{2}}\mathit{\mu }{{\mathit{v}}^{\mathrm{\prime }}}_{\mathrm{\infty }}^{\mathrm{2}}\mathrm{=}\frac{\mathrm{1}}{\mathrm{2}}\mathit{\mu }{\mathit{v}}_{\mathrm{\infty }}^{\mathrm{2}}\mathrm{+}\mathrm{\Delta }{\mathit{E}}_{\mathrm{AB}}\mathit{,}$(3)where ΔE_AB is the change in the binding energy of the binary. The minimum velocity v_c of the impactor necessary to disrupt the binary is such that ΔE_AB = E_AB or, equivalently, E_tot = 0. This gives (Hut & Bahcall 1983) 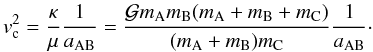${\mathit{v}}_{\mathrm{c}}^{\mathrm{2}}\mathrm{=}\frac{\mathit{\kappa }}{\mathit{\mu }}\frac{\mathrm{1}}{{\mathit{a}}_{\mathrm{AB}}}\mathrm{=}\frac{\mathrm{𝒢}{\mathit{m}}_{\mathrm{A}}{\mathit{m}}_{\mathrm{B}}\mathrm{(}{\mathit{m}}_{\mathrm{A}}\mathrm{+}{\mathit{m}}_{\mathrm{B}}\mathrm{+}{\mathit{m}}_{\mathrm{C}}\mathrm{)}}{\mathrm{(}{\mathit{m}}_{\mathrm{A}}\mathrm{+}{\mathit{m}}_{\mathrm{B}}\mathrm{)}{\mathit{m}}_{\mathrm{C}}}\frac{\mathrm{1}}{{\mathit{a}}_{\mathrm{AB}}}\mathrm{·}$(4)It will prove useful to write the incoming velocity of the impactor v_∞ in units of v_c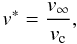${\mathit{v}}^{\mathrm{\ast }}\mathrm{=}\frac{{\mathit{v}}_{\mathrm{\infty }}}{{\mathit{v}}_{\mathrm{c}}}\mathit{,}$(5)which gives an adimensional expression for the incoming velocity. Furthermore, v_∞ can be written in terms of the semimajor axis of the hyperbolic orbit as: 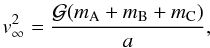${\mathit{v}}_{\mathrm{\infty }}^{\mathrm{2}}\mathrm{=}\frac{\mathrm{𝒢}\mathrm{(}{\mathit{m}}_{\mathrm{A}}\mathrm{+}{\mathit{m}}_{\mathrm{B}}\mathrm{+}{\mathit{m}}_{\mathrm{C}}\mathrm{)}}{\mathit{a}}\mathit{,}$(6)where a is the the semimajor axis of m_C with respect to the center of mass of the binary m_A + m_B. Recalling expression (4), we may now write the relationship between a and v^∗ as 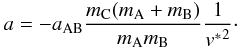$\mathit{a}\mathrm{=}\mathrm{-}{\mathit{a}}_{\mathrm{AB}}\frac{{\mathit{m}}_{\mathrm{C}}\mathrm{(}{\mathit{m}}_{\mathrm{A}}\mathrm{+}{\mathit{m}}_{\mathrm{B}}\mathrm{)}}{{\mathit{m}}_{\mathrm{A}}{\mathit{m}}_{\mathrm{B}}}\frac{\mathrm{1}}{{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}}\mathrm{·}$(7)Similarly, we can obtain the eccentricity of the hyperbolic orbit of m_C as 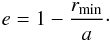$\mathit{e}\mathrm{=}\mathrm{1}\mathrm{-}\frac{{\mathit{r}}_{\min }}{\mathit{a}}\mathrm{·}$(8)Finally, if we define ϵ₀ as the value of the eccentric anomaly at the beginning of the simulation (when r = r₀), we can calculate the initial position and velocity of m_C using the usual expressions for hyperbolic motion (e.g. Butler 2005).

2.2. Complete set of variables for the scattering problem

The set (v_∗,r_min,ϵ₀) defines the initial conditions for the impactor m_C, with respect to the center of mass of m_A + m_B, assuming that the differential gravitational interactions from both components do not significantly perturb the two-body hyperbolic orbit (see Hut & Bahcall 1983, for a similar approach). However, even if this condition is not satisfied, and the orbit of the incoming star is seriously affected by the two central bodies, the values of (v_∗,r_min) are still indicative of the “unperturbed” motion of m_C, and therefore may still be referred to as variables of the problem.

To complete the description of the system, we must give the initial conditions for each of the binary components at a given time. These can be uniquely specified by the set of m_A-centric orbital elements of m_B: (a_B,e_B,I_B,λ_B,ω_B,Ω_B), where the inclination I_B is given with respect to the orbital plane of the incoming impactor. Since the value of ϵ is already a variable of the system, it appears less complicated to specify the value of the mean longitude λ_B at the time of maximum approach of the impacter (i.e. r = r_min). From the two-body solution we can then calculate the value of the mean longitude at the initial time ϵ = ϵ₀ and calculate the position and velocity vectors of m_A and m_B at the beginning of the simulation.

As with the initial conditions for m_C, it is not expected that the orbits of the binary stars remain constant in time. Accordingly, the values for the orbital elements adopted as initial conditions are also “unperturbed” values, in the same way as the impact parameter b is the unperturbed minimum distance between the projectile and the target.

Last of all, and since our ultimate aim will be to study the exoplanet detected around γ-Cephei-A, we will also assume that a small planetary mass m_p orbits the central star m_A. The initial m_A-centric orbit of the planet will be circular and specified by values of (a_p,I_p,λ_p,Ω_p), where λ_p is once again given at the time when r_C = r_min.

To summarize, we need to set initial values for 16 independent variables in order to get a full description of the scattering event. These are 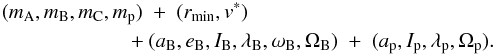$\begin{array}{ccc}& & \mathrm{\left(}{\mathit{m}}_{\mathrm{A}}\mathit{,}{\mathit{m}}_{\mathrm{B}}\mathit{,}{\mathit{m}}_{\mathrm{C}}\mathit{,}{\mathit{m}}_{\mathrm{p}}\mathrm{\right)}\mathrm{+}\mathrm{\left(}{\mathit{r}}_{\min }\mathit{,}{\mathit{v}}^{\mathrm{\ast }}\mathrm{\right)}\\ & & \end{array}$(9)We recall that the m_A-centric orbital elements of m_B are assumed to correspond to the point at which the impactor has its maximum approach if the impactor had zero mass.

Of course, previous knowledge of the dynamical system implies that some variables are already known, such as most of the masses and the main orbital elements. However, this still leaves us with a significant number of degrees of freedom to explore.

3. The numerical code

Once we set the values for the stellar masses and initial conditions, we integrated the equations of motion using an N-body code to simulate the scattering event. Dynamically, the problem may be characterized as a hierarchical (or nested) full four-body problem, in which all mutual gravitational interactions are taken into account.

For the simulations described in this work we employed a code constructed around a Bulrisch-Stoer integrator with an error tolerance of ll = 13. Since the scattering event is expected to be extremely sensitive to the initial conditions, especially if the impact parameter is small, we performed a series of preliminary runs that included back integrations from the final configurations. In all cases there was no significant difference between the two branches of the same trajectory.

Our working hypothesis is that the current γ-Cephei system could be the outcome of a stellar scattering event that either modified the orbit of the secondary star or caused an exchange of massive bodies. To study whether this is possible, we employes the concept of reverse integration. In other words, our initial conditions were the present day orbital configuration of the γ-Cephei system plus an additional star m_C in an arbitrary outward-bound hyperbolic orbit. We then integrated the system backwards in time to reproduce the hypothetical scattering event and find the “initial conditions” that led to the present system. It is important to stress that this procedure can only be employed in purely conservative systems where the equations of motion are time-reversible. Therefore, we did not consider the effects of any non-conservative force such as gas drag of tidal effects between the bodies.

We considered that a simulation yields a positive result when the following two conditions are met:

• the planet m_p remains bounded to m_A in an orbit with moderate to low eccentricity (e.g. e_p < 0.1);

• the region around m_p becomes compatible with planetary formation according to standard core-accretion scenario. This could either be a consequence of a significant increase in the semimajor axis of the secondary binary component, or a stellar exchange in which m_A becomes a single star.

Since the equations of motion of the N-body problem are time-reversible, the final outcomes of our simulations would then constitute possible initial conditions that could explain the current planetary system.

3.1. Possible outcomes

Depending on the relative magnitudes between v_∞ and ΔE_AB, we can list five possible outcomes of a hyperbolic fly-by: de-excitation, excitation, resonance, ionization, and exchange. The reader is referred to Heggie (1975) for more details, including explicit conditions for each type.

Not all possible outcomes are relevant for the case at hand. For example, resonance is a transitory state, at least in the point-mass approximation, and following complex interactions between all three stars, at least one will leave the system in a hyperbolic orbit. Ionization implies that all three stars acquire unbounded motion with respect to the other two; the original binary is then destroyed, but not replaced. Since in our case we worked with a reverse temporal axis, this would mean that the present-day γ-Cephei is the outcome of a triple encounter of isolated stars, a highly improbable situation, to say the least.

Since our aims are more restrictive and focused on finding possible formation mechanisms for γ-Cephei-A-b, we prefer to redefine the possible outcomes according to what Pfahl (2005) calls “scenarios”. These are (Fig. 1):

• Type I: the impactor m_C captures the secondary component m_B during the encounter, leaving behind m_A as a single star with the planet still bounded in a quasi-circular orbit.

• Type II: while there is no exchange in the memberships, the binary m_A + m_B acquires a sufficiently wide orbit to allow planetary formation in the region around m_p.

• Type III: the incoming star m_C changes place with m_B where this star is expelled from the system. The new binary m_A + m_C is sufficiently wide to allow planetary formation around the location of m_p.

Both types I and III are cataloged as exchange in Heggie’s nomenclature, while type II corresponds to an excitation. Marzari & Barbieri (2007a) only discussed type-II outcomes.

In addition to the types listed before, we also found a few cases of three other types of outcomes. Although these were very rare and have only a negligible effect on the statistical analysis performed later on, we will nevertheless include them here for completeness and for a full understanding of the complexity of the problem. These will be referred to as types IV to VI, and correspond to the following scenarios:

• Type IV: the impactor m_C not only captures the secondary component m_B during the encounter (which would be cataloged as type I), but also the planet that originally orbited m_A. The final configuration then includes a new binary m_B + m_C with the planet orbiting m_C.

• Type V: the impactor m_C carries away both m_A and its planet m_p, but in the final configuration the planet now orbits m_C.

• Type VI: the passage of the impactor m_C only captures the planet from the original binary, leaving behind a planet-less m_A + m_B system.

As mentioned in the previous section (see Eq. (2)), we need to specify a total of 16 parameters/variables. Of these, however, several will be fixed to represent the γ-Cephei system. For the masses we adopted the values 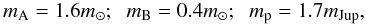${\mathit{m}}_{\mathrm{A}}\mathrm{=}\mathrm{1.6}{\mathit{m}}_{\mathrm{\odot }}\mathrm{;}{\mathit{m}}_{\mathrm{B}}\mathrm{=}\mathrm{0.4}{\mathit{m}}_{\mathrm{\odot }}\mathrm{;}{\mathit{m}}_{\mathrm{p}}\mathrm{=}\mathrm{1.7}{\mathit{m}}_{\mathrm{Jup}}\mathit{,}$(10)while for the m_A-centric orbit of m_B we assumed: 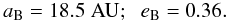${\mathit{a}}_{\mathrm{B}}\mathrm{=}\mathrm{18.5}\mathrm{AU}\mathrm{;}{\mathit{e}}_{\mathrm{B}}\mathrm{=}\mathrm{0.36.}$(11)Finally, we assumed for the m_A-centric semimajor axis of the planet m_p, a_p = 2.1 AU. The remaining ten parameters where considered to be unknown and free to modify in our series of runs.

3.2. Test runs

Not all variables are created equal, and some are expected to be more influential in determining the outcome of the scattering event. The aim of these preliminary series of runs is to estimate how each parameter affects the dynamics and what may be preferential values.

We began with three series of runs, each with fixed values of the impactor mass. The values adopted for each run are m_C = 0.2 (series 1), m_C = 0.4 (series 2) and m_C = 1.0 (series 3), with values given in solar masses. All orbits are assumed to lie on the same plane (i.e. I_i = 0, and Ω_i indeterminate) and the remaining angles are taken equal to zero. At the beginning of each integration, the impactor is set at a distance from the binary equal to r₀ = 50Q_B, where Q_B = a_B(1 + e_B) is the apocentric distance between both components. Since the orbital elements of the planet and binary are given at r = r_min, the outcome of the scattering event is not dependent on the value of r₀, as long as it is chosen to be sufficiently large.

Thus, in each series we have only two free parameters left: (r_min,v^∗). For each series we chose a total of 2.5 × 10⁵ values chosen from an equispaced 500 × 500 grid within the intervals: 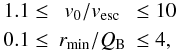$\begin{array}{ccc}\mathrm{1.1}\mathrm{\le }& {\mathit{v}}_{\mathrm{0}}\mathit{/}{\mathit{v}}_{\mathrm{esc}}& \mathrm{\le }\mathrm{10}\\ \mathrm{0.1}\mathrm{\le }& {\mathit{r}}_{\min }\mathit{/}{\mathit{Q}}_{\mathrm{B}}& \end{array}$(12)where v₀ is the magnitude of the initial velocity at r = r₀ and v_esc the escape velocity at that point. Thus, we consider initial speeds ranging from almost parabolic orbits to highly hyperbolic fly-bys. After some simple algebraic calculations, we find that the corresponding interval in v^∗ is approximately 0.08 ≤ v^∗ ≤ 1.7.

Figure 2 shows the post-scattering m_A-centric orbital elements of the secondary star of the resulting binary system. Since the central star becomes isolated in type-I interactions, only type II (left) and type III (right) are analyzed. In the first case, m_B remains bounded to m_A, so the eccentricity and semimajor axis plotted are those of m_B. In type-III outcomes, however, the final binary is now m_A + m_C, so the orbital elements are those of m_C with respect to m_A. Black squares show those runs in which the planetary orbit remained almost circular (e.g. e_p < 0.1), while those in which m_p was severely perturbed are shown in brown.

In most cases the resulting distribution is V-shaped, roughly delimited on the left by apocentric distances Q ≥ 25 AU, which corresponds to the apocentric distance of the original binary system. The black squares, on the other hand, are mostly located with q ≥ 12 AU, which is also the pericentric distance of the original system. It therefore appears that if the new binary has a lower value of q, roughly independent of the eccentricity, its gravitational perturbations on the planet would be sufficient to increase its eccentricity beyond the imposed limit e_p = 0.1. Of course this analysis is qualitative and does not rigorously represent every solution, but it does give an overall picture of the behavior.

Not all black squares are categorized as positive solutions. As mentioned previously, the final system must also permit for planetary formation, i.e., allow for an in-situ accretion of m_p. Since the present-day γ-Cephei system is too compact to allow for accretional collisions in the planetesimal swarm (e.g. Thébault et al. 2004; Paardekooper et al. 2008), we must ask about the minimum distance between binary components at which this may be avoided.

Unfortunately, there is no easy answer to this question, but we may obtain a rough idea from previous numerical studies of planetesimal dynamics in binary systems. Thébault et al. (2006) presented a detailed calculation of the impact velocity of different-sized planetesimals located at a = 1 AU in generic binary systems with m_A = 1 and m_B = 0.5, both in units of solar mass. For every point in a grid of values of (a_B,e_B) these authors calculated the average impact velocity Δv between a 2.5 km and a 5 km solid body, and drew level curves of constant Δv. According to the authors, accretional collisions are guaranteed for Δv < 10 m/s, denoting regions where the encounter speeds are practically unaffected by the secondary star. Collisions with 10 < Δv < 100 m/s are less certain, but may still allow for planetary formation even if some erosion is expected.

Since the impact velocity at any given location is primarily dictated by the forced eccentricity e_f excited by the secondary star on the planetesimal swarm, we can use the results by Thébault et al. (2006) to extrapolate their findings to other binary systems. As determined by Heppenheimer (1978), a first-order expression (in the masses) for the forced eccentricity at a given semimajor axis a may be written as 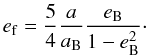${\mathit{e}}_{\mathrm{f}}\mathrm{=}\frac{\mathrm{5}}{\mathrm{4}}\frac{\mathit{a}}{{\mathit{a}}_{\mathrm{B}}}\frac{{\mathit{e}}_{\mathrm{B}}}{\mathrm{1}\mathrm{-}{\mathit{e}}_{\mathrm{B}}^{\mathrm{2}}}\mathrm{·}$(13)A second-order expression was calculated recently by Giuppone et al. (2011), which depends explicitly on the stellar masses. However, the difference between both values is only relevant for high values of e_f, which is beside the purpose of the present study.

Using expression (13) of Thébault’s system we can calculate (for our case) the critical value of the forced eccentricity associated to Δv = 10 m/s and to Δv = 100 m/s. We can then use these as reference values and, once again applying (13), estimate the values of a_B and e_B that give the same value of e_f for a given semimajor axis a. Since the forced eccentricity increases with a, a_B and e_B, in principle we should expect accretional collisions for lower values of all these parameters.

To complete this setup, we must specify a value for a. Since the exoplanet detected in γ-Cephei has a semimajor axis of 2.1 AU, even an in-situ formation with little planetary migration requires a sufficiently large feeding zone that would extend beyond the snow line to accrete the necessary mass. For the present study, we chose a = 4 AU; in other words, we required that the entire region up to 4 AU satisfies the conditions established in Thébault et al. (2006). Although this upper limit may appear rather arbitrary, we consider it as illustrative of the dynamics and not as an actual proposal for the formation process itself.

The orange curves in each frame of Fig. 2 show the values of the eccentricity and semimajor axis of the binary system that yield (within the approximation described above) the two values of the impact velocities mentioned before. All binaries located to the right and below each curve satisfy this ad-hoc condition of accretional collision.

Figure 3 focuses on the type-II outcomes for m_C = 0.4   M_⊙. The top frame shows the distribution of orbital parameters of the binary as a function of the minimum distance r_min of the impactor, in units of Q_B. For illustration purposes, we have also drawn the curves of q_B = a_B(1 − e_b) = 12 AU and Q_B = a_B(1 + e_b) = 25 AU, both corresponding to the original values of the system. Thus, the original orbit is located at the intersection point between both curves.

Since distant encounters (i.e. large values of r_min) imply lower perturbations, the final configuration remains close to the original orbit. However, as the distance decreases, the resulting orbits spread significantly, most of them increasing both q_B and Q_B.

A comparison with the curves of constant Δv also shows that the positive solutions occur primarily for impactors whose minimum distance lies between one and three times the apocentric distance of the original binary. Closer encounters are too destructive, while more distant fly-bys are not able to modify the system sufficiently to overcome the planetary formation constraints.

The lower plot shows the distribution of final orbits as a function of the velocity at infinity of m_C, in units of the escape velocity of the system. Low incoming speeds cause a more or less random spread of solutions around the original configuration, mainly as a consequence of the resonance interactions. Higher speeds generate more ordered distributions. Once again, positive solutions are mainly found for intermediate values, between two and six times the escape velocity.

Finally, the percentage of positive results are summarized in Table 1, were we have extended the series to include a total of five values of m_C between 0.2   M_⊙ and 1   M_⊙. For most impactor masses, type I positive solutions are the most common because they contain no restrictions to the orbit of the outgoing binary. We recall that in this type of outcome the central star m_A becomes isolated and the new binary is composed of m_B + m_C. All other types of solutions are rare, as already noted by Marzari & Barbieri (2007a), usually less than 1% of all scattering events. If we consider the very restrictive Δv < 10 m/s limit, only a few 0.01% of the encounters yield final configurations suitable for planetary formation around m_A.

4. Full numerical simulations

We now repeated the simulations, this time with random values of all angular variables (I_B,λ_B,ϖ_B,Ω_B,λ_p,ϖ_p). In other words, we extended the experiments to the 3D case and considered arbitrary orientations of the orbits of both the binary and the planet. However, in all cases we considered the planet initially in the same orbital plane as the secondary, i.e. I_p = I_B and Ω_p = Ω_B. One of the aspects we wished to study is the change in the mutual inclination between the planet and the binary perturber after the passage of the impactor. It was already noted in Marzari & Barbieri (2007a,b) that high inclinations between the impactor and the binary may lead to greater disruptions of the system, so these configuration may cause large variations in I_p, leaving behind planetary systems with high inclinations with respect to the plane of the binary.

Figure 4 shows the eccentricity and semimajor axis distribution of the resulting binaries, where the left-hand plots show the type-II outcomes and the right-hand graphs correspond to type III. As with Fig. 2, the symbols in brown show all the outcomes while those in black maintained the planet in an almost circular orbit (e_p < 0.1). Compared with Fig. 2, we see a greater proportion of positive results for type-II outcomes, but a significant decrease in positive results for type III (see Table 2). In fact, the number of Type III outcomes with relative encounter speed Δv < 10 m/s expected for small planetesimals is less than 0.01% for all impactor masses. Results also show a serious reduction in the positive outcomes of type-I encounters, which are now typically only half those found in our test runs.

Finally, Fig. 5 shows the distribution of final inclinations i_mut of the planetary orbit with respect to that of the binary component. In type-II outcomes (left-hand plots), the secondary remains the original companion m_B, therefore i_mut measures the perturbation of the fly-by on the original system. Although most orbits remain relatively aligned, especially those corresponding to positive results, we also note a significant amount of highly inclined orbits, some even retrograde with respect to the binary orbit.

The right-hand plots in Fig. 5 correspond to type-III outcomes, in which the new binary system is now composed of m_A + m_C. Because the new companion is captured and not primordial, in principle there should be little correlation between the orbits of m_p and m_C; consequently the values of i_mut should be fairly random. However, the results of the simulations, especially those classified as positive, show a marked correlation. This seems to indicate that only the fly-bys that occur near the orbital plane of the original binary lead to systems suitable for planetary formation. The difference in the plots between the black and red curves gives the impression that most of the encounters with large I_B lead to highly eccentric planets, and positive results occur primarily with I_B ~ 0.

5. Distribution functions for the free parameters

To gain a more accurate understanding of the probability to form the γ-Cephei system through the process explained in these paper, we must weight the results showed in the previous sections by assigning a distribution function (DF) to each of the free parameters, r_min, v^∗ and m_C.

As mentioned earlier, the parameter r_min appears more suitable than the impact parameter b for describing the two-body dynamics of the scattering problem. However, to find the corresponding DF, we must first relate r_min with b and v^∗.

For a hyperbolic keplerian orbit we may write 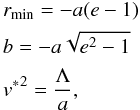$\begin{array}{ccc}& & {\mathit{r}}_{\min }\mathrm{=}\mathrm{-}\mathit{a}\mathrm{(}\mathit{e}\mathrm{-}\mathrm{1}\mathrm{)}\\ & & \mathit{b}\mathrm{=}\mathrm{-}\mathit{a}\sqrt{{\mathit{e}}^{\mathrm{2}}\mathrm{-}\mathrm{1}}\\ & & \end{array}$(14)where a and e are the semimajor axis and eccentricity of the orbit of the incoming body m_C and Λ = a_ABm_C(m_A + m_B)/(m_Am_B). Introducing the last two expressions of (14) into the first, and after some simple algebraic manipulations, we obtain 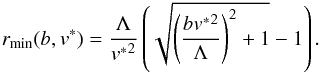${\mathit{r}}_{\min }\mathrm{\left(}\mathit{b,}{\mathit{v}}^{\mathrm{\ast }}\mathrm{\right)}\mathrm{=}\frac{\mathrm{\Lambda }}{{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}}\left(\sqrt{{\left(\frac{\mathit{b}{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}}{\mathrm{\Lambda }}\right)}^{\mathrm{2}}\mathrm{+}\mathrm{1}}\mathrm{-}\mathrm{1}\right)\mathit{.}$(15)Following Hut & Bahcall (1983) we assumed a distribution of close encounters uniform in b². To estimate the distribution probability of v ^∗ , we first need to determine the DF of the relative encounter velocities between a single star and a binary. Again following Hut & Bahcall (1983), the thermal distribution function of velocities for stars of equal mass m is 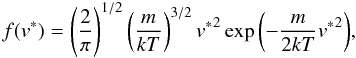$\mathit{f}\mathrm{\left(}{\mathit{v}}^{\mathrm{\ast }}\mathrm{\right)}\mathrm{=}{\left(\frac{\mathrm{2}}{\mathit{\pi }}\right)}^{\mathrm{1}\mathit{/}\mathrm{2}}{\left(\frac{\mathit{m}}{\mathit{kT}}\right)}^{\mathrm{3}\mathit{/}\mathrm{2}}{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}\exp \left(\mathrm{-}\frac{\mathit{m}}{\mathrm{2}\mathit{kT}}{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}\right)\mathit{,}$(16)where k is Boltzmann’s constant and T is a temperature-like parameter in analogy with a velocity DF of gas particles. Below we will express these variables in terms of the thermal velocity dispersion v_th.

Binaries formed from equal-mass stars have a combined mass 2m, and a thermal DF 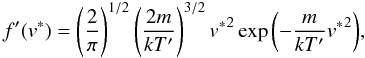${\mathit{f}}^{\mathrm{\prime }}\mathrm{\left(}{\mathit{v}}^{\mathrm{\ast }}\mathrm{\right)}\mathrm{=}{\left(\frac{\mathrm{2}}{\mathit{\pi }}\right)}^{\mathrm{1}\mathit{/}\mathrm{2}}{\left(\frac{\mathrm{2}\mathit{m}}{\mathit{k}{\mathit{T}}^{\mathrm{\prime }}}\right)}^{\mathrm{3}\mathit{/}\mathrm{2}}{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}\exp \left(\mathrm{-}\frac{\mathit{m}}{\mathit{k}{\mathit{T}}^{\mathrm{\prime }}}{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}\right)\mathit{,}$(17)where T′ = T for equipartition of translational energy, and T′ = 2T if the binaries have the same velocity dispersion as single stars (Hut & Bahcall 1982). The real value for T′ lies somewhere in the middle of these extremes.

Finally, we can calculate the distribution of relative velocities of single stars in the instantaneous rest frame of a binary. It is again a Maxwellian distribution but with an effective mass m^∗ and temperature T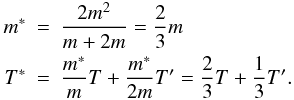^∗: $\begin{array}{ccc}{\mathit{m}}^{\mathrm{\ast }}& \mathrm{=}& \frac{\mathrm{2}{\mathit{m}}^{\mathrm{2}}}{\mathit{m}\mathrm{+}\mathrm{2}\mathit{m}}\mathrm{=}\frac{\mathrm{2}}{\mathrm{3}}\mathit{m}\\ {\mathit{T}}^{\mathrm{\ast }}& \mathrm{=}& \end{array}$(18)And we have for the velocities 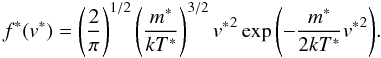${\mathit{f}}^{\mathrm{\ast }}\mathrm{\left(}{\mathit{v}}^{\mathrm{\ast }}\mathrm{\right)}\mathrm{=}{\left(\frac{\mathrm{2}}{\mathit{\pi }}\right)}^{\mathrm{1}\mathit{/}\mathrm{2}}{\left(\frac{{\mathit{m}}^{\mathrm{\ast }}}{\mathit{k}{\mathit{T}}^{\mathrm{\ast }}}\right)}^{\mathrm{3}\mathit{/}\mathrm{2}}{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}\exp \left(\mathrm{-}\frac{{\mathit{m}}^{\mathrm{\ast }}}{\mathrm{2}\mathit{k}{\mathit{T}}^{\mathrm{\ast }}}{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}\right)\mathit{.}$(19)From now on we will characterize the temperature T ^∗  by the thermal velocity dispersion in the relative velocities: 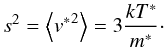${\mathit{s}}^{\mathrm{2}}\mathrm{=}\mathrm{⟨}{{\mathit{v}}^{\mathrm{\ast }}}^{\mathrm{2}}\mathrm{⟩}\mathrm{=}\mathrm{3}\frac{\mathit{k}{\mathit{T}}^{\mathrm{\ast }}}{{\mathit{m}}^{\mathrm{\ast }}}\mathrm{·}$(20)Although these expressions were obtained for equal-mass binaries, the same procedure can be extended to other masses. The velocity dispersion is the classical parameter used to characterize the relative velocities of different types of stellar systems. Typical values for s are extremely dependent on the environment, and may be as low as 0.3 km s^-1 in open clusters, or up to two orders of magnitude higher in the solar neighborhood (see Binney & Tremaine 2008, for a detailed analysis).

From Eqs. (14), (15), (19) and (20), we can calculate the probability function P(r_min,v^∗)   dr_min   dv^∗ for a given value of s. Results are shown in Fig. 6 for three magnitudes of the velocity dispersion, and adopting values for dr_min and dv^∗ from a 100 × 100 grid of initial conditions in the plane.

As expected, higher velocity dispersions increase the probability of encounters at higher values of v^∗. For s = 1 km s^-1, only encounters with v₀ ~ v_esc are relevant and most of the solutions discussed in the lower plot of Fig. 3 will have negligible weight in the overall outcome probability. On the other hand, for s = 10 km s^-1 the spread in v^∗ is much larger and even high incoming speeds are statistically pertinent.

We can now incorporate these distribution functions into the results shown in Table 2 to give more realistic probabilities of positive outcomes. Before discussing these results, we must also incorporate a distribution function for the impactor mass. For this we have adopted the so-called universal initial mass function proposed by Kroupa (2001) which, in the mass interval between  ~0.1   M_⊙ and  ~1   M_⊙, can be expressed by a multiple-part power-law ξ(m) ∝ m ^− α_i with $\begin{array}{ccc}{\mathit{\alpha }}_{\mathrm{1}}& \mathrm{=}& \mathrm{1.3}\mathrm{if}\mathrm{0.08}\mathrm{\le }\mathit{m}\mathit{/}{\mathit{M}}_{\mathrm{\odot }}\mathit{<}\mathrm{0.5}\\ {\mathit{\alpha }}_{\mathrm{2}}& \mathrm{=}& \end{array}$(21)and where ξ(m)   dm is the number of single stars expected in the mass interval  [m,m + dm] . This distribution function is shallower than the classical Salpeter (1955) prescription for small stellar masses but, at least for our application, both give similar results.

Taking into consideration all distribution functions, we can now estimate the final probability for favorable scattering outcomes, integrated over the impactor mass m_C and initial values for r_min and v^∗. Results are shown in Table 3 (which adds all positive type I + type II + type III outcomes), where we have considered three different possible values for the velocity dispersion s of background stars. We have also performed separate calculations assuming that the maximum impact speeds for planetesimals leading to accretional collisions is either 10 m/s or 100 m/s. We recall that the first is a very strict limit in which all collisions should be constructive (Thébault et al. 2006), while the higher impact velocity allows some disruptions to take place.

Contrary to expectations, results are not extremely sensitive to the adopted value for s. For very stringent accretional restrictions, we find that around 1.5% of all stellar scattering events lead to favorable outcomes, while this number increases to  ~5.5% if we allow higher impact speeds. This seems to imply that given a “normal” planetary system consisting in either (i) a planet around a single star interacting with a binary stellar system, or (ii) a planet in a circumstellar orbit around a wide binary interacting with a single star, the final result could be a system similar to γ-Cephei in (roughly) 1–5% of cases.

6. Conclusions

The discovery of at least four exoplanets in circumstellar orbits in tight binary systems has raised the question of their formation history. So far, all attempts to explain their origin via normal in-situ formation processes have been unsuccessful, and we wonder whether other more exotic mechanisms may have played a role. Following the suggestion of Marzari & Barbieri (2007a), in this work we have analyzed whether these systems, in particular γ-Chepei, could have begun their lives in other dynamical configurations more suitable for planetary formation, attaining their present structure later on as a consequence of a close encounter with a background singleton.

Following a series of numerical simulations of time-reversed stellar encounters, whose results were later weighted adopting classical expressions for probability distributions for stellar mass, relative velocities and impact cross-sections, we have found that between 1 and 5 percent of fly-bys between a planetary system and background stars could lead to planets in tight binary systems. Although this number may not seem high, it could in fact explain why planets in tight binaries are not more numerous, which would indeed be the case if in-situ planetary formation were possible.

However, we must remain cautious. Although we have attempted to give some estimate about the probability outcomes, given a sufficiently large number of initial conditions and values in the parameter space, it is possible to obtain almost any result from a scattering event. This does not mean that the event actually happened or that the explanation lies there. However, as Sir Arthur Conan Doyle said through his character Sherlock Holmes: “Once you eliminate the impossible, whatever remains, no matter how improbable, must be the truth.”

Acknowledgments

This work has been partially supported by the Argentinian Research Council – CONICET –, and by the Universidad Nacional de Córdoba (UNC). The authors wish to express their gratitude to Francesco Marzari for helpful suggestions and a detailed review of this work.

References

All Tables

All Figures