| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A87 | |
| Number of page(s) | 9 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201219245 | |
| Published online | 02 August 2012 | |
Coronae above accretion disks around black holes: the effect of Compton cooling
1 Max-Planck-Institut für Astrophysik, Karl-Schwarzschildstr. 1, 85740 Garching, Germany
e-mail: emm@mpa-garching.mpg.de
2 National Astronomical Observatories, Chinese Academy of Sciences, 20A Datun Road, Chaoyang District, 100012 Beijing, PR China
Received: 19 March 2012
Accepted: 12 June 2012
Context. The geometry of the accretion flow around stellar mass and supermassive black holes depends on the accretion rate. Broad iron emission lines originating from the irradiation of cool matter can indicate that there is an inner disk below a hot coronal flow.
Aims. These emission lines have been detected in X-ray binaries. Observations with the Chandra X-ray Observatory, XMM Newton, and Suzaku have confirmed the presence of these emission lines also in a large fraction of Seyfert-1 active galactic nuclei (AGN). We investigate the accretion flow geometry for which broad iron emission lines can arise in hard and soft spectral states.
Methods. We study an ADAF-type coronal flow, where the ions are viscously heated and electrons receive their heat only by collisions from the ions and are Compton cooled by photons from an underlying cool disk.
Results. For a strong mass flow in the disk and the resulting strong Compton cooling only a very weak coronal flow is possible. This limitation allows the formation of ADAF-type coronae above weak inner disks in the hard state, but almost rules them out in the soft state.
Conclusions. The observed hard X-ray luminosity in the soft state, of up to 10% or more of the total flux, indicates that there is a heating process that directly accelerates the electrons. This might point to the action of magnetic flares of disk magnetic fields reaching into the corona. Such flares have also been proposed by observations of the spectra of X-ray black hole binaries without a thermal cut-off around 200 keV.
Key words: accretion, accretion disks / X-rays: galaxies / black hole physics / galaxies: active / magnetic fields / galaxies: Seyfert
© ESO, 2012
1. Introduction
With the advent of XMM-Newton observations, it has become obvious that broad iron emission lines are common in Seyfert galaxies (Nandra et al. 2007). The number of sources with detections of strong disk lines is growing with the increasing number of new observations by XMM-Newton, Chandra, and Suzaku. These Fe K-shell emission lines are the strongest X-ray emission lines in most AGN and X-ray binaries (see the review by Miller 2007). Averaging AGN X-ray spectra from deep Chandra fields Falocco et al. (2011) significantly detected the broad component of the Fe line in the X-ray spectra of low luminosity AGN at low redshift.
Since iron emission lines can be understood as the reaction of an accretion disk to irradiation by an external source of hard X-rays, the obvious question is under which conditions the accretion geometry contains an inner disk and above it a hot coronal flow/ADAF. An inner disk is necessary to explain the relativistic lines. As commonly accepted, the mass accretion rate determines whether an optically thick and geometrically thin disk reaches inward to the innermost stable circular orbit (ISCO) or the disk is truncated and replaced by an advection-dominated optically thin hot flow in the inner region. A detailed definition of these states is given by Remillard & McClintock (2006). For very high accretion rates, a third, so-called steep-power law state can exist, which is observed during some outbursts of X-ray binaries. Though in principle the accretion flow geometry is the same for X-ray binaries and AGN (Narayan et al. 1998), it is easier to distinguish between different spectral states for galactic sources than for AGN. Walton et al. (2012) analyzed high quality spectra of the stellar-mass black hole binary XTE J1650-500 and the active galaxy MCG-6-30-15 and argued that the similarity of broad iron line features shows that the excess in both sources is of the same nature.
During the hard/low state, the power-law flux from the ADAF in the inner region is the main source of radiation. If the disk is truncated, no relativistic iron emission lines should be produced. However, from the earliest studies a broad iron emission line has been detected for Cygnus X-1 in low state (Barr et al. 1985). Now Chandra and XMM-Newton observations have firmly established the existence of a relativistic Fe K emission line in spectra of several X-ray binaries. Reis et al. (2010) analyzed the X-ray spectra of black hole binaries in the canonical low/hard state and found that the accretion disk reaches inward to the ISCO. These detections were made mostly during outburst decline and can theoretically be understood in terms of re-condensation of gas into an inner disk (Meyer et al. 2007) in the hard spectral state, as a transient phenomenon following the state transition. This accretion flow geometry, an outer truncated disk, and inside only a weak inner disk and above it the main flow via a corona/ADAF, is the situation where broad iron emission lines are expected. There may be a gap between the outer standard disk and such a weak inner disk.
During the high/soft (thermal) state, the flux is dominated by the radiation from the inner disk. The observations of X-ray binaries have identified an additional hard power-law flux, sometimes with a non-thermal tail, the power-law flux that is evidence of the co-existence of disk and hot flow. In this case then, one has to keep in mind that heat conduction and the possible exchange of mass and angular momentum between disk and hot flow can be significant. Investigations of the spectra of X-ray binaries, especially Cyg X-1 (Ibragimov et al. 2005), led to the conclusion that magnetic flares are needed to explain the non-thermal radiation.Hints to magnetic fields also come from accretion disk winds, which are ubiquitous in black hole binaries in the soft state, as pointed out by Ponti et al. (2012). Miller et al. (2008) modeled spectra observed for GRO J1655-4 and concluded that these disk winds are probably related to magnetic fields.
The interpretation of spectra is less clear for AGN. Despite the large number of observations, it is difficult to classify the source as in hard or soft state. Vasudevan & Fabian (2009) presented spectral energy distributions for a sample of AGN, based on contemporaneous optical, ultraviolet, and X-ray observations, and determined the ratio of bolometric to Eddington luminosity, using the black hole mass measurements of Peterson et al. (2004). Tanaka et al. (1995) first observed an asymmetric disk line profile in the Seyfert-1 AGN MCG-6-30-15, which remains a very important source for studies of relativistic disk lines. If a relativistic line is detected, one might conclude that an inner disk exists, which is either (1) in the soft state, a standard disk inward to the ISCO with irradiation from a coronal layer or (2) in the hard state, only a very weak inner disk below the standard ADAF. The latter case seems to occur in X-ray binaries as a transient phenomenon of the intermediate spectral state. One might expect to find the same accretion flow geometry for AGN. Meyer-Hofmeister & Meyer (2011) investigated the situation using Seyfert galaxies for which emission lines were clearly present (Nandra et al. 2007; Miller 2007), but found that some of these sources were apparently in the soft rather than the hard state.
That broad iron emission lines are common in Seyfert AGN suggests that they are not a transient phenomenon and that the accretion geometry then corresponds to a soft state disk with a hot coronal layer/ADAF above, at least for some of the observed sources. In this paper we investigate the structure of the hot coronal flow above a standard disk under the influence of Compton cooling. In Sect. 2, we give a short summary of broad iron emission lines detected in X-ray binaries and AGN. Section 3 concerns the physics of interaction of disk and corona around supermassive and stellar-size black holes. We determine the limitation of the coronal flow caused by Compton cooling (Sect. 4). The restriction in the case of a strong disk mass flow is so low that the observed hard power-law flux in a number of sources requires an additional heating process, e.g. one produced by magnetic flares. This is consistent with the conclusions derived by Ibragimov et al. (2005) from fitting X-ray binary spectra with a non-thermal tail and no cut-off at energies between 100 keV and 200 keV (Sect. 5). Whether the situation is similar for AGN is difficult to judge since for these sources, a non-thermal power-law flux does not seem to be indicated, but cannot be not generally excluded. In Sect. 6, we refer to observations for X-ray binaries that detect evidence of non-thermal Comptonization. A discussion of questions related to our results follows in Sect. 6.
2. Detection of broad iron emission lines in Seyfert AGN and X-ray binaries
Broad iron emission lines provide information on the accretion process in the innermost region around the black hole. If the line profile is asymmetric, the extent of the red compared to the blue wing allows us to derive measures of the black hole spin. Miller (2007) presented a review of relativistic X-ray lines from both the inner accretion disks of Seyfert AGN and disks around stellar-size black holes. The recent XMM-Newton and Suzaku surveys were discussed, in which broad Fe lines were found to be common. Nandra et al. (2007) found broad iron emission lines for 73% of the sources in his sample of 30 Seyfert galaxies observed with XMM-Newton. Bhayani & Nandra (2011) achieved an improved fit of these data, finding evidence of broad iron lines in 11 sources for which originally the lines could not be detected. Reeves et al. (2006) report the detection of relativistic disk lines and reflection in six of seven Seyfert AGN in a Suzaku survey. These observations also show that the disk reflection spectrum follows the same variability pattern as the iron line (see discussion in Miller 2007). The much cooler accretion disks in AGN allow us to easily separate disk radiation from the iron emission line in the spectrum. In X-ray binaries, the radiation from the disk and the corona, which in both cases both lies in the range of commonly observed X-rays and iron emission lines would be more difficult to be recognized.
A priori it is unclear what the detection of so many iron emission lines in Seyfert galaxies means with respect to the accretion flow geometry. Brighter sources with high mass accretion rates in the high/soft spectral state may be overrepresented in the samples. However, Nandra et al. (2007) found a mean spectral index of Γ = 1.86 for their sample, which according to the definition of Remillard & McClintock (2006) would correspond to a low/hard state.
In X-ray binaries, the spectral state can usually be determined. In these systems, the broad iron emission lines are primarily found in the low/hard spectral state, either during a rise to an outburst or, more often, an outburst decline, at times when the accretion rate has not yet decreased to very low values below about 0.001 of the Eddington rate. These lines were detected in connection with very weak inner disk components. Hence the iron emission lines appear to be a transient phenomenon, that has been found for quite a number of well-known X-ray binaries (for compilations of the detections, see Miller 2007; Meyer-Hofmeister et al. 2009; Reis 2010). These iron lines seem to require cool material below a hot flow close to the central black hole. This has sometimes been taken as a contradiction to the “truncated disk picture” in the hard state. However, these weak inner disks could well form by the re-condensation of gas from the hot flow (Liu et al. 2006; Meyer et al. 2007; Taam et al. 2008). For some Seyfert AGN with observed broad iron emission lines, the accretion flow geometry might be the same. On the other hand, “best candidates”, for the presence of broad iron emission lines in Nandra et al. (2007) and Miller (2007) seem to have an Eddington scaled accretion rate above 0.1, hence are probably in the soft spectral state (Meyer-Hofmeister & Meyer 2011).
3. Advection-dominated accretion flows
The origin of hard X-rays observed in accretion flows onto compact objects is commonly attributed to the inverse Compton scattering of cool photons from outside on hot electrons in the accreting plasma. The high electron temperature results naturally from the effective heating and rather poor radiative cooling of the tenuous plasma. Major heating processes here are the collisional heating by hot ions generated by the “frictional” release of gravitational energy in the accreting flow, the dissipation of magnetic energy in the corona of an underlying accretion disk, and conceivably the strong irradiation by an external source of high energy photons.
An advection-dominated optically thin hot flow, which was discussed by Ichimaru (1977) and both introduced and investigated in detail by Narayan and collaborators (see Narayan et al. 1998, for references), is presumably present in many X-ray sources, stellar-mass objects and AGN. The hard spectrum mainly results from the hot plasma in an inner region around the black hole. The appearance of magnetic fields is nearly unavoidable in accretion flows of conductive plasma and in particular they are thought to provide the frictional heating in accretion disks by the magneto-rotational instability. These fields may well reach out to an overlying corona and there produce magnetic heating e.g. by flares. Irradiation from a central source can heat the corona above the disk, as in the case of Her X-1 (Schandl & Meyer 1994).
3.1. Interaction between corona and disk
An inner hot flow is usually surrounded by a standard Shakura-Sunyaev type accretion disk. The change from disk accretion to a hot flow can arise from thermal conduction from a hot corona, that evaporates the disk underneath in a way that depends on the accretion rate (Meyer & Meyer-Hofmeister 1994; Liu et al. 2002). In a typical low/hard state with accretion rates below a few percent of the Eddington accretion rate (ṀEdd), the inner disk is evaporated and recedes outward to distances of several hundred Schwarzschild radii.
The opposite process, the condensation of gas from the hot flow onto a cool disk below, is also possible (Liu et al. 2006; Meyer et al. 2007) and can help to sustain a very weak inner disk after an outburst. In such a hard-intermediate state, accretion rates are around 0.001 to 0.01 ṀEdd. An inner weak disk can explain the broad Fe K emission lines in the spectra of X-ray binaries in the hard spectral state. The modeling is supported by an analysis of observations for GX 339-4 (Liu et al. 2007; Taam et al. 2008). A hot corona above a very weak cool disk in a hard/low spectral state differs from a pure ADAF: the existence of a cool disk underneath the corona by vertical thermal conduction sets up an electron temperature profile connecting the hot corona and cool disk, and the electron temperature near the base of the corona finally becomes so low that Coulomb coupling between the ions and electrons becomes effective and ion and electron temperatures become equal.
In the high/soft spectral state, if the underlying disk is strong, another case of an interaction between disk and corona is present. The inverse Compton scattering of cool disk photons by hot electrons leads to an efficient cooling of the electrons. We study under which circumstances this process can completely cool the corona.
In the following, we distinguish between a standard ADAF present in the inner region in the hard spectral state and an “ADAF-type corona” as a coronal flow above a weak or strong disk. Common to both cases is that only the ions are thought to be directly heated by the release of gravitational energy in the accreting gas, and the electrons only receive their heat by collisional coupling to the ions.
3.2. The two-temperature ADAF-type corona in the inner region
A two-temperature flow is present if electrons are cooled preferentially. In general, the collisions between ions and electrons reduce a temperature difference. At large distances, larger than a few hundred Schwarzschild radii, ions and electrons are thermally coupled.
We consider here the changes that occur to the structure of the coronal flow when a disk exists below the hot flow. If there is no additional heat input from a disk underneath, then such an “ADAF-type corona” will be similar to a standard ADAF where the electrons receive their heat only from collisions with the hot ions, which in turn have been heated by the release of potential energy. We use the analytical relations of Narayan & Yi (1995b). Total pressure p, electron density ne, viscous dissipation of energy q + , and isothermal sound speed cs depend on the black hole mass m, the accretion rate ṁc in the ADAF, the distance r from the black hole, and the viscosity parameter α as 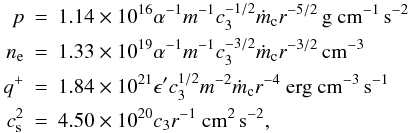 (1)where m, ṁc, and r are in units of solar mass, Eddington rate (ṀEdd = 1.39 × 1018m g/s), and Schwarzschild radius, respectively. We denote by ṁc the ADAF accretion rate because we later introduce ṁd, the accretion rate in a disk beneath the ADAF. The coefficients depend on the ratio of specific heats of the magnetized plasma γ
(1)where m, ṁc, and r are in units of solar mass, Eddington rate (ṀEdd = 1.39 × 1018m g/s), and Schwarzschild radius, respectively. We denote by ṁc the ADAF accretion rate because we later introduce ṁd, the accretion rate in a disk beneath the ADAF. The coefficients depend on the ratio of specific heats of the magnetized plasma γ![\begin{eqnarray} c_3=\frac{10+4{\epsilon}'}{9\alpha^2}\left[ \left( 1+\frac{18\alpha^2}{(5+2\epsilon')^2} \right)^{1/2} -1 \right]\approx {2\over 5+2\epsilon'}, \hspace{0.5cm} \end{eqnarray}](/articles/aa/full_html/2012/08/aa19245-12/aa19245-12-eq16.png) (2)with
(2)with 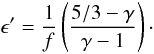 (3)The parameter f = (q+ − q−)/q+, which is the ratio of the advected energy to heat generated, measures the degree to which the flow is advection- dominated, where q − is the energy lost. This means that in a standard ADAF f is close to 1.
(3)The parameter f = (q+ − q−)/q+, which is the ratio of the advected energy to heat generated, measures the degree to which the flow is advection- dominated, where q − is the energy lost. This means that in a standard ADAF f is close to 1.
The expressions depend on the ratio of specific heats of the magnetized plasma γ = (8−3β)/(6−3β) (Esin 1997), where β is the ratio of gas pressure to total pressure. We adopt the value β = 0.8, resulting from shearing box simulations in a collisionless plasma (Sharma et al. 2006).
As long as the ions are not significantly cooled by the transfer of energy to the electrons they take their energy inward with the flow. This determines the virial-like ADAF temperature of the ions. However, if the ions lose a certain fraction of their energy to the electrons, their temperature becomes accordingly lower. For a sufficiently low electron temperature, electrons and ions become thermally coupled. The rate of collisional energy transfer from ions to electrons given by Stepney (1983), is approximated (Liu et al. 2002) as 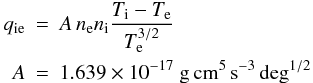 (4)where Te, Ti are the electron and ion temperatures, and ne, ni are the electron and ion number densities.
(4)where Te, Ti are the electron and ion temperatures, and ne, ni are the electron and ion number densities.
This energy transfer increases with decreasing electron temperature. When the collisional heat transfer from ions to electrons is able to take away nearly all the heat that the ions have gained, i.e. qie = (1 − f)q+, f small, coupling occurs.
We use the analytical relations for the case f = 0.1 (as shown later an appropriate approximation). The electron temperature at which coupling occurs can then be roughly estimated to be 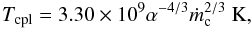 (5)which is independent of distance r.
(5)which is independent of distance r.
We note that a low electron temperature can also result from electron cooling by thermal conduction to the underlying disk. These coupling processes were discussed in the context of the re-condensation of gas onto a weak inner disk (Meyer et al. 2007).
3.3. The relation between Ti and Te
The ion temperature is the result of viscous heating and collisional cooling by electrons. This collisional cooling depends only on the ADAF parameters and the electron temperature and is independent of the nature of the electron cooling processes. The relation between ion and electron temperature describes the possible combinations of the two temperatures in the case of any cooling process leading to a temperature decrease.
The gas pressure of the accreting gas is given by 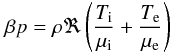 (6)with μi = 1.23 and μe = 1.14 for a hydrogen mass fraction of 0.75. From Eq. (1) we derive a relation between Ti and Te
(6)with μi = 1.23 and μe = 1.14 for a hydrogen mass fraction of 0.75. From Eq. (1) we derive a relation between Ti and Te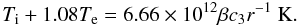 (7)In the above equation c3 contains the parameter f, which is determined by f = 1 − qie/q + . Thus, c3 is an implicit function of Te, Ti, ne, and ni. Given α, β, ṁc, and distance r, the relation between Ti and Te is the solution of the implicit Eq. (7).
(7)In the above equation c3 contains the parameter f, which is determined by f = 1 − qie/q + . Thus, c3 is an implicit function of Te, Ti, ne, and ni. Given α, β, ṁc, and distance r, the relation between Ti and Te is the solution of the implicit Eq. (7).
 |
Fig. 1 The change of ion temperature with electron temperature for given rates of coronal mass flow ṁc at distance r = 30, α = 0.2 and β = 0.8. |
 |
Fig. 2 Relation between ion and electron temperature, for different distances from the black hole, and ṁc = 0.01, α = 0.2. |
Figure 1 shows the relation for various mass flow rates ṁc in an ADAF at distance r = 30. Three branches are displayed. A first branch in the uppermost part of the figure describes the standard ADAF: the ion temperature is high, ions and electrons are thermally decoupled, and the ions obtain the virial-like temperature of an ADAF. If the electron temperature decreases owing to a cooling process, collisional coupling increases, more heat is drained from the ions, the ion temperature starts to decrease, and the electron temperature finally reaches a minimum. A second branch of possible combinations of values Ti and Te then appears: the ion temperature decreases further, and the electron temperature rises again. This is due to the rate of collisional energy transfer from ions to electrons for these Ti, Te values and the corresponding density values (Eq. (4)). This second branch is an unstable structure, corresponding to the solution found by Shapiro et al. (1976), the instability depending on the cooling process (Piran 1978). At sufficiently low ion temperature a third branch then appears where the ion and electron temperature become equal. These three branches correspond to the possible configurations for the different cooling processes of electrons and ions, should not be considered as consecutive structures. In the following section, we discuss the effect of especially Compton cooling.
The advected energy fraction f decreases from 1 at the upper right end of the Ti – Te curve towards zero at the one-temperature end, with f about 0.1 at the upper bend of the curve. In the limit of very small f, the corona is no longer spherical and the density of the coronal gas increases strongly towards the equatorial plain (Narayan & Yi 1995a).
For the Compton cooling process, we discuss here only an optically thin flow. The scattering optical depth of an ADAF similarity solution (Narayan & Yi 1995b) is 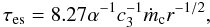 (8)and becomes ≥ 1 for low values of f.
(8)and becomes ≥ 1 for low values of f.
We note that for larger optical depth the cooling efficiency of the disk photons is higher and the derived limits on the allowed coronal flow are even lower.
Figure 2 shows the change in the relation with distance. r = 30 is a typical distance for an inner region, a finding that is important for the radiation, which determines the spectrum. In the innermost area, r = 3 the temperatures might be affected by processes that are not considered here. r = 300 is already a distance where the ion temperature is not very high compared to the electron temperature, indicating that there is a transition to the farther outward located one-temperature ADAF.
The relation between ion and electron temperatures in Figs. 1 and 2 for small distances shows an interesting hysteresis. When cooling increases, e.g. owing to an increase in the accretion rate in the disk underneath, the ion temperature can abruptly drop to the value Ti = Te. On the other hand, starting from a one-temperature flow, allowing temperatures to increase, the plasma remains at one temperature until it reaches a critical value where ions become uncoupled from the electrons, cannot be cooled efficiently, and assume the virial-like temperature of the two-temperature ADAF. The two transition temperatures are different. The reason for the difference is that as long as the ions are coupled with electrons their temperature remains low, the density is large, and the coupling remains strong.
4. Compton cooling: a weak ADAF-type corona above a strong disk in soft spectral state
In a hot advection-dominated coronal flow above an underlying disk conduction cooling and Compton cooling are in general the most important cooling processes. When conduction cooling is not important the electron temperature is determined by the inverse Compton scattering by photons from the disk. The Compton cooling rate is 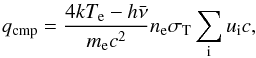 (9)with σT the Thomson scattering cross section, σ the Stefan Boltzman constant,
(9)with σT the Thomson scattering cross section, σ the Stefan Boltzman constant, 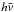 the mean photon energy, and ui the energy density of the cooling/heating photons. There are three sources of Compton cooling: photons from the disk below, photons from the innermost disk region and hard radiation from the hot flow. In the first two cases the term
the mean photon energy, and ui the energy density of the cooling/heating photons. There are three sources of Compton cooling: photons from the disk below, photons from the innermost disk region and hard radiation from the hot flow. In the first two cases the term 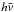 in general can be neglected compared to the thermal electron energy. The contribution from the disk underneath is
in general can be neglected compared to the thermal electron energy. The contribution from the disk underneath is 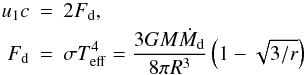 (10)where ui is the energy density of the photon field, M the black hole mass, Ṁd the disk accretion rate, R the radius, and RS the Schwarzschild radius.
(10)where ui is the energy density of the photon field, M the black hole mass, Ṁd the disk accretion rate, R the radius, and RS the Schwarzschild radius.
For the contribution of the inner disk region, we assume that it is diluted in proportion to 1/R2 at distances larger than about 5RS. The inclination angle δ under which the assumed flat inner disk appears at coronal height z is given by tanδ = R/z. For a density distribution ρ ∝ exp( − z2/H2) with scale height 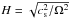 , for a rotational velocity Ω, we obtain a mean height
, for a rotational velocity Ω, we obtain a mean height 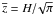 . With this mean height, the corresponding projection of the disk area with respect to the line of sight yields
. With this mean height, the corresponding projection of the disk area with respect to the line of sight yields 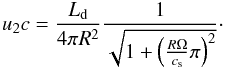 (11)We take the central luminosity as
(11)We take the central luminosity as 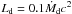 . This leads to the sum of the contributions
. This leads to the sum of the contributions 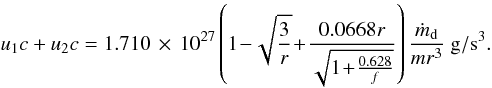 (12)The second contribution becomes more important than the first for r larger than about 30. The contribution of hard radiation is proportional to the mass flow rate in the corona and can be neglected in the soft state.
(12)The second contribution becomes more important than the first for r larger than about 30. The contribution of hard radiation is proportional to the mass flow rate in the corona and can be neglected in the soft state.
Bremsstrahlung cooling is less important than Compton cooling when Compton cooling is significant for a soft state disk underneath the corona. In addition, conduction cooling is much less efficient than Compton cooling for the low mass flow rates in the corona, as derived in the following.
4.1. A limit to the mass flow rate in the corona
To derive the mass flow rate in the corona, we evaluate the electron temperature for the case that Compton cooling qcmp balances collisional heating qie. We use Eq. (1) to determine the relation between Te, ṁc, and ṁd for a given distance r and α. Here f = 0.1 is again an appropriate approximation for which the temperature difference Ti − Te in the formula for qie can be approximated by Ti since the value of Te is small compared to that for Ti, yielding 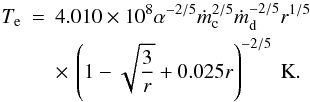 (13)Now, if Compton cooling brings the electron temperature (Eq. (13)), down below the coupling temperature (Eq. (5)) no two-temperature coronal flow can exist for lower electron temperatures. This yields an upper limit to the mass flow rate in the ADAF-type corona. For a given value ṁd, this rate limit ṁc can be determined using Te = Tcpl (f = 0.1). For a rate higher than this limit the electron temperature would be higher, but the coupling temperature would increase even more, preventing any coronal flow from existing. The rate limit is given by
(13)Now, if Compton cooling brings the electron temperature (Eq. (13)), down below the coupling temperature (Eq. (5)) no two-temperature coronal flow can exist for lower electron temperatures. This yields an upper limit to the mass flow rate in the ADAF-type corona. For a given value ṁd, this rate limit ṁc can be determined using Te = Tcpl (f = 0.1). For a rate higher than this limit the electron temperature would be higher, but the coupling temperature would increase even more, preventing any coronal flow from existing. The rate limit is given by 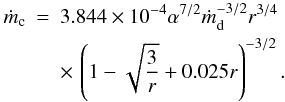 (14)In Fig. 3, we show the resulting coronal mass flow rates and their dependence on both ṁd and radius. For a mass flow rate in the disk ṁd = 0.1 − 0.2 ṀEdd, which is typical of a soft spectral state, the accretion rate possible in the ADAF-type corona is very low, below 10-3 ṀEdd. Only for a weak mass flow in the disk of around a few percent of ṀEdd, typical of an intermediate state, is the maximal ṁc slightly higher, at around 0.02 ṀEdd.
(14)In Fig. 3, we show the resulting coronal mass flow rates and their dependence on both ṁd and radius. For a mass flow rate in the disk ṁd = 0.1 − 0.2 ṀEdd, which is typical of a soft spectral state, the accretion rate possible in the ADAF-type corona is very low, below 10-3 ṀEdd. Only for a weak mass flow in the disk of around a few percent of ṀEdd, typical of an intermediate state, is the maximal ṁc slightly higher, at around 0.02 ṀEdd.
We note that our evaluation is very simplified and cannot give detailed numbers, but it becomes clear that Compton cooling leads to a severe reduction in the coronal mass flow. Narayan et al. (1998) indeed pointed already out that bremsstrahlung cooling can reduce the coronal flow.
 |
Fig. 3 The effect of Compton cooling: upper limit to the mass flow rate ṁc in the ADAF-corona for different mass flow rates ṁd in the disk and distances, α = 0.2 (approximation for f = 0.1). Rates ṁd = 0.1 − 0.2 correspond to a typical soft state, and rates ≤ 0.01 to an intermediate state. |
 |
Fig. 4 Ion and electron temperature Ti and Te under Compton cooling by photons from a disk underneath as function of disk mass flow rate ṁd. Solid lines: coronal mass flow rate ṁc = 0.01, dashed lines: ṁc = 0.001; left panel: R = 3 RS, right panel: R = 30 RS; α = 0.2. |
4.2. Ion and electron temperatures affected by Compton cooling
We determine how the mass flow in the disk affects the coronal mass flow changing its nature from a typical two-temperature ADAF with f close to 1 to a one-temperature flow with f → 0. As stated above, we assume again that (1 − f)q + = qie = qcmp, that is all the energy obtained by collisions with ions (qie) is cooled by the Compton scattering of the disk photons. The disk mass flow is then 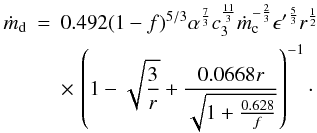 (15)This analytical formula is only valid for Te ≪ Ti. However, by evaluating the implicit formula without this approximation one can study how ion and electron temperatures change in depending on the cooling provided by a mass flow rate in the disk underneath. The result is shown in Fig. 4. With rising ṁd, the ion temperature decreases monotonously, whereas the electron temperature first decreases, then rises again, and finally decreases again. The non-monotonic behavior of the electron temperature is more pronounced for lower mass flow rates in the corona and smaller radii. (If r = 3 were approached, the description of both the ADAF and Compton cooling would have to be modified.)
(15)This analytical formula is only valid for Te ≪ Ti. However, by evaluating the implicit formula without this approximation one can study how ion and electron temperatures change in depending on the cooling provided by a mass flow rate in the disk underneath. The result is shown in Fig. 4. With rising ṁd, the ion temperature decreases monotonously, whereas the electron temperature first decreases, then rises again, and finally decreases again. The non-monotonic behavior of the electron temperature is more pronounced for lower mass flow rates in the corona and smaller radii. (If r = 3 were approached, the description of both the ADAF and Compton cooling would have to be modified.)
For a given value ṁc, there is a critical rate ṁd beyond which no solution exists. The critical rate ṁd is higher for lower ṁc, i.e. a higher mass flow in the disk allows only a smaller mass flow in the corona. Figure 4 shows that there can be two solutions for the same ṁd, a standard ADAF solution with electrons poorly coupled to the ions, a high ion temperature, and a SLE-type solution with lower ion temperature (and close to the black hole, a third one-temperature solution). The SLE branch approaches a one-temperature solution. For low temperatures, the densities in the coronal flow are higher and Compton cooling from a certain amount of photons becomes more efficient, that is a very small increase in ṁd leads to a temperature decrease. For very low ion temperatures the ADAF then becomes optically thick, e.g. for Ti ≤ 5 × 109 and ṁc = 0.01 and for Ti ≤ 5 × 108 and ṁc = 0.001 at r = 30 RS. The effect of cooling by the disk photons then differs.
We performed a stability analysis of the Compton cooling process, following the procedure performed by Narayan & Yi (1995b) who considered other cooling processes, other than cooling by a disk underneath. We also find that the SLE branch is unstable, as illustrated in Fig. 4 by the again increasing electron temperature, following an initial decrease.
4.3. Comparison with observations
The comparison with observations highlights a discrepancy. Observations of X-ray binaries and Seyfert galaxies (in soft spectral state) have found evidence of a coronal flow that is clearly higher than the upper limits derived in our analysis. In their definition of spectral states, Remillard & McClintock (2006) indeed refer to an upper limit to the non-thermal component of 25% of the flux at 2 − 20 keV). The existence of such a high power-law flux points to some additional heating of electrons that is able to compensate the Compton cooling.
In 2001, Merloni & Fabian pointed out that the coronal energy content derived from observationally determined electron temperatures and optical depth is insufficient to account for the observed X-ray luminosities, and conclude that, if ion-electron coupling is poor as assumed, an additional electron-heating mechanism, e.g. magnetic flaring, is required.
We here show that coronal flows can be sustained even if up to 90% of the ion heating is drained to the electrons, but that owing to the intricate dependence of the ion-electron coupling on both electron temperature and density, a coronal flow can thus be sustained only for a very low mass flow rate, depending on the Compton cooling providing a mass flow rate in the disk, that insufficient to account for the observed relatively high and hard X-ray radiation.
For such a process magnetic flares have been often proposed. This explanation is supported by the observation of a non-thermal tail for several X-ray binaries in a soft state. For AGN, only a few observations include this high-energy range in the spectrum. For some sources, a cut-off seems to be indicated, but the general situation is unclear.
5. Observed non-thermal Comptonization
Grove et al. (1998) used observations with OSSE on the Compton Gamma Ray Observatory (CGRO) of seven transient galactic black hole candidates to investigate the high-energy extension of the hard state. They found three sources with hard spectra below 100 keV and exponential cut-off consistent with thermal Comptonization, and four sources, with relatively soft spectra, spectral indices Γ ~ 2.5−3, and no evidence of a spectral break. The authors argued that photons from the disk in the high soft state cool the electrons in an inner advection-dominated Comptonization region. Our analysis of the Compton cooling effect is consistent with this picture.
Observations of a hard power-law tail and several investigations of spectra of Cyg X-1 have proven the existence of non-thermal Comptonization (Gilfanov et al. 1999; Frontera et al. 2001; McConnell et al. 2002). McConnell et al. (2002) used observations from CGRO and BeppoSAX which extending over the energy range from 20 keV to 10 MeV and derived constraints on the magnetic field in the hot flow based on the presence of a non-thermal tail. They emphasized the similarity between black hole binaries in the hard state and Seyfert galaxies and mentioned that similar tails could also be present in the AGN spectra. A detailed analysis of the broad-band spectra of Cyg X-1 was presented by Ibragimov et al. (2005, see also references therein). Beloborodov (1999) proposed a situation different from the soft state and modeled the hard spectrum of Cyg X-1 suggesting, that during the hard spectral state a large fraction of luminosity is released in a magnetic corona atop a cold accretion disk, via compact bright flares, the magnetic energy is generated by the magneto-rotational instability. Poutanen & Fabian (1999) also argued that magnetic flares cause the short-time spectral variability of Cygnus X-1.
For GRS 1915+105, evidence of non-thermal Comptonization was also found and discussed first by Grove et al. (1998), then Zdziarski et al. (2001, 2005). For GRO J1655-40, a high-energy cut-off during the rising phase of an outburst and its disappearance in the high/soft state was found by Joinet et al. (2008) (INTEGRAL observations along with RXTE and Swift data). The studies of GX 339-4 by Motta et al. (2009) showed the evolution of the high-energy cut-off during the brightening of the source and also the final disappearance in the soft state.
Zdziarski et al. (2000) summarized the spectra of Seyfert galaxies observed by the OSSE detector aboard CGRO and pointed out that constraints on the form of the individual soft γ-ray properties are rather weak owing to the limited quality of photon statistics. In the case of the bright radio-quiet Seyfert galaxy, NGC 4151, the spectrum above 50 keV is well described by thermal Comptonization. The spectrum of the bright Seyfert galaxy MCG-6-30-15 was modeled with a relativistic reflection model in the range 0.5−200 keV by Chiang & Fabian (2011), but for the soft γ-ray range no information is available.
6. Discussion
Our results evoke a number of questions. Observations of X-ray binaries may allow us to gain information on particular features of the accretion flow geometry. For AGN, it is more difficult to determine the spectral state of a source, since there are large uncertainties in e.g. the bolometric luminosity measurements, as described by Raimundo et al. (2012).
6.1. Dichotomy in the relation between ion and electron temperature
The run of the Ti and Te curves in Fig. 4 shows that for small distances two temperature solutions are possible for the same value of Compton cooling by photons originating from the disk underneath. This indicates that different combinations of Ti and Te are possible for either an increasing or a decreasing mass flow rate in the outer disk. During the transition from hard to soft spectral state and the reverse transition, the mass flow rates can be expected to allow such a temperature dichotomy in the hot flow. Stiele et al. (2011) found in their study of GX 339-4 interesting differences in the spectra when the source moves through both softening and hardening in the hardness-intensity diagram (HID), and argue that type B quasi-periodic oscillations (QPO) are related to the electron temperature distribution.
6.2. Limitation of the hot coronal flow?
Dunn et al. (2010) show in their diagrams of disk fraction and power-law fraction luminosities how for several black hole binaries these contributions change during the outburst cycles. In the soft state, the power-law flux strongly fluctuates. The average amount of power-law flux is in the range of a few up to ten percent of the total flux. An even higher power-law flux of up to 17% of the total flux was found in Swift/BAT observations of GX 339-4 during the 2010 outburst (Cadolle Bel et al. 2011; Shidatsu et al. 2011). This flux decreased within a short time after outburst maximum. However, the power-law flux observed for XTE J1752-223 during the 2009 − 2010 outburst (Swift/BAT observations), which is also a comparable fraction of the total flux, did persist for the entire outburst duration (Nakahira et al. 2012).
Within the picture developed here, a power-law flux higher than the limitation by Compton cooling, which is around 1% of the total flux, should indicate that electrons are accelerated in another way, e.g. by magnetic flares. The magnetic flares otherwise should yield non-thermal Comptonization, leading to a hard power-law tail in the spectrum up to energies higher than 200 keV. One might therefore expect that in the observations the two features appear together, i.e. that (1) the power-law flux is higher than the limitation found in our analysis and (2) there is a hard power-law tail in the spectrum due to the presence of magnetic flares.
6.3. Corona and disk during the intermediate state
The two accretion flow configurations with either a disk reaching inward to the ISCO or an ADAF in the inner region, and either dominant soft or hard radiation, are commonly accepted. However, during the change from one of these states to the other the accretion flow geometry is difficult to constrain.
During outburst rise, and a rising mass flow from further out, one can imagine that the inner edge of the truncated disk is continuously shifted inward, and that the soft radiation becomes dominant. During an outburst decline, the geometry of the accretion flow might be more complicated and depend on the process initiating the change from disk accretion to an ADAF. The efficiency of this process, which is theoretically understood as a siphon process leading to the evaporation of the disk (Meyer et al. 2000; Liu et al. 2002), has a maximum at a certain distance of probably a few hundred Rs (depending on parameters such as the ratio of gas pressure to total pressure, Qiao & Liu 2012). This means that the standard disk will first disappear there and that a gap might open between the outer standard disk and an inner weak disk. (In spectral fits, it might be difficult to distinguish between the inner edge of the standard disk and that of a weak inner disk.) The amount of mass in the inner disk is continuously reduced by diffusion, but disappears only slowly possible owing to the re-condensation of gas from the corona into the inner disk (Liu et al. 2006). The re-condensation only works as long as ṁ ≥ 10-3. So the weak inner disks are a natural feature of the intermediate state, at the soft-to-hard state transition. Observational evidence of a thermal component in the spectra of quite a number of sources support this picture. The iron emission lines then are the reaction of the inner accretion disk to irradiation.
For the intermediate state of Cyg X-1, Ibragimov et al. (2005) discussed an Fe Kα emission line. Observations with Chandra, XMM-Newton, and Suzaku revealed relativistic iron emission lines for several X-ray binaries in the hard (probably hard-intermediate) state, and also for Seyfert AGN (Nandra et al. 2007; Miller 2007). Additional information is provided by Swift observations (Reynolds & Miller 2011).
The more complex accretion flow geometry in the intermediate state does not contradict the fundamental picture of the two main flow patterns, either a disk or an ADAF in the inner region.
6.4. Magnetic flares in the accretion disk?
If magnetic flares are important for the power-law flux in the soft state, the strength of the magnetic fields is of interest, and maybe also changes in the magnetic field during the outburst cycles. Advective concentration in the inner parts of accretion disks was investigated for binary stars by Meyer (1996). The global, three-dimensional magnetohydrodynamic simulations of Tchekhovskoy et al. (2011) show that a large amount of magnetic flux can be transported to the center. This could lead to magnetic flares in the inner region, the acceleration of electrons, and a resulting power-law flux. The different amounts of power-law flux recently observed for GX 339-4 and XTE J1752-223, as discussed above, could well be due to different amounts of flux being accumulated at the center during different outbursts. Dunn et al. (2011) demonstrate in their analysis of the power-law flux during outbursts of the sources 4U 1543-47, GRO J1655-40, GX 339-4, H1743-322, XTE J1550-564, and XTE J1859+226 that there is a remarkable difference in the variability of the power-law flux in the soft and in the hard spectral state. This variability in the soft state could be caused by flare activity, which is also a sign of magnetic fields.
6.5. An effect of mass outflow from the corona?
Accretion disk winds have been found for many galactic X-ray binaries in soft spectral state (Ponti et al. 2012), and especially the microquasar GRS 1915+105 (Neilsen et al. 2011). How would such a wind loss influence the results for ADAF/coronal flows?
Wind loss leads to an inward successive decrease in the local mass accretion rate and also takes up energy from the corona. The reduction in the accretion rate can be approximately followed by our semi-local analysis with a radially decreasing rate.
The impact of a reduced ion heating can be estimated by noting that the ADAF-type coronal flow is sustained until the coupling to the electrons takes away about 90% of the ion heating rate. Even if wind cooling were to take away 50% of the gravitational energy released to the ions, the ADAF character would still remain until electron coupling took away the rest. Owing to the very sensitive dependence of the electron-ion coupling in this temperature range, such wind loss would probably have a minor effect on the local Te − Ti relation and the consequential limits to the coronal mass flow.
7. Conclusions
When broad iron emission lines are observed from a region close to an accreting black hole, obviously both a coronal hot flow and a disk irradiated by X-rays from this hot flow are present. Such an accretion flow geometry either exists in the soft spectral state, with a standard disk + weak coronal flow, or in the hard-intermediate state with a weak inner disk + strong coronal flow.
In the first case, a standard disk in the soft state + corona, the coronal mass flow rate ṁc is expected to be low, as the result of the Compton cooling for an ADAF-type corona, e.g. ṁc ≤ 0.001 for ṁd = 0.1. The observation of a higher coronal flux points to an additional acceleration of the electrons in the corona, as might result from flares of disk magnetic fields. Magnetic flares might yield a tail of non-thermal radiation in the spectrum, as observed for X-ray binaries in soft state. From energy considerations, Merloni & Fabian (2001) pointed out the need for additional electron heating, proposing that this is generated by magnetic flares. Support for this idea also comes from observations of black hole binaries, especially GRO J1655-40. The growing evidence of magnetic processes could be important for the understanding of jet production.
In the second case, of a weak inner disk in the hard-intermediate state + corona, a coronal flow stronger than that in the soft state is possible. The more complex accretion flow geometry, that is expected presumably near the soft/hard spectral transition, might be present for quite some time as a transient phenomenon, until the weak inner disk disappears with a decreasing accretion rate during the outburst decline. Differences in the relation between ion and electron temperatures of the coronal flow between the hard/soft and the soft/hard transition might be the cause of changes in the variability character.
For X-ray binaries with observed broad iron emission lines, it is possible to determine the spectral state and analyze the accretion flow geometry. This is much more difficult for AGN (Raimundo et al. 2012). However, the possible appearance of broad iron emission lines in different configurations of accretion flow geometry allows us to understand that these lines are very common in Seyfert-1 AGN (Nandra et al. 2007; Miller 2007).
Acknowledgments
We thank Werner Collmar for information about γ-ray observations. B. F. Liu thanks the Alexander-von-Humboldt Foundation for support and acknowledges support by the National Natural Science Foundation of China (grants 11033007 and 11173029) and by the National Basic Research Program of China-973 Program 2009CB824800.
References
- Barr, P., White, N. E., & Page, C. G. 1985, MNRAS, 216, 65 [Google Scholar]
- Beloborodov, A. M. 1999, ApJ, 510, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Bhayani, S., & Nandra, K. 2011, MNRAS, 416, 629 [NASA ADS] [Google Scholar]
- Cadolle Bel, M., Rodriguez, J., D’Avanzo, P., et al. 2011, A&A, 534, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, C.-Y., & Fabian, A. C. 2011, MNRAS, 414, 2345 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, R. J. H., Fender, R. P., & Körding, E. G. 2011, MNRAS, 411, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Esin, A. A. 1997, ApJ, 482, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Falocco, S., Carrera, F. J., Corral, A., et al. 2012, A&A, 538, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frontera, F., Palazzi, E., Zdziarski, A. A., et al. 2001, ApJ, 546, 1027 [NASA ADS] [CrossRef] [Google Scholar]
- Gilfanov, M. 2010, in The Jet Paradigm – From Microquasars to Quasars, Lect. Notes Phys., 794 (Springer), 17 [Google Scholar]
- Gilfanov, M., Churazov, E., & Revnivtsev, W. 1999, A&A, 352, 182 [NASA ADS] [Google Scholar]
- Grove, J. E., Johnson, W. N., Kroeger, R. A., et al. 1998, ApJ, 500, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Joinet, A., Kalemci, E., & Senziani, F. 2008, ApJ, 679, 655 [NASA ADS] [CrossRef] [Google Scholar]
- Ibragimov, A., Poutanen, J., Gilfanov, M., et al. 2005, MNRAS, 362, 1435 [NASA ADS] [CrossRef] [Google Scholar]
- Ichimaru, S. 1977, ApJ, 214, 840 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B. F., Mineshige, S., Meyer, F., et al. 2002, ApJ, 575, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B. F., Meyer, F., & Meyer-Hofmeister, E. 2006, A&A, 454, L9 [Google Scholar]
- Liu, B. F., Taam, R. E., Meyer-Hofmeister, E., et al. 2007, ApJ, 671, 695 [NASA ADS] [CrossRef] [Google Scholar]
- McClintock, J. E., & Remillard, R. A. 2006, in Compact Stellar X-ray Sources, eds. W. H. G. Lewin, & M. van der Klis (Cambridge University Press), Cambridge Astrophys. Ser., 39, 157 [Google Scholar]
- McConnell, M. L., Zdziarski, A. A., Bennett, K., et al. 2002, ApJ, 572, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., & Fabian, A. C. 2001, MNRAS, 321, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer, F. 1996, in Accretion Disks – New Aspects, eds. E. Meyer-Hofmeister, & H. Spruit, Lect. Notes Phys., 487 (Springer), 338 [Google Scholar]
- Meyer, F., & Meyer-Hofmeister, E. 1994, A&A, 288, 175 [NASA ADS] [Google Scholar]
- Meyer, F., Liu, B. F., & Meyer-Hofmeister, E. 2007, A&A, 463, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer-Hofmeister, E., Liu, B. F., & Meyer, F. 2005, A&A, 432, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer-Hofmeister, E., Liu, B. F., & Meyer, F. 2009, A&A, 508, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer-Hofmeister, E., & Meyer, F. 2011, A&A, 527, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, J. M. 2007, ARA&A, 45, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Raymond, J., Reynolds, C. S., et al. 2008, ApJ, 680, 1359 [NASA ADS] [CrossRef] [Google Scholar]
- Motta, S., Belloni, T., & Homan, J. 2009, MNRAS, 400, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Nakahira, S., Koyama, S., Ueda, Y., et al. 2012, PASJ, 64, 13 [NASA ADS] [Google Scholar]
- Nandra, K., Neill, P. O., George, L. M., et al. 2007, MNRAS, 382, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995a, ApJ, 444, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., & Yi, I. 1995b, ApJ, 452, 710 [NASA ADS] [CrossRef] [Google Scholar]
- Narayan, R., Mahadevan, R., & Quataert, E. 1998, in Theory of Black Hole Accretion Disks, eds. M. A. Abramowicz, G. Bjornson, & J. E. Pringle (Cambridge Univ. Press), 148 [Google Scholar]
- Neilsen, J., Remillard, R. A., & Lee, J. C. 2011, ApJ, 737, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Piran, T. 1978, ApJ, 221, 652 [NASA ADS] [CrossRef] [Google Scholar]
- Ponti, G., Fender, R. P., Begelman, M. C., et al. 2012, MNRAS, 422, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Poutanen, J., & Fabian, A. C. 1999, MNRAS, 306, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Qiao, E., & Liu, B. F. 2012, ApJ, 744, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Raimundo, S. I., Fabian, A. C., Vasudevan, R. V., et al. 2012, MNRAS, 419, 2529 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, J. N., Fabian, A. C., Kataoka, J., et al. 2006, Astron. Nachr., 327, 1067 [Google Scholar]
- Reis, R. C., Miller, J. M., & Fabian, A. C. 2009, MNRAS, 395, L52 [NASA ADS] [CrossRef] [Google Scholar]
- Reis, R. C., Fabian, A. C., & Miller, J. M. 2010, MNRAS, 402, 836 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, M. T., & Miller, J. M. 2011, ApJ, submitted [arXiv:1112.2249] [Google Scholar]
- Schandl, S., & Meyer, F. 1994, A&A, 289, 149 [NASA ADS] [Google Scholar]
- Shapiro, S. L., Lightman, A. P., & Eardley, D. M. 1976, ApJ, 204, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Sharma, P., Hammet, W., Quataert, E., et al. 2006, ApJ, 637, 952 [NASA ADS] [CrossRef] [Google Scholar]
- Shidatsu, M., Ueda, Y., Nakahira, S., et al. 2011, PASJ, 63, 803 [NASA ADS] [Google Scholar]
- Stepney, S. 1983, MNRAS, 202, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Stiele, H., Motta, S., Muños-Darias, T., et al. 2011, MNRAS, 418, 1746 [NASA ADS] [CrossRef] [Google Scholar]
- Taam, R. E., Liu, B. F., Meyer, F., et al. 2008, ApJ, 688, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Tanaka, Y., Nandra, K., Fabian, A. C., et al. 1995, Nature, 375, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Tchekhovskoy, A., Narayan, R., McKinney, J. C., et al. 2011, MNRAS, 418, 79 [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2007, MNRAS, 381, 1235 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., & Fabian, A. C. 2009, MNRAS, 392, 1124 [NASA ADS] [CrossRef] [Google Scholar]
- Walton, D. J., Reis, R. C., Cackett, E. M., et al. 2012, MNRAS, 422, 2510 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Poutanen, J., & Johnson, W. N. 2000, ApJ, 542, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Grove, J. E., Poutanen, J., et al. 2001, ApJ, 554, L48 [Google Scholar]
- Zdziarski, A. A., Gierliński, M., & Rao, A. R., et al. 2005, MNRAS, 360, 825 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 The change of ion temperature with electron temperature for given rates of coronal mass flow ṁc at distance r = 30, α = 0.2 and β = 0.8. |
| In the text | |
 |
Fig. 2 Relation between ion and electron temperature, for different distances from the black hole, and ṁc = 0.01, α = 0.2. |
| In the text | |
 |
Fig. 3 The effect of Compton cooling: upper limit to the mass flow rate ṁc in the ADAF-corona for different mass flow rates ṁd in the disk and distances, α = 0.2 (approximation for f = 0.1). Rates ṁd = 0.1 − 0.2 correspond to a typical soft state, and rates ≤ 0.01 to an intermediate state. |
| In the text | |
 |
Fig. 4 Ion and electron temperature Ti and Te under Compton cooling by photons from a disk underneath as function of disk mass flow rate ṁd. Solid lines: coronal mass flow rate ṁc = 0.01, dashed lines: ṁc = 0.001; left panel: R = 3 RS, right panel: R = 30 RS; α = 0.2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


