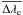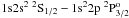EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 543 (July 2012) A&A, 543 (2012) A44 Full HTML
Free Access
Issue
A&A
Volume 543, July 2012
Article Number A44
Number of page(s) 9
Section Atomic, molecular, and nuclear data
DOI https://doi.org/10.1051/0004-6361/201219438
Published online 25 June 2012

© ESO, 2012

1. Introduction

The improved resolution and sensitivity of current satellite-borne X-ray telescopes (Chandra, XMM-Newton and Suzaku) are allowing the study of weak spectral features which are nonetheless of astrophysical interest. This is the case of light odd-Z and iron-peak elements (excluding iron and nickel) whose absorption K lines have been observed in the high-resolution Chandra spectrum of the micro quasar GRO J1655-40, thus enabling abundances determinations (Kallman et al. 2009).

The first detection of helium-like Cr and Mn emission K lines in clusters has been reported by Tamura et al. (2009). They used Suzaku observations of the central region of the Perseus cluser and analyzed X-ray spectra from the intracluster medium recorded by the X-ray Imaging Spectrometer (XIS) to determine the Cr and Mn abundances.

Nobukawa et al. (2010) recorded Suzaku XIS X-ray spectra of the Galactic center region and discovered K-shell emission lines of “neutral” (lowly-ionized) atoms. Amongst these, the lowly-ionized chromium and manganese Kα lines were found. They also observed the helium-like Cr and Mn Kα lines.

Suzaku XIS spectra of Tycho’s supernova remnant (SNR) were taken by Tamagawa et al. (2009).They observed for the first time significant Kα line emission from the trace species chromium and manganese at energies of 5.48 keV and 5.95 keV, respectively. From Moseley’s law and the K line wavelengths and Kβ/Kα line ratios of the iron ions reported in Mendoza et al. (2004), they concluded that the charge state of these ions is consistent with Cr xv–xvi and Mn xv–xvi. Following this observation, Badenes et al. (2008) proposed a new method for measuring the metallicity of type Ia supernova progenitors using manganese and chromium K lines in SNR.

Recently X-ray emission K lines of radioactive scandium (33Sc) have been detected at 4.1 keV from a 237 ks Chandra spectrum of the youngest (~100 years) galactic SNR G1.9+0.3 (Borkowski et al. 2010). Deeper observations should impose more constraints on nucleosynthesis models of type Ia supernovae.

Moreover, Astro-H, the next generation of X-ray observatory, with a 7 eV resolution in the spectral range around 6 keV, will challenge our knowledge on the atomic processes involving the iron peak elements at play in astrophysical plasmas.

Following extensive work by Palmeri et al. (2002; 2003a,b), Bautista et al. (2003; 2004), Mendoza et al. (2004) and Kallman et al. (2004) on Fe K lines; García et al. (2005) on the K-shell photoabsorption of O ions; Palmeri et al. (2008a) on the Ne, Mg, Si, S, Ar and Ca K lines; Palmeri et al. (2008b) on the Ni K lines; García et al. (2009) on the K-shell photoionization and photoabsorption of N ions; by Witthoeft et al. (2009) on K-shell photoionization and photoabsorpton of Ne, Mg, Si, Ar and Ca ions and the more recent studies on Al K lines (Palmeri et al. 2011), radiative and Auger parameters are now calculated for the modeling of the K lines of all the ions belonging to the F, Na, P, Cl, K, Sc, Ti, V, Cr, Mn, Co, Cu and Zn isonuclear sequences up to the singly ionized members. Level energies, transition wavelengths, radiative transition probabilities, radiative and Auger widths and K-vacancy level fluorescence yields have been determined using HFR, a Hartree-Fock method with relativistic corrections (Cowan 1981). The main goals are the improvement of the atomic database of the XSTAR modeling code for photoionized plasmas (Bautista & Kallman 2001), and the preparation of ionic targets (configuration expansions and orbitals) for the lengthy computations of the K-shell photoabsorption and photoionization cross sections, where both radiative and Auger dampings are key effects (Palmeri et al. 2002).

The outline of the present report is as follows. The numerical calculations are briefly described in Sect. 2, while a detailed analysis of the results based on comparisons with previous experimental and theoretical values is carried out in Sect. 3. The two supplementary electronic tables are briefly explained in Sect. 4, and some conclusions are finally drawn in Sect. 5.

2. Calculations

Three independent atomic structure packages have been used. The bulk of the atomic data is computed with the Hartree-Fock with relativistic corrections (HFR) method of Cowan (1981). Data accuracy is assessed by comparing with two other approaches: the multiconfiguration Breit-Pauli method, which incorporates a scaled Thomas-Fermi-Dirac (TFD) statistical potential as implemented in AUTOSTRUCTURE (Badnell 2011), and the GRASP code (Grant et al. 1980; Grant & McKenzie 1980; McKenzie et al. 1980) based on the multiconfiguration Dirac-Fock method.

In HFR and AUTOSTRUCTURE, wave functions are calculated with a Hamiltonian that includes Breit-Pauli relativistic corrections 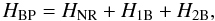HBP=HNR+H1B+H2B,\begin{equation} % H_{\rm BP} = H_{\rm NR} + H_{\rm 1B} + H_{\rm 2B}, \end{equation}(1)where HNR is the usual nonrelativistic Hamiltonian. The one-body relativistic operators 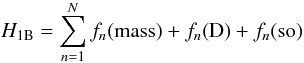H1B=∑n=1Nfn(mass)+fn(D)+fn(so)\begin{equation} % H_{\rm 1B} = \sum^N_{n=1} f_n({\rm mass}) + f_n({\rm D}) + f_n({\rm so}) \end{equation}(2)represent the spin-orbit interaction, fn(so), the non-fine-structure mass variation, fn(mass), and the one-body Darwin correction, fn(D). The two-body Breit operators are given by 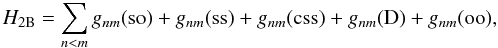H2B=∑n<mgnm(so)+gnm(ss)+gnm(css)+gnm(D)+gnm(oo),\begin{equation} % H_{\rm 2B} = \sum_{n<m} g_{nm}({\rm so}) + g_{nm}({\rm ss}) + g_{nm}({\rm css}) + g_{nm}({\rm D}) + g_{nm}({\rm oo}), \label{breit} \end{equation}(3)where the fine-structure terms are gnm(so) (spin-other-orbit and mutual spin-orbit) and gnm(ss) (spin-spin), and the non-fine-structure counterparts are gnm(css) (spin-spin contact), gnm(D) (two-body Darwin), and gnm(oo) (orbit-orbit). HFR computes energies, A-values, and Auger rates with nonorthogonal orbital bases, which are generated by optimizing the average energy of each configuration. It also neglects the part of the Breit interaction (Eq. (3)) that cannot be reduced to a one-body operator. AUTOSTRUCTURE can use both orthogonal and nonorthogonal orbital bases for all the electronic configurations considered, which enables estimates of relaxation effects. In this study, we used non-orthogonal orbitals in order to consider the relaxation effects. Auger rates are computed in both HFR and AUTOSTRUCTURE in a distorted wave approach. The Auger decay channels considered in the present calculations and the configuration-interaction (CI) expansions used are the same as in our previous papers on the Fe isonuclear sequence (Bautista et al. 2003; Palmeri et al. 2003a,b; Mendoza et al. 2004). Concerning the open-3d-shell ions, we employ the formula given in Palmeri et al. (2001) for single-configuration averaged Auger decay rates 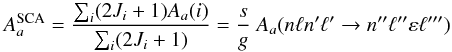AaSCA=∑i(2Ji+1)Aa(i)∑i(2Ji+1)=sg Aa(nℓn′ℓ′→n′′ℓ′′εℓ′′′)\begin{equation} % A^{\rm SCA}_a = \frac{\sum_i (2J_i+1) A_a(i)}{\sum_i (2J_i+1)} = \frac{s}{g}~ A_a (n\ell n'\ell' \rightarrow n''\ell'' \varepsilon\ell''') \end{equation}(4)which is based on the total Auger rate formula determined by Kucas et al. (1995) using a general group-diagrammatic summation method and where the sum runs over all the levels of the autoionizing configuration, s/g is a statistical factor given in Eqs. (15), (16) of Palmeri et al. (2001) that contains the dependence on the active shell (nℓ, n′ℓ′, n′′ℓ′′) occupancy, and Aa(nℓn′ℓ′ → n′′ℓ′′εℓ′′′) is the two-electron autoionization rate which is a function of the radial integrals and for which the complete expression is given in Eq. (11) of Palmeri et al. (2001). The SCA Auger rates using this formula are expected to be as accurate as those obtained in a level-by-level single-configuration approach. In this work, the radial integrals are determined by the HFR method. This approach was used originally by Griffin et al. (1985) to calculate distorted wave dielectronic recombination cross sections in the Li-like ions. On the other hand, AUTOSTRUCTURE Auger rates are calculated level by level but a single-configuration approximation is still used for these ions due to the complexity of their atomic structures.

Our third package is GRASP which is an implementation of the multiconfiguration Dirac-Fock (MCDF) method where the atomic state function (ASF) is represented as a superposition of configuration state functions (CSF) of the type 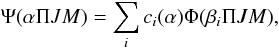Ψ(αΠJM)=∑ici(α)Φ(βiΠJM),\begin{equation} % \Psi(\alpha \Pi J M) = \sum_i c_i(\alpha) \Phi(\beta_i \Pi J M), \label{grasp} \end{equation}(5)where Ψ and Φ are, respectively, the ASF and CSF. Π, J and M are the relevant quantum numbers: parity, total angular momentum and its associated total magnetic number, respectively, and α and βi stand for all the other quantum numbers that are necessary to describe unambiguously the ASFs and CSFs. The summation in Eq. (5) is up to nc, the number of CSFs in the expansion, and each CSF is built from antisymmetrised products of relativistic spin orbitals. The ci coefficients, together with the orbitals, are optimized by minimizing an energy functional. The latter is built from one or more eigenvalues of the Dirac-Coulomb Hamiltonian depending on the optimization strategy adopted. In the present work, we have used the extended average level (EAL) option in which the (2J + 1) weighted trace of the Hamiltonian is minimized. The transverse Breit interaction as well as other quantum electrodynamics (QED) interactions, namely the vacuum polarization and self-energy, have been included in the Hamiltonian matrix as perturbations. This code does not treat the continuum, and has thus been exclusively employed in comparisons of the radiative data for bound-bound transitions.

Grid middleware combined with Python scripts have been used in a computer grid to calculate the HFR atomic data for all the ions in one go. The final electronic tables were generated automatically using Python scripts during a single multi-node job. The AUTOSTRUCTURE and MCDF-EAL calculations, on the other hand, were run in parallel for specific ions on a local cluster in order to estimate the accuracy of the HFR data.

3. Results and discussions

Detailed comparisons with previous data have been carried out in order to obtain accuracy estimates and detect weak points. In the following sections, we give a concise account of our computations of level energies and radiative and Auger widths for K-vacancy states and wavelengths and radiative transition probabilities for K lines in members of the F, Na, P, Cl, K, Sc, Ti, V, Cr, Mn, Co, Cu, and Zn isonuclear sequences, each ion denoted hereafter by its electron number N and atomic number Z. Some of the characteristics of the unresolved transition arrays (UTAs) are studied in the singly-ionized (Zc = Z − N + 1 = 2) ions with 11 ≤ Z ≤ 30, namely the λKα1, λKα2 and λKβ UTA centroid wavelengths, the Kα2/Kα1 and Kβ/Kα intensity ratios, the KLM/KLL and KMM/KLL Auger channel ratios and the K-shell fluorescence yield ωK. As a matter of fact, xstar simulations of iron K lines showed that K lines of second and third-row ions will appear in astrophysical spectra as UTAs (Palmeri et al. 2003b).

Table 1

Comparison between EBIT and HFR K-vacancy level energies.

3.1. Energy levels

In Table 1, the HFR, AUTOSTRUCTURE and MCDF-EAL energies for fine structure K-vacancy levels are compared with experimental values determined from the available EBIT wavelengths for resonance lines (Beiersdorfer et al. 1989; 1991; Chantler et al. 2000; Smith et al. 1995). Reasonably good agreement is found for HFR, with discrepancies ranging from a few tenths of an eV to  ~ 3 eV. This level of accuracy is expected with HFR for K-vacancy levels of highly charged ions as reported in our previous studies. Concerning AUTOSTRUCTURE, the differences with the EBIT energies are somewhat larger ranging from a few tenths of an eV to  ~ 8 eV. This is not due to the relaxation effects that are considered in our AUTOSTRUCTURE calculations but it is probably due to the use of the less accurate scaled TFD statistical potential. Regarding MCDF-EAL, the calculated energies are systematically smaller than experiment with differences ranging from a few tenths of an eV to  ~ 4 eV. Here the systematic is due to the missing relaxation effects.

Table 2

Comparison between HFR, experimental and RMBPT K-edge energies in neutral atoms.

Table 2 shows a comparison between our HFR K-edge energies in neutral atoms with measurements in the solid and gas phases (Deslattes et al. 2003) and the theoretical values by Deslattes et al. (2003) obtained by means of the Relativistic Many Body Perturbation Theory (RMBPT) method. In the HFR calculations, the K-edge energy was estimated by taking the difference between the energy of fine-structure ground level of the neutral atom and that of the lowest fine-structure K-vacancy level of the singly ionized ion. The solid-state measurements are systematically lower than both HFR and RMBPT calculations by ~10−15 eV. This kind of discrepancy vanishes when comparing the free-atom calculations (HFR and RMBPT) with the available gas-phase experimental values, suggesting a solid-state effect in the interpretation of the above-mentioned systematic. The agreement with the gas-phase measurements is similar for HFR and RMBPT, where differences range from  − 4.5 eV in zinc to 3.5 eV in cobalt for HFR, and from  − 7.7 eV in scandium to 0.8 eV in cobalt for RMBPT.

Table 3

Comparison between HFR and experimental UTA wavelengths in singly-ionized ions.

In conclusion, these comparisons suggest an accuracy of a few eV for our HFR K-vacancy level energies.

thumbnail Fig. 1

Average wavelength differences between HFR and experiment (in mÅ), Δλe\hbox{$\overline{\Delta \lambda_{\rm e}}$}, for K lines of ions belonging to three isoelectronic sequences as function of the effective charge, Zc = Z − N + 1. Full squares: Be-like sequence (N = 4); open diamonds: O-like sequence (N = 8); full circles: F-like sequence (N = 9). Experimental data for ions with Zc ≤ 15 are taken from the laser-produced plasma (Faenov et al. 1994) and plasma focus discharge in argon (Biémont et al. 2000) experiments. EBIT measurements (Beiersdorfer et al. 1991; Smith et al. 1995; Decaux et al. 1997) are considered for ions with Zc > 15. Experimental error bars are included.

3.2. Wavelengths

In Fig. 1, we plot as function of the effective charge, Zc = Z − N + 1, the average wavelength difference (in mÅ) between HFR and experiment, 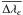Δλe\hbox{$\overline{\Delta \lambda_e}$}, for K lines of ions belonging to three isoelectronic sequences, namely beryllium (N = 4), oxygen (N = 8) and fluorine (N = 9). 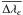Δλe\hbox{$\overline{\Delta \lambda_e}$} is computed using the formula 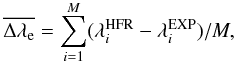Δλe=∑i=1M(λiHFR−λiEXP)/M,\begin{equation} % \overline{\Delta \lambda_{\rm e}} = \sum_{i=1}^{M} (\lambda_{i}^{\rm HFR} - \lambda_{i}^{\rm EXP}) / M, \end{equation}(6)where M is the number of available experimental wavelengths. For ions with Zc ≤ 15, the experimental wavelengths 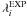λiEXP\hbox{$\lambda_{i}^{\rm EXP}$} are taken from the laser-produced plasma experiment of Faenov et al. (1994) and the plasma focus discharge in argon of Biémont et al. (2000); for ions with Zc > 15, the wavelengths measured using an EBIT are considered (Beiersdorfer et al. 1991; Smith et al. 1995; Decaux et al. 1997). The HFR wavelengths 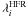λiHFR\hbox{$\lambda_{i}^{\rm HFR}$} are calculated in this work for phosphorus, vanadium and cobalt; in Palmeri et al. (2003a) for iron; in Palmeri et al. (2008a) for magnesium, silicon, sulphur and argon and in Palmeri et al. (2011) for aluminium. The experimental error bars are also displayed. It may be noticed that HFR wavelengths are shorter than experiment, and that the differences grow, on average, with the effective charge along each isoelectronic sequences where they span a range from less than 1 mÅ (Zc = 24) to 24 mÅ (Zc = 6). The trends differ from a given isoelectronic sequence to the other, and consequently, we did not attempt to correct our calculated wavelengths.

Table 3 presents a comparison of centroid wavelengths for the Kα1 ( [1s1/2]  →  [2p3/2] ), Kα2 ( [1s1/2]  →  [2p1/2] ) and Kβ ( [1s1/2]  →  [3p1/2,3/2] ) UTAs calculated with HFR for singly-ionized ions with those measured in the solid (Deslattes et al. 2003). These centroid wavelengths have been calculated using the following formula for a given UTA: 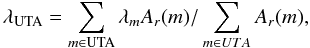λUTA=∑m∈UTAλmAr(m)/∑m∈UTAAr(m),\begin{equation} % \lambda_{\rm UTA} = \sum_{m \in {\rm UTA}} \lambda_m A_r(m) / \sum_{m \in UTA} A_r(m), \end{equation}(7)where λUTA is the centroid wavelength, λm is the wavelength of the m fine-structure transition belonging to the UTA and Ar(m) is the corresponding radiative transition probability. As the HFR method uses κ-averaged relativistic orbitals, the Kα1 and Kα2 UTAs had to be separated using plots of the transition probability as function of the wavelengths; however, this was not possible in ions with weak 2p orbital spin-orbit interaction, i.e. in Na ii, P ii, Cl ii and K ii. Figure 2 gives two examples of such plots in Na ii (upper panel) and in Cu ii (lower panel). In Table 3, it may be appreciated that the HFR Kα centroid wavelengths are shorter than the measurements in the solid: absolute differences decrease with Z ranging from ~ 10 mÅ for sodium to  ~0.5 mÅ for zinc. In fact, relative differences are approximatively constant with a value of better than  ~10-3. Concerning the Kβ UTA, the differences are affected by the delocalization of the 3p orbital in the crystals of sodium, phosphorus and chlorine, and by the fact that, in the iron-peak elements, the  [1s1/2]  →  [3d3/2,5/2] hole transition (Kβ5) is E1-forbidden in the free atom (weak and therefore neglected in our HFR calculations) and E1-allowed (i.e. strong) in the solid (Török et al. 1996). Nevertheless, one can see that they are surprisingly small (less than 1 mÅ) in the iron-peak elements.

From these comparisons, we can say that our HFR wavelengths have in general a relative accuracy of better than  ~10-3.

thumbnail Fig. 2

HFR spectra (transition probability as function of wavelength) for fine-structure Kα transitions in Na ii (upper panel) and in Cu ii (lower panel). In singly-ionized copper, Kα1 and Kα2 UTAs are clearly resolved.

thumbnail Fig. 3

1s2s2 2S1/2−1s22p 2P1/2o\hbox{${\rm 1s2s^2~^2S_{1/2} - 1s^22p~^2P^o_{1/2}}$} to 1s2s2 2S1/2−1s22p 2P3/2o\hbox{${\rm 1s2s^2~^2S_{1/2} - 1s^22p~^2P^o_{3/2}}$} line intensity ratio as function of the atomic number, Z, along the lithium isoelectronic sequence. Full circles: HFR calculations (this work); open circles: MCDF-EAL calculations (this work); open triangles up: MCDF-EAL calculations (Beiersdorfer et al. 1991); open triangles down: MCDF-OL calculations (Beiersdorfer et al. 1991); open squares: EBIT measurements (Beiersdorfer et al. 1991).

3.3. Transition probabilities, radiative and Auger widths

Figure 3 shows the 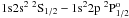1s2s2 2S1/2−1s22p 2P1/2o\hbox{${\rm 1s2s^2~^2S_{1/2} - 1s^22p~^2P^o_{1/2}}$} to 1s2s2   2S1/2 – 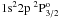1s22p 2P3/2o\hbox{${\rm 1s^22p~^2P^o_{3/2}}$} line intensity ratio as function of the atomic number, Z, along the lithium isoelectronic sequence. These transitions are only possible through the interaction between the configurations 1s2s2 and 1s2p2. These line intensities were measured by Beiersdorfer et al. (1991) using EBIT sources for vanadium, chromium, manganese, iron, nickel and germanium. They also estimated theoretical values as ratios of radiative transition probabilities using the MCDF method with two different optimization options (EAL and OL). We report the transition probability ratios calculated with HFR in this work (Z = 9, 11, 15, 17, 19, 21 − 25, 27, 29, 30, 32) and in our previous studies (Palmeri et al. 2003a; 2008a; 2011). We have also carried out MCDF-EAL calculations in fluorine, phosphorus, calcium, vanadium, chromium, manganese, iron, nickel and germanium. Our HFR and MCDF-EAL calculations agree and display exactly the same trend along the sequence. The EBIT measurements are in good agreement with our theoretical values (HFR and MCDF-EAL) except in manganese and iron where our theoretical ratios are slightly outside the experimental error bars. The theoretical values of Beierdorfer et al. (1991) are somewhat higher than ours for ions with Z ≥ 25.

thumbnail Fig. 4

Transition probability ratio with respect to HFR as function of HFR transition probability for strong K lines (A > 1013   s-1) in Ti xvii. Circles: MCDF calculations (Chen et al. 1997); squares: MCDF-EAL calculations (this work); diamonds: AUTOSTRUCTURE calculations (this work). Average ratios are respectively 1.42  ±  1.70 (Chen et al. 1997), 1.00  ±  0.17 (MCDF-EAL) and 1.05  ±  0.36 (AUTOSTRUCTURE). A straight line of equality has been drawn.

In Fig. 4, the HFR radiative transition probabilities are compared with the MCDF values of Chen et al. (1997) and with our MCDF-EAL and AUTOSTRUCTURE calculations for the strong K lines (AHFR > 1013 s-1) in C-like titanium (Ti xvii). It may be noticed that the scatter between Chen et al. and HFR is significant. Moreover, the MCDF A-values become systematically higher than HFR for values greater than 1014 s-1, the average ratio with respect to HFR being 1.42  ±  1.70 (the scatter range is given in terms of the standard deviation). This discrepancy contrasts with the good agreement found with our MCDF-EAL and AUTOSTRUCTURE transition probabilities with average ratios of 1.00  ±  0.17 and 1.05  ±  0.36, respectively. This type of situation was also encountered in C-like argon where the MCDF A-values calculated by Chen et al. were found to be problematic (Palmeri et al. 2008a). Cancelation effects impacting the HFR line strengths (Cowan 1981) explain the disagreements (ratios of more than 1.5 and less than 0.5) found for some transitions with HFR A-values close to 1013 s-1. For these particular transitions, the resulting HFR transition probabilities are weaker than they should be and are affected by important numerical inaccuracies.

thumbnail Fig. 5

Radiative width ratio with respect to HFR as function of HFR radiative width in Ti xvii. Circles: MCDF calculations (Chen et al. 1997); squares: MCDF-EAL calculations (this work); diamonds: AUTOSTRUCTURE calculations (this work). Average ratios are respectively 1.27  ±  0.12 (Chen et al. 1997), 1.01  ±  0.04 (MCDF-EAL) and 1.02  ±  0.05 (AUTOSTRUCTURE). A straight line of equality has been drawn.

Figure 5 is the equivalent of Fig. 4 for the radiative widths. Values by Chen et al. (1997) are on average higher than HFR with an average ratio of 1.27  ±  0.12, reflecting the situation found for the transition probabilities. Both of our MCDF-EAL and AUTOSTRUCTURE calculations agree well with HFR, with average ratios of 1.01  ±  0.04 and 1.02  ±  0.05, respectively.

The HFR Auger widths in Ti xvii are compared with AUTOSTRUCTURE and the MCDF calculation of Chen et al. (1997) in Fig. 6. Here again, widths by Chen et al. are noticeably larger than HFR (the average ratio is 1.22  ±  0.16) while our AUTOSTRUCTURE values agree with HFR to within 4%.

thumbnail Fig. 6

Auger width ratio with respect to HFR as function of HFR Auger width in Ti xvii. Circles: MCDF calculations (Chen et al. 1997); diamonds: AUTOSTRUCTURE calculations (this work). Average ratios are respectively 1.22  ±  0.16 (Chen et al. 1997) and 0.94  ±  0.04 (AUTOSTRUCTURE). A straight line of equality has been drawn.

3.4. UTA intensity ratios, Auger channel ratios and K-shell fluorescence yields

In Table 4, the HFR Kα2/Kα1 UTA intensity ratios for singly-ionized ions with 21 ≤ Z ≤ 30 are compared with our AUTOSTRUCTURE and MCDF-EAL results and with the measured UTA intensity ratios of Hölzer et al. (1997). The agreement between all four data sets is within a few percents.

Table 4

Comparison between HFR and other Kα2/Kα1 UTA line ratios.

Table 5

Comparison between HFR and other Kβ/Kα UTA line ratios.

Table 6

Comparison between HFR and other KLM/KLL Auger channel ratios.

In Table 5, we compare between the calculated Kβ/Kα UTA intensity ratios for singly ionized ions with 15 ≤ Z ≤ 30 using our three independent methods (HFR, AUTOSTRUCTURE and MCDF-EAL) with measurements in solids (Hölzer et al. 1997; Bé et al. 1998; Öz 2006) and the empirical fit of Schönfeld & Janssen (1996). The solid-state measurements and the empirical fit values are scaled down by a factor of 0.9 for elements with 17 ≤ Z ≤ 30 in order to remove the radiative Auger and the solid-state Kβ5 emission contributions not considered in our three free atom models (Török et al. 1996; Bé et al. 1998; Verma 2000). AUTOSTRUCTURE values agree with HFR to within ~ 15% while the MCDF ratios are systematically higher than HFR by ~10%. The solid-state measurements of Hölzer et al. (1997) and Bé et al. (1998) are closer to our MCDF values than to HFR except in cobalt and copper, while the ratios measured by Öz (2006) agree generally better with the latter calculations. Concerning the empirical fit of Schönfeld & Janssen (1996), their values are on average closer to HFR than to AUTOSTRUCTURE and MCDF by, respectively, 2  ±  7%, 6  ±  6% and 5  ±  8%.

We compare our theoretical KLM/KLL Auger channel ratios with experiment for singly-ionized ions with 11 ≤ Z ≤ 30 in Table 6. AUTOSTRUCTURE failed to calculate the Auger rates in V ii, Cr ii and Mn ii due to the memory limits of our computer. With the exception of sodium, the agreement between HFR and AUTOSTRUCTURE is better than 10%. The HFR ratio in Na ii is closer to the measurement carried out in the gas phase by Hillig et al. (1974) than AUTOSTRUCTURE. The measurements in the solid of Kovalik et al. (1988; 1990; 2004) support our HFR calculations.

Table 7 is the equivalent of Table 6 for the KMM/KLL Auger channel ratios. The absence of AUTOSTRUCTURE values for Z = 23 − 25 is due to the same reasons than for the KLM/KLL ratios. Here, the discrepancies between HFR and AUTOSTRUCTURE ratios are around 10 − 30%. The solid-state measurements of Kovalik et al. (2004) in zinc support both of our HFR and AUTOSTRUCTURE ratios, while the experimental values obtained in manganese by Kovalik et al. (1990) are higher than our HFR calculation.

Table 7

Comparison between HFR and other KMM/KLL Auger channel ratios.

Table 8

Comparison between HFR and other K-shell fluorescence yields, ωK.

Table 9

Valence and K-vacancy levels in chromium (Z = 24) ions with electron number 2 ≤ N ≤ 3.

Table 8 presents a comparison of our HFR and AUTOSTRUCTURE K-shell fluorescence yields with experiment (Hubbell et al. 1994; Durak & Özdemir 2001) and with empirical fit values (Bambynek 1984; Hubbell et al. 1994; Durak & Özdemir 2001) are presented for singly-ionized ions with 11 ≤ Z ≤ 30. The lack of AUTOSTRUCTURE values for Z = 23 − 25 is due to the same reasons as for the Auger channel ratios. AUTOSTRUCTURE yields are systematically lower than HFR values by on average a few percents (up to 16% in sodium); this is essentially due to shorter AUTOSTRUCTURE Auger widths as it was found previously in Ti xvii. Although the HFR yields are generally in good agreement with experiment and empirical fits (within 10%), AUTOSTRUCTURE does somewhat better (~5%).

4. Supplementary electronic tables

Tables of computed level energies, wavelengths, radiative transition probabilities, absorption oscillator strengths, radiative and Auger widths, and K-shell fluorescence yields in iron peak and odd-Z elements can be accessed electronically at the CDS. The sizes of the two ASCII tables, one for the levels and the other for the lines, are respectively 4 MB (more than 50 thousand fine-structure levels) and 159 MB (more than 3 million fine-structure K lines). The printed version shows data for chromium (Z = 24) ions with electron number N ≤ 3.

Table 10

K-vacancy transitions in chromium (Z = 24) ions with electron number 2 ≤ N ≤ 3.

In Table 9 levels are identified with the vector (Z,N,i,2S + 1,L,2J,Conf) where Z is the atomic number, N is the electron number, i is the level index, 2S + 1 is the spin multiplicity, L is the total orbital angular momentum quantum number, J is the total angular momentum quantum number, and Conf is the level configuration assignment. For each level, the computed HFR energy and its radiative width Ar(i) are listed. For K-vacancy levels, the Auger width Aa(i) and the K-shell fluorescence yield ωK(i) are also given. In Table 10 transitions are identified with the vector (Z,N,k,i) where k and i are the upper and lower level indices, respectively, tabulating its computed wavelength λ, radiative transition probability Ar(k,i), weighted oscillator strength gf(i,k), and cancelation factor CF as defined by Cowan (1981).

5. Summary and conclusion

Extensive data sets containing energy levels, wavelengths, radiative transition probabilities, absorption oscillator strengths, radiative and Auger widths and fluorescence yields have been computed with the HFR method for more than 3 million fine-structure K lines of iron peak and odd-Z elements.

Comparisons with EBIT energies for K-vacancy levels of highly charged ions and with experimental and RMBPT K-edge energies in neutral atoms suggest an accuracy for our HFR K-vacancy level energies of a few eV. From comparisons with hot plasma and EBIT experiments for highly charged ions and with UTA Kα and Kβ centroid wavelengths measured in solids, we can estimate that the HFR K line wavelengths have in general a relative accuracy of better than  ~10-3.

Concerning the HFR decay rates, comparisons between our three independent methods, on the one hand, with available experimental and empirical fit values of radiative line, Auger channel ratios and K-shell fluorescence yields, on the other, lead to an accuracy estimate of better than ~20% for rates greater than 1013 s-1.

The present radiative and Auger widths will be used in the computation of the K-shell photoionization cross sections of these ions which are required in XSTAR (Kallman & Bautista 2001) for the modeling of some interesting K-shell spectral features.

Acknowledgments

This work was funded in part by the NASA Astronomy and Physics Research and Analysis Program. P.P. and P.Q. are respectively Research Associate and Senior Research Associate of the Belgian FRS-FNRS. Computations were carried out on the BEgrid grid, the Belgian Grid for Research (Belnet, Belgium: http://www.begrid.be), the HMEM (UCL/CÉCI, Belgium: http://www.uclouvain.be/cism; http://www.ceci-hpc.be) and iSCF (FUNDP/UMONS, Belgium: http://www.scf.fundp.ac.be) clusters.

References

  1. Badenes, C., Bravo, E., & Hughes, J. 2008, ApJ, 680, L33 [NASA ADS] [CrossRef] [Google Scholar]
  2. Badnell, N. R. 2011, Comp. Phys. Commun., 182, 1528 [Google Scholar]
  3. Bambynek, W. 1984, X-84 Proc. X-Ray and Inner-Shell Processes in Atoms, Molecules and Solids, Leipzig Aug. 20 − 23, ed. A. Meisel, VEB Druckerei, Thomas Münzer, Langensalza [Google Scholar]
  4. Bautista, M. A., & Kallman, T. R. 2001, ApJS, 134, 139 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bautista, M. A., Mendoza, C., Kallman, T. R., & Palmeri, P. 2003, A&A, 403, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bautista, M. A., Mendoza, C., Kallman, T. R., & Palmeri, P. 2004, A&A, 418, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Bé, M.-M., Lépy, M.-C., Plagnard, J., & Duchemin, B. 1998, Appl. Radiat. Isot., 49, 1367 [Google Scholar]
  8. Behar, E., & Netzer, H. 2002, ApJ, 570, 165 [NASA ADS] [CrossRef] [Google Scholar]
  9. Beiersdorfer, P., Bitter, M., von Goeler, S., & Hill, K. W. 1989, Phys. Rev. A, 40, 150 [NASA ADS] [CrossRef] [Google Scholar]
  10. Beiersdorfer, P., Chen, M. H., Marrs, R. E., Schneider, M. B., & Walling, R. S. 1991, Phys. Rev. A, 44, 396 [NASA ADS] [CrossRef] [Google Scholar]
  11. Biémont, E., Quinet, P., Faenov, A. Ya., et al. 2000, Phys. Scr., 61, 555 [NASA ADS] [CrossRef] [Google Scholar]
  12. Borkowski, K. J., Reynolds, S. P., Green, D. A., et al. 2010, ApJ, 724, L161 [NASA ADS] [CrossRef] [Google Scholar]
  13. Chantler, C. T., Paterson, D., Hudson, L. T., et al. 2000, Phys. Rev. A, 62, 042501 [NASA ADS] [CrossRef] [Google Scholar]
  14. Chen, M. H., Reed, K. J., McWilliams, D. M., et al. 1997, ADNDT, 65, 289 [Google Scholar]
  15. Cowan, R. D. 1981, The Theory of Atomic Structure and Spectra (Berkeley: University of California Press) [Google Scholar]
  16. Decaux, V., Beiersdorfer, P., Kahn, S. M., & Jacobs, V. L. 1997, ApJ, 482, 1076 [NASA ADS] [CrossRef] [Google Scholar]
  17. Deslattes, R. D., Kessler, E. G., Indelicato, P., et al. 2003, Rev. Mod. Phys., 75, 35 [NASA ADS] [CrossRef] [Google Scholar]
  18. Durak, R., & Özdemir, Y. 2001, Rad. Phys. Chem., 61, 19 [Google Scholar]
  19. Faenov, A. Ya., Pikuz, S. A., & Shlyaptseva, A. S. 1994, Phys. Scr. 49, 41 [Google Scholar]
  20. García, J., Mendoza, C., Bautista, M. A., et al. 2005, ApJS, 158, 68 [NASA ADS] [CrossRef] [Google Scholar]
  21. García, J., Kallman, T. R., Witthoeft, M., et al. 2009, ApJS, 185, 477 [NASA ADS] [CrossRef] [Google Scholar]
  22. Grant, I. P., & McKenzie, B. J. 1980, J. Phys. B, 13, 2671 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
  23. Grant, I. P., McKenzie, B. J., Norrington, P. H., Mayers, D. F., & Pyper, N. C. 1980, Comput. Phys. Commun., 21, 207 [NASA ADS] [CrossRef] [Google Scholar]
  24. Griffin, D. C., Pindzola, M. S., & Bottcher, C. 1985, Phys. Rev. A, 31, 568 [NASA ADS] [CrossRef] [Google Scholar]
  25. Hillig, H., Cleff, B., Mehlhorn, W., & Schmitz, W. 1974, Z. Phys., 268, 225 [Google Scholar]
  26. Hölzer, G., Fritsch, M., Deutsch, M., Härtwig, J., & Förster, E. 1997, Phys. Rev. A, 56, 4554 [NASA ADS] [CrossRef] [Google Scholar]
  27. Hubbell, J. H., Trehan, P. N., Singh, N., et al. 1994, J. Phys. Chem. Ref. Data, 23, 339 [NASA ADS] [CrossRef] [Google Scholar]
  28. Kallman, T., & Bautista, M. 2001, ApJS, 133, 221 [NASA ADS] [CrossRef] [Google Scholar]
  29. Kallman, T. R., Palmeri, P., Bautista, M. A., Mendoza, C., & Krolik, J. H. 2004, ApJS, 155, 675 [NASA ADS] [CrossRef] [Google Scholar]
  30. Kallman, T. R., Bautista, M. A., Goriely, S., et al. 2009, ApJ, 701, 865 [NASA ADS] [CrossRef] [Google Scholar]
  31. Kovalík, A., Ryšavý, M., Brabec, V., et al. 1988, Phys. Scr., 37, 871 [NASA ADS] [CrossRef] [Google Scholar]
  32. Kovalík, A., Brabec, V., Novák, J., et al. 1990, J. Electron Spectrosc. Relat. Phenom., 50, 89 [CrossRef] [Google Scholar]
  33. Kovalík, A., Lubashevsky, A. V., Inoyatov, A., et al. 2004, J. Electron Spectrosc. Relat. Phenom., 134, 67 [CrossRef] [Google Scholar]
  34. Kucas, S., Karazija, R., & Jonauskas, V. 1995, Phys. Scr., 52, 639 [NASA ADS] [CrossRef] [Google Scholar]
  35. McKenzie, B. J., Grant, I. P., & Norrington, P. H. 1980, Comput. Phys. Commun., 21, 233 [NASA ADS] [CrossRef] [Google Scholar]
  36. Mendoza, C., Kallman, T. R., Bautista, M. A., & Palmeri, P. 2004, A&A, 414, 377 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Nobukawa, M., Koyama, K., Tsuru, T. G., Ryu, S. G., & Tatischeff, V. 2010, PASJ, 62, 423 [NASA ADS] [Google Scholar]
  38. Öz, E. 2006, JQSRT, 97, 41 [NASA ADS] [Google Scholar]
  39. Palmeri, P., Quinet, P., Zitane, N., & Vaeck, N. 2001, J. Phys. B, 34, 4125 [NASA ADS] [CrossRef] [Google Scholar]
  40. Palmeri, P., Mendoza, C., Kallman, T. R., & Bautista, M. A. 2002, ApJ, 577, L119 [NASA ADS] [CrossRef] [Google Scholar]
  41. Palmeri, P., Mendoza, C., Kallman, T. R., & Bautista, M. A. 2003a, A&A, 403, 1175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Palmeri, P., Mendoza, C., Kallman, T. R., Bautista, M. A., & Meléndez, M. 2003b, A&A, 410, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Palmeri, P., Quinet, P., Mendoza, C., et al. 2008a, ApJS, 177, 408 [NASA ADS] [CrossRef] [Google Scholar]
  44. Palmeri, P., Quinet, P., Mendoza, C., et al. 2008b, ApJS, 179, 542 [NASA ADS] [CrossRef] [Google Scholar]
  45. Palmeri, P., Quinet, P., Mendoza, C., et al. 2011, A&A, 525, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Schönfeld, E., & Janssen, H. 1996, Nucl. Instr. Meth. Phys. Res. A, 369, 527 [Google Scholar]
  47. Smith, A. J., Beiersdorfer, P., Decaux, V., et al. 1995, Phys. Rev. A, 51, 2808 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  48. Tamagawa, T., Hayato, A., Nakamura, S., et al. 2009, PASJ, 61, S167 [NASA ADS] [Google Scholar]
  49. Tamura, T., Maeda, Y., Mitsuda, K., et al. 2009, ApJ, 705, L62 [NASA ADS] [CrossRef] [Google Scholar]
  50. Török, I., Papp, T., Pálinkás, J., et al. 1996, Nucl. Instr. Meth. Phys. Res. B, 114, 9 [NASA ADS] [CrossRef] [Google Scholar]
  51. Verma, H. R. 2000, J. Phys. B, 33, 3407 [NASA ADS] [CrossRef] [Google Scholar]
  52. Witthoeft, M. C., Bautista, M. A., Mendoza, C., et al. 2009, ApJS, 182, 127 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Comparison between EBIT and HFR K-vacancy level energies.

In the text
Table 2

Comparison between HFR, experimental and RMBPT K-edge energies in neutral atoms.

In the text
Table 3

Comparison between HFR and experimental UTA wavelengths in singly-ionized ions.

In the text
Table 4

Comparison between HFR and other Kα2/Kα1 UTA line ratios.

In the text
Table 5

Comparison between HFR and other Kβ/Kα UTA line ratios.

In the text
Table 6

Comparison between HFR and other KLM/KLL Auger channel ratios.

In the text
Table 7

Comparison between HFR and other KMM/KLL Auger channel ratios.

In the text
Table 8

Comparison between HFR and other K-shell fluorescence yields, ωK.

In the text
Table 9

Valence and K-vacancy levels in chromium (Z = 24) ions with electron number 2 ≤ N ≤ 3.

In the text
Table 10

K-vacancy transitions in chromium (Z = 24) ions with electron number 2 ≤ N ≤ 3.

In the text

All Figures

thumbnail Fig. 1

Average wavelength differences between HFR and experiment (in mÅ), Δλe\hbox{$\overline{\Delta \lambda_{\rm e}}$}, for K lines of ions belonging to three isoelectronic sequences as function of the effective charge, Zc = Z − N + 1. Full squares: Be-like sequence (N = 4); open diamonds: O-like sequence (N = 8); full circles: F-like sequence (N = 9). Experimental data for ions with Zc ≤ 15 are taken from the laser-produced plasma (Faenov et al. 1994) and plasma focus discharge in argon (Biémont et al. 2000) experiments. EBIT measurements (Beiersdorfer et al. 1991; Smith et al. 1995; Decaux et al. 1997) are considered for ions with Zc > 15. Experimental error bars are included.
In the text
thumbnail Fig. 2

HFR spectra (transition probability as function of wavelength) for fine-structure Kα transitions in Na ii (upper panel) and in Cu ii (lower panel). In singly-ionized copper, Kα1 and Kα2 UTAs are clearly resolved.
In the text
thumbnail Fig. 3

1s2s2 2S1/2−1s22p 2P1/2o\hbox{${\rm 1s2s^2~^2S_{1/2} - 1s^22p~^2P^o_{1/2}}$} to 1s2s2 2S1/2−1s22p 2P3/2o\hbox{${\rm 1s2s^2~^2S_{1/2} - 1s^22p~^2P^o_{3/2}}$} line intensity ratio as function of the atomic number, Z, along the lithium isoelectronic sequence. Full circles: HFR calculations (this work); open circles: MCDF-EAL calculations (this work); open triangles up: MCDF-EAL calculations (Beiersdorfer et al. 1991); open triangles down: MCDF-OL calculations (Beiersdorfer et al. 1991); open squares: EBIT measurements (Beiersdorfer et al. 1991).
In the text
thumbnail Fig. 4

Transition probability ratio with respect to HFR as function of HFR transition probability for strong K lines (A > 1013   s-1) in Ti xvii. Circles: MCDF calculations (Chen et al. 1997); squares: MCDF-EAL calculations (this work); diamonds: AUTOSTRUCTURE calculations (this work). Average ratios are respectively 1.42  ±  1.70 (Chen et al. 1997), 1.00  ±  0.17 (MCDF-EAL) and 1.05  ±  0.36 (AUTOSTRUCTURE). A straight line of equality has been drawn.
In the text
thumbnail Fig. 5

Radiative width ratio with respect to HFR as function of HFR radiative width in Ti xvii. Circles: MCDF calculations (Chen et al. 1997); squares: MCDF-EAL calculations (this work); diamonds: AUTOSTRUCTURE calculations (this work). Average ratios are respectively 1.27  ±  0.12 (Chen et al. 1997), 1.01  ±  0.04 (MCDF-EAL) and 1.02  ±  0.05 (AUTOSTRUCTURE). A straight line of equality has been drawn.
In the text
thumbnail Fig. 6

Auger width ratio with respect to HFR as function of HFR Auger width in Ti xvii. Circles: MCDF calculations (Chen et al. 1997); diamonds: AUTOSTRUCTURE calculations (this work). Average ratios are respectively 1.22  ±  0.16 (Chen et al. 1997) and 0.94  ±  0.04 (AUTOSTRUCTURE). A straight line of equality has been drawn.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.