| Issue |
A&A
Volume 543, July 2012
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 14 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201218807 | |
| Published online | 21 June 2012 | |
Error characterization of the Gaia astrometric solution
I. Mathematical basis of the covariance expansion model
Lund Observatory, Lund University, Box 43, 22100 Lund, Sweden
e-mail: Berry.Holl@astro.lu.se; Lennart.Lindegren@astro.lu.se
Received: 11 January 2012
Accepted: 1 May 2012
Context. Accurate characterization of the astrometric errors in the forthcoming Gaia Catalogue will be essential for making optimal use of the data. This includes the correlations among the estimated astrometric parameters of the stars as well as their standard uncertainties, i.e., the complete (variance-)covariance matrix of the relevant astrometric parameters.
Aims. Because a direct computation of the covariance matrix is infeasible due to the large number of parameters, approximate methods must be used. The aim of this paper is to provide a mathematical basis for estimating the variance-covariance of any pair of astrometric parameters, and more generally the covariance matrix for multidimensional functions of the astrometric parameters. The validation of this model by means of numerical simulations will be considered in a forthcoming paper.
Methods. Based on simplifying assumptions (in particular that calibration errors can be neglected), we derive and analyse a series expansion of the covariance matrix of the least-squares solution. A recursive relation for successive terms is derived and interpreted in terms of the propagation of errors from the stars to the attitude and back. We argue that the expansion should converge rapidly to useful precision. The recursion is vastly simplified by using a kinematographic (step-wise) approximation of the attitude model.
Results. Low-order approximations of arbitrary elements from the covariance matrix can be computed efficiently in terms of a limited amount of pre-computed data representing compressed observations and the structural relationships among them. It is proposed that the user interface to the Gaia Catalogue should provide the tools necessary for such computations.
Key words: astrometry / catalogs / methods: data analysis / methods: statistical / space vehicles: instruments
© ESO, 2012
1. Introduction
The space astrometry mission Gaia, planned for launch in 2013 by the European Space Agency (ESA), will provide the most comprehensive and accurate catalogue of astrometric data for galactic and astrophysical research in the coming decades. It will observe roughly 1 billion stars, quasars and other point like objects (hereafter called “sources”) for which the five astrometric parameters (position, parallax and proper motion) will be determined. For sources down to ~17th magnitude radial velocities will also be measured, giving the full 6-dimensional position and velocity components. Compared with the Hipparcos Catalogue (ESA 1997) the Gaia Catalogue will contain roughly 10 000 times more astrometric data with 10–100 times smaller standard uncertainties, for a mainly complementary set of fainter sources.
The Gaia satellite is in principle self-calibrating (Lindegren & Bastian 2011), meaning that besides the astrometric parameters additional “nuisance” parameters (e.g., for spacecraft attitude and instrument calibration) are self-consistently estimated from the regular observations. The derived catalogue of astrometric parameters will however not be perfect: every derived parameter has an error1, ultimately resulting from a very large number of microscopic stochastic processes, such as photon detection and thruster noise, propagating through the astrometric solution. The actual errors in the Gaia Catalogue are of course unknown, but can nevertheless be statistically characterized, and it is the purpose of this paper to derive some tools for this. For most applications it is sufficient to consider the first and second (central) moments of the errors, i.e., their expected values (biases), variances, and covariances; equivalently the latter two can be represented by the standard uncertainties and correlation coefficients. We assume that biases are negligible, and therefore concentrate on the second moments, which are most generally described by the variance-covariance matrix of the estimated parameters (hereafter simply referred to as the covariance matrix).
Knowledge of the covariances is needed when estimating the uncertainty of quantities that combine more than one astrometric parameter. We need to consider both the covariances between the different astrometric parameters of the same source and between different sources. An example of the first kind could be the uncertainty of the transverse velocity of a star, computed from its parallax and proper motion. Two examples of the second kind are discussed in Holl et al. (2012a): the computation of the mean parallax of stars in a cluster, and the determination of the acceleration of the solar system barycentre using the apparent proper motions of cosmological objects scattered over the celestial sphere. The complete covariance matrix for a final catalogue containing 109 sources will have a data volume of the order of ~108 Terabyte (TB), which is totally impractical to compute, store and query efficiently with current techniques. It is therefore clearly desirable that the variances and covariances of selected astrometric parameters could be derived from some smaller set of pre-computed data. This is obviously possible, at least in principle, since the total volume of raw data generated by Gaia is only ~70 TB. However, it is far from obvious whether and how it can be done in practice, i.e., efficiently and accurately enough.
The main goal of this study is to set up a mathematical and computational framework for estimating the covariance of any pair of astrometric parameters obtained as part of the astrometric core solution for Gaia (Lindegren et al. 2012). Following Holl et al. (2012a), in addition to considering a single scalar quantity y = f(x) depending on some subset of n astrometric parameters x = (x1, ..., xn), we generally want to characterize the joint errors of m different scalar quantities y = (y1, ..., ym) depending on x. Introducing the m × n Jacobian matrix J with elements Jμν = ∂yμ/∂xν we have 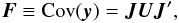 (1)where U = Cov(x) is the covariance matrix of the relevant subset of the astrometric parameters.
(1)where U = Cov(x) is the covariance matrix of the relevant subset of the astrometric parameters.
In the present Paper I we derive analytical approximations for (subsets of) the complete covariance matrix, or more generally for expressions like Eq. (1), using a series expansion model. In Holl et al. (2012b, Paper II) this model will be quantitatively validated by means of numerical simulations of the astrometric solution. Section 2 outlines how the astrometric parameters are derived from Gaia observations and contains a brief discussion about the nature of the errors. In Sect. 3 we derive the formal series expansion of the covariance matrix in terms of the normal matrix used in the least-squares adjustment. Section 4 introduces a crucial simplification allowing successive terms in the series expansion to be recursively computed from a data set of realistic size as described in Sect. 5. Additional considerations of the resulting matrix structures and of the necessary approximations are made in the appendices.
2. Constructing an astrometric solution from observations
2.1. Observing with Gaia
Located near the second Lagrange point (L2), 1.5 million km from the Earth, Gaia will be continuously spinning with a period of six hours. In the plane orthogonal to the spin axis it has two fields of view of ~0.5 deg2 that are separated by a large angle, 106.5°, known as the basic angle. The simultaneous observation of two widely separated parts of the celestial sphere is essential for the definition of absolute parallaxes and a globally consistent reference frame (Lindegren & Bastian 2011). The spin axis makes an angle of 45° to the solar direction, and precesses around this direction with a period of 63 days. This combination of spinning and precessional motions, known as the Nominal Scanning Law (NSL) of Gaia, ensures a reasonably uniform sky coverage over the mission lifetime of 5 years (Fig. 1), with an average of 72 field-of-view transits for any position on the celestial sphere.
 |
Fig. 1 Colour-coded map of the expected number of field-of-view transits experienced by sources at different celestial positions in a 5 year mission. The projection uses equatorial coordinates, with right ascension running from −180° to +180° right-to-left. The blue line is the ecliptic. The average number of field transits in this plot is 88, although the value that is normally used for performance evaluation is 72 (accounting for dead time). An over-abundance of transits occurs at 45° away from the ecliptic plane due to the difference between the 45° spin axis angle with respect to the sun and the 90° angle between spin axis and the fields of view. |
 |
Fig. 2 Schematic layout of the CCDs in the focal plane of Gaia. Due to the satellite spin, a source enters the focal plane from the left in the along-scan (AL) direction. All sources brighter than G = 20 mag are detected by one of the skymappers (SM1 or SM2, depending on the field of view) and then tracked over the subsequent CCDs dedicated to astrometry (AF1–9), photometry (BP and RP), and radial-velocity determination (RVS1–3). In addition there are special CCDs for interferometric Basic-Angle Monitoring (BAM), and for the initial mirror alignment using Wavefront Sensors (WFS). |
The two fields of view are projected onto the same focal plane, schematically shown in Fig. 2. Due to the satellite’s spin, the images of the sources will enter the focal plane from the left in the figure and move over the various CCDs in the along-scan (AL) direction (the perpendicular direction is called across-scan, AC). In this study we are only concerned with observations made with the skymapper (SM1–2) and astrometric (AF1–9) CCDs, since only they are used for direct astrometric measurements. SM1 is only used in the preceding field of view, and SM2 only in the following; each field-of-view transit therefore generates 10 astrometric observations (1 SM and 9 AF), leading to an average of 720 astrometric observations per source over 5 years.
The charge image built up in each CCD is transported in “time delay and integration” (TDI) mode (similar to drift scanning) to compensate for the satellite’s spinning motion, providing an effective integration time of about 4.4 s per CCD. Only a small fraction of the pixels read out from the CCD are kept; these typically form a small window of 6 × 12 pixels (AL × AC) around each source. Moreover, these pixels are usually binned in the AC direction, resulting in a one-dimensional profile from which only the AL image coordinate can be determined. However, some of the observations (in particular all SM observations and the AF observations of bright stars) retain resolution in the AC direction, allowing both image coordinates to be determined.
It is usually a good enough approximation to regard the resulting observation as instantaneous, and occurring at an instant that is half an integration time before the CCD readout (Bastian & Biermann 2005). This instant is called the CCD observation time and is denoted tl, where l is an index uniquely identifying each observation. Since Gaia has a nominally constant spin rate, we can without loss of generality express tl (or rather the AL error or residual) in equivalent angular units.
For some observations, the AC image coordinate μl is also determined. Although AC measurements in both fields of view are required to determine all components of the attitude, and therefore must be part of the astrometric core solution, they contribute only marginally to the source parameters. This is partly a consequence of geometrical factors (cf. Lindegren & Bastian 2011), partly because the total weight of the AC measurements is only about 1% of the total weight of the AL measurements. In the theoretical part of this study we therefore neglect the AC data, although they are by necessity included in the numerical experiments in Paper II.
2.2. Nature of the observation errors
The basic Gaia measurements thus consist mainly of the observation times tl, determined by means of a location estimation procedure where a calibrated line-spread function is fitted to the observed pixel values (see Lindegren et al. 2012, Sect. 3.5). Due to statistical errors in the pixel values, caused mainly by photon noise and to a much smaller extent by readout and discretization noise, the estimated tl will deviate from its true value by an error which we denote 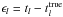 . Depending mainly on the magnitude of the source, the errors typically have standard deviations in the range 0.1 to 1 mas for the AL position of the source in the CCD frame.
. Depending mainly on the magnitude of the source, the errors typically have standard deviations in the range 0.1 to 1 mas for the AL position of the source in the CCD frame.
In this study we make three crucial assumptions about the nature of the AL observation errors ϵl:
-
1.
the observations are unbiased:E [ϵl] = 0;
-
2.
each observation has a finite and known standard deviation σl, where
![\hbox{$\sigma_l^2=\text{E}[\epsilon_l^2]$}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq33.png) ;
; -
3.
the errors of different observations are statistically independent and therefore uncorrelated: E [ϵlϵm] = 0 for l ≠ m.
In the numerical experiments of Paper II the errors are generated as independent pseudo-random normal variates, 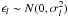 . That the errors are normally distributed (i.e., Gaussian) is an expedient but not necessary assumption in this study, since we only consider the propagation of first- and second-order moments of the errors, not the probability density functions.
. That the errors are normally distributed (i.e., Gaussian) is an expedient but not necessary assumption in this study, since we only consider the propagation of first- and second-order moments of the errors, not the probability density functions.
The first assumption (of unbiased errors) requires that modelling errors are completely negligible, which will not be true for the real Gaia mission. For example, in order to perform the astrometric core solution it will be assumed that certain instrument parameters are constant over a time interval that is sufficiently long to permit a precise calibration of these parameters. In reality they are of course variable also on shorter timescales, resulting in modelling errors at any particular time. Another example is the effect of Charge Transfer Inefficiency (CTI) in the CCDs, which after calibration may have residual biases that depend in a very complicated way on the source, the degree of radiation damage of the CCDs, and the illumination histories of the CCDs prior to the observations. The net effect of CTI on image location estimations and Gaia astrometry is discussed in Prod’homme et al. (2012) and Holl et al. (2012c), while other causes of systematic errors will be discussed elsewhere. Since the present study is only concerned with the propagation of random errors, the assumption of unbiasedness is motivated.
The second assumption (known σl) is reasonable for the real Gaia data processing, because the initial treatment of the CCD data, and in particular the image location process, is done using algorithms that provide accurate estimates of the standard uncertainties of the estimated quantities. In this study σl is taken to be a known function of the magnitude of the source. In some cases we will assume that all sources have the same magnitude, making σl constant and the resulting astrometric uncertainties scale with the assumed σl. In those cases its precise value is thus uncritical.
The third assumption (independent errors) reflects the stochastic nature of the main noise contributions, namely photon noise (which is strictly independent) and readout noise (which is to a high degree uncorrelated from one pixel to the next). Even if the noise in adjacent pixels might be somewhat correlated, it is difficult to see how it could produce correlations on a macroscopic level, i.e., between different CCD transits. It is important to remember that we are here talking about the intrinsic errors of the image location in the pixel stream, not about the apparently correlated errors that arise from (for example) inadequate attitude modelling (this would be covered by assumption 1) or the random (but temporally correlated) attitude errors; the latter will be included in the error propagation model.
2.3. Astrometric solution for Gaia
The baseline method for determining the astrometric parameters of sources observed by Gaia is the so-called Astrometric Global Iterative Solution (AGIS; Lindegren et al. 2012). This is an iterative least-squares estimation of the five astrometric parameters (position, parallax and proper motion) for a subset of ~108 well-behaved (apparently single) primary sources, with additional unknowns for the instrument attitude, calibration and global parameters. The total number of unknowns is ~5 × 108. The feasibility of a direct (non-iterative) solution was studied by Bombrun et al. (2010), who found it to be infeasible considering current and near-future available storage and floating-point capabilities. Mathematically, the result of the iterative solution is however equivalent to a direct solution, provided that a sufficient number of iterations are performed (Bombrun et al. 2012).
In this paper we will neglect the influence of instrument and global calibration. Although the expected total number of global parameters is quite small (≲102) it is known that even the inclusion of a single global parameter can sometimes have a profound effect on the astrometric solution. An example is the parametrised post-Newtonian parameter γ, which has a significant correlation with the parallax zero point (Hobbs et al. 2010). The treatment of such effects is beyond the scope of this paper. Also, global parameters are often “experimental” in the sense that they are introduced to test various possible deviations from the standard theory (in this case general relativity), but not necessarily retained in the final solution.
Neglecting instrument calibration is partly motivated by the smaller number of parameters involved: ≲106 calibration parameters, versus ≳2 × 107 for the attitude, and ≃5 × 108 for the astrometric parameters of the primary sources. In contrast to the global parameters, only a small fraction of the observations are affected by any given calibration parameter. Conversely, each calibration parameter depends on a very large number of observations spread over many different sources over the whole celestial sphere. The calibration parameters are therefore not greatly affected by localised errors on the sky and are relatively straightforward to estimate (e.g., by accumulating a map of average positional residuals across the field of view). In contrast, both the attitude and source parameters may have a very local influence on the sky, which could render their disentanglement more difficult (cf. van Leeuwen 2007, Sect. 1.4.6). Large-scale experiments including calibration parameters have confirmed that the calibration parameters have an insignificant effect on the estimated source parameters (Lindegren et al. 2012, Sect. 7). Moreover, in the iterative solution the calibration parameters generally converge much quicker than the source and attitude parameters, which suggests that the calibration is an “easy” part of the solution. However, we emphasize that these considerations apply to the propagation of the random observational errors (essentially photon noise); modelling errors in the instrument calibration (e.g., Holl et al. 2012c) and attitude representation are expected to be non-negligible in the real data, but are not part of the present study (cf. Sect. 6).
When instrument calibration, global parameters, and across-scan measurements are ignored the resulting simplified problem can be written ![\begin{equation} \label{eq:samin} \min_{\vec{s},\,\vec{a}} \sum_l \left[ \frac{ t_l - f_l(\vec{s}_i,\,\vec{a}) }{ \sigma_l } \right]^2\, , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq47.png) (2)where the sub-vector si contains the five astrometric parameters α, δ, ϖ, μα∗, and μδ for each source i, and a is a single vector containing all the attitude parameters. The observational uncertainties σl are fixed and known (assumption 2 in Sect. 2.2). The function f is in principle highly non-linear, but the initial data treatment provides an initial approximation to all the unknowns which is good enough (e.g., with errors | Δ | < 10-6 rad ≃ 0.2 arcsec) for subsequent calculations to work with the linearised functions (resulting in errors of the order of Δ2 < 10-12 rad ≃ 0.2 μas). The minimization is made globally with respect to the complete set of astrometric and attitude parameters, s and a.
(2)where the sub-vector si contains the five astrometric parameters α, δ, ϖ, μα∗, and μδ for each source i, and a is a single vector containing all the attitude parameters. The observational uncertainties σl are fixed and known (assumption 2 in Sect. 2.2). The function f is in principle highly non-linear, but the initial data treatment provides an initial approximation to all the unknowns which is good enough (e.g., with errors | Δ | < 10-6 rad ≃ 0.2 arcsec) for subsequent calculations to work with the linearised functions (resulting in errors of the order of Δ2 < 10-12 rad ≃ 0.2 μas). The minimization is made globally with respect to the complete set of astrometric and attitude parameters, s and a.
2.4. Nature of the parameter errors
As already mentioned, the characterization of the astrometric errors will here focus on the computation of the covariance matrix (or selected parts of it), as it contains, in principle, all the available information about the errors under the given assumptions. To illustrate this point, let u and v be any two of the parameters (astrometric or attitude) estimated as part of the solution. Their errors are eu = u − utrue and ev = v − vtrue. Because of the linearity of the model, the error in any parameter is a linear combination of errors from individual observations. As we assume that the observation errors are unbiased (assumption 1 in Sect. 2.2) the same will be true for the parameter errors, i.e., E [eu] = E [ev] = 0. The observational errors are approximately Gaussian, but even if they are not, the large number of observations contributing to each parameter and their statistical independence (assumption 3 in Sect. 2.2) will in practice result in a Gaussian distribution of the parameter errors by virtue of the Central Limit Theorem (e.g., Rice 2006). The error of a single parameter is then completely described by the variance ![\hbox{$\text{Var}[e_u]\equiv\text{E}[(e_u-\text{E}(e_u))^2]=\text{E}[e_u^2]=\sigma_u^2$}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq65.png) and the joint distribution of eu and ev by the covariance matrix
and the joint distribution of eu and ev by the covariance matrix ![\begin{equation} \label{eq:Cove} \begin{bmatrix} ~\text{E}[e_ue_u] &~& \text{E}[e_ue_v]~ \\ ~\text{E}[e_ve_u] &~& \text{E}[e_ve_v]~ \end{bmatrix} = \begin{bmatrix} \sigma_u^2 &~& \rho_{uv}\sigma_u\sigma_v~ \\ ~\rho_{uv}\sigma_u\sigma_v &~& \sigma_v^2 \end{bmatrix} , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq68.png) (3)where ρuv is the correlation coefficient.
(3)where ρuv is the correlation coefficient.
Generalizing to the full set of (astrometric and attitude) parameters, we have the complete covariance matrix C which can be estimated as 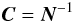 (4)where N is the normal matrix built up by combing all observation equations as detailed in Sect. 3.1. (As discussed in Sect. 3.2, the pseudo-inverse should in principle be used.) For any pair of parameters (u,v) the relevant elements in Eq. (4) can be obtained from C by extracting the elements at the intersections of the rows and columns corresponding to u and v. In practice we are mainly concerned with the covariances of the astrometric parameters, which constitute the sub-matrix U introduced in Eq. (1). As mentioned in the introduction, the data volume of such a covariance matrix for 109 sources (some 108 TB) is likely to be prohibitive even at the time when the final catalogue will become available. In the next section we start out by considering the formal expressions for the “impossible” matrices C and U, but it should be borne in mind that the principal aim is to evaluate selected elements in U or more generally expressions like Eq. (1).
(4)where N is the normal matrix built up by combing all observation equations as detailed in Sect. 3.1. (As discussed in Sect. 3.2, the pseudo-inverse should in principle be used.) For any pair of parameters (u,v) the relevant elements in Eq. (4) can be obtained from C by extracting the elements at the intersections of the rows and columns corresponding to u and v. In practice we are mainly concerned with the covariances of the astrometric parameters, which constitute the sub-matrix U introduced in Eq. (1). As mentioned in the introduction, the data volume of such a covariance matrix for 109 sources (some 108 TB) is likely to be prohibitive even at the time when the final catalogue will become available. In the next section we start out by considering the formal expressions for the “impossible” matrices C and U, but it should be borne in mind that the principal aim is to evaluate selected elements in U or more generally expressions like Eq. (1).
3. Formal derivation of the covariances
3.1. Structure of the normal equations
When using a linear expansion around some reference values of the unknowns, the resulting system of linear equations (the observation equations) can be written in matrix form. Observation equations for different sources involve disjoint source parameter sub-vectors si but the same attitude vector a. Sorting all the observations by the source index i and collecting them in separate matrices for the source and attitude unknowns, we can write the observation equations as 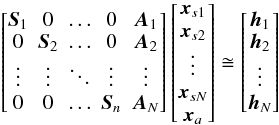 (5)(Bombrun et al. 2010). Here N is the number of sources, and xsi, xa denote the displacements around the source and attitude reference values. The matrices Si, Ai, and hi collect all the coefficients and residuals related to source i:
(5)(Bombrun et al. 2010). Here N is the number of sources, and xsi, xa denote the displacements around the source and attitude reference values. The matrices Si, Ai, and hi collect all the coefficients and residuals related to source i: 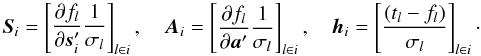 (6)We use l ∈ i as a shorthand for “observations l that involve source i”. The square brackets in Eq. (6) should thus be understood as matrices with one row for each observation of the source. The prime in
(6)We use l ∈ i as a shorthand for “observations l that involve source i”. The square brackets in Eq. (6) should thus be understood as matrices with one row for each observation of the source. The prime in 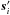 denotes matrix transpose, so that
denotes matrix transpose, so that 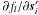 is a matrix of size 1 × 5. If oi is the number of observations of source i, the dimensions of the matrices in Eq. (6) are, respectively, oi × 5, oi × dim(a), and oi × 1. Each equation has been normalised by the standard uncertainty σl, and therefore represents an observation of unit standard deviation. According to assumption 3 in Sect. 2.2, the covariance of the right-hand side is then the identity matrix.
is a matrix of size 1 × 5. If oi is the number of observations of source i, the dimensions of the matrices in Eq. (6) are, respectively, oi × 5, oi × dim(a), and oi × 1. Each equation has been normalised by the standard uncertainty σl, and therefore represents an observation of unit standard deviation. According to assumption 3 in Sect. 2.2, the covariance of the right-hand side is then the identity matrix.
Equation (5) can be written compactly as 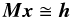 (7)where M is a very sparse matrix. This system is over-determined: there are (many) more observation equations than unknowns. Due to measurement errors there does not exist a solution that simultaneously satisfies all the equations; we indicate this by using “ ≅ ” instead of an equality in Eqs. (5) and (7). The least-squares solution minimises the 2-norm of the post-fit residual vector, ∥h − Mx∥, and is classically found by solving the normal equations
(7)where M is a very sparse matrix. This system is over-determined: there are (many) more observation equations than unknowns. Due to measurement errors there does not exist a solution that simultaneously satisfies all the equations; we indicate this by using “ ≅ ” instead of an equality in Eqs. (5) and (7). The least-squares solution minimises the 2-norm of the post-fit residual vector, ∥h − Mx∥, and is classically found by solving the normal equations 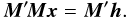 (8)It is well known that, under the given assumptions, the least-squares estimate
(8)It is well known that, under the given assumptions, the least-squares estimate 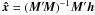 is unbiased, and that its covariance matrix is given by (M′M)-1. Since the objective of this paper is to characterize the astrometric solution in terms of its covariance matrix, we need to concentrate on the normal matrix N = M′M and its inverse. The basic problem is that these matrices are so large that it is not feasible to calculate the inverse directly. From Eq. (5) we have
is unbiased, and that its covariance matrix is given by (M′M)-1. Since the objective of this paper is to characterize the astrometric solution in terms of its covariance matrix, we need to concentrate on the normal matrix N = M′M and its inverse. The basic problem is that these matrices are so large that it is not feasible to calculate the inverse directly. From Eq. (5) we have ![\begin{equation} \label{eq:normMatrix} \vec{N}= \left[\begin{array}{cccc|c} \vec{S}_1'\vec{S}_1^{} & 0 & \cdots & 0 & \vec{S}_1'\vec{A}_1^{} \\[3pt] 0 & \vec{S}_2'\vec{S}_2^{} & \cdots & 0 & \vec{S}_2'\vec{A}_2^{} \\[0pt] \vdots & \vdots & \ddots & \vdots & \vdots \\[3pt] 0 & 0 & \cdots & \vec{S}_n'\vec{S}_n^{} & \vec{S}_n'\vec{A}_n^{} \\[4pt] \cline{1-5} \\[-10pt] &&&&\\[-10pt] \vec{A}_1'\vec{S}_1^{} & \vec{A}_2'\vec{S}_2^{} & \cdots & \vec{A}_n'\vec{S}_n^{} & \sum_i \vec{A}_i'\vec{A}_i^{} \\ \end{array}\right] = \begin{bmatrix} \vec{P} & \vec{R} \\[3pt] \vec{R}' & \vec{Q} \\ \end{bmatrix} , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq99.png) (9)where the lines divide N into the sub-matrices P, R, and Q, the structures of which are outlined below.
(9)where the lines divide N into the sub-matrices P, R, and Q, the structures of which are outlined below.
In the following we use indices i, j, and k (ranging from 1 to N) to denote the different primary sources, while p, q, and r are reserved for the different attitude parameters (in the range from 1 to P) and l for the observations. As before, l ∈ i means an observation of source i, but we now introduce also l ∈ p for an observation depending on ap (the attitude parameter with index p), that is an observation for which ∂fl/∂ap ≠ 0. Similarly, l ∈ i ∩ p indicates an observation of source i depending on ap, and l ∈ p ∩ q an observation depending on both ap and aq; finally, p ∈ i means that there is at least one observation of source i depending on ap. With this slight abuse of indices and notations from set theory we can write the relevant sums in a concise way which is quite easy to interpret, keeping in mind that i always refers to a source, p to an attitude parameter, and so on. (See Appendix A for more precise definitions.)
The source normal matrix P is a block-diagonal matrix of size 5N × 5N, with blocks Pi of size 5 × 5 (the number of astrometric parameters per source) along the main diagonal. From Eqs. (6) and (9) we find 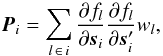 (10)where
(10)where 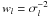 is the weight of observation l. Provided that the source is sufficiently observed (which is a condition for primary sources) Pi is positive definite, and so is P. Because of the block-diagonal structure of P its inverse is also block-diagonal with
is the weight of observation l. Provided that the source is sufficiently observed (which is a condition for primary sources) Pi is positive definite, and so is P. Because of the block-diagonal structure of P its inverse is also block-diagonal with 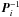 along the diagonal; thus P-1 is trivially computed.
along the diagonal; thus P-1 is trivially computed.
The structure of the P × P matrix Q depends on the attitude parametrisation used (see Sect. 4) but is typically band-diagonal. The general expression for the matrix element is 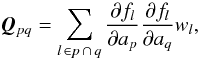 (11)which is 0 if no observation depends on both ap and aq.
(11)which is 0 if no observation depends on both ap and aq.
The off-diagonal sub-matrices R and R′ are very sparse but have a complicated structure due to the scanning law. Each 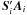 in Eq. (9) consists of a row of P blocks of size 5 × 1; for source i the block in column p is given by
in Eq. (9) consists of a row of P blocks of size 5 × 1; for source i the block in column p is given by 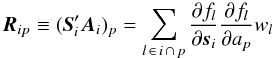 (12)which is 0 if no observation of source i depends on ap. From Eq. (12) it is clear that R is responsible for the coupling between source and attitude parameters. Because a given source is observed quite infrequently, the matrix is typically very sparse.
(12)which is 0 if no observation of source i depends on ap. From Eq. (12) it is clear that R is responsible for the coupling between source and attitude parameters. Because a given source is observed quite infrequently, the matrix is typically very sparse.
3.2. Rank deficiency of the normal equations
Thanks to the scanning law of Gaia and the choice of primary sources and attitude parametrisation, it follows that the sub-matrices P and Q are positive definite. The complete normal matrix is however singular, having a 6-dimensional null space due to the (internally) undefined orientation and spin of the reference system in which the source and attitude parameters are expressed. This means that C = N-1 does not exist and that the normal equations have an infinitude of solutions. Notwithstanding this predicament, the normal equations can be solved by iteration, as is done in AGIS, and the only corrective action needed is to modify the null-space component of the converged solution, through a rigid-body rotation, to agree with the (externally defined) reference frame (Lindegren et al. 2012, Sect. 6.1). However, even without such external data it is possible to produce a pseudo-solution by aligning the converged AGIS solution with the initial catalogue values used to start up the iterations. This projects the solution (in terms of corrections to the initial values) into the orthogonal complement of the null space.
For the characterization of the astrometric errors it is in principle desirable to use , the pseudo-inverse of the normal matrix. This means that C does not include the uncertainty of the reference frame itself. Indeed, the latter may be several times larger than the positional uncertainties of the most precise stars, due to the scarcity and faintness of extragalactic objects suitable for linking with the VLBI frame (Bourda et al. 2008). On the other hand, since Gaia will in effect define the optical reference frame for the foreseeable future, this uncertainty is largely arbitrary and irrelevant for most purposes. Thus it is better not to include it in C, which implies using the pseudo-inverse, and to characterize the frame errors separately.
Although the singularity of N formally invalidates the series expansion of the inverse derived in the next section, our conjecture is that the expansion converges and provides a useful approximation of C. In order to obtain the pseudo-inverse, it may be necessary to project the rows and columns of C into the orthogonal complement of the null space, but probably this has almost negligible impact on the values, thanks to the very large number of parameters. Ultimately, the accuracy of the approximation will be ascertained by numerical experiments, as reported in Paper II. For the subsequent development the singularity of N is ignored.
3.3. Series expansion of the covariance matrix
The complete covariance matrix for the least squares problem of Eq. (8) is C = N-1, which can be written as ![\begin{equation} \label{eq:C} \vec{C} \equiv \begin{bmatrix} \vec{U} & \vec{W} \\[3pt] \vec{W}' & \vec{V} \end{bmatrix} = \begin{bmatrix} \vec{P} & \vec{R} \\[3pt] \vec{R}' & \vec{Q} \end{bmatrix}^{-1} \, , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq133.png) (13)using the same block partition as in the normal matrix of Eq. (9), an important difference being that the covariance matrix is not sparse, but typically full. Block U gives us the covariances of the astrometric parameters of all the sources, V contains the covariances of the attitude parameters, and W the cross-covariances between the source and attitude parameters. We are mainly interested in U, although for some purposes V may also be required (e.g., to get the covariances for secondary sources, which depend on the attitude parameters but do not contribute to the estimation of the attitude).
(13)using the same block partition as in the normal matrix of Eq. (9), an important difference being that the covariance matrix is not sparse, but typically full. Block U gives us the covariances of the astrometric parameters of all the sources, V contains the covariances of the attitude parameters, and W the cross-covariances between the source and attitude parameters. We are mainly interested in U, although for some purposes V may also be required (e.g., to get the covariances for secondary sources, which depend on the attitude parameters but do not contribute to the estimation of the attitude).
Formally, the block-diagonal components of C are readily obtained by elimination as 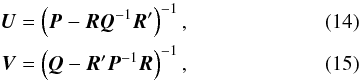 whereupon the off-diagonal block is given by either of the expressions in
whereupon the off-diagonal block is given by either of the expressions in 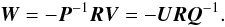 (16). But while it is practically feasible to invert P and Q thanks to their simple block-diagonal and band-diagonal structures, this is not the case for the matrices in the right-hand sides of Eqs. (14) and (15). Indeed, Bombrun et al. (2010) considered in detail these matrices (called Rs and Ra in that paper), and concluded that any direct solution method, such as Cholesky decomposition, is infeasible for the Gaia application with current computing resources. The reason is that the terms added to P and Q in Eqs. (14), (15) cause significant fill-in which cannot be reduced to any simple structure, e.g., by re-ordering of the parameters. Equation (14) therefore does not solve our problem.
(16). But while it is practically feasible to invert P and Q thanks to their simple block-diagonal and band-diagonal structures, this is not the case for the matrices in the right-hand sides of Eqs. (14) and (15). Indeed, Bombrun et al. (2010) considered in detail these matrices (called Rs and Ra in that paper), and concluded that any direct solution method, such as Cholesky decomposition, is infeasible for the Gaia application with current computing resources. The reason is that the terms added to P and Q in Eqs. (14), (15) cause significant fill-in which cannot be reduced to any simple structure, e.g., by re-ordering of the parameters. Equation (14) therefore does not solve our problem.
Using the Woodbury formula2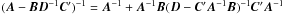 (e.g., Björck 1996), valid for arbitrary matrices A, B, C, D with non-singular A and D, it is possible to re-write Eqs. (14), (15) as
(e.g., Björck 1996), valid for arbitrary matrices A, B, C, D with non-singular A and D, it is possible to re-write Eqs. (14), (15) as 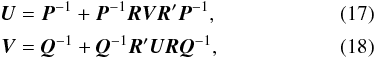 which only require the inversion of P and Q. On the other hand, these are now implicit relations since the expression for U depends on V and vice versa.
which only require the inversion of P and Q. On the other hand, these are now implicit relations since the expression for U depends on V and vice versa.
Equations (17) and (18) have a very simple and clear interpretation. In Eq. (17) the first term P-1 is the covariance of the source parameters in the absence of attitude errors (i.e., for V = 0). The second term is the contribution due to the uncertainty of the attitude (since in reality V > 0). Similarly, in Eq. (18) the first term Q-1 is the covariance of the attitude errors obtained by fitting the attitude model to the noisy observations, using error-free source parameters (i.e., for U = 0). The second term is the contribution from the uncertainty of the source parameters. Inserting Eq. (18) into (17) and expanding recursively gives 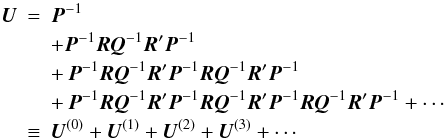 (19)Successive terms have a clear physical interpretation in terms of the propagation of the observational errors alternately from the sources to the attitude, and from the attitude to the sources. For example, U(0) is the covariance of the source parameters due to the observation noise but with perfect attitude; U(1) the additional uncertainty from the attitude errors due to the noisy observations but assuming true source parameters; U(2) the additional uncertainty due to the source errors obtained with perfect attitude propagating through the attitude back to the sources; and so on. A corresponding expansion can be made for the attitude:
(19)Successive terms have a clear physical interpretation in terms of the propagation of the observational errors alternately from the sources to the attitude, and from the attitude to the sources. For example, U(0) is the covariance of the source parameters due to the observation noise but with perfect attitude; U(1) the additional uncertainty from the attitude errors due to the noisy observations but assuming true source parameters; U(2) the additional uncertainty due to the source errors obtained with perfect attitude propagating through the attitude back to the sources; and so on. A corresponding expansion can be made for the attitude: 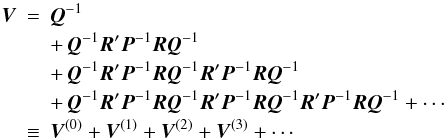 (20)in which successive terms can be similarly interpreted.
(20)in which successive terms can be similarly interpreted.
The terms in Eqs. (19) and (20) follow the simple recursions 3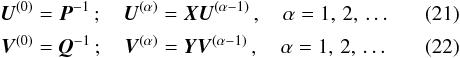 where
where 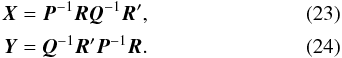 X is a matrix consisting of N × N blocks of size 5 × 5; the (i,j)th block is
X is a matrix consisting of N × N blocks of size 5 × 5; the (i,j)th block is 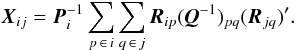 (25)The corresponding expression for the (scalar) elements of Y is
(25)The corresponding expression for the (scalar) elements of Y is 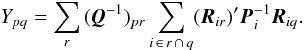 (26)Now consider the case that Q-1 is a full matrix (which would happen, for example, if the attitude is modelled by a single continuous spline over the whole mission). Then Xij is clearly non-zero for any combination of i and j. From Eq. (21) we have
(26)Now consider the case that Q-1 is a full matrix (which would happen, for example, if the attitude is modelled by a single continuous spline over the whole mission). Then Xij is clearly non-zero for any combination of i and j. From Eq. (21) we have 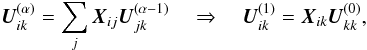 (27)so that in this case already U(1) is a full matrix. Since Xik involves a large number of elements from Q-1, it is clear that the computation of a single block in U(1) is already a heavy task. Considering the next term U(2), we see from the left part of Eq. (27) that the computation of the single block
(27)so that in this case already U(1) is a full matrix. Since Xik involves a large number of elements from Q-1, it is clear that the computation of a single block in U(1) is already a heavy task. Considering the next term U(2), we see from the left part of Eq. (27) that the computation of the single block 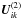 requires knowledge of
requires knowledge of 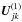 for every j, making it utterly impracticable. Similar considerations apply to the recursion of the attitude covariance using Eq. (26). To proceed, we clearly need to introduce some radical simplifications.
for every j, making it utterly impracticable. Similar considerations apply to the recursion of the attitude covariance using Eq. (26). To proceed, we clearly need to introduce some radical simplifications.
4. The kinematographic approximation
4.1. Assumptions
The attitude parameters define the spatial orientation of the instrument as a function of time. For Gaia the attitude will be modelled by quaternions whose components are fitted by cubic splines on a (more or less regular) knot sequence with knot separations of ~5–30 s (Lindegren et al. 2012, Sect. 3.3). Instead of the non-intuitive four-component quaternions we can think of the attitude as being represented by three angles: one describing the AL angle (i.e., the rotational phase around the spin axis), and two describing the AC components of the attitude (i.e., the direction of the spin axis). To first order, however, is is only the errors in the AL direction that matter (see Lindegren & Bastian 2011), and as discussed in Sect. 2.1 we only consider the AL observations in our analytical model. The partial derivative of fl with respect to the AL attitude is ≃−1 for observations in both fields of view. (The sign is negative because a larger AL attitude angle would result in an earlier observation time.)
The use of cubic splines means that each observation depends on four spline coefficients for each attitude component. The structure of Q in Eq. (9) is therefore in general band-diagonal. The spline representation is “local” in the sense that the fitted spline at point t is largely independent of data that are more distant from t than a few times the knot separation Δt. To first order, one can therefore approximate the attitude by means of a sequence of independent satellite orientations at discrete points in time, separated by the typical spline correlation time. Formally, the time line is divided into a sequence of attitude “bins” of length B ≃ Δt, and the AL attitude error is treated as constant in each bin.
Another way of looking at this is as follows. Suppose that Gaia, instead of being continuously scanning, had been designed to operate in the “step and stare” mode: successive exposures of length B are taken, with an almost instantaneous re-orientation of the satellite in the AL direction between exposures. In the limit B → 0 we recover the continuous scanning, except that the number of degrees of freedom for the attitude representation (one set of angles per time point) would go to infinity. For the accuracy analysis, the correct number of degrees of freedom can be preserved by choosing B equal to the knot separation of the attitude spline. The circumstance that the transition from one point to the next is continuous for Gaia but discrete in our model is expected to have only a second-order effect on the error characterization. Subsequently we will refer to the successive points in time as “attitude points” (at the centre of the corresponding bin) and indexed p = 1, 2, ..., P.
This “kinematographic” approximation, adopted for our analytical model, greatly simplifies the representation of Q which changes from band-diagonal to block-diagonal form. This is significant because the inverse of a band-diagonal matrix is in general full, while that of a block-diagonal matrix is another block-diagonal matrix. Each block has the length of the number of attitude orientation components, but as we will from now on only consider the AL attitude angle, both Q and its inverse are diagonal matrices. Together with the very mild approximation that ∂fl/∂aq ≃ − 1 for all AL observations we have simply 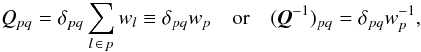 (28)using the Kronecker delta and introducing wp for the total weight of the observations depending on ap. In the kinematographic model l ∈ p stands for an observation in the attitude bin associated with attitude point p.
(28)using the Kronecker delta and introducing wp for the total weight of the observations depending on ap. In the kinematographic model l ∈ p stands for an observation in the attitude bin associated with attitude point p.
The structure of R is also simplified: a particular element is associated with exactly one source and one attitude point, and it is non-zero only if that source was observed at that point in time. From Eq. (12) we find 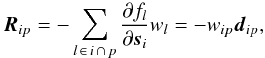 (29)where
(29)where 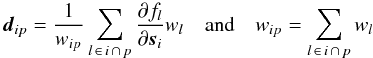 (30)are the mean derivative (a 5 × 1 vector) and total weight of the observations of source i at point p. Formally we may take wip = 0 (and dip undefined) if the source was not observed at this point.
(30)are the mean derivative (a 5 × 1 vector) and total weight of the observations of source i at point p. Formally we may take wip = 0 (and dip undefined) if the source was not observed at this point.
A more detailed analysis of the kinematographic approximation (outlined in Appendix C) suggests that it can be improved by using 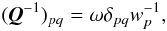 (31)instead of the second part of Eq. (28), where ω is a “fudge factor” accounting for the non-zero correlation width of the cubic attitude spline. We expect ω ≃ 1 if the ratio of the bin length to the attitude spline knot interval is appropriately chosen. As will be shown in Appendix C the situation is slightly more complex. Nevertheless, we already introduce ω in all subsequent expressions resulting from the series expansion of the covariance matrix.
(31)instead of the second part of Eq. (28), where ω is a “fudge factor” accounting for the non-zero correlation width of the cubic attitude spline. We expect ω ≃ 1 if the ratio of the bin length to the attitude spline knot interval is appropriately chosen. As will be shown in Appendix C the situation is slightly more complex. Nevertheless, we already introduce ω in all subsequent expressions resulting from the series expansion of the covariance matrix.
4.2. Recursion formulae
With the above assumptions Eqs. (25), (26) simplify to ![\begin{eqnarray} \label{eq:X3} \vec{X}_{ij} &= &\omega\vec{P}_i^{-1} \sum_{p\,\in\, i} \frac{w_{ip}w_{jp}}{w_p}\vec{d}_{ip}\vec{d}_{jp}' ,\\[3pt] \label{eq:Y3} Y_{pq} &=& \omega\hspace{-3pt}\sum_{i\,\in\, p\,\cap\,q} \frac{w_{ip}w_{iq}}{w_p}\,\vec{d}_{ip}' \vec{P}^{-1}_i \vec{d}_{iq} , \end{eqnarray}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq186.png) and the recursions in Eqs. (21), (22) become:
and the recursions in Eqs. (21), (22) become: ![\begin{eqnarray} \label{eq:Urec} \vec{U}^{(\alpha)}_{ik} &=& \omega\vec{P}^{-1}_i\sum_{p\,\in\, i}\,\sum_{j\,\in\,p} \frac{w_{ip}w_{jp}}{w_p}\, \vec{d}_{ip}\vec{d}_{jp}' \vec{U}^{(\alpha-1)}_{jk} ,\\[3pt] \label{eq:Vrec} V^{(\alpha)}_{pr} &= &\omega\sum_q \sum_{i\,\in\, p\,\cap\,q} \frac{w_{ip}w_{iq}}{w_p}\, \vec{d}_{ip}' \vec{P}^{-1}_i \vec{d}_{iq} V^{(\alpha-1)}_{qr} , \end{eqnarray}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq187.png) starting from
starting from 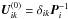 and
and 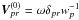 . Note that the last factors appearing in the recursion formulae may be zero for some combinations of indices jk or qr.
. Note that the last factors appearing in the recursion formulae may be zero for some combinations of indices jk or qr.
4.3. The first-order terms
The double sums in Eqs. (34), (35) in general involve a large, but not huge number of terms. However, for α = 1 the last factors vanish except when j = k and q = r, respectively. The first-order terms are therefore quite simple: ![\begin{eqnarray} \label{eq:U1} \vec{U}^{(1)}_{ik} &=& \omega\vec{P}^{-1}_i\sum_{p\,\in\, i\,\cap\,k}\frac{w_{ip}w_{kp}}{w_p}\, \vec{d}_{ip}\vec{d}_{kp}' \vec{P}^{-1}_{k} \, ,\\[3pt] \label{eq:V1} V^{(1)}_{pr} &= &\omega\hspace{-3pt}\sum_{i\,\in\, p\,\cap\,r} \frac{w_{ip}w_{ir}}{w_pw_r}\, \vec{d}_{ip}' \vec{P}^{-1}_i \vec{d}_{ir} \, . \end{eqnarray}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq195.png) In particular, the diagonal blocks/elements are:
In particular, the diagonal blocks/elements are: ![\begin{eqnarray} \label{eq:U1diag} \vec{U}^{(1)}_{ii} &= &\omega\vec{P}^{-1}_i\sum_{p\,\in\, i}\frac{w_{ip}^2}{w_p}\, \vec{d}_{ip}\vec{d}_{ip}' \vec{P}^{-1}_{i} \, ,\\[3pt] \label{eq:V1diag} V^{(1)}_{pp} &=& \omega\sum_{i\,\in\, p} \frac{w_{ip}^2}{w_p^2}\, \vec{d}_{ip}' \vec{P}^{-1}_i \vec{d}_{ip} \, . \end{eqnarray}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq196.png) From Eq. (36) is clear that
From Eq. (36) is clear that 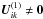 only if the two sources i and k are observed simultaneously at some attitude point (including the trivial case i = k). This is usually the case if the two sources are close together on the sky (typically within about 0.7°, corresponding to the size of the field of view), but sometimes also for sources separated by an angle close to the basic angle (106.5°), thanks to the optical superposition of the two fields of view. Thus, i must be linked to some p, which in turn must be linked to k.
only if the two sources i and k are observed simultaneously at some attitude point (including the trivial case i = k). This is usually the case if the two sources are close together on the sky (typically within about 0.7°, corresponding to the size of the field of view), but sometimes also for sources separated by an angle close to the basic angle (106.5°), thanks to the optical superposition of the two fields of view. Thus, i must be linked to some p, which in turn must be linked to k.
Indeed, the structure of both this term and of all subsequent terms in the expansion is entirely determined by the multitude of links established by the observations between the different sources and the attitude points. Such relationships may be described by means of concepts in graph theory (see Appendix B), and we will adopt some of the terminology here. Thus, any source or attitude point is called a vertex (of the graph describing the structure of the observations), and i and p are adjacent vertices if source i was observed at point p, i.e., if wip > 0. If, in addition, k is adjacent to p, then there exists a walk from i to k (via p), which has a length of 2 steps if i ≠ k, or 0 if i = k. There may of course be even longer walks from i to k via other sources and attitude points. The length of the shortest walk between any two vertices is called the distance4 and denoted d. The condition for non-zero 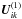 can now be concisely written as d(i,k) ≤ 2.
can now be concisely written as d(i,k) ≤ 2.
4.4. Second and higher order terms
Considering now the second-order term 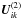 in Eq. (34), i.e., for α = 2, we know from the previous section that the last factor is non-zero only if d(j,k) ≤ 2, while the double sum requires that d(i,j) ≤ 2. Together, these conditions imply (using the triangle inequality, Eq. (B.1)) that d(i,k) ≤ 4 is required for the second-order term to be non-zero. A similar consideration applied to Eq. (35) shows that
in Eq. (34), i.e., for α = 2, we know from the previous section that the last factor is non-zero only if d(j,k) ≤ 2, while the double sum requires that d(i,j) ≤ 2. Together, these conditions imply (using the triangle inequality, Eq. (B.1)) that d(i,k) ≤ 4 is required for the second-order term to be non-zero. A similar consideration applied to Eq. (35) shows that 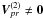 only if d(p,r) ≤ 4. Generalizing, it can be shown (cf. Appendix B) that, for arbitrary α ≥ 0,
only if d(p,r) ≤ 4. Generalizing, it can be shown (cf. Appendix B) that, for arbitrary α ≥ 0, ![\begin{eqnarray} \label{eq:Uz} \vec{U}^{(\alpha)}_{ik} \ne \vec{0} &&\quad\text{only if}\quad d(i,k)\le 2\alpha ,\\[3pt] \label{eq:Vz} V^{(\alpha)}_{pr} \ne 0 &&\quad\text{only if}\quad d(p,r)\le 2\alpha . \end{eqnarray}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq212.png) In order to compute
In order to compute 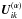 for arbitrary order α, it is necessary to consider the sources and attitude points on all possible walks from i to k of length ≤ 2α.
for arbitrary order α, it is necessary to consider the sources and attitude points on all possible walks from i to k of length ≤ 2α.
As every source is connected to several hundred attitude points, and several thousand stars are typically observed at every attitude point, it is clear that the recursions in Eqs. (34), (35) involve a rapidly increasing number of sources and attitude points for higher α. Indeed, numerical experiments by Holl et al. (2012a) suggest that d(i,k) ≤ 6 for any pair (i,k). This implies that, for α ≥ 6, the calculation of 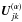 even for a single pair (i,k) would involve all the (primary) sources. Thus, it is in practice necessary to truncate the series expansion after only a few terms. This raises a number of interesting questions, e.g.: what is the accuracy of the expansion when including only terms up to a certain order α? Which data are needed to compute successive terms? How does the complexity of the calculations grow with α? How should the calculations be organised to minimise the number of floating-point operations and/or memory usage? A further issue is the accuracy of the kinematographic approximation itself and the relevance of the fudge factor ω: because of the errors involved in this approximation, it may not be meaningful to include expansion terms above a certain order.
even for a single pair (i,k) would involve all the (primary) sources. Thus, it is in practice necessary to truncate the series expansion after only a few terms. This raises a number of interesting questions, e.g.: what is the accuracy of the expansion when including only terms up to a certain order α? Which data are needed to compute successive terms? How does the complexity of the calculations grow with α? How should the calculations be organised to minimise the number of floating-point operations and/or memory usage? A further issue is the accuracy of the kinematographic approximation itself and the relevance of the fudge factor ω: because of the errors involved in this approximation, it may not be meaningful to include expansion terms above a certain order.
We intend to give a partial answer to these questions in the remainder of this paper and in Paper II, where the series expansion is numerically compared with the results of simulated astrometric solutions.
4.5. Interpretation and convergence
By means of a few further approximations it is possible to interpret the first-order term in Eq. (36) in a way that sheds some light on its expected magnitude and the rate of convergence of the series expansion. It should be noted that the approximations introduced in this section are not needed for the practical computation of the terms; they are only meant to provide order-of-magnitude estimates. We note that Eq. (10) can be written 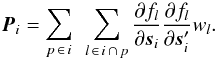 (42)During the short time interval represented by the attitude point p, the position angle of the AL direction across the source is practically constant. The same is true for the celestial direction to the source itself. As a consequence, the partial derivatives in Eq. (42) can be regarded as constant for l ∈ i ∩ p and equal to the weighted average dip defined in Eq. (30). Thus, to a good approximation we have
(42)During the short time interval represented by the attitude point p, the position angle of the AL direction across the source is practically constant. The same is true for the celestial direction to the source itself. As a consequence, the partial derivatives in Eq. (42) can be regarded as constant for l ∈ i ∩ p and equal to the weighted average dip defined in Eq. (30). Thus, to a good approximation we have 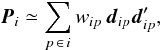 (43)and therefore
(43)and therefore 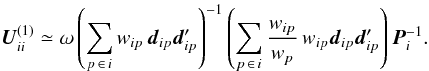 (44)If ηi = wip/wp is the same for all p ∈ i, then η can be taken out of the sum and we find
(44)If ηi = wip/wp is the same for all p ∈ i, then η can be taken out of the sum and we find 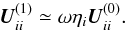 (45)Thus, the first order term is smaller than the zero-order by a factor equal to the weight ratio of source i to all the sources observed at the same time. In reality this weight ratio may vary quite a lot between different attitude points, but the above relation may still give a correct order-of-magnitude estimate if ηi is taken to be the mean value of wip/wp for p ∈ i. Since typically thousands of primary stars are observed together at any attitude point, the relative weight of any single sources is usually quite small, so that ηi ≪ 1, in which case the first-order term is just a small correction to the previous term.
(45)Thus, the first order term is smaller than the zero-order by a factor equal to the weight ratio of source i to all the sources observed at the same time. In reality this weight ratio may vary quite a lot between different attitude points, but the above relation may still give a correct order-of-magnitude estimate if ηi is taken to be the mean value of wip/wp for p ∈ i. Since typically thousands of primary stars are observed together at any attitude point, the relative weight of any single sources is usually quite small, so that ηi ≪ 1, in which case the first-order term is just a small correction to the previous term.
Considering now the cross-term 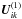 for i ≠ k, its size should be compared with the corresponding diagonal blocks Uii and Ukk, for which we may for the present purpose use the zero-order approximations
for i ≠ k, its size should be compared with the corresponding diagonal blocks Uii and Ukk, for which we may for the present purpose use the zero-order approximations 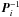 and
and 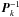 . Defining a dimensionless “block correlation coefficient”
. Defining a dimensionless “block correlation coefficient” 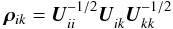 (46)in analogy with the usual (scalar) correlation coefficient, we have
(46)in analogy with the usual (scalar) correlation coefficient, we have ![\begin{eqnarray} \label{eq:blockCorr1} \vec{\rho}_{ik}^{(1)} &\equiv& \vec{U}_{ii}^{-1/2}\vec{U}_{ik}^{(1)}\vec{U}_{kk}^{-1/2}\nonumber\\[3pt] &\simeq&\vec{P}_i^{1/2}\vec{U}_{ik}^{(1)}\vec{P}_k^{1/2}\nonumber\\[3pt] &=&\omega\vec{P}^{-1/2}_i\sum_{p\,\in\, i\,\cap\,k}\frac{w_{ip}w_{kp}}{w_p}\, \vec{d}_{ip}\vec{d}_{kp}' \vec{P}^{-1/2}_{k}\nonumber\\ &\simeq&\omega\sqrt{\eta_i\eta_k}~\left(\sum_{p\,\in\, i}\! \vec{d}_{ip}\vec{d}_{ip}'\right)^{-1/2}\, \left(\sum_{p\,\in\, i\,\cap\, k} \!\vec{d}_{ip}\vec{d}_{kp}'\right)\, \left(\sum_{p\,\in\, k} \!\vec{d}_{kp}\vec{d}_{kp}'\right)^{-1/2} \, , \end{eqnarray}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq235.png) (47)where, in the last approximation, we introduced wip ≃ ηiwp and wkp ≃ ηkwp similarly to what was done for Eq. (45), and assumed wp to be roughly constant for all p.
(47)where, in the last approximation, we introduced wip ≃ ηiwp and wkp ≃ ηkwp similarly to what was done for Eq. (45), and assumed wp to be roughly constant for all p.
In order to proceed further and obtain a rough estimate of the size of the (block) correlation, we need to rely on statistical arguments. We note that the vectors dip contain the partial derivatives of the AL coordinate with respect to the five astrometric parameters and thus depend only on the time and geometry of the observations (for example, it is nearly the same for all sources observed in the same field of view at a given time). The most important cases of non-zero 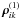 will occur when the two sources i and k are fairly close to one another on the sky, so that they are frequently observed together (with the same p). In such cases we have dip ≃ dkp and the three sums in Eq. (47) mainly differ in the number of terms that they contain. If κ(i,k) denotes the number of attitude points that the two sources have in common, so that κ(i,i), κ(i,k), and κ(k,k) are the number of terms in the three sums, we have very approximately
will occur when the two sources i and k are fairly close to one another on the sky, so that they are frequently observed together (with the same p). In such cases we have dip ≃ dkp and the three sums in Eq. (47) mainly differ in the number of terms that they contain. If κ(i,k) denotes the number of attitude points that the two sources have in common, so that κ(i,i), κ(i,k), and κ(k,k) are the number of terms in the three sums, we have very approximately 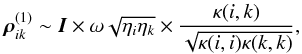 (48)where I is the 5 × 5 identity matrix. The second factor is the fudge factor (of order unity) times the geometric mean of the two weight ratios, which is typically small as discussed above. The last factor measures the degree of overlap between the two sources and is always in the range from 0 to 1. Thus we conclude that the first-order block correlation between any two sources is typically ≪ 1. Similar arguments can be advanced for the first-order term of V and for the higher-order terms of both U and V, making it plausible that the series expansions converge rather rapidly.
(48)where I is the 5 × 5 identity matrix. The second factor is the fudge factor (of order unity) times the geometric mean of the two weight ratios, which is typically small as discussed above. The last factor measures the degree of overlap between the two sources and is always in the range from 0 to 1. Thus we conclude that the first-order block correlation between any two sources is typically ≪ 1. Similar arguments can be advanced for the first-order term of V and for the higher-order terms of both U and V, making it plausible that the series expansions converge rather rapidly.
Equation (48) predicts that the statistical correlation between two neighbouring sources, for any of the astrometric parameters, will decrease with their angular separation in proportion to the degree of overlap of their observations. This result, derived under more restrictive assumptions in Holl et al. (2011), qualitatively explains the spatial correlation curves obtained in small-scale simulations (Holl et al. 2010)5.
In Sect. 3.3 we noted that the successive terms in Eq. (19) can be interpreted as the propagation of the observational errors back and forth between the source parameters and the attitude parameters. This resembles the so-called “simple iteration” scheme originally devised for the astrometric global iterative solution (Sect. 4.5 in Lindegren et al. 2012), in which the source and attitude parameters are alternately updated. Although the simple iteration converges to a valid solution, it is slow when applied to the astrometric problem: hundreds of iterations are required for full numerical convergence (Bombrun et al. 2012). One might conclude that the covariance series expansion requires a similar, prohibitively large number of terms for a useful accuracy. This is not the case, however, for the following reasons. First, the relevant quantities to compare are the RMS astrometric errors, which reach a stable level in the iterative solution in much fewer iterations than required for the parameters to obtain their final values: compare for example the two left panels in Fig. 3 of Bombrun et al. (2012). Secondly, while the astrometric solution typically starts from initial parameter values that are quite far from the final (converged) values, the appropriate analogy for the covariance expansion is to start the iterations from the true parameter values: U(0) is the source covariance due to the observation noise, assuming the true attitude parameters; propagating this uncertainty to the attitude parameters and then back to the source parameters gives the next term U(1); and so on. If the simple iterations are started from the true parameter values they will surely come very close to the final astrometric solution in just a few iterations. Although these arguments are qualitative and not very precise, they support the previous conclusion that the covariance expansion may only need a small number of terms.
5. Practical computation of covariances
5.1. A more convenient recursion
Although arbitrary elements of U can be computed, in principle to arbitrary order, using the recursion relations derived in Sect. 4, a more efficient approach will be described here which directly focuses on the computation of the covariance matrix F in Eq. (1) for a given Jacobian J. Note that the covariance matrix of the five astrometric parameters of a single source, or the joint covariances of the parameters of selected sources, can be obtained by specifying a trivial Jacobian filled with 0’s and 1’s in the appropriate places. It is assumed that we are only interested in data for a moderate number (s) of sources, so that F is of manageable size.
From Eqs. (19) and (1) we have 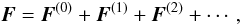 (49)where F(α) = JU(α)J′. Introducing
(49)where F(α) = JU(α)J′. Introducing 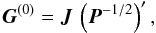 (50)where P − 1/2 is any square root of P-1 (such that
(50)where P − 1/2 is any square root of P-1 (such that 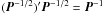 , for example the inverse of the upper-triangular Cholesky factor of P), we may write successive terms as
, for example the inverse of the upper-triangular Cholesky factor of P), we may write successive terms as 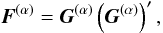 (51)with the recursion
(51)with the recursion ![\begin{equation} \label{eq:Grec} \vec{G}^{(\alpha)} = \left\{ \begin{array}{ll} \vec{G}^{(\alpha-1)}\vec{H} &\quad\text{if }\alpha\text{ is odd,}\\[6pt] \vec{G}^{(\alpha-1)}\vec{H}' &\quad\text{if }\alpha\text{ is even,} \end{array} \right. \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq254.png) (52)where
(52)where 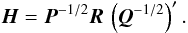 (53)Thanks to the kinematographic approximation, the expression for H becomes extremely simple – it has the same structure as R, with a non-zero element of size 5 × 1 at position (i,p) only if source i was observed at attitude point p:
(53)Thanks to the kinematographic approximation, the expression for H becomes extremely simple – it has the same structure as R, with a non-zero element of size 5 × 1 at position (i,p) only if source i was observed at attitude point p: 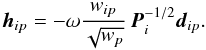 (54)With N primary sources (5N astrometric parameters), P attitude points, and considering the joint covariance of s sources (where s ≪ N), the full size of J is 5s × 5N and G(α) has the same size when α is even. However, because H is 5N × P, we see that the full size of G(α) is 5s × P when α is odd. Therefore, the recursions in Eq. (52) alternate between matrices of two different sizes, and the new version (of order α) may overwrite the previous version (of order α − 2) in memory. Naturally, since both forms of G(α) are very sparse, at least for small α, sparse matrix methods should be used for their storage and manipulation. The squaring of the terms in Eq. (51) and the accumulation of F in Eq. (49) only need a few small matrices of size 5s × 5s.
(54)With N primary sources (5N astrometric parameters), P attitude points, and considering the joint covariance of s sources (where s ≪ N), the full size of J is 5s × 5N and G(α) has the same size when α is even. However, because H is 5N × P, we see that the full size of G(α) is 5s × P when α is odd. Therefore, the recursions in Eq. (52) alternate between matrices of two different sizes, and the new version (of order α) may overwrite the previous version (of order α − 2) in memory. Naturally, since both forms of G(α) are very sparse, at least for small α, sparse matrix methods should be used for their storage and manipulation. The squaring of the terms in Eq. (51) and the accumulation of F in Eq. (49) only need a few small matrices of size 5s × 5s.
The recursions successively fill in more and more columns in G(α). For any α, the non-zero columns in G(α) correspond to the sources (even α) or attitude points (odd α) that have been involved so far. Applying Eq. (52) fills in the attitude points or sources that are connected to any of the previous set.
5.2. Computation of attitude covariance
Successive terms of the series expansion of the attitude covariance V are computed by an almost identical algorithm. With 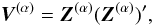 (55)and starting from
(55)and starting from 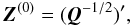 (56)we obtain the recursion
(56)we obtain the recursion ![\begin{equation} \label{eq:Zrec} \vec{Z}^{(\alpha)} = \left\{ \begin{array}{ll} \vec{Z}^{(\alpha-1)}\vec{H}' &\quad\text{if }\alpha\text{ is odd,}\\[6pt] \vec{Z}^{(\alpha-1)}\vec{H} &\quad\text{if }\alpha\text{ is even,} \end{array} \right. \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq269.png) (57)where H has the same meaning as before.
(57)where H has the same meaning as before.
5.3. Data needed for the recursion
Equations (52) and (54) show that all terms of the series expansion for F (and indeed for V as well) can be calculated from a limited set of pre-computed data, essentially comprising:
-
for every source i the inverse Cholesky factor
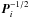 (15 reals);
(15 reals); -
for every source–attitude point combination ip with at least one observation, the 5 × 1 array hip according to Eq. (54) (5 reals);
-
for every attitude point p, the inverse square root of the weight
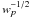 (1 real);
(1 real); -
information defining the structure of the connections, e.g., for every source a list of the attitude points at which it was observed, and for every attitude point a list of the sources observed at that point.
In order to estimate the total size of the required data, let us pessimistically assume N = 109 sources (i.e., including secondary sources) and P = 3 × 107 attitude points (a 5 yr mission with 15% dead time and a knot separation equal to the integration time per CCD, or ≃ 4.5 s). Because there are on average 72 field-of-view transits per source (Sect. 2.1) and every field-of-view transit generates 10 AL observations (1 SM and 9 AF), this results in 15 + 5 × 72 × 10 = 3615 reals per source for the first two items; a negligible amount for the third item; and some 72 × 10 = 720 integers per source for the last item. Uncompressed, and assuming 4 bytes per real or integer, the total size is of the order of 20 TeraByte (TB). (For comparison, storing the full source covariance matrix U would require 2 million TB, and the full attitude covariance matrix V about 2000 TB.) Significant savings may be possible by utilizing the large overlap in sources observed on sequential attitude points, and the fact that dip is virtually the same for the 10 CCD crossings of a given source in a field-of-view transit. However, we conclude that the storage and pre-computation of all the data needed to compute arbitrary terms in the covariance expansion is entirely feasible even without these potential savings.
These estimates are based on the kinematographic approximation, the validity of which has not been established at this point. However, in Paper II we show that the present model, using a third-order expansion (α = 3), is accurate enough to predict variances to better than 1% and correlations within the statistical uncertainty of the numerical experiments. It is therefore a valid basis for calculating the required data volumes.
6. Discussion and conclusions
Based on a series expansion of the inverse of the normal equations matrix for the source and attitude parameters, we have presented a method to estimate the covariances of arbitrary parameters in Gaia’s astrometric core solution. To obtain a practically feasible algorithm it has been necessary to introduce a number of simplifications and assumptions, and even so it is only possible to compute the first few terms of the expansion. In the subsequent Paper II (Holl et al. 2012b) we use numerical simulations of the astrometric core solution to test and validate some of these assumptions.
Exactly as in any least-squares estimation, the covariances derived from the inverse normal equations matrix are formal in the sense that they merely describe how the initially assigned observational uncertainties are propagated to the estimated parameters. The resulting covariances are correct to the extent that the assumptions in Sect. 2.2 hold for the real data. Fortunately, at least some of the assumptions can be tested once the real data become available: for example, the assumed observational uncertainties can be checked by inspecting the residuals of the least-squares fit, and modelling errors can be revealed by the presence of certain patterns in the residuals. For a fully realistic error characterization it is necessary to feed this information back into the covariance model. The mechanism for this is not discussed here and should be the subject of further studies. Conceivably it could involve a modification of 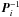 and Q-1 using the “excess source noise” and “excess attitude noise” derived in the astrometric core solution (Sect. 3.6 in Lindegren et al. 2012). In any case the adopted mechanism needs to be validated against large-scale simulations of the Gaia data and the subsequent data processing, based on more detailed models of expected perturbations (cf. Appendix D in Lindegren et al. 2012). Of particular concern are residual CTI effects (Holl et al. 2012c) and attitude modelling errors, which are not independent from one observation to the next and therefore cannot be modelled in the same way as the (uncorrelated) observation noise considered in this paper.
and Q-1 using the “excess source noise” and “excess attitude noise” derived in the astrometric core solution (Sect. 3.6 in Lindegren et al. 2012). In any case the adopted mechanism needs to be validated against large-scale simulations of the Gaia data and the subsequent data processing, based on more detailed models of expected perturbations (cf. Appendix D in Lindegren et al. 2012). Of particular concern are residual CTI effects (Holl et al. 2012c) and attitude modelling errors, which are not independent from one observation to the next and therefore cannot be modelled in the same way as the (uncorrelated) observation noise considered in this paper.
Notwithstanding these shortcomings, we believe that the present covariance model provides a sound mathematical basis for a more complete characterization of the astrometric errors in the Gaia Catalogue. An implementation of the corresponding algorithms outlined in Sect. 5 should be part of the future user interface to the Gaia Catalogue.
We always take “error” to mean the (signed) difference between the estimated and true values of a quantity, and use the term “standard uncertainty” (rather than “standard error”, “mean error”, or similar) to designate the statistical uncertainty of the estimate, in the sense of a standard deviation.
This name is also given to other variants of the formula, especially when D is the identity matrix (e.g., Stewart 1998; Press et al. 2007). The form given here is also referred to as the binomial inverse theorem (Wikipedia). For a historical review, see Henderson & Searle (1981).
The distance between two sources must be an even number, and the same holds for the distance between two attitude points. On the other hand, the distance between a source and an attitude point is an odd number. If no walk exists between two vertices, we take the distance to be infinite. This should not happen in the graphs considered here.
In a study of spatial correlations in the Hipparcos parallaxes, van Leeuwen (1999, 2007) similarly related the drop-off of spatial correlations with angular separation to the diminishing degree of coincidence of the reference great circles ( ≃ scans) in which the stars were observed.
As shown in Fig. C.1 (bottom), the correlation length equals the knot interval for the theoretical covariance functions considered here. This is generally true for a uniform, one-dimensional spline. However, as will be shown in Paper II, when the cubic spline represents the components of the attitude quaternion, we have in general L < Δt4, and it is therefore necessary to distinguish between the two quantities.
Acknowledgments
B. Holl’s work was supported by the European Marie-Curie research training network ELSA (MRTN-CT-2006-033481). L. Lindegren gratefully acknowledges support by the Swedish National Space Board. The authors thank the referee and the editor for comments that helped to improve the paper.
References
- Bastian, U., & Biermann, M. 2005, A&A, 438, 745 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Björck, Å. 1996, Numerical Methods for Least Squares Problems (Philadelphia, PA, USA: Society for Industrial and Applied Mathematics) [Google Scholar]
- Bombrun, A., Lindegren, L., Holl, B., & Jordan, S. 2010, A&A, 516, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bombrun, A., Lindegren, L., Hobbs, D. L., et al. 2012, A&A, 538, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourda, G., Charlot, P., & Le Campion, J.-F. 2008, A&A, 490, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chartrand, G., & Lesniak, L. 2005, Graphs & digraphs, 4th edn. (Chapman & Hall/CRC) [Google Scholar]
- ESA 1997, The Hipparcos and Tycho Catalogues, ESA SP-1200 [Google Scholar]
- Henderson, H. V., & Searle, S. R. 1981, SIAM Rev., 23, 53 [CrossRef] [Google Scholar]
- Hobbs, D., Holl, B., Lindegren, L., et al. 2010, in IAU Symp. 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 315 [Google Scholar]
- Holl, B., Hobbs, D., & Lindegren, L. 2010, in IAU Symp. 261, ed. S. A. Klioner, P. K. Seidelmann, & M. H. Soffel, 320 [Google Scholar]
- Holl, B., Lindegren, L., & Hobbs, D. 2011, in EAS Publ. Ser., 45, 117 [Google Scholar]
- Holl, B., Lindegren, L., & Hobbs, D. 2012a, in Workshop on Astrostatistics and Data Mining in Large Astronomical Databases, La Palma, 30 May–3 June 2011, ed. L. Sarro, J. De Ridder, L. Eyer, & W. O’Mullane, in press [Google Scholar]
- Holl, B., Lindegren, L., & Hobbs, D. 2012b, A&A, 543, A15 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holl, B., Prod’homme, T., Lindegren, L., & Brown, A. 2012c, MNRAS, 422, 2786 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., & Bastian, U. 2011, in GAIA: At the Frontiers of Astrometry, EAS Publ. Ser., 45, 109 [Google Scholar]
- Lindegren, L., Lammers, U., Hobbs, D., et al. 2012, A&A, 538, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Press, W., Teukolsky, S., Vetterling, W., & Flannery, B. 2007, Numerical Recipes: The Art of Scientific Computing, 3rd edn. (Cambridge University Press) [Google Scholar]
- Prod’homme, T., Holl, B., Lindegren, L., & Brown, A. G. A. 2012, MNRAS, 419, 2995 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, J. 2006, Mathematical Statistics and Data Analysis (Duxbury Press) [Google Scholar]
- Stewart, G. 1998, Matrix Algorithms: Basic decompositions (SIAM) [Google Scholar]
- van Leeuwen, F. 1999, in Harmonizing Cosmic Distance Scales in a Post-HIPPARCOS Era, ed. D. Egret, & A. Heck, ASP Conf. Ser., 167, 52 [Google Scholar]
- van Leeuwen, F. 2007, Hipparcos, the New Reduction of the Raw Data, Astrophys. Space Sci. Lib., 350 [Google Scholar]
Appendix A: Notations
List of variables.
Table A.1 lists some important variables in the paper. Italics are used for scalar quantities, lower-case boldface for vectors (column matrices), upper-case boldface for (two-dimensional) matrices, and calligraphic style for sets. A′ is the transpose of A.
In Sect. 3.1 we introduced short-hand notations such as l ∈ i for the observations (having index l) of source i; a more precise definition is as follows. Each observation l is associated with a certain set of sources, designated 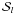 , and with a certain set of attitude points, designated
, and with a certain set of attitude points, designated 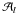 . Then:
. Then: 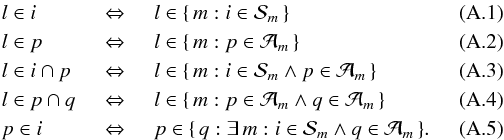 Normally (and certainly in this paper) there is exactly one source for each observation, so
Normally (and certainly in this paper) there is exactly one source for each observation, so 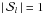 for every l (where | | indicates the size of the set). Moreover, in the kinematographic approximation we have
for every l (where | | indicates the size of the set). Moreover, in the kinematographic approximation we have  for every l. In this approximation every observation l is therefore uniquely associated with one source and one attitude point. This allows some simplification of the definitions above (e.g., the set in Eq. (A.4) is empty if p ≠ q), but we retain the more general formulation for future reference.
for every l. In this approximation every observation l is therefore uniquely associated with one source and one attitude point. This allows some simplification of the definitions above (e.g., the set in Eq. (A.4) is empty if p ≠ q), but we retain the more general formulation for future reference.
Appendix B: The structure of the normal equations as a graph
 |
Fig. B.1 Left: schematic representation of the structure of the normal matrix in Eq. (9), with non-zero elements marked in grey. In this example the number of sources is N = 20, and the number of attitude points P = 15. There are five parameters per source; hence the 5 × 5 block structure in the upper-left part. The first source was observed at attitude points 1 and 7 the second source at 7 and 12, etc. Centre: the matrix obtained by collapsing the blocks in the normal matrix to single elements (actually I + K, where K is the adjacency matrix). Right: the non-trivial part E of the adjacency matrix. |
 |
Fig. B.2 Structure of successive powers of the matrix EE′, where E is as shown in Fig. B.1. Non-zero elements are marked in grey. |
 |
Fig. B.3 Structure of successive powers of the matrix E′E, where E is as shown in Fig. B.1. Non-zero elements are marked in grey. (E′E)α is a P × P matrix (where P is the number of attitude points) with the same fill structure as V(α). |
In Sect. 4.3 some relationships relevant for computing the covariance expansion were described in terms borrowed from graph theory. Here we provide some elementary definitions and further illustrations of the concepts, adapted to the present problem. For a general introduction to graph theory the reader is referred to standard textbooks such as Chartrand & Lesniak (2005).
A graph consists of a set of vertices and a set of edges that connect pairs of distinct vertices. Two vertices are adjacent if there is an edge in the graph joining them. A walk is a sequence of edges connecting one vertex to another. Two vertices are disconnected if there exists no walk between them. The length of the walk is the number of edges. The length of the shortest walk between two vertices is the distance between them. If the two vertices are disconnected, we may take the distance to be infinite. Let n be the order of the graph, i.e., the size of the vertex set. The adjacency matrix of the graph is a symmetric n × n matrix K = [Kuv] such that Kuv = 1 if the uth and vth vertices are adjacent, and Kuv = 0 otherwise. We have the following useful theorem (see, e.g., Chartrand & Lesniak 2005, Theorem 1.7):
For a graph with adjacency matrix K, the (u,v)th element of Kα, α ≥ 1, is the number of different walks of length α from vertex 6u to vertex v.
It follows that the distance d(u,v) between vertices u and v is the smallest power α for which ![\hbox{$[\vec{K}^\alpha]_{uv}>0$}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq333.png) . We have d(u,v) = d(v,u) ≥ 0 for all pairs u, v, with d(u,v) = 0 if and only if u = v. We also have the triangle inequality
. We have d(u,v) = d(v,u) ≥ 0 for all pairs u, v, with d(u,v) = 0 if and only if u = v. We also have the triangle inequality 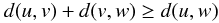 (B.1)for all triples u, v, w of vertices.
(B.1)for all triples u, v, w of vertices.
In a bipartite graph the vertex set can be divided into two disjoint sets  and
and  , such that every edge connects one element in
, such that every edge connects one element in  to one element in
to one element in  . It is clear that the structure of the observations in the kinematographic approximation can be described by means of a bipartite graph: the sets
. It is clear that the structure of the observations in the kinematographic approximation can be described by means of a bipartite graph: the sets  and
and  correspond to the (primary) sources and attitude points, respectively, and there is an edge connecting
correspond to the (primary) sources and attitude points, respectively, and there is an edge connecting 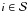 and
and 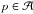 if and only if wip > 0. Using the same matrix partitioning as in Eq. (9), the adjacency matrix can be written
if and only if wip > 0. Using the same matrix partitioning as in Eq. (9), the adjacency matrix can be written ![\appendix \setcounter{section}{2} \begin{equation} \label{eq:adjK} \vec{K} = \begin{bmatrix} \vec{0} & \vec{E}~ \\[3pt] ~\vec{E}' & \vec{0} \end{bmatrix} , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq343.png) (B.2)where the elements of the non-trivial part of the adjacency matrix, E, are Eip = 1 if wip > 0 and Eip = 0 otherwise. The even powers of K are:
(B.2)where the elements of the non-trivial part of the adjacency matrix, E, are Eip = 1 if wip > 0 and Eip = 0 otherwise. The even powers of K are: ![\appendix \setcounter{section}{2} \begin{equation} \label{eq:adjKeven} \vec{K}^{2\alpha} = \begin{bmatrix} ~(\vec{E}\vec{E}')^\alpha & \vec{0} \\[3pt] \vec{0} & (\vec{E}'\vec{E})^\alpha~ \end{bmatrix} , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq346.png) (B.3)and the odd powers:
(B.3)and the odd powers: ![\appendix \setcounter{section}{2} \begin{equation} \label{eq:adjKodd} \vec{K}^{2\alpha+1} = \begin{bmatrix} \vec{0} & (\vec{E}\vec{E}')^\alpha\vec{E}~ \\[3pt] ~(\vec{E}'\vec{E})^\alpha\vec{E}' & \vec{0} \end{bmatrix} . \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq347.png) (B.4)The structure of E is similar to that of R in Eq. (9), in the sense that each non-zero element in E corresponds to a non-zero 5 × 1 submatrix in R, and similarly for the zero elements. Since P-1 and Q-1 are (block) diagonal matrices in the kinematographic approximation, it can be seen from Eqs. (19) and (20) that U(α) has the same structure as
(B.4)The structure of E is similar to that of R in Eq. (9), in the sense that each non-zero element in E corresponds to a non-zero 5 × 1 submatrix in R, and similarly for the zero elements. Since P-1 and Q-1 are (block) diagonal matrices in the kinematographic approximation, it can be seen from Eqs. (19) and (20) that U(α) has the same structure as 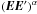 , while V(α) has the same structure as (E′E)α. The conditions for non-zero blocks or elements in the series expansions of U and V, Eqs. (40), (41), then follow from the theorem above.
, while V(α) has the same structure as (E′E)α. The conditions for non-zero blocks or elements in the series expansions of U and V, Eqs. (40), (41), then follow from the theorem above.
Figures B.1–B.3 illustrate the structures of the normal matrix, the corresponding adjacency matrix, and the successive powers of EE′ and E′E for an extremely simple (and of course totally unrealistic) example with 20 sources and 15 attitude points. In this example 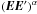 is completely filled for α ≥ 4, which means that the largest distance between any two sources is 8; while (E′E)α is filled for α ≥ 5, which means that the largest distance between any two attitude points is 10.
is completely filled for α ≥ 4, which means that the largest distance between any two sources is 8; while (E′E)α is filled for α ≥ 5, which means that the largest distance between any two attitude points is 10.
Appendix C: Estimating the “fudge factor” ω
 |
Fig. C.1 Top: the along-scan attitude measurements (symbolised by the dots) schematically fitted by a first-order spline (dashed line) and a cubic spline (solid curve), using the same uniform knot sequence with knot interval Δt. Bottom: the theoretical autocovariance functions of the two splines, normalised as described in the text. In both diagrams the timescale is shown in units of Δt. |
The fudge factor ω was introduced in Eq. (31) to account for a possible underestimation of the along-scan (AL) attitude error variance in the kinematographic approximation. With a view to obtain an a priori estimate of ω, we now take a closer look at the expected statistical properties of the attitude errors.
In the kinematographic approximation the AL attitude error is assumed to be constant within the attitude bin around each attitude point p. Mathematically, it can therefore be described as a spline of order M = 1, for which the knots coincide with the boundaries of the attitude bins7. On the other hand, cubic splines (of order M = 4) are used to model the attitude in the astrometric solution. It is therefore relevant to compare the statistical properties of splines of different orders, in particular first-order versus fourth-order splines. For simplicity we assume that the splines are uniform, i.e., defined on knot sequences with a constant knot interval Δt. Figure C.1 (top) illustrates the modelling of the AL attitude measurement errors (represented by the dots) by means of a cubic spline (solid curve, representing the attitude errors in the astrometric solution), and a first-order spline (dashed line, representing the kinematographic approximation). In this diagram we have assumed that Δt is the same for the two splines; in general they could however be different.
Let eM(t) be a spline of order M representing the AL attitude errors on a uniform knot sequence with knot interval ΔtM. We assume that the errors are unbiased, E [eM(t)] = 0, and describe the second-order statistics by means of the autocovariance function ![\appendix \setcounter{section}{3} \begin{equation} \label{appB01} C_M(\tau\,|\,\Delta t_M) = \text{E}_t\left[ e_M(t) e_M(t+\tau) \right] , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq356.png) (C.1)where the dependence on ΔtM is made explicit by the second argument of the autocovariance function. Et signifies an average over t as well as the ensemble average over different random realisations of the measurement noise. In particular, CM(0 | ΔtM) is the time-averaged AL attitude variance. The autocovariance function can be theoretically calculated for an infinite, uniform knot sequence under the assumption that the measurements are sufficiently densely and uniformly distributed in time that one can ignore the statistical variation of astrometric weight between knot intervals and within each knot interval. Let ẇ = dw/dt be the rate at which the astrometric weight of the AL attitude measurements is accumulated. The weight per knot interval is then wM = ẇΔtM. It turns out that this theoretical CM(τ | ΔtM) is a spline of order 2M such that
(C.1)where the dependence on ΔtM is made explicit by the second argument of the autocovariance function. Et signifies an average over t as well as the ensemble average over different random realisations of the measurement noise. In particular, CM(0 | ΔtM) is the time-averaged AL attitude variance. The autocovariance function can be theoretically calculated for an infinite, uniform knot sequence under the assumption that the measurements are sufficiently densely and uniformly distributed in time that one can ignore the statistical variation of astrometric weight between knot intervals and within each knot interval. Let ẇ = dw/dt be the rate at which the astrometric weight of the AL attitude measurements is accumulated. The weight per knot interval is then wM = ẇΔtM. It turns out that this theoretical CM(τ | ΔtM) is a spline of order 2M such that  and CM(mΔtM | ΔtM) = 0 for integer m ≠ 0. The details of this calculation are not given here, but the results for M = 1 and 4 are shown in the bottom part of Fig. C.1 in the form of the normalized autocovariance functions
and CM(mΔtM | ΔtM) = 0 for integer m ≠ 0. The details of this calculation are not given here, but the results for M = 1 and 4 are shown in the bottom part of Fig. C.1 in the form of the normalized autocovariance functions 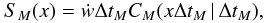 (C.2)which only depend on M. The autocovariance functions for different orders are similar in the sense that they have the same variance and correlation length8, provided that ΔtM is the same. Choosing the attitude bin width B equal to the knot interval of the cubic spline, and ω = 1, therefore gives an autocovariance function in the kinematographic approximation that in a certain sense optimally matches the true autocovariance. We might naively think that this also gives the best estimate of the attitude covariance matrix.
(C.2)which only depend on M. The autocovariance functions for different orders are similar in the sense that they have the same variance and correlation length8, provided that ΔtM is the same. Choosing the attitude bin width B equal to the knot interval of the cubic spline, and ω = 1, therefore gives an autocovariance function in the kinematographic approximation that in a certain sense optimally matches the true autocovariance. We might naively think that this also gives the best estimate of the attitude covariance matrix.
However, the differences between S1 and S4 become significant when combining the observations from different CCDs in the astrometric field (AF). As described in Sect. 2.1, a source is normally observed on n = 9 successive CCDs in the AF, with a temporal spacing of T = 4.85 s as set by the angular separation of the CCDs in the focal plane and the satellite spin rate. During such a field-of-view passage the observation geometry (i.e., ∂fl/∂si) as well as the weights wl remain nearly constant for a given source. The relevant AL attitude error for the determination of si is therefore not eM(t) but the mean value of the n equidistant points sampled by the CCDs9, or 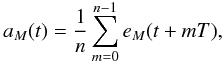 (C.3)where the time argument of aM arbitrarily refers to the first CCD observation. The corresponding autocovariance function is
(C.3)where the time argument of aM arbitrarily refers to the first CCD observation. The corresponding autocovariance function is ![\appendix \setcounter{section}{3} \begin{equation} \label{appB10} \text{E}_t\left[ a_M(t) a_M(t+\tau) \right] = \frac{1}{n} \sum_{m=-n+1}^{n-1} \left(1-\frac{|m|}{n}\right) C_M(mT+\tau) . \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq376.png) (C.4)In particular, the variance of the averaged attitude error is found to be
(C.4)In particular, the variance of the averaged attitude error is found to be ![\appendix \setcounter{section}{3} \begin{equation} \label{appB04} \text{Var}[a_M] = \frac{1}{n\dot{w}\Delta t_M} \sum_{m=-n+1}^{n-1} \left(1-\frac{|m|}{n}\right) S_M(mT/\Delta t_M) , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq377.png) (C.5)which in general is not the same for different M, even if ΔtM is kept constant. For example, Var [a4] > Var [a1] means that the astrometric effects of the attitude errors are larger than predicted in the kinematographic approximation (with ω = 1). Our conjecture is that this can be corrected by applying a fudge factor equal to the variance ratio, or
(C.5)which in general is not the same for different M, even if ΔtM is kept constant. For example, Var [a4] > Var [a1] means that the astrometric effects of the attitude errors are larger than predicted in the kinematographic approximation (with ω = 1). Our conjecture is that this can be corrected by applying a fudge factor equal to the variance ratio, or ![\appendix \setcounter{section}{3} \begin{equation} \label{appB05} \omega = \frac{\text{Var}[a_4]}{\text{Var}[a_1]} = \frac{(T/L)\sum_{m=-n+1}^{n-1} \left(1-\frac{|m|}{n}\right) S_4(mT/L)} {(T/B)\sum_{m=-n+1}^{n-1} \left(1-\frac{|m|}{n}\right) S_1(mT/B)} , \end{equation}](/articles/aa/full_html/2012/07/aa18807-12/aa18807-12-eq379.png) (C.6)where we have put Δt1 = B (the attitude bin width in the kinematographic approximation) and Δt4 = L (the correlation length of the cubic attitude spline)10. Table C.1 gives ω computed according to Eq. (C.6) for several different combinations of the dimensionless numbers L/T and B/T, i.e., the correlation length and attitude bin width expressed in units of the temporal separation of the CCD observations (T = 4.85 s for Gaia). We note that for any L/T it is possible to choose B/T such that ω = 1. However, since the choice of B/T also affects the correlation length of a1(t), a better matching of the attitude covariance functions in Eq. (C.4) should be possible by using both B/T and ω as free parameters in the kinematographic model. In Paper II these theoretical results are compared with empirical determinations from numerical simulations.
(C.6)where we have put Δt1 = B (the attitude bin width in the kinematographic approximation) and Δt4 = L (the correlation length of the cubic attitude spline)10. Table C.1 gives ω computed according to Eq. (C.6) for several different combinations of the dimensionless numbers L/T and B/T, i.e., the correlation length and attitude bin width expressed in units of the temporal separation of the CCD observations (T = 4.85 s for Gaia). We note that for any L/T it is possible to choose B/T such that ω = 1. However, since the choice of B/T also affects the correlation length of a1(t), a better matching of the attitude covariance functions in Eq. (C.4) should be possible by using both B/T and ω as free parameters in the kinematographic model. In Paper II these theoretical results are compared with empirical determinations from numerical simulations.
Theoretical values of the fudge factor ω for different combinations of the dimensionless numbers L/T and B/T.
All Tables
Theoretical values of the fudge factor ω for different combinations of the dimensionless numbers L/T and B/T.
All Figures
 |
Fig. 1 Colour-coded map of the expected number of field-of-view transits experienced by sources at different celestial positions in a 5 year mission. The projection uses equatorial coordinates, with right ascension running from −180° to +180° right-to-left. The blue line is the ecliptic. The average number of field transits in this plot is 88, although the value that is normally used for performance evaluation is 72 (accounting for dead time). An over-abundance of transits occurs at 45° away from the ecliptic plane due to the difference between the 45° spin axis angle with respect to the sun and the 90° angle between spin axis and the fields of view. |
| In the text | |
 |
Fig. 2 Schematic layout of the CCDs in the focal plane of Gaia. Due to the satellite spin, a source enters the focal plane from the left in the along-scan (AL) direction. All sources brighter than G = 20 mag are detected by one of the skymappers (SM1 or SM2, depending on the field of view) and then tracked over the subsequent CCDs dedicated to astrometry (AF1–9), photometry (BP and RP), and radial-velocity determination (RVS1–3). In addition there are special CCDs for interferometric Basic-Angle Monitoring (BAM), and for the initial mirror alignment using Wavefront Sensors (WFS). |
| In the text | |
 |
Fig. B.1 Left: schematic representation of the structure of the normal matrix in Eq. (9), with non-zero elements marked in grey. In this example the number of sources is N = 20, and the number of attitude points P = 15. There are five parameters per source; hence the 5 × 5 block structure in the upper-left part. The first source was observed at attitude points 1 and 7 the second source at 7 and 12, etc. Centre: the matrix obtained by collapsing the blocks in the normal matrix to single elements (actually I + K, where K is the adjacency matrix). Right: the non-trivial part E of the adjacency matrix. |
| In the text | |
 |
Fig. B.2 Structure of successive powers of the matrix EE′, where E is as shown in Fig. B.1. Non-zero elements are marked in grey. |
| In the text | |
 |
Fig. B.3 Structure of successive powers of the matrix E′E, where E is as shown in Fig. B.1. Non-zero elements are marked in grey. (E′E)α is a P × P matrix (where P is the number of attitude points) with the same fill structure as V(α). |
| In the text | |
 |
Fig. C.1 Top: the along-scan attitude measurements (symbolised by the dots) schematically fitted by a first-order spline (dashed line) and a cubic spline (solid curve), using the same uniform knot sequence with knot interval Δt. Bottom: the theoretical autocovariance functions of the two splines, normalised as described in the text. In both diagrams the timescale is shown in units of Δt. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


