| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A126 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201218849 | |
| Published online | 14 May 2012 | |
Cosmic-ray-induced ionization in molecular clouds adjacent to supernova remnants
Tracing the hadronic origin of GeV gamma radiation
1
Ruhr-Universität Bochum, Fakultät für Physik &
Astronomie,
44780
Bochum
Germany
e-mail: florian.schuppan@rub.de
2
Dept. of Earth and Space Sciences, Chalmers University of
Technology, Onsala Space Observatory, 439 92
Onsala,
Sweden
3
Unit for Space Physics, North-West University,
2520
Potchefstroom, South
Africa
4
Université Denis Diderot-Paris 7, Laboratoire APC,
Bâtiment Condorcet, Case
7020, 75205
Paris Cedex 13,
France
5
Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117
Heidelberg,
Germany
Received:
19
January
2012
Accepted:
22
March
2012
Context. Energetic gamma rays (GeV to TeV photon energy) have been detected toward several supernova remnants (SNRs) that are associated with molecular clouds. If the gamma rays are produced mainly by hadronic processes rather than leptonic processes like bremsstrahlung, then the flux of energetic cosmic ray nuclei (>1 GeV) required to produce the gamma rays can be inferred at the site where the particles are accelerated in SNR shocks. It is of great interest to understand the acceleration of the cosmic rays of lower energy (<1 GeV) that accompany the energetic component. These particles of lower energy are most effective in ionizing interstellar gas, which leaves an observable imprint on the interstellar ion chemistry. A correlation of energetic gamma radiation with enhanced interstellar ionization can thus be used to support the hadronic origin of the gamma rays and to constrain the acceleration of ionizing cosmic rays in SNR.
Aims. We propose a method to test the hadronic origin of GeV gamma rays from SNRs associated with a molecular cloud.
Methods. We use observational gamma ray data for each SNR known to be associated with a molecular cloud, modeling the observations to obtain the underlying proton spectrum under the assumption that the gamma rays are produced by pion decay. Assuming that the acceleration mechanism does not only produce high energy protons, but also low energy protons, this proton spectrum at the source is then used to calculate the ionization rate of the molecular cloud. Ionized molecular hydrogen triggers a chemical network forming molecular ions. The relaxation of these ions results in characteristic line emission, which can be predicted.
Results. We show that the predicted ionization rate for at least two objects is more than an order of magnitude above Galactic average for molecular clouds, hinting at an enhanced formation rate of molecular ions. There will be interesting opportunities to measure crucial molecular ions in the infrared and submillimeter-wave parts of the spectrum.
Key words: astroparticle physics / radiation mechanisms: non-thermal / ISM: clouds / cosmic rays / ISM: supernova remnants / gamma rays: ISM
© ESO, 2012
1. Introduction
The origin of cosmic rays (CRs) is an open question in astrophysics. The cosmic ray
spectrum below the knee, at energy/nucleon E < 1015 eV is
believed to be associated with cosmic ray acceleration in supernova remnants (SNRs, Bell 1978b; Blandford
& Ostriker 1978; Blandford &
Eichler 1987). However, there is no conclusive proof for this until now. There is
an excess in GeV-TeV gamma rays observed from SNRs associated with molecular clouds, see
e.g. Abdo et al. (2009), Abdo et al. (2010c) and Aharonian et al.
(2008). These signals might be caused by bremsstrahlung or inverse Compton
scattering of electrons in a leptonic scenario, or by the decay of neutral pions formed by
proton-proton scattering in a hadronic scenario. So far, it is not known which of these
processes is dominant. Investigating which is the dominant process is important to
understand the origin of cosmic rays. In the hadronic scenario, high energy protons are
accelerated in the SNR shocks and then escape to interact with ambient protons, in
particular in molecular clouds in the direct vicinity of the SNR. It is also likely that low
energy protons (E < 1 GeV) are accelerated in the SNR, but these
protons fall below the threshold for pion formation, so that no conclusions concerning the
low energy CR spectrum can be drawn from gamma ray observations. However, low energy protons
are very efficient in ionizing molecular gas. Therefore, ionization signatures provide
information about the density of low energy cosmic rays. The main product of the ionization
of molecular hydrogen, H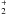 ,
initiates a chain of chemical reactions that yield additional ions like
H
,
initiates a chain of chemical reactions that yield additional ions like
H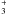 ,
OH+, H2O+, H3O+ and HeH+
(Black 2007; McCarthy et al. 2006). These molecules are most likely formed in rotationally and
vibrationally excited states, the corresponding wavelength for relaxation in the UV or IR,
respectively. If the abundances of these molecules are sufficiently large, the UV or IR
signals might be detectable and offer conclusions concerning the source of cosmic rays. A
correlation study of molecular clouds bright in GeV gamma rays and showing ionization
features might be useful to find the dominant process in forming GeV gamma rays. In this
paper, the ionization rate of molecular hydrogen is calculated for each SNR known to
interact with a molecular cloud. In contrast to former work (Becker et al. 2011), here the spectral shape of the primary particle spectral
energy distribution (SED) below kinetic energies of E ~ 1 GeV is
altered in order to take the unknown spectral behavior into consideration, rather than
altering the minimum energy of particles contributing to the ionization process. The paper
is structured as follows: in Sect. 2 the competing
processes active while particles are being accelerated and their influence on the spectral
shape of the CRs is discussed, in Sect. 3 the spectrum
of the primary protons is calculated by considering loss processes and the acceleration
mechanism, in Sect. 4 the ionization rate for each SNR
associated with a molecular cloud is calculated, in Sect. 5 the uncertainties are discussed, in Sect. 6
the ionization signatures to be expected are shown, in Sect. 7 first observational evidence for an enhanced ionization rate in correlation with
GeV gamma ray emission is summarized and in Sect. 8, a
summary of the paper as well as an outlook to future work is given.
,
OH+, H2O+, H3O+ and HeH+
(Black 2007; McCarthy et al. 2006). These molecules are most likely formed in rotationally and
vibrationally excited states, the corresponding wavelength for relaxation in the UV or IR,
respectively. If the abundances of these molecules are sufficiently large, the UV or IR
signals might be detectable and offer conclusions concerning the source of cosmic rays. A
correlation study of molecular clouds bright in GeV gamma rays and showing ionization
features might be useful to find the dominant process in forming GeV gamma rays. In this
paper, the ionization rate of molecular hydrogen is calculated for each SNR known to
interact with a molecular cloud. In contrast to former work (Becker et al. 2011), here the spectral shape of the primary particle spectral
energy distribution (SED) below kinetic energies of E ~ 1 GeV is
altered in order to take the unknown spectral behavior into consideration, rather than
altering the minimum energy of particles contributing to the ionization process. The paper
is structured as follows: in Sect. 2 the competing
processes active while particles are being accelerated and their influence on the spectral
shape of the CRs is discussed, in Sect. 3 the spectrum
of the primary protons is calculated by considering loss processes and the acceleration
mechanism, in Sect. 4 the ionization rate for each SNR
associated with a molecular cloud is calculated, in Sect. 5 the uncertainties are discussed, in Sect. 6
the ionization signatures to be expected are shown, in Sect. 7 first observational evidence for an enhanced ionization rate in correlation with
GeV gamma ray emission is summarized and in Sect. 8, a
summary of the paper as well as an outlook to future work is given.
2. Acceleration and diffusion
Since the primary particle spectra at energies below ~1 GeV at the source are
not known, especially in the context of cosmic ray-induced ionization (e.g. Nath & Biermann 1994; Indriolo et al. 2009), the competing processes affecting these particles
are discussed and compared in this section. In particular, it is of importance at what
energy the ionization timescale is shorter than the acceleration timescale and vice versa to
ensure that acceleration is unaffected. The acceleration timescale is given in Jokipii (1987), Biermann
et al. (2009) as 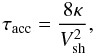 (1)where κ is
the diffusion coefficient and Vsh is the shock velocity. The
diffusion coefficient may well differ inside the cloud and outside the cloud. Outside the
cloud, the diffusion coefficient has to be low enough to allow for efficient acceleration,
while inside the cloud the diffusion coefficient has to be sufficiently large for the
particles to penetrate the cloud within the age of the SNR. For a typical age of
T = 104 yr and a penetration depth of
R = 30 pc (Becker et al. 2011), the
diffusion coefficient for a particle of
p = 1 GeV c-1 would have to be
(1)where κ is
the diffusion coefficient and Vsh is the shock velocity. The
diffusion coefficient may well differ inside the cloud and outside the cloud. Outside the
cloud, the diffusion coefficient has to be low enough to allow for efficient acceleration,
while inside the cloud the diffusion coefficient has to be sufficiently large for the
particles to penetrate the cloud within the age of the SNR. For a typical age of
T = 104 yr and a penetration depth of
R = 30 pc (Becker et al. 2011), the
diffusion coefficient for a particle of
p = 1 GeV c-1 would have to be
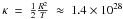 cm2 s-1.
Introducing a momentum dependence in the diffusion coefficient,
cm2 s-1.
Introducing a momentum dependence in the diffusion coefficient,
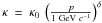 , and applying this value
for the cloud’s interior, the acceleration timescale can be written as
, and applying this value
for the cloud’s interior, the acceleration timescale can be written as
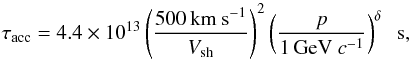 (2)where c
is the speed of light and p is the momentum of the particle. This includes
a scaling to a typical value of the shock velocity for middle-aged remnants,
Vsh = 500 km s-1 (Abdo et al. 2010c).
(2)where c
is the speed of light and p is the momentum of the particle. This includes
a scaling to a typical value of the shock velocity for middle-aged remnants,
Vsh = 500 km s-1 (Abdo et al. 2010c).
The momentum loss rate dp/dt at a given momentum
p by ionization or excitation is given by Lerche & Schlickeiser (1982) as
![\begin{eqnarray} \frac{{\rm d}p}{{\rm d}t} &=& -5 \times 10^{-19}~ q^2 \left(\frac{n}{\rm cm^{-3}} \right)\left(\frac{p}{m c} \right)^{-2} \nonumber\\ &&\times \left[11.3 + 2 \ln{\left(\frac{p}{m c} \right)} \right]~{\rm eV~cm^{-1}}, \end{eqnarray}](/articles/aa/full_html/2012/05/aa18849-12/aa18849-12-eq28.png) (3)where
q is the charge of the particle, n is the number density
of the interacting region, m is the mass of the particle and
c is the speed of light. A more general expression can be found in Mannheim & Schlickeiser (1994). Neglecting the
logarithmic dependence in the square bracket, since p is of the order of
~1 GeV c-1, the ionization timescale for protons is
calculated as
(3)where
q is the charge of the particle, n is the number density
of the interacting region, m is the mass of the particle and
c is the speed of light. A more general expression can be found in Mannheim & Schlickeiser (1994). Neglecting the
logarithmic dependence in the square bracket, since p is of the order of
~1 GeV c-1, the ionization timescale for protons is
calculated as 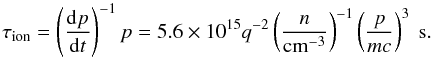 (4)These two timescales are
compared in Fig. 1, where q = 1,
n = 100 cm-3 and
Vsh = 500 km s-1 were used as a typical set of
parameters. The momentum dependence of the diffusion coefficient is shown for
δ = 1/3 as well as for δ = 0.6, as
discussed in Blasi & Amato (2012), and
references therein. There it is reported that a value of δ = 1/3
would favor second order Fermi acceleration and at the same time explain the observed ratios
of B/C and fit the anisotropy of cosmic rays observed at Earth better than
δ = 0.6. However, this would require an injection spectrum of
N(E) ∝ E-2.4, which is
challenging for non-linear diffusive shock acceleration (NLDSA) in SNRs. On the other hand,
δ = 0.6 would favor NLDSA and match the detected spectra of cosmic
rays including nuclei heavier than helium, but result in an anisotropy larger than observed.
The shock velocity Vsh = 500 km s-1 is typical for
older SNRs, as e.g. W51C (Abdo et al. 2009). For
younger SNRs, the shock velocity can reach values of
Vsh ~ 10 000 km s-1.
(4)These two timescales are
compared in Fig. 1, where q = 1,
n = 100 cm-3 and
Vsh = 500 km s-1 were used as a typical set of
parameters. The momentum dependence of the diffusion coefficient is shown for
δ = 1/3 as well as for δ = 0.6, as
discussed in Blasi & Amato (2012), and
references therein. There it is reported that a value of δ = 1/3
would favor second order Fermi acceleration and at the same time explain the observed ratios
of B/C and fit the anisotropy of cosmic rays observed at Earth better than
δ = 0.6. However, this would require an injection spectrum of
N(E) ∝ E-2.4, which is
challenging for non-linear diffusive shock acceleration (NLDSA) in SNRs. On the other hand,
δ = 0.6 would favor NLDSA and match the detected spectra of cosmic
rays including nuclei heavier than helium, but result in an anisotropy larger than observed.
The shock velocity Vsh = 500 km s-1 is typical for
older SNRs, as e.g. W51C (Abdo et al. 2009). For
younger SNRs, the shock velocity can reach values of
Vsh ~ 10 000 km s-1.
 |
Fig. 1 Ionization and acceleration timescale for protons, n = 100 cm-3 and Vsh = 500 km s-1. |
In the environment described by the chosen parameters, at a particle momentum of p ≥ 0.8 GeV c-1, almost independent of the actual momentum dependence of the diffusion coefficient, the acceleration timescale is shorter than the ionization timescale, indicating that ionization losses do occur, but do not suppress the acceleration process effectively above this momentum. Therefore, the ionization losses do affect the spectral index of the primary proton SED significantly, but only at momenta p ≤ 1 GeV c-1.
Furthermore, adiabatic deceleration might in principle occur and alter the spectral shape of the primary proton SED, especially for momenta p ≥ 1 GeV c-1 (see Lerche & Schlickeiser 1982). The momentum loss for primary particles with momenta p ≥ 1 GeV c-1 by adiabatic deceleration dominates the ionization losses, while below this energy the ionization losses dominate losses by adiabatic deceleration (see Lerche & Schlickeiser 1982). However, the primary proton SED at these energies is obtained from modeling the GeV gamma ray emission via π0-decay using the Kamae model (Kamae et al. 2006; Karlsson & Kamae 2008). The lowest observable photon energy Eγ ≈ 100 MeV corresponds to a primary proton energy of Ep = 1 GeV. Thus, above 1 GeV the spectrum of primary protons needed is directly known and would already include modulation effects on the SED caused by adiabatic deceleration. Yet, there is no direct information about the low energy cosmic rays, so the estimate of the low energy cosmic ray spectrum has to be made very carefully.
3. Primary proton SED
To calculate ionization by cosmic ray protons in a molecular cloud, the cosmic ray proton spectrum at the cloud is required. There is no observational data of the particle spectrum at the source: only the spectrum after propagation to Earth is known. Due to larger uncertainties in the description of the propagation process, especially due to the lack of knowledge of the exact magnetic field configuration, the spectrum at the source cannot be described easily from the observed data. If the magnetic field is known, it can be taken into consideration following Padovani & Galli (2011). Gamma ray emission from hadronic interactions is, on the other hand, very well suited to derive the primary particle spectrum above ~1 GeV, since the gamma spectrum follows the primary spectrum. This gamma ray emission was detected e.g. by the Fermi-LAT instrument. Assuming that the detected gamma radiation is mainly caused by the decay of neutral pions from inelastic proton-proton interactions at the cloud, the primary proton SED can be found modeling the gamma ray detections. The spectral shape of this SED is gained modeling the gamma ray emission from neutral pion decay, induced by inelastic proton-proton interactions, and fitting the modeled gamma ray spectrum to the observational data. Loss processes for the primary particles are summarized in Sect. 3.1, acceleration processes are discussed in Sect. 3.2 and finally the calculation of the normalization of the primary proton SED is described in detail in Sect. 3.3.
3.1. Loss processes
The primary protons accelerated by the SNR can suffer momentum losses on their way to the molecular cloud. Yet, it should be stressed here that the spectral shape gained from modeling the gamma ray emission via neutral pion decay, on the other hand, provides the primary proton spectrum at the location of the formation of the neutral pions, the molecular cloud, since they decay in less than 10-16 s (Particle Data Group 2010). The gamma rays emitted from the decay of these pions do hardly suffer energy losses. Therefore, the primary proton spectrum at the location of the cloud is obtained. Low energy protons are very likely accelerated in the same place as the high energy protons, so in this cloud there is not only the formation of pions, but also ionization to be expected. Furthermore, deceleration of high energy protons additionally increases the number of low energy protons (Padovani et al. 2009). Since the spectrum obtained from modeling holds for the location of the molecular cloud, no additional momentum losses have to be considered. However, the primary proton SED can only be considered as known from the modeling down to energies of roughly 1 GeV, as mentioned above. Below this energy, there is no observational information about the primary proton spectrum available. Ionization, on the other hand, will only be effective below 1 GeV, with the cross section for the direct ionization of molecular hydrogen by an incoming proton peaking at about 100 keV and rapidly declining with increasing proton energy (Padovani et al. 2009, and references therein). This makes estimates for the primary proton spectrum below ~1 GeV rather uncertain and a crucial part of the calculation of the ionization rate. It is well possible and most probable that the power law behavior of the primary proton SED is not to be extrapolated to lower energies, because the acceleration mechanisms in these energy domains may differ. In order to account for loss processes which are effective for energies below ~1 GeV as well as the unknown acceleration mechanism at these energies, here the primary proton spectrum derived from modeling is attenuated to lower energies by the choice of a broken power law with positive spectral index 1 ≤ a ≤ 2, E+a, which is compatible with predictions of Skilling & Strong (1976), for three different lower break energies Elb. It should be mentioned that Zirakashvili & Ptuskin (2008) and Ellison & Bykov (2011) predict a concave spectrum for the primary particles escaping SNRs and entering nearby molecular clouds. The models used there apply for young SNRs with an age of 103 yrs or younger, while here all examined SNRs are at least middle-aged, about 104 yrs or older. For old SNRs, Bozhokin & Bykov (1994) modeled the penetration of a broad cosmic ray proton spectrum into a molecular cloud, assuming a diffusion coefficient with momentum dependence κ ∝ p0.33 and κ ∝ p0.5. Their results motivate further examination of SNRs interacting with a molecular cloud, as e.g. Bykov et al. (2000) modeled the spectrum of cosmic ray electrons interacting with a molecular cloud for the case of IC 443, where they also derived a profile of the ionization rate due to primary electrons in the shocked part of the cloud. Recently, Yan et al. (2011) investigated the acceleration of protons in SNRs and the generation of gamma rays in nearby molecular clouds, taking into account the streaming instability and background turbulence.
3.2. Acceleration mechanism
Fermi acceleration (Fermi 1949) is the very first approach to stochastically accelerate charged particles at shock fronts and the model has been further developed to the theory of diffusive shock acceleration (DSA) (Krymskii 1977; Bell 1978b,a; Blandford & Ostriker 1978; Schlickeiser 1989a,b). A variety of concrete models concerning the acceleration mechanism at work in SNRs have been established in the past (e.g. Scott & Chevalier 1975; Blandford & Eichler 1987; Blasi 2005; Zirakashvili & Aharonian 2010; Eichler & Pohl 2011; Drury 2011, and references therein). Recently, Uchiyama et al. (2010) described an alternate model where the focus is not on escaped CR particles, but strong adiabatic compression behind the SNR shock wave in the cloud leads to DSA of pre-existing cosmic rays. With their model, they are capable of modeling both the observed synchrotron radiation and gamma ray emission from certain SNRs associated with a molecular cloud, in particular W51C, W44 and IC 443. However, there is no direct evidence which process actually is responsible for the acceleration. Furthermore, propagation effects and possibly reacceleration are important. The unknown nature of the actual acceleration mechanism leads to a huge variety in possible CR spectra below ~1 GeV, which is shown in Fig. 1 of Indriolo et al. (2009), where several propagated primary spectra are summarized. But since the modeling of the primary particle spectrum fitting the observed gamma ray emission via neutral pion decay does offer the spectral shape of the primaries at the source above 1 GeV, the primary spectra used in this work are independent of the actual acceleration mechanism. The only assumption made is that the major contribution to the GeV gamma ray emission from the sources is caused by neutral pion decay, which shall be tested this way.
3.3. Calculation of the proton SED normalization
In this subsection a detailed description of the calculation of the normalization of the
proton SED using the observed gamma spectrum is given. Known is the flux of gamma rays
detected at Earth, 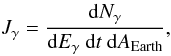 (5)in units of
GeV-1 s-1 cm-2. What can be calculated from
observations is the normalization of the flux of high energy protons interacting with the
cloud and thus forming neutral pions causing the gamma radiation, which is continued to
lower energies in order to calculate the ionization rate of the cloud next to the SNR.
This flux is needed not at Earth but at the SNR,
(5)in units of
GeV-1 s-1 cm-2. What can be calculated from
observations is the normalization of the flux of high energy protons interacting with the
cloud and thus forming neutral pions causing the gamma radiation, which is continued to
lower energies in order to calculate the ionization rate of the cloud next to the SNR.
This flux is needed not at Earth but at the SNR, 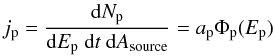 (6)in units of
GeV-1 s-1 cm-2. For instance, for W51C,
(6)in units of
GeV-1 s-1 cm-2. For instance, for W51C,
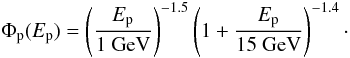 (7)Here,
Φp(Ep) is a dimensionless spectral function and
ap is the normalization factor in units of
GeV-1 s-1 cm-2. The latter enters the calculation of
the ionization rate. In order to obtain this value, the proton flux at the source is
calculated from the observed gamma ray spectrum.
(7)Here,
Φp(Ep) is a dimensionless spectral function and
ap is the normalization factor in units of
GeV-1 s-1 cm-2. The latter enters the calculation of
the ionization rate. In order to obtain this value, the proton flux at the source is
calculated from the observed gamma ray spectrum.
The calculation of the formation of gamma rays via neutral pion decay is described in
detail in e.g. Kelner & Aharonian (2008).
In this paper, the equation for the formation rate of gamma rays in the energy interval
(Eγ,
Eγ + dEγ)
and a unit volume from the decay of neutral pions is reported as:
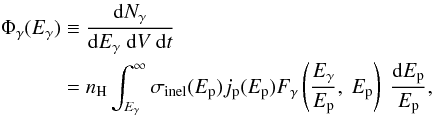 (8)where
nH is the density of the ambient medium and
σinel(Ep) is the cross section
of inelastic proton-proton interactions1. The
function
Fγ(x, Ep)
describes the number of photons in the energy interval
(x,x + dx) per collision and is a dimensionless
probability density distribution function.
(8)where
nH is the density of the ambient medium and
σinel(Ep) is the cross section
of inelastic proton-proton interactions1. The
function
Fγ(x, Ep)
describes the number of photons in the energy interval
(x,x + dx) per collision and is a dimensionless
probability density distribution function.
The result of the formula mentioned above is the number of gamma rays formed from neutral
pion decay per unit time, unit energy and unit volume at the location of the hadronic
interactions, in units of GeV-1 s-1 cm-3. To transform
this quantity into the quantity detected, the result first has to be multiplied by the
volume of the interaction region in order to obtain the total number of gamma rays formed
from neutral pion decay per unit time and unit energy:
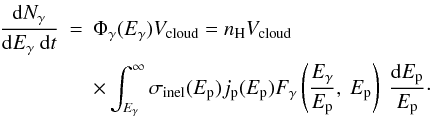 (9)Assuming
that these gamma rays are emitted isotropically, the fraction that is detected at Earth
per unit area can be gained from this by dividing by
(4
(9)Assuming
that these gamma rays are emitted isotropically, the fraction that is detected at Earth
per unit area can be gained from this by dividing by
(4 ) to account
for the solid angle:
) to account
for the solid angle:
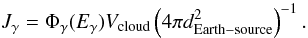 (10)Using Eqs. (6), (8) and (10), the photon spectrum at Earth can be
written as
(10)Using Eqs. (6), (8) and (10), the photon spectrum at Earth can be
written as 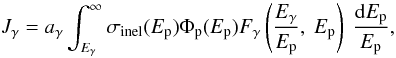 (11)where
(11)where 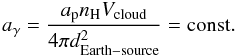 (12)is the
normalization constant of the gamma spectrum. This factor is determined by high-energy
gamma observations of the sources.
(12)is the
normalization constant of the gamma spectrum. This factor is determined by high-energy
gamma observations of the sources.
For the calculation of ionization rates, the proton SED normalization,
ap has to be calculated. This is done using conservation of
energy:
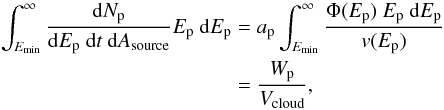 (13)where
(13)where
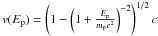 is the
velocity of the particle depending on its kinetic energy Ep
and Wp is the total proton energy budget of protons with a
minimum energy of Emin. Solving this for
ap gives:
is the
velocity of the particle depending on its kinetic energy Ep
and Wp is the total proton energy budget of protons with a
minimum energy of Emin. Solving this for
ap gives: 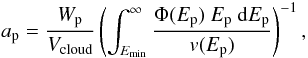 (14)where
ap is in units of
GeV-1 s-1 cm-2. So the entire expression for the
normalization of the gamma spectrum from neutral pion decay,
aγ, can be written as
(14)where
ap is in units of
GeV-1 s-1 cm-2. So the entire expression for the
normalization of the gamma spectrum from neutral pion decay,
aγ, can be written as 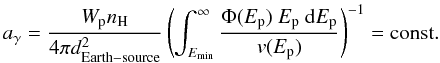 (15)The gamma
normalization is therefore independent of the cloud volume, while the proton SED
normalization, ap, depends on this volume.
(15)The gamma
normalization is therefore independent of the cloud volume, while the proton SED
normalization, ap, depends on this volume.
The modeling of the gamma rays is done using the Kamae model (Kamae et al. 2006; Karlsson & Kamae 2008) in order to obtain the value of aγ. Here, a factor of 1.85 is multiplied to the resulting spectrum in order to take helium and heavier nuclei into account, as suggested by Mori (2009). Here, the model is modified by these two factors and will be referred to as the modified Kamae model.
For a given spectral shape of the proton SED, Φp(Ep), the gamma ray spectrum normalization, aγ, can be found from modeling. For a given distance of the object from Earth, dEarth − source, and lower integration threshold, Emin, this leads to a certain value for the product Wp·nH for each object. Because there are no precise estimates of the average hydrogen densities of the objects, nH, here a value of nH = 100 cm-3 is assumed. The result for Wp simply scales inversely with nH, if nH should turn out to be different. With a value for Wp, the proton SED normalization ap is calculated for each object. Since ap is already implicitly including the solid angle interval, the multiplication by 4π in Eq. (17) is not performed.
4. Calculation of the ionization rate
In general, ionization by particles is mainly caused by two different kinds of particles,
namely electrons and protons. One has to consider direct ionization by electrons as well as
protons on the one hand and ionization by electron capture of protons on the other hand. The
full expression for the ionization rate following Padovani
et al. (2009) is ![\begin{eqnarray} \zeta^{\rm{H_2}} &=& 4\pi \sum_k \int_{E_{\rm{min}}}^{E_{\max}} j_k(E_k)[1 + \phi_k(E_k)]\sigma_{k}^{\rm ion}(E_k){\mathrm{d}}E_k \notag\\ &&+ 4\pi \int_{0}^{E_{\max}}j_{\rm p}(E_{\rm p})\sigma_{\rm p}^{\rm e.c.}(E_{\rm p}){\mathrm{d}}E_{\rm p}, \end{eqnarray}](/articles/aa/full_html/2012/05/aa18849-12/aa18849-12-eq85.png) (16)where
Emin is the minimum energy of particles considered to
contribute to the ionization process, jk is the
number of CR particles of species k (k = e or p,
respectively) per unit time, area, solid angle and energy interval,
(16)where
Emin is the minimum energy of particles considered to
contribute to the ionization process, jk is the
number of CR particles of species k (k = e or p,
respectively) per unit time, area, solid angle and energy interval,
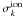 is the ionization
cross section for particles of species k,
is the ionization
cross section for particles of species k,
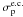 is the
electron capture cross section for protons and
φk is a number taking into account that
ionization may not only be due to ionization by a primary particle k, but
also by the electrons set free during this ionization, called secondary ionization. A closer
look at the orders of magnitude for the different summands shows that only the contribution
from primary proton ionization is significant at the considered energies. The other
ionization processes by protons have cross sections which are significantly lower than the
one for direct ionization by primary protons, as can be seen in Fig. 1 of Padovani et al. (2009).
is the
electron capture cross section for protons and
φk is a number taking into account that
ionization may not only be due to ionization by a primary particle k, but
also by the electrons set free during this ionization, called secondary ionization. A closer
look at the orders of magnitude for the different summands shows that only the contribution
from primary proton ionization is significant at the considered energies. The other
ionization processes by protons have cross sections which are significantly lower than the
one for direct ionization by primary protons, as can be seen in Fig. 1 of Padovani et al. (2009).
Ionization by primary electrons is neglected here for two reasons: first, the ionization cross sections for these processes are lower than the corresponding ones for protons. Second, while protons hardly lose energy on their way from the SNR to the molecular cloud, electrons can suffer energy losses. However, since the primary CR spectra near the peak of the corresponding ionization cross section (~105 eV) is unknown, it is possible that primary electrons do contribute to the ionization rate significantly, as discussed in Padovani et al. (2009). Because the focus of this work is on the contribution of CR protons, here it is assumed that the contribution of primary electrons to the total ionization rate is dominated by the contribution of primary protons and secondary electrons. In fact, ionization by secondary electrons is an important aspect, but it only increases the ionization rate by less than a factor of 2. The resulting ionization rates derived here are rather lower limits, due to neglecting the contribution of primary electrons.
Since only primary particles with a minimum kinetic energy of 105 eV can penetrate the cloud (as will be discussed below), this contribution seems negligible. On the other hand, protons penetrating the cloud will lose energy gradually, so in principle the effect of secondary ionization needs to be calculated differentially, as was done in Padovani et al. (2009). This will be done in future work and thus the ionization rates calculated here are lower limits.
Neglecting the aforementioned ionization processes, the calculation reduces to:
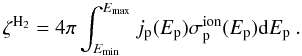 (17)For the examined SNRs
the lower limit of integration, Emin, depends on the hydrogen
density. This is due to the fact that the CR particles have to penetrate the molecular cloud
before interacting with the gas, and lower energy particles are decelerated on shorter
length scales than higher energetic ones and therefore do not contribute noticeably to the
ionization. However, deceleration of high energy particles populates the low energy part of
the spectrum. The stopping length of the particles depends on the hydrogen density, and thus
does the lower integration limit. Indriolo et al.
(2009) suggest a lower integration threshold of 2 MeV for diffuse clouds as
originally suggested by Spitzer & Tomasko
(1968), nH < 103 cm-3, and
a lower integration threshold of 10 MeV for dense clouds,
nH > 103 cm-3. But since this
effect is not well understood in quantitative terms, 100 MeV for dense clouds or 100 keV for
diffuse clouds in the direct vicinity of the SNR might be considered as well. The direct
ionization cross section for primary protons used is reported by Padovani et al. (2009) in Eqs. (5) and (6).
(17)For the examined SNRs
the lower limit of integration, Emin, depends on the hydrogen
density. This is due to the fact that the CR particles have to penetrate the molecular cloud
before interacting with the gas, and lower energy particles are decelerated on shorter
length scales than higher energetic ones and therefore do not contribute noticeably to the
ionization. However, deceleration of high energy particles populates the low energy part of
the spectrum. The stopping length of the particles depends on the hydrogen density, and thus
does the lower integration limit. Indriolo et al.
(2009) suggest a lower integration threshold of 2 MeV for diffuse clouds as
originally suggested by Spitzer & Tomasko
(1968), nH < 103 cm-3, and
a lower integration threshold of 10 MeV for dense clouds,
nH > 103 cm-3. But since this
effect is not well understood in quantitative terms, 100 MeV for dense clouds or 100 keV for
diffuse clouds in the direct vicinity of the SNR might be considered as well. The direct
ionization cross section for primary protons used is reported by Padovani et al. (2009) in Eqs. (5) and (6).
Using the proton spectra obtained from modeling the gamma ray detections, the ionization
rate by primary protons is calculated from Eq. (17). These spectra are varied in the spectral index a below the
lower break energy Elb. Additionally, the lower break energy
Elb is varied. The minimum energy of protons penetrating the
cloud and thus contributing to the ionization process considered is
Emin = 10 MeV as a conservative approximation. The Galactic
average ionization rate of molecular hydrogen in molecular clouds is
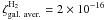 s-1,
as reported by Neufeld et al. (2010). It should be
noted that this average value is subject to variations between approximately
10.5 × 10-16 s-1 at maximum and
0.5 × 10-16 s-1 or less, possibly connected to propagation effects
(Indriolo & McCall 2012). The proton
spectra of the sources are either of the form
s-1,
as reported by Neufeld et al. (2010). It should be
noted that this average value is subject to variations between approximately
10.5 × 10-16 s-1 at maximum and
0.5 × 10-16 s-1 or less, possibly connected to propagation effects
(Indriolo & McCall 2012). The proton
spectra of the sources are either of the form
![\begin{equation} j_{\rm p}(E_{\rm p}) = \left\{\begin{array}{ll} a_{\rm p}\left(\frac{E_{\rm lb}}{E_0}\right)^{-s}\left(1+\frac{E_{\rm lb}}{E_{\rm br}}\right)^{-\Delta s} ~\left(\frac{E_{\rm p}}{E_{\rm lb}}\right)^{a} &\qquad (E_{\rm p} \leq E_{\rm lb}) \\[2mm] a_{\rm p}\left(\frac{E_{\rm p}}{E_0}\right)^{-s}\left(1+\frac{E_{\rm p}}{E_{\rm br}}\right)^{-\Delta s}~ & \qquad (E_{\rm p} > E_{\rm lb}),\end{array}\right. \end{equation}](/articles/aa/full_html/2012/05/aa18849-12/aa18849-12-eq102.png) (18)or
of the form
(18)or
of the form ![\begin{equation} j_{\rm p}(E_{\rm p}) = \left\{\begin{array}{ll} a_{\rm p}~\left(\frac{E_{\rm lb}}{E_0}\right)^{-s} \exp{\left(-\frac{E_{\rm lb}}{E_{\rm cutoff}}\right)} \left(\frac{E_{\rm p}}{E_{\rm lb}}\right)^{a} & \qquad (E_{\rm p} \leq E_{\rm lb}) \\[2mm] a_{\rm p}\left(\frac{E_{\rm p}}{E_0}\right)^{-s} \exp{\left(-\frac{E_{\rm p}}{E_{\rm cutoff}}\right)} &\qquad(E_{\rm p} > E_{\rm lb}),\end{array}\right. \end{equation}](/articles/aa/full_html/2012/05/aa18849-12/aa18849-12-eq103.png) (19)where
ap is the normalization factor,
E0 = 1 GeV or 1 TeV (see Table 1), Ebr is the location of the spectral break,
s ≡ αl is the lower spectral index,
Δs + s ≡ αh is the higher
spectral index, Ecutoff is the higher cutoff energy,
Elb is the location of the lower spectral break and
a = 2.0,1.5 or 1.0 the spectral index below the lower break
Elb. It should be mentioned that the spectral break in the
primary proton spectrum is partly due to the fact that it is given in terms of the kinetic
energy Ep. Diffusive shock acceleration produces a power law in
momentum, so expressing this spectral behavior in terms of the kinetic energy
Ep, the spectrum deviates from a power law in kinetic energy
near the rest energy of the particle, ~1 GeV for protons. Because the particles
are accelerated at the supernova shock front which in some cases penetrates the molecular
cloud, both acceleration and ionization can occur in the same place and at the same time. To
account for the unknown acceleration mechanism below E ~ 1 GeV,
the lower spectral break Elb is introduced. Below this break
energy, the particle spectrum is assumed to decrease rapidly toward lower particle energies
as to give a conservative lower limit on the ionization rate. For
Elb ≤ 1 GeV, this does not change the resulting gamma ray
spectrum from neutral pion decay.
(19)where
ap is the normalization factor,
E0 = 1 GeV or 1 TeV (see Table 1), Ebr is the location of the spectral break,
s ≡ αl is the lower spectral index,
Δs + s ≡ αh is the higher
spectral index, Ecutoff is the higher cutoff energy,
Elb is the location of the lower spectral break and
a = 2.0,1.5 or 1.0 the spectral index below the lower break
Elb. It should be mentioned that the spectral break in the
primary proton spectrum is partly due to the fact that it is given in terms of the kinetic
energy Ep. Diffusive shock acceleration produces a power law in
momentum, so expressing this spectral behavior in terms of the kinetic energy
Ep, the spectrum deviates from a power law in kinetic energy
near the rest energy of the particle, ~1 GeV for protons. Because the particles
are accelerated at the supernova shock front which in some cases penetrates the molecular
cloud, both acceleration and ionization can occur in the same place and at the same time. To
account for the unknown acceleration mechanism below E ~ 1 GeV,
the lower spectral break Elb is introduced. Below this break
energy, the particle spectrum is assumed to decrease rapidly toward lower particle energies
as to give a conservative lower limit on the ionization rate. For
Elb ≤ 1 GeV, this does not change the resulting gamma ray
spectrum from neutral pion decay.
Here, jp(Ep) = dNp/(dEp dt dAsource) is the number of CR protons per unit time, area and energy at the source. The spectral shapeof the proton spectrum Φp(Ep) for each object is found modeling the gamma ray detections by Fermi-LAT (see references Abdo et al. 2009, 2010a–d; Castro & Slane 2010) assuming hadronic interactions to form neutral pions, which decay via gamma-gamma coincidences to be the cause of the gamma ray emission. The spectral information about all sources is given in Table 1.
Table of parameters used.
 |
Fig. 2 Modeled gamma ray spectrum and Fermi-LAT observational data. The modeled spectrum shown is for Elb = 1 GeV and a = 2.0, but the spectra for Elb down to 30 MeV and a down to 1.0 practically coincide with the spectrum shown due to the low cross section below 1 GeV. |
To calculate the primary proton SED, observational data about the distance d of the object from Earth and the approximate volume of the cloud is required (see Eqs. (11) and (15)). The values used here are shown in Table 1. The calculation of the ionization rate is discussed here at the example of W51C, but for the other objects the same procedure is done to obtain the result.
In the case of W51C, for d = 6 kpc (Abdo
et al. 2009), Elb = 1 GeV, a = 2.0 and
Emin = 107 eV, only the total proton energy budget
of protons with a minimum kinetic energy of Emin,
Wp and the average hydrogen density of the cloud are free
parameters (see Eq. (15)). The product of
these two quantities needs to be 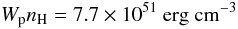 (20)to
produce the modeled gamma spectrum shown in Fig. 2. As
can be seen, the modeled spectrum matches the detections well.
(20)to
produce the modeled gamma spectrum shown in Fig. 2. As
can be seen, the modeled spectrum matches the detections well.
Because there is no precise estimate of the average density of the cloud, here nH = 100 cm-3 is assumed, thus offering the required value of Wp. The result for Wp simply scales inversely with nH, if nH should turn out to be different.
The normalization factor of the proton SED, ap is calculated following Eq. (14), where Wp is the total interacting proton energy budget and the volume of the source Vcloud is assumed to be spherical with a radius taken from observations (Abdo et al. 2009, 2010a–d; Castro & Slane 2010). The lower integration limit indicates the minimum energy of particles contributing to ionization processes. As a conservative approximation, here Emin = 10 MeV is used. The result for each object is shown in Table 2.
Proton SED normalization ap for each source for different lower break energies Elb and spectral indices a below the lower break energy in [erg-1 s-1 cm-2].
With this normalization one can compute the ionization rate due to primary proton ionization performing the integration (17) for different values of Elb and a fixed value of Emax = 1 GeV. The lower break energy is of large importance for the result, because the ionization cross section is the largest at low energies and declines rapidly with increasing energy. The upper integration limit may be any value from 1 GeV or higher because of the low ionization cross section for high energies. Changing Emax to 1 PeV does not change the ionization rate significantly. However, changing Elb from 1 GeV to a different value results in a different gamma spectrum normalization aγ, as can be seen in Eq. (15).
 |
Fig. 3 Ionization rates versus lower break energy Elb for different spectral indices below this break: a = 2.0 (solid black line), a = 1.0 (dotted red line). |
Figure 3 shows that even choosing a large value for the lower break energy would result in an ionization rate at least an order of magnitude greater than the Galactic average for molecular clouds, reported to be about 2 × 10-16 s-1 by Neufeld et al. (2010), for at least two objects, namely W49B and 3C 391. The different lines refer to different values for the power law index a. As can be seen, the value of a does influence the ionization rate, but only to a rather small extent. The ionization rate is much more sensitive to the choice of the lower break energy Elb. If Elb = 100 MeV can be used, only the ionization rate for W51C would be lower than the Galactic average for molecular clouds, while the other objects would exceed this value for all spectral indices a. If even a value for Elb as low as 30 MeV is suitable, the ionization rate for all objects would be greater than the Galactic average for molecular clouds.
If even protons with a minimum energy of Emin = 2 MeV could penetrate the cloud and thus contribute to the ionization, the ionization rates would increase further due to the maximum value of the ionization cross section at E = 100 keV, as Fig. 1 in Padovani et al. (2009) shows. According to Indriolo et al. (2009), this might be reasonable and would increase the ionization rate by 4–40% for a = 1 and Elb = 30 MeV. For larger values of a and Elb, this enhancement of the ionization rate would be significantly lower.
The resulting ionization rates for each SNR known to be associated with a molecular cloud are given in Table 3.
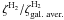 for all objects, calculated for different spectral indices a below
the lower spectral break Elb and different lower break
energies Elb.
for all objects, calculated for different spectral indices a below
the lower spectral break Elb and different lower break
energies Elb.
5. Uncertainties
As mentioned above, since there is no observational data concerning the primary proton SED
for energies below E ~ 1 GeV, the spectral behavior in this
low energy domain is unknown. However, assuming a positive spectral index
a = 2 is rather conservative and should offer a lower limit on the
spectrum and therefore on the ionization rate. This is due to the fact that for an injection
spectrum of ∝ p−s, for a loss term of
ṗ ∝ p-2 like ionization losses, would
be modified as ∝ p3−s, and the power law
indices for the sources discussed are s = 1.5–2.45. However, this is
likely to be the largest uncertainty. Furthermore, there is no precise estimate of the
average density of the molecular clouds, so a value of
nH = 100 cm-3 is assumed. This is also a
major source of uncertainty. The primary proton SED scales linearly with the inverse value
of nH (see Eq. (12)). Should the average density differ from the assumed value, then most likely
it will be larger and therefore the primary proton SED and the ionization rate would
decrease. Another critical parameter is the volume of the cloud. This is a particularly
difficult aspect, since only the primary proton SED does depend on it (see Eq. (14)), but not the resulting gamma spectrum (see
Eq. (15)). The radii used here refer to
the whole SNRs and should therefore offer upper limits on the cloud volume, which would
result in lower limits for the primary proton SEDs and thus the ionization rates. With this
respect, our calculations therefore represent a conservative approach. The distance of the
object from Earth enters the primary proton SED and the ionization rate as
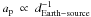 (see Eq. (12)), so the results are more
sensitive on the lower break energy Elb than on the distance.
(see Eq. (12)), so the results are more
sensitive on the lower break energy Elb than on the distance.
Taking all the uncertainties discussed into consideration, still at least two sources, namely W49B and 3C 391, remain with an unusually large ionization rate at least one order of magnitude greater than the Galactic average for molecular clouds. Quite a few sources drop below Galactic average values in the most conservative scenario. This is not expected, since ionization at the accelerator itself is not likely to be lower than on average, but rather higher. Thus, we would rather expect the primary spectrum to extend toward lower energies or the interaction volume to be significantly smaller.
6. Signatures
The enhanced ionization rate in the molecular clouds triggers a chemical network, forming a variety of ionized molecules in rotationally and vibrationally excited states, see e.g. Black (1998) and Black (2007). Once these molecules are sufficiently abundant, their relaxation results in characteristic line emission. Though in principle similar chemical signatures could be produced by X-ray ionization, X-rays have a much shorter penetration depth (Beskin et al. 2003) and therefore are not capable of ionizing the cloud’s interior as effectively as cosmic rays. This implies that the detection of chemical signatures similar to those shown in Becker et al. (2011) would be a strong argument for a proton SED capable of producing these large ionization rates, which in turn would be a very strong argument for hadronic interactions as the dominant process in forming the detected gamma radiation in the GeV regime. Uncertainties do not allow the prediction of the exact value, but the statement that in general, an enhanced ionization rate is expected. Observations of the objects with e.g. Herschel and ALMA will give a better idea of exact values in the future. First results of such observations are summarized in Sect. 7.
In steady state the number densities of the transient ions O+, OH+,
H2O+, and HeH+ are expected to be proportional to
ζH (Herbst & Klemperer
1973). In fully molecular regions, where
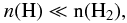 (21)of a low ionization level
(21)of a low ionization level
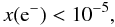 (22)competing processes
almost do not interrupt the sequence of H-atom abstraction reactions. So nearly each
ionization of hydrogen leads to the formation of H
(22)competing processes
almost do not interrupt the sequence of H-atom abstraction reactions. So nearly each
ionization of hydrogen leads to the formation of H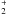 ,
H
,
H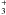 ,
OH+, H2O+, and H3O+. The
time-scales to achieve steady state are very short,
,
OH+, H2O+, and H3O+. The
time-scales to achieve steady state are very short,
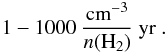 (23)These time-scales are
shorter than the age of the SNRs dealt with here.
(23)These time-scales are
shorter than the age of the SNRs dealt with here.
As stated also in Becker et al. (2011), the concrete
ionization signatures to expect from the enhanced ionization rates cannot be predicted
quantitatively yet. However, the statement that enhanced ionization signatures are to be
expected can clearly be made. These signatures would be characteristic rotation-vibration
emission lines from abundant ionized molecules as e.g.
H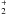 and
H
and
H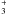 (see
Becker et al. 2011, for an example of such a
spectrum). The environments of SNR-MC systems are therefore considered to be optimal for a
first time direct detection of H
(see
Becker et al. 2011, for an example of such a
spectrum). The environments of SNR-MC systems are therefore considered to be optimal for a
first time direct detection of H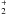 .
Should such ionization signatures be detected in spatial correlation with the GeV gamma ray
emission from an SNR associated with a molecular cloud, this would provide a strong hint at
inelastic proton-proton scattering as the dominant process in forming these gamma rays.
.
Should such ionization signatures be detected in spatial correlation with the GeV gamma ray
emission from an SNR associated with a molecular cloud, this would provide a strong hint at
inelastic proton-proton scattering as the dominant process in forming these gamma rays.
7. First experimental evidence
In two sight lines in the IC443 complex, Indriolo et al.
(2010) found a large column density of H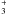 ,
,
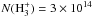 cm-2,
indicating an enhanced ionization rate of
ζH2 ~ 2 × 10-15 s-1.
This favors a less conservative calculation of the ionization rate in this region, as
mentioned in Sect. 5. Dense molecular gas associated
with the W28 SNR shows evidence of heating and chemistry driven by shock waves (Nicholas et al. 2011, 2012), but the high excitation of ammonia molecules in one molecular core can also
be interpreted in terms of ion chemistry driven by an enhanced rate of ionization as
outlined in the next subsection. A derivation of the ionization rate is given in Sect. 7.1. In a molecular cloud of W51C, Ceccarelli et al. (2011) derived an enhanced ionization rate by
measurements of the DCO+/HCO+ ratio of
ζH2 ~ 10-15 s-1,
which also favors a less conservative calculation of the ionization rate. These detections
encourage additional observations toward the direction of the discussed SNR-MC systems, in
particular toward the very promising candidates W49B and 3C 391.
cm-2,
indicating an enhanced ionization rate of
ζH2 ~ 2 × 10-15 s-1.
This favors a less conservative calculation of the ionization rate in this region, as
mentioned in Sect. 5. Dense molecular gas associated
with the W28 SNR shows evidence of heating and chemistry driven by shock waves (Nicholas et al. 2011, 2012), but the high excitation of ammonia molecules in one molecular core can also
be interpreted in terms of ion chemistry driven by an enhanced rate of ionization as
outlined in the next subsection. A derivation of the ionization rate is given in Sect. 7.1. In a molecular cloud of W51C, Ceccarelli et al. (2011) derived an enhanced ionization rate by
measurements of the DCO+/HCO+ ratio of
ζH2 ~ 10-15 s-1,
which also favors a less conservative calculation of the ionization rate. These detections
encourage additional observations toward the direction of the discussed SNR-MC systems, in
particular toward the very promising candidates W49B and 3C 391.
7.1. RADEX modeling for W28
The W28 SNR is a prominent example of an association of partly resolved HESS γ-ray sources and dense, shocked molecular gas, as revealed by the molecular line observations of Nicholas et al. (2011, 2012). In particular, the cm-wave inversion transitions of ammonia (NH3) show peak intensities that coincide with the positions of peaks in γ-ray emission and radio synchrotron emission. Conventionally NH3 emission is thought to probe dense molecular gas and the relative intensities of the inversion transitions are considered to be good indicators of kinetic temperature. Nicholas et al. (2011) identified a molecular cloud Core 2 that is associated with the γ-ray source HESS J1801−233 and where the (J,K) = (3,3) inversion line of NH3 is unusually intense compared with the (1,1) and (2,2) lines of lower excitation. Moreover, they clearly detected emission in the (6,6) line and weakly in the (9,9) line at the same position. From a three-dimensional radiative transfer analysis of their most sensitive NH3 spectra, Nicholas et al. (2011) determined a best-fitting hydrogen number density of nH = 103.45 cm-3 and a kinetic temperature T = 95 K, but excluded the weak (9,9) line from the analysis and noted that the model underestimates the intensity of the (6,6) line. This analysis makes the standard assumption that the excitation is controlled by inelastic collisions of H2 with NH3 in competition with the radiative transitions. The NH3 lines in Core 2 have unusually large line widths, indicating Doppler velocity dispersions exceeding 5 km s-1. Both the relatively high kinetic temperature and large velocity dispersion might result from the dynamical interaction of the expanding SNR with a dense molecular cloud. We have considered an alternative explanation of the high excitation of NH3, which might apply in a region of enhanced cosmic-ray ionization rate. A chemical formation source for the highly excited inversion levels would naturally account for the superthermal line widths: the newly formed molecules would be translationally hot – they gain kinetic energy from the enthalpy change in the chemical formation process. If NH3 is formed in a sequence of exoergic ion-molecule reactions that are initiated by cosmic-ray ionization of hydrogen and/or nitrogen, then the formation process itself, mainly
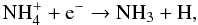 leaves the
product NH3 molecules initially in highly excited rotational states, which
relax rapidly by submm-wave rotational transitions. However, all steps in this radiative
cascade that pass through rotational states (J,K) with
J = K, leave molecules stranded in the lower inversion
level, because all these levels are highly metastable. If the rate of formation of
NH3 is high enough, compared with the rates of inelastic collisions, then the
formation process itself can account for observable populations of highly excited states.
Indeed, this mechanism of “formation pumping” can mimic a collisionally excited component
of molecular gas at a temperature >100 K, which would otherwise be needed to
populate such metastable states as (6,6) and (9,9), which lie at energies
E(J,K)/k = 408 K and 853 K above
the ground state, respectively.
leaves the
product NH3 molecules initially in highly excited rotational states, which
relax rapidly by submm-wave rotational transitions. However, all steps in this radiative
cascade that pass through rotational states (J,K) with
J = K, leave molecules stranded in the lower inversion
level, because all these levels are highly metastable. If the rate of formation of
NH3 is high enough, compared with the rates of inelastic collisions, then the
formation process itself can account for observable populations of highly excited states.
Indeed, this mechanism of “formation pumping” can mimic a collisionally excited component
of molecular gas at a temperature >100 K, which would otherwise be needed to
populate such metastable states as (6,6) and (9,9), which lie at energies
E(J,K)/k = 408 K and 853 K above
the ground state, respectively.
We have calculated models of the non-LTE excitation of NH3 in which the
formation and destruction processes are included together with the inelastic collisions
involving H2 and e− and all relevant radiative processes, through
use of the RADEX code as described by van der Tak et al.
(2007). There are too many free parameters and too many uncertainties in
collisional rates to permit a fully optimized model. However, the observed intensities of
the inversion lines of NH3 are reproduced fairly well in a model at kinetic
temperature Tk = 80 K with densities of
H2, e−, and H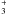 of
1000 cm-3, 0.1 cm-1, and 0.03 cm-3, respectively. The
fractional abundance of ammonia relative to H2 is 7.7 × 10-8 over a
region of path length L = 1.3 × 1019 cm = 4.2 pc, which
corresponds to the extent of the strong emission observed in the (3,3) inversion line in
cloud Core 2. The H
of
1000 cm-3, 0.1 cm-1, and 0.03 cm-3, respectively. The
fractional abundance of ammonia relative to H2 is 7.7 × 10-8 over a
region of path length L = 1.3 × 1019 cm = 4.2 pc, which
corresponds to the extent of the strong emission observed in the (3,3) inversion line in
cloud Core 2. The H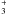 ions are included in order to account for the relative amounts of NH3 in
ortho-symmetry states, (3,3), (6,6), (9,9), and in para-symmetry states, (1,1) and (2,2),
through reactive collisions that change the nuclear-spin symmetry of the molecule. In this
model, the highly excited states are populated largely by the formation process itself,
and the inferred rate of formation is 7.7 × 10-13 ammonia
molecules cm-3 s-1. This is balanced by a destruction rate of
approximately 10-8 s-1. These rates would require that
ions are included in order to account for the relative amounts of NH3 in
ortho-symmetry states, (3,3), (6,6), (9,9), and in para-symmetry states, (1,1) and (2,2),
through reactive collisions that change the nuclear-spin symmetry of the molecule. In this
model, the highly excited states are populated largely by the formation process itself,
and the inferred rate of formation is 7.7 × 10-13 ammonia
molecules cm-3 s-1. This is balanced by a destruction rate of
approximately 10-8 s-1. These rates would require that
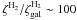 and thus imply a lower
spectral break in the cosmic ray spectrum at Elb ~ 10
MeV (see Table 3).
and thus imply a lower
spectral break in the cosmic ray spectrum at Elb ~ 10
MeV (see Table 3).
The high abundance and high excitation of NH3 observed in molecular Core 2 by
Nicholas et al. (2011) could be explained as the
result of rapid formation in an ion-driven chemistry. As discussed by Nicholas et al., the
NH3 might result from shock-driven chemistry, which would also fit well with
the other tracers of molecular shocks that they describe. The clearest way to distinguish
between these two explanations would be observations of molecular ions like
H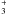 and H3O+, which would be expected to have greatly enhanced
abundances if the cosmic ray ionization rate is unusually high.
and H3O+, which would be expected to have greatly enhanced
abundances if the cosmic ray ionization rate is unusually high.
8. Conclusions and outlook
In this paper we compute ionization rates for molecular clouds known to be associated with SNRs based on the assumption that the GeV gamma ray emission from these objects is due to neutral pion decay formed in proton-proton scattering in the molecular clouds. The computed ionization rates for at least two objects are above Galactic average for molecular clouds in the most conservative scenario. Therefore ionization signatures in the form of rotation-vibration line emission from molecular ions are likely to be detected from these two objects. The spatial correlation of the detection of GeV gamma rays on the one hand and rotation-vibration line emission from molecular ions on the other hand would strongly hint at the hadronic origin of the detected GeV gamma ray excess, explaining both detections by one population of cosmic ray particles. However, there is the caveat that low energy CRs are efficient in ionizing, whereas high energy CRs are responsible for the gamma radiation. One can expect that low and high energy CRs are accelerated in the same objects, but an extrapolation of the high energy CR spectrum inferred from the gamma ray detections to low energies is not exempt from problems. Still, recent observations hint at enhanced ionization rates in molecular clouds associated with SNRs, e.g. Nicholas et al. (2011) and Ceccarelli et al. (2011), in support of the presented model.
In future work, differential propagation of the primary protons into the molecular cloud as well as the consideration of secondary ionization are planned to be implemented to offer more precise predictions concerning the ionization signatures to be expected.
Kelner & Aharonian (2008) use the CR density, while here the CR flux is used.
Acknowledgments
We would like to thank R. Schlickeiser and P. L. Biermann for helpful and inspiring discussions. We also want to thank the referee, Marco Padovani, for very helpful comments, which further improved the quality of this paper. J.K.B., S.C. and F.S. acknowledge funding from the DFG, Forschergruppe “Instabilities, Turbulence and Transport in Cosmic Magnetic Fields” (FOR1048, Project BE 3714/5-1) and from the Junges Kolleg (Nordrheinwestfälische Akademie der Wissenschaften und der Künste). J.H.B. is grateful to the Swedish
National Space Board for support. We further acknowledge the support by the Research Department of Plasmas with Complex Interactions (Bochum).
References
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2009, ApJ, 706, L1 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010a, ApJ, 718, 348 [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010b, ApJ, 722, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010c, Science, 327, 1103 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Abdo, A. A., Ackermann, M., Ajello, M., et al. 2010d, ApJ, 712, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Aharonian, F., Akhperjanian, A. G., Barres de Almeida, U., et al. 2008, A&A, 483, 509 [Google Scholar]
- Becker, J. K., Black, J. H., Safarzadeh, M., & Schuppan, F. 2011, ApJ, 739, L43 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978a, MNRAS, 182, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, A. R. 1978b, MNRAS, 182, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Beskin, V., Henri, G., Menard, F., Pelletier, G., & Dalibard, J. 2003, Accretion disks, jets and high-energy phenomena in astrophysics, École d’été de Physique des Houches, Session LXXVIII (Heidelberg: Springer) [Google Scholar]
- Biermann, P. L., Becker, J. K., Meli, A., et al. 2009, Phys. Rev. Lett., 103, 061101 [Google Scholar]
- Black, J. H. 1998, Faraday Discussions, 109, 257 [Google Scholar]
- Black, J. H. 2007, in Molecules in Space and Laboratory, ed. J. L. Lemaire, & F. Combes [Google Scholar]
- Blandford, R., & Eichler, D. 1987, Phys. Rep., 154, 1 [Google Scholar]
- Blandford, R. D., & Ostriker, J. P. 1978, ApJ, 221, L29 [Google Scholar]
- Blasi, P. 2005, in Magnetic Fields in the Universe: From Laboratory and Stars to Primordial Structures, ed. E. M. de Gouveia dal Pino, G. Lugones, & A. Lazarian, AIP Conf. Ser., 784, 407 [Google Scholar]
- Blasi, P., & Amato, E. 2012, J. Cosmol. Astropart. Phys., 1, 10 [Google Scholar]
- Bozhokin, S. V., & Bykov, A. M. 1994, Astron. Lett., 20, 503 [NASA ADS] [Google Scholar]
- Bykov, A. M., Chevalier, R. A., Ellison, D. C., & Uvarov, Yu. A. 2000, ApJ, 538, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Castro, D., & Slane, P. 2010, ApJ, 717, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Ceccarelli, C., Hily-Blant, P., Montmerle, T., et al. 2011, ApJ, 740, L4 [Google Scholar]
- Drury, L. O. 2011, MNRAS, 415, 1807 [NASA ADS] [CrossRef] [Google Scholar]
- Eichler, D., & Pohl, M. 2011, ApJ, 738, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., & Bykov, A. M. 2011, ApJ, 731, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Fermi, E. 1949, Phys. Rev., 75, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Herbst, E., & Klemperer, W. 1973, ApJ, 185, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Fields, B. D., & McCall, B. J. 2009, ApJ, 694, 257 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Blake, G. A., Goto, M., et al. 2010, ApJ, 724, 1357 [NASA ADS] [CrossRef] [Google Scholar]
- Jokipii, J. R. 1987, ApJ, 313, 842 [Google Scholar]
- Kamae, T., Karlsson, N., Mizuno, T., Abe, T., & Koi, T. 2006, ApJ, 647, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Karlsson, N., & Kamae, T. 2008, ApJ, 674, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Kelner, S. R., & Aharonian, F. A. 2008, Phys. Rev. D, 78, 034013 [NASA ADS] [CrossRef] [Google Scholar]
- Krymskii, G. F. 1977, Akademiia Nauk SSSR Doklady, 234, 1306 [NASA ADS] [Google Scholar]
- Lerche, I., & Schlickeiser, R. 1982, MNRAS, 201, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Mannheim, K., & Schlickeiser, R. 1994, A&A, 286, 983 [NASA ADS] [Google Scholar]
- McCarthy, M. C., Gottlieb, C. A., Gupta, H., & Thaddeus, P. 2006, ApJ, 652, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Mori, M. 2009, Astropart. Phys., 31, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Nath, B. B., & Biermann, P. L. 1994, MNRAS, 267, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Goicoechea, J. R., Sonnentrucker, P., et al. 2010, A&A, 521, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nicholas, B., Rowell, G., Burton, M. G., et al. 2011, MNRAS, 411, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholas, B. P., Rowell, G., Burton, M. G., et al. 2012, MNRAS, 419, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., & Galli, D. 2011, A&A, 530, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Particle Data Group 2010, J. Phys. G: Nucl. Part. Phys., 37, 075021 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 1989a, ApJ, 336, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schlickeiser, R. 1989b, ApJ, 336, 264 [NASA ADS] [CrossRef] [Google Scholar]
- Scott, J. S., & Chevalier, R. A. 1975, ApJ, 197, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Skilling, J., & Strong, A. W. 1976, A&A, 53, 253 [NASA ADS] [Google Scholar]
- Spitzer, Jr., L., & Tomasko, M. G. 1968, ApJ, 152, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Uchiyama, Y., Blandford, R. D., Funk, S., Tajima, H., & Tanaka, T. 2010, ApJ, 723, L122 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yan, H., Finkelstein, S. L., Huang, K.-H., et al. 2011, ApJ, 745, 140 [Google Scholar]
- Zirakashvili, V. N., & Aharonian, F. A. 2010, ApJ, 708, 965 [NASA ADS] [CrossRef] [Google Scholar]
- Zirakashvili, V. N., & Ptuskin, V. S. 2008, ApJ, 678, 939 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Proton SED normalization ap for each source for different lower break energies Elb and spectral indices a below the lower break energy in [erg-1 s-1 cm-2].
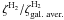 for all objects, calculated for different spectral indices a below
the lower spectral break Elb and different lower break
energies Elb.
for all objects, calculated for different spectral indices a below
the lower spectral break Elb and different lower break
energies Elb.
All Figures
 |
Fig. 1 Ionization and acceleration timescale for protons, n = 100 cm-3 and Vsh = 500 km s-1. |
| In the text | |
 |
Fig. 2 Modeled gamma ray spectrum and Fermi-LAT observational data. The modeled spectrum shown is for Elb = 1 GeV and a = 2.0, but the spectra for Elb down to 30 MeV and a down to 1.0 practically coincide with the spectrum shown due to the low cross section below 1 GeV. |
| In the text | |
 |
Fig. 3 Ionization rates versus lower break energy Elb for different spectral indices below this break: a = 2.0 (solid black line), a = 1.0 (dotted red line). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


