| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 5 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118762 | |
| Published online | 19 April 2012 | |
Research Note
Association of individual meteors with their parent bodies
1
Institut de Mécanique Céleste et de Calcul des Éphémérides – Observatoire
de Paris,
77 avenue Denfert-Rochereau,
75014
Paris,
France
e-mail: rudawska@imcce.fr
2
Arecibo Observatory, HC03 Box 53995, Arecibo
00612, Puerto Rico, USA
Received:
30
December
2011
Accepted:
16
February
2012
Context. The main problem in establishing a parent body for a meteoroid stream is the choice of a reliable meteoroid stream identification method. There are several identification methods based on three components: a dynamical similarity function, a threshold value, and meteoroid stream search algorithm.
Aims. The French Meteor Network, developed in the CABERNET project (PODET-MET), will soon provide a large amount of meteor observation data aiming to establish a parent body for each observed meteor. We therefore aim to obtain the value of the upper limit to the criteria that we can later use for data provided by the French Meteor Network.
Methods. We tested four D-criteria, using artificial data sets for which the parent body is known. We obtained threshold values and applied them to the Armagh Observatory meteor database. A detailed comparison is made between a similarity function based on the orbital elements and the function defined by quasi-invariants.
Results. We detected major meteoroid streams in the Armagh Observatory meteor database. A few meteors were also found to be associated with the asteroid 2005 UW6 – an asteroids not considered as a possible parent body for Taurid complex before. However, the problem of finding the appropriate threshold value that would work with all meteoroid streams is still open.
Key words: meteorites, meteors, meteoroids / minor planets, asteroids: general / comets: general
© ESO, 2012
1. Introduction
As soon as a meteoroid leaves its parent body, its orbit is constantly perturbed. The meteoroid endures planetary perturbations, mutual collisions, and non-gravitational (radiative) forces. Each orbit is independent but evolves in a similar way as the other particles ejected by the parent body. Hence, the existence of a structure composed of meteoroids with similar orbits (called a meteoroid stream) is maintained over a long period of time (i.e. as long as the perturbations still allows one to define the stream).
Our goal is to develop a method that allows us to perform a quick and effective search for parent bodies and apply it to each observed meteor. The outcome of this method will be a probability of association between a meteoroid and either a comet or asteroid, that will unveil the genetic relations between small bodies of the Solar System, and advance our knowledge of the origin and evolution of the entire Solar System. In this paper, we focus on determining a method to associate an individual meteor with a given parent body.
2. Orbital similarity functions
The similarity between the orbits A and B is established by a measure of the distance between these orbits. Depending on the number of parameters required to a given similarity function, the distance between two orbits might be measured in a five-dimensional phase space (Southworth & Hawkins1963; Drummond1981; Jopek1993), seven-dimensional phase (Jopek et al.2008), or other.
In our survey, we decided to test four D-criteria: DSH of Southworth & Hawkins (1963), DH of Jopek (1993), DV of Jopek et al. (2008), and DJ of Jenniskens (2008). We rejected Drummond’s criterion (Drummond1981) because of its conceptual similarity with DSH and DH. Furthermore, we also rejected criteria with dedicated application to a given stream as in Steel et al. (1991) and Asher et al. (1993). We also did not test the Valsecchi et al. criterion (1999).
Southworth & Hawkins (1963) defined the
similarity function DSH using the formula ![\begin{eqnarray} D_{\rm SH}^{2}=[e_{\rm B}-e_{\rm A}]^2+[q_{\rm B}-q_{\rm A}]^{2}+\left[2\sin\frac{I_{\rm BA}}{2}\right]^{2} \nonumber \\ +\left[\frac{e_{\rm B}+e_{\rm A}}{2}\right]^{2}\left[2\sin\frac{\pi_{\rm BA}}{2}\right]^{2} , \label{eq:Dsh} \end{eqnarray}](/articles/aa/full_html/2012/05/aa18762-11/aa18762-11-eq5.png) (1)where
eA and eB is the eccentricity, and
qA and qB is the perihelion
distance of two orbits, IBA is the angle between two orbital
planes, and πBA is the distance of the longitudes of perihelia
measured from the intersection of the orbits.
(1)where
eA and eB is the eccentricity, and
qA and qB is the perihelion
distance of two orbits, IBA is the angle between two orbital
planes, and πBA is the distance of the longitudes of perihelia
measured from the intersection of the orbits.
Jopek (1993) suggested a distance function that is a
hybrid of DSH and the Drummond function (1981) ![\begin{eqnarray} D_{\rm H}^{2} & = & [e_{\rm B}-e_{\rm A}]^{2}+\left[\frac{q_{\rm B}-q_{\rm A}}{q_{\rm B}+q_{\rm A}}\right]^{2}+\left[2\sin \frac{I_{\rm BA}}{2}\right]^{2} \nonumber \\ & & +\left[\frac{e_{\rm B}-e_{\rm A}}{2}\right]^{2}\left[2 \sin \frac{\pi_{\rm BA}}{2}\right]^{2} \cdot \end{eqnarray}](/articles/aa/full_html/2012/05/aa18762-11/aa18762-11-eq12.png) (2)An
orbit can also be described by vectorial elements: the angular momenta
h,
(2)An
orbit can also be described by vectorial elements: the angular momenta
h, 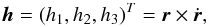 the
Laplace vector e,
the
Laplace vector e, 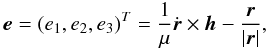 and
the orbital energy E,
and
the orbital energy E, 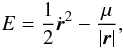 where
μ = k2, k is the Gauss
constant, whereas r and
where
μ = k2, k is the Gauss
constant, whereas r and
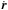 are the heliocentric vectors of the position and velocity of the meteoroid. Using those
elements, Jopek et al. (2008) proposed a new metric
for meteoroid stream identification
are the heliocentric vectors of the position and velocity of the meteoroid. Using those
elements, Jopek et al. (2008) proposed a new metric
for meteoroid stream identification 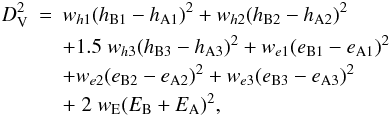 (3)where
w are weight coefficients. In the survey, we used values of weight
coefficients taken from Jopek et al. (2008).
(3)where
w are weight coefficients. In the survey, we used values of weight
coefficients taken from Jopek et al. (2008).
Jenniskens (2008) used dynamical invariants for
meteoroid stream identification, which earlier were introduced by Babadzhanov (1989). The metric DJ has the form
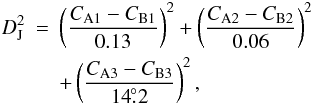 (4)where
the first invariant corresponds to the z-component of the orbital angular
momentum
(4)where
the first invariant corresponds to the z-component of the orbital angular
momentum 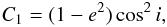 the
second one is taken from the secular model of Lidov
the
second one is taken from the secular model of Lidov 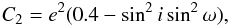 while
the third invariant is the longitude of perihelion
while
the third invariant is the longitude of perihelion
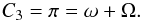 The
longitude of perihelion is used here because its changes are slower than any changes in
ω and Ω themselves.
The
longitude of perihelion is used here because its changes are slower than any changes in
ω and Ω themselves.
The association is stated if D(OA,OB) < Dc, where Dc is an assumed constant threshold below which two orbits OA and OB are considered to be similar.
There are several meteoroid stream identification methods. However, there are still unsolved problems such as the choice of cluster analysis method or the optimal threshold value of D-criterion. In this study, we focus on finding threshold values of similarity functions. We used alternatively two cluster analysis methods: a single linking method to search for showers (a meteor to meteor search), and an iterative technique to look for a parent body (a meteor to asteroid or comet search).
3. Data preparation
To test each and every function, we generate artificial data for which we know exactly the parent body, as well as the year of ejection.
The model of generation and evolution of meteoroid stream in the solar system is taken from Vaubaillon et al. (2005). We tested the meteoroid streams of the Leonids, Perseids, Draconids, and τ-Herculids.
The comet’s orbital parameters are taken from Rocher1, and integrated over an arc of orbits within three astronomical units. In the simulation, the meteoroids are released at regular time intervals (one day), with ejection velocity taken from Crifo & Rodionov (1997). The physical parameters (size of nucleus) are taken from the JPL horizons website. When a test particle crosses the ecliptic plane, its orbital parameters are saved if it is sufficiently close to the Earth (within 0.05 astronomical units from our planet). The orbital elements of each particle is then used to look for possible parent bodies, among all known comets and asteroids. We assume that the tested method works if it is able to identify the correct parent body and we determine the conditions needed to reach this goal. Table 1 shows the streams and the year of ejection chosen for this study.
Simulated datasets used to compute the criterion.
The streams and year of ejection were chosen for the following reasons:
-
Both the Jupiter family comets and long period comets are taken into account and can be compared.
-
Only meteor showers with identified trails are considered; as a consequence, the simulated data are close enough to the Earth to be considered as impacting the planet. The distance between the trajectory of the Earth and that of the particle is 0.01 astronomical units.
-
A wide range of number of revolutions are considered, allowing one to study the robustness of the methods with the dynamical age (perturbation) of the stream.
 |
Fig. 1 Threshold values found for the tested dissimilarity functions ∗ DSH, ° DH, + DV, and × DJ. |
4. Searching for an upper limit to the D-criteria
Meteoroid stream identification method is sensitive to the adopted threshold value Dc. The threshold value itself depends on the orbital evolution of the meteoroid stream whose origin we wish to determine. Thus, for more dispersed streams, we need to a apply higher threshold value than for less perturbed ones.
We determine which value of the threshold, a given method requires to correctly identify a parent body for 70% (also 80% and 90%) of the generated sample of meteors. The results are plotted in Fig. 1, where the outcomes of 50% and 60% of the identifications have also been included.
In comparison to our results for τ Herculids, the values of the threshold is smaller for the rest of the stream samples. which means that τ Herculids is a more dispersed stream than the Draconids. Moreover, the τ Herculids stream is much more perturbed than the 1767 Leonids trail, for which we obtained the lowest threshold values for the similarity functions that we used.
Since DSH and DH functions are conceptually similar, we expected to receive comparable results. The esults plotted in Fig. 1 confirm this. The threshold values for these two functions are slightly different – DH is a little bit smaller than DSH. A significant difference between them is visible for τ Herculids.
The question is now how do these results refer to real data from meteor observations?
5. Armagh Observatory meteor database
The Northern Irish meteor network (Atreya & Christou 2008) consists of three Watec 902DM2s cameras at Armagh Observatory, and one at Bangor, approximately 73 km away, to perform double station observations. The two designated double-station cameras are equipped with 6 mm, F0.8 (medium angle) Computar lens, while the two remaining cameras at the Armagh Observatory are equipped with 3.8 mm, F0.8 (wide-angled) Computar lens. The pixel resolution is 0.08 degrees for the medium angled camera and 0.14 degrees for a wide-angled camera.
SPARVM (Software for Photometric and Astrometric Reduction of Video Meteors), developed during the Ph.D. work at Armagh Observatory of Atreya (2009) was used to reduce the double station meteors captured from this network. Various criteria such as the number of stars available for astrometric calibration, residuals of the third degree polynomial astrometric fitting, and deviation from the original pointing of the cameras used for the astrometric calibration of the images. The astrometric uncertainty in themeteor position is estimated to be 0.3 pixel and the uncertainty in the transformation from pixel coordinates to equatorial coordinate systems (RA, Dec) is 0.2 pixels. The double station meteors are reduced using Ceplecha (1987) method and the orbital elements are computed using SPICE2.
The current Armagh Observatory meteor database contains meteors observed from 25 June 2005 until 31 December 2007. However, the videos from Bangor were corrupted between 19 August 2007 and 8 December 2007, thus there are no double station meteors during this time interval. There are 457 meteoroids orbits in the database, and for the meteors recorded by more than one camera, the average solutions computed from all possible cameras are shown. The double station database contains the unique ID, the date and time of the meteor occurrence, RA and Dec of the radiant, V∞, and finally the orbital elements qo, a, e, i, Ω, ω, and Mo.
Upper limit to the threshold values for tested similarity functions.
 |
Fig. 2 Associations detected by our survey plotted as a function of U and cosθ defined in Valsecchi et al. 1999. The results shows associations found in the m-m search with DV function. The upper solid line is the cutoff for Earth-intersecting parabolic orbits. The lower line represents objects on Aten-like orbits, a < 1 AU. |
6. Results
The previously determined thresholds (Table 2) were used to analyse a sample of the Armagh Observatory meteor data (Atreya2009). This is the first study of this kind for this database. We extracted 433 meteor orbits, removing hyperbolic orbits. We then looked for associations in two steps. First, we searched for a parent body for each meteor (m-pb search). In this case, we hereafter talk about a connection. Second, we looked for the associations between different meteors with a single-neighbour linking technique (m-m search). In this case, we hereafter talk about an association. Here we compare the results obtained using the DSH and DV functions.
The orbits of meteoroids are constantly perturbed because they are affected by planetary perturbations and non-gravitational (radiative) forces. Depending on the threshold value, one meteor might not be connected with its parent body using an m-pb search. Fortunately, each meteoroid orbit is independent but evolves in a way similar to the other particles ejected by the parent body. Hence, the meteoroid structure is maintained over a long period of time, which mainly depends on the occurrence of close encounters with giant planets. The m-m search then allows one to find the association of a given meteoroid with its stream, and hence with its parent body.
Detected major meteoroid streams in the Armagh meteor sample (see text for more details).
Table 3 shows the list of the major streams detected in the Armagh meteor sample. The second and third columns of the table gives the number of members identified by two functions: DSH and DV (using the m-m search). The fourth column gives the number of members MC commonly found by the two functions. The fifth column provides the number of meteors (from the m-m search) correctly associated with an already known parent body (in m-pb search). For example, in an m-m search, using DV we found 18 Perseids (Dc = 8.87 × 10-4), while with DSH (Dc = 8.4010 × 10-2) we found only 7. These 7 meteors were also identified by DV. However, in an m-pb search with the DSH function, only 3 meteors pointed towards comet 109P/Swift-Tuttle as a parent body. The same search with the DV function shows a connection with the comet for 6 meteors.
Using the DSH with the m-m search, we detected 28 associations (i.e. potential showers) where only 5 of them included more than 5 members. Using the DV function, 46 associations were detected, and 13 of them have more than 5 members.
We found an interesting group of Taurids, which includes 25 members. Fourteen of them show association with asteroids that are already considered as the possible parents bodies of the Taurid complex (e.g. Oljato, 2007 RU17 or 2003 WP21). For four meteors (two observed in 2005 Nov. 12, and 2006 Nov. 9 and Nov. 11) we found a connection with asteroid 2005 UW6. Those meteor orbital elements, the Tisserand coefficient, and parent body candidates (for all of which DV < Dc) are listed in Table 4. It is possible that three other meteors might have a similar link with this asteroid. This means that we might have identified one additional Taurids’ parent body, which had never been considered before. However, further study is needed to confirm this association.
In one case (namely o4), the parent body of one of the meteors appeared to be asteroid 5025 P-L. 5025 P-L is an asteroid that is associated with the Taurid complex (Asher et al. 1993; Babadzhanov 2001). This suggests that this group might be part of one of Taurid substreams. Results for the other groups are inconclusive.
7. Discussion
Using the DV criterion we found 7 other associations, which are indicated in Fig. 2 and marked by open circles. The associationes o1 and o2 are close to the Perseid stream, and were observed during typical Perseid activity, whereas o6 is located close to the Orionid stream. This suggests that if the threshold value for DV function were slightly higher in the m-m search the association o1 and o2 would be related to the Perseids, and o6 to the Orionids.
We might then be tempted to simply increase the threshold. However, four other groups (o3, o4, o5, and o7) each found connections with several asteroids as pointed out in Table 4. In an attempt to determine one unique parent body, one might be tempted to simply decrease the threshold, which is in contradiction with the previous point.
As a consequence, it seems hard to determine a unique threshold that is suitable for all showers. In our approach, we decided to adopt a rather conservative point of view and use the threshold obtained in Sect. 4. The main reason is that these thresholds allow us to identify the main showers (e.g. Perseids), and a closer (manual) look allows us to decide whether a close association also belongs to the stream. In the case of a minor shower, many different parent bodies were found, allowing us to identify common potential parent bodies, such as 2005 UW6 as previously mentioned. In other words, this is a compromise between too many and too few parent body candidates.
Meteors in Armagh Observatory meteor data associated with asteroid 2005 UW6.
8. Conclusion
We have compared four dissimilarity functions to determine a threshold value that can help our search for the parent body of meteor observed by the French Meteor Network, developed in the CABERNET project (PODET-MET). We obtained threshold values for four criteria using artificial data from numerical simulations and applied them to the Armagh Observatory meteor database.
Finally, we compared our results for two dissimilarity functions DSH (Southworth & Hawkins1963) and DV (Jopek et al.2008). We detected five major meteoroid streams using both the DSH and DV methods. The DV function enabled us to find a few other associations that had not been identified using the DSH method. The reason for this is the rather rigorous threshold value of DSH that we adopted. On the other hand, the threshold value of DV chosen here is in a good agreement with the result obtained by Rudawska (2010).
We did not obtain one specific value of threshold that would fit all cases. The ideal threshold depends on the sample, the stream we search, and the cluster analysis method. Long period streams appear to be most easily identified using a high threshold value, whereas Jupiter-family streams need a lower value. However, the high concentration of possible parent bodies allows us to identify a common potential parent that may strengthen the case for an association. One interesting case that we found this way is the connection between the Taurids and asteroid 2005 UW6. It suggests that this asteroid might be considered as a possible parent body of the Taurid complex. No observation was conducted in 2007 to confirm this. It would be extremely instructive to obtain further observations of meteors from (especially) the period between November 9 and 12 in order to ascertain whether there is any association with asteroid 2005 UW6. The future high accuracy observations that
are to be performed with the CABERNET camera will help us to answer this question.
References
- Asher, D. J., Clube, S. V. M., & Steel, D. I. 1993, MNRAS, 264, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Atreya, P. 2009, Ph.D. Thesis, The Queens Univ. of Belfast [Google Scholar]
- Atreya, P., & Christou, A. 2008, EM&P, 102, 263 [NASA ADS] [Google Scholar]
- Babadzhanov, P. B. 1989, 3. International Symposium on Asteroids, Comets, Meteors, 4, 4 [Google Scholar]
- Babadzhanov, P. B. 2001, A&A, 373, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceplecha, Z. 1987, Bull. Astron. Inst. Czechoslovakia, 38, 222 [Google Scholar]
- Crifo, J. F., & Rodionov, A. V. 1997, Icarus, 127, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Drummond, J. D. 1981, Icarus, 45, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Jenniskens, P. 2008, Icarus, 194, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J. 1993, Icarus, 106, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Jopek, T. J., Rudawska, R., & Bartczak, P. J. 2008, EM&P, 102, 73 [Google Scholar]
- Rudawska, R. 2010, In Ph.D. Dissertation, A. M. University, Poznan (in polish) [Google Scholar]
- Southworth, R. B., & Hawkins, G. S. 1963, Smithson. Contr. Astrophys., 7, 261 [Google Scholar]
- Steel, D. I., Asher, D. J., & Clube, S. V. M. 1991, MNRAS, 251, 632 [NASA ADS] [Google Scholar]
- Valsecchi, G. B., Jopek, T. J., & Froeschle, C. 1999, MNRAS, 304, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Vaubaillon, J., Colas, F., & Jorda, L. 2005, A&A, 439, 751 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Detected major meteoroid streams in the Armagh meteor sample (see text for more details).
All Figures
 |
Fig. 1 Threshold values found for the tested dissimilarity functions ∗ DSH, ° DH, + DV, and × DJ. |
| In the text | |
 |
Fig. 2 Associations detected by our survey plotted as a function of U and cosθ defined in Valsecchi et al. 1999. The results shows associations found in the m-m search with DV function. The upper solid line is the cutoff for Earth-intersecting parabolic orbits. The lower line represents objects on Aten-like orbits, a < 1 AU. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


