| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A60 | |
| Number of page(s) | 9 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201118635 | |
| Published online | 27 April 2012 | |
Variation in sunspot properties between 1999 and 2011 as observed with the Tenerife Infrared Polarimeter
1 Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6, 79104 Freiburg, Germany
e-mail: rrezaei@kis.uni-freiburg.de; wolfgang@kis.uni-freiburg.de
2 Instituto de Astrofísica de Canarias (CSIC), Vía Lactéa, 38205 La Laguna, Tenerife, Spain
3 Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
e-mail: cbeck@iac.es
Received: 13 December 2011
Accepted: 21 February 2012
Aims. We study the variation in the magnetic field strength and the umbral intensity of sunspots during the declining phase of the solar cycle No. 23 and in the beginning of cycle No. 24.
Methods. We analyze a sample of 183 sunspots observed from 1999 until 2011 with the Tenerife Infrared Polarimeter (TIP) at the German Vacuum Tower Telescope (VTT). The magnetic field strength is derived from the Zeeman splitting of the Stokes-V signal in one near-infrared spectral line, either Fe i 1564.8 nm, Fe i 1089.6 nm, or Si i 1082.7 nm. This avoids the effects of the unpolarized stray light from the field-free quiet Sun surroundings that can affect the splitting seen in Stokes-I in the umbra. The minimum umbral continuum intensity and umbral area are also measured.
Results. We find that there is a systematic trend for sunspots in the late stage of the solar cycle No. 23 to be weaker, i.e., to have a smaller maximum magnetic field strength than those at the start of the cycle. The decrease in the field strength with time of about 94 Gyr-1 is well beyond the statistical fluctuations that would be expected because of the larger number of sunspots close to cycle maximum (14 Gyr-1). In the same time interval, the continuum intensity of the umbra increases with a rate of 1.3 (±0.4)% of Ic yr-1, while the umbral area does not show any trend above the statistical variance. Sunspots in the new cycle No. 24 show higher field strengths and lower continuum intensities than those at the end of cycle No. 23, interrupting the trend.
Conclusions. Sunspots have an intrinsically weaker field strength and brighter umbrae at the late stages of solar cycles compared to their initial stages, without any significant change in their area. The abrupt increase in field strength in sunspots of the new cycle suggests that the cyclic variations are dominating over any long-term trend that continues across cycles. We find a slight decrease in field strength and an increase in intensity as a long-term trend across the cycles.
Key words: Sun: photosphere / Sun: magnetic topology / sunspots / Sun: evolution
© ESO, 2012
1. Introduction
Morphological and physical studies of sunspots have been described for several decades (Bray & Loughhead 1964). It was already known half a century ago that larger umbrae are darker and show higher magnetic field strength. Albregtsen & Maltby (1978) first reported a systematic variation in the umbral intensity in the infrared as a function of the solar cycle, with darker umbrae appearing in the early phase of the cycle (see also Albregtsen & Maltby 1981). Adjabshirzadeh & Koutchmy (1983) attributed this variation to the change in the number of umbral dots within the solar cycle. This was dismissed by Albregtsen et al. (1984), who showed that the measured variations cannot be solely caused by umbral dots. Subsequent studies of the umbral intensity and the magnetic field strength established a relation between the continuum intensity and the magnetic field strength in sunspot umbrae (Kopp & Rabin 1992; Martinez Pillet & Vazquez 1993): the greater the field strength, the lower the intensity. While new high-resolution observations are still consistent with this empirical relation, no clear explanation has been provided (see, however, Schüssler et al. 1994).
The variation in the field strength of sunspots in the last two cycles has been the subject of several studies (Livingston 2002; Penn et al. 2003; Norton & Gilman 2004; Penn & MacDonald 2007; Leonard & Choudhary 2008; Schad & Penn 2010). Livingston (2002) measured the separation of the σ-components of Stokes-I of the Fe i line at 1564.8 nm, which is a Zeeman triplet with an effective Landé-factor of 3.0, and concluded that sunspots in cycle No. 23 were intrinsically weaker than those in cycle No. 22. A similar data set was also used in subsequent works (Livingston et al. 2006; Penn & Livingston 2011). These authors found that the field strength of sunspots was stronger at the beginning of cycle No. 22 than at its end. Although the magnetic sensitivity of the infrared Fe i 1564.8 nm line is high (Rüedi et al. 1995), the influences of scattered light and line blends in the intensity profiles on the measurement motivates one to employ more accurate methods to derive the field strength. It is not clear how dynamo theory can explain such cyclic dependency (e.g., Ossendrijver 2003).
In this contribution, we used spectropolarimetric data in the Fe i 1564.8 nm line and other near-IR lines to evaluate the cyclic variation in the magnetic field strength of sunspots. We used full Stokes spectra to determine the magnetic field strength rather than solely the intensity profiles. The advantage with respect to the stray light contamination is that the intensity in the quiet Sun (QS) surroundings is higher than in the umbra, whereas exactly the opposite relation holds for the polarization signal. Therefore intensity spectra in the umbra are contaminated by contributions from the QS, but the splitting of Stokes-V is not. Another advantage of this sample compared to the previously mentioned works is that the majority of sunspots were observed with an active image correction; i.e., the spatial resolution of our data set is better than observations prior to the advent of correlation trackers or adaptive optics (AO).
Section 2 describes the observations used. The data analysis methods are explained in Sect. 3. Section 4 gives the results, together with numerical tests. The findings are discussed in Sect. 5. Section 6 provides the conclusions.
2. Observations
We analyzed a sample of 231 sunspots observed from 1999 to 2011 with the Tenerife Infrared Polarimeter (TIP-I and TIP-II, respectively; Martínez Pillet et al. 1999; Collados et al. 2007). All observation were carried out at the German Vacuum Tower Telescope (VTT, Schröter et al. 1985). The observed maps usually cover a sunspot and the surrounding QS area. For some of the data taken with TIP-I using its small field of view (FOV) of about 30′′, the sunspots’ penumbra was not fully covered. Each data set consists of full Stokes profiles in magnetically sensitive infrared lines such as Fe i 1564.8 m, Fe i 1089.6 nm, or Si i 1082.7 nm. Table 1 summarizes the atomic parameters of the selected spectral lines. Out of the 231 maps, 99 were observed at 1.56 μm and 84 at 1.1 μm. The remaining 48 maps mainly come from the earliest observations with TIP-I and were taken in some uncommon wavelength ranges, often covering molecular lines. These data could therefore not be used without considerable effort. We thus only selected those observations in which one of the three spectral lines listed in Table 1 was recorded. That amounted to 183 full Stokes sunspot maps covering the descending phase of cycle No. 23 and the rise of cycle No. 24.
The low temperature of umbrae allows certain molecules to form. As a result, the umbral profiles are usually contaminated with molecular blends (e.g., the FTS atlas of umbral profiles of Wallace et al. 2000). Figure 1 shows examples of umbral Stokes-I and V profiles at 1.56 μm for two different heliocentric angles (μ = 0.58 and 0.76). The difference in the continuum level of the Stokes-I profiles is real. As seen in this figure, there are several strong blends around the Fe i 1565.2 nm line that corrupt not only the intensity profile but also the Stokes-Q/U/V profiles of this line (bottom panel, Fig. 1). For this reason, we decided not to use the Fe i 1565.2 nm line. The molecular blends are, however, useful for determining of atmospheric stratifications in inversions of umbral spectra (e.g., Mathew et al. 2003). There are several blends around the Fe i 1564.8 nm line as well (e.g., Livingston et al. 2006, their Table 1). The main blend in this line is a CO line to the blue of the line center wavelength. It is, however, weaker than the OH blends near the Fe i 1565.2 nm line.
 |
Fig. 1 Sample of two umbral profiles. The solid (dashed) line corresponds to a sunspot at μ = 0.58 (0.76). The continuum intensity of the quiet Sun profiles corresponding to each of them is unity. The short vertical lines mark four OH spectral lines, while the long vertical line denotes the Fe i 1564.8 nm line. Top: Stokes-I, bottom: Stokes-V. |
Atomic properties of the observed spectral lines (Nave et al. 1994).
The spatial and spectral resolution, as well as the rms noise level, is different for each map. A careful analysis of the individual sunspots was done to take the diversity of the data into account. While the data until 2005 were recorded using a correlation tracker for real-time image correction (CT, Ballesteros et al. 1996), the Kiepenheuer-Institute adaptive optics system (KAOS, von der Lühe et al. 2003) was utilized for all later data to improve the spatial resolution.
The old TIP-I camera (Martínez Pillet et al. 1999) was used until mid 2006, providing a slit length of 27 arcsec at a spatial sampling of 0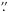 36 per pixel. The integration of the new TIP-II camera (Collados et al. 2007) increased the slit length and at the same time doubled the spatial and spectral resolution because of the larger CCD chip and the smaller pixel size. Examples of data sets with the old and new TIP systems are shown in Fig. 2. The top panel shows a TIP-I data set with CT correction, while the bottom panel shows a data set recorded with TIP-II taken with AO correction. An overview of the data up to 2009 is available online in the TIP archive1. The header of each file contains information about, among other things, the location of the spot, scanning steps, and the integration time. This allowed us to retrieve the position and dimension of the sunspots. We used this information to calculate the area of the umbra and the sunspot as a whole. The calibration of the data as well as the cross-talk correction was performed in the same manner as in Schlichenmaier & Collados (2002).
36 per pixel. The integration of the new TIP-II camera (Collados et al. 2007) increased the slit length and at the same time doubled the spatial and spectral resolution because of the larger CCD chip and the smaller pixel size. Examples of data sets with the old and new TIP systems are shown in Fig. 2. The top panel shows a TIP-I data set with CT correction, while the bottom panel shows a data set recorded with TIP-II taken with AO correction. An overview of the data up to 2009 is available online in the TIP archive1. The header of each file contains information about, among other things, the location of the spot, scanning steps, and the integration time. This allowed us to retrieve the position and dimension of the sunspots. We used this information to calculate the area of the umbra and the sunspot as a whole. The calibration of the data as well as the cross-talk correction was performed in the same manner as in Schlichenmaier & Collados (2002).
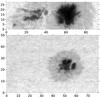 |
Fig. 2 Example of TIP scans. Top: sunspot on 24 May 2001, recorded in Fe i 1089.6 nm with CT correction. Bottom: sunspot on 17 July 2011, recorded in Si i 1082.7 nm with AO image stabilization. Tick marks are in arcseconds. |
3. Data analysis
For each data set, an average QS profile was calculated using a region in the FOV outside of the penumbra. We used two of the spectral lines covered in each wavelength range to determine the spectral dispersion for each map. Then, the rms noise of the polarization signal, σ, was estimated in a continuum band. After that, the amount of separation between the two lobes of Stokes-V was measured for all locations on the map with a maximum Stokes-V amplitude larger than 12 σ. “Lobes” were defined as local maxima in the polarization signal of Stokes-V that a) were larger than the five wavelength pixels to the left and right and b) had an amplitude above the 12-σ level (cf. Beck 2006; Rezaei et al. 2008). This conservative threshold ensures that we only analyze clear antisymmetric Stokes-V profiles with a drawback that we have some gaps in the maps in the neutral lines of Stokes-V where the polarization signal strongly decreases. Because there are only a few data sets close to the limb (μ < 0.5), the neutral line only passed through the umbra in a couple of cases. In particular, the missing values in the neutral line do not affect our results concerning the maximum magnetic field strength in umbrae. Whenever the profile exhibited more than two lobes, the two lobes most separated in wavelength were selected. Finally, we constructed maps of the magnetic field strength from the determined location of the two lobes in the Stokes-V profiles and the spectral dispersion in the strong field approximation (Stix 2002; Landi degl’Innocenti & Landolfi 2004): 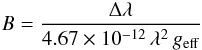 (1)where λ and Δλ are in nm and B is in Gauss. In the strong field limit, the separation of the two lobes is independent of the inclination angle, hence of the location of the spot on the disk. The signal amplitude is, however, affected by the inclination angle, but we do not use it here. In a plot of the maximum field strength vs. cosine of the heliocentric angle (not shown here), we did not find any significant trend.
(1)where λ and Δλ are in nm and B is in Gauss. In the strong field limit, the separation of the two lobes is independent of the inclination angle, hence of the location of the spot on the disk. The signal amplitude is, however, affected by the inclination angle, but we do not use it here. In a plot of the maximum field strength vs. cosine of the heliocentric angle (not shown here), we did not find any significant trend.
The uncertainty of the estimated field strength was calculated using standard error propagation applied to Eq. (1). The main source of uncertainty stems from the measurements of the separation of the lobes, whereas the effective Landé factor and the rest wavelength are known with high accuracy. We assumed an error of 0.1 pixels in the derivation of the position. This translates then into a (random error) σB of about 20 to 60 G, depending on the wavelength range and the dispersion of the spectra. The value is comparable to the formal error attributed to field strength in inversions of the Fe i line at 1564.8 nm (Beck et al. 2007). There are also systematic errors caused by gradients of the field strength with height in the atmosphere. With a typical measured vertical gradient of the magnetic field strength of 1−2 G km-1 (e.g., Schmidt & Balthasar 1994; Westendorp Plaza et al. 2001), this systematic error amounts to some 20−40 G difference in the measurements between μ = 1 and μ = 0.5.
Besides the maps of the magnetic field strength, we also determined the continuum intensity and the area of each sunspot. To define the umbra and penumbra, we produced at first an umbral mask using a variable threshold in continuum intensity. Using a fixed threshold did not produce satisfactory results because the umbral contrast varies with wavelength (e.g., Mattig 1971; Albregtsen & Maltby 1981; Chapman & Meyer 1981; Maltby et al. 1986; Tritschler & Schmidt 2002). Using those (initial) masks, we constructed contours for the umbra and penumbra manually. Light bridges were excluded from the umbral masks. In some data sets, such as shown in the top panel of Fig. 2, the penumbra was not covered completely, so the penumbral area and the total sunspot area are underestimated in a few cases. The continuum intensities were not corrected for the limb-darkening effect. There was no significant trend in the minimum continuum intensity vs. the cosine of the heliocentric angle.
A code was attributed to each spot describing its type in terms of complexity, completeness, and similar morphological characteristics (see Sect. 4.1). In the case of complex active regions (e.g., the top panel of Fig. 2), only the largest spot in the map was selected.
The continuum intensity sample is not fully homogeneous because we have the continuum intensity in two different wavelength windows (1.1 and 1.6 μm). As mentioned above, sunspots have higher contrasts at shorter wavelengths. We multiplied the continuum intensity of sunspots at 1.1 μm with a factor of 1.3 to have the same scale as in 1.6 μm, both in scatter plots and histograms (Sect. 4). This coefficient of relative umbral intensities of 1.3 corresponds to an umbral temperature of about 4200 K. The intensities in each wavelength range were normalized to the intensity in the QS surroundings of the sunspot. For a temperature of about 6000 K in the QS, the ratio of continuum intensities in the Planck curve is IQS(λ = 1100 nm)/IQS(λ = 1565 nm) ~ 2.77; i.e., the intensity at the shorter wavelength has to be multiplied by 2.77 to be normalized to IQS(λ = 1565 nm). This yields a relative umbral intensity Iumbra(λ = 1100 nm)/IQS(λ = 1565 nm) = 1/1.3·2.77 ~ 2.13, when the umbral intensity at 1565 nm is set to unity. A ratio of 2.13 in the intensities I(λ = 1100 nm)/I(λ = 1565 nm) is obtained in the Planck curve for T = 4165 K. The value fits to previous determinations of umbral temperatures (e.g., Maltby et al. 1986; Collados et al. 1994; Mathew et al. 2003; Solanki 2003; Sánchez Cuberes et al. 2005; Beck 2008).
4. Results
4.1. Empirical relations
Figure 3 shows the scatter plot of the minimum umbral intensity vs. the maximum field strength, Bmax. By “minimum” we mean the average of the ten pixels with the lowest intensity. Similarly by Bmax, we mean the average of the ten pixels with the largest field strength. These pixels partly overlap those with the lowest intensity. Different symbols in the plot indicate morphological details of each sunspot. Triangles denote sunspots whose penumbra touches the map border, although they have a complete umbra. Circles mark sunspots in complex active region. This group of sunspots sometimes have extended or incomplete penumbrae.
 |
Fig. 3 Variation in the minimum continuum intensity in the umbra as a function of maximum magnetic field strength. The 1.1 μm data were multiplied by a factor 1.3. Red and black symbols mark the 1.1 and 1.6 μm data, respectively. P-incomplete and U-incomplete mark sunspots whose penumbra and umbra were not fully covered in the map. The solid line shows a least-squared fit, and the dashed lines indicate the 1σ interval. Numbers in parenthesis denote the 1σ uncertainty. |
 |
Fig. 4 Variation in the minimum continuum intensity in the umbra as a function of area. Top: total sunspot area, bottom: umbral area. The solid lines indicate bisector least-squared fit to all data points expect complex sunspots (circles). The dashed lines show the 1σ interval. Symbols are like Fig. 3. |
 |
Fig. 5 Variation in the maximum magnetic field strength in the umbra as a function of area. Top: total sunspot area, bottom: umbral area. Symbols are like Fig. 3. Linear fits are similar to Fig. 4. |
 |
Fig. 6 Variation in the maximum magnetic field strength (left), minimum continuum intensity (midddle), and umbral area (right) vs. time. Symbols show the individual sunspots while the blue filled circles mark the annual averages. The linear fits was performed for individual data points between the two vertical lines. The dashed vertical lines mark maximum and minimum of cycle 23. Symbols are like in Fig. 3. |
As a result, a triangle, for instance, does not exclude the spot belonging to a complex active region. Reverse triangles mark those objects that are either a pore or more like a protospot: they do not have a fully fledged penumbra. In rare cases, the map does not fully cover the umbra. These objects are marked with asterisks. As seen in Fig. 3, there is a tight correlation between the continuum intensity and the field strength. The classical or Pearson correlation (Cp), as well as the nonparametric Spearman correlation coefficients (Cs), were calculated (Press et al. 1992). We find correlation coefficients of Cp = 0.80 and Cs = 0.76. The offset of 11% (solid line, Fig. 3) above unit continuum intensity for B ≡ 0 G matches stray light estimates in the umbra well, where stray light levels between 8% and 15% were found for similar data (e.g., Rezaei et al. 2007; Beck 2008; Beck et al. 2011).
Figure 4 shows the variation in minimum continuum intensity vs. area. In this figure as well as Fig. 5, we do not show the error bars because they are usually smaller than the size of the symbols. There are a few points that are off the main trend. A close inspection showed that those sunspots belong to complex active regions and have extended penumbrae. If we omit their extended penumbrae, their areas shrink significantly. As seen in Fig. 4, there is an anticorrelation between the minimum continuum intensity and umbral (sunspot) area. The correlation coefficients are Cp = –0.43 and Cs = –0.40 (Cp = –0.48 and Cs = –0.57), respectively. This is consistent with earlier findings: larger umbrae are intrinsically cooler. The linear fits in Figs. 4 and 5 are bisector fits. That means we assume that both variables are independent (Akritas & Bershady 1996). For these four fits, the complex sunspots (circles) were excluded. A standard least-square fit results in shallower slopes. Assuming a linear relation between the Bmax and minimum intensity with the sunspot/umbral area is equivalent to the relation used by other authors (e.g., Schad & Penn 2010), who fit a quadratic function between these quantities and the umbral radius.
Figure 5 shows the variation in the Bmax vs. area. The trend is clearer with the sunspot area than the umbral area. We find a positive correlation between the maximum field strength and the umbral (sunspot) area (Fig. 5). For Bmax vs. umbral (sunspot) area, we find Cp = 0.26 and Cs = 0.20 (Cp = 0.25 and Cs = 0.39), respectively. If we skip the complex sunspots with the largest area, the correlation coefficient increases significantly. We created two random vectors of the same size as our TIP sample and calculated their correlations. After repeating this experiment for 1000 times, the standard deviation both for the Pearson and Spearman correlations were σC = 0.07, so the found correlation coefficients are well above the distribution of purely random numbers.
Part of the scatter in Figs. 4 and 5 is real because there is a diversity in properties of simple and complex sunspots, as well as differences between fully developed and forming sunspots (Collados et al. 1994). As discussed in Sect. 3, the separation of the two lobes of Stokes-V in the strong-field regime is not a function of the inclination angle nor the heliocentric angle.
4.2. Temporal evolution
Figure 6 shows the temporal evolution of the maximum field strength, the minimum continuum intensity, and the umbral area. A decrease in the magnetic field strength is seen in the diagram (left panel). We examined correlations to check for any systematic trend of Bmax with the solar cycle. To this extent, we selected the time span between the two dashed lines in Fig. 6. The correlation coefficient for the magnetic field strength is about Cp = –0.57 and Cs = –0.43 for the Pearson and Spearman definitions, respectively. This indicates the significance of the decrease in magnetic field strength in the declining phase of solar cycle No. 23.
We used a Bayesian method (e.g., Gregory & Loredo 1992; Gregory 2005) to fit a straight line to the individual data points between 2001 and 2009. To this end, a Markov Chain Monte Carlo (MCMC) method was utilized with one million iterations (Patil et al. 2010). This resulted in a linear fit with an offset of 2915 ( ± 30) G and a slope of –94 ( ± 7) Gyr-1. The solid line in Fig. 6 shows the best-fit line. The dashed line shows a standard least-square linear fit whose slope is –88 ( ± 14) Gyr-1. The extension of the solid line (Fig. 6) to 2012 demonstrates that the decrease in the field strength does not continue in cycle No. 24. If we use the range of 2000 to 2009 instead, the slopes drop to –59 ( ± 8) Gyr-1 and –56 ( ± 14) Gyr-1 for the Bayesian and least-square methods, respectively.
As seen in the middle panel of Fig. 6, there is a weak tendency in sunspots such that the umbra is brighter at the end of the cycle. Both linear fits have a common slope of 1.3 ( ± 0.4)% Ic yr-1. From the relation between the umbral intensity and Bmax (Sect. 4.1), one expects to find an increase in the continuum intensity because we find a decrease in the field strength. The amount of decrease of Bmax during the declining phase is about 750 G, leading to a predicted increase in the minimum intensity of some 14% of Ic. As a result, the expected slope for the temporal evolution of minimum intensity based on the empirical relation between Bmax and intensity (Fig. 3) is about 1.8% yr-1, consistent with the linear fit within the 1σ uncertainty range.
The correlation coefficient of the umbral area vs. time (right panel, Fig. 6) in the same time interval is Cp = 0.05 and Cs = 0.12 for the Pearson and Spearman correlation coefficients, respectively. It stays insignificant for the deprojected area of the umbra. The corresponding coefficients for the sunspot area are Cp = –0.06 and Cs = –0.03, respectively, so such correlations are not significant (recall the limit of σC = 0.07 for purely random variables, Sect. 4.1). That means that within the scatter and statistics of our data, there is no systematic change in the umbral size with the solar cycle.
4.3. Distribution of parameters
The probability density function (PDF) of the maximum field strength is shown in Fig. 7. A Kolmogorov-Smirnov test was applied to find the best PDF for the data (Press et al. 1992). This test allows one to reject that the observed and fit distributions are significantly different. A normal distribution with an average field strength of 2.6 kG and a variance of 0.3 kG reproduces the observed PDF of the field strength well. There is no umbra with a magnetic field strength below about 1.8 kG. The assumed normal distribution thus exceeds the observed PDF for field strengths below that value. In the limit of extremely large field strengths above about 3 kG, the best-fit PDF also does not matches the observed one perfectly. This will presumably be caused by the poor statistics of those few umbrae with a maximum field strength above 3 kG in the observations, and the selection of the largest sunspot in complex active regions.
 |
Fig. 7 Probability density function of the maximum magnetic field strength. The red curve is the best-fit normal distribution to the data using a Bayesian method. |
4.4. Numerical experiment
To investigate the influence of noise and systematic effects on the derived slope of Bmax with the phase of the solar cycle, we performed three numerical tests. This allowed us to evaluate the amount and importance of spurious signals in our results. In particular, we tried to evaluate the significance of the trend of field strength with the phase of the solar cycle (–94 Gyr-1).
First experiment:
assume that the maximum magnetic field strength of sunspots has a constant distribution at any moment of a solar cycle, i.e., the PDF of the maximum field strength, Bmax, is the same for each year and is given by Fig. 7. The number of sunspots close to a solar maximum is about 100 times more than at the solar minimum (cf. Fig. 8). Therefore, the statistics of sunspots around the time of maximum activity is better and will sample the PDF correctly, whereas close to minimum activity strong deviations from the true PDF may occur because of the sparse sample. This can lead to an apparent temporal trend in field strength caused purely by the variation of the sample size, where both a decrease or an increase in the field strength can result. To reject the hypothesis that the measured systematic variation of –94 Gyr-1 is caused only by the large number of sunspots close to the maximum of a cycle and the low number close to the minimum (Fig. 8), we performed the following test.
Figure 8 shows the yearly sunspot number from the Solar Influences Data Center (SIDC) during cycle No. 23 and the early years of cycle No. 24 (SIDC-team 2011). For each year from 1999 through 2009, we created a sample of Bmax, according to the observed distribution of field strengths (Fig. 7). The size of the sample population was set to the annual sunspot number, making the PDFs of the the field strength in individual years roughly identical within the statistical fluctuations. We then analyzed this synthetic temporal sample in the same manner as the real data. Using both the Bayesian (Sect. 4.2) and the least-square methods, we fit a straight line to measure any change of the mean of Bmax. The test was repeated 100 times. The average and rms of the resulting slopes were zero and 11 Gyr-1, respectively. The two methods resulted in identical average and rms slopes. The sample of 100 slopes had a maximum and minimum of +23 and –26 Gyr-1, respectively. We note that, if one plots all such artificial solar cycle curves, the width of the region covering the 100 curves increases toward the end of the cycle as expected because of the poorer statistics. That means the upper boundary for statistical fluctuations of less than 30 Gyr-1 as the sole reason for the observed systematic trend is significantly smaller than the slope we have derived from the observations.
 |
Fig. 8 Yearly sunspot number. The solid line shows the SIDC annual sunspot number. The filled circles mark the number of TIP maps in each year. |
Second experiment:
although the first test showed that the trend is real, it is not clear how far it is influenced by the statistical fluctuations. We performed a second numerical experiment to elaborate on this issue. Like the first test, we created artificial samples of Bmax. The sample size for each year was as in the first test. The PDF of the Bmax was, however, different for each year in the sense that the mean value of the PDF was decreased by –94 Gyr-1. Because of the lower number of sunspots at the end of the cycle, it is then possible to get a slope that is too flat or too steep compared to the actually imposed slope. The number of repetitions and the analysis method were identical to the first experiment. The average and rms of the slopes derived in the second experiment were –94 and 12 Gyr-1, respectively, both for the Bayesian and least-square methods. The maximum and minimum slopes of the sample were –68 and –130 Gyr-1, respectively. That means that with a complete sample the measured slope can be off by about 36 Gyr-1 in a worst case scenario.
Third experiment:
the second experiment showed that, if there is a real trend in Bmax with the phase of the solar cycle, it is measurable despite the different statistics of sunspots at the maximum and minimum of the cycle. However, we do not have all of the sunspots in our sample, only those that were observed with TIP. This can introduce a significantly larger uncertainty in the derived slope compared to the second experiment. Therefore, we repeated the second numerical test with one change: instead of using the annual sunspot number of SIDC, we used the statistics of the TIP sample. The resulting slopes then spanned a range between –130 and –66 Gyr-1 with an average of –84 and a standard deviation of 9 Gyr-1. This means the statistics of the TIP sample has about the same amount of uncertainty as the complete sample with a caveat that it underestimates the correct trend by 10 Gyr-1, well within the 1σ range of 14 Gyr-1. This ensures us that the slope of –94 Gyr-1 is significant and measurable with the statistics of our sample.
5. Discussion
5.1. Tracers of the solar cycle
The number of sunspots and sunspot groups are the most common indicators for studying the solar cycle (Hathaway et al. 2002,and references therein). Nevertheless, other parameters with more straightforward physical meanings show similar, if not better traces of cyclic variations. These parameters, such as the magnetic field strength of sunspots, usually have a caveat: their systematic recording started only in the early 20th century. In other words, they cannot compete with the 400-year record of sunspot numbers. Recent investigations of the sunspot numbers also indicate that large sunspots correlate better with chromospheric and coronal indicators of the solar cycle such as the 10.7 cm radio flux (Kilcik et al. 2011).
5.2. Continuum intensity vs. magnetic field strength
Our results reproduce earlier observations regarding the general behavior of the maximum magnetic field and minimum continuum intensity of sunspots: the greater the field strength, the lower the continuum intensity. Our Fig. 3 compares reasonably well with Fig. 2 of Livingston (2002). Similar curves of the relation between intensity and field strength for this and other wavelength ranges are given in literature (e.g., Martinez Pillet & Vazquez 1993; Lites et al. 1993; Keppens & Martinez Pillet 1996; Stanchfield et al. 1997; Norton & Gilman 2004; Leonard & Choudhary 2008; Wesolowski et al. 2008; Schad & Penn 2010), where those of Gurman & House (1981) and Livingston (2002) match ours closest because of the pronounced linear behavior. In some of the works the relation between intensity and field strength was derived inside a single sunspot, not for a sunspot sample, sometimes also yielding clearly nonlinear relations.
5.3. Temporal evolution of Bmax
Solar cycle No. 23 was weaker than cycle No. 22 (e.g., Ataç & Özgüç 2006). Livingston (2002) report that sunspots in cycle No. 23 had an excess of smaller and brighter umbrae compared to cycle No. 22. Using 1.56 μm Kitt Peak data, Penn & Livingston (2011) suggest that the strengths of sunspots has steadily decreased since the last solar maximum. Although our finding (Fig. 6) in the declining phase of cycle No. 23 is consistent with them, we do find an increase in Bmax since the beginning of the solar cycle No. 24. As seen in the lefthand panel of Fig. 6, the average field strength of the years 2010 and later are well above the linear trend that indicates the extrapolation of the decrease during the declining phase of cycle No. 23. That is in contrast to Fig. 1 of Penn & Livingston (2011), who predict a continuous decrease in the sunspot field strength and consequently on the solar magnetic activity across cycles. We note, however, that the field strength at the start of cycle No. 24 seems to be slightly lower than at the same stage in cycle No. 23, and the continuum intensity correspondingly slightly higher. This will have to be confirmed by additional data in the following years.
The weakening rate of the magnetic field strength in the descending phase of cycle No. 23 in the TIP data is about –94 ( ± 14) Gyr-1. Penn & Livingston (2006) reported –52 Gyr-1. The size of our sample is smaller than that of Livingston (2002), as well as Penn & Livingston (2006). However, the precision of the measurements, and the calibration accuracy is superior to the mentioned references because of using vector-polarimetric data instead of intensity profiles.
Watson et al. (2011) used Soho magnetograms and analyzed more than 30 000 sunspots. They reported a systematic decrease of –70 Gyr-1 in the declining phase of the cycle No. 23, in agreement with our results. These results should be taken with care because the Soho/MDI instrument cannot accurately measure the magnetic field in sunspots because of line saturation effects (Berger & Lites 2003). Pevtsov et al. (2011) compiled observations of seven (former Soviet) solar observatories. They report a rate of –119 Gyr-1 for cycle No. 23, which is the strongest rate in the four cycles they studied. Despite some (systematic) uncertainty in part of their data around 1965, they did not find any significant secular trend in field strength over four and a half solar cycles.
5.4. Temporal evolution of umbral intensity
Albregtsen & Maltby (1978) and Albregtsen et al. (1984) found that the amount of variation in the umbral intensity during a cycle is about 10% (see also, Maltby 1992). Our results are therefore consistent with their analysis. Mathew et al. (2007) used Soho data and did not find any significant enhancement in the umbral intensity as a function of the solar cycle phase. In contrast, Penn & MacDonald (2007) find a cycle-dependent oscillation of the umbral intensity. Our data show an increase in the umbral continuum intensity with the phase of the solar cycle. We find a slope of 1.3 ( ± 0.4)% Ic(1.56 μm)% yr-1 in the TIP data of cycle No. 23. Our results are consistent with the observations of Albregtsen et al. (1984), who reported an increase of 1.2 and 1.9% per year in cycles No. 20 and 21, as well as with Penn & Livingston (2006) who find an increase of 1.9% per year from 2000 to 2006.
5.5. Umbral area
Brants & Zwaan (1982) found that larger umbrae have a higher field strength, similar to Kopp & Rabin (1992) and Martinez Pillet & Vazquez (1993). We find a similar trend in our results (Fig. 5). Recently, Watson et al. (2011) report a dependence of the area of the largest sunspots on the solar cycle. This, however, does not imply any trend in the size of individual sunspots. Like Penn & MacDonald (2007), we did not find any systematic trend between the phase of the solar cycle and the sunspot size. These observations therefore hint at a constant distribution of the sunspot area, e.g., a log-normal distribution with a fixed slope (Bogdan et al. 1988). The larger number of sunspots close to the maximum of a cycle naturally increases the number of large sunspot groups. Because these large sunspots are located at the tail of the distribution, they are prone to larger statistical fluctuations compared to other quantities resulting from all sunspots such as Bmax. The lack of a systematic change of sunspot area is still puzzling because we measure a difference of some 700 G between the average Bmax in the maximum and minimum of cycle No. 23, comparable to the 600 G reported by Penn & Livingston (2006). Taking Fig. 5 at face value that shows the relation between field strength and area, a rate of –28 arcsec2 yr-1 would be expected. A least-square fit to the average umbral areas per year resulted, however, only in a slope of 2 ( ± 4)arcsec2 yr-1. It was already mentioned by Brants & Zwaan (1982) that the scatter between Bmax and umbral size is partly intrinsic. Penn & MacDonald (2007) suggest that the relation between the Bmax and umbral area might vary during a solar cycle. Therefore, it remains an open question to verify whether the diversity of physical conditions in different umbrae vary with the solar cycle in a sense that it prevents a cyclic trend of umbral size.
Mathew et al. (2007) report a clear trend between the umbral intensity and the umbral size in Soho data (see also Wesolowski et al. 2008). Although the umbral contrast is lower at 1.56 μm, there is a similar trend in our data as well. As seen in Fig. 4, larger sunspots have a lower continuum intensity than smaller sunspots, in agreement with previous studies (Brants & Zwaan 1982; Kopp & Rabin 1992).
5.6. Implications for the solar irradiance
An excess or lack of large dark umbrae changes the total solar irradiance (TSI, e.g., Steinegger et al. 1990). Our finding thus also has some implications for the TSI variations in solar cycle No. 24. There are long term variations in the solar activity and irradiance (e.g., Tapping et al. 2007; Fröhlich 2009; Shapiro et al. 2011). In particular, because the Sun apparently had an unusually active period in the last couple of decades (Usoskin et al. 2003; Bonev et al. 2004), we cannot completely rule out the existence of a long term trend. However, in spite of suggestions that cycle No. 24 and the preceding activity minimum are very different from previous ones (Tripathy et al. 2010; ?), the influence of a long term trend seems to be less than the cycle-dependent pattern on the timescale of a solar cycle.
6. Conclusion
A sample of sunspot maps observed with the Tenerife Infrared Polarimeter was analyzed to elaborate on a possible dependence of the magnetic field strength of sunspots on the phase of the solar cycle. The vector-polarimetric data enabled us to use full Stokes measurements to estimate the variation in Bmax rather than only using intensity profiles as used in case of Kitt Peak data. We found a significant decrease in the measured magnetic field strength from the maximum to the minimum of the sunspot cycle No. 23 with a rate of –94 ( ± 14) Gyr-1. At the same time, the minimum umbral continuum intensity increases by 1.3 ( ± 0.4)% of Ic yr-1, while there is no significant trend of the umbral area with the phase of the solar cycle. The magnetic field strength of sunspots increased at the beginning of solar cycle No. 24. This indicates that the observed trend of Bmax is likely to be a cyclic pattern rather than a long-term evolution. Comparing the field strength in the early stages of cycle Nos. 23 and 24, we find a slight reduction in Bmax in the new cycle that, however, will need to be confirmed by additional data in the future.
http://www3.kis.uni-freiburg.de/~cbeck/TIP_archive/TIP_archivemain.html. If you are interested in using the data, please contact mcv@iac.es.
Acknowledgments
The German VTT is operated by the Kiepenheuer-Institut für Sonnenphysik at the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias (IAC). We are grateful to Manuel Collados (IAC) for providing the data. We also thank Juan M. Borrero for reading the manuscript. R.R. acknowledges fruitful discussions at the workshop on “Filamentary Structure and Dynamics of Solar Magnetic Fields”, as well as “Extracting Information from spectropolarimetric observations: comparison of inversion codes” at the ISSI in Bern. C.B. acknowledges partial support by the Spanish Ministry of Science and Innovation through projects AYA 2007-63881 and AYA 2010-18029.
References
- Adjabshirzadeh, A., & Koutchmy, S. 1983, A&A, 122, 1 [NASA ADS] [Google Scholar]
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Albregtsen, F., & Maltby, P. 1978, Nature, 274, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Albregtsen, F., & Maltby, P. 1981, Sol. Phys., 71, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Albregtsen, F., Joras, P. B., & Maltby, P. 1984, Sol. Phys., 90, 17 [Google Scholar]
- Ataç, T., & Özgüç, A. 2006, Sol. Phys., 233, 139 [Google Scholar]
- Ballesteros, E., Collados, M., Bonet, J. A., et al. 1996, A&AS, 115, 353 [NASA ADS] [Google Scholar]
- Beck, C. 2006, Ph.D. Thesis, Albert-Ludwigs-University, Freiburg [Google Scholar]
- Beck, C. 2008, A&A, 480, 825 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Bellot Rubio, L. R., Schlichenmaier, R., & Sütterlin, P. 2007, A&A, 472, 607 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, C., Rezaei, R., & Fabbian, D. 2011, A&A, 535, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, T. E., & Lites, B. W. 2003, Sol. Phys., 213, 213 [Google Scholar]
- Bogdan, T. J., Gilman, P. A., Lerche, I., & Howard, R. 1988, ApJ, 327, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Bonev, B. P., Penev, K. M., & Sello, S. 2004, ApJ, 605, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Brants, J. J., & Zwaan, C. 1982, Sol. Phys., 80, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Bray, R. J., & Loughhead, R. E. 1964, Sunspots (Chapman Hall) [Google Scholar]
- Chapman, G. A., & Meyer, A. D. 1981, in The Physics of Sunspots, ed. L. E. Cram, & J. H. Thomas, 446 [Google Scholar]
- Collados, M., Martinez Pillet, V., Ruiz Cobo, B., del Toro Iniesta, J. C., & Vazquez, M. 1994, A&A, 291, 622 [NASA ADS] [Google Scholar]
- Collados, M., Lagg, A., Díaz Garcí A, J. J., et al. 2007, in The Physics of Chromospheric Plasmas, ed. P. Heinzel, I. Dorotovič, & R. J. Rutten, ASP Conf Ser., 368, 611 [Google Scholar]
- Fröhlich, C. 2009, A&A, 501, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gregory, P. C. 2005, Bayesian Logical Data Analysis for the Physical Sciences: A Comparative Approach with “Mathematica” Support, ed. P. C. Gregory (Cambridge University Press) [Google Scholar]
- Gregory, P. C., & Loredo, T. J. 1992, ApJ, 398, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Gurman, J. B., & House, L. L. 1981, Sol. Phys., 71, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Hathaway, D. H., Wilson, R. M., & Reichmann, E. J. 2002, Sol. Phys., 211, 357 [Google Scholar]
- Jain, K., Tripathy, S. C., & Hill, F. 2011, ApJ, 739, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Keppens, R., & Martinez Pillet, V. 1996, A&A, 316, 229 [NASA ADS] [Google Scholar]
- Kilcik, A., Yurchyshyn, V. B., Abramenko, V., et al. 2011, ApJ, 731, 30 [CrossRef] [Google Scholar]
- Kopp, G., & Rabin, D. 1992, Sol. Phys., 141, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Landi degl’Innocenti, E. & Landolfi, M. 2004, Polarization in Spectral Lines, Astrophys. Space Sci. Lib. (Kluwer Academic Publishers) [Google Scholar]
- Leonard, T., & Choudhary, D. P. 2008, Sol. Phys., 252, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lites, B. W., Elmore, D. F., Seagraves, P., & Skumanich, A. P. 1993, ApJ, 418, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W. 2002, Sol. Phys., 207, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Livingston, W., Harvey, J. W., Malanushenko, O. V., & Webster, L. 2006, Sol. Phys., 239, 41 [Google Scholar]
- Maltby, P. 1992, in Sunspots. Theory and Observations, ed. J. H. Thomas, & N. O. Weiss, NATO ASIC Proc., 375, 103 [Google Scholar]
- Maltby, P., Avrett, E. H., Carlsson, M., et al. 1986, ApJ, 306, 284 [Google Scholar]
- Martinez Pillet, V., & Vazquez, M. 1993, A&A, 270, 494 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., Collados, M., Sánchez Almeida, J., et al. 1999, in High Resolution Solar Physics: Theory, Observations, and Techniques, ASP Conf. Ser., 183, 264 [NASA ADS] [Google Scholar]
- Mathew, S. K., Lagg, A., Solanki, S. K., et al. 2003, A&A, 410, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathew, S. K., Martínez Pillet, V., Solanki, S. K., & Krivova, N. A. 2007, A&A, 465, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mattig, W. 1971, Sol. Phys., 18, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Nave, G., Johansson, S., Learner, R. C. M., Thorne, A. P., & Brault, J. W. 1994, ApJS, 94, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, A. A., & Gilman, P. A. 2004, ApJ, 603, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Ossendrijver, M. 2003, A&ARv, 11, 287 [Google Scholar]
- Patil, A., Huard, D., & Fonnesbeck, C. J. 2010, Jour Stat Software, 35, 4 [Google Scholar]
- Penn, M. J., & Livingston, W. 2006, ApJ, 649, L45 [Google Scholar]
- Penn, M. J., & Livingston, W. 2011, in The Physics of the Sun and Star Spots, IAU Symp., 273, 126 [NASA ADS] [Google Scholar]
- Penn, M. J., & MacDonald, R. K. D. 2007, ApJ, 662, L123 [NASA ADS] [CrossRef] [Google Scholar]
- Penn, M. J., Walton, S., Chapman, G., Ceja, J., & Plick, W. 2003, Sol. Phys., 213, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Pevtsov, A. A., Nagovitsyn, Y. A., Tlatov, A. G., & Rybak, A. L. 2011, ApJ, 742, L36 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical recipes in FORTRAN, The art of scientific computing, 2nd edn. (Cambridge University Press) [Google Scholar]
- Rezaei, R., Schlichenmaier, R., Beck, C. A. R., Bruls, J. H. M. J., & Schmidt, W. 2007, A&A, 466, 1131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rezaei, R., Bruls, J. H. M. J., Schmidt, W., et al. 2008, A&A, 484, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rüedi, I., Solanki, S. K., & Livingston, W. 1995, A&A, 302, 543 [NASA ADS] [Google Scholar]
- Sánchez Cuberes, M., Puschmann, K. G., & Wiehr, E. 2005, A&A, 440, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schad, T. A., & Penn, M. J. 2010, Sol. Phys., 262, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Schlichenmaier, R., & Collados, M. 2002, A&A, 381, 668 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmidt, W., & Balthasar, H. 1994, A&A, 283, 241 [NASA ADS] [Google Scholar]
- Schröter, E. H., Soltau, D., & Wiehr, E. 1985, Vistas Astron., 28, 519 [Google Scholar]
- Schüssler, M., Caligari, P., Ferriz-Mas, A., & Moreno-Insertis, F. 1994, A&A, 281, L69 [Google Scholar]
- Shapiro, A. I., Schmutz, W., Rozanov, E., et al. 2011, A&A, 529, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- SIDC-team 2011, Monthly Report on the International Sunspot Number, online catalogue, http://www.sidc.be/sunspot data/ [Google Scholar]
- Solanki, S. K. 2003, A&ARv, 11, 153 [Google Scholar]
- Stanchfield, II, D. C. H., Thomas, J. H., & Lites, B. W. 1997, ApJ, 477, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Steinegger, M., Brandt, P. N., Schmidt, W., & Pap, J. 1990, Ap&SS, 170, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Stix, M. 2002, The Sun: An Introduction, 2nd edn. (Berlin: Springer-Verlag) [Google Scholar]
- Tapping, K. F., & Valdés, J. J. 2011, Sol. Phys., 272, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Tapping, K. F., Boteler, D., Charbonneau, P., et al. 2007, Sol. Phys., 246, 309 [Google Scholar]
- Tripathy, S. C., Jain, K., Hill, F., & Leibacher, J. W. 2010, ApJ, 711, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Tritschler, A., & Schmidt, W. 2002, A&A, 382, 1093 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Usoskin, I. G., Solanki, S. K., Schüssler, M., Mursula, K., & Alanko, K. 2003, Phys. Rev. Lett., 91, 211101 [Google Scholar]
- von der Lühe, O., Soltau, D., Berkefeld, T., & Schelenz, T. 2003, in Innovative Telescopes and Instrumentation for Solar Astrophysics. ed. S. L. Keil, & S. V. Avakyan, SPIE, 4853, 187 [Google Scholar]
- Wallace, L., Hinkle, K., & Livingston, W. 2000, An atlas of sunspot umbral spectra in the visible, from 15 000 to 25 500 cm-1 (3920 to 6664 [Å]) (National Optical Astronomy Observatories) [Google Scholar]
- Watson, F. T., Fletcher, L., & Marshall, S. 2011, A&A, 533, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wesolowski, M. J., Walton, S. R., & Chapman, G. A. 2008, Sol. Phys., 248, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Westendorp Plaza, C., del Toro Iniesta, J. C., Ruiz Cobo, B., et al. 2001, ApJ, 547, 1130 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Sample of two umbral profiles. The solid (dashed) line corresponds to a sunspot at μ = 0.58 (0.76). The continuum intensity of the quiet Sun profiles corresponding to each of them is unity. The short vertical lines mark four OH spectral lines, while the long vertical line denotes the Fe i 1564.8 nm line. Top: Stokes-I, bottom: Stokes-V. |
| In the text | |
 |
Fig. 2 Example of TIP scans. Top: sunspot on 24 May 2001, recorded in Fe i 1089.6 nm with CT correction. Bottom: sunspot on 17 July 2011, recorded in Si i 1082.7 nm with AO image stabilization. Tick marks are in arcseconds. |
| In the text | |
 |
Fig. 3 Variation in the minimum continuum intensity in the umbra as a function of maximum magnetic field strength. The 1.1 μm data were multiplied by a factor 1.3. Red and black symbols mark the 1.1 and 1.6 μm data, respectively. P-incomplete and U-incomplete mark sunspots whose penumbra and umbra were not fully covered in the map. The solid line shows a least-squared fit, and the dashed lines indicate the 1σ interval. Numbers in parenthesis denote the 1σ uncertainty. |
| In the text | |
 |
Fig. 4 Variation in the minimum continuum intensity in the umbra as a function of area. Top: total sunspot area, bottom: umbral area. The solid lines indicate bisector least-squared fit to all data points expect complex sunspots (circles). The dashed lines show the 1σ interval. Symbols are like Fig. 3. |
| In the text | |
 |
Fig. 5 Variation in the maximum magnetic field strength in the umbra as a function of area. Top: total sunspot area, bottom: umbral area. Symbols are like Fig. 3. Linear fits are similar to Fig. 4. |
| In the text | |
 |
Fig. 6 Variation in the maximum magnetic field strength (left), minimum continuum intensity (midddle), and umbral area (right) vs. time. Symbols show the individual sunspots while the blue filled circles mark the annual averages. The linear fits was performed for individual data points between the two vertical lines. The dashed vertical lines mark maximum and minimum of cycle 23. Symbols are like in Fig. 3. |
| In the text | |
 |
Fig. 7 Probability density function of the maximum magnetic field strength. The red curve is the best-fit normal distribution to the data using a Bayesian method. |
| In the text | |
 |
Fig. 8 Yearly sunspot number. The solid line shows the SIDC annual sunspot number. The filled circles mark the number of TIP maps in each year. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


