| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A109 | |
| Number of page(s) | 5 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118585 | |
| Published online | 10 May 2012 | |
Sun-grazing orbit of the unusual near-Earth object 2004 LG
1 Institute of Astronomy, Faculty of Mathematics and Physics, Charles University, V Holešovičkách 2, 18000 Prague, Czech Republic
e-mail: vokrouhl@cesnet.cz
2 Southwest Research Institute, 1050 Walnut St, Suite 300, Boulder, CO 80302, USA
e-mail: davidn@boulder.swri.edu
Received: 5 December 2011
Accepted: 9 March 2012
Context. Near-Earth objects (NEOs) typically end their existence by falling into the Sun. Because the orbit evolution timescale is long, however, it is unlikely that we will witness such events or predict them happening in a foreseeable future.
Aims. We studied the orbital dynamics of NEOs to understand whether predictions of Sun impact are possible for individual bodies, and if so, whether special cases can be identified where the Sun impact is expected to happen in ≲100 ky.
Methods. We identified an unusual NEO on a Sun-grazing orbit, 2004 LG, and numerically integrated its orbit to understand its dynamical history and future evolution.
Results. We found that the orbit of 2004 LG is strongly affected by the Kozai resonance. In about 9 ky from now, when the orbital eccentricity will reach the maximum value during its current Kozai cycle, 2004 LG has a greater than 25% probability of falling into the Sun. The probability of Sun impact is >50% over the next 100 ky. 2004 LG was exposed to extreme solar radiation in the past and will be exposed to even more extreme solar radiation in the future. For example, we found that 2004 LG was approaching the Sun to within only ≃5.6 solar radii some 3 ky ago, and its surface was baked at temperatures ≃2500 K. Spectroscopic observations of 2004 LG would therefore be useful in characterizing the effects of extreme irradiation on NEOs’ surfaces. Our forward orbital integrations showed that 2004 LG will reach a very low orbital perihelion distance (<1.6 solar radii) at 9 ky from now, indicating its surface will be scorched at temperatures exceeding 4500 K while the interior will be exposed to strong solar tides and thermal stresses. The object will probably not maintain its physical integrity.
Key words: minor planets, asteroids: general / comets: general
© ESO, 2012
1. Introduction
Small bodies in the inner part of the solar system whose orbits become decoupled from Jupiter (semimajor axis <2.5 AU) are eventually expected to (i) disintegrate through a collision with another small body, tidally disrupt in the planetary or solar gravity fields, undergo rotational fission, or (ii) directly hit a major body such as a planet or the Sun. For (ii), the solar impact is statistically most likely because planets, including the Earth or Venus, are relatively small targets.
A number of comets have been seen to fall into the Sun or disintegrate in its immediate vicinity (e.g., Marsden 2005, for a review). Numerical simulations, used to study the origin and orbital evolution of comets, also confirm the solar impact as a possible end-state, although not the most likely one (see, e.g., Duncan et al. 2004)1. Studies of the orbital fate of asteroids evolving into unstable orbits from the chaotic (resonant) zones surrounding the asteroid main belt (e.g., Farinella et al. 1994; Gladman et al. 1997, 2000) show that most of the bodies eventually fall into the Sun. This is because asteroids have no, or only weak, gravitational coupling to Jupiter (especially for orbits originating in the inner and middle parts of the asteroid belt).
The solar impacts in the above-mentioned simulations were typically obtained for a synthetic population of particles and impacts occurred on very long timescales. Even in the few cases of orbital simulations of real objects, such as Eros or Itokawa, the solar impacts were inferred on a statistical basis (e.g., Michel et al. 1998; Michel & Yoshikawa 2006). This is because the impacts were recorded over timescales much longer than those allowing deterministic orbit propagation. Thus, with exception of a few very rare cases (e.g., comet P96/Machholz; e.g., Bailey et al. 1992; Bailey 1996; Levison & Dones 2007), no definite predictions about the solar impacts were made for specific bodies.
Equinoctial orbital elements and their formal uncertainty for 2004 LG as of MJD 53 333.862633629 (middle of the currently available observation arc).
As a part of an independent project (Vokrouhlický et al. 2012), we noted the case of 2004 LG. This near-Earth asteroid (NEA) has an unusually small c = η cosi value2, 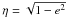 with e the eccentricity and i the inclination. In particular, c ≃ 0.144 for 2004 LG, by far the smallest in the studied group of NEAs. Additionally, it has a fairly small value of the semimajor axis a (a ≃ 2.066 AU), which prompted us to look closer at the orbital evolution of this object. Searching among other populations of small bodies we found that only an unusual comet P96/Machholz, and a group of sungrazing comets that are believed to originate from P96/Machholz (e.g., Sekanina & Chodas 2005), have c and a somewhat similar to 2004 LG (c ≃ 0.141 and a ≃ 3.02 AU for P96/Machholz). Typical values of c for Jupiter-family comets are c > 0.5 (including the comet 2P/Encke) and their semimajor axis values are a > 2.5 AU (with the exception of the comet 2P/Encke), while typical semimajor axis values for long-period comets are a > 5.2 AU (Jupiter’s value).
with e the eccentricity and i the inclination. In particular, c ≃ 0.144 for 2004 LG, by far the smallest in the studied group of NEAs. Additionally, it has a fairly small value of the semimajor axis a (a ≃ 2.066 AU), which prompted us to look closer at the orbital evolution of this object. Searching among other populations of small bodies we found that only an unusual comet P96/Machholz, and a group of sungrazing comets that are believed to originate from P96/Machholz (e.g., Sekanina & Chodas 2005), have c and a somewhat similar to 2004 LG (c ≃ 0.141 and a ≃ 3.02 AU for P96/Machholz). Typical values of c for Jupiter-family comets are c > 0.5 (including the comet 2P/Encke) and their semimajor axis values are a > 2.5 AU (with the exception of the comet 2P/Encke), while typical semimajor axis values for long-period comets are a > 5.2 AU (Jupiter’s value).
In Sect. 2 we use direct numerical integration to explore the orbital evolution of 2004 LG. Discussion and conclusions are provided in Sect. 3.
2. Orbital evolution of 2004 LG
The object known as 2004 LG was discovered on June 9, 2004 during regular observations of the LINEAR project, and was subsequently followed by various stations. At the end of April 2007, the body was recovered by the Spacewatch program, and another set of observations covering a short orbital arc was acquired. Because the orbit of 2004 LG is close to the exterior 3/1 mean motion resonance with the Earth, the geometry of the 2004 and 2007 observations was similar. Finally, 2004 LG was detected by the WISE spacecraft on June 12, 2010. Observations from these three apparitions constitute the database available for the orbital solution of 2004 LG, which we list in Table 1. The orbit determination also allows us to estimate the absolute magnitude of 2004 LG to be ≃ 17.9 mag. Since the analysis of the WISE infrared observations has not been reported yet, we can only estimate 2004 LG’s size to be 0.8 − 1.5 km for reasonable values of the geometric albedo. No other physical parameters for this body are presently known.
Obviously, the orbit determination provides also a full covariance matrix Σ of solution for all six osculating elements ET = (a,k,h,q,p,λ) at a given epoch. Because of the repeating observing geometry, some of the correlations are high and need to be taken into account when constructing initial conditions for our orbital integrations. This is because to explore the orbital evolution for 2004 LG, one needs apart from the best-fit solution E ⋆ , to investigate the orbital evolution of nearby orbits (geometrical clones). The clones are chosen such that their distribution p(E) in the six-dimensional orbital-element space is proportional to ![\hbox{$\exp\left[-\frac{1}{2} \Delta{\bf E}^{\rm T}\cdot {\boldmath\Sigma} \cdot \Delta{\bf E}\right]$}](/articles/aa/full_html/2012/05/aa18585-11/aa18585-11-eq45.png) , where ΔE = E − E ⋆ (e.g., Milani & Gronchi 2010).
, where ΔE = E − E ⋆ (e.g., Milani & Gronchi 2010).
Most of the numerical integrations were performed using the SWIFT_RMVS package3. Several control runs were also performed using the Burlish-Stoer integrator with adaptive stepsize. We did not see any significant differences in results obtained with the two codes. Because the orbit of 2004 LG reaches very small perihelion distances, we included a post-Newtonian potential term effectively simulating the general relativistic perihelion precession using the formulation by Nobili & Roxburgh (1986; see also Nobili et al. 1989). While only approximate, this formulation is easily implemented in SWIFT_RMVS thanks to its simple potential form. Moreover, we note that the overall relativistic effect in the orbit of 2004 LG is not fundamental for our investigation. The corresponding perihelion advance at maximum eccentricity reached by the orbit of 2004 LG is only ~2.5 larger than that of Mercury. This is because the semimajor axis of 2004 LG always remains larger than 2 AU.
More importantly, we had to use a short integration timestep of 0.01 − 0.03 d in our simulations, because the eccentricity reached very high values during the simulation (>0.99). Fortunately, even with this small timestep the accumulation of rounding-off errors is small, because we are interested in evolution timescales ≤105 y. Except for the Newtonian and relativistic gravitational perturbations from the Sun and planets we did not consider other dynamical effects in the orbit of 2004 LG. We shall return to this question, and justify it partly, in Sect. 3.
 |
Fig. 1 Numerical integration of the nominal orbit of 2004 LG up to 8.9 ky when the heliocentric distance became smaller than solar radius. The upper three panels show the time evolution of the osculating semimajor axis (top), eccentricity (middle) and inclination (bottom). Each of them is affected by resonance phenomena that produce large-scale oscillations: the semimajor axis oscillates due to effects of the J4/1 mean motion resonance with Jupiter, eccentricity and inclination show correlated oscillations due to the Kozai resonance (with smaller effects of the J4/1 resonance too). The bottom-most panel shows the resonance angle φJ41 = 4λJ − λ − 3ϖ. |
2.1. Future orbital evolution
Propagation of the nominal orbit of 2004 LG (i.e., with the orbital elements from Table 1) provides a first look at the fundamental dynamical effects in its evolution (Fig. 1). The semimajor axis undergoes large-amplitude (≃0.015 AU) and long-period (≃500 y) oscillations in the 4/1 mean motion resonance with Jupiter. The corresponding principal resonance angle φJ41 = 4λJ − λ − 3ϖ librates with small amplitude, see Fig. 1, bottom panel. The slow drift of the resonance center seen in this panel is a somewhat unusual effect, likely related to an extreme eccentricity and inclination regime and other secular phenomena affecting the orbit. The eccentricity and inclination undergo a long-term evolution characteristic of the Kozai dynamics (e.g., Kozai 1962; Bailey et al. 1992), namely correlated and large-amplitude oscillations with a conservation of the c = η cosi integral (see also Fig. 3). Using the current osculating orbital elements with the inclination relative to the Laplacian plane of the solar system, we estimate that e ≃ 0.9884 will be reached during the Kozai cycle (see, e.g., Kinoshita & Nakai 2007; or for a more accurate formulation, Milani & Gronchi 2010, and proper elements available at the AstDyS website). With the current osculating semimajor axis of ≃ 2.066 AU, this would indicate a minimum perihelion distance of ≃5 solar radii. However, effects of the J4/1 mean motion change the situation. Small, but important, oscillations in eccentricity and inclination produce a small decrease of c. The maximum eccentricity achieved during the Kozai cycle then exceeds ≃0.9976. When the semimajor axis approaches its minimum value during its resonance cycle, the pericenter of the orbit becomes smaller than the solar radius at time ≃8.9 ky. Indeed, our simulation was stopped at this time, indicating a direct impact of 2004 LG onto the Sun.
While this is interesting by itself, a more important problem is to understand how typical the solar impact is for all possible orbits originating from the close neighborhood of the nominal orbit. An objective approach is to consider a certain number of geometric clones of 2004 LG, constructed according to the scheme outlined above, and propagate their orbits to the future. Figure 2 shows results from orbit propagation of 1000 clones of 2004 LG for 100 ky to the future. About 27% of all clones share the same fate as the nominal solution and hit the Sun in ≃9 ky. Pushing the time to 100 ky in the future, the fraction of clones that hit the Sun increases to about 56%. The clones that do not hit the Sun during the next 100 ky reside on trajectories that approach the Sun at a very close distance. We note that all our clones reached q < 1.6 solar radii in ≃9 ky.
 |
Fig. 2 Results of a numerical integration of 1000 orbital clones of 2004 LG. The ordinate shows the percentage of clones that reached a given solar distance in <10 ky in the future (solid line) or in 100 ky in the future (dashed line). The solar distance is shown in units of solar radius. The upper abscissa shows an effective subsolar temperature due to solar irradiation. |
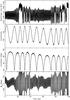 |
Fig. 3 Same as in Fig. 1, but for the backward evolution of the nominal orbit of 2004 LG; the abscissa is time in the past in ky. |
The effective subsolar temperature 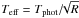 for zero or low albedo values is given at the upper abscissa in Fig. 2 (Tphot ≃ 5780 K is the photospheric temperature and R is the heliocentric distance in solar radii; e.g., Bertotti et al. 2003). A more accurate thermophysical model could indicate a slightly lower temperature, but still high enough to confirm our argument4. Additionally, assuming a proton density ≃ 108 cm-3 at the heliocentric distance of ≃ 1.5 solar radii (e.g., Bertotti et al. 2003) and taking the pericentric speed of ≃ 600 km s-1 (basically the escape velocity from the Sun), the kinetic energy density by which solar atmosphere plasma hits the surface is comparable to the energy density of the radiation field. Both factors must cause a significant damage to the body, or at least alter its surface properties. The whole body will be also exposed to strong effects of the solar tidal field and experience significant thermal stress at distances <2 solar radii (e.g., Holsapple & Michel 2006, 2008, and references therein; and Čapek & Vokrouhlický 2010, and references therein).
for zero or low albedo values is given at the upper abscissa in Fig. 2 (Tphot ≃ 5780 K is the photospheric temperature and R is the heliocentric distance in solar radii; e.g., Bertotti et al. 2003). A more accurate thermophysical model could indicate a slightly lower temperature, but still high enough to confirm our argument4. Additionally, assuming a proton density ≃ 108 cm-3 at the heliocentric distance of ≃ 1.5 solar radii (e.g., Bertotti et al. 2003) and taking the pericentric speed of ≃ 600 km s-1 (basically the escape velocity from the Sun), the kinetic energy density by which solar atmosphere plasma hits the surface is comparable to the energy density of the radiation field. Both factors must cause a significant damage to the body, or at least alter its surface properties. The whole body will be also exposed to strong effects of the solar tidal field and experience significant thermal stress at distances <2 solar radii (e.g., Holsapple & Michel 2006, 2008, and references therein; and Čapek & Vokrouhlický 2010, and references therein).
2.2. Past orbital evolution
We now turn our attention to the orbital history of 2004 LG. We concentrate on discussing the short-term timescales, leaving the more extensive work on possible evolutionary paths from putative source zones aside5.
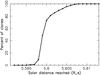 |
Fig. 4 Results from numerical propagation of 500 orbital clones of 2004 LG. The ordinate shows the percentage of clones that reached a given solar distance during the past maximum of the eccentricity cycle (some 3 ky ago). The distance is given in units of solar radius. |
First, the propagation of the nominal orbit backward in time reveals that maximum values of eccentricity reached during the Kozai cycles systematically increased since 25 ky ago (Fig. 3). In particular, the lowest perihelium distance reached some 3 ky ago, during the last eccentricity maximum, was ≃5.6 solar radii only, and was ≃ 10 solar radii during the previous cycle. The orbit is seen to interact with the J4/1 mean motion resonance, temporarily dropping and regaining location in it. Deterministic predictions are therefore not possible beyond a few Kozai oscillations.
We again substantiated the previous results by propagating 500 clones of 2004 LG backward in time and determined the distribution of the minimum solar distances reached within the past 3.5 ky (covering the last maximum of the eccentricity oscillation). Figure 4 shows the result. The minimum solar distance distribution is tightly constrained with a characteristic value of ≃5.6 solar radii. This better confinement, compared to Fig. 2, is a combination of two factors: (i) shorter timescale of propagation, and (ii) larger perihelion distance. At the minimum distances reached, some 5.596 solar radii, the effective subsolar temperature was ≃2440 K. We thus find that 2004 LG underwent a sequence of unusually close approaches to the Sun recently, and that its surface properties could have been significantly altered in the strong solar radiation environment. To appreciate the uniqueness of 2004 LG, consider for comparison the more than twice as large distance to the Sun for the past orbital evolution of comet P96/Machholz, whose perihelion distance reached ~14 solar radii some 4 ky ago (e.g., Gonczi et al. 1992; Bailey et al. 1992). Similarly, none of the known asteroids had such a close approach to the Sun within the past thousands of years.
3. Discussion and conclusions
We first comment on the validity of the dynamical model that we used for the orbit propagation of 2004 LG. The relevant gravitational effects were taken into account, but one is usually concerned with the role of non-gravitational forces. As far as we know, cometary activity has not been reported for 2004 LG from its sparse observations. While we cannot rule out a low level of activity, or even a more regular activity in the past, we shall neglect it in our considerations at this moment. Still, there are additional non-gravitational forces efficient enough to perturb orbits of comets and asteroids.
As the perihelion distance of the orbit becomes very small, one may wonder if the denser solar wind environment (or an extended solar atmosphere) might become important for the dynamics of 2004 LG. Because of the strong decrease of solar wind density with the heliocentric distance, we assume that the solar wind drag can be approximated by an instantaneous kick at the orbital pericenter (e.g., Bertotti et al. 2003). Denoting ρsw ≃ 10-16 g/cm3 the mass density of the solar wind at about 1.5 − 2 solar radii, ρbulk ≃ 1 − 2 g/cm3 the bulk density of 2004 LG, D ≃ 1 km its size and vp ≃ 600 km s-1 its pericenter speed, we estimate the eccentricity change of δe ~ −6 (ρsw/ρbulk) (vp/D) ~ 10-13 per revolution. The braking effects of the circumsolar dust cloud can be estimated using the formulation and data from Mann et al. (2000). Assuming the volume density of ~10 μm dust grains evaporating below ≃ (2.5−3) solar radii distance can reach up to ~10-14 cm-3, we obtain even weaker effects than from the solar wind particles. These effects are negligible for the orbital evolution of 2004 LG.
Second, the finite value of the surface thermal inertia of small bodies results in a photon thrust called the Yarkovsky effect (e.g., Bottke et al. 2006). We roughly estimate the expected rate of secular change in the orbital semimajor axis. A typical maximum value at ≃ 2 AU heliocentric distance would be da/dt ≃ 2 × 10-4 AU/My for a kilometer-sized body. The extreme eccentricity reached during the Kozai cycle of 2004 LG (see Figs. 1 and 3) could increase this expected da/dt by up to two orders of magnitude (see, e.g., Spitale & Greenberg 2001), making thus a maximum expected cumulative change δa ~ 2 × 10-4 AU in the semimajor axis during 10 ky timescale (relevant for Fig. 1 simulation). However, because of the resonant confinement of the orbit, the typical semimajor axis drift due to the Yarkovsky effect translates into a correlated change in eccentricity (see, e.g., Brož & Vokrouhlický 2008; Brož et al. 2011). Using the quasi-conserved quantity ∝ 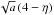 in the J4/1 mean motion resonance (
in the J4/1 mean motion resonance (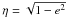 ; e.g., Morbidelli 2002), we therefore estimate an upper bound on a cumulative change in eccentricity caused by the thermal forces to be δe ≃ 2 η (δa/a) ≃ 2 × 10-5. This weak effect is not likely to affect the results significantly.
; e.g., Morbidelli 2002), we therefore estimate an upper bound on a cumulative change in eccentricity caused by the thermal forces to be δe ≃ 2 η (δa/a) ≃ 2 × 10-5. This weak effect is not likely to affect the results significantly.
Our work has interesting implications for the orbital history of 2004 LG. The very small perihelion distance of 2004 LG reached some 3 ky ago is unusual in the current population of NEAs. While most NEAs ultimately end up falling into the Sun, for most of their lifetime they typically stay away from the extreme solar proximity. For example, the simulations of Marchi et al. (2009) indicate that only ~1% of NEAs spend ~(1−1000) ky on orbits with a perihelion smaller than 0.1 AU, and this fraction quickly drops for smaller perihelion distances. In fact, their simulations did not have enough resolution to estimate the likelihood of the 2004 LG case.
The very high temperatures to which the surface of 2004 LG was exposed recently may have produced significant alterations. It would be thus interesting to obtain spectral observations of this body. These observations can be challenging because the object is faint and near the galactic plane at oppositions, or at low solar elongations when closer to the Earth. As far as orbit-determination improvements are concerned, perhaps a precovery search among the data taken in the 1990s might help, because the observational conditions for 2004 LG were better.
Looking ahead to the future, we note that the solar tide and thermal stresses, as well as subsurface gas pressure build-up are going to be severe when the orbit will begin to reach solar distances of ≤ 2 solar radii in about 8 ky from now. 2004 LG may not maintain its physical integrity during this period (e.g., Marsden 2005; Brown et al. 2011). Note that some sungrazing comets were seen to survive a single perihelion passage with q comparable to the predicted values of 2004 LG orbit, but these cases were rare (see, e.g., the case of comet C/2011 W3 (Lovejoy), Gundlach et al. 2012). Moreover, 2004 LG will be undergoing dozens of such close passages during up to several centuries. Even if 2004 LG withstands the effects of solar tide, which is uncertain (e.g., Holsapple & Michel 2006, 2008), it will suffer from strong mass loss. For reference we note that for an assumed ice composition, Brown et al. (2011) predicted a few percent mass fractional loss for a single perihelion passage at ~2 solar radii distance and a body of ~1015 g mass (appropriate for 2004 LG). While we do not have the expertise to evaluate these effects in more detail, we hope our results for 2004 LG may stimulate additional studies in this direction (e.g., extending the work of Brown et al. 2011, to a broader class of mineralogical compositions).
Parameter c is an integral of motion in an idealized secular model of asteroid motion introduced by Kozai (e.g., Kozai 1962; Morbidelli 2002). For asteroid orbits, c is nearly conserved unless located in one of the strong secular resonances. Note that objects impacting the Sun must be on orbits with a very high eccentricity, and consequently have very small c value. Therefore, the small value of c for 2004 LG makes it not only exceptional among NEAs, but also a candidate object for a possible solar impact.
Note, however, that for high temperatures the role of heat conduction decreases, which can be expressed by a small value of the thermal parameter (e.g., Spencer et al. 1989). This implies that the above estimate of the peak temperature is quite good (we thank Michael Muller for pointing this out).
Acknowledgments
The work of D.V. was supported by grants GACR 205/08/0064 and by the Research Program MSM0021620860 of the Ministry of Education. The work of D.N. was supported by the NASA Planetary Geology
and Geophysics program. We thank Michael Muller for his referee report that helped to improve this paper.
References
- Bailey, M. E. 1996, EMP, 72, 57 [Google Scholar]
- Bailey, M. E., Chambers, J. E., & Hahn, G. 1992, A&A, 257, 315 [NASA ADS] [Google Scholar]
- Bertotti, B., Farinella, P., & Vokrouhlický, D. 2003, Physics of the Solar System (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
- Bottke, W. F., Morbidelli, A., Jedicke, R., et al. 2002, Icarus, 156, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Bottke, W. F., Vokrouhlický, D., Rubincam, D. P., & Nesvorný, D. 2006, Ann. Rev. Earth Planet. Sci., 34, 157 [Google Scholar]
- Brown, J. C., Potts, H. E., Porter, L. J., & Le Chat, G. 2011, A&A, 535, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brož, M., & Vokrouhlický, D. 2008, MNRAS, 390, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Brož, M., Vokrouhlický, D., Morbidelli, A., Nesvorný, D., & Bottke, W. F. 2011, MNRAS, 414, 2716 [NASA ADS] [CrossRef] [Google Scholar]
- Čapek, D., & Vokrouhlický, D. 2010, A&A, 519, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, M., Levison, H., & Dones, L. 2004, in Comets II, ed. M. C. Festou et al. (Tucson: Arizona University Press), 193 [Google Scholar]
- Gladman, B. J., Migliorini, F., Morbidelli, A., et al. 1997, Science, 277, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Gladman, B., Michel, P., & Froeschlé, Ch. 2000, Icarus, 146, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Gonczi, R., Rickman, H., & Froeschlé, C. 1992, MNRAS, 254, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Greenstreet, S., Ngo, H., & Gladman, B. 2012, Icarus, 217, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gundlach, B., Blum, J., Skorov, Y. V., & Keller, H. U. 2012, Icarus, submitted [arXiv:1203.1808] [Google Scholar]
- Holsapple, K. A., & Michel, P. 2006, Icarus, 183, 331 [Google Scholar]
- Holsapple, K. A., & Michel, P. 2008, Icarus, 193, 283 [NASA ADS] [CrossRef] [Google Scholar]
- Farinella, P., Froeschlé, Ch., Froeschlé, C., et al. 1994, Nature, 371, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Knežević, Z., Lemaitre, A., & Milani, A. 2002, in Asteroids III, ed. W. F. Bottke et al. (Tucson: Arizona University Press), 603 [Google Scholar]
- Kozai, Y. 1962, AJ, 67, 591 [Google Scholar]
- Levison, H. F., & Dones, L. 2007, in Encyclopedia of the Solar System, ed. L.-A. McFadden et al. (Amsterdam: Academic Press), 575 [Google Scholar]
- Mann, I., Krivov, A., & Kimura, H. 2000, Icarus, 146, 658 [Google Scholar]
- Marchi, S., Delbò, M., Morbidelli, A., Paolicchi, P., & Lazzarin, M. 2009, MNRAS, 400, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Marsden, B. G. 2005, ARA&A, 43, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, P., & Yoshikawa, M., 2006, A&A 449, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michel, P., Farinella, P., & Froeschlé, Ch. 1998, AJ, 116, 2023 [NASA ADS] [CrossRef] [Google Scholar]
- Milani, A., & Gronchi, G. F. 2010, Theory of Orbit Determination (Cambridge: Cambridge University Press) [Google Scholar]
- Morbidelli, A. 2002, Modern Celestial Mechanics: Aspects of Solar System Dynamics (Taylor & Francis, Cambridge Scientific Publishers) [Google Scholar]
- Nobili, A.-M., & Roxburgh, I. W. 1986, in Relativity in Celestial Mechanics and Astrometry, ed. J. Kovalevsky, & V. A. Brumberg (Dordrecht: D. Reidel Publ.), 105 [Google Scholar]
- Nobili, A.-M., Milani, A., & Carpino, M. 1989, A&A, 210, 313 [NASA ADS] [Google Scholar]
- Sekanina, Z., & Chodas, P. W. 2005, ApJS, 161, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Spencer, J. R., Lebofsky, L. A., & Sykes, M. V. 1989, Icarus, 78, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Spitale, J., & Greenberg, R. 2001, Icarus, 149, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Vokrouhlický, D., Pokorný, P., & Nesvorný, D. 2012, Icarus, 219, 150 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Equinoctial orbital elements and their formal uncertainty for 2004 LG as of MJD 53 333.862633629 (middle of the currently available observation arc).
All Figures
 |
Fig. 1 Numerical integration of the nominal orbit of 2004 LG up to 8.9 ky when the heliocentric distance became smaller than solar radius. The upper three panels show the time evolution of the osculating semimajor axis (top), eccentricity (middle) and inclination (bottom). Each of them is affected by resonance phenomena that produce large-scale oscillations: the semimajor axis oscillates due to effects of the J4/1 mean motion resonance with Jupiter, eccentricity and inclination show correlated oscillations due to the Kozai resonance (with smaller effects of the J4/1 resonance too). The bottom-most panel shows the resonance angle φJ41 = 4λJ − λ − 3ϖ. |
| In the text | |
 |
Fig. 2 Results of a numerical integration of 1000 orbital clones of 2004 LG. The ordinate shows the percentage of clones that reached a given solar distance in <10 ky in the future (solid line) or in 100 ky in the future (dashed line). The solar distance is shown in units of solar radius. The upper abscissa shows an effective subsolar temperature due to solar irradiation. |
| In the text | |
 |
Fig. 3 Same as in Fig. 1, but for the backward evolution of the nominal orbit of 2004 LG; the abscissa is time in the past in ky. |
| In the text | |
 |
Fig. 4 Results from numerical propagation of 500 orbital clones of 2004 LG. The ordinate shows the percentage of clones that reached a given solar distance during the past maximum of the eccentricity cycle (some 3 ky ago). The distance is given in units of solar radius. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


