EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 541 (May 2012) A&A, 541 (2012) A30 Full HTML
Free Access
Issue
A&A
Volume 541, May 2012
Article Number A30
Number of page(s) 10
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201118187
Published online 24 April 2012

© ESO, 2012

1. Introduction

Since the first numerical simulations of core collapse supernovae in the 1960s (Colgate & White 1966; Arnett 1968a), enormous progress has been made on both the hydrodynamics and the microphysics. The effects of hydrodynamical instabilities, rotation, convection, and general relativity (GR) have been analysed and implemented in modern simulations. Several steps forward have also been made from the microphysical point of view, mainly concerning the nuclear equation of state and the knowledge of neutrino properties. Despite these improvements, a unified consensus on the supernova explosion scenario is still to be achieved. Different groups have been working in order to introduce more realistic physics. On the one hand, a detailed treatment of neutrino physics has been implemented in spherically symmetric models both in Newtonian gravity (Rampp & Janka 2000) and in GR (Liebendörfer et al. 2001). On the other hand, multi-dimensional codes have been developed with different approximation schemes for neutrino transport. New algorithms based either on implicit, adaptive grid solvers for hydrodynamics with the Boltzmann equation for neutrino transport (Liebendörfer et al. 2004), or explicit, conservative schemes with a Riemann-solver for hydrodynamics coupled with an implicit solver for the neutrino equations (such as the variable Eddington factor, Rampp & Janka 2002; and the “ray-by-ray-plus” method, Müller et al. 2010), were employed. Moreover, a significant effort has been made in order to implement a set of nuclear reactions other than the ones treated in Bruenn (1985). All state-of-the-art simulations of core collapse supernova, however, performed in Newtonian gravity (e.g. Rampp & Janka 2000; Thompson et al. 2003), in Newtonian gravity with relativistic corrections in the Newtonian potential (e.g. Buras et al. 2003, 2006a), in full GR (e.g. Mezzacappa et al. 2001; Liebendörfer et al. 2001, 2003, 2004, 2005), and with different equations of state (e.g. Janka et al. 2005; Sumiyoshi et al. 2005), agree with the results obtained in the 1980s and 1990s (e.g. Myra & Bludman 1989; Swesty et al. 1994). Namely, the prompt shock is not able to drive a supernova explosion, except in the case of small iron cores (Baron & Cooperstein 1990) or very soft equations of state (Baron et al. 1987). Even in the case of the delayed mechanism, spherically symmetric simulations, as well as 2- and 3-dimensional models with convection (e.g. Janka & Müller 1996; Burrows et al. 1995; Buras et al. 2006a) give a similar outcome: no successful explosion can be obtained for progenitors more massive than 10 M⊙.

More recently, it has been stressed that success in the numerical simulations might be attained by taking into account hydrodynamical instabilities, like standing accretion shock instability (SASI), which would act during shock stagnation, helping the neutrino energy deposition and the shock revival (Foglizzo 2002; Blondin et al. 2003; Foglizzo et al. 2007). Indeed, in the simulations performed by the Garching group, the onset of a SASI-aided explosion was obtained for a 11.2 M⊙ and a 15 M⊙ progenitor (Buras et al. 2006b; Marek & Janka 2009), producing an explosion energy of ~1051 erg. Some different mechanisms, such as magneto-hydrodynamical effects (e.g. Burrows et al. 2007) or acoustic power associated with the accreting proto-neutron star (Burrows et al. 2006) have also been proposed. Very recently, Nordhaus et al. (2010) investigated the dependence on spatial dimension of the neutrino heating mechanism in core collapse supernova. The authors claimed that the tendency of the models to explode increases monotonically with the dimension of the simulation, but these results were not confirmed by the study performed by Hanke et al. (2011). Despite the crucial role played by hydrodynamics, however, the correct treatment of how microphysics comes into play in the models is one of the major challenges for compact stars (and specifically core collapse supernovae) physics.

In particular, weak processes act in a crucial way throughout the collapse and the proto-neutron star formation. Electron capture on free protons and on exotic nuclei controls the neutronisation phase during collapse, until the formation of an almost deleptonised central compact object, the neutron star. Neutrinos, produced thermally and in such weak processes, escape freely from the star in the first phase of collapse. The rising density increases their diffusion timescale and, for densities  ≳1012 g cm-3, neutrinos become trapped, driving the system towards β equilibrium. After bounce, neutrinos are still trapped and diffuse outwards. Few hundreds of seconds after bounce, they carry out the energy gained in the collapse, contributing to the shock wave revival. We refer to the review by Bethe (1990) for a complete discussion of these phenomena and their relevance to supernova explosions.

Among the processes mediated by weak interaction, the electron capture is the main one acting during the infall phase. It determines the lepton fraction evolution and, as a consequence, the mass of the inner core. Indeed, at the onset of the collapse, the mass of the core is roughly the Chandrasekhar mass associated to the initial lepton fraction (i.e. the electron fraction at the beginning of the collapse) (Shapiro & Teukolski 1983): 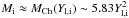. As the collapse proceeds, and before bounce, the density and the velocity profiles of the core obey a self-similar solution, and the mass of the homologous inner core can be determined from the value of the Chandrasekhar mass associated to the final (equilibrium) lepton fraction (Goldreich & Weber 1980): 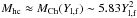. Therefore, a larger lepton fraction after trapping corresponds to a larger homologous core. The importance of the weak interaction rates and their effects in the supernova collapse dynamics have been demonstrated by different numerical simulations. In the pre-supernova stage, remarkable changes in the central electron fraction and entropy were noticed when using the shell model Monte Carlo rates (Langanke & Martínez-Pinedo 2000) instead of the Fuller et al. (1980, 1982) ones (Heger et al. 2001). Namely, the new rates result in higher (of about 0.01−0.015) central values of the electron fraction at the onset of core collapse, which in turn increases the Chandrasekhar mass, in lower (larger) core entropies for stars with M ≲ 20   M⊙ (M ≳ 20   M⊙), and generally smaller iron core masses (the reduction was by about 0.05   M⊙ for progenitors with M < 20   M⊙). In the collapse phase, the more recent rates calculated in the so-called hybrid model proposed by Langanke et al. (2001) have been included in the supernova simulations performed by the Oak Ridge and Garching collaboration and compared with the previous results employing the rates derived in Bruenn (1985). The outcome of the simulations has shown significant changes in the collapse trajectories and neutrino spectra (see e.g. Hix et al. 2003; Janka et al. 2007; Langanke et al. 2003). Indeed, an increase of the electron capture in the denser regions and a reduced electron capture in the outer regions have been observed for the new rates, leading to a shift of the position of the shock formation inwards of about 16% in the core mass and to a 10% smaller velocity across the shock. Moreover, the parameter study of Hix et al. (2005) shows that each increase of the rate of capture by a factor 10 corresponds roughly to the same decrease (~0.1   M⊙) of the mass of the homologous core.

In this work, we focus on the impact of a specific nuclear input during the core collapse phase of type II supernovae. By means of a one-dimensional Newtonian numerical simulation, we study the effect of the temperature dependence of the in-medium nucleon mass. In the article by Donati et al. (1994, Paper I from now on), a first investigation of the temperature dependence of the nuclear symmetry energy on the dynamics of the collapse was carried out in a one-zone (uniform mean density) model. This approach is easy to implement and nevertheless is able to incorporate the important physics coming into play. It is indeed suitable to make a preliminary study of the core deleptonisation during the infall epoch before core bounce, when the collapse is homologous (Esptein & Pethick 1981; Fuller 1982; Ray et al. 1984). The one-zone collapse simulation showed that the temperature dependence of the symmetry energy, Esym(T), derived from the temperature dependence of the nucleon effective mass m∗(T), yields a lower rate of neutronisation along the collapse. After Paper I, a further investigation of this particular issue related to electron capture has been conducted in the article by Fantina et al. (2009, Paper II). Although it is still based on a one-zone approximation, several improvements have been made over Paper I: (i) the treatment of electron capture on nuclei was switched from the statistical temperature-independent approach of Bethe et al. (1979, BBAL) to the temperature-dependent two-level transition fully described in Fuller (1982); (ii) neutrinos were included; neutrino trapping was set to start at a given density ρtr while in Paper I neutrinos were always streaming out freely (Yν = 0) and β equilibrium could never be reached; (iii) the initial conditions of the simulations were updated according to the recent pre-supernova conditions found after implementing improved shell model Monte Carlo capture rates in evolutionary stellar codes (Heger et al. 2001). The results obtained in Paper II confirmed those in Paper I, namely a systematic reduction of the neutronisation during the collapse phase and, as a consequence, a gain in the dissociation energy of the shock. This is expected for larger values of Esym, which in turn yield higher values of the electron fraction, Ye, at neutrino trapping density. Indeed, a larger lepton fraction after trapping corresponds to a larger homologous core. The shock wave, which forms at its edge after core bounce, will have less material to traverse in its way out of the iron core, and hence it will dissipate less energy in the photo-dissociation of tightly bound nuclei.

The purpose of the present article is to investigate within a more realistic hydrodynamical one-dimensional collapse simulation the extent to which the temperature dependence of the nucleon effective mass can affect the deleptonisation and the dynamics of the collapsing stellar core. In particular, we will analyse the position of formation of the shock wave, which is the first crucial hint in determining the possible success of the supernova explosion.

The paper is organised as follows: in Sect. 2 our physical model is described; in Sect. 3 the results obtained in such a framework are discussed; finally, in Sect. 4 we will give our conclusions and outlooks.

2. Description of the model

2.1. Hydrodynamics and neutrino transport

Our simulations are carried out with a Newtonian, spherically symmetric (1D) code (Blottiau 1989). The hydrodynamics and neutrino transport are coupled and solved by an implicit finite-differencing scheme written in Lagrangian coordinates. The core is divided into 40 zones, and the envelope into 60 zones, giving a total number of Nzone = 100. This grid spacing might raise some questions about the precision of the spatial grid. However, this spacing is sufficient to correctly reproduce the dynamical features we are interested in (collapse and shock formation) in a short computational time (few tens of hours), and allows a more precise neutrino energy resolution. The shock is treated in the shock tracking fashion; the prescription for the artificial viscosity is similar to the one given by Noh (1978). Unlike the latter, we set the artificial viscosity to a non-zero value only when the divergence (and not the gradient as in the paper by Noh 1978) of the velocity field is negative, a condition which ensures that the matter is in the compression phase. The system of conservation equations to be solved for each mass shell (i.e. mass, momentum and energy conservation, plus the electron number evolution equation) reads (Blottiau 1989; we also refer to Mihalas & Mihalas 1999, textbook for a complete treatment of the radiation hydrodynamics): 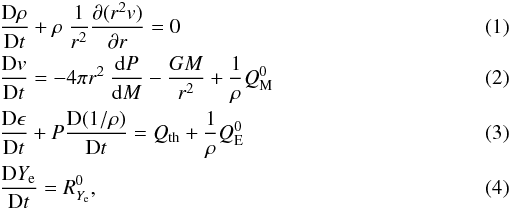where D is the Lagrangian derivative, ρ is the baryon density, Ye is the electron fraction, v is the infall velocity, P is the pressure, M is the enclosed mass, and ϵ is the specific internal energy (per unit mass). The source terms account respectively for the momentum (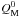) and energy (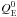) exchange from neutrinos to matter, the energy rate coming from dissociation reactions plus the nuclear thermal excitation energy (Qth), and the change in the electron fraction due to electron capture (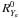). The superscript “0” refers to the comoving frame. An equation of state (EoS) P(ρ,T,Ye) is needed to close the system. Moreover, the transport equation for neutrinos has to be solved in each mass shell. The Boltzmann transport equation in spherical symmetry, neglecting 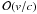terms, reads: (5)where f ≡ f(t,r,μ,ω) is the neutrino distribution function (where r is the distance of the considered fluid element from the centre of the star, μ is the cosine of the angle between the propagation direction of the neutrino and the outward radial direction, and ω is the neutrino energy). The collision integral, 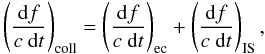(6)accounts for the emission and absorption from electron capture on nuclei and free protons (labelled as “ec”), and elastic scattering off nuclei and off nucleons (labelled as “IS”): where j(ω) is the neutrino emissivity, λ(a)(ω) is the neutrino absorption mean free path, 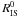is the isoenergetic scattering kernel, φ is the azimuthal angle of one neutrino relative to the other, and θ is the scattering angle: cosθ = μμ′ + [(1 − μ2)(1 − μ′2)] 1/2cosφ (Bruenn 1985). In the terms above, we have kept explicitly the energy dependence, while the spatial and time dependence has been suppressed for notational convenience. For the application considered in this paper, the neutrino-electron scattering has not been considered and only electron neutrinos have been taken into account. Indeed, other neutrino flavours come into play only in later stages of supernova collapse (see e.g. Janka et al. 2007).

For completeness, we report here the expressions for the source terms, according to Bruenn (1985): 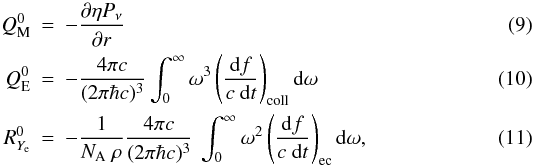where NA is Avogadro’s number, η is defined after Eq. (15) and Pν is the neutrino pressure: 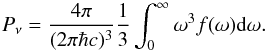(12)Finally, the nuclear thermal energy (per baryon) stored in excited states reads (Bethe et al. 1983): 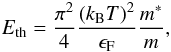(13)where kB is the Boltzmann constant and ϵF ≃ 40 MeV is the nuclear kinetic Fermi energy (Bethe et al. 1983). In the original work by Blottiau (Blottiau 1989), the nucleon effective mass m∗ (being m the bare nucleon mass) was density and isospin dependent, according to Eq. (3.6) in Bethe et al. (1983). Since the purpose of this article is to focus only on its temperature dependence, we have replaced this expression according to the parametrisation derived in Paper I, as explained in Sect. 2.2.

Neutrino transport is treated in the multi-group flux-limited diffusion approximation (MGFLDA) (Bruenn et al. 1978; Bowers & Wilson 1982a,b; Mellor 1988). In the diffusion approximation, the transport equation to be solved for each energy bin reads (Bowers & Wilson 1982a): 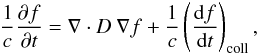(14)with the following choice for the diffusion coefficient (Bruenn 1985; Mellor et al. 1988): 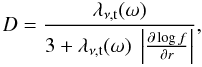(15)which defines η as: D/λν,t(ω) = η/3. The total neutrino mean free path, λν,t(ω), is given by: 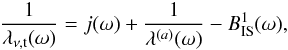(16)where 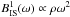is the first momentum of the isoenergetic scattering kernel 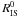. The neutrino energy is resolved in Nbin = 40 geometrically increasing energy groups from 10-2 MeV to 300 MeV. As noticed by Bruenn (1985), as a result of the MGFLDA, an additional term, which corresponds to the change in the neutrino distribution function due to compression or expansion of matter, must be taken into account. We follow the prescription in Appendix A of Bruenn (1985), where the author has pointed out that to treat consistently the energy exchange between matter and neutrinos for an arbitrary neutrino mean free path, only a fraction η(r,ω) of neutrinos must be affected by the compression/expansion term; the remaining fraction, 1 − η(r,ω), of the neutrino distribution function evolves according to the usual MGFLDA equation.

2.2. Equation of state

The star is divided into two distinct regions: the core and the envelope. The complex initial structure and composition of the envelope, determined by the different nuclear burning stages, are described by dividing it into shells. We impose the existence of a mean representative nucleus, following the results of the common stellar evolution codes (see e.g. Woosley & Weaver 1995; Woosley et al. 2002). Going from the edge of the inner core towards the surface, in the case of a 15 M⊙ progenitor with a core of about 1.26 M⊙, we distinguish: a silicon shell (up to 1.68 M⊙, where A = 28, Z = 14), an oxygen shell (up to 2.59 M⊙, where A = 16, Z = 8), a helium shell (up to 4.43 M⊙, where A = 4, Z = 2), and a hydrogen outer shell (A = 1, Z = 1). The electron fraction in the envelope is fixed to 0.5, and matter is treated as an ideal gas of baryons, electrons and photons. Therefore, in the following, we will discuss the EoS in the core. The original version of our Newtonian code (Blottiau 1989) relied on the EoS derived by BBAL. This EoS is based on a compressible liquid drop model, and the ensemble of nuclear species is approximated by a “mean nucleus” (the one which minimises the total energy of the system), in a sea of alpha particles, free neutrons and (fewer) protons. The composition is determined by the Saha equation for the dissociation of nuclei into α particles and neutrons, and of α particles into nucleons. For the high density region (above ~2 × 1013 g cm-3), the BBAL EoS is matched to the EoS derived in Suraud (1985) which models the transition from nuclei to nuclear matter.

At present, two hadronic EoSs are commonly used in core collapse simulations: the one by Lattimer & Swesty (1991, LS), and the one by Shen et al. (1998), which employ different nuclear interactions but are based on the same assumption that matter is formed by a mixture of non-interacting alpha particles, free neutrons and protons, and a single heavy nucleus, in addition to electron, positron and photon gas. Therefore, we have introduced in the code the LS EoS, routine version (v.2.7), open source and available from the Stony Brook group1. We have modified it in order to be able to run it at lower densities (Fantina 2010; Oertel & Fantina 2010), so that a unique EoS can be used in all the mass shells of the core.

However, both in Papers I and II, the BBAL EoS was implemented. The main reason for adopting such an EoS relies on the fact that it is fully analytical, and thus the implementation of the temperature dependent in-medium nucleon mass is easier, while it would be lengthly and not straightforward to introduce it in EoSs such as the LS one, and it would be impossible to do it in the Shen et al. (1998) EoS. Since we want to compare our results to the ones in Papers I and II, we have to employ the same input physics. We have thus chosen to run the code with the BBAL EoS, matched to the EoS derived in Suraud (1985) for the high density range. In contrast with the one-zone code, where the independent variables are chosen to be the density, the temperature and the electron fraction, the hydrodynamical code works with (ρ,ϵ,Ye) as independent variables. A routine which recovers the temperature from the internal energy has therefore been supplied.

The implementation of the temperature dependent in-medium nucleon mass is done as explained in Papers I and II. In Paper I, the T-dependence of the nuclear symmetry energy was derived from that of the nucleon effective mass m∗ in the range 0 < T < 2 MeV, due to the coupling of the mean field single-particle levels to the collective surface vibrations of the nucleus, calculated in the quasi-particle random phase approximation (QRPA). The influence of temperature on pairing in nuclei is therefore effectively included in the model. The nucleon effective mass was written as a product of two terms, the k-mass mk, due to the non-locality (or momentum dependence) of the mean field, and the ω-mass mω, due to the energy dependence of the mean field. The typical scale of variation of the k-mass with respect to temperature is of  ≈ 8 MeV, which is larger than the temperature encountered during the collapse phase where nuclei are expected to exist. Therefore, the question of the temperature dependence of m∗ can be formulated in terms of the temperature dependence of the ω-mass, keeping the k-mass temperature-independent. In particular, in Paper I, the value of mk was fixed to 0.76. The value of mω was found to decrease with temperature in the range 0 < T < 2 MeV. The numerical results, obtained for different nuclei, were parametrised with the following analytical expression: (17)where mω(T = 0) is the ω-mass calculated at zero temperature and T0 gives the typical scale of variation of mω with respect to T. We will adopt the “standard” average values of these two parameters: mω/m = 1.7 and T0 = 2 MeV. Their meaningful physical ranges are: 1.4 ≲ mω/m ≲ 1.8 and 1.9 ≲ T0 ≲ 2.1, which account for the dependence on the nucleus under study (Donati et al. 1994). In analogy to the results of the Fermi gas model and assuming that only the kinetic part of the symmetry energy depends on the effective mass, it has been argued in Paper I that the temperature dependence of Esym can be obtained by the following analytical expression: (18)where Z and A stand for the charge and mass number of the nucleus under study, kF = 1.35 fm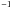 is the Fermi momentum at saturation density and s(0) = s(T = 0)  ≈ 30 MeV is the symmetry coefficient at zero temperature. The decrease of m∗ in the interval of temperatures 0 − 1 MeV was found to correspond to an increase of the nuclear symmetry energy, Esym, of ~8% (see Eqs. (17)–(18)). Several years later, Dean et al. (2002), using the shell model Monte Carlo framework, investigated directly the temperature dependence of the nuclear symmetry energy. Studying several isobaric pairs with mass number A = 56 − 66, the authors found a variation of the symmetry energy coefficient of ~6% in the temperature interval T = 0.33 − 1.23 MeV, in agreement with the results of Paper I.

The symmetry energy enters in the bulk nuclear energy and, as a consequence, in the neutron chemical potential, μn, and in the neutron-proton energy difference, 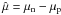: 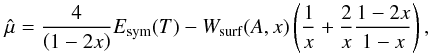(19)where x: = Z/A and Wsurf(A,x) = 290x2(1 − x)2A − 1/3 is the surface energy (Bethe et al. 1983). These quantities appear in the expressions for the free particle abundancies, in the Q-value of the electron capture reaction (see Eq. (23)), and in the nuclear entropy (Bethe et al. 1983): 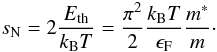(20)Thus, the temperature dependence of the in-medium nucleon mass and of the nuclear symmetry energy affects both the EoS of the system, and the electron capture rates on nuclei. In particular, the increase of the nuclear symmetry energy, Esym, yields an increase of the neutron-proton energy difference 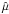. This is shown in Fig. 1 (upper panels) where Esym(T), Eq. (18), and 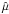, Eq. (19), are plotted as a function of temperature for three selected nuclei of astrophysical interest: 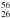Fe, 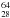Ni and 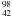Mo (the past two are among those studied in Paper I). We notice that most of the increase of Esym(T) is located in the temperature interval 0 − 4 MeV, which is the relevant one for the collapse phase. In the same temperature range, 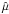increases by about a factor 2. One therefore expects that the increase of Esym with T would inhibit the electron capture on nuclei, resulting in a larger electron fraction during the deleptonisation phase. This theoretical prediction was indeed confirmed by the one-zone collapse simulations performed in Papers I and II. The numerical results obtained within our one-dimensional collapse simulations will be shown in Sect. 3. The lower panels of Fig. 1 display the impact of the temperature dependence of m∗ on the nuclear thermal energy2 and the corresponding entropy. The solid (dashed) lines represent the case where m∗ = m∗(0) (m∗ = m∗(T)) in Eqs. (13) and (20). Since these two quantities are plotted per baryon, there is no dependence on the mass number of the nucleus. Also in this case, the most of the effect due to the temperature dependence of the in-medium nucleon mass lies in the range T = 0 − 4 MeV (shown by the insets). At 2 MeV, the difference between Eth(m∗(0)) and Eth(m∗(T)) and between sN(m∗(0)) and sN(m∗(T)) is of about 26%, while at 4 MeV, this difference decreases to about 9%.

thumbnail Fig. 1

Upper panels: nuclear symmetry energy and neutron-proton energy difference as a function of temperature, for the nuclei Fe, Ni, Mo. Lower panels: nuclear thermal excitation energy and corresponding entropy (see text for details).

2.3. Treatment of electron capture

Electron capture is treated using the prescription given by Bruenn (1985). In order to explore the sensitivity of the model to uncertainties in the nuclear electron capture rates, we have performed a parameter study, each time varying the strength of the electron capture on nuclei. This is actually analogous to vary the parameter γ2 in the model described in Papers I and II.

We report for completeness and further discussions the expressions of the neutrino emissivity and the absorption mean free path for electron capture rates on nuclei as given in Bruenn (1985): where GF is the Fermi coupling constant, nbXh/A is the number density of the parent nucleus species, 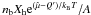the number density of excited (Z − 1,A) nuclei, gA = 1.23 is the axial coupling constant, fe is the Fermi distribution, me the electron mass, and: 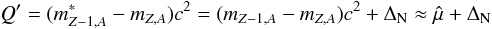(23)is the Q-value of the capture reaction3. The excitation energy of the nuclear Gamow-Teller (GT) resonance, ΔN, is set to 3 MeV (Bethe et al. 1979; Bruenn 1985). The product 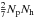represents an estimate of the typical GT matrix element |MGT|2 for the capture on nuclei: and it is meant to reproduce the zero-order shell model results (Fuller et al. 1982; Bruenn 1985). For simplicity and reproducibility of the results, we take the Bruenn (1985) capture rates as reference, and we then change by hand the product NpNh. The same procedure has been adopted e.g. in the paper by Hix et al. (2005).

3. Results

In order to perform a comparison with the literature, we have run the simulations of the collapse of a 15 M⊙ progenitor with a core of ~1.3   M⊙ using the routine version of the LS EoS (1991), version v2.7, modified to make it work at lower densities (Fantina 2010; Oertel & Fantina 2010). In Fig. 2 we plot the velocity (upper left panel), density (upper right panel), electron fraction (lower left panel) profiles as a function of the enclosed mass at bounce, and the evolution of the central lepton fraction (lower right panel) as a function of the increasing central density. The bounce is defined as the time when the maximum central density is reached. The results in Fig. 2 are shown for the value of the compressibility modulus K = 180 MeV and the “standard” Bruenn (1985) capture rates on nuclei. The bounce is located around 0.65 M⊙, which is in reasonable agreement with the Newtonian simulations showed by, e.g., Hix et al. (2005).

thumbnail Fig. 2

Velocity (upper left panel), density (upper right panel), electron fraction (lower left panel) profiles as a function of the enclosed mass at bounce, and the evolution of the central lepton fraction (lower right panel) as a function of the increasing central density, for the run with the LS EoS (K = 180 MeV) and Bruenn (1985) capture rates on nuclei.

We now analyse the influence of the temperature dependence of the in-medium nucleon mass. To do this, we run simulations employing the BBAL EoS matched to the Suraud EoS. In the expression for m∗, the value of the k-mass mk is fixed at 0.76, and mω is given by Eq. (17), as explained in Sect. 2.2. We have actually tested in our simulations the effect of the inclusion of the temperature dependence of the k-mass, according to a parametrisation which fits the results of Brueckner Hartree-Fock calculations (Vidaña, priv. comm.), and we have found no significant differences in the collapse trajectories. For each set of parameters, we run the code twice: either with m∗(T) or with m∗(0), i.e. taking or not into account the temperature dependence of the in-medium nucleon mass. A parameter study of the effect of the temperature dependence of m∗ is represented in Fig. 3, where the velocity and the lepton fraction profiles are shown at bounce for different strengths of electron capture rates on nuclei (from top to bottom panels): the “standard” Bruenn prescription (Bruenn 1985) with the product NpNh given by Eqs. (24)–(25), or fixing the product NpNh equal to 1 and 10 (consistent with the present theoretical uncertainties of the capture rates). We observe in all cases the same systematic behaviour: the deleptonisation is slightly reduced when the temperature dependence of the nucleon effective mass is considered, and the shock wave formation is shifted outwards. In Table 1 the maximum central density, together with the enclosed mass and central lepton fraction at shock formation, are listed. In the third and fourth column, in parentheses, the “thermal” variation δT due to the temperature dependence of the nucleon effective mass in nuclei is given: δTMb: = Mb|T − Mb|0 (for the enclosed mass), and δTYl,b: = Yl,b|T − Yl,b|0 (for the lepton fraction). We notice that the “thermal” variations of the lepton fraction (last column in Table 1) are in good agreement with the results obtained in Paper II. Despite the small values of δTYl ≃ 0.003 − 0.005, the effects on the position of the formation of the shock wave are quite large, namely δTMb ≃ 0.08 − 0.1   M⊙. This might be due to the influence of the temperature dependence of the in-medium nucleon mass on the EoS of the system rather than its influence on the electron capture rates. However, because of the non-linear relation among the T-dependent nucleon effective mass, the EoS (chemical potentials, abundancies, nuclear thermal excitation energy) and the Q-value of the capture reaction, it is difficult to decouple the different contributions. Nevertheless we want to investigate this question. Therefore, we have run a simulation, for the “standard” reference Bruenn capture rates, removing the contribution of the T-dependence of the nucleon effective mass from the nuclear thermal excitation energy (Eq. (13)). Indeed, in Paper II, the corresponding entropy term was claimed to have a non-negligible effect on the collapse trajectory. To this purpose, we have set m∗(T) = m∗(0) in Eq. (13), leaving the other equations containing m∗(T) unchanged. The results of the simulation are shown in Fig. 4. Since the expression for the Q-value is not modified, the effect of the temperature dependence of the nucleon effective mass is still acting on the capture rates. Indeed, even removing the contribution of m∗(T) in the nuclear thermal excitation energy, we still observe almost the same effect on the final lepton fraction at bounce (Fig. 4, right panel), i.e. the deleptonisation is reduced (δTYl ≃ 0.005), as in the case where m∗(T) is implemented everywhere. However, it is clear from the left panel, where the velocity profile at bounce is displayed, that the inclusion of m∗(T) in the nuclear thermal excitation energy turns out to be non-negligible in the collapse dynamics. Indeed, when the temperature dependence of the in-medium nucleon mass is implemented except in the nuclear thermal excitation energy (dashed-dotted line), the shock wave is forming at Mb ≃ 0.87   M⊙, to be compared with Mb ≃ 0.82   M⊙ when m∗ = m∗(0) and with Mb ≃ 0.90   M⊙ when m∗(T) is fully implemented. In conclusion, the contribution of the temperature dependence of the nucleon effective mass in the nuclear thermal excitation energy accounts for a non-negligible fraction of the global effect. This confirms the statement in Paper II (Sect. 2).

Table 1

Central density, enclosed mass, central lepton fraction at bounce, for different strengths of the electron capture on nuclei, and for m∗ = m∗(0) or m∗ = m∗(T).

We also notice that in the “standard” case (Fig. 3, upper panels), the shock is forming at ~0.8   M⊙, i.e. outwards with respect to the simulations carried by, e.g., Hix et al. (2005). This might come from the EoS adopted (BBAL together with the Suraud EoS), instead of the LS one (cf. Fig. 2). We also stress that the neutrino-electron scattering, which is expected to move the position of the formation of the shock wave inwards of about 0.1 M⊙ (Bethe 1990), is not included in our simulations.

thumbnail Fig. 3

Velocity (left panels), and lepton fraction (right panels) profiles as a function of the enclosed mass at bounce (see text for details).

thumbnail Fig. 4

Velocity (left panel), and lepton fraction (right panel) profiles as a function of the enclosed mass at bounce (see text for details). The capture rates are the “standard” ones by Bruenn (1985).

In order to further investigate the effect of the temperature dependence of the in-medium nucleon mass on the EoS during infall, we plot in Fig. 5 the pressure (left panel) and the specific internal energy (right panel) of the innermost zone in the core, as a function of the increasing central density, up to about nuclear matter density. The solid (dashed) lines correspond to the simulation where m∗ = m∗(0) (m∗ = m∗(T)) has been set. We notice that the effect is cumulative and non-linear, and the difference between the collapse trajectories δTP and δTϵ builds up as the density increases. As an example, at ρ ~ 3 × 1012 g cm-3 (ρ ~ 2.4 × 1014 g cm-3), the “thermal” difference in the pressure is δTP ≈ 4% (δTP ≈ 14%) and the “thermal” difference in the specific energy is δTϵ ≈ 5% (δTϵ ≈ 9%).

thumbnail Fig. 5

Pressure (left panel) and specific internal energy (right panel) as a function of the increasing central density. The capture rates are the “standard” ones by Bruenn (1985).

The position of the formation of the shock is undoubtedly a first crucial indication to estimate the possible fate of the shock wave. However, in order to evaluate the efficiency of the shock wave, it is important to follow the time evolution of the fluid trajectories and the propagation of the shock. In Fig. 6, the first few milliseconds of the time evolution of the radii of different mass shells are displayed as a function of the post-bounce time. The core is shown, together with the first shells of the envelope. Both panels show the results of the simulation where we employed the “standard” Bruenn (1985) capture rates, and the BBAL matched to the Suraud (1985) EoS. The left (right) panel corresponds to the simulation in which we set m∗ = m∗(0) (m∗ = m∗(T)). The lines indicate the trajectories of the fluid elements spaced by ~0.06   M⊙. We notice from Fig. 6 the collapse of the innermost shells, followed by the bounce (at t = tb) and the formation and propagation of the shock. Figure 6 also shows that the inclusion in the simulation of the temperature dependence of the in-medium nucleon mass not only shifts the position of the shock wave formation (see Fig. 3), but also leads to a gain in the position of the shock front in the first few milliseconds after bounce. Indeed, as an example, at 2 ms after bounce, the shock front is at ~90 km in the case illustrated by panel a), and at ~100 km in panel b). At 10 ms after bounce, the shock front is at ~130 km in the case illustrated by panel a), and at ~180 km in panel b). If compared to the position of the shock stagnation usually found in 1D simulations (around 100–200 km), the gain found after implementing the temperature dependence of the nucleon effective mass in nuclei (about 10% after 2 ms, and about 30% after 10 ms) is not negligible.

thumbnail Fig. 6

Time evolution (with respect to the time of bounce) of the trajectories of fluid elements spaced with an interval of ~0.06   M⊙, starting from the lowest mass shell at 0.059   M⊙. In the simulations we set a) m∗(0); b) m∗(T). The capture rates on nuclei are the “standard” ones by Bruenn (1985).

4. Conclusions

In this paper we have studied the impact of the temperature dependence of the nucleon effective mass in nuclei in a core collapse supernova simulation by means of a one-dimensional Newtonian code with neutrino transport treated in the MGFLDA. We have implemented this temperature dependence in the BBAL EoS, for comparison with Papers I and II, finding a systematic reduction of the deleptonisation during the collapse phase, in agreement with the results presented in Paper II. Moreover, we have evaluated the position of the formation of the shock wave. It is shifted outwards by a significative amount when the T-dependence of the in-medium nucleon mass is taken into account. Furthermore, we have shown that the shock front, in the first few milliseconds after the core bounce, is located outwards of about 10 km (50 km) at 2 ms (10 ms) after bounce in the simulation where we set m∗ = m∗(T). Therefore, even if we do not expect dramatic changes in the outcome of the simulation, we conclude that the implementation of the temperature dependence of the nucleon effective mass has a non-negligible effect on the shock wave propagation. We also notice that the temperature dependence of the in-medium nucleon mass has an important impact on the nuclear thermal excitation energy of the system.

Therefore, it would be interesting to include this effect in the GR framework, which has been shown to be physically relevant in compact star models (e.g. Bruenn et al. 2001; Dimmelmeier et al. 2006; Liebendörfer et al. 2001), and into multi-dimensional simulations, which are undoubtedly required to correctly reproduce the supernova mechanism, in particular during the long-term post-bounce evolution. The inclusion of such a temperature dependence in more realistic and commonly used EoSs, such as the LS one, or more recent EoSs based on statistical distribution of nuclei, is a further point to investigate.

However, different thermal effects other than the one discussed in this work can play a role in the supernova mechanism, and it is hard to determine a priori which ones are the most relevant to change considerably the picture. As far as concerning the EoS, it would be worth elaborating on the impact of temperature on the cluster structure at sub-saturation density, as well as on the temperature dependence of some key quantities such as the nuclear surface energy and the curvature parameter of the nuclear symmetry energy (Ksym) in asymmetric matter. In particular, the value of Ksym has been shown to be relevant for the estimation of the thickness of the neutron star crust (Vidaña et al. 2009). Nevertheless, this is not a straightforward task: supernova simulations rely most on tabulated EoSs and thus it is difficult to play with the different parameters. Finite temperature effects have a crucial role also in the calculation of the electron capture rates. It has been proved (Langanke et al. 2001) that the Gamow-Teller transitions, which dominate the electron capture cross sections, are unblocked by configuration mixing and thermal excitations for all temperatures relevant for supernova collapse, increasing the capture cross section with respect to the independent particle model picture. The peak and width of the Gamow-Teller strength are also affected by the temperature. Generally speaking, it has been noticed that, with increasing temperature, the Gamow-Teller peak is shifted downwards in energy and its strength is reduced. This makes the unblocking sensitive to temperature and lowers the energy threshold for the capture (see e.g. Civitarese & Ray 1999; Dzhioev et al. 2010; Radha et al. 1997). It is thus necessary to include these finite temperature effects in numerical simulations of core collapse to judge which among them can substantially modify the outcome of the simulations.

2

The thermal energy also represents the average excitation energy over the density of states.

3

The neutron and proton chemical potentials do not include the rest mass. Thus, the neutron-proton mass difference has to be explicitly included in computing the Q-value, Eq. (23).

Acknowledgments

We acknowledge Paola Donati (University of Milan), Micaela Oertel and Jérôme Novak from LUTh, Observatoire de Paris-Meudon, and Thierry Foglizzo from CEA, Service d’Astrophysique, for very fruitful discussions. This work has been supported by CompStar, a Research Networking Programme of the European Science Foundation, by the ANR NExEN and SN2NS, and by the exchanged fellowship program of the Université Paris-Sud XI. A.F.F. has been also supported by the Communauté française de Belgique – Actions de Recherche Concertées, and by the F.R.S.-FNRS (Belgium) via the contract of Chargé de Recherches.

References

  1. Arnett, W. D. 1968a, ApJ, 153, 341 [NASA ADS] [CrossRef] [Google Scholar]
  2. Arnett, W. D. 1968b, Nature, 219, 1344 [NASA ADS] [CrossRef] [Google Scholar]
  3. Baron, E., & Cooperstein, J. 1990, ApJ, 353, 597 [NASA ADS] [CrossRef] [Google Scholar]
  4. Baron, E., Bethe, H. A., Brown, G. E., Cooperstein, J., & Kahana, S. 1987, Phys. Rev. Lett., 59, 736 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bethe, H. A. 1990, Rev. Mod. Phys., 62, 801 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bethe, H. A., Brown, G. E., Applegate, J., & Lattimer, J. M. 1979, Nucl. Phys. A, 324, 487 [NASA ADS] [CrossRef] [Google Scholar]
  7. Bethe, H. A., Brown, G. E., Cooperstein, J., & Wilson, J. R. 1983, Nucl. Phys. A, 403, 625 [NASA ADS] [CrossRef] [Google Scholar]
  8. Blondin, J. M., Mezzacappa, A., & DeMarino, C. 2003, ApJ, 584, 971 [NASA ADS] [CrossRef] [Google Scholar]
  9. Blottiau, P. 1989, Ph.D. Thesis, Université Paris VII, Paris, France [Google Scholar]
  10. Bowers, R. B., & Wilson, J. R. 1982a, ApJS, 50, 115 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bowers, R. B., & Wilson, J. R. 1982b, ApJ, 263, 366 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bruenn, S. W. 1985, ApJS, 58, 771 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bruenn, S. W., Buchler, J. R., & Yueh, W. R. 1978, Ap&SS, 59, 261 [NASA ADS] [CrossRef] [Google Scholar]
  14. Bruenn, S. W., De Nisco, K. R., & Mezzacappa, A. 2001, ApJ, 560, 326 [NASA ADS] [CrossRef] [Google Scholar]
  15. Buras, R., Rampp, M., Janka, H.-Th., & Kifonidis, K. 2003, Phys. Rev. Lett., 90, 0241101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  16. Buras, R., Janka, H.-Th., Rampp, M., & Kifonidis, K. 2006a, A&A, 457, 281 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Buras, R., Rampp, M., Janka, H.-Th., & Kifonidis, K. 2006b, A&A, 447, 1049 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Burrows, A., Hayes, J., & Fryxell, B. A. 1995, ApJ, 450, 830 [NASA ADS] [CrossRef] [Google Scholar]
  19. Burrows, A., Livne, E., Dessart, L., Ott, C. D., & Murphy, J. 2006, New Astron. Rev., 50, 487 [NASA ADS] [CrossRef] [Google Scholar]
  20. Burrows, A., Dessart, L., Livne, E., Ott, C. D., & Murphy, J. 2007, ApJ, 664, 416 [NASA ADS] [CrossRef] [Google Scholar]
  21. Civitarese, O., & Ray, A. 1999, Phys. Scr., 59, 352 [NASA ADS] [CrossRef] [Google Scholar]
  22. Colgate, S. A., & White, R. H. 1966, ApJ, 143, 626 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dean, D.J., Langanke, K., & Sampaio, J. M. 2002, Phys. Rev. C, 66, 045802 [NASA ADS] [CrossRef] [Google Scholar]
  24. Dimmelmeier, H., Cerdá-Durán, P., Marek, A., & Faye, G. 2006, AIP Conf. Proc., 861, 600 [NASA ADS] [CrossRef] [Google Scholar]
  25. Donati, P., Pizzochero, P. M., Bortignon, P. F., & Broglia, R. A. 1994, Phys. Rev. Lett., 72, 2835 (Paper I) [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  26. Dzhioev, A. A., Vdovin, A. I., Ponomarev, V. Y., et al. 2010, Phys. Rev. C, 81, 015804 [NASA ADS] [CrossRef] [Google Scholar]
  27. Epstein, R. I., & Pethick, C. J. 1981, ApJ, 243, 1003 [NASA ADS] [CrossRef] [Google Scholar]
  28. Fantina, A. F. 2010, Supernovae theory: study of electro-weak processes during gravitational collapse of massive stars, Ph.D. Thesis, Université Paris-Sud 11, Orsay, France, and Università degli Studi di Milano, Milano, Italy [Google Scholar]
  29. Fantina A. F.,Donati, P., & Pizzochero, P. M. 2009, Phys. Lett. B, 676, 140 (Paper II) [NASA ADS] [CrossRef] [Google Scholar]
  30. Foglizzo, T. 2002, A&A, 392, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Foglizzo, T., Galletti, P., Scheck, L., & Janka, H.-Th. 2007, ApJ, 654, 1006 [NASA ADS] [CrossRef] [Google Scholar]
  32. Fuller, G. M. 1982, ApJ, 252, 741 [Google Scholar]
  33. Fuller, G. M., Fowler, W. A., & Newman, M. J. 1980, ApJS, 42, 447 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fuller, G. M., Fowler, W. A., & Newman, M. J. 1982, ApJ, 252, 715 [NASA ADS] [CrossRef] [Google Scholar]
  35. Fuller, G. M., Fowler, W. A., & Newman, M. J. 1985, ApJ, 293, 1 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  36. Goldreich, P., & Weber, S. V. 1980, ApJ, 238, 991 [NASA ADS] [CrossRef] [Google Scholar]
  37. Hanke, F., Marek, A., Mueller, B., & Janka, H.-T. 2011 [arXiv:1108.4355] [Google Scholar]
  38. Heger, A., Langanke, K., Martínez-Pinedo, G., & Woosley, S. E. 2001, Phys. Rev. Lett., 86, 1678 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  39. Hix, W. R., Messer, O. E. B., Mezzacappa, A., et al. 2003, Phys. Rev. Lett., 91, 201102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  40. Hix, W. R., Messer, O. E. B., Mezzacappa, A., et al. 2005, Nucl. Phys. A, 758, 31c [NASA ADS] [CrossRef] [Google Scholar]
  41. Janka, H.-Th., & Müller, E. 1996, A&A, 306, 167 [NASA ADS] [Google Scholar]
  42. Janka, H.-Th., Buras, R., Kitaura Joyanes, F. S., et al. 2005, Nucl. Phys. A, 758, 19c [NASA ADS] [CrossRef] [Google Scholar]
  43. Janka, H.-Th., Langanke, K., Marek, A., Martínez-Pinedo, G., & Müller, B. 2007, Phys. Rep., 442, 38 [NASA ADS] [CrossRef] [Google Scholar]
  44. Langanke, K., & Martínez-Pinedo, G. 2000, Nucl. Phys. A, 673, 481 [NASA ADS] [CrossRef] [Google Scholar]
  45. Langanke, K., Kolbe, E., & Dean, D. J. 2001, Phys. Rev. C, 63, 032801 [NASA ADS] [CrossRef] [Google Scholar]
  46. Langanke, K., Martínez-Pinedo, G., Sampaio, J. M., et al. 2003, Phys. Rev. Lett., 90, 241102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  47. Lattimer, J. M., & Swesty, F. D. 1991, Nucl. Phys. A, 535, 331 [NASA ADS] [CrossRef] [Google Scholar]
  48. Liebendörfer, M., Mezzacappa, A., Thielemann, F.-K., et al. 2001, Phys. Rev. D, 63, 103004 [NASA ADS] [CrossRef] [Google Scholar]
  49. Liebendörfer, M., Mezzacappa, A., Messer, O. E. B., et al. 2003, Nucl. Phys. A, 719, 144c [NASA ADS] [CrossRef] [Google Scholar]
  50. Liebendörfer, M., Messer, O. E. B., Mezzacappa, A., et al. 2004, ApJS, 150, 263 [NASA ADS] [CrossRef] [Google Scholar]
  51. Liebendörfer, M., Rampp, M., Janka, H.-Th., & Mezzacappa, A. 2005, ApJ, 620, 840 [NASA ADS] [CrossRef] [Google Scholar]
  52. Marek, A., & Janka, H.-Th. 2009, ApJ, 694, 664 [NASA ADS] [CrossRef] [Google Scholar]
  53. Mellor, Ph. 1988, Modélisation des Supernovae de type II: simulation du transport des neutrinos, Ph.D. Thesis, Université Paris VII, Paris, France [Google Scholar]
  54. Mellor, Ph., Chièze, J. P., & Basdevant, J. L. 1988, A&A, 197, 123 [NASA ADS] [Google Scholar]
  55. Mezzacappa, A., Liebendörfer, M., Messer, O. E. B., et al. 2001, Phys. Rev. Lett., 86, 1935 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  56. Mihalas, D., & Weibel-Mihalas, B. 1999, Foundation of Radiation Hydrodynamics (Mineola New York USA: Dover Publications Inc.) [Google Scholar]
  57. Müller, B., Janka, H.-Th., & Dimmelmeier, H. 2010, ApJS, 189, 104 [NASA ADS] [CrossRef] [Google Scholar]
  58. Myra, E. S., & Bludman, S. A. 1989, ApJ, 340, 384 [NASA ADS] [CrossRef] [Google Scholar]
  59. Noh, W. F. 1978, J. Comp. Phys., 72, 78 [Google Scholar]
  60. Nordhaus, J., Burrows, A., Almgren, A., & Bell, J. 2010, ApJ, 720, 694 [NASA ADS] [CrossRef] [Google Scholar]
  61. Oertel, M., & Fantina, A. F. 2010, SF2A-2010: Proc. Annual meeting of the French Society of Astronomy and Astrophysics, 185 [Google Scholar]
  62. Radha, P. B., Dean, D. J., Koonin, S. E., Langanke, K., & Vogel, P. 1997, Phys. Rev. C, 56, 3079 [NASA ADS] [CrossRef] [Google Scholar]
  63. Rampp, M., & Janka, H.-Th. 2000, ApJ, 539, L33 [NASA ADS] [CrossRef] [Google Scholar]
  64. Rampp, M., & Janka, H.-Th. 2002, A&A, 396, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Ray, A., Chitre, S. M., & Kar, K. 1984, ApJ, 285, 766 [NASA ADS] [CrossRef] [Google Scholar]
  66. Shapiro, S. L., & Teukolsky, S. A. 1983, Black holes, White Dwarfs, and Neutron Stars (New York, USA: John Wiley & Sons) [Google Scholar]
  67. Shen, H., Toki, H., Oyamatsu, K., & Sumiyoshi, K. 1998, Nucl. Phys. A, 637, 435 [NASA ADS] [CrossRef] [Google Scholar]
  68. Sumiyoshi, K., Yamada, S., Suzuki, H., et al. 2005, ApJ, 629, 922 [NASA ADS] [CrossRef] [Google Scholar]
  69. Suraud, E. 1985, A&A, 143, 108 [NASA ADS] [Google Scholar]
  70. Swesty, F. D., Lattimer, J. M., & Myra, E. S. 1994, ApJ, 425, 195 [NASA ADS] [CrossRef] [Google Scholar]
  71. Thompson, T. A., Burrows, A., & Pinto, P. A. 2003, ApJ, 592, 434 [NASA ADS] [CrossRef] [Google Scholar]
  72. Vidaña, I., Providência, C., Polls, A., & Rios, A. 2009, Phys. Rev. C, 80, 045806 [NASA ADS] [CrossRef] [Google Scholar]
  73. Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [NASA ADS] [CrossRef] [Google Scholar]
  74. Woosley, S. E., Heger, A., & Weaver, T. A. 2002, Rev. Mod. Phys., 74, 1015 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

Central density, enclosed mass, central lepton fraction at bounce, for different strengths of the electron capture on nuclei, and for m∗ = m∗(0) or m∗ = m∗(T).

In the text

All Figures

thumbnail Fig. 1

Upper panels: nuclear symmetry energy and neutron-proton energy difference as a function of temperature, for the nuclei Fe, Ni, Mo. Lower panels: nuclear thermal excitation energy and corresponding entropy (see text for details).
In the text
thumbnail Fig. 2

Velocity (upper left panel), density (upper right panel), electron fraction (lower left panel) profiles as a function of the enclosed mass at bounce, and the evolution of the central lepton fraction (lower right panel) as a function of the increasing central density, for the run with the LS EoS (K = 180 MeV) and Bruenn (1985) capture rates on nuclei.
In the text
thumbnail Fig. 3

Velocity (left panels), and lepton fraction (right panels) profiles as a function of the enclosed mass at bounce (see text for details).
In the text
thumbnail Fig. 4

Velocity (left panel), and lepton fraction (right panel) profiles as a function of the enclosed mass at bounce (see text for details). The capture rates are the “standard” ones by Bruenn (1985).
In the text
thumbnail Fig. 5

Pressure (left panel) and specific internal energy (right panel) as a function of the increasing central density. The capture rates are the “standard” ones by Bruenn (1985).
In the text
thumbnail Fig. 6

Time evolution (with respect to the time of bounce) of the trajectories of fluid elements spaced with an interval of ~0.06   M⊙, starting from the lowest mass shell at 0.059   M⊙. In the simulations we set a) m∗(0); b) m∗(T). The capture rates on nuclei are the “standard” ones by Bruenn (1985).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.