| Issue |
A&A
Volume 541, May 2012
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 10 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117763 | |
| Published online | 26 April 2012 | |
Interstellar polarization and grain alignment: the role of iron and silicon⋆
1
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail: voshchinnikov@mpia.de
2
Sobolev Astronomical Institute, St. Petersburg University,
Universitetskii prosp. 28, 198504
St. Petersburg,
Russia
e-mail: nvv@astro.spbu.ru
3
Isaac Newton Institute of Chile, St. Petersburg Branch,
Russia
4
IUCAA, Post Bag 4, Ganeshkhind, 411 007
Pune,
India
Received: 25 July 2011
Accepted: 9 March 2012
We compiled the polarimetric data for a sample of lines of sight with known abundances of Mg, Si, and Fe. We correlated the degree of interstellar polarization P and polarization efficiency (the ratio of P to the colour excess E(B − V) or extinction AV) with dust phase abundances. We detect an anticorrelation between P and the dust phase abundance of iron in non silicate-containing grains [Fe(rest)/H]d, a correlation between P and the abundance of Si, and no correlation between P/E(B − V) or P/AV and dust phase abundances. These findings can be explained if mainly the silicate grains aligned by the radiative mechanism are responsible for the observed interstellar linear polarization.
Key words: dust, extinction / ISM: abundances / polarization
Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The modelling of interstellar polarization includes light scattering calculations for aligned non-spherical particles. It is usually performed for particles of simple shapes (infinite cylinders or homogeneous spheroids) and the particles are very often assumed to be perfectly aligned (Mathis 1986; Kim & Martin 1995; Draine & Fraisse 2009). The reasons for these simplifications are a poor knowledge of alignment mechanisms (see Lazarian 2009, for a recent review) and the impossibility of light scattering calculations for complex aggregate particles of intermediate and large sizes (Michel et al. 1996; Farafonov & Il’in 2006; Borghese et al. 2007; Min 2009).
According to standard concepts (Krügel 2003; Whittet 2003), the alignment of interstellar grains may be magnetic or radiative. Magnetic alignment occurs if pure iron or iron components in dust grains interact with the magnetic field. Radiative torque alignment (RAT alignment) arises from an azimuthal asymmetry of the light scattering by non-spherical particles. Magnetic inclusions can enhance RAT alignment (Lazarian & Hoang 2008). The amount of iron in dust grains can be found from dust phase abundances. Using them, we can estimate the grain composition and, as a consequence, the scattering and polarizing properties of interstellar dust.
In this paper, we analyse the relation between the interstellar polarization and dust phase abundances of Mg, Si, and Fe previously compiled by Voshchinnikov & Henning (2010, VH10). We assume that all silicon and magnesium and a part of iron are incorporated into amorphous silicates. We correlate the amount of the remaining iron as well as dust phase abundances of Mg, Si, and Fe with the polarization degree P or polarization efficiency (the ratio of P to the colour excess E(B − V) or extinction AV) and draw some conclusions on grains producing interstellar polarization and favourite alignment mechanism.
2. Polarization and alignment mechanisms
The fact that interstellar grains polarize starlight has important implications. It requires the simultaneous fulfilment of the following conditions in a given direction.
-
1.
Dust grains must be non-spherical.
-
2.
Dust grains must have sizes close to the wavelength of incident radiation because big particles do not polarize the transmitted radiation even if they are perfectly orientated (Voshchinnikov et al. 2000).
-
3.
Dust grains must have specific magnetic properties to interact with the interstellar magnetic field.
-
4.
Dust grains must be aligned.
-
5.
The direction of alignment must not coincide with the line of sight.
-
6.
The distribution of aligned grains along the line of sight must be quite regular to exclude the cancellation of polarization.
The most discussed item is the alignment mechanism. A very popular alignment mechanism is the magnetic alignment (Davis-Greenstein (DG) type orientation, Davis & Greenstein 1951) based on the paramagnetic relaxation of grain material containing about one percent of iron impurities. The DG mechanism requires a stronger magnetic field than average galactic magnetic field (~3−5 μG; Heiles & Crutcher 2005). Because of this problem, it has been suggested that the polarizing grains contain small clusters of iron, iron sulfides, or iron oxides with superparamagnetic or ferromagnetic properties (Jones & Spitzer 1967). This leads to an enhancement of the imaginary part of the magnetic susceptibility of grain material χ″ by a factor 10–100 and alignment can occur through the DG mechanism. This scenario is supported by laboratory experiments (Djouadi et al. 2007; Belley et al. 2009). A significant enhancement of χ″ is also possible in mixed MgO/FeO/SiO grains (Duley 1978) or in H2O ice mantle grains containing magnetite (Fe3O4) precipitates (Sorrell 1994; 1995).
A very important factor of any alignment mechanism is grain rotation. The faster it is, the more effective the grain alignment should be. The DG mechanism assumes thermally rotating grains. Purcell (1979) suggested a mechanism of supra-thermal spin alignment (“pinwheel” mechanism) where the grains are spun up to very high velocities as a result of the desorption of H2 molecules from their surfaces.
Fast rotation can also arise because of radiation torques when asymmetrical grains scatter the radiation (Dolginov et al. 1979; Draine & Weingartner 1997), which can lead to grain alignment in an anisotropic radiation field. Radiation torque is a manifestation of the radiation pressure force possessing a transversal component directed perpendicular to the direction of the incident radiation. This component was measured in laboratory experiments (Abbas et al. 2004; Krauß & Wurm 2004). It can be easily calculated for cylindrical (Voshchinnikov & Il’in 1983) and spheroidal (Voshchinnikov 1990; Il’in & Voshchinnikov 1998) grains and estimated for fluffy aggregates (Kimura & Mann 1998). The transversal component is larger for dielectric particles and plays an important role in the motion of interplanetary and circumstellar grains (Il’in & Voshchinnikov 1998; Kimura et al. 2002; Kocifaj & Klac˘ka 2004).
The theory of RAT alignment is well developed (Lazarian & Hoang 2007). Recent observations of interstellar polarization in the vicinity of luminous stars (Andersson & Potter 2010; Matsumura et al. 2011; Andersson et al. 2011) have been used for confirmation of the RAT alignment mechanism. However, the discussed models are phenomenological, they are not based on correct light scattering calculations of interstellar polarization. One of the reasons is that the alignment function for the RAT mechanism is unknown. Another reason is a requirement of advanced light scattering methods because fast rotation can only occur for grains of very specific (helical) shape (Dolginov et al. 1979; Lazarian & Hoang 2007). This is highly improbable from the point of view of grain growth in the interstellar medium.
In any event, since both magnetic alignment and radiative alignment depend on iron inclusions, we can expect that polarization and/or polarization efficiency should increase with the growth of iron fraction in dust grains. A goal of our investigation is to check this suggestion using the available data on interstellar polarization and element abundances.
3. Results and discussion
We compiled the polarimetric data for a sample of 196 targets with known dust phase abundances collected in VH10. Polarimetric observations of 13 stars in the V band were performed by one of the authors (HKD) in October 2011 at a 2 m telescope of the IUCAA Girawali Observatory (Pune, India). The polarization degree P in percent with 1σ error and the corresponding reference are given in Table 1 (Cols. 9 and 13). The total number of stars with measured polarization is 172. Columns 10 and 11 contain the ratios of P to the colour excess E(B − V) and visual extinction AV1, which characterizes the polarization
 |
Fig. 1 Polarization according to colour excess for 172 stars from Table 1. Variable stars and stars with peculiar spectra are marked. The straight line shows the empirical upper limit for interstellar polarization (Serkowski et al. 1975). |
efficiency of the interstellar medium in a given direction. In Table 1, the extinction AV and the ratio P/E(B − V) were calculated assuming 1σ error for E(B − V) equal to 0.01.
We marked stars with a peculiar spectrum (“s”) and variable stars (“v”). For these, a part of the observed polarization may be intrinsic. However, the positions of these stars on the diagram P vs. E(B − V) do not look unusual (see Fig. 1). In the direction of variable stars or stars with peculiar spectrum where the interstellar polarization was determined from polarization of surrounding stars, we used this interstellar polarization (labelled “i”). The polarimetric data are mainly related to the visual part of spectrum (V band). For stars marked “m” the value of the maximum polarization Pmax is given. The major part of observations was taken from the catalogues of Heiles (2000), Serkowski et al. (1975), and Efimov (2009). In the latter case, we used Pmax obtained for the Serkowski curve approximated according to Whittet et al. (1992).
Voshchinnikov & Henning (2010) found a sharp distinction in abundances of Mg, Si, and Fe for sightlines located at low (| b| < 30°) and high (| b| > 30°) galactic latitudes. For high-latitude stars the ratios Mg/Si and Fe/Si in dust are close to 1.5. For disk stars these ratios are reduced to ~1.2 and ~1.05 for Mg and Fe, respectively. The derived numbers indicate that the dust grains cannot be just a mixture of only olivine (Mg2xFe2−2xSiO4) and pyroxene (MgyFe1−ySiO3) silicates (here 0 ≤ x,y ≤ 1). Some amount of magnesium or iron (or both) should be embedded into other materials.
Based on the discussion of alignment mechanisms (Sect. 2), we suggest that the interstellar polarization is probably be related to the amount of iron in dust grains. We assume that all silicon and all magnesium are embedded into amorphous silicates of olivine composition (Mg2xFe2−2xSiO4, where x = [Mg/H] d/(2 [Si/H] d) as is a part of iron. The remaining part of Fe can be found as ![\begin{equation} \left [{\rm {Fe(rest)}/{H}} \right ]_{\rm d} = \left [{\rm {Fe}/{H}} \right ]_{\rm d} - (2\,\left [{\rm {Si}/{H}} \right ]_{\rm d} - \left [{\rm {Mg}/{H}} \right ]_{\rm d}). \label{fer} \end{equation}](/articles/aa/full_html/2012/05/aa17763-11/aa17763-11-eq26.png) (1)It is expected to be in the form of various iron oxides (FeO, Fe2O3, Fe3O4) and/or metallic iron, which confers magnetic properties to the grains.
(1)It is expected to be in the form of various iron oxides (FeO, Fe2O3, Fe3O4) and/or metallic iron, which confers magnetic properties to the grains.
 |
Fig. 2 Polarization of 95 stars according to the remaining dust phase abundance of Fe as given by Eq. (1) normalized to the cosmic abundance of iron. Halo stars with |b| > 30° and disk stars with |b| ≤ 30° and low (E(B − V) ≤ 0.2) and high (E(B − V) > 0.2) reddening are shown with different symbols. Filled symbols correspond to sightlines where the abundances of three elements (Mg, Si, and Fe) are measured. Open symbols correspond to sightlines where the abundances of two elements (Fe and Mg or Si) are known. The number of stars is indicated in parentheses in the legend. |
Our choice of Mg-rich silicates with the olivine stoichiometry is based on the theoretical and observational studies of dust composition in circumstellar environments (Gail 2010; Molster et al. 2010; Sturm et al. 2010) and on the interpretation of the observed interstellar silicate absorption profiles (Min et al. 2007; van Breemen et al. 2011). Probably the single exception is the oxygen-rich AGB star T Cep, whose peak wavelength in the IR features suggests the presence of Fe-rich silicates (Niyogi et al. 2011).
Pearson correlation coefficients between polarization, extinction, and element abundances in the dust phase.
Using Eq. (1), we calculated the dust phase abundance of Fe incorporated into non-silicate materials [Fe(rest)/H]d (see Col. 13 in Table 1). Then these abundances were normalized to the solar (cosmic) abundance of iron ([Fe/H]⊙ = 31.6 ppm, Asplund et al. 2009)2 and we correlated them with the polarization and polarization efficiency. The results are shown in Figs. 2 and 3 and in Table 2 (rows 1–3). The abundances of the three elements Mg, Si, and Fe were measured only for the 28 targets with known polarization. They are plotted in the figures using filled symbols. To increase the sample volume, we calculated [Fe(rest)/H]d for sightlines where the abundances of two elements (Fe and Mg or Si) were known. In this case, we use the average abundance of the third (lacking) element as given in rows 2−5 of Table 2 in VH10. These data are shown by open symbols in Figs. 2 and 3. Clearly, the amount of Fe in non-silicates is quite high, especially for low-reddened (E(B − V) ≲ 0.2) and halo (| b| > 30°) stars. There is also a tendency for a decline in polarization (see Fig. 2) with transition from high-reddened to low-reddened stars, which likely reflects a fall of the column density of polarizing grains. An exception is the sightline towards the star N 195 (CPD –59 2603), where the dust phase abundance of Si is very low. There are also three targets (NN 78, 81, and 89) where the calculated values of [Fe(rest)/H]d are negative. We excluded these four stars from the correlation analysis (rows 1–3 in Table 2).
As indicated in Fig. 2, there is a negative correlation between the polarization degree P and the amount of remaining iron. This is inconsistent with the common suggestion about the great role of iron-rich grains in the production of polarization. Because P is proportional to the column density of polarizing grains, we can conclude that the increase of the iron content in non-silicate grains does not enhance polarization. These particles may be spherical, very large or very small in comparison with radiation wavelength, or they may be less aligned. It is also important that metallic iron or iron oxides have high refractive indices, and particles consisting of these materials scatter less radiation compared with (Mg, Fe)-silicates, which prevents radiative torques. Therefore, we can conservatively estimate that the radiative alignment is the favourite alignment mechanism of the interstellar grains.
 |
Fig. 4 Interstellar polarization according to dust phase abundance of iron. Halo stars with |b| > 30° and disk stars with |b| ≤ 30° and low (E(B − V) ≤ 0.2) and high (E(B − V) > 0.2) reddening are shown with different symbols. The number of stars is indicated in parentheses in the legend. |
Because in calculating [Fe(rest)/H]d we removed all Si and Mg and a part of Fe from the dust phase, we expect a positive correlation between the polarization and the abundances of the eliminated elements. Figures 4–6 show the dependence of interstellar polarization on dust phase abundances of iron, magnesium, and silicon. Evidently, there is only a weak correlation between P and [Fe/H]d or [Mg/H]d and a strong correlation between P and [Si/H]d. Therefore, we can establish that polarization is more likely produced by silicates. These findings are evidence in favour of the assumption of Mathis (1986) that only the silicate grains are aligned and contribute to the observed polarization, while the carbonaceous grains are either spherical or randomly aligned. Note that a poor alignment of carbonaceous grains compared with silicate grains also follows from the consideration of disalignment caused by thermal flipping or discrete charging (Weingartner 2006). Another verification of this suggestion is the absence of any correlation between the polarization efficiency P/E(B − V) or P/AV and dust phase abundances of elements (see Table 2 and Fig. 3). This is because dust grains of all types (silicate, carbonaceous, iron-rich, etc.) contribute to the observed extinction AV and most likely to the colour excess E(B − V) = AB − AV, while only the silicates seems to be responsible for the observed polarization. Thus, the absence of correlation between the ratio of the total to selective extinction RV and the wavelength of maximum polarization λmax observed in many cases (e.g., Whittet et al. 2001; Andersson & Potter 2007) can be easily understood.
4. Conclusions
The main results of the paper can be formulated as follows.
-
1.
We compiled the polarimetric data for a sample of196 lines of sight with known dust phaseabundances of Mg, Si, and Fe collected in Voshchinnikov &Henning (2010). The total number of stars with measuredpolarization is 172. Polarimetric observations of 13 stars arepresented for the first time in this paper.
-
2.
Assuming that all Si and Mg and a part of Fe are incorporated into amorphous silicates of olivine composition, we calculated the dust phase abundance of the remaining iron. The fraction of iron not included in silicates [Fe(rest)/H]d is quite high: changing from ~0.1 of cosmic abundance of Fe for reddened disk (| b| < 30°, E(B − V) > 0.2) stars to ~0.8 for halo (| b| > 30°) stars.
-
3.
We detect an anticorrelation between P and [Fe(rest)/H]d (rcorr. = −0.638) and a correlation between P and dust phase abundances of Si (rcorr. = 0.736). We conclude that it is more likely that polarization is produced by silicates and is not produced by iron-rich non-silicate grains. Because silicate grains scatter more radiation than grains of other types (carbonaceous, iron oxides, etc.), these findings can be interpreted in favour of the radiative alignment of interstellar grains.
-
4.
We found no correlation between the polarization efficiency (the ratio of P to the colour excess E(B − V) or extinction AV) and the dust phase abundances of Mg, Si, or Fe. This fact can be explained if we assume that dust grains of all types contribute to AV and E(B − V), while only the silicates are responsible for the observed polarization.
Online material
Polarization of stars with known dust phase abundances.
Acknowledgments
We thank Albina Timirbaeva for assistance in collecting the observational data, Andrei Berdyugin for sending the polarimetric data, and Vladimir Il’in, Svitlana Zhukovska, and Alex Lazarian for stimulating discussions. We are grateful to the anonymous referee for comments and suggestions. The work was partly supported by the grants RFBR 10-02-00593 and 11-02-92695.
References
- Abbas, M. M., Craven, P. D., Spann, J. F., et al. 2004, ApJ, 614, 781 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, B.-G., & Potter, S. B. 2007, ApJ, 665, 369 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, B.-G., & Potter, S. B. 2010, ApJ, 720, 1045 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, B.-G., & Wannier, P. G. 1997, ApJ, 491, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Andersson, B.-G., Pintado, O., Potter, S. B., Straizys, V., & Charcos-Llorens, M. 2011, A&A, 534, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Belley, F., Ferré, E. C., Martín-Hernândez, F., et al. 2009, Earth Plan. Sci. Lett., 284, 516 [Google Scholar]
- Borghese, F., Denti, P., & Saija, R. 2007, Scattering by model non-spherical particles, second edition (Heidelberg: Springer) [Google Scholar]
- Das, H. K., Voshchinnikov, N. V., & Il’in, V. B., 2010 MNRAS, 404, 265 [NASA ADS] [Google Scholar]
- Davis, L., & Greenstein, J. L. 1951, ApJ, 114, 206 [Google Scholar]
- Djouadi, G., Gattacecca, J., d’Hendecourt, L., et al. 2007, A&A, 468, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dolginov, A. Z., Gnedin, Yu. N., & Silant’ev, N. A. 1979, Propagation and Polarization of Radiation in Cosmic Medium (Moscow: Nauka) [Google Scholar]
- Duley, W. W. 1978, ApJ, 219, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Fraisse, A. A. 2009, ApJ, 626, 1 [NASA ADS] [Google Scholar]
- Draine, B. T., & Weingartner, J. C. 1997, ApJ, 480, 663 [Google Scholar]
- Efimov, Yu. S. 2009, Bull. CrAO, 105, 82 [Google Scholar]
- Elias, N. M., Koch, R. H., & Pfeiffer, R. J. 2008, A&A, 489, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Farafonov, V. G., & Il’in, V. B. 2006, in Light Scattering Reviews, ed. A. A. Kokhanovsky (Springer), 1, 125 [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. L. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gail, H.-P. 2010, in Astromineralogy, second edition, ed. Th. Henning (Springer), Lect. Notes Phys., 815, 61 [Google Scholar]
- Ghosh, K., Iyengar, K. V. K., Ramsey, B. D., & Austin, R. A. 1999, AJ, 118, 1061 [NASA ADS] [CrossRef] [Google Scholar]
- Harries, T. J., Howarth, I. D., & Evans, C. J. 2002, MNRAS, 337, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 2000, AJ, 119, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Crutcher, R. 2005, in Cosmic Magnetic Fields, ed. R. Wielebinski, & R. Beck, Lect. Notes Phys., 664, 137 [Google Scholar]
- Jones, R. V., & Spitzer, L. 1967, ApJ, 147, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Il’in, V. B., & Voshchinnikov, N. V. 1998, A&AS, 128, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kim, S.-H., & Martin, P. G. 1995, ApJ, 444, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, H., & Mann, I. 1998, JQSRT, 60, 425 [NASA ADS] [Google Scholar]
- Kimura, H., Okamoto, H., & Mukai, T. 2002, Icarus, 157, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Kocifaj, M., & Klačka, J. 2004, JQSRT, 89, 165 [NASA ADS] [Google Scholar]
- Krauß, O., & Wurm, G. 2004, JQSRT, 89, 179 [Google Scholar]
- Krügel, E. 2003, The Physics of Interstellar Dust (London: Institute of Physics Publishing) [Google Scholar]
- Larson, K. A., Whittet, D. C. B., & Hough, J. H. 1996, ApJ, 472, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A. 2009, in Cosmic Dust – Near and Far, ed. Th. Henning et al., ASP Conf. Ser., 414, 482 [Google Scholar]
- Lazarian, A., & Hoang, T. 2007, MNRAS, 378, 910 [Google Scholar]
- Lazarian, A., & Hoang, T. 2008, ApJ, 676, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, J. L., & Le Borgne, J. F. 1987, A&A, 186, 322 [NASA ADS] [Google Scholar]
- Marraco, H. G., Vega, E. I., & Vrba, F. J. 1993, AJ, 105, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. G., Clayton, G. C., & Wolff, M. J. 1999, ApJ, 510, 905 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S. 1986, ApJ, 308, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumura, M., Kameura, Y., Kawabata, K. S., et al. 2011, PASJ, 63, L43 [NASA ADS] [Google Scholar]
- McDavid, D. 2000, AJ, 119, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Michel, B., Henning, Th., Stognienko, R., & Rouleau, F. 1996, ApJ, 468, 834 [NASA ADS] [CrossRef] [Google Scholar]
- Min, M. 2009, in Cosmic Dust – Near and Far, ed. Th. Henning et al., ASP Conf. Ser., 414, 356 [Google Scholar]
- Min, M., Waters, L. B. F. M., de Koter, A., et al. 2007, A&A, 462, 667 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molster, F. J., Waters, L. B. F. M., & Kemper, F. 2010, in Astromineralogy, second edition, ed. Th. Henning (Springer), Lect. Notes Phys., 815, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Niyogi, S. G., Speck, A. K., & Onaka, T. 2011, ApJ, 733, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Oudmaijer, R. D., & Drew, J. E. 1999, MNRAS, 305, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Patriarchi, P., Morbidelli, L., & Perinotto, M. 2003, A&A, 410, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poeckert, R., Bastien, P., & Landstreet, J. D. 1979, AJ, 84, 812 [Google Scholar]
- Purcell, E. M. 1979, ApJ, 231, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Roche, P., Larionov, V., Tarasov, A. E., et al. 1997, A&A, 322, 139 [NASA ADS] [Google Scholar]
- Serkowski, K., Mathewson, D. S., & Ford, V. L. 1975, ApJ, 196, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Sorrell, W. H. 1994, MNRAS, 268, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Sorrell, W. H. 1995, MNRAS, 273, 187 [NASA ADS] [Google Scholar]
- Sturm, B., Bouwman, J., Henning, Th., et al. 2010, A&A, 518, L129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valencic, L. A., Clayton, J. C., & Gordon, K. D. 2004, ApJ, 616, 912 [NASA ADS] [CrossRef] [Google Scholar]
- van Breemen, J. M., Min, M., Chiar, J. E., et al. 2011, A&A, 526, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vega, E. I., Orsatti, A. M., & Marraco, H. G. 1994, AJ, 108, 1834 [NASA ADS] [CrossRef] [Google Scholar]
- Vink, J. S., Davies, B., Harries, T. J., Oudmaijer, R. D., & Walborn, N. R. 2009, A&A, 505, 743 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voshchinnikov, N. V. 1990, SvA, 33, 429 [NASA ADS] [Google Scholar]
- Voshchinnikov, N. V., & Henning, Th. 2010, A&A, 517, A45 (VH10) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voshchinnikov, N. V., & Il’in, V. B. 1983, SvA Lett., 9, 101 [NASA ADS] [Google Scholar]
- Voshchinnikov, N. V., Il’in, V. B., Henning, Th., Michel, B., & Farafonov, V. G. 2000, JQSRT, 65, 877 [CrossRef] [Google Scholar]
- Wegner, W. 2002, BaltA, 11, 1 [Google Scholar]
- Wegner, W. 2003, AN, 324, 219 [NASA ADS] [Google Scholar]
- Weingartner, J. C. 2006, ApJ, 647, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Weitenbeck, A. J. 2008, AcAstr, 58, 433 [Google Scholar]
- Whittet, D. C. B. 2003, Dust in the Galactic Environments, second edition (Bristol: Institute of Physics Publishing) [Google Scholar]
- Whittet, D. C. B., Martin, P. G., Hough, J. H., et al. 1992, ApJ, 386, 562 [NASA ADS] [CrossRef] [Google Scholar]
- Whittet, D. C. B., Gerakines, P. G., Hough, J. H., & Shenoy, S. S. 2001, ApJ, 547, 872 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Pearson correlation coefficients between polarization, extinction, and element abundances in the dust phase.
All Figures
 |
Fig. 1 Polarization according to colour excess for 172 stars from Table 1. Variable stars and stars with peculiar spectra are marked. The straight line shows the empirical upper limit for interstellar polarization (Serkowski et al. 1975). |
| In the text | |
 |
Fig. 2 Polarization of 95 stars according to the remaining dust phase abundance of Fe as given by Eq. (1) normalized to the cosmic abundance of iron. Halo stars with |b| > 30° and disk stars with |b| ≤ 30° and low (E(B − V) ≤ 0.2) and high (E(B − V) > 0.2) reddening are shown with different symbols. Filled symbols correspond to sightlines where the abundances of three elements (Mg, Si, and Fe) are measured. Open symbols correspond to sightlines where the abundances of two elements (Fe and Mg or Si) are known. The number of stars is indicated in parentheses in the legend. |
| In the text | |
 |
Fig. 3 Same as in Fig. 2, but now for polarization efficiency P/E(B − V). |
| In the text | |
 |
Fig. 4 Interstellar polarization according to dust phase abundance of iron. Halo stars with |b| > 30° and disk stars with |b| ≤ 30° and low (E(B − V) ≤ 0.2) and high (E(B − V) > 0.2) reddening are shown with different symbols. The number of stars is indicated in parentheses in the legend. |
| In the text | |
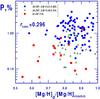 |
Fig. 5 Same as in Fig. 4, but now for magnesium. |
| In the text | |
 |
Fig. 6 Same as in Fig. 4, but now for silicon. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


