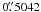| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A88 | |
| Number of page(s) | 8 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201118678 | |
| Published online | 02 April 2012 | |
Quasi full-disk maps of solar horizontal velocities using SDO/HMI data
1 Université de Toulouse, UPS-OMP, IRAP, Toulouse, France
e-mail: thierry.roudier@irap.omp.eu
2 CNRS, IRAP, 14 avenue Edouard Belin, 31400 Toulouse, France
3 LESIA, Observatoire de Paris, Section de Meudon, 92195 Meudon, France
4 CALMIP, DTSI Université Paul Sabatier, Université de Toulouse 31062 Toulouse, France
5 Lockheed Martin Advance Technology Center, Palo Alto, CA, USA
6 Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Strasse 2, 37191 Katlenburg-Lindau, Germany
7 Institut für Astrophysik, Georg-August Universität Göttingen, 37077 Göttingen, Germany
8 Astronomical Institute, Academy of Sciences of the Czech Republic (v. v. i.), Fričova 298, 25165 Ondřejov, Czech Republic
9 Astronomical Institute, Faculty of Mathematics and Physics, Charles University in Prague, V Holešovičkách 2, 18000 Prague 8, Czech Republic
Received: 19 December 2011
Accepted: 18 February 2012
Aims. For the first time, the motion of granules (solar plasma on the surface on scales larger than 2.5 Mm) has been followed over the entire visible surface of the Sun, using SDO/HMI white-light data.
Methods. Horizontal velocity fields are derived from image correlation tracking using a new version of the coherent structure tracking algorithm. The spatial and temporal resolutions of the horizontal velocity map are 2.5 Mm and 30 min, respectively.
Results. From this reconstruction, using the multi-resolution analysis, one can obtain to the velocity field at different scales with its derivatives such as the horizontal divergence or the vertical component of the vorticity. The intrinsic error on the velocity is ~0.25 km s-1 for a time sequence of 30 min and a mesh size of 2.5 Mm. This is acceptable compared to the granule velocities, which range between 0.3 km s-1 and 1.8 km s-1. A high correlation between velocities computed from Hinode and SDO/HMI has been found (85%). From the data we derive the power spectrum of the supergranulation horizontal velocity field, the solar differential rotation, and the meridional velocity.
Key words: Sun: granulation / Sun: rotation / Sun: general
© ESO, 2012
1. Introduction
The Sun is a star whose plasma flows are the main source of its magnetic evolution and activity. The coupling of these motions and the magnetic field in the convection zone is the driver of the magnetic activity through the dynamo process. The description of the physical properties of the convective zone requires the knowledge of these motions at all scales in space and time.
Determining plasma motions inside the Sun is a difficult task. While local helioseismology can be used to infer vector flows in three dimensions just below the solar surface, this is only possible for spatial scales larger than 5 Mm and temporal scales longer than several hours (Jackiewicz et al. 2008; Gizon et al. 2010; Švanda et al. 2011).
From the analysis of the proper motion of photospheric structures (solar granules), it has been shown (Rieutord et al. 2001) that it is possible to get the horizontal plasma flow on the Sun surface. In more detail, using numerical simulation in a large horizontal box, Rieutord et al. (2001) show that granule motions are highly correlated with horizontal flows when the scale is larger than ~2500 km; at smaller scale, granule motions should be considered as (solar) turbulent noise. Such techniques have been used on relatively small fields of view (few arcminutes) and usually located at the disk center.
Very recently, Hinode and SDO satellites produced time sequences of images of the solar surface without disturbance from the terrestrial atmosphere (seeing). These observations allow us to simultaneously measure horizontal velocities at different spatial resolutions and to study long-time sequences of velocities over the full Sun (HMI/SDO).
In this paper, we describe a method for determining horizontal velocities from proper motions of the solar structures observed on the full-disk Sun. For the first time, the motion of granules (solar plasma flows on the surface on scales larger than 2.5 Mm) has been followed over the full visible Sun surface. Horizontal velocity fields are derived from granule tracking using a new version of the coherent structure tracking (CST) algorithm (Rieutord et al. 2007).
We first present in some detail the algorithm based on granule tracking, which is able to give a reconstruction of the velocity field at all scales larger than the sampling scale. The CST also offers the possibility of selecting specific structures according to their nature, size, lifetime, etc. and study their motion. In the next section we discuss the different steps of the algorithm, the segmentation and interpolation processes, and a comparison of Hinode and SDO flow maps. We illustrate the method with applications such as the calculation of the kinetic power spectrum of supergranulation, and the measurement of the solar differential rotation and meridional flow at the central meridian. Discussion and conclusions follow.
2. Observations
2.1. Hinode observations
We used data sets of the Solar Optical Telescope (SOT), on-board the Hinode1 mission (e.g. Suematsu et al. 2008; Ichimoto et al. 2004). The SOT has a 50 cm primary mirror with a spatial resolution of about 0.2′′ at 550 nm. For our study, we used blue continuum observations at 450.45 nm from the Hinode/SOT BFI (BroadBand Filter Imager). The observations were recorded on August 30, 2010 from 08:04:33 to 10:59:36 UT. Solar rotation is compensated to observe exactly the same region of the Sun. The time step is 60 s and the field of view is 76.7″ × 76.7″ with a pixel scale of 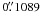 . After alignment, the useful field-of-view is reduced to
. After alignment, the useful field-of-view is reduced to 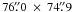 .
.
To remove the effects of the oscillations, we applied a subsonic Fourier filter. This filter is defined by a cone in the k − ω space, where k and ω are spatial and temporal frequencies. All Fourier components with ω/k ≤ V = 7 km s-1 were retained to keep only convective motions (Title et al. 1989).
2.2. SDO-HMI observations
The Helioseismic and Magnetic Imager onboard the Solar Dynamics Observatory (HMI/SDO) yields uninterrupted high-resolution observations of the entire disk. This gives a unique opportunity for mapping surface flows on various scales (spatial and temporal). Using the HMI/SDO white-light data from August 30, 2010, we derived horizontal velocity fields from image granulation tracking using a newly developed version of the CST algorithm. The time step is 45 s with a pixel scale of 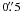 . HMI/SDO white-light data from April 10, 2010, July 10, 2010 and May 12,13, 2011 are used to measure solar differential rotation during 24 h for each of them.
. HMI/SDO white-light data from April 10, 2010, July 10, 2010 and May 12,13, 2011 are used to measure solar differential rotation during 24 h for each of them.
 |
Fig. 1 Full Sun HMI/SDO white-light on August 30, 2010 (left) and the segmented map, in which about 500 000 granules are detected (right). |
3. The new CST method
Granule tracking is a difficult task because of the complex evolution on granules depending of their size. Granule fragmentation and mixing must be managed very carefully to avoid the generating noise. We pursue here the development of a method called coherent structure tracking, or CST, which determines the horizontal motion of granules in the field of view (Rieutord et al. 2007). The preceding version was developed for a field of a few arcminutes, generally located at the disk center of the Sun where the solar rotation was removed by alignment of the frames. The application of the CST to HMI/SDO data requires a new granule time labeling methode which takes care of the motion caused by the solar rotation to avoid misidentification. Indeed, in the preceding CST version the time labeling was processed by following the barycenter of the granule. The solar rotation that is present in HMI/SDO data and the evolution of granules like the birth of a new (small) granule close to an existing granule between two frames can lead to misidentification of barycenters. This leads to a bad temporal labeling and generates noticeable noise in the final velocity maps.
 |
Fig. 2 Close-up view of the field around a spot as delineated in Fig. 1 (top left) with its segmentation (top right). Below, resulting velocity field from granule tracking (note the clear signature of the moat flow associated with the spot near x = 50, y = 100). |
3.1. Segmentation and granule identification
To identify a granule one needs to establish a local criterion to decide whether a given pixel belongs to a given structure. This criterion needs to be local to avoid threshold effects due to large-scale variations of the intensity. The most efficient segmentation algorithm for solar granulation is an adaptated version of Strous′ segmentation (curvature-based criterion Strous 1994) described in Rieutord et al. (2007). This image segmentation is very efficient at removing large-scale intensity fluctuations. An example is shown in Fig. 1. To summarize, it consists of the following steps:
-
Calculation of the “minimal curvature image”: for each pixel, theminimal curvature among the four directions is computed.
-
Detection of the granules as non-negative curvature pixels in the minimal curvature image.
-
Extension of the detected granules with points whose minimal curvature value is higher than a given (negative) threshold, while keeping a minimal distance of one pixel between each granule.
Once the image has been segmented, each granule needs to be identified. This operation, called connected-component labeling, is an algorithmic application of the graph theory, where subsets of connected components are uniquely labeled based on a given heuristic. Connected-component labeling is used to detect the connected regions in the binary digital images produced by our segmentation algorithm. In this labeling process, a pixel belongs to a granule if it shares at least one side with another pixel of the granule.
3.2. Measuring the velocities
Once the granules have been labeled in each frame, their trajectories are identified by comparing two consecutive images. During their lifetime, granules can split or merge into multiple objects. Disappearance or appearance between two successive frames must be taken into account. Then, the life of coherent objects (i.e. granules) is defined between its appearance and disappearance if the granule does not split or merge. When the granule splits, the life of granule is stopped and its “children” are considered as new granules. In the same way, when granules merge, the lives of the granules that merge are stopped and the new granule issued from the merging is considered as a new granule. Thus, we can follow a coherent structure between their birth and death. In the previous CST version, the temporal labeling of the coherent structure was performed from one frame to the next by following the barycenter trajectory (Roudier et al. 1999; Rieutord et al. 2007) and was essentially applied to the aligned data where large-scale motions were removed (solar rotation, drifts, etc.). However, when this method is applied to the HMI/SDO data, it generates some misidentifications of the barycenters between close granules because of the high value of the rotation velocity (around 2 km s-1). To avoid this extra noise, we now performed a time labeling of granules, that takes into account a common granule area between image t and t + 1. This method ensures the temporal link between two snapshots of an evolving granule and improves their temporal labeling.
Hence, each coherent structure (i) is defined by six values:
-
1.
birth time Tbi and death time Tdi;
-
2.
(Xi,Yi)b and (Xi,Yi)d the positions at time Tbi and Tdi;
-
3.
Vx and Vy are in the heliocentric-cartesian coordinates (Thompson 2006), respectively the horizontal component of velocity in x (x increasing toward solar west) and in y (increasing toward solar north).
From the birth and death locations and lifetimes of each coherent structure, we derived a trajectory and mean velocity. To reduce the noise, coherent structures with a lifetime shorter than 180 s were ignored.
If one analyzes a long times series of images, it is useful to determine the time evolution of the velocity field; for this purpose a time window lasting δt was used and trajectories were restricted to the time window. Hence, for a given time window, we derived a set of trajectories and velocities. The values of the velocities are of course not uniformly distributed in the field of view, and we need to know how they constrain the velocity field at a given scale: small-scale components are weakly constrained while large-scale ones are highly constrained. The maximum resolution for the velocity field is given by the density of trajectories. As pointed out in Rieutord et al. (2001), granules cannot be used to trace plasma flow below a scale of 2.5 Mm (except for very rapid flows like in an “explosion” of granules); thus the determination of a large-scale flow needs a mesh size not smaller than 1.25 Mm.
Rieutord et al. (2007) indicated that the minimum size of the velocity mesh grid is related to the temporal resolution. They showed that one typical granule trajectory occupies a “volume” of 1200 Mm2 s. When the “space-time” resolution does not reach this limit, many granules contribute to the velocity in one mesh point. Their mean velocity is considered as the true local velocity but local fluctuations around this may also give some information on the local strength of convection. Because granules do not sample the field of view uniformly, a reconstruction of the velocity field along with its derivatives such as the divergence D = ∂xVx + ∂yVy or the z-component of vorticity ζ = ∂xVy − ∂yVx requires some interpolation. Like Rieutord et al. (2007) we used the multi-resolution analysis for the interpolation, which limits the effects of noise and error propagation.
The smallest spatial and temporal resolutions achieved in the horizontal velocity map produced using the new CST algorithm are 2.5 Mm and 30 min, respectively.
Figure 2 shows some details around a sunspot in the intensity field and its segmentation where granules are visible; we plot an enlargement of the flow fields around the sunspot where divergent structures and the sunspot moat are clearly visible.
On the full Sun white-light observation around 5 × 105 granules are detected. During a time tracking of 30 min around 2.2 × 106 coherent structures are identified. This number increases up to 7.5 × 106 for a time sequence of two-hours. We show an example of the full Sun Vx and Vy in Figs. 3 and 4 components from a two-hour sequence with a spatial resolution of 2.5 Mm. Arrows indicate the location of supergranules that are visible also on the Doppler map (Fig. 5). Owing to the radial flows within supergranules, two supergranules are marked in the Vx map close to the western limb where they are easier to identify than in the east-west component of the flow (and vice versa for the Vy map). The circle inside the solar grid in Fig. 6 represents the limit up to which the projected Vx and Vy are correctly measured. Beyond this circle, granule tracking is difficult and errors increase rapidly as we near the limb. The useful field lies in the latitude and longitude range between ± 60° in latitude and longitude for a two-hour sequence. Because this field covers a large part of the visible Sun area (80%), we define it as a quasi full-disk map of photospheric horizontal velocities.
 |
Fig. 3 Full Sun Vx component from a two-hour sequence, spatial resolution 2.5 Mm. Arrows indicate the location of supergranule visible also on the Doppler map. |
 |
Fig. 4 Full Sun Vy component from two-hour sequence, spatial resolution 2.5 Mm. Arrow indicates the location a supergranule visible also on the Doppler map. |
 |
Fig. 5 Averaged Dopplergram from two-hour sequence where the solar rotation has been removed. Arrows indicate the location of supergranule. |
 |
Fig. 6 Solar grid where the dark circle indicates the limit of the validity of the horizontal velocity measurement. |
4. Precision
 |
Fig. 7 Solar granulation from Hinode (1 pixel = |
Following Tkaczuk et al. (2007), we can estimate the error propagation on the velocity of the CST algorithm. Over an image, granules are much less dense than pixels, therefore the velocity field is sampled on a much coarser grid whose elements are of size δ here 2.5 Mm. The velocity at a grid coordinate (x,y) is assumed to be the average of the velocity of granules whose average coordinates belong to the domain D around (x,y) (i.e. in [x − δ/2,x + δ/2] , [y − δ/2,y + δ/2]). The spatial resolution of the velocity field is given by the mesh size δ. If we assume that the dispersion on the barycenter is the same for the whole time series (σ), and that the time interval Δtk (of the granule k) is the same for all granules (i.e. all granules have the same lifetime Δt), then the expression of the dispersion of the average velocity (Tkaczuk et al. 2007) is 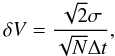 (1)where N is the number of trajectories falling in D. We found for the full Sun white-light SDO data for a time sequence of 30 min and a mesh size of 2.5 Mm, that N = 8. The precision of the location of the barycenter of granule is estimated to half a pixel, which represents
(1)where N is the number of trajectories falling in D. We found for the full Sun white-light SDO data for a time sequence of 30 min and a mesh size of 2.5 Mm, that N = 8. The precision of the location of the barycenter of granule is estimated to half a pixel, which represents 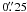 (183 km). With a median lifetime of 405 s δV = 0.22 km s-1, which is good enough at a scale of 2500 km, i.e. at the scale where granule motion traces the large-scale plasma flows. Tkaczuk et al. (2007) showed that precise velocity values need many granules in a grid element and a long-time interval. In other words, errors are less if a coarse resolution in space and time is used.
(183 km). With a median lifetime of 405 s δV = 0.22 km s-1, which is good enough at a scale of 2500 km, i.e. at the scale where granule motion traces the large-scale plasma flows. Tkaczuk et al. (2007) showed that precise velocity values need many granules in a grid element and a long-time interval. In other words, errors are less if a coarse resolution in space and time is used.
When moving to the limb, the detection of granules becomes more difficult but the mesh size δ covers a larger area on the Sun’s surface. Both phenomena more or less cancel each other out and we find that close to the limb N = 7 and δV = 0.24 km s-1.
Accordingly, we estimate that an error of δV = 0.25 km s-1 for the HMI/SDO data for a time sequence of 30 min is acceptable since most of the granules are showing velocities in the range 0.3–1.8 km s-1 in our analysis. This error seems to be large, but this is due in great part to the pixel size 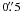 , which allows us to follow only the large granules on the Sun surface. However, when the velocities are averaged in space and time this error decreases for example down to 0.06 km s-1 at the disk center with a window of 20″ × 20″ for a 24-h sequence (see below). This estimate error of the smoothed data is very similar to the one deduced from helioseismology analysis, which is found to be 30 m/s for one day data (Table 2 of Švanda et al. 2011).
, which allows us to follow only the large granules on the Sun surface. However, when the velocities are averaged in space and time this error decreases for example down to 0.06 km s-1 at the disk center with a window of 20″ × 20″ for a 24-h sequence (see below). This estimate error of the smoothed data is very similar to the one deduced from helioseismology analysis, which is found to be 30 m/s for one day data (Table 2 of Švanda et al. 2011).
5. Comparison of HINODE and SDO velocity fields
To determine the quality of the velocities measured with white-light HMI/SDO data, quasi simultaneous observations of the Sun’s surface with very high spatial resolution were obtained with the Hinode satellite during three-hours. The data were carefully aligned, k-ω filtered and resized at the same scale (1 pixel = 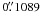 ). The Hinode data were also degraded to the spatial resolution of HMI/SDO for a detailed comparison. Three temporal sequences were treated exactly in the same way. We applied the CST to these sequences and show the results in Fig. 7. The correlation between velocities of the different sequences is about 85% and one can easily recognize common patterns between the time series. The histograms of the velocity in Fig. 8 are very similar for all sequence, indicating that the amplitudes are also correctly measured. For comparison, local correlation tracking (LCT) was applied to the same one-hour sequence. This flow field is shown in the bottom of Fig. 7. Here we also find a good correlation (about 75%) between velocities computed by CST and LCT. The LCT velocities are lower, however than the CST velocities by 15%, likely because of the spatial window size used in the LCT to convolve the data (Roudier et al. 1999).
). The Hinode data were also degraded to the spatial resolution of HMI/SDO for a detailed comparison. Three temporal sequences were treated exactly in the same way. We applied the CST to these sequences and show the results in Fig. 7. The correlation between velocities of the different sequences is about 85% and one can easily recognize common patterns between the time series. The histograms of the velocity in Fig. 8 are very similar for all sequence, indicating that the amplitudes are also correctly measured. For comparison, local correlation tracking (LCT) was applied to the same one-hour sequence. This flow field is shown in the bottom of Fig. 7. Here we also find a good correlation (about 75%) between velocities computed by CST and LCT. The LCT velocities are lower, however than the CST velocities by 15%, likely because of the spatial window size used in the LCT to convolve the data (Roudier et al. 1999).
 |
Fig. 9 Solar differential rotation on April 10, 2010, July 10, 2010, May 12, 2011, and May 13, 2011. We plot the rotation law determined by spectroscopic method (Howard & Harvey 1970) in the four panels ω = 13.76−1.74 × sin2λ − 2.19 × sin4λ (λ = latitude, ω = angular velocity in deg/day), giving an equatorial velocity of 1.93 km s-1. |
The high correlation between velocities and the quasi-identical amplitudes of the velocities indicate a good agreement between velocities measured with Hinode data (high spatial resolution) and HMI/SDO data (low spatial resolution). This allows us to use HMI/SDO data with some confidence in determining the horizontal flows across the Sun.
6. Power spectrum of the solar supergranulation
The kinetic energy distribution among the scales is represented by the power spectrum of the velocity field. Like Rieutord et al. (2008), we computed the kinetic energy spectral density E(k) for a time window of 120 min and spatial field of 650″ × 650″ centered on the disk center on August 30, 2010.
The spectrum shown in Fig. 10 is very similar to that exhibited in Fig. 2 of Rieutord et al. (2008). It exhibits the kinetic energy contained in the supergranulation. With SDO data, we find the maximum of the spectral density at a wavelength of 35.8 Mm quite close to 36 Mm found by Rieutord et al. (2008) and the FWHM of the peak indicates that supergranulation occupies the range of scales of [19, 56] Mm compared to [20, 75] Mm for Rieutord et al. (2008). Our time sequence is shorter by a factor 3.75 but our field of view is 3.5 larger (400″ × 300″ for Rieutord et al. 2008). Like Rieutord et al., we indicate the best-fit power-law (3 and –2), which mimics the sides of the supergranulation spectral peak. At small scales below k = 0.1 Mm-1 we observe E(k) ∝ k due to the decorrelated random noise. Our present result confirms the previous findings.
7. Solar differential and meridional flow determination
There is a long history of inconsistent measurements of solar rotation (Beck 2000). One of the first applications of the CST algorithm on HMI/SDO data is to measure the horizontal velocities over 24 h on the central meridian. Owing to computational time, we used a band of 50″ along the central meridian and 48 time-sequences of 30 min. Then, 98 spatial windows of 50″ × 20″ were used to obtain the horizontal flow fields at different latitudes for each time-sequence of 30 min. Finally, we averaged all 30 min time-sequences for each latitude to obtain the final Vx and Vy over 24 h. The Vx are corrected for the Earth’s orbital motion to obtain the sidereal rotation of the Sun, and Vy was also corrected for the B0 evolution during 24 h. This is the first time that solar rotation has been determined from granule displacement measurements over the full solar disk. Figure 9 shows the differential rotation computed in this way for four different dates close to the solar minimum.
The standard deviation of the velocity field close to the disk center is 0.06 km s-1 (24 h sequence). Owing to the change in size of the Sun in diameter of (1.4 pixel on the detector) (SDO Earth orbit) and also to the B0 evolution during 24 h, the field of good measurement was reduced to − 50° and + 45° in longitude and ± 50° in latitude around the disk center. This limitation will be improved in the near future (new observations on 10 December 2011) by reducing the effects of dilatation and contraction of the Sun’s diameter on the CCD.
Our results of April 10, 2010 agree with the spectroscopic determination of the solar rotation of Howard & Harvey (1970) but the rotation seems slightly faster on the other dates with an equatorial velocity of 1.99 km s-1. The daily Wolf numbers are 8, 14, 33, and 26 and 8, 16.1, and 41.6 monthly. We expect differences with Howard & Harvey (1970), simply because we are not studying the same time period. The solar differential rotation appears to change in time particularly at high latitudes, but we need a more extensive analysis to confirm these variations.
 |
Fig. 10 Kinetic energy spectra of the horizontal velocities. The vertical dashed line emphasizes the 10 Mm scale, which is usually taken as upper limit of mesogranular scale. Two power laws are shown on each side of the peak, as well as that of the small-scale noise. |
 |
Fig. 11 Meridionnal velocity at different latitudes across the central meridian on April 10, 2010, quiet Sun. |
The meridional flows with Vrms = 90 m s-1, given by the Vy component for 24 h, is plotted in Fig. 11 for a quiet Sun on April 10 2010 between −50° and +45° in latitude. Because the Vrms of the mean meridional flow is 90 m s-1, the expected signal of 20 m s-1 is completely hidden. Several days are required to reduce the Vrms amplitude and determine the meridional velocity. This work is scheduled for the near future because we must also include the Sun’s diameter evolution on the SDO detector over a long period of time (Earth orbit).
8. Discussion and conclusions
Determining horizontal velocity fields on the solar surface is crucial for understanding the dynamics of the phostosphere, the distribution of magnetic fields and its influence on the structures of the solar atmosphere (filaments, jets, etc.).
We have shown that the reconstruction of the velocity field can be achieved over the Sun’s entire visible surface with HMI/data by using CST. From this reconstruction, by using the multi-resolution analysis, one can also compute the velocity field at different scales along with its derivatives such as divergence and curl. An uncertainty in the velocity of about 0.25 km s-1 for a time sequence of 30 min and a mesh of 2.5 Mm is acceptable if compared to the granule velocities which range between 0.3 km s-1 and 1.8 km s-1. The kinetic energy power spectra obtained on a large field of the Sun confirms the previous quantitative studies of the dynamic of the Sun’s surface. The first determination of the solar rotation using granule tracking demonstrates the potential of our method for studying the evolution of solar rotation on short-time scales. The method can also be used to remove the solar rotation for studying smaller scale evolution (supergranulation flows, etc.).
In a near future, it will be possible to derive the velocities on the solar surface in the local coordinates system (Vr,Vθ,Vφ) from the line-of-sight component velocity (Vdop) and horizontal velocity fields on the solar surface (Vx, Vy). In particular, it will be possible to compare the spherical analysis of the Sun’s motions to those of numerical simulations, thus improving our knowledge of the physical properties of the Sun.
Contemplating the CST method and the HMI/SDO data, many applications can be envisioned on time scales ranging from 30 min to several days or even months with spatial scales ranging form 2.5 Mm up to the radius of the Sun. This opens a new
field of study allowing, e.g., a measure of the influence of photospheric motions on the dynamics of the outer solar atmosphere such as the triggering of filament eruptions, see Roudier et al. (2008). Many other applications will be possible on phenomena that surface motions involve.
Today, 12 min of processor time are required to compute 30 min of solar observations. Improvement of the code is in progress. Currently, the Fortran90 CST code is parallelized in a shared memory approach involving OpenMP. We experienced good scaling on a production data set (full sun) with 73.16% parallel efficiency on 24 cores. Tests were conducted on an SGI Altix UV ccNUMA node with 96 cores and 1TB of RAM. This CST code (Fortran90) will be implemented in the German Data Center for SDO and in the Joint Science Operations Center, and will be available to solar community.
Acknowledgments
We thank the Hinode/SOT team for assistance in acquiring and processing the data. Hinode is a Japanese mission developed and launched by ISAS/JAXA, collaborating with NAOJ as a domestic partner, NASA and STFC (UK) as international partners. Support for the post-launch operation is provided by JAXA and NAOJ (Japan), STFC (UK), NASA, ESA, and NSC (Norway). We thank the HMI team members for their hard work.We thank the German Data Center for SDO and BASS2000 for providing HMI/SDO data. The German Data Center for SDO is supported by the German Aerospace Center (DLR). We thank F. Rincon for comments. This work was granted access to the HPC resources of CALMIP under the allocation 2011-[P1115]. This work was supported by the CNRS Programme National Soleil Terre. We thank the anonymous referee for suggestions and careful reading of the manuscript.
References
- Beck, J. G. 2000, Sol. Phys., 191, 47 [Google Scholar]
- Gizon, L., Birch, A. C., & Spruit, H. C. 2010, ARA&A, 48, 289 [Google Scholar]
- Howard, R., & Harvey, J. 1970, Sol. Phys., 12, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Ichimoto, K., Tsuneta, S., Suematsu, Y., et al. 2004, in Optical, Infrared, and Millimeter Space Telescopes, ed. J. C. Mather, SPIE Conf., 5487, 1142 [Google Scholar]
- Jackiewicz, J., Gizon, L., & Birch, A. C. 2008, Sol. Phys., 251, 381 [Google Scholar]
- Rieutord, M., Roudier, T., Ludwig, H.-G., Nordlund, Å., & Stein, R. 2001, A&A, 377, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Roudier, T., Roques, S., & Ducottet, C. 2007, A&A, 471, 687 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieutord, M., Meunier, N., Roudier, T., et al. 2008, A&A, 479, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roudier, T., Rieutord, M., Malherbe, J., & Vigneau, J. 1999, A&A, 349, 301 [NASA ADS] [Google Scholar]
- Roudier, T., Švanda, M., Meunier, N., et al. 2008, A&A, 480, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strous, L. 1994, Ph.D. Thesis, University of Utrecht [Google Scholar]
- Suematsu, Y., Tsuneta, S., Ichimoto, K., et al. 2008, Sol. Phys., 249, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Thompson, W. T. 2006, A&A, 449, 791 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Title, A. M., Tarbell, T. D., Topka, K. P., et al. 1989, ApJ, 336, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Tkaczuk, R., Rieutord, M., Meunier, N., & Roudier, T. 2007, A&A, 471, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Švanda, M., Gizon, L., Hanasoge, S. M., & Ustyugov, S. D. 2011, A&A, 530, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Figures
 |
Fig. 1 Full Sun HMI/SDO white-light on August 30, 2010 (left) and the segmented map, in which about 500 000 granules are detected (right). |
| In the text | |
 |
Fig. 2 Close-up view of the field around a spot as delineated in Fig. 1 (top left) with its segmentation (top right). Below, resulting velocity field from granule tracking (note the clear signature of the moat flow associated with the spot near x = 50, y = 100). |
| In the text | |
 |
Fig. 3 Full Sun Vx component from a two-hour sequence, spatial resolution 2.5 Mm. Arrows indicate the location of supergranule visible also on the Doppler map. |
| In the text | |
 |
Fig. 4 Full Sun Vy component from two-hour sequence, spatial resolution 2.5 Mm. Arrow indicates the location a supergranule visible also on the Doppler map. |
| In the text | |
 |
Fig. 5 Averaged Dopplergram from two-hour sequence where the solar rotation has been removed. Arrows indicate the location of supergranule. |
| In the text | |
 |
Fig. 6 Solar grid where the dark circle indicates the limit of the validity of the horizontal velocity measurement. |
| In the text | |
 |
Fig. 7 Solar granulation from Hinode (1 pixel = |
| In the text | |
 |
Fig. 8 Velocity histograms from CST and LCT are plotted in Fig. 7. |
| In the text | |
 |
Fig. 9 Solar differential rotation on April 10, 2010, July 10, 2010, May 12, 2011, and May 13, 2011. We plot the rotation law determined by spectroscopic method (Howard & Harvey 1970) in the four panels ω = 13.76−1.74 × sin2λ − 2.19 × sin4λ (λ = latitude, ω = angular velocity in deg/day), giving an equatorial velocity of 1.93 km s-1. |
| In the text | |
 |
Fig. 10 Kinetic energy spectra of the horizontal velocities. The vertical dashed line emphasizes the 10 Mm scale, which is usually taken as upper limit of mesogranular scale. Two power laws are shown on each side of the peak, as well as that of the small-scale noise. |
| In the text | |
 |
Fig. 11 Meridionnal velocity at different latitudes across the central meridian on April 10, 2010, quiet Sun. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.