| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A62 | |
| Number of page(s) | 10 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201118102 | |
| Published online | 27 March 2012 | |
Transit-timing measurements with the model-independent barycenter method: application to the LHS 6343 system⋆
1 Centro de Astrofísica, Universidade do Porto, Rua das Estrelas, 4150-762 Porto, Portugal
e-mail: moshagh@astro.up.pt
2 Departamento de Física e Astronomia, Faculdade de Ciências, Universidade do Porto, Rua do Campo Alegre, 4169-007 Porto, Portugal
3 Institute for Astronomy and NASA Astrobiology Institute, University of Hawaii-Manoa, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
Received: 15 September 2011
Accepted: 7 February 2012
We present a model-independent technique for calculating the time of mid-transits. This technique, named “barycenter method”, uses the light-curve’s symmetry to determine the transit timing by calculating the transit light-curve barycenter. Unlike the other methods of calculating mid-transit timing, this technique does not depend on the parameters of the system and central star. We demonstrate the capabilities of the barycenter method by applying this technique to some known transiting systems including several Kepler confirmed planets. Results indicate that for complete and symmetric transit lightcurves, the barycenter method achieves the same precision as other techniques, but with fewer assumptions and much faster. Among the transiting systems studied with the barycenter method, we focus in particular on LHS 6343C, a brown dwarf that transits a member of an M+M binary system, LHS 6343AB. We present the results of our analysis, which can be used to set an upper limit on the period and mass of a possible second small perturber.
Key words: planetary systems / methods: data analysis
Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The success of the transit-timing variation (TTV) method in characterizing planets around the stars Kepler 9 (Holman et al. 2010) and Kepler 11 (Lissauer et al. 2011) and in detecting a planet around star Kepler 19 (Ballard et al. 2011) strongly suggests that TTV method has come of age and is now among the main mechanisms for detecting extrasolar planets. This method, which is based on modeling the variations that appear in the times of the transits of a planet due to the perturbations of other objects, has been shown by many authors to be capable of detecting small Earth-sized planets, moons of giant planets, and stellar companions around variety of stars (Miralda-Escudé 2002; Holman & Murray 2005; Agol et al. 2005; Kipping 2009; Montalto 2010; Schwarz et al. 2011; Haghighipour & Kirste 2011).
Because the interaction between the transiting planet and the perturbing body(ies) is gravitational if there are no magnetic fields, the amplitude of the TTV strongly depends on the masses of these objects and their orbital architecture. As shown by Holman & Murray (2005), Agol et al. (2005), and Haghighipour & Kirste (2011), the amplitude of a TTV signal varies with the mass and distance of the perturbing body. The latter has been used in several null detections to place an upper limit on the mass and orbital parameters of a hypothetical perturber (Bean 2009; Csizmadia et al. 2010; Adams et al. 2010, 2011; Maciejewski et al. 2010, 2011a,b).
The TTV amplitude is strongly amplified when the transiting and perturbing planets are in a mean-motion resonance. For instance, as shown by Agol et al. (2005); Steffen et al. (2007); Agol & Steffen (2007); Haghighipour et al. (2009); Haghighipour & Kirste (2011), a planet as small as Earth can produce large and detectable TTVs on a transiting Jupiter-like body in or near a resonance. This characteristic of resonant transiting systems makes the TTV method a powerful technique for detecting low-mass planets.
The fact that different orbital configurations of the transiting and perturbing bodies can produce similar TTVs has made the inference of the mass and orbital elements of the perturber from the measurements of the transiting planet’s TTVs a very complicated task. Several attempts have been made to overcome these difficulties (Nesvorný & Morbidelli 2008; Nesvorný 2009; Nesvorný & Beaugé 2010; Meschiari & Laughlin 2010). However, the complications still exist, particularly when the system is in or near a resonance. As shown by García-Melendo & López-Morales (2011), continuous observations by Kepler and CoRoT are expected to resolve some of these difficulties.
Determining variations in transit timing requires precise measurements of the times of mid-transits. To compute a mid-transit time, it is necessary to develop a theoretical light-curve that best models the observational measurements of the intensity of the light of a star. When studying transiting planets, many authors use the analytical methodology developed by Mandel & Agol (2002) for this purpose. In this method, the light-curve of a star is calculated using an analytical formula that contains several parameters such as the coefficients of the star’s limb darkening, the ratio of the radius of the planet to that of the star, the semimajor axis of the planet (or its orbital period), and the planet’s orbital inclination. To measure the individual mid-transit times, it is customary to hold all parameters (except mid-transit time) constant during the fitting procedure. As a result, the measurement of the time of each mid-transit will be vulnerable to systematic errors. In other words, any modification to the values of any of the above-mentioned parameters (which may be obtained when observing the system for longer times) will change the fitted light-curve and result in different values of the times of mid-transits. Subsequently, the values of the TTVs obtained in these systems will also change.
We used a model-independent methodology, first introduced by Szabó et al. (2006), to calculate the time of mid-transit. We call this technique the barycenter method because it calculates the mid-transit times by using the definition of the transit light-curve barycenter and its symmetry. We describe this methodology in Sect. 2 and present examples of its application to some of the already known transiting systems in Sect. 3. In Sect. 4, we apply this technique to the system of LHS 6343 and explain its implications for the transit timing of the system. We analyze the derived O–C diagram of LHS 6343 in Sect. 5, and in Sect. 6 we conclude this study by summarizing our analysis and reviewing the results.
2. Barycenter method
As mentioned earlier, to determine the variations in the transit timing of a planet, a precise calculation of the times of its mid-transits is required. The mid-transit times are determined by fitting an analytically obtained light-curve to the observational data, and calculating the time of the mid-point of each individual transit on the latter curve. When the transiting body is planetary, the synthetic light-curve is usually produced using the algorithm developed by Mandel & Agol (2002). In the majority of cases, the times of mid-transits are calculated by keeping all other parameters (e.g. stellar radius, planet radius, orbital period, and two limb darkening coefficients) constant during the fitting procedure. This is particularly important when the number of points inside a transit is small (e.g., 6–9 points). In such cases, fitting the observed data can lead to imprecise results.
Another technique for calculating times of mid-transits is the “trapezoid method” (Alonso et al. 2009). In this method, a trapezoid function is fitted to the observational data and the best light-curve is determined by varying the depth, duration, and shape of the trapezoid. The time of mid-transit is then calculated by identifying the mid-point of each transit on the best-fit trapezoidal curve.
In systems where the transiting/eclipsing body is a stellar companion, the time of each mid-transit/eclipse is calculated using the methodology developed by Kwee & van Woerden (1956). This method has been used by Deeg et al. (2000, 2008) to calculate eclipse timing variations of eclipsing binaries caused by a circumbinary planet, and is based on the assumption that in an unperturbed system, the light-curve of the transited/eclipsed star is symmetric. In this method, the mid-point of an eclipsing light-curve is determined by folding the light-curve around one point of the transit, and calculating the differences between the points on the two parts of the folded light-curve. The point where these differences become minimum corresponds to the point of mid-transit.
The method developed by Kwee & van Woerden (1956) has the advantage that unlike the method of Mandel & Agol (2002), it does not depend on the parameters of the central star. However, for the measurements of the mid-transit times to be accurate, this method requires very many points, which are obtained through the interpolation of points from the results of observation. As a result, in transiting systems with few data points (e.g., the transiting systems identified in the long cadence of Q0 to Q2 data sets from Kepler), using this method is not practical.
In this section, we explain a methodology that employs similar idea as the method by Kwee & van Woerden (1956) (i.e., using light-curve’s symmetry) and as such is independent of the system’s stellar parameters. This method was first presented by Szabó et al. (2006) and later used by Simon et al. (2007) and Kipping (2011) to study the possibility of the detection of exomoons. It calculates the exact moment of mid-transit using the definition of the transit light-curve barycenter. We call this methodology the “barycenter method”. Unlike the method by Kwee & van Woerden (1956), the barycenter method can be applied to transit planetary systems with few data points.
To define the transit light-curve barycenter, we use a normalized graph of the flux of the central star. As shown in Fig. 1, the flux of the star outside the transit is detrended and normalized to 1. For a point i with a flux fi inside the transit, the corresponding value of the light-loss of the system is equal to 1 − fi. Similar to the barycenter point of a number of massive objects, we now define a barycenter for the points on the graph of the normalized flux. In this definition, the time of mid-transit will then be given by 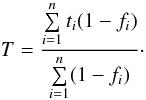 (1)In Eq. (1), n represents the number (rank) of the data points in the observation, and ti is Julian Day (JD) of the observation point i. To obtain more precise results, we only consider the points that are inside the transit light-curve. A point is inside the transit if its light-loss (1 − fi) is higher than the standard deviation of flux outside the transit.
(1)In Eq. (1), n represents the number (rank) of the data points in the observation, and ti is Julian Day (JD) of the observation point i. To obtain more precise results, we only consider the points that are inside the transit light-curve. A point is inside the transit if its light-loss (1 − fi) is higher than the standard deviation of flux outside the transit.
 |
Fig. 1 Schematic view of the barycenter method. |
3. Application of the barycenter method to known transiting systems
3.1. HAT-P-7b
To test the capability of the barycenter method and the validity of its results, we used this technique to calculate the times of mid-transits in several known transiting planetary systems. In addition to the timing, transits may also show variations in their durations and depths. However, our focus is only on the variations in the times of mid-transits. Our first case was the transiting planet HAT-P-7b (Kepler-2b). HAT-P-7 was observed in short and long cadences as a calibration target for Kepler. In the short cadence mode, the light-curve of HAT-P-7 consisted of approximately 355 points in each transit. We used the results of the observations as reported in Q0 data set, and calculated the time of mid-transit for the first transit of this planet. Figure 2 shows the results (the first point from the left). The error bar on each point was determined using the bootstrap technique (Wall & Jenkins 2003). As shown here, the time of mid-transit obtained from the barycenter method is consistent with those obtained from the trapezoid method and the model by Mandel & Agol (2002).
To evaluate the sensitivity of each of these techniques to the number of points in a transit, we reduced the number of points in the light-curve by regular sampling, and calculated the time of mid-transit using all three methods. Results are shown in Fig. 2. As expected, the sizes of the error bars indicating the uncertainties at each point increase for fewer data points. However, as Fig. 2 shows, the times of mid-transits obtained by all three methods are close and agree with one another.
 |
Fig. 2 Comparison between the results of mid-transit of HAT-P-7b first transit, obtained by the Mandel & Agol method (black circle), the trapezoid method (red square) and the barycenter method (blue triangle). |
3.2. Kepler-1b to Kepler-9c
We also applied the barycenter method to the confirmed planets of the Kepler-1 to Kepler-9 systems. Table 1 shows the results and their corresponding uncertainties. The uncertainties were calculated using the equation 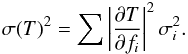 (2)Table 1 also shows the values of the mid-transit times of these planets as reported by Holman et al. (2010) and Ford et al. (2011) using the model of Mandel & Agol (2002). As shown here, the results obtained from the barycenter method agree very well with the previously reported values.
(2)Table 1 also shows the values of the mid-transit times of these planets as reported by Holman et al. (2010) and Ford et al. (2011) using the model of Mandel & Agol (2002). As shown here, the results obtained from the barycenter method agree very well with the previously reported values.
 |
Fig. 3 Differences between the values of mid-transit timing obtained by the barycenter method and the Mandel & Agol method for Kepler-1b to Kepler-4b (Holman et al. 2010; Ford et al. 2011). |
Figures 3 and 4 show the differences between the values of mid-transit times obtained by the barycenter method and those reported by Holman et al. (2010) and Ford et al. (2011). The error bar at each point was calculated by taking the quadratic sum of the uncertainties shown in Table 1. Table 2 lists standard deviations of these differences and their average error bars. As can be seen from Fig. 3 and Table 2, Kepler-4b shows large error bars compared to those of other planets because of its shallow transits. This figure also shows that the standard deviation of Kepler-3b, as listed in Table 2, is larger than its average error, which can be attributed to the non-symmetric shapes of the first and sixth transits of this planet (see Fig. 5). These short-lived anomaly flux variations can be explained by different mechanisms such as the presence of active regions (dark spots) or a second transiting body (Rabus et al. 2009; Sanchis-Ojeda et al. 2011; Sanchis-Ojeda & Winn 2011; Silva-Valio 2008; Nutzman et al. 2011; Deming et al. 2011).
Comparison of standard deviation of the difference between two methods and the average error bar obtained by quadratic sum.
 |
Fig. 5 Asymmetries in the first and sixth transits of Kepler-3b (maybe due to starspots). |
Since in both the barycenter method and the method of Mandel & Agol (2002) it is assumed that the light-curve is symmetric, these methods are sensitive to missing points in the observation of a transit. This can be seen from Table 2 for Kepler-6b and Kepler-9b. The standard deviations of these two planets are larger than their average errors, which could have been caused by a missing point in the observation of the first transit of Kepler-6b and fifth transit of Kepler-9b (Fig. 6). To illustrate this effect, we made an artificial light-curve for a transiting planet and calculated the time of its mid-transit using the model of Mandel & Agol (2002). We then removed one point from the light-curve and calculated the time of mid-transit using both the barycenter method and the method of Mandel & Agol (2002). As shown in Fig. 7, and in agreement with Csizmadia et al. (2010), the results obtained by both methods show large deviations when the missing point was in ingress or egress (deviation ~500 s). On the other hand, both methods become less sensitive when the missing point is close to the bottom of the light curve. This experiment suggested that both the barycenter and the Mandel & Agol methods require the full coverage of observation data in transit, and a missing point in the observation data may cause a large offset in the results.
We also examined the applicability of the barycenter method to the long integration time of Kepler’s long cadence observations (29.42 min) (Kipping 2010). Using the algorithm by Mandel & Agol (2002), we generated an artificial light-curve with bins of long integration times (we chose a point every 6 s and used the mean of 270 of those points as the observed flux). We changed the beginning time of each binning and studied the variations of mid-transit times as determined by the barycenter method. Results point to a deviation of no more than 4 s for the mid-transit times.
 |
Fig. 6 Asymmetries in the first transit of Kepler-6b and fifth transit of Kepler-9b, caused by missing point of observation. |
 |
Fig. 7 Deviations of mid-transit timing from the known values as calculated by Mandel & Agol, and the barycenter methods for a synthetic light curve with one missing point. The x-axis presents the rank of missing points in light curve. |
Parameters of the LHS 6343 system according to Johnson et al. (2011).
Transit timing of LHS 6343, as measured by the barycenter method and O–C values in days were calculated according to the new linear ephemeris.
 |
Fig. 8 Strange non-symmetric shape of third (blue square), fifth (green triangle), and eighth (red circle) transit of LHS 6343. |
4. The LHS 6343 system and its transit timing
LHS 6343 is a close, M+M binary system with a separation of ~20 AU. The primary of this binary, LHS 6343 A (KIC 10002261, RA = 19h10m14.33s, Dec = 46 °57′25.50′′), has a mass of 0.37 M⊙ and the mass of the secondary, LHS 6343 B, is approximately 0.30 M⊙ (see Table 3). The publicly available Q0 and Q1 data sets from Kepler revealed four deep transits in the light-curve of this system. By analyzing these data, Johnson et al. (2011) showed that these transits are produced by a third object, LHS 6343 C, which orbits LHS 6343 A every 12.71 days. As determined by these authors, LHS 6343 C is a brown dwarf with a mass of ~63 MJ and is located at a distance 0.08 AU from LHS 6343 A.
In preparation for applying the barycenter method to the light-curve of LHS 6343, we analyzed each transit of this system separately. Our initial analysis of the light-curve of LHS 6343 at the time of the release of Q0 and Q1 data sets pointed to a non-symmetric transit (transit number 3) among the initial four transits of this system. We recall that the barycenter method is based on the symmetry of the shape of a transit. The release of the Q2 data set provided us with seven more transits, of which our analysis identified transits number 5 and 8 as asymmetric. Figure 8 shows these non-symmetric transits. We note that these anomalies may be caused by starspots. To better portray the anomalies in the shapes of these transits, we used Mandel & Agol’s methodology and obtained the best fit to all 11 transits of this system. Figure 9 shows the residuals of each single transit with respect to this best fit. As shown here, the residuals of the third, fifth, and eighth transits are larger than 1 − σ (closer to 2 − σ) because of their anomalies inside their transits.
As mentioned for Kepler-9b, developing a model to explain these anomalies would require many observational points inside each transit and will depend on several parameters such as the size and latitude of starspots, their lifetimes, the rotational period of the star, and the orientation of the rotation axis of the star relative to the orbit of transiting brown dwarf. Although an interesting project on its own, developing such a model is beyond the scope of our study. Also, given that with the currently available data, the number of points in each transit is limited to only 5 or 6, such a model may not even be entirely realistic. Therefore, because the basis of the barycenter method is on the symmetry of a transit, and also to restrain false positive TTVs, we decided to exclude the most asymmetric transits (i.e., transits 3, 5, and 8) from our analysis. Table 4 lists the times of the mid-transits of the remaining eight transits of the system calculated using the barycenter method. To estimate the corresponding errors of each mid-transit time, we used the bootstrap method (Wall & Jenkins 2003) and considered the standard deviation inside each transit as the initial uncertainty. Note that the standard deviation inside a transit may be larger than outside due to crossing over starspots. To check the validity of our error estimation, we also calculated the values of errors using Eq. (2) and the methodology used by Doyle & Deeg (2004). Our calculations showed that the values of the errors obtained from all three methods have the same order of magnitude.
 |
Fig. 9 Residual of the best fit of the Mandel & Agol method to all transits of LHS 6343 (just inside transit). |
To obtain the variations in the transit timing of the system, we applied a linear fit to the eight mid-transit times in Table 4. Results suggested a period of P = 12.713815 days, corresponding to a semimajor axis of 0.076–0.080 AU for the transiting body. These results closely agree with the results reported by Johnson et al. (2011).
Given that LHS 6343 is a binary system and the transiting object (LHS 6343 C) orbits the primary star, the three-body system of LHS 6343 AC-B forms a hierarchical three-body system. We examined the stability of LHS 6343 C in this system by numerically integrating its orbit. Results indicated that this object is stable for long times. We refer the reader to a recent article by Borkovits et al. (2011) and references therein, where the authors have presented a detailed analysis of the dynamics and transit/eclipse timing variations of hierarchical tripe systems.
 |
Fig. 10 Diagram of the transit-timing variations of LHS 6343. |
5. Analyzing the O–C diagram of LHS 6343
The times of mid-transits obtained from the barycenter method show small deviations from their linear fit. Figure 10 and the right column of Table 4 show these deviations and their corresponding uncertainties for each mid-transit time. In this section, we analyze these deviations from the linear fit of transit timings and discuss their implications for the possible existence of a second smaller object around the primary LHS 6343 A.
Because it is in a hierarchical tripe configuration, LHS 6343 C is continuously subject to the gravitational perturbation of the secondary star. These perturbations affect the orbit of this object and cause variations in the times of its transit (for a detailed analysis of TTVs in hierarchical tripe systems we refer the reader to Borkovits et al. 2011). Given that the semimajor axis of the binary (~20 AU) and its projected separation (19–21 AU) are much larger than the semimajor axis of LHS 6343 C, it would be important to determine to what degree the variations in the transit timing of this object have been caused by the binary’s light-travel time (LTT) effect. To examine this possibility, we used the methodology presented by Montalto (2010) and calculated LTTs for different values of the semimajor axis and eccentricity of the binary. We changed the values of the projected separation of the binary using the distribution given by Duquennoy & Mayor (1991), and performed 10 000 LTT-calculations for randomly chosen values of the binary eccentricity between 0 and 0.9. In all our simulations, we considered the system to be coplanar. We identified the systems for which the value of LTT was between 1 s and 6 s. Figures 11 and 12 show the results for a timespan of three years (duration of Kepler’s primary mission). As shown here, systems with LTTs between 4.5 s and 5.5 s constitute the majority of the cases (we recall that the minimum reported value of TTV that can be detected by Kepler is ~10 s, see Ford et al. 2011). Figure 13 shows the results of all our simulations for LTTs between 5 s and 6 s in more detail. As shown in this figure, the values of LTTs do not exceed 6 s, which implies that during the period spanned by the present public release of the Kepler observations data (~144 days), the contribution of the binary LTT to the variations in the transit timing of LHS 6343 C is negligible.
 |
Fig. 11 Values of LTTs of LHS 6343 for different values of the binary semimajor axis. |
 |
Fig. 12 Values of LTTs of LHS 6343 for different values of the binary eccentricity. |
 |
Fig. 13 Graph of LTTs between 5 s and 6 s for different values of the binary semimajor axis and eccentricity. |
The fact that the contribution of LTT to the O–C values, as listed in Table 4, is negligibly small implies that in modeling these deviations from the linear fit of transit timings, one can safely ignore the effect of the secondary star.
To examine whether these deviations could be caused by an additional body in the system, we considered the two-body system of LHS 6343 AC, and calculated the O–C values for different values of the mass, semimajor axis, and orbital eccentricity of a hypothetical perturber around the primary LHS 6343 A. To reduce the amount of calculations (which could be large because of the large size of the parameter-space), we limited our study to only circular and coplanar systems. Figure 14 shows the results for different values of the initial angular position of the hypothetical third body. A comparison between these results and the values of the O–C in the right column of Table 4 suggests that a perturber with a mass ranging from 0.1 to 1 MJ may be able to produce these values when in an orbit with a period ranging from ~3.5 to 8P (where P = 12.713815 days is the orbital period of LHS 6343 C) around LHS 6343 A. To determine an upper limit for the mass of the perturber, we calculated the O–C values for different values of the mass and semimajor axis of this object, and compared the results with the values of O–C as shown in Fig. 10. Figure 15 shows the maximum values of the mass of the perturber for which the value of χ2 between the O–C obtained from the model and those listed in Table 4 are lower than 3. As shown in this figure, the mass of the perturber cannot be larger than one Jupiter-mass.
 |
Fig. 14 Values of TTVs in the system of LHS 6343AC due to a hypothetical perturber. The system is assumed to be circular and coplanar. Each panel shows TTVs for a different value of the angular phase of the perturber. The units on the color scale are in seconds. |
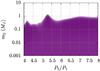 |
Fig. 15 Maximum mass of the perturber on circular orbit reproducing the TTVs as in Fig. 10, as a function of its orbital period. |
6. Conclusion
We presented a technique called the barycenter method for calculating the time of the mid-transit in transit-timing studies. This method is based on the symmetry of the light-curve, and has the advantage that is independent of the parameters of the system. In other words, unlike other techniques for calculating the mid-transit timing, the results obtained from the barycenter method will not change by changing the assumption on the parameters of the central star. However, the fact that this method requires symmetry in the light-curve implies that when the transit curve is not perfectly symmetric (i.e., when observational points are missing, or because of starspots), large offsets may appear in the mid-transit timing measurements. The application of the barycenter method to several known transiting systems showed that the results obtained from this technique are comparable with those obtained from other methods. Our study indicates that for complete and symmetric transit lightcurves, the barycenter method achieves the same precision as in the model of Mandel & Agol (2002), but with fewer assumptions and much faster.
We used the barycenter method to calculate the times of mid-transits of the M+M binary star LHS 6343. Our results indicated that as suggested by Johnson et al. (2011), the primary of this system is host to a smaller object with a period of ~12.7 days. A study of the variations in the transit timing of this body (LHS 6343 C) points to the possibility that a small object with a mass no larger than 1 MJ may exist around LHS 6343 A, which can produce the O–C values lower than the upper values presented here. Whether such an object actually exists requires more transit data and more observations of this system.
Online material
Transit timing of Kepler-1b - Kepler-9c, measured by both methods.
Acknowledgments
We acknowledge the support by the European Research Council/European Community under the FP7 through Starting Grant agreement number 239953, and by Fundação para a Ciência e a Tecnologia (FCT) in the form of grant reference PTDC/CTE-AST/098528/2008. N.C.S. also acknowledge the support from FCT through program Ciência 2007 funded by FCT/MCTES (Portugal) and POPH/FSE (EC). G.B. thanks the Paris Observatory for providing the necessary computational resources for this work. N.H. acknowledges support from the NASA/EXOB program through grant NNX09AN05G and from the NASA Astrobiology Institute under Cooperative Agreement NNA04CC08A at the Institute for Astronomy, University of Hawaii.
References
- Adams, E. R., López-Morales, M., Elliot, J. L., Seager, S., & Osip, D. J. 2010, ApJ, 714, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Adams, E. R., López-Morales, M., Elliot, J. L., Seager, S., & Osip, D. J. 2011, ApJ, 728, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Agol, E., & Steffen, J. H. 2007, MNRAS, 374, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso, R., Alapini, A., Aigrain, S., et al. 2009, A&A, 506, 353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballard, S., Fabrycky, D., Fressin, F., et al. 2011, ApJ, 743, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L. 2009, A&A, 506, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borkovits, T., Csizmadia, S., Forgács-Dajka, E., & Hegedüs, T. 2011, A&A, 528, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Csizmadia, S., Renner, S., Barge, P., et al. 2010, A&A, 510, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deeg, H. J., Doyle, L. R., Kozhevnikov, V. P., et al. 2000, A&A, 358, L5 [NASA ADS] [Google Scholar]
- Deeg, H. J., Ocaña, B., Kozhevnikov, V. P., et al. 2008, A&A, 480, 563 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deming, D., Sada, P. V., Jackson, B., et al. 2011, ApJ, 740, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Doyle, L. R., & Deeg, H.-J. 2004, in Bioastronomy 2002: Life Among the Stars, ed. R. Norris, & F. Stootman, IAU Symp., 213, 80 [Google Scholar]
- Duquennoy, A., & Mayor, M. 1991, A&A, 248, 485 [NASA ADS] [Google Scholar]
- Ford, E. B., Rowe, J. F., Fabrycky, D. C., et al. 2011, ApJS, 197, 2 [NASA ADS] [CrossRef] [Google Scholar]
- García-Melendo, E., & López-Morales, M. 2011, MNRAS, 417, L16 [NASA ADS] [Google Scholar]
- Haghighipour, N., Agol, E., Eastman, J. D., et al. 2009, astro2010: The Astronomy and Astrophysics Decadal Survey, 109 [Google Scholar]
- Haghighipour, N., & Kirste, S. 2011, Cel. Mech. Dyn. Astron., 111, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Holman, M. J., & Murray, N. W. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Holman, M. J., Fabrycky, D. C., Ragozzine, D., et al. 2010, Science, 330, 51 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Johnson, J. A., Apps, K., Gazak, J. Z., et al. 2011, ApJ, 730, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2009, MNRAS, 392, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2010, MNRAS, 408, 1758 [NASA ADS] [CrossRef] [Google Scholar]
- Kipping, D. M. 2011, MNRAS, 416, 689 [NASA ADS] [Google Scholar]
- Kwee, K. K., & van Woerden, H. 1956, Bull. Astron. Inst. Netherlands, 12, 327 [Google Scholar]
- Lissauer, J. J., Fabrycky, D. C., Ford, E. B., et al. 2011, Nature, 470, 53 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Maciejewski, G., Dimitrov, D., Neuhäuser, R., et al. 2010, MNRAS, 407, 2625 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, G., Dimitrov, D., Neuhäuser, R., et al. 2011a, MNRAS, 411, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, G., Errmann, R., Raetz, S., et al. 2011b, A&A, 528, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Meschiari, S., & Laughlin, G. P. 2010, ApJ, 718, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda-Escudé, J. 2002, ApJ, 564, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Montalto, M. 2010, A&A, 521, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nesvorný, D. 2009, ApJ, 701, 1116 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Beaugé, C. 2010, ApJ, 709, L44 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvorný, D., & Morbidelli, A. 2008, ApJ, 688, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Nutzman, P. A., Fabrycky, D. C., & Fortney, J. J. 2011, ApJ, 740, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Rabus, M., Alonso, R., Belmonte, J. A., et al. 2009, A&A, 494, 391 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanchis-Ojeda, R., & Winn, J. N. 2011, ApJ, 743, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchis-Ojeda, R., Winn, J. N., Holman, M. J., et al. 2011, ApJ, 733, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, R., Haghighipour, N., Eggl, S., Pilat-Lohinger, E., & Funk, B. 2011, MNRAS, 414, 2763 [NASA ADS] [CrossRef] [Google Scholar]
- Silva-Valio, A. 2008, ApJ, 683, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, A., Szatmáry, K., & Szabó, G. M. 2007, A&A, 470, 727 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steffen, J. H., Gaudi, B. S., Ford, E. B., Agol, E., & Holman, M. J. 2007 [arXiv:0704.0632] [Google Scholar]
- Szabó, G. M., Szatmáry, K., Divéki, Z., & Simon, A. 2006, A&A, 450, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wall, J. V., & Jenkins, C. R. 2003, Practical Statistics for Astronomers (Cambridge University Press) [Google Scholar]
All Tables
Comparison of standard deviation of the difference between two methods and the average error bar obtained by quadratic sum.
Transit timing of LHS 6343, as measured by the barycenter method and O–C values in days were calculated according to the new linear ephemeris.
All Figures
 |
Fig. 1 Schematic view of the barycenter method. |
| In the text | |
 |
Fig. 2 Comparison between the results of mid-transit of HAT-P-7b first transit, obtained by the Mandel & Agol method (black circle), the trapezoid method (red square) and the barycenter method (blue triangle). |
| In the text | |
 |
Fig. 3 Differences between the values of mid-transit timing obtained by the barycenter method and the Mandel & Agol method for Kepler-1b to Kepler-4b (Holman et al. 2010; Ford et al. 2011). |
| In the text | |
 |
Fig. 4 Same as in Fig. 3 for Kepler-5b to Kepler-9c. |
| In the text | |
 |
Fig. 5 Asymmetries in the first and sixth transits of Kepler-3b (maybe due to starspots). |
| In the text | |
 |
Fig. 6 Asymmetries in the first transit of Kepler-6b and fifth transit of Kepler-9b, caused by missing point of observation. |
| In the text | |
 |
Fig. 7 Deviations of mid-transit timing from the known values as calculated by Mandel & Agol, and the barycenter methods for a synthetic light curve with one missing point. The x-axis presents the rank of missing points in light curve. |
| In the text | |
 |
Fig. 8 Strange non-symmetric shape of third (blue square), fifth (green triangle), and eighth (red circle) transit of LHS 6343. |
| In the text | |
 |
Fig. 9 Residual of the best fit of the Mandel & Agol method to all transits of LHS 6343 (just inside transit). |
| In the text | |
 |
Fig. 10 Diagram of the transit-timing variations of LHS 6343. |
| In the text | |
 |
Fig. 11 Values of LTTs of LHS 6343 for different values of the binary semimajor axis. |
| In the text | |
 |
Fig. 12 Values of LTTs of LHS 6343 for different values of the binary eccentricity. |
| In the text | |
 |
Fig. 13 Graph of LTTs between 5 s and 6 s for different values of the binary semimajor axis and eccentricity. |
| In the text | |
 |
Fig. 14 Values of TTVs in the system of LHS 6343AC due to a hypothetical perturber. The system is assumed to be circular and coplanar. Each panel shows TTVs for a different value of the angular phase of the perturber. The units on the color scale are in seconds. |
| In the text | |
 |
Fig. 15 Maximum mass of the perturber on circular orbit reproducing the TTVs as in Fig. 10, as a function of its orbital period. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


