| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A117 | |
| Number of page(s) | 15 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201117540 | |
| Published online | 06 April 2012 | |
Strong interactions between g- and p-modes in the hybrid γ Doradus-δ Scuti CoRoT star ID 105733033⋆,⋆⋆
1 Laboratoire Lagrange, UMR7293, Université de Nice Sophia-Antipolis, CNRS, Observatoire de la Côte d’Azur, 06300 Nice, France
2 Université de Toulouse, UPS-OMP, IRAP, 65000 Tarbes, France
e-mail: philippe.mathias@irap.omp.eu
3 CNRS, IRAP, 57 Avenue d’Azereix, BP 826, 65008 Tarbes, France
4 University of Vienna, Institute for Astronomy, Türkenschanzstrasse 17, 1180 Vienna, Austria
5 Instituut voor Sterrenkunde, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
Received: 22 June 2011
Accepted: 26 January 2012
Context. The presence of stellar p- and g-modes allows us to test stellar structure models in great detail from the core to the envelope. As the driving mechanisms are not yet fully understood, the first important step is to provide clear evidence of these pulsation modes.
Aims. Recent space missions have confirmed that the γ Doradus and the δ Scuti observational instability strips overlap and consequently that many stars may be hybrids. CoRoT ID 105733033 is an excellent example of these hybrid pulsators as it shows g- and p-modes with almost similar amplitudes in two clearly distinct frequency domains. We present a detailed frequency analysis of the CoRoT star ID 105733033, which is obtained with a classical Fourier analysis.
Methods. After removing residual instrumental effects from the CoRoT light curve of N2 level, frequencies with an amplitude as small as 0.1 mmag were determined with Period04 and SigSpec up to 50 d-1, although if deemed necessary lower amplitudes and higher frequencies were also investigated. The frequency spectrum of CoRoT ID 105733033 clearly consists of two distinct ranges, which are typical of γ Doradus and δ Scuti pulsation. Focus was placed on the identification of linear combinations and frequencies due to the coupling between γ Doradus and δ Scuti modes.
Results. We detect 198 γ Doradus type frequencies in the range [0.25;4] d-1, of which 180 are not combination frequencies, and 24 of them are separated by a constant period-interval ΔP = 0.03074 d. According to the asymptotic theory, these 24 frequencies correspond to a series of g-modes of the same ℓ-degree and different radial orders n. We also detect 246 δ Scuti type frequencies in the range [10.1;63.4] d-1. The dominant frequency F = 12.6759 d-1 was identified as the fundamental radial mode. Our most noteworthy result is that all the main γ Doradus frequencies fi are also detected in the δ Scuti domain as F ± fi with four times smaller amplitudes. Once these frequencies were removed, only 59 can be considered as individual δ Scuti frequencies.
Conclusions. A coupling between g- and p-modes is proposed to be a tool for detecting g-modes in the Sun, but this coupling has never yet been observed. Our present study may be valuable input to theoretical studies, addressing the mutual influence of g- and p-mode cavities and the deviation from classical theory. Furthermore, we identify a sequence of g-modes belonging to the same ℓ but with consecutive orders n.
Key words: asteroseismology / stars: oscillations / techniques: photometric / stars: variables: general
The CoRoT space mission was developed and is operated by the French space agency CNES, with participation of ESA’s RSSD and Science Programmes, Austria, Belgium, Brazil, Germany, and Spain.
Full Table 1 is available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
The knowledge of solar and stellar interiors has improved tremendously in the past few decades due to both theoretical work such as new opacity tables (Cox et al. 1992) for the destabilisation of β Cephei and SPB stars and the convection/pulsation coupling for γ Doradus stars (Guzik et al. 2000; Dupret et al. 2004), and new observing facilities such as the space missions CoRoT (Baglin et al. 2006), MOST (Walker et al. 2003), and Kepler (Borucki et al. 1997; Christensen-Dalsgaard et al. 2008).
Until recently, δ Scuti and γ Doradus stars seemed to be clearly distinct, even if their respective instability strips overlap within a small region. A few hybrid star candidates have been identified e.g. by Henry & Fekel (2005), Rowe et al. (2006), and Handler (2009). The hybrid stars have become extremely interesting targets because p- and g-modes probe different regions of the stellar interiors. The presence of both types of modes in a same star provides complementary model constraints.
With the availability of space observations, considerably lower-amplitude pulsation modes have become detectable compared with ground observations. The instability strips (IS) of δ Scuti and γ Doradus stars have been found to overlap and their respective hot and cool borders have become seemingly less well-defined. In addition, many CoRoT and Kepler stars do not show in their pulsation spectra a clear distinction between their γ Doradus and δ Scuti-frequency regions.
In this paper, we discuss the very interesting case of a star being unambiguously hybrid, with a frequency gap between 4 d-1 and 10 d-1, and indications of strong interactions between the p- and g-modes. The data are described in Sect. 2, and the frequency analysis is presented in Sect. 3. The frequency spectrum is discussed in Sect. 4 for the low-frequency region (γ Doradus domain) and in Sect. 5 for the high-frequency region (δ Scuti domain). A theoretical interpretation of the interaction of the γ Doradus-δ Scuti modes is given in Sect. 5. The effects of the rotation are discussed in Sect. 6 and some conclusions are provided in Sect. 7.
2. The CoRoT data
The observations of CoRoT ID 105733033 were collected during CoRoT’s second long run, LRc02, which targeted the Galactic center. We used the reduced N2 light curves (Auvergne et al. 2009) throughout this paper. The observations lasted 145 days, from 2008, April 15th to September 7th. Among the 388 950 measurements obtained with a temporal resolution of 32 s, we retained only the 345 908 points flagged “0” by the CoRoT pipeline, the other measurements being affected by instrumental effects such as straylight, cosmic rays, and perturbation by Earth eclipses.
The light curve is recorded in “chromatic” light i.e., in three non-calibrated bands unevenly spanning the wavelength interval 370–950 nm, obtained by the insertion of a prism just in front of the exo-planet CCD. To increase the signal-to-noise ratio (S/N), we added the three components of the colour bands to a “white” light curve. Unless specified otherwise, we refer in the following to the “white” light curve.
CoRoT data are known to be affected by several instrumental effects, such as long-term trends and jumps due to cosmic rays (Auvergne et al. 2009). In addition, many individual measurements can be considered as outliers. The data of the most significant outliers (mainly high-flux data points caused by cosmic ray impacts) were removed by an iterative procedure during the Fourier analysis. Jumps were corrected by applying simple vertical shifts to the data. The resulting light curve is represented at different timescales in Fig. 1 and clearly contains both low and high frequency components. As noted by Balona et al. (2011) for other high amplitude γ Doradus stars, the light curve displays sometimes a Blazhko-like behaviour: the maxima vary far more than the minima. This effect can also be observed for our star. In the following, the timescale is labeled in units of the CoRoT Julian day (JD), where the starting CoRoT JD corresponds to HJD 2 445 545.0 (2000, January 1st at UT 12:00:00).
 |
Fig. 1 Light curve of the star CoRoT ID 105733033 corrected for long-term trends, jumps, and outliers (see text) with different timescales. From top to bottom, the complete light curve over 145 d, then a subset over 22 d and finally a zoom into a 3.5 d subset. |
Information provided by the EXODAT database (Deleuil et al. 2009) indicates that the star has an A5V spectral type and magnitude V = 12.8. The conversion of the flux values to magnitudes of CoRoT ID 105733033 is calibrated to a CoRoT magnitude of C = 12.543. The BEST survey of the LRc02 field classifies the star as a pulsating star of SX Phoenicis type (Kabath et al. 2009) and 2MASS provides (J = 11.445, H = 11.205, K = 11.094). The CoRoT contamination factor is very small (1.7%), hence we assume that the signal originates entirely from CoRoT ID 105733033.
3. Frequency analysis of the CoRoT dataset
The frequency analysis was performed on the filtered data using two independent methods: Period04 (Lenz & Breger 2005) and SigSpec (Reegen 2007). We first used the Period04 package and searched the interval [0;100] d-1 i.e., well below the Nyquist frequency. However, since the computations were very time-consuming, we limited our search mostly to the interval [0;50] d-1, and explored the second part of the interval only every 50 newly detected frequencies. For each detected frequency, the amplitude and phase were calculated by a least-squares sine fit. The data were then prewhitened and a new analysis was performed on the residuals. We did not use the option improve all, available in the Period04 package, which computes a multi-sine fit. From experience, it is known that the frequency differences derived from an individual least-squares sine fit relative to a multi-sine fit, depend largely on the quality of the spectral window, which in our case of CoRoT is characterized by a very high duty cycle. Tests have confirmed that differences smaller than 0.001 d-1 are typical in our case of frequencies higher than 0.05 d-1, except in cases of a small-amplitude frequency within a 1/ΔT-bin close to a large amplitude one. Our analysis was conducted until a S/N = 3.9 was reached, slightly below the usual S/N = 4 value (Breger et al. 1993; Kuschnig et al. 1997) and corresponding to an amplitude of about 0.1 mmag, which resulted in a detection of 559 frequencies.
The uncertainties in the frequencies, amplitudes, and phases were computed with the formulae proposed by Montgomery & O’Donoghue (1999) providing a 3σ estimate. However, as we used a step size of 1/20ΔT in the Fourier analysis, and since the accuracies of the frequencies were not improved by a multi-sine fit, the uncertainties in the frequencies are certainly no smaller than 1/40ΔT. Therefore, the frequency uncertainties are 1/40ΔT when the aforementioned formal 3σ estimate is smaller. Some of the lowest frequencies are actually linked to instrumental fluctuations, which were not corrected by the reduction pipeline. Once the 559 frequencies are removed, the periodogram of the residuals shows that some signal is still present (Fig. 2) but mainly located in high-density peak regions, and many of the peaks are actually residuals of previously detected frequencies.
In a next step, the frequency analysis was repeated by applying SigSpec to the data filtered with a cubic spline function to get rid of the main CCD variations. However, this procedure also eliminated possible low-frequency pulsations. To be consistent with the Period04 results, the program was stopped after detecting 600 frequencies. The threshold magnitude turned out to be about 0.08 mmag.
The results of the two methods agree fairly well. With SigSpec, we detected fewer low-frequencies since the data were prewhitenened with a cubic spline, but some additional frequencies emerged with marginal amplitudes between 0.08 and 0.1 mmag. The main difference concerns the frequency values derived by the two techniques, which can amount sometimes to 0.004 d-1, but remains well within the Rayleigh criterion of 0.007 d-1. As we needed consistency to detect couplings, we used Period04 in the following.
The next step consisted in the sorting of stellar and non-stellar frequencies. As usual for CoRoT data, we eliminated both the frequencies corresponding to the orbital frequency forb = 13.97 d-1 and its harmonics, and the 2fsid = 2.0054 d-1 value due to the passage over the South Atlantic Anomaly, which occurs twice each sidereal day (Auvergne et al. 2009). Small-amplitude frequencies separated by 1/ΔT from a large-amplitude frequency were ignored in the following as the effects of the spectral window (data set length).
 |
Fig. 2 Amplitude spectra computed with Period04 for the 444 retained frequencies. From top to bottom: the amplitudes in μmag, and the same with a logarithmic scale, the Fourier spectrum computed from the residuals, and the spectral window normalized to unity, but plotted only to 0.1 in amplitude. |
As usual in the CoRoT data, variations in the properties of the CCD perturb the lowest part of the periodogram, so we decided to analyze only frequencies higher than 0.25 d-1. We made an exception of the low amplitude frequency F144 = 0.2482 d-1 as it corresponds to the coupling f1 − f4. We tested our 0.25 d-1 limit in Sect. 5 and found that it is realistic.
As a result, 444 frequencies were retained that have no clear instrumental origin (in Table 1, only the first 25 frequencies are given here and the full table is only available electronically, and in Fig. 2). These frequencies can be divided into two main groups: 198 in the interval [0.2483;3.9936] d-1, corresponding to the typical γ Doradus frequency domain, and 246 in the interval [10.1038;63.3800] d-1, which is typical of the δ Scuti domain. No frequency with an amplitude larger than 0.1 mmag was detected in the interval [4;10] d-1, except perhaps an isolated frequency f = 5.6038 d-1 with an amplitude of 0.09 mmag.
The first 25 stellar frequencies.
This clear distinction between low- and high-frequency regions may be the consequence of a quite low angular rotation velocity Ω. Following the rotation perturbation theory, the observed frequencies are indeed shifted from the co-moving frame ones by a quantity that is, to first order, proportional to Ω. Hence, in the case of rapid rotators, the “observed” frequency spectrum might differ significantly from those measured in a “co-rotating” frame and the two frequency regions might even overlap. It is thus imperative to obtain a spectrum of this star, which allows us to measure v sin i and estimate the rotation velocity Ω. Unfortunately, no spectroscopy is yet available for CoRoT ID 105733033. However, the clear gap between rather compact low- and high-frequency regions strongly argues in favor of a slow angular rotation, which we therefore predict. A low Ω would also be consistent with a rotation period of 20.57 d, which is proposed by us in Sect. 6. In the following, we therefore assume that the observed frequencies do not differ significantly from the co-rotating ones.
4. The γ Doradus domain
From the Fourier analysis, we found 198 frequencies in the range [0.2483;3.9936] d-1, of which 176 were detected between 0.25 and 2.6 d-1 (Fig. 3). In the following, we re-numbered the 198 frequencies in order of decreasing amplitude, starting from f1. The main frequency is f1 = 0.7428 d-1 with an amplitude A1 = 11.15 mmag. Data phased with this frequency are represented in Fig. 4. The shape of the curve is nearly sinusoidal, hence only 2f1 is detected with an amplitude of 0.77 mmag.
We identified 17 cases in which a linear combination of detected γ Doradus frequencies coincide to within Δ = 0.001 d-1 with 17 other detected frequency (Table 2). This Δ refers to the uncertainty in the lowest amplitude frequencies (see Table 1).
Another interesting finding is the presence of coupling between p- and g-modes (see Sect. 5), where we found for 82% of the 50 candidates with the largest amplitudes a frequency difference between coupled modes and observed frequencies of less than 0.001 d-1. On the other hand, in the case of the 100 lowest amplitude g-modes (for which no coupling is expected) we found in only 1.5% of the possibilities a difference smaller than 0.001 d-1. We interpret this finding as support of the chosen value of Δ = 0.001 d-1. A few expected combinations were not detected, e.g. f1 + f5, as they were masked by pulsation frequencies with higher amplitudes (within a distance smaller than 1/ΔT). After elimination of harmonics and coupled frequencies, 180 independent frequencies of γ Doradus type were retained.
Linear combinations of frequencies detected in the γ Doradus domain.
In the case of large radial numbers n, the first order asymptotic theory (Tassoul 1980) predicts for g-modes of the same degree ℓ, a constant period spacing between consecutive radial orders n. Searching in Table 1 for equidistant γ Doradus periods, we found a series of 24 asymptotic ones with a mean separation of ΔP = 0.03074 ± 0.00005 d (Fig. 5). The periods extend from 0.693 d to 1.593 d with the highest concentration being between 1.009 d and 1.439 d. In this region, we detected 15 consecutive and equidistant periods among the 18 possible. Most of them have relatively large amplitudes, and are indeed among the largest amplitude g-mode frequencies detected. Further away from the central region, the amplitudes decrease, but we detected 9 other periods fitting the sequence. Several values are missing in the asymptotic series probably owing to their low amplitudes. The 24 retained periods correspond to n-values ranging from − 23 to + 8, with the largest amplitude period P1 = 1.3470 d (f1 = 0.7428 d-1) being arbitrarily taken as order zero. The sequence is listed in Table 3 and illustrated in Fig. 6.
 |
Fig. 3 Enlargement of Fig. 2 [second] showing the detected frequencies in the γ Doradus domain. The ordinates are on a logarithmic scale. |
 |
Fig. 4 Data phased with the main γ Doradus frequency f1 = 0.7428 d-1. |
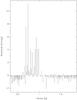 |
Fig. 5 Plot of the frequencies detected in the interval [0.4; 1.8] d-1. “Positive” amplitude frequencies represent the identified asymptotic frequency series, while the “negative” ones are the other detected frequencies in this interval. |
 |
Fig. 6 γ Doradus periods that obey the asymptotic period spacing law as a function of radial order n with an arbitrary zero point [top]. The bottom part shows the residuals of this period spacing; a straight line has been added for better visibility. |
5. The δ Scuti domain
In the δ Scuti frequency domain, we retained 246 frequencies in the interval [10.1038;63.3800] d-1 (Table 1, Fig. 7). One frequency clearly dominates the spectrum, F = 12.6759 d-1, with an amplitude A1 = 27.08 mmag. Figure 7 represents a light curve that has been phased with frequency F. The curve is very asymmetric and unsurprisingly harmonics up to 5F were detected. The Fourier parameters φ21 = 4.03 rad (phase difference of first overtone and twice the phase of fundamental frequency) and R21 = 0.26 (the amplitude ratio of first overtone to fundamental frequency) were in perfect agreement with those of fundamental radial pulsators (Poretti 2001). Hence, we can conclude that F is a radial mode.
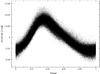 |
Fig. 7 Data phased with the main δ Scuti frequency F = 12.6759 d-1. |
Asymptotic frequencies.
To corroborate the identification of this pulsation mode, we have only the measurements provided by the EXODAT database (Deleuil et al. 2009), which are indicative of an A5V spectral type. On the basis of this classification, the star would have an absolute magnitude of MV = +2.0 mag and an effective temperature of Teff = 8000 K. The period-luminosity relation given by Templeton et al. (2002) supports the identification of the main frequency F as a radial fundamental mode. Likewise, using the equation given by Poretti et al. (2008)MV = −1.83( ± 0.08) − 3.65( ± 0.07)log P, we also obtain for the absolute magnitude: MV = + 2.20( ± 0.16) mag.
The most remarkable property of CoRoT ID 105733033 is the coupling of most of the δ Scuti frequencies with γ Doradus ones: the first tens of γ Doradus frequencies fi are present in the δ Scuti domain as F ± fi. We also detected 2F ± fi and 3F ± fi for the γ Doradus frequencies with the largest amplitudes. For the 40 first γ Doradus frequencies fi, both F − fi and F + fi frequencies are present except for a few ambiguous cases. Coupling with lower amplitude γ Doradus frequencies (up to f100) were also detected as F − fi or F + fi, but not so regularly. We were able to detect 146 couplings within the limit of Δf = 0.001 d-1: 110 for F ± fi, 30 for 2F ± fi, and 6 for 3F ± fi. The three first groups of coupling are presented in Table 4, the complete list being presented in Table 1.
First three groups of coupled γ Doradus and δ Scuti frequencies.
 |
Fig. 8 Top: enlargement of Fig. 2 [second] showing the detected frequencies in the δ Scuti domain. Bottom: the δ Scuti frequencies without linear combinations with γ Doradus frequencies. The ordinates are on a logarithmic scale. |
The amplitude ratios of the γ Doradus frequencies to the associated high frequencies of δ Scuti characteristics are remarkably constant, being 4.1 ± 0.1 (Afi/(AF ± fi)), 15 ± 1 (Afi/(A2F ± fi)), and 53 ± 4 (Afi/(A3F ± fi)). The amplitudes of the F − fi frequencies were slightly larger (1.3%) than those of F + fi. We also note that the beatings of F ± fi frequencies are in phase with the fi frequencies i.e., the highest amplitude of the beating of F and F ± fi occurs when the light curve of fi reaches a maximum.
Thus, it appears that a fundamental property of this star is the coupling between g- and p-modes. This coupling was previously predicted for the Sun (Kennedy et al. 1993). Following this study, the low-frequency g-modes, trapped in the stellar interior, induce slow periodic thermodynamic perturbations in the envelope, leading to a frequency modulation of the outer p-modes. This causes the formation of a pair of spectral sidelobes (not to be confused with sidelobes caused by the spectral window!) that are symmetric relative to the unperturbed p-mode frequency. This is exactly what we see for our F ± fi peaks. A complementary study (Lou 2001) shows that, in principle, a spectrum of sidelobes would appear to be centered on each p-mode frequency and that the spectral structure may be complicated by the presence of several g-modes. The predicted amplitude ratio of the first sidelobe As to the central p-mode Ap is 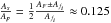 , but this ratio was not measured by us.
, but this ratio was not measured by us.
On the other hand, measured sidelobe amplitudes are directly linked to the amplitude of the respective “parent” g- and p-modes. The first non-radial mode of δ Scuti-type (p1) also contains sidelobes. The amplitude ratio of F to p1 is 23, where the sidelobes of the p1 ± fi peaks are “only” nine times smaller than those corresponding to F ± fi. Hence, the relationship does not seem to be linear. In conclusion, except for the influence of the amplitudes of the concerned modes, the coupling mechanism proposed by Kennedy et al. (1993) and Lou (2001) operates in this star. Initiated first as a help to the detection of g-modes in the Sun, there is no obvious reason for not assuming that this mechanism operates in other stars.
Without all the coupling frequencies 100, δ Scuti-type frequencies remained. For a list of “pure” δ Scuti frequencies, we also discarded frequencies with | kF ± fi − Fmeasured | ≤ Δ = 0.0015 d-1 (instead of our standard Δ = 0.0010 d-1), if their amplitude ratio was compatible with the value of three obtained in our “standard” case. We derived 25 of these possible couplings, which are all of F ± fi type.
We used this interaction mechanism in order to test the low frequency region. If γ Doradus-type frequencies, fi, lower than 0.25 d-1 and with amplitudes larger than 0.4 mmag were to exist, we should detect them as F ± fi. No such frequencies were detected, so we conclude that the lower limit for γ Doradus frequencies really is about 0.25 d-1.
The physical characteristics of the star (mass, effective temperature, radius, evolutionary state...), are uncertain, as was previously mentioned at the beginning of this section. Using the values computed by Fitch (1981), the frequencies associated with the first overtones 1O, 2O, and 3O should be close to respectively 16.55, 20.66, and 24.85 d-1. Values associated with the 1O and 2O modes are located in regions that have a low density of frequencies, and the frequencies F98 = 16.4019 d-1 (A98 = 0.49 mmag) and F215 = 20.7007 d-1 (A215 = 0.25 mmag) could correspond to these modes. As neither the fundamental stellar parameters, nor the true errors of the models, are known with sufficient accuracy, we can only speculate that the overtones are a correct interpretation.
The non-radial δ Scuti frequencies were renamed in order of decreasing amplitude starting from p1 ≡ F33 (see also Table 1). They are presented in the lower part of Fig. 8. These frequencies are dominated by p1 = 13.8566 d-1 with an amplitude of 1.18 mmag and all the others have amplitudes smaller than 0.5 mmag. We detected three couplings between p1 and the γ Doradus frequencies f3, f5, and f6 according to p1 + fi. The mean amplitude ratio Ap1/(Ap1 + fi) is 35 i.e., about nine times larger than the corresponding ratio associated to F.
We also detected 9 couplings between F and other δ Scuti type frequencies. Therefore, we end up with 59 independent δ Scuti frequencies, three of which are probably associated with radial modes, and the 56 others with non-radial modes.
6. Rotation
We searched for equidistant frequencies that could be related to rotational splitting. The only possibilities we found were quadruplet components formed by p31 ≡ F381 = 12.5776 d-1, p29 ≡ F360 = 12.6276 d-1, F = 12.6759 d-1 and p41 ≡ F444 = 12.7231 d-1. The separations are respectively 0.0500, 0.0483, and 0.0473 d-1. The radial fundamental mode F cannot of course lead to any rotational splitting, but its high amplitude may conceal a non-radial ℓ = 2 mode that could be responsible for the aforementioned detected quadruplet. Another interpretation is that the star belongs to a binary system, and that the equidistant peaks are actually orbital sidelobes to the central pulsation frequency modulated by the Doppler effect, as proposed by Shibahashi & Kurtz (2012).
Among the frequencies below 0.25 d-1 (see Sect. 3) was a frequency at 0.04862 d-1 that has an amplitude of A = 1.46 mmag, which is close to the separation values mentioned in the previous paragraph.
A possible interpretation of this low frequency could be the rotation of the star with a period of 20.57 d causing light variations associated for instance with surface inhomogeneities. We note that a phase plot (Fig. 9) of the residuals after prewhitening with the pulsation frequencies, when using the candidate rotation period looks reasonable. This rotation period would also be long enough to account for the two clearly distinct groups of γ Doradus and δ Scuti frequencies because the observed frequency spectrum should not differ significantly from the co-rotating one. Our speculations concerning a rotation period of course have to be taken with the utmost caution as the very low frequency range is populated by signal caused by instrumental effects, imperfect data reduction, g-modes, and combination frequencies. A dedicated spectroscopic observing program focused on the detection of rotation and eventual binarity effects in this star would be needed to resolve the ambiguities. However, the evidence presented in this paper is both consistent and plausible.
 |
Fig. 9 Binned data phased with the candidate rotation frequency f = 0.0486 d-1, corresponding to a rotation period of 20.57 d. Different symbols refer to different rotation cycles and data averaged in steps of 0.1 in phase. |
7. Summary
The star CoRoT ID 105733033 appears to be a very powerful test case for hybrid star studies. First, its frequency spectrum is quite rich. Second, two separate domains are clearly detected, with 198 frequencies in the range of [0.2483;3.9936] d-1, which is typical for g-modes, and 246 frequencies in the range of [10.1038;63.3800] d-1, typical of p-modes. Among these frequencies, 180 and 59 are respectively neither combination frequencies nor caused by coupling between g and p-modes, hence seem to represent pure γ Doradus and δ Scuti pulsation modes. The sole exception is the frequency f = 5.6038 d-1, but with an amplitude slightly smaller than 0.1 mmag, which is our chosen lower magnitude limit. This gap between the two domains is a strong indication of slow rotation, since the modes in the observer’s frame are not mixed.
We found 17 linear combinations among the γ Doradus frequencies. More are probably present, but the time coverage of our data may not be sufficiently long to detect them. The asymptotic theory is very well-illustrated by this star, which has 24 periods that are equidistant at intervals of ΔP = 0.03074 d.
The high-frequency region shows a dominant peak F that could be identified with the radial fundamental mode. It is most remarkable that of the 246 δ Scuti frequencies, only about 70 ( ≈ 30%) seem really independent of a γ Doradus frequency. Twice as many (146) couplings of the form kF ± fi were detected. Depending on Δ, which is the minimum frequency difference to allow for a clear determination of neighbouring frequencies, this number could increase to 171 and more. Additional coupled frequencies are certainly present, but hidden in the noise or too close to a frequency of larger amplitude.
Kallinger & Matthews (2010) claimed that the several hundreds of δ Scuti-type frequencies detected in A-F type stars observed by CoRoT and Kepler could not all be attributed to pulsation. Since the observable amplitudes of modes with ℓ larger than 4, which are required to explain the large number of pulsation modes, suffer strong cancellation effects when integrated over the stellar disk, only some tens of frequencies should be detected. The authors demonstrated that many low amplitude frequencies could alternatively be the signature of non-white granulation background noise and that fewer than about 100 of the frequencies of the investigated stars are actually stellar p-modes. In our case, we detected “only” 59 independent modes. Therefore, only ℓ-values up to 5 are necessary to attribute the frequencies to p-modes, but significantly higher ℓ values are discussed nowadays for Kepler data. However, as the granulation level is not known for CoRoT ID 105733033, we cannot be entirely sure that all the 59 δ Scuti- type frequencies are really associated with pulsation.
We also detected equidistant frequencies very close to F that could be interpreted as a signature of rotational splitting or Doppler effect modulation. If this were indeed true, the rotation or binary period of the star would be 20.57 d.
We have clearly established the influence of the γ Doradus variations on the δ Scuti behaviour, and convincingly confirmed the thermodynamical and mechanical interactions between the two p- and g-mode cavities, as predicted many years ago as a tool for detecting g-modes in the Sun (Kennedy et al. 1993; Lou 2001).
We now know that the instability strips of γ Doradus and δ Scuti stars are not as clearly defined as previously thought (Uytterhoeven et al. 2011), and the star CoRoT ID 105733033 might be the Rosetta stone for hybrid stars, where coupling similar to those detected in the present paper should be systematically searched for. We are presently studying other candidates in the CoRoT exofield (see e.g. Mathias et al. 2009; Hareter et al. 2010).
Online material
List of the 444 frequencies of stellar origin detected by Period04.
Acknowledgments
The authors wish to thank E. Poretti and F.-X. Schmider for useful comments. W. W. Weiss is supported by the Austrian Research Fond (project P22691-N16). The authors thank their anonymous referee for his helpful suggestions.
References
- Auvergne, M., Bodin, P., Boisnard, L., et al. 2009, A&A, 506, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baglin, A., Michel, E., Auvergne, M., et al. 2006, ESASP, 624, 34 [Google Scholar]
- Balona, L. A., Guzik, J. A., Uytterhoeven, K., et al. 2011, MNRAS, 415, 3531 [NASA ADS] [CrossRef] [Google Scholar]
- Borucki, W. J., Koch, D. G., Dunham, E. W., & Jenkins, J. M. 1997, ASP Conf., 119, 153 [Google Scholar]
- Breger, M., Stich, J., Garrido, R., et al. 1993, A&A, 271, 482 [NASA ADS] [Google Scholar]
- Chapellier, E., Rodriguez, E., Auvergne, M., et al. 2011, A&A, 525, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Christensen-Dalsgaard, J., Arentoft, T., Brown, T. M., et al. 2008, J. Phys. Conf. Ser., 118, 2039 [Google Scholar]
- Cox, A. N., Morgan, S. M., Rogers, F. J., et al. 1992, ApJ, 393, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Cuypers, J., Aerts, C., De Cat, P., et al. 2009, A&A, 499, 967 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deleuil, M., Meunier, J. C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Dupret, M.-A., Grigahcéne, A., Garrido, R., et al. 2004, A&A, 414, 17 [Google Scholar]
- Fitch, W. S. 1981, ApJ, 249, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Guzik, J. A., Kaye, A. B., Bradley, P. A., et al. 2000, ApJ, 542, 57 [Google Scholar]
- Handler, G. 2009, MNRAS, 398, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Hareter, M., Reegen, P., Miglio, A., et al. 2010 [arXiv:1007.3176] [Google Scholar]
- Henry, G. W., & Fekel, F. C. 2005, AJ, 129, 2026 [NASA ADS] [CrossRef] [Google Scholar]
- Kabath, P., Fruth, T., Rauer, H., et al. 2009, AJ, 137, 3911 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., & Matthews, J. M. 2010, ApJ, 711, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, J. R., Jefferies, S. M., & Hill, F. 1993, ASP Conf. Ser., 42, 273 [Google Scholar]
- Kuschnig, R., Weiss, W. W., Gruber, R., et al. 1997, A&A, 328, 544 [NASA ADS] [Google Scholar]
- Lenz, P., & Breger, M. 2005, CoAst, 146, 53 [Google Scholar]
- Lou, Y.-Q. 2001, ApJ, 556, L121 [NASA ADS] [CrossRef] [Google Scholar]
- Mathias, P., Chapellier, E., Bouabid, M., et al. 2009, AIP Conf. Ser., 1170, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Montgomery, M. H., & O’Donoghue, D. 1999, DSSN, 13, 28 [Google Scholar]
- Poretti, E. 2001, A&A, 371, 986 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poretti, E., Clementini, G., Held, E. V., et al. 2008, ApJ, 685, 947 [NASA ADS] [CrossRef] [Google Scholar]
- Reegen, P. 2007, A&A, 467, 1353 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rowe, J. F., Matthews, J. M., & Cameron, C. 2006, Commun. Asteroseismol., 148, 34 [Google Scholar]
- Shibahashi, H., & Kurtz, D. W. 2012, MNRAS, accepted [arXiv:1202.0105] [Google Scholar]
- Tassoul, M. 1980, ApJS, 43, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Templeton, M., Basu, S., & Demarque, P. 2002, ApJ, 576, 963 [NASA ADS] [CrossRef] [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, A., et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, G., Matthews, J. M., Kuschnig, R., et al. 2003, PASP, 115, 1023 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Light curve of the star CoRoT ID 105733033 corrected for long-term trends, jumps, and outliers (see text) with different timescales. From top to bottom, the complete light curve over 145 d, then a subset over 22 d and finally a zoom into a 3.5 d subset. |
| In the text | |
 |
Fig. 2 Amplitude spectra computed with Period04 for the 444 retained frequencies. From top to bottom: the amplitudes in μmag, and the same with a logarithmic scale, the Fourier spectrum computed from the residuals, and the spectral window normalized to unity, but plotted only to 0.1 in amplitude. |
| In the text | |
 |
Fig. 3 Enlargement of Fig. 2 [second] showing the detected frequencies in the γ Doradus domain. The ordinates are on a logarithmic scale. |
| In the text | |
 |
Fig. 4 Data phased with the main γ Doradus frequency f1 = 0.7428 d-1. |
| In the text | |
 |
Fig. 5 Plot of the frequencies detected in the interval [0.4; 1.8] d-1. “Positive” amplitude frequencies represent the identified asymptotic frequency series, while the “negative” ones are the other detected frequencies in this interval. |
| In the text | |
 |
Fig. 6 γ Doradus periods that obey the asymptotic period spacing law as a function of radial order n with an arbitrary zero point [top]. The bottom part shows the residuals of this period spacing; a straight line has been added for better visibility. |
| In the text | |
 |
Fig. 7 Data phased with the main δ Scuti frequency F = 12.6759 d-1. |
| In the text | |
 |
Fig. 8 Top: enlargement of Fig. 2 [second] showing the detected frequencies in the δ Scuti domain. Bottom: the δ Scuti frequencies without linear combinations with γ Doradus frequencies. The ordinates are on a logarithmic scale. |
| In the text | |
 |
Fig. 9 Binned data phased with the candidate rotation frequency f = 0.0486 d-1, corresponding to a rotation period of 20.57 d. Different symbols refer to different rotation cycles and data averaged in steps of 0.1 in phase. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


