EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 540 (April 2012) A&A, 540 (2012) A12 Full HTML
Free Access
Issue
A&A
Volume 540, April 2012
Article Number A12
Number of page(s) 6
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201117006
Published online 15 March 2012

© ESO, 2012

1. Introduction

The investigation of the thermal evolution of neutron stars is a powerful tool for probing the inner composition of these objects. The cooling of neutron stars has been investigated by many authors, where many different microscopic models were assumed (see Schaab et al. 1996; Page et al. 2004, 2006, 2009; Blaschke et al. 2000; Grigorian et al. 2005; Blaschke et al. 2006; Negreiros et al. 2010). Most of the research on the thermal evolution of compact stars focus on objects older than 10 to 100 years, which is comprehensible if one considers that the thermal data currently available to us is for pulsars with estimated ages the same as or greater than 330 years (Page et al. 2004, 2009). We discuss the thermal evolution of young neutron stars, in the little explored time window that spans ages greater than 1 min (just after the proto-neutron star regime, Prakash et al. 2001) to ages  ≤ 10–100 years, when the neutron star becomes isothermal (see Gnedin et al. 2001, for details).

We discuss the possibility that the late X-ray emission (URCA hereafter1) following a few GRBs associated with supernovae (SNe); e.g. URCA-1 in GRB980425-SN1998bw (Ruffini et al. 2004; Fraschetti et al. 2005; Bernardini et al. 2008), URCA-2 in GRB030329-SN2003dh (Bernardini et al. 2004, 2005b), and URCA-3 in GRB031203-SN2003lw (Bernardini et al. 2005a; Ruffini et al. 2007a, 2008) (see Fig. 3 for details), might actually be created from young (t ~  1 min–(10–100) years), hot (T ~ 107–108 K) neutron stars that are remnants of the SN (Ruffini et al. 2007a) and which we here call neo-neutron stars. Relevant also are the observations of the isolated Type Ic supernova SN 1994I (Immler et al. 2002) and SN 2002ap (Soria et al. 2004), which present late emissions similar to the ones observed in URCA-1, URCA-2, and URCA-3.

Here we propose a revision of the boundary conditions usually employed in the thermal cooling theory of neutron stars, in order to match the proper conditions of the atmosphere at young ages. We also discuss the importance of the thermal processes taking place in the crust, which also have strong effects on the initial stages of thermal evolution. We stress that we are not calling the validity of the current treatment of the atmosphere of compact stars into question but, instead, we point out the need of extending them to appropriately describe the conditions of neo-neutron stars.

2. Cooling of young, hot neutron stars

There are three important ingredients that govern the thermal evolution of a compact star: 1) the microscopic input, which accounts for the neutrino emissivities, specific heat, and thermal conductivity; 2) the macroscopic structure of the star, namely its mass, radius, pressure profile, crust size, etc.; and 3) the boundary condition on the surface of the star, which provides a relationship between the mantle temperature and that of the atmosphere, the latter being what we ultimately observe. These ingredients have been studied extensively, and a comprehensive review can be found in Page et al. (2006). As discussed in Gnedin et al. (2001), during the initial stages of thermal evolution (ages  ≤ 10−100 years), the core and the crust of the neutron star are thermally decoupled. This is because the high-density core is emitting neutrinos at a much higher rate than the crust, which causes it to cool down more quickly. This effectively means that, initially, the neutron star is cooling “inside out”, with the core colder than the outer layers. This scenario is schematically depicted in Fig. 1.

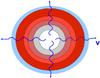thumbnail Fig. 1

Schematic representation of the cooling of a young neutron star. Due to stronger neutrino emissivities, the core of the star cools down more quickly than the crust, causing the star to cool inside out. Darker and lighter areas represent higher and lower temperatures, respectively.

The dominant neutrino emission processes in the crust are given by the Bremsstrahlung, plasmon decay, and electron-positron annihilation processes. Following the footsteps of Gnedin et al. (2001), we calculate the thermal evolution of neutron stars, by artificially adding a phenomenological source of heat (see details in Sect. 4). This allow us to estimate how much heat is needed, so that the thermal evolution of a neo-neutron star matches the X-ray light curve of late emission of GRB-SN.

After this initial core-crust decoupled state, the “cooling wave” originated in the core reaches the crust, and the object becomes isothermal. The time scale of this process is between 10 and 100 years, depending on the properties of the crust (Gnedin et al. 2001). This means that the crust shields the core during the initial stages of thermal evolution, and all the information we might obtain at this stage refers only to the crust and to the atmosphere of the star. This raises another issue about the atmosphere of the star. The thermal connection between the mantle and the atmosphere is what defines the photon luminosity, which is what we observe. Therefore, the appropriate description of the atmosphere is key to correctly understanding the thermal evolution of neutron stars. In the usual approach, the thermal relaxation time of the atmosphere is assumed to be much shorter than that of the neutron star; furthermore, neutrino emissions from the atmosphere are also considered to be negligible (see Gudmundsson et al. 1983). Under these assumptions, and assuming a plane-parallel approximation (which is reasonable since the atmosphere is  ~100 m thick), one can get a relationship between the temperature of the mantle Tb and the temperature of atmosphere Te or, equivalently, the luminosity Le. Gudmundsson et al. (1983) originally found a Tb-Te relationship that depends on the surface gravity of the neutron star. This relationship was developed further by Potekhin et al. (1997) to account for the possibility of mass accreted in the initial stages and of magnetic fields effects. As pointed out by Gudmundsson et al. (1983), such assumptions for the atmosphere of the star are only valid for objects older than a few tens of years, when the temperature has dropped below 109 K for densities below 1010 g/cm3. In fact, we see that the current boundary conditions yields temperatures  ~107 K (L ~ 1037 erg/s, equivalently) for young neutron stars (age  < 1–10 years). This should raise some suspicion since proto-neutron stars studies (see Prakash et al. 2001, and references therein) indicate that neutron stars just after this regime have temperatures  ~1010–1011 K.

The properties of the atmosphere of a sufficiently hot, nascent neutron star should differ significantly from those considered in Gudmundsson et al. (1983) and Potekhin et al. (1997), especially since at hot temperatures (T ≳ 109 K) the atmosphere might not be transparent to neutrinos, and thus the neutrino transport equations have to be considered. The coupled equations of neutrino and photon transport, in the atmosphere of a neutron star, were solved by Salpeter & Shapiro (1981), and Duncan et al. (1986). In these works the authors performed detailed calculations of the atmosphere properties of hot neutron stars. They found the following photon luminosity, as observed at infinity, 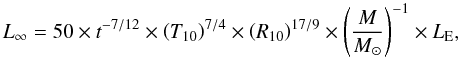L∞=50×t−7/12×(T10)7/4×(R10)17/9×(MM⊙)-1×LE,\begin{equation} \label{eq:Lshapiro} L_\infty = 50\times t^{-7/12}\times\left(T_{10}\right)^{7/4}\times\left(R_{10}\right)^{17/9}\times\left(\frac{M}{M_\odot}\right)^{-1} \times L_{\rm E}, \end{equation}(1)where t is time in seconds, T10 is the initial temperature in units of 10 MeV, R10 the neutron star radius in units of 10 km, M the neutron star mass, and LE ~ 2.0 × 1038 erg/s is the Eddington luminosity. Duncan et al. (1986) found that the above expression should be valid for at least the initial 100 s. In Fig. 2 we can see how the luminosity of the star changes for the first 100 s, for stars with different initial temperatures.

thumbnail Fig. 2

Luminosity of a hot nascent neutron star as observed at infinity given by Eq. (1) during the initial 100 s (Duncan et al. 1986), with the initial temperatures indicated. The neutron star is assumed to have a mass of 1.4   M⊙ and a radius of 13 km.

thumbnail Fig. 3

Synthetic light curves of GRB980425 A) (Ruffini et al. 2004; Fraschetti et al. 2005; Bernardini et al. 2008), GRB030329 B) (Bernardini et al. 2004, 2005b) and GRB031203 C) (Bernardini et al. 2005a; Ruffini et al. 2007a, 2008). The solid curves represent the hard X-ray emission (10–200 keV range) and the triangles are 2–10 keV flux points. The optical luminosities of the SNe accompanying these GRBs are also reported with crosses (see Ruffini et al. 2007a, for details). The curves fitting the late X-ray luminosity (URCAs) are qualitative cooling curves based on Canuto (1978); see also Ruffini et al. (2004, 2007a, 2008), Bernardini et al. (2004, 2005a,b, 2008), and Fraschetti et al. (2005) for details.

According to these results, during the initial 100 s, the photon luminosity emerging from the atmosphere will be higher than the Eddington luminosity. This implies that there will be mass loss, owing to neutrino-driven winds from the young atmosphere. As shown by Duncan et al. (1986), the total mass loss only becomes appreciable for neutron stars with large radii and high initial temperatures. For a typical neutron star with the canonical mass of 1.4   M⊙, a radius of 13 km and initial temperature of  ~1011 K, the total mass loss was estimated to be  ~6.2 × 10-6   M⊙.

In addition to the high luminosities associated to the atmosphere of young neutron stars, one also needs to consider fallback onto the surface of the neutron star. Potekhin et al. (1997) discuss how fallback, at earlier stages of evolution, would modify the properties of the atmosphere, hence of the boundary conditions. Once more in this investigation, however, such a fallback is assumed to have happened at early times, and the modified boundary conditions are only valid if the fallback has already ceased. Chevalier (1989) studied the fallback onto young neutron stars and found that, while there is an envelope, a luminosity near the Eddington limit should be present. Furthermore, the authors have found that in this case the energy from the envelope can be radiated away in about one year. This timescale, however, might be lengthened if rotation effects are accounted for during the fallback. In addition to that, Turolla et al. (1994) discuss the possibility of “hot solutions” for the atmosphere of neutron stars undergoing spherical accretion. It is shown that for L ≥ 10-2   LE the temperature at the atmosphere of a neutron star might be  ~109–1011 K.

Table 1

GRBs associated to SNe and URCAs.

thumbnail Fig. 4

X-ray light curves of the counterparts of GRB980425-SN1998bw and of two Type Ic SNe not accompanied by GRBs: SN1994I (“normal”) and SN2002ap (broadlined). The data are from Pian et al. (2000), Immler et al. (2002), Kouveliotou et al. (2004), and Soria et al. (2004).

thumbnail Fig. 5

Thermal evolution of neo-neutron stars for selected values of the heating source H0 =  [1012,5 × 1012,1015]  erg/g/s and for an initial temperature of the atmosphere T0 = 8.7 × 106 K. The observed data represents the X-ray light curve associated with the URCAs.

3. Late X-ray emission in GRBs associated to supernovae: URCAs

It seems clear to us that, after the analysis of the scenario described above, we must extend the current model for the boundary conditions used in cooling calculations, to include the effects of a high-temperature atmosphere, possibly with super-Eddington luminosity. Up until this point, however, little attention has been given to the thermal evolution of young neutron stars, mainly due to the absence of observational data of neutron stars with ages  < 330 years. It has been recently proposed (see Ruffini et al. 2007a, for details) that the long-lasting X-ray emission called URCA there (see Fig. 3) of a few GRBs associated to SNe; URCA-1 in GRB980425-SN1998bw (Ruffini et al. 2004; Fraschetti et al. 2005; Bernardini et al. 2008), URCA-2 in GRB030329-SN2003dh (Bernardini et al. 2004, 2005b), and URCA-3 in GRB031203-SN2003lw (Bernardini et al. 2005a; Ruffini et al. 2007a, 2008), might actually originate in the compact star remnant of the SN: a neo-neutron star. In this scenario the GRB is described as the core collapse of a massive star, whose remnant is a black hole. This massive star is supposed to be in a binary system, whose companion is on the verge of becoming an SN. The GRB triggers the SN explosion in the companion star, which in turns leaves behind a neutron star (Ruffini et al. 2001). An alternative scenario has been recently suggested in which the so-called GRB is actually not a GRB but the observed X-ray emission stems from a collapsing core: a proto-neutron star leading directly to a SN explosion (Ruffini 2011). Such a process, if confirmed, will naturally explain the observations of the X-ray outburst 080109/SN 2008D (Soderberg et al. 2008). This concept is very similar to the one of a proto-black hole as introduced in Ruffini et al. (2011, 2010a); Izzo et al. (2011); Penacchioni et al. (2012), where the emission from the collapsing core is clearly distinguished from the GRB. In that case, the collapsing core leads to the formation of the black hole, while in the present case it forms a neutron star.

Both scenarios form a neo-neutron star, and they are supported by the observation of supernova 1979C (Patnaude et al. 2011), where a similar X-ray light curve also followed the SN. In Fig. 3 we show the X-ray light curve associated with the URCAs.

From Fig. 3 we can see that the X-ray luminosities of these sources are of the same magnitude as what is expected for neo-neutron stars, as discussed above. In Table 1 we summarize the representative parameters of the four GRB-SN systems, including the very high kinetic energy observed in all SNe (Mazzali 2006). We have also included the association GRB060218-SN2006aj (see Dainotti et al. 2007, 2010, for details). It must be noted that similar prolonged X-ray emission has also been observed in connection with other Type Ic SN not associated with GRBs, such as SN1994I (Immler et al. 2002) and SN2002ap (Soria et al. 2004) (see Fig. 4 for details).

4. Neo-neutron star luminosity and the URCAs

Another important ingredient for the cooling of young neutron stars are the crust properties. As illustrated in Fig. 1, due to the stronger neutrino emission from the core, the core and crust are thermally decoupled during the initial stages. For that reason, the initial stages of the thermal evolution reflect the properties of the crust, while the core remains invisible. Thus the proper description of the crust structure and composition is also fundamental for understanding the initial thermal stages in the evolution of a neutron star. We now briefly discuss the current understanding of the crustal processes and how it might be related to the data available from the URCAs.

There are several active emission mechanisms in the neutron star crust, e.g. e-ion Bremsstrahlung, plasmon decay, e+-e− annihilation, e-e and n-n Bremsstrahlung, synchrotron emission, as well as Cooper pair processes for temperatures below the critical temperature for superfluidity Tcrit. However, as shown by Yakovlev et al. (2001), the first three processes are the dominant ones for temperatures above 108 K, which is the regime we are interested in. For instance, synchrotron emission channels might become slightly relevant, but only for T < 108 K and for very high magnetic fields  > 1014 G. The Cooper pair mechanism, possibly important for objects a few hundred years old like Cas A (see e.g. Page et al. 2011; Shternin et al. 2011, for details), is irrelevant in the present case since we are dealing with neutron star ages below ten years and thus temperatures well above Tcrit.

At temperatures T ~ 3 × 109 K, we can write for the most important emission processes in the crust, ϵB~1021 ergs-1 cm-3,ϵP~1022 ergs-1 cm-3,ϵep~1019 ergs-1 cm-3,\begin{eqnarray} \epsilon_{\rm B} \sim 10^{21}~ \textrm{erg s}^{-1}\,\textrm{cm}^{-3},\\ \epsilon_{\rm P} \sim 10^{22} ~\textrm{erg s}^{-1}\,\textrm{cm}^{-3},\\ \epsilon_{\rm ep} \sim 10^{19}~ \textrm{erg s}^{-1}\,\textrm{cm}^{-3}, \end{eqnarray}where ϵi denotes the emissivity, and the indexes B, P, ep denote the Bremsstrahlung, plasmon decay, and pair annihilation processes, respectively.

To estimate the amount of heat needed to match the theoretical thermal evolution of a neo-neutron star to the light curve of the URCAs, we added a phenomenological source of heat parametrized by 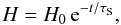H=H0 e−t/τS,\begin{equation} \label{eq:H} H = H_0\,{\rm e}^{-t/\tau_{\rm S}} , \end{equation}(5)with H0 the magnitude of the heat source, and τS the time scale in which it is active. For our calculations we set τS = 1 year.

In addition, we introduced a phenomenological boundary condition for the early stages of evolution of the surface temperature Ts that follows the form 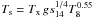Ts=Tx gs141/4T80.55\hbox{$T_{\rm s} = T_{\rm x}\,gs_{14}^{1/4} T_8^{0.55}$} K, where Tx = 0.87 × 106 + (T0 − 0.87 × 106)   e − t/τS K, T8 is the mantle temperature Tb in units of 108 K, T0 is the initial temperature of the atmosphere, and gs14 is the surface acceleration of gravity in units of 1014 cm/s2. With this new boundary condition, we can mimic the high temperature of the atmosphere for young neutron stars by setting the temperature at early times to a higher value and, for times greater than τS, it asymptotically goes to its traditional value  ~0.87 × 106 K.

In Fig. 5 we show the cooling curves of neo-neutron stars resulting from the presence of the heating source given by Eq. (5), in addition to the traditional cooling processes of neutron stars. The cooling curves are obtained self-consistently by exactly solving the full, general relativistic energy transport and balance equations as described in Schaab et al. (1996), Page et al. (2006) and Negreiros et al. (2010). We also show the observed data for the X-ray light curve associated with the URCAs. This allows us to identify the key factor leading to the matching of the neo-neutron star luminosity with the X-ray emission of the URCAs.

5. Discussion and conclusions

The major role played by the neutrino emissions from the crust of a neo-neutron star in its initial stages of the object is illustrated in Fig. 5. In addition, by calibrating our additional heating source at early times to H0 ~ 1012–1015 erg/g/s, we find striking agreement of the luminosity obtained from the cooling of a neo-neutron stars with the prolonged (t = 108–109 s) X-ray emission observed in GRB associated with an SN (see Fig. 5 for details). This could indicate that something might be missing in our current understanding of the crust of neutron stars. It might be that, as is the case for the atmosphere, we need to develop our current models for the crust further, so as to describe properly the properties of neo-neutron stars. The traditional thermal processes taking place in the crust might be enhanced by the extremely high temperature conditions of neo-neutron star and, additional heating processes not yet studied within this context could also take place under such conditions and deserve further analysis.

Particularly interesting in this respect are the processes of e+e− pair creation expected to occur in the interphase between the core and the crust during the neutron star formation leading to the appearance of critical fields (see Ruffini et al. 2007b; Ruffini 2008; Rueda et al. 2010a,b; Popov 2010; Ruffini et al. 2010b; Rotondo et al. 2011b,c; Rueda et al. 2011a; Rotondo et al. 2011d,a; Rueda et al. 2011b, for details)

It is also worth mentioning that the additional heating source needed at early times, H0 ~ 1012–1015 erg/g/s (or H0 ~ 10-6–10-3 MeV/Nucleon/s), is in striking agreement with the heat released from nuclear fusion reactions, radiative neutron captures, and photodisintegrations in the early stages of neutron star mergers found by Goriely et al. (2011a,b). Both fission and β-decays have also been included there: i.e neutron-induced fission, spontaneous fission, β-delayed fission, photofission, and β-delayed neutron emission.

All this suggests the exciting possibility that we are, for the first time, observing a nascent hot neutron star. This possibility alone warrants further study of this subject, so we might obtain a more concrete picture of the thermal evolution of neo-neutron stars. A proposal has been recently submitted by E. Pian et al. to the Chandra satellite to observe whether a similar prolonged X-ray emission also exists in GRB100316D that is associated with SN2010bh (Pian et al. 2011). We also encourage dedicated observations of isolated SNe in view of the similarities between URCA-1–URCA-3 and the Type Ic supernova SN 1994I (Immler et al. 2002) and SN 2002ap (Soria et al. 2004).

1

The names URCA-1 and URCA-2 mentioned here were given to these sources when presented for the first time at the MG10 meeting held in Rio de Janeiro in the town of Urca. The location of the MG10 meeting was very close to the “Cassino da Urca” where George Gamow and Mario Schoenberg conceived the process of neutrino emission for the cooling process of neutron stars, which also took the name from the town of Urca, the Urca process (see e.g. detailed history in Ruffini et al. 2005; Gamow 1970).

Acknowledgments

We thank the referee for very interesting remarks.

References

  1. Bernardini, M. G., Bianco, C. L., Chardonnet, P., et al. 2004, in Gamma-Ray Bursts: 30 Years of Discovery, ed. E. Fenimore, & M. Galassi, AIP Conf. Ser., 727, 312 [Google Scholar]
  2. Bernardini, M. G., Bianco, C. L., Chardonnet, P., et al. 2005a, ApJ, 634, L29 [NASA ADS] [CrossRef] [Google Scholar]
  3. Bernardini, M. G., Bianco, C. L., Ruffini, R., et al. 2005b, in The Tenth Marcel Grossmann Meeting, On recent developments in theoretical and experimental general relativity, gravitation and relativistic field theories, ed. M. Novello, S. Perez Bergliaffa, & R. Ruffini (Singapore: World Scientific), 2459 [Google Scholar]
  4. Bernardini, M. G., Bianco, C. L., Caito, L., et al. 2008, in The Eleventh Marcel Grossmann Meeting, ed. R. T. Jantzen, H. Kleinert, & R. Ruffini (Singapore: World Scientific) [Google Scholar]
  5. Blaschke, D., Klahn, T., & Voskresensky, D. 2000, ApJ, 533, 406 [NASA ADS] [CrossRef] [Google Scholar]
  6. Blaschke, D., Voskresensky, D., & Grigorian, H. 2006, Nucl. Phys. A, 774, 815 [NASA ADS] [CrossRef] [Google Scholar]
  7. Canuto, V. 1978, in Physics and Astrophysics of Neutron Stars and Black Holes, ed. R. Giacconi, & R. Ruffini, 448 [Google Scholar]
  8. Chevalier, R. A. 1989, ApJ, 346, 847 [NASA ADS] [CrossRef] [Google Scholar]
  9. Dainotti, M. G., Bernardini, M. G., Bianco, C. L., et al. 2007, A&A, 471, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Dainotti, M., Bernardini, M. G., Bianco, C. L., et al. 2010, J. Kor. Phys. Soc., 56, 1588 [NASA ADS] [CrossRef] [Google Scholar]
  11. Duncan, R. C., Shapiro, S. L., & Wasserman, I. 1986, ApJ, 309, 141 [NASA ADS] [CrossRef] [Google Scholar]
  12. Fraschetti, F., Bernardini, M. G., Bianco, C. L., et al. 2005, in The Tenth Marcel Grossmann Meeting, On recent developments in theoretical and experimental general relativity, gravitation and relativistic field theories, ed. M. Novello, S. Perez Bergliaffa, & R. Ruffini (Singapore: World Scientific), 2451 [Google Scholar]
  13. Galama, T. J., Vreeswijk, P. M., van Paradijs, J., et al. 1998, Nature, 395, 670 [NASA ADS] [CrossRef] [Google Scholar]
  14. Gamow, G. 1970, My world line: An informal autobiography, ed. G. Gamow (New York, NY, USA: Viking Press) [Google Scholar]
  15. Gnedin, O. Y., Yakovlev, D. G., & Potekhin, A. Y. 2001, MNRAS, 324, 725 [NASA ADS] [CrossRef] [Google Scholar]
  16. Goriely, S., Bauswein, A., & Janka, H.-T. 2011a, ApJ, 738, L32 [Google Scholar]
  17. Goriely, S., Chamel, N., Janka, H.-T., & Pearson, J. M. 2011b, A&A, 531, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Greiner, J., Peimbert, M., Estaban, C., et al. 2003, GCN Circ., 2020 [Google Scholar]
  19. Grigorian, H., Blaschke, D., & Voskresensky, D. 2005, Phys. Rev. C, 71, 1 [Google Scholar]
  20. Gudmundsson, E. H., Pethick, C. J., & Epstein, R. I. 1983, ApJ, 272, 286 [NASA ADS] [CrossRef] [Google Scholar]
  21. Immler, S., Wilson, A. S., & Terashima, Y. 2002, ApJ, 573, L27 [NASA ADS] [CrossRef] [Google Scholar]
  22. Iwamoto, K., Mazzali, P. A., Nomoto, K., et al. 1998, Nature, 395, 672 [NASA ADS] [CrossRef] [Google Scholar]
  23. Izzo, L., Ruffini, R., Penacchioni, A. V., et al. 2011, A&A, submitted [Google Scholar]
  24. Kaneko, Y., Ramirez-Ruiz, E., Granot, J., et al. 2007, ApJ, 654, 385 [NASA ADS] [CrossRef] [Google Scholar]
  25. Kouveliotou, C., Woosley, S. E., Patel, S. K., et al. 2004, ApJ, 608, 872 [NASA ADS] [CrossRef] [Google Scholar]
  26. Mazzali, P. 2006, Talk presented at the congress, Swift and GRBs: unveiling the relativistic universe, Venice, Italy [Google Scholar]
  27. Mirabal, N., Halpern, J. P., An, D., Thorstensen, J. R., & Terndrup, D. M. 2006, ApJ, 643, L99 [NASA ADS] [CrossRef] [Google Scholar]
  28. Negreiros, R., Dexheimer, V., & Schramm, S. 2010, Phys. Rev. C, 82, 1 [Google Scholar]
  29. Page, D., Lattimer, J., Prakash, M., & Steiner, A. W. 2004, ApJS, 155, 623 [NASA ADS] [CrossRef] [Google Scholar]
  30. Page, D., Geppert, U., & Weber, F. 2006, Nucl. Phys. A, 777, 497 [NASA ADS] [CrossRef] [Google Scholar]
  31. Page, D., Lattimer, J., Prakash, M., & Steiner, A. W. 2009, ApJ, 707, 1131 [NASA ADS] [CrossRef] [Google Scholar]
  32. Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. W. 2011, Phys. Rev. Lett., 106, 081101 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  33. Patnaude, D., Loeb, A., & Jones, C. 2011, New Astron., 16, 187 [NASA ADS] [CrossRef] [Google Scholar]
  34. Penacchioni, A. V., Ruffini, R., Izzo, L., et al. 2012, A&A, 538, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Pian, E., Amati, L., Antonelli, L. A., et al. 2000, ApJ, 536, 778 [NASA ADS] [CrossRef] [Google Scholar]
  36. Pian, E., et al. 2011, Proposal for Chandra Observations: The X-Ray Remnant of XRF100316D/SN2010BH [Google Scholar]
  37. Popov, V. 2010, in The Sun, the stars, the universe and general relativity, ed. R. Ruffini, & G. Vereshchagin, AIP Conf. Ser., 1205, 127 [Google Scholar]
  38. Potekhin, A. Y., Chabrier, G., & Yakovlev, D. G. 1997, A&A, 323, 415 [NASA ADS] [Google Scholar]
  39. Prakash, M., Lattimer, J., Pons, J., Steiner, A., & Reddy, S. 2001, Phys. Neutron Star Int., 364 [Google Scholar]
  40. Prochaska, J. X., Bloom, J. S., Chen, H.-W., et al. 2004, ApJ, 611, 200 [NASA ADS] [CrossRef] [Google Scholar]
  41. Rotondo, M., Rueda, J. A., Ruffini, R., & Xue, S.-S. 2011a, Phys. Rev. D, sumbitted [arXiv:1107.2777] [Google Scholar]
  42. Rotondo, M., Rueda, J. A., Ruffini, R., & Xue, S.-S. 2011b, Phys. Rev. C, 83, 045805 [NASA ADS] [CrossRef] [Google Scholar]
  43. Rotondo, M., Rueda, J. A., Ruffini, R., & Xue, S.-S. 2011c, Phys. Lett. B, 701, 667 [NASA ADS] [CrossRef] [Google Scholar]
  44. Rotondo, M., Ruffini, R., Xue, S.-S., & Popov, V. 2011d, IJMPD, 20, 1995 [NASA ADS] [CrossRef] [Google Scholar]
  45. Rueda, J. A., Rotondo, M., Ruffini, R., & Xue, S.-S. 2010a, J. Korean Phys. Soc., 57, 560 [NASA ADS] [CrossRef] [Google Scholar]
  46. Rueda, J. A., Ruffini, R., & Xue, S.-S. 2010b, in The Sun, the stars, the universe and general relativity, ed. R. Ruffini, & G. Vereshchagin, AIP Conf. Ser., 1205, 143 [Google Scholar]
  47. Rueda, J. A., Rotondo, M., Ruffini, R., & Xue, S.-S. 2011a, IJMPD, 20, 1789 [NASA ADS] [CrossRef] [Google Scholar]
  48. Rueda, J. A., Ruffini, R., & Xue, S. 2011b, Nucl. Phys. A, in press [arXiv:1104.4062] [Google Scholar]
  49. Ruffini, R. 2008, in Path Integrals – New Trends and Perspectives, ed. W. Janke, & A. Pelster, 207 [Google Scholar]
  50. Ruffini, R. 2011, in Proceedings of the Third Galileo-Xu Guangqi Meeting, ed. Z. Cao, X. Chen, R. Ruffini, S.-S. Xue, C. Zhang, & S. Zhang, to appear [Google Scholar]
  51. Ruffini, R., Bianco, C. L., Chardonnet, P., Fraschetti, F., & Xue, S.-S. 2001, ApJ, 555, L117 [Google Scholar]
  52. Ruffini, R., Bernardini, M. G., Bianco, C. L., et al. 2004, Adv. Space Res., 34, 2715 [NASA ADS] [CrossRef] [Google Scholar]
  53. Ruffini, R., Bernardini, M. G., Bianco, C. L., et al. 2005, in The Tenth Marcel Grossmann Meeting, On recent developments in theoretical and experimental general relativity, gravitation and relativistic field theories, ed. M. Novello, S. Perez Bergliaffa, & R. Ruffini (Singapore: World Scientific), 369 [Google Scholar]
  54. Ruffini, R., Bernardini, M. G., Bianco, C. L., et al. 2007a, in The 6th Integral Workshop – The Obscured Universe, ed. S. Grebenev, R. Sunyaev, C. Winkler, A. Parmar, & L. Ouwehand, ESA SP-622, 561 [Google Scholar]
  55. Ruffini, R., Rotondo, M., & Xue, S.-S. 2007b, IJMPD, 16, 1 [NASA ADS] [CrossRef] [Google Scholar]
  56. Ruffini, R., Bernardini, M. G., Bianco, C. L., et al. 2008, in Relativistic Astrophysics Legacy and Cosmology – Einstein’s Legacy, ed. B. Aschenbach, V. Burwitz, G. Hasinger, & B. Leibundgut, 399 [Google Scholar]
  57. Ruffini, R., Chakrabarti, S. K., & Izzo, L. 2010a, Adv. Space Res., submitted [Google Scholar]
  58. Ruffini, R., Vereshchagin, G., & Xue, S. 2010b, Phys. Rep., 487, 1 [NASA ADS] [CrossRef] [Google Scholar]
  59. Ruffini, R., Izzo, L., Penacchioni, A. V., et al. 2011, PoS(Texas2010), 101 [Google Scholar]
  60. Salpeter, E. E., & Shapiro, S. L. 1981, ApJ, 251, 311 [NASA ADS] [CrossRef] [Google Scholar]
  61. Schaab, C., Weber, F., Weigel, M., & Glendenning, N. K. 1996, Nucl. Phys. A, 605, 531 [NASA ADS] [CrossRef] [Google Scholar]
  62. Shternin, P. S., Yakovlev, D. G., Heinke, C. O., Ho, W. C. G., & Patnaude, D. J. 2011, MNRAS, 412, L108 [NASA ADS] [Google Scholar]
  63. Soderberg, A. M., Berger, E., Page, K. L., et al. 2008, Nature, 453, 469 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  64. Soria, R., Pian, E., & Mazzali, P. A. 2004, A&A, 413, 107 [Google Scholar]
  65. Turolla, R., Zampieri, L., Colpi, M., & Treves, A. 1994, ApJ, 426, L35 [NASA ADS] [CrossRef] [Google Scholar]
  66. Yakovlev, D. G., Kaminker, A. D., Gnedin, O. Y., & Haensel, P. 2001, Phys. Rep., 354, 1 [NASA ADS] [CrossRef] [Google Scholar]

All Tables

Table 1

GRBs associated to SNe and URCAs.

In the text

All Figures

thumbnail Fig. 1

Schematic representation of the cooling of a young neutron star. Due to stronger neutrino emissivities, the core of the star cools down more quickly than the crust, causing the star to cool inside out. Darker and lighter areas represent higher and lower temperatures, respectively.
In the text
thumbnail Fig. 2

Luminosity of a hot nascent neutron star as observed at infinity given by Eq. (1) during the initial 100 s (Duncan et al. 1986), with the initial temperatures indicated. The neutron star is assumed to have a mass of 1.4   M⊙ and a radius of 13 km.
In the text
thumbnail Fig. 3

Synthetic light curves of GRB980425 A) (Ruffini et al. 2004; Fraschetti et al. 2005; Bernardini et al. 2008), GRB030329 B) (Bernardini et al. 2004, 2005b) and GRB031203 C) (Bernardini et al. 2005a; Ruffini et al. 2007a, 2008). The solid curves represent the hard X-ray emission (10–200 keV range) and the triangles are 2–10 keV flux points. The optical luminosities of the SNe accompanying these GRBs are also reported with crosses (see Ruffini et al. 2007a, for details). The curves fitting the late X-ray luminosity (URCAs) are qualitative cooling curves based on Canuto (1978); see also Ruffini et al. (2004, 2007a, 2008), Bernardini et al. (2004, 2005a,b, 2008), and Fraschetti et al. (2005) for details.
In the text
thumbnail Fig. 4

X-ray light curves of the counterparts of GRB980425-SN1998bw and of two Type Ic SNe not accompanied by GRBs: SN1994I (“normal”) and SN2002ap (broadlined). The data are from Pian et al. (2000), Immler et al. (2002), Kouveliotou et al. (2004), and Soria et al. (2004).
In the text
thumbnail Fig. 5

Thermal evolution of neo-neutron stars for selected values of the heating source H0 =  [1012,5 × 1012,1015]  erg/g/s and for an initial temperature of the atmosphere T0 = 8.7 × 106 K. The observed data represents the X-ray light curve associated with the URCAs.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.