| Issue |
A&A
Volume 540, April 2012
|
|
|---|---|---|
| Article Number | A65 | |
| Number of page(s) | 9 | |
| Section | Celestial mechanics and astrometry | |
| DOI | https://doi.org/10.1051/0004-6361/201116952 | |
| Published online | 27 March 2012 | |
Dynamical parameter determinations in Pluto’s system⋆
Expected constraints from the New Horizons mission to Pluto
1 Institut de Mécanique Céleste et de Calcul des Éphémérides-Observatoire de Paris, UMR 8028 du CNRS, Université Pierre et Marie Curie, Université Lille 1, 77 avenue Denfert Rochereau, 75014 Paris, France
e-mail: beauvalet@imcce.fr
2 Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
Received: 24 March 2011
Accepted: 16 February 2012
Pluto is the multiple system that has been observed the longest. Yet, the masses of its smallest satellites, Nix and Hydra, which were discovered in 2005, are still imprecisely known, because of the short time span and number of available observations. We present a numerical model that takes into account the second order gravity fields and Pluto’s orbital motion in the solar system. We investigated the dynamical parameters that may be reliably determined today. We also assessed the possible improvements on the parameter uncertainties with the future increase of observations, including the New Horizons mission. Fitting our model to simulated data, we show that the precision of observations prevents the quantification of the polar oblateness J2 and equatorial bulge c22 of Pluto and Charon. Similarly, we show that the masses are on the detection limit. In particular, unless 25 observations are made every year, the mass of Nix may be constrained with confidence only with New Horizons data. Hydra’s mass will only be constrained by the probe. The recent discovery of P4 might change this situation, but our knowledge of this object is still too vague to draw any conclusion.
Key words: methods: numerical / Kuiper belt: general / planets and satellites: fundamental parameters / celestial mechanics / planets and satellites: individual: Pluto
Tables 4 and 5 are available in electronic form at http://www.aanda.org
© ESO, 2012
1. Introduction
Pluto’s system is now the multiple system that has been observed the longest. It consists of four bodies: Pluto, its most massive satellite Charon, which was discovered in 1978 (Christy & Harrington 1978), and the smaller satellites Nix and Hydra, discovered in 2005 (Weaver et al. 2005, 2006). Charon’s mass is about one tenth of Pluto’s mass, making it one of the most massive satellites with respect to its primary in the solar system. Indeed, they should be considered as a binary object because the center of mass of the system is not inside Pluto. The most popular formation scenario for the pair is a collision between two massive Kuiper Belt objects, which created Pluto and Charon (Canup 2005). The formation of the other satellites is also discussed, with a possible in-situ formation (accretion from the remains of Charon’s formation) or a capture scenario. Their color is the same as that of Charon (Stern et al. 2007). The farthest satellite, Hydra, orbits at only 3% of Hill’s radius around Pluto, making it one of the most compact systems (Stern et al. 2006). These facts favor the accretion scenario, but a more definitive clue would be given by the estimation of their densities.
While the sizes and masses of Pluto and Charon are known through stellar occultations and satellite period estimates, respectively, that is not the case for Nix and Hydra. The best estimate of the system’s masses has been made by Tholen et al. (2008) with masses (GM) for Nix and Hydra 0.039 ± 0.034 km3 s-2 and 0.021 ± 0.042 km3 s-2, respectively, while no successful stellar occultation of them has been made. No estimate of Pluto and Charon’s harmonic gravity fields is available. Constraining these parameters will greatly help in characterizing Pluto’s and Charon’s interiors.
The system has yet to be explored by in situ spacecraft. This situation will change in 2015 with the arrival of the New Horizons mission (Stern & Spencer 2003). This mission will provide observations of Pluto and its companions, astrometry, surface imaging, and spectroscopy of the bodies’ surface. The probe will not orbit around Pluto’s system, it will only cross the system before escaping the solar system. The high resolution of the probe’s observations is expected to improve the precision in our current estimates of the masses of the system’s bodies (Weaver et al. 2007).
The purpose of this paper is to determine how much about the dynamical parameters of the system we can know today. We also investigate how this knowledge will evolve, before and after New Horizons’ flyby with an observation rate similar to previous years (about ten observations per year) and a similar astrometric precision. To do so we have developed a numerical model of Pluto’s system (Sect. 2). We estimated which dynamical parameters are likely to be determined from observations today and considered the existence of opportune observation moments for mass determination (Sect. 3). Finally, we studied how the precision on these parameters may evolve with increasing observations (Sect. 4).
2. Dynamical model
We describe Pluto’s system as an 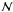 +4-body problem. The number
+4-body problem. The number 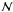 refers to the bodies introduced in the model that do not belong to Pluto’s system: the Sun and the eight planets, for which the Moon’s mass is added to that of the Earth. The number 4 is for Pluto, Charon, Nix and Hydra.
refers to the bodies introduced in the model that do not belong to Pluto’s system: the Sun and the eight planets, for which the Moon’s mass is added to that of the Earth. The number 4 is for Pluto, Charon, Nix and Hydra.
We calculated the equations of motion of Pluto, Charon, Nix, and Hydra in an inertial reference frame centered on the barycenter of the solar system, not a plutocentric one to avoid the additional inertial forces. Only Pluto and Charon are described as oblate. We also took into account the fact that Pluto and Charon are in a double spin-orbit resonance, which means that they have the same rotation period, equal to Charon’s revolution period.
We use the following notation:
 and we obtain the following equation of motion for the integrated body i:
and we obtain the following equation of motion for the integrated body i:
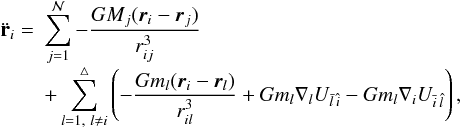 (1)where the function of the oblateness is written, depending on the coordinates (ri,φi,λi) providing the position of i in the spherical equatorial coordinates system linked to l:
(1)where the function of the oblateness is written, depending on the coordinates (ri,φi,λi) providing the position of i in the spherical equatorial coordinates system linked to l: ![\begin{equation} U_{\bar{i}\, \hat{l}}= -\frac{R_l^2 }{r_{il}^3} \left[J_{2}^{(l)}\left(\frac{3}{2}\sin^2 (\phi_i) -\frac{1}{2}\right) -3 c_{22}^{(l)}\cos^2(\phi_i) \cos(2\lambda_i)\right]\text{.} \end{equation}](/articles/aa/full_html/2012/04/aa16952-11/aa16952-11-eq13.png) (2)The expressions of
(2)The expressions of 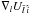 and
and 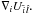 have been developed in Lainey et al. (2004) in a planetocentric reference frame. We used the same expressions for a plutocentric reference frame and computed them in the International Celestial Reference Frame (ICRF) through a transformation matrix using the spherical coordinates of Pluto’s rotation pole from the IAU convention (Seidelmann et al. 2007). The prime meridian of Pluto is considered to be in the direction of Charon because of the double spin-orbit resonance, and conversely. Indeed, the optical libration caused by Charon’s eccentricity has an amplitude of 2eC (Murray & Dermott 2000), where eC is Charon’s eccentricity. This means 6 × 10-3 rad difference in the orientation of Charon, causing an effect far weaker on the longitude. Accordingly, this effect can be neglected at our level of accuracy.
have been developed in Lainey et al. (2004) in a planetocentric reference frame. We used the same expressions for a plutocentric reference frame and computed them in the International Celestial Reference Frame (ICRF) through a transformation matrix using the spherical coordinates of Pluto’s rotation pole from the IAU convention (Seidelmann et al. 2007). The prime meridian of Pluto is considered to be in the direction of Charon because of the double spin-orbit resonance, and conversely. Indeed, the optical libration caused by Charon’s eccentricity has an amplitude of 2eC (Murray & Dermott 2000), where eC is Charon’s eccentricity. This means 6 × 10-3 rad difference in the orientation of Charon, causing an effect far weaker on the longitude. Accordingly, this effect can be neglected at our level of accuracy.
The masses of Pluto’s system and the initial state vectors for each moon were taken from Tholen et al. (2008). Using the DE406 JPL ephemeris (Standish 1998), we obtained Pluto’s initial positions and velocities, as well as the masses and position of the Sun and the planets.
The values of the oblate gravity field coefficients J2 and c22 come from a theoretical approach. Following Turcotte & Schubert (2002), assuming a constant density body and given the notation ωl the angular velocity of the l body, we have 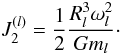 (3)Pluto and Charon are in a double spin-orbit resonance. Hence, Pluto’s rotation period is estimated from Charon’s revolution to be about six days. This leads, for Pluto and Charon, to
(3)Pluto and Charon are in a double spin-orbit resonance. Hence, Pluto’s rotation period is estimated from Charon’s revolution to be about six days. This leads, for Pluto and Charon, to 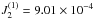 and
and 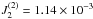 . The tesseral coefficient c22 value gives an idea of Pluto’s and Charon’s deformation due to their mutual interaction in double spin-orbit resonance. In the hydrostatic case, the value of c22 is (Zharkov et al. 1985)
. The tesseral coefficient c22 value gives an idea of Pluto’s and Charon’s deformation due to their mutual interaction in double spin-orbit resonance. In the hydrostatic case, the value of c22 is (Zharkov et al. 1985) 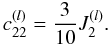 (4)Hence the values of c22 we considered for Pluto and Charon are
(4)Hence the values of c22 we considered for Pluto and Charon are 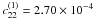 and
and 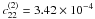 , respectively.
, respectively.
We integrated numerically our model with the 15th order Gauss-Radau integrator developed by Everhart (1985), which we chose for its accuracy and speed.
We fitted the initial conditions and parameters with a linear least-square procedure without any constraints. To obtain the values of the partial derivatives needed for it, we used the following relation (Lainey et al. 2004): ![\begin{equation} \frac{\partial}{\partial c_l}\left(\frac{\mathrm{d}^2 \vec{r}_i}{\mathrm{d}t^2}\right)=\frac{1}{M_i}\left[\sum_j\left( \frac{\partial\vec{F}_i}{\partial \vec{r}_j}\frac{\partial \vec{r}_j}{\partial c_l} + \frac{\partial\vec{F}_i}{\partial \dot{\vec{r}}_j}\frac{\partial \dot{\vec{r}}_j}{\partial c_l}\right) + \frac{\partial\vec{F}_i}{\partial c_l}\right]\text{,} \end{equation}](/articles/aa/full_html/2012/04/aa16952-11/aa16952-11-eq26.png) (5)where cl is a parameter we need to adjust. The values of the ∂ri/∂cl coefficients were then computed through numerically integrating the previous equation simultaneously with the equations of motion. For more details on the variational equations used, we refer to Lainey et al. (2004).
(5)where cl is a parameter we need to adjust. The values of the ∂ri/∂cl coefficients were then computed through numerically integrating the previous equation simultaneously with the equations of motion. For more details on the variational equations used, we refer to Lainey et al. (2004).
While we are fitting initial Cartesian coordinates in Sect. 3, initial elliptical elements are fitted in Sect. 4 for better convergence (Taylor 1998).
3. Parameter determinations
We are challenged by the great distance of Pluto’s system to the Sun. This leads to a large uncertainty in the observations once they are transformed into kilometers. Since an unmodeled physical effect can partly vanish when fitting a dynamical model to the observations, we have to quantify the part of its influence after the fitting.
Therefore, we used the following procedure. We computed simulated positions using Eq. (1) and the inital conditions and parameters described above. These simulated data are obtained by taking into account the effect we aim to test, a mass, an initial position or a polar oblateness coefficient. We then fitted a version of our model that does not include the parameter we aim to test. The obtained residuals may then be compared to the precision of the observations (Lainey & Tobie 2005).
3.1. Oblate gravity fields
The main effect of the influence of Pluto’s polar oblateness will be the precession of the satellite orbits. The effect will be easier to detect in two cases. First, for satellites close to the planet, because their precession will be faster. Second, for a satellite that has been observed for a long time, because the difference in longitude will grow with time.
To test the influence of the oblate gravity fields, we simulated data on a time span of about 30 years, the time span since Charon’s discovery. A sampling of ten days for the four bodies’ Cartesian positions was considered. We used the values of J2 and c22 given in the previous section. We then fitted only the values of the cartesian initial positions and velocities to the data. We did not fit the value of the masses because of the possible correlations between them and the oblate gravity fields. As a result, this situation is the most favorable one for detecting the influence of these coefficients. The post-fit residuals are shown in Fig. 1.
 |
Fig. 1 Post-fit residuals of a model without Pluto’s and Charon’s J2 and c22, fitted to simulated observations with a non-zero value of these coefficients. Only the initial positions and velocities were fitted. |
The residuals for Pluto are at most about 7 km, 4 km for Charon, 3 km for Nix, and 4 km for Hydra. Evidently, the residuals are all linearly increasing with time, except for Hydra. Because the system lies about 30 AU away, it means a difference of about 0.2 mas and 0.3 mas for the satellites and Pluto, respectively. Pluto’s system is really compact, consequently both Nix and Hydra are in the light of Pluto and Charon on the observations. In the observations from 2002–2003 of Nix and Hydra, the precision on the astrometry of Charon were about 3 mas. The oldest observations of Charon where it can be separated from Pluto are speckle interferometry observations from 1985 and 1983, whose precision were estimated to be 80 mas. Most recent observations of Charon probably have an accuracy better than 3 mas, but the precision of the older observations prevents us from detecting this 0.3 mas effect after 30 years of observations. Therefore we conclude that the effect of the oblate gravity fields cannot be detected today thanks to the observations.
Our hypothesis on the constant density of Pluto and Charon is most probably not true, but the value of the J2 coefficient will not be drastically modified. As a result, we would still be confronted with the very same problem as before, where the uncertainty of the observations will prevent us from detecting the effect of the most massive bodies’ oblateness.
Concerning the insight the New Horizons mission will provide on this topic, the minimum precision required for detecting the effect of J2 and c22 on the satellites will only be attained seven days before the closest approach between the probe and Pluto’s system. This will provide only a few points in a short timespan compared to the observations already available. Moreover, the center of mass will not be determined with a one-pixel precision because of the size of the satellites on the image at the time of the closest approach. Because the residuals show a linear increase with time, we can deduce that a good precision of the observations in this short timespan will probably not be enough to provide the value of Pluto’s and Charon’s oblate gravity fields.
 |
Fig. 2 Post-fit residuals of a model with a massless Hydra fitted to simulated observations with GM4 = 0.021 ± 0.042 km3 s-2. Only the initial positions and velocities were fitted. |
3.2. Masses
The current uncertainties in the masses of Pluto and Charon are a small percentage compared to their masses, but that is not the case for Nix and Hydra. When comparing the perturbations of the satellites on each other, the main perturbation on Nix will be caused by Hydra and vice versa. Consequently, the mutual interactions between the smallest satellites will be the best way to determine their masses.
As already mentioned, Tholen et al. (2008) have given values for the masses of the system’s bodies. Unfortunately, the 1-σ error bar for Nix and Hydra are nearly the same as the estimated value, giving GM values of Gm3 = 0.039 ± 0.034 km3 s-2 and Gm4 = 0.021 ± 0.042 km3 s-2, respectively. Because of the low value of the masses and these large error bars, we tried to determine whether we could obtain reliable mass estimates in the coming years. To do so, we used the same method as used before for the oblate gravity fields. We simulated observations with the masses given by Tholen et al. (2008), and fitted our model with a massless Hydra to derive whether fitting the initial positions and velocities only would absorb the difference. Because the two small moons have been discovered in 2005 and precovery observations have been obtained in 2002, we simulated data over eight years only, with a ten day sampling period. The result is given in Fig. 2.
 |
Fig. 3 Post-fit residuals of a model with a massless Nix fitted to simulated observations with GM3 = 0.039 ± 0.034 km3 s-2. Only the initial positions and velocities were fitted. |
The low post-fit residuals on Pluto’s and Charon’s positions are explained by the small influence of Hydra on their orbits. The post-fit residuals of Nix’s position are higher, about 40 km (i.e. 2 mas). The precision of the astrometric positions on the prediscovery observations from Buie et al. (2006) for Nix and Hydra are 15 and 9 mas, respectively. In Tholen et al. (2008), the uncertainties are slightly greater.
In principle, a 2 mas signal in the 9 mas noise of Nix’s observations should be detectable. Of course, in this case, the number of observations will become a major concern. With too few observations, it will be impossible to detect the effect of the masses with confidence, because both the noise and the too few positions will prevent us from detecting a clear tendency in the signal (see Sect. 4 for an analysis on the precision of the masses depending on the number of observations). The currently unpublished observations from HST have been made with the WFPC2 of the HST, which means with a pixel size of 46 mas. The astrometry from the HST images comes from the motion of Pluto on the CCD plane, one star at most being visible on the image. In this case, the uncertainty on Pluto’s motion causes an uncertainty on the relative position of its satellites. Accordingly, we do not expect the uncertainty on the astrometric positions of the satellites to be reduced by much from their current value, even with observations made especially to detect the faint satellites.
To test the influence of Nix’s mass (whose estimate in Tholen et al. 2008, is higher than Hydra’s), we used the very same method. The result is shown in Fig. 3. The residuals are higher than before, and because the current mass tested is twice the previous one, the post-fit residuals are also about twice as high.
The masses of the satellites obviously have an influence on the residuals, but they are not adequately constrained from current estimates. Because of this, the masses can be greater than their current estimates. To quantify how the residuals increase with the satellites masses, we used the same method as before, and fitted a model for which Nix’s mass is 2-σ greater than its estimated value, hence a mass about three times bigger than previously. The result is shown in Fig. 4. The residuals are three times higher than before. The uncertainty on the masses implies that Nix could be three times more massive, and Hydra five times more massive if we consider the 2-σ uncertainty. This would imply at most residuals of 10 and 12 mas, respectively.
If the real masses of the satellites are larger than previously estimated, the problem of the number of observations and noise will be less important than for the masses from Tholen et al. (2008). But on the other hand, if the masses are smaller, the observation noise will become more difficult to overcome. The problem is that the currently estimated masses induce residuals on the very limit of the current best precision of observations, and they are not as numerous and regular as in the previous simulations. Yet, residuals will grow as a longer time span of the observations is available, hence easier possible detection. Disregarding these problems of parameter correlations and the number of observations, the masses as currently estimated are within the range of detection and do not appear to be numerical artifacts.
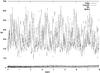 |
Fig. 4 Post-fit residuals of a model with a massless Nix fitted to simulated observations with GM3 = 0.107 km3s-2. Only the initial positions and velocities were fitted. |
3.3. Sense and sensitivity
Because mass determination can be a tricky problem that depends on the amount of observations, we have tried to determine the best opportunities for new observations. To do so, we used the same approach as Emelyanov (2005) and calculated the value of the sensitivity function 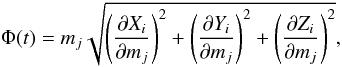 (6)where t is the date of observation, Xi, Yi and Zi the Cartesian coordinates of the perturbed body, and mj the mass of the perturbing satellite. This quantity stands for the influence of the mass of a satellite on another body’s position. Accordingly, the higher its value, the stonger the influence, the easier it is to detect. We calculated this value about every five hours to be sure not to miss an interesting opportunity. Figure 5 shows the sensitivity function of Charon’s and Hydra’s position with respect to Nix’s mass, while Fig. 6 shows the sensitivity function of Charon’s and Nix’s position with respect to Hydra’s mass.
(6)where t is the date of observation, Xi, Yi and Zi the Cartesian coordinates of the perturbed body, and mj the mass of the perturbing satellite. This quantity stands for the influence of the mass of a satellite on another body’s position. Accordingly, the higher its value, the stonger the influence, the easier it is to detect. We calculated this value about every five hours to be sure not to miss an interesting opportunity. Figure 5 shows the sensitivity function of Charon’s and Hydra’s position with respect to Nix’s mass, while Fig. 6 shows the sensitivity function of Charon’s and Nix’s position with respect to Hydra’s mass.
We can only see the growth of the curves and oscillation amplitudes around a mean value. The amplitude of the oscillations is coherent with those obtained from the tests on our model capability to detect the masses of the small satellites. Though their values are not the same, we still have higher oscillations from the influence of Nix, whose mass is bigger than Hydra’s, than from those of Hydra.
The sensitivity function does not take into account the possible correlations between the parameters. As a result, we cannot quantify the effect that these correlations would have on the satellites’ motion from the signal, and consequently, we cannot quantify the effect of the masses on the satellites’ motion. But we also looked at the maximum of the oscillations and found a clear regularity, most probably related to a combination of proper frequencies of the satellites’ orbits. The regularity of the oscillations suggests that specific observation moments may be determined to enhance the detection of the masses, once our model will be fitted to the observations.
 |
Fig. 5 Sensitivity function of Charon’s and Hydra’s position with respect to Nix’s mass. |
 |
Fig. 6 Sensitivity function of Charon’s and Nix’s position with respect to Hydra’s mass. |
4. Evolution of the uncertainty on mass determinations
As mentioned in the previous section, the currently estimated masses of the smallest satellites can be clearly determined once enough observations is available. Yet this does not tell us whether we could obtain it when considering the currently available sets of observations, and how the precision of this determination will evolve in the future.
Here, our method is to simulate data at the dates of the observations, fit our model to it, and then extract the statistical 1-σ precision given by the least-squares procedure. The difference to the previous methods is that we now fit all the parameters (initial conditions and masses), and that problems from correlations and observation uncertainties will arise. We no longer fit our model to absolute Cartesian coordinates, but to spherical ones relative to Pluto (Δα, Δδ). The advantage of working with simulated data is that we do not have to face convergence problems because of observation accuracy. The precision that will be given is the formal 1-σ from the least-squares fit.
The dates we used for the simulated data of Nix and Hydra are the same as those of the prediscovery observations (Buie et al. 2006), which give also Charon’s positions, those of the discovery (Weaver et al. 2005) and those of Hydra and Charon from Sicardy et al. (2006). We added simulations corresponding to Charon’s observations from Tholen & Buie (1997). We also assumed that observations of the system will be carried out every year from the ground or HST, near Pluto’s opposition. For these hypothetical observations, we assumed that about ten of them will be made every year, the current rythm being about ten observations every two years, and that their precision would be those given in Buie et al. (2006), that is, 3 mas for Charon, 9 mas for Hydra, and 15 mas for Nix.
Our reason for not decreasing these error bars is that in the most recent fit to observations made (Tholen et al. 2008), the uncertainties have been raised and the pixel size of the unpublished observations is greater than those of the published ones, as said in Sect. 3.2. Moreover, no drastic evolution of the precision of observations may be expected before the arrival of New Horizons, the next generation of ground telescope are still projects, and the next generation of space telescope will not be launched before 2015.
We did not simulate the observations from cycle 15 and 17 of the HST, because they were still unpublished when we were writing this paper, and because one set of additional data is not expected to change the conclusions on the uncertainty of the masses drastically. Therefore we simulated ten observations in 2010 while twelve have been made in reality (Tholen et al. 2010), and we did not simulate data in 2007.
The dates for these simulations are given in Table 1. We also simulated data that will reproduce the schedule of New Horizons’ observations, coming from Young et al. (2008) and Young et al. (2010). The schedule and uncertainties used are given in Table 4. To know whether extending the New Horizons mission in Pluto’s system would significantly improve its results, we added a set of simulated observations after the probe’s flyby of the system, following a symmetric pattern to last phase of the mission. During this phase, only Nix and Hydra are observed. The schedule of the simulated data as well as the uncertainties attached to each date are given in Table 5. To reproduce the fact that at the time of the closest approach, the satellite’s center of mass will probably not be determined with a one-pixel precision, we increased the uncertainty. Considering the observations of Deimos by the probe Mars Express (Oberst et al. 2006), the uncertainty on the center of figure is about one sixth of the Deimos radii and 500 m for Phobos. In the case of New Horizons, the satellites will probably be darker, so there will be a longer exposure and there will possibly be stars beside them. Consequently, we expect the astrometric determination to be easier. To reproduce the difficulty of localizing the objects’ center of light, we set the precision on the satellites observations to be at best one eighth of the satellites’ diameter.
The simulated positions of the satellites are given with respect to Pluto. We have five sets of simulated data:
-
1992–2006: reproduces the existing observations describedabove;
-
1992–2014: reproduces the existing observations described above and the future ground-based observations made before the New Horizons’ flyby in Pluto’s system;
-
1992–2006+NH: reproduces the existing observations described above and the observations made by New Horizons;
-
1992–2014+NH: reproduces the existing observations described above, the future ground-based observations, and the observations made by New Horizons;
-
1992–2014+extended NH: reproduces the existing observations described above, the future ground-based observations, and the observations made by New Horizons assuming the observations of Pluto’s system are extended.
The results for all these simulations and the number of simulated data used for each body are given in Table 2.
Dates used for the simulation of observations between 2010 and 2014.
1-σ error bars on the masses given by least-squares method using different sets of simulated observations, using m1 = 870.3 km3 s-2, m2 = 101.4 km3 s-2, m3 = 0.039 km3 s-2 and m4 = 0.021 km3 s-2.
The error bars of the masses found for the 1992–2006 period are consistent with those from Tholen et al. (2008), and the error bars have the same order of magnitude as the mass estimates for Nix and Hydra.
Between the set for the 1992–2006 period and that for 1992–2014, we can see that the uncertainty on the masses of Pluto and Charon decrease less noticeably than those of Nix and Hydra. Yet, the relative uncertainties on these latter ones remain very high.
While considering the different sets, we can see that the most significant improvement in the determination of the masses will be given by New Horizons data. The main advantage of observing the system before the probe’s flyby is to precisely determine the orbit of the satellites and help constrain the mass of Nix, but only New Horizons will enable us to obtain statistical error bars whose order of magnitude is lower than the current estimated masses. That Nix’s mass will become less constrained than that of Hydra, while the situation is different now, can be explained because New Horizons will obtain more extensive observations of this satellite. One aspect that can be discussed is the uncertainty we attached to New Horizons simulations. We used Phobos and Deimos as an example for the determination of the satellites’ center. These satellites are far from spherical, hence the difficulties in determining the center. Nix and Hydra are possibly more spherical because of their expected greater size, and therefore the precision on their center might be better than in our simulations. This can also lower the uncertainty on the masses, but not significantly. Because of the difference between the pixel size and the precision of the determination of the center of mass, the extension of the mission presented here would not be useful to constrain the masses much more, and so would not be a good option for enhancing the detection of masses.
Now we can consider the question of the value of the masses. The statistical uncertainty from the least-squares method only depends on the uncertainty of the observations, the partial derivatives, and the correlations between the parameters. When considering the uncertainty attached to one mass, the factors described before do not explicitly depend on this mass. Therefore, if one satellite’s mass is higher than its estimate, its error will not change much from the case where the estimate is the lower mass. That is, the relative error will decrease, but not the absolute one. Accordingly, if we consider that both satellites are 2-σ more massive than their current estimation, and using the σ from Table 2, we obtain m3 = 0.087 km3 s-2 and m4 = 0.093 km3 s-2. It means that the masses would be known to 11 and 20%, respectively, in 2014. While New Horizons would not improve this relative uncertainty much for Nix, that is not the case for Hydra, whose mass would be known with a 3% uncertainty.
We assume that the mass will be determined with sufficient confidence if the 2-σ uncertainty is less than half the mass of the satellite. In 2014, we can see that the uncertainty on Nix’s mass will be 0.010 km3 s-2. If we compare this with the estimated mass in Tholen et al. (2008), we can see that the condition given above will be fulfilled. This means that if the real mass of Nix is about the same or greater than its current estimation, we will know it with confidence before the New Horizons mission. If Nix is less massive, we can determine which value of the mass New Horizons will enable us to detect with confidence. Because the uncertainty on Nix’s mass from the New Horizons data is expected to be 0.0076 km3 s-2, the minimum corresponding mass is 0.030 km3 s-2. When using the same method for Hydra, we find that the mass of Hydra would have to be greater than 0.075 km3 s-2 to be known before 2014, and that its lowest value detectable from the New Horizons data is 0.010 km3 s-2.
We then investigated how many ground-based observations would be needed to obtain a comparable precision as the one we obtained before with New Horizons. To do so, we simulated observations at random dates during 50 days each year around Pluto’s opposition, beginning in 2011. We used two different densities of simulations. In the first set, with the highest density, we simulated 100 observations each year (set 1999–2014 HD), and about 25 for the second one (set 1999–2014 LD). The uncertainties obtained for these simulated dates are given in Table 3.
1-σ error bars on the masses given by the least-squares method using two sets of simulated observations with different densities, using m1 = 870.3 km3 s-2, m2 = 101.4 km3 s-2, m3 = 0.039 km3 s-2, and m4 = 0.021 km3 s-2.
Clearly, our most dense set gives a lower uncertainty for Nix’s mass than what would be achieved with New Horizons in our previous simulation. Yet, that is not the case for the mass of the other objects of the system. This is because New Horizons will observe the system very regularly during several months, a situation harder to achieve for HST and ground-based observations. Nix’s mass can be constrained with only 25 observations per year. We would then obtain only from ground-based/HST observations a precision similar to what we expect with the New Horizons data and ten ground-based/HST observations per year.
5. Conclusion
We have developed a numerical model of a multiple system’s motion around the Sun with the possibility to include the oblate gravity fields. The first application of this model to Pluto’s system has led us to conclude that the oblate gravity fields of Pluto and Charon will not be substantially more constrained from astrometry in the coming years, even considering New Horizons’ data. Concerning the masses, we are limited today by the accuracy of the observations. A study on the error bars also shows that substantial improvement in mass determinations of all bodies except for possibly Nix must await New Horizons’ flyby of Pluto’s system.
Astrometric observations from New Horizons should succeed in significantly constraining Nix’s and Hydra’s mass and radii, if the masses are not too low compared with their current estimates. If the masses are lower than their current estimates, we can determine a highest possible value from New Horizons error bars, that is 0.0076 km3 s-2 for Nix, and 0.0028 km3 s-2 for Hydra. This will provide the first estimates or highest values of the two moon densities and, as a result, may shed light on the question of their origin.
This should not be considered a reason not to observe the system. The discovery of the new satellite P4 clearly indicates that this system could still be a source of discoveries, and as such, new observations are still necessary. Indeed, the recent discovery of P4 could challenge some of these results depending on the interactions between this satellite and the other bodies of the system. P4 orbits around Pluto on an orbit between Nix and Hydra. Its mass is expected to be far lower than those of Nix and Hydra from its magnitude. If its trajectory is strongly disturbed by mutual effects with the other two satellites, then we might expect P4 to be the key to obtain the masses of Nix and Hydra before the arrival of New Horizons if the rate of observations is not increased. One must keep in mind, nonetheless, that this is only one possible configuration of the system among others.
Indeed, we still have very few observations of the satellite nor do we have data on its astrometric precision.
That the masses remain strongly unconstrained while the motion of the satellites is known with a fairly good precision means that the masses are not heavily constrained by said motions. Observing the system remains imperative for constraining the orbit of the satellites, to prepare the New Horizons arrival as well as potential stellar occultations by these bodies. Indeed, their ephemeris is doomed to diverge if no new observations are available.
One key point of our model is that it is able to simultaneously fit the primary’s motion (in our application, Pluto) and those of its satellites. The next step is now to adjust our model to real observations.
Online material
New Horizons observation schedule, as currently planned, for the listed targets and anticipated measurement precision.
Dates, precision and targets used for the simulation of New Horizons extension.
Acknowledgments
Support for this work (R.P.B.) was provided by NASA, as a member of the New Horizons Mission science team. The authors thank the New Horizons Pluto Encounter Planning team for providing the parameters in Table 4.
References
- Buie, M. W., Grundy, W. M., Young, E. F., Young, L. A., & Stern, S. A. 2006, AJ, 132, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Canup, R. M. 2005, Science, 307, 546 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Christy, J. W., & Harrington, R. S. 1978, AJ, 83, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Emelyanov, N. V. 2005, A&A, 438, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, held in Rome, Italy, June 11–15, 1984 (Dordrecht: Reidel), ed. A. Carusi, & G. B. Valsecchi, Proc. IAU Colloq., 83, Astrophys. Space Sci. Lib., 115, 185 [Google Scholar]
- Lainey, V., & Tobie, G. 2005, Icarus, 179, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Lainey, V., Duriez, L., & Vienne, A. 2004, A&A, 420, 1171 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murray, C. D., & Dermott, S. F. 2000, Solar System Dynamics, ed. C. D. Murray, & S. F. Dermott [Google Scholar]
- Oberst, J., Matz, K. D., Roatsch, T., et al. 2006, A&A, 447, 1145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seidelmann, P. K., Archinal, B. A., A’Hearn, M. F., et al. 2007, Cel. Mech. Dyn. Astron., 98, 155 [Google Scholar]
- Sicardy, B., Ageorges, N., Marco, O., et al. 2006, PLUTO III (HYDRA), Tech. Rep., IAU Electronic Telegram [Google Scholar]
- Standish, E. M. 1998, Tech. Rep., Jet Prop. Lab. Interoffice Memo. 312.F-98-04 [Google Scholar]
- Stern, S. A., Mutchler, M. J., Weaver, H. A., & Steffl, A. J. 2007, in Lunar and Planetary Institute Science Conference Abstracts, 38, 1722 [Google Scholar]
- Stern, S. A., & Spencer, J. 2003, Earth Moon and Planets, 92, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, S. A., Weaver, H. A., Steffl, A. J., et al. 2006, Nature, 439, 946 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, D. B. 1998, A&A, 330, 362 [NASA ADS] [Google Scholar]
- Tholen, D. J., & Buie, M. W. 1997, Icarus, 125, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Tholen, D. J., Buie, M. W., Grundy, W. M., & Elliott, G. T. 2008, AJ, 135, 777 [NASA ADS] [CrossRef] [Google Scholar]
- Tholen, D. J., Buie, M. W., & Grundy, W. M. 2010, in BAAS, 42, AAS/Division for Planetary Sciences Meeting Abstracts # 42, 984 [Google Scholar]
- Turcotte, D. L., & Schubert, G. 2002, Geodynamics, 2nd edn., ed. D. L. Turcotte, & G. Schubert [Google Scholar]
- Weaver, H. A., Stern, S. A., Mutchler, M. J., et al. 2005, IAU Circ., 8625, 1 [NASA ADS] [Google Scholar]
- Weaver, H. A., Stern, S. A., Mutchler, M. J., et al. 2006, Nature, 439, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Weaver, H. A., Gibson, W. C., Tapley, M. B., Young, L. A., & Stern, S. A. 2007, Overview of the New Horizons Science Payload, Tech. Rep., Johns Hopkins University Applied Physics Laboratory, http://www.boulder.swri.edu/pkb/ [Google Scholar]
- Young, L. A., Stern, S. A., Weaver, H. A., et al. 2008, Space Sci. Rev., 140, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Young, L. A., Olkin, C., Spencer, J., et al. 2010, New Horizons: Plans for Nix and Hydra, in 2010 Nix-Hydra Meeting, Baltimore, MD, https://webcast.stsci.edu/webcast/detail.xhtml?talkid=1914&parent=1 [Google Scholar]
- Zharkov, V. N., Leontjev, V. V., & Kozenko, V. A. 1985, Icarus, 61, 92 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
1-σ error bars on the masses given by least-squares method using different sets of simulated observations, using m1 = 870.3 km3 s-2, m2 = 101.4 km3 s-2, m3 = 0.039 km3 s-2 and m4 = 0.021 km3 s-2.
1-σ error bars on the masses given by the least-squares method using two sets of simulated observations with different densities, using m1 = 870.3 km3 s-2, m2 = 101.4 km3 s-2, m3 = 0.039 km3 s-2, and m4 = 0.021 km3 s-2.
New Horizons observation schedule, as currently planned, for the listed targets and anticipated measurement precision.
All Figures
 |
Fig. 1 Post-fit residuals of a model without Pluto’s and Charon’s J2 and c22, fitted to simulated observations with a non-zero value of these coefficients. Only the initial positions and velocities were fitted. |
| In the text | |
 |
Fig. 2 Post-fit residuals of a model with a massless Hydra fitted to simulated observations with GM4 = 0.021 ± 0.042 km3 s-2. Only the initial positions and velocities were fitted. |
| In the text | |
 |
Fig. 3 Post-fit residuals of a model with a massless Nix fitted to simulated observations with GM3 = 0.039 ± 0.034 km3 s-2. Only the initial positions and velocities were fitted. |
| In the text | |
 |
Fig. 4 Post-fit residuals of a model with a massless Nix fitted to simulated observations with GM3 = 0.107 km3s-2. Only the initial positions and velocities were fitted. |
| In the text | |
 |
Fig. 5 Sensitivity function of Charon’s and Hydra’s position with respect to Nix’s mass. |
| In the text | |
 |
Fig. 6 Sensitivity function of Charon’s and Nix’s position with respect to Hydra’s mass. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


