| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 12 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201118031 | |
| Published online | 30 January 2012 | |
3D simulations of pillar formation around HII regions: the importance of shock curvature
Laboratoire AIM Paris-Saclay (CEA/Irfu – Uni. Paris Diderot – CNRS/INSU), Centre d’études de Saclay, 91191 Gif-Sur-Yvette, France
e-mail: pascal.tremblin@cea.fr
Received: 6 September 2011
Accepted: 3 November 2011
Aims. Radiative feedback from massive stars is a key process for understanding how HII regions enhance or inhibit star formation in pillars and globules at the interface with molecular clouds. We aim to contribute by modelling the interactions between ionization and gas clouds to better understand the processes at work. We study in detail the impact of modulations on the cloud-HII region interface and density modulations inside the cloud.
Methods. We ran 3D hydrodynamical simulations based on Euler equations coupled with gravity using the HERACLES code. We implemented a method to solve ionization/recombination equations and took into account typical heating and cooling processes at work in the interstellar medium that are caused by ionization/recombination physics.
Results. UV radiation creates a dense shell compressed between an ionization front and a shock ahead. Interface modulations produce a curved shock that collapses on itself, which leads to stable growing pillar-like structures. The narrower the initial interface modulation, the longer the resulting pillar. We interpret pillars resulting from density modulations in terms of the ability of these density modulations to curve the shock ahead of the ionization front.
Conclusions. The shock curvature is a key process for understanding the formation of structures at the edge of HII regions. Interface and density modulations at the edge of the cloud have a direct impact on the morphology of the dense shell during its formation. Deeper inside the cloud, structures have less influence because of the high densities reached by the shell during its expansion.
Key words: stars: formation / HII regions / ISM: structure / methods: numerical
© ESO, 2012
1. Introduction
Radiative feedback from massive stars could be an important process to explain the star-formation rates on galactic scales. Its role in complexe structures such as giant molecular clouds is still a matter of debate (see Dale et al. 2007; Price & Bate 2009; Dale & Bonnell 2011). When the UV radiation from the massive objects photoionizes the surrounding gas, a “bubble” of hot ionized gas expands around the star: the HII region (see Purcell et al. 2009, for example). While star formation is inhibited inside the bubble, the small-scale compression at the edge of the HII region seems to form elongated structures (pillars) and globules owing to its expansion in which the star-formation activity seems enhanced (see Deharveng et al. 2010, for example). Different models investigate this process.
First studies of HII regions (e.g. Strömgren 1939; Elmegreen & Lada 1977) showed how UV radiation leads to the formation of an ionization front and of a shock ahead. The gas is compressed between them, forming a dense shell that may lead to fragmentation, gravitational collapse, and star formation, this is the collect-and-collapse scenario (Elmegreen & Lada 1977).
Another scenario was proposed by Bertoldi (1989), the radiation-driven implosion scenario. He looked at the photoevaporation of spherical neutral clouds and found that the ionization front drives a shock into the cloud, leading to the compression of the initial structure into a compact globule. This scenario has been studied in detail with numerical simulations for years (see Lefloch & Lazareff 1994; Williams et al. 2001; Kessel-Deynet & Burkert 2003). Recently, Bisbas et al. (2011) and Gritschneder et al. (2009) looked at the implosion of isothermal spherical clouds with smoothed particle hydrodynamics (SPH) codes. Using a grid code, Mackey & Lim (2010) produced elongated structures from dense spherical clumps using the shadowing effects of these structures.
In the past decade, the importance of the initial turbulence in the cloud has been studied with 3D simulations at different scales. Mellema et al. (2006) presented simulations of the formation of the HII region that agree well with observations. The interplay between ionization and magnetic fields has been studied by Krumholz et al. (2007) and later by Arthur et al. (2011) in the context of HII region formation, and these authors found that magnetic fields tend to suppress the small-scale fragmentation. On larger scales Dale et al. (2007) looked at the impact of ionization feedback on the collapse of molecular clouds, finding a slight enhancement of star formation with ionization, while Dale & Bonnell (2011) found almost no impact. On a smaller scale, Lora et al. (2009) found that the angular momentum of the resulting clumps is preferentially oriented perpendicular to the incident radiation. Gritschneder et al. (2010) showed that pillars arise preferentially at high turbulence and that the line-of-sight velocity structure of these pillars differs from a radiation-driven-implosion scenario.
These HII regions are seen in many massive molecular clouds and are the object of a great number of observational studies: in the Rosette nebula (Schneider et al. 2010), M16 (Andersen et al. 2004), 30 Doradus (Walborn et al. 2002), Carina nebula (Smith et al. 2000), the Elephant Trunk nebula (Reach et al. 2004), the Trifid nebula (Lefloch et al. 2002), M17 (Jiang et al. 2002), or the Horsehead nebula (Bowler et al. 2009). Spitzer observations also provide a wide range of HII regions, which were studied in detail by Deharveng et al. (2010). Pillars and globules are frequently observed and present density clumps which may lead to star formation. The different scenarii described above can be constrained thanks to these observations.
The present study focuses on “simple” situations to highlight the key mechanisms at work in the interaction between a HII region and a cloud. We present the numerical methods needed for this study followed by two different set-ups, cloud-HII region interface modulation and density modulation inside the cloud, and finally a study of the different stages of evolution of the resulting pillars. A following paper will investigate these situations in a more complete set-up, which will include turbulence inside the cloud.
2. Numerical methods
We considered a molecular cloud impacted by the UV radiation of an OB cluster to study how structures develop at the interface between the resulting HII region and the cloud. Section 2.1 describes the method used to simulate gas hydrodynamic in the molecular cloud with the HERACLES code (González et al. 2007). Section 2.2 describes the numerical method used to take into account the UV radiation from the OB cluster and the resulting ionization/recombination reactions. Thermal processes from these reactions and the heating and cooling rates used in the molecular cloud are described in Sect. 2.3.
2.1. Hydrodynamic
Our simulations were performed with the HERACLES code1. It is a grid-based code using a second-order Godunov scheme to solve Euler equations. These equations are given in Eq. (1) including a gravitationnal potential Φ, constrained by the Poisson equation: △ Φ = 4πGρ![\begin{eqnarray} \label{eulergrav} \frac{\partial \rho} {\partial t} + \nabla \cdot (\rho \vec{V}) & = & 0 , \notag\\[-3mm] \frac{\partial \rho \vec{V}}{\partial t} + \nabla \cdot [\rho \vec{V} \otimes \vec{V} + pI] & = & - \rho \nabla \Phi ,\notag \\[-3mm] \frac{\partial E} {\partial t} + \nabla \cdot [(E + p) \vec{V} ] & = & - \rho(\vec{V} \cdot \nabla \Phi) + \Lambda(\rho,T) . \end{eqnarray}](/articles/aa/full_html/2012/02/aa18031-11/aa18031-11-eq3.png) (1)We used an ideal gas equation of state, so that E = p/(γ − 1) + 0.5ρV2 with γ = 5/3. Λ(ρ,T) corresponds to the heating and cooling processes detailed in Sect. 2.3, leading to a polytropic gas of index around 0.7 at equilibrium (for ρ = 500/cm3). All other variables have their usual meaning.
(1)We used an ideal gas equation of state, so that E = p/(γ − 1) + 0.5ρV2 with γ = 5/3. Λ(ρ,T) corresponds to the heating and cooling processes detailed in Sect. 2.3, leading to a polytropic gas of index around 0.7 at equilibrium (for ρ = 500/cm3). All other variables have their usual meaning.
2.2. Ionization
The stationnary equation governing radiative tranfer in spherical geometry is given by 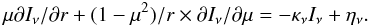 (2)μ is equal to cosθ and θ is the polar angle, Iν(r,μ,ν) is the spectral intensity at a radius r in the direction defined by μ at the frequency ν, κν(r,ν) is the absorption coefficient and ην(r,ν) is the source term. Radiation is coming from a point source such that Iν(r,μ,ν) = Fν(r,ν) × δ1(μ), in which δ1(μ) is a Dirac distribution whose peak is at μ = 1 corresponding to the direction θ = 0 in spherical coordinates. Integrating Eq. (2) over μ leads to Eq. (3), in which the absorption coefficient and the source term are given by Eq. (4)
(2)μ is equal to cosθ and θ is the polar angle, Iν(r,μ,ν) is the spectral intensity at a radius r in the direction defined by μ at the frequency ν, κν(r,ν) is the absorption coefficient and ην(r,ν) is the source term. Radiation is coming from a point source such that Iν(r,μ,ν) = Fν(r,ν) × δ1(μ), in which δ1(μ) is a Dirac distribution whose peak is at μ = 1 corresponding to the direction θ = 0 in spherical coordinates. Integrating Eq. (2) over μ leads to Eq. (3), in which the absorption coefficient and the source term are given by Eq. (4) ![\begin{eqnarray} \label{transfer2} \partial F_\nu/\partial r +2/r\times F_\nu &=& -\kappa_\nu F_\nu + \eta_\nu \\[-1mm] \label{etakappa} \eta_\nu(r,\nu) &=& S_*(\nu)\delta_{0}(r) \notag\\[-1mm] \kappa_\nu(r,\nu) &=& \sigma n_{H_0} \nu^3_1/\nu^3. \end{eqnarray}](/articles/aa/full_html/2012/02/aa18031-11/aa18031-11-eq22.png) hν1 is equal to 13.6eV, σ is the ionizing cross section for photons at frequency ν1 and nH0(x) the density of neutral hydrogen atoms. δ0(r) is a Dirac peak at r = 0 and S ∗ is the flux from the central OB cluster. The radiation from the cluster is approximated by a unique source of radius r ∗ at a distance r0 of the computational domain, S ∗ corresponds to a diluted Planckian function at the star temperature
hν1 is equal to 13.6eV, σ is the ionizing cross section for photons at frequency ν1 and nH0(x) the density of neutral hydrogen atoms. δ0(r) is a Dirac peak at r = 0 and S ∗ is the flux from the central OB cluster. The radiation from the cluster is approximated by a unique source of radius r ∗ at a distance r0 of the computational domain, S ∗ corresponds to a diluted Planckian function at the star temperature 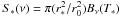 . By dividing Eq. (3) with hν to obtain an equation on the number of photons rather than radiative energies and averaging ν between ν1 and + ∞ to keep track only of the ionizing photons, we obtain
. By dividing Eq. (3) with hν to obtain an equation on the number of photons rather than radiative energies and averaging ν between ν1 and + ∞ to keep track only of the ionizing photons, we obtain 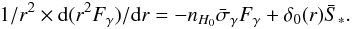 (5)Fγ is now the number of ionizing photons per unit of surface and time arriving in the radial direction and
(5)Fγ is now the number of ionizing photons per unit of surface and time arriving in the radial direction and 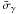 is the average cross-section over the Planckian source at T∗ and
is the average cross-section over the Planckian source at T∗ and 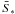 the rate of emission of ionizing photons by the stars. We can obtain plane-parallel equations in the limit r → ∞.
the rate of emission of ionizing photons by the stars. We can obtain plane-parallel equations in the limit r → ∞.
We now compute the equations for photo-chemistry. We set X to be the fraction of ionization X = nH + /nH in which nH = nH + + nH0, it follows the dynamic of the gas as an advected quantity. The variation of protons is the number of incoming photons that are going to interact minus the number of protons that will be used for recombination. The number of interacting photons in a volume dvcell is given by the number of incoming photons threw a surface dsin multiplied by the probability of interaction given by the cross-section, 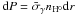 leading to
leading to 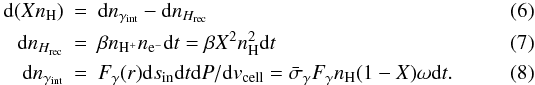 The dilution term ω = (dsindr/dvcell) is equal to
The dilution term ω = (dsindr/dvcell) is equal to 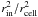 in spherical coordinates and to 1 in the plan-parallel limit. rin is the radial position of the entrance surface for incoming photons dsin and rcell is the radial position of the centre of the volume dvcell. β gives the rate of recombination and is equal to 2 × 10-10T-0.75 cm3/s, in which T is the temperature of thermodynamic equilibrium between all species (see Black 1981).
in spherical coordinates and to 1 in the plan-parallel limit. rin is the radial position of the entrance surface for incoming photons dsin and rcell is the radial position of the centre of the volume dvcell. β gives the rate of recombination and is equal to 2 × 10-10T-0.75 cm3/s, in which T is the temperature of thermodynamic equilibrium between all species (see Black 1981).
2.3. Thermal processes
Thermal processes are taken in account by adding the heating and cooling rate Λ(ρ,T) in the equation of energy conservation in Eq. (1).
In the ionized phase we consider two processes that have a major impact on the thermodynamic of the gas, the photoelectric heating caused by the massive star UV flux and the cooling through recombination of electrons onto protons. The energy eγ(T∗) given by ionizing photons is the integrated value of Iν/hν(hν − hν1) between ν1 and + ∞ on the incoming spectrum Iν. In the following we will assume a Planckian distribution Bν(T∗) with T∗ = 35 000 K, which gives eγ(T∗) = 1eV. Therefore the heating rate is given by Eq. (9). The cooling term is the loss of the thermal energy of electrons used by recombination given by Eq. (10) 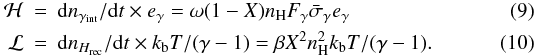 At the equilibrium between ionization and recombination, the recombination rate is equal to the ionization rate dnγint = dnHrec. Therefore the temperature is given by (γ − 1)eγ/kb when thermodynamic equilibrium is achieved in the ionized phase, which is equal to 7736 K. The corresponding isothermal curve in the pressure-density plane is drawn in Fig. 1.
At the equilibrium between ionization and recombination, the recombination rate is equal to the ionization rate dnγint = dnHrec. Therefore the temperature is given by (γ − 1)eγ/kb when thermodynamic equilibrium is achieved in the ionized phase, which is equal to 7736 K. The corresponding isothermal curve in the pressure-density plane is drawn in Fig. 1.
 |
Fig. 1 Thermodynamic equilibrium in the pressure-density plane for the highly and weakly ionized phases. |
In the weakly ionized phase we simulate the radiative heating and cooling of the interstellar medium (ISM) by adding five major processes following the work of Audit & Hennebelle (2005) and Wolfire et al. (1995, 2003):
-
photoelectric heating by UV radiation with a flux equal toG0/1.7, in which G0 is the Habing flux;
-
cooling by atomic fine-structure lines of CII;
-
cooling by atomic fine-structure lines of OI;
-
cooling by H (Lyα);
-
cooling by electron recombination onto positively charged grains.
The UV flux used in this phase is an ambient low flux, additional to the UV flux Fγ from the massive stars, which is used in our ionization process described in Sect. 2.2. This heating and cooling function is only valid for the dense cold and weakly ionized phase. Therefore these processes are weighted by 1 − X and contribute only in the weakly ionized phase. In this phase, the ionization fraction used for the thermal processes is a function of the temperature and is given by Wolfire et al. (2003) (typically around 10-4). The thermodynamic equilibrium in the pressure-density plane is given in Fig. 1.
The transition at the ionization front is very sharp as it can be seen on the tests in Sect. 2.4. Therefore the fraction of the gas in between the two phases is small and is not dynamically significant.
 |
Fig. 2 Expansion of an HII region in a homogenous medium (nH = 500 cm-3, T ≈ 25 K, S∗ = 1050γionizing/s). Case 1 is a simulation where the gas temperature is instantaneously at 7736 K if the ionization fraction is exceeds 0.5. Case 2 takes into account the time evolution of the temperature given by Eqs. (9) and (10). The analytic solution is computed from Eq. (12) if the thermal equilibrium is reached instantaneously. The Strömgren radius is given by Eq. (11). |
2.4. 1D spherical test: HII region expansion in spherical geometry
We first started by testing our numerical algorithms in a simple 1D spherical test that can be compared to analytical solution. Starting from a region with nH = 500 cm-3 and T ≈ 25 K, we switched on a photon flux coming from a typically O4 star with 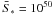 γionizing/s. In the beginning the typical time for ionization/recombination was much shorter than the hydrodynamical typical timescale. Therefore there was a first phase of development in which the hydrodynamic was frozen and the medium was ionized in a small sphere around the source. The radius of this sphere is controlled by the Strömgren formula given in Eq. (11) (see Strömgren 1939). Ionization stoped when all photons were used to compensate recombinations inside the sphere. In our example this radius is Rs = 2.38 pc
γionizing/s. In the beginning the typical time for ionization/recombination was much shorter than the hydrodynamical typical timescale. Therefore there was a first phase of development in which the hydrodynamic was frozen and the medium was ionized in a small sphere around the source. The radius of this sphere is controlled by the Strömgren formula given in Eq. (11) (see Strömgren 1939). Ionization stoped when all photons were used to compensate recombinations inside the sphere. In our example this radius is Rs = 2.38 pc 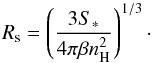 (11)If the thermal equilibrium between ionization and recombination is reached instantaneously, it is possible to compute an analytic expression of the time evolution of the ionization front (Spitzer 1978)
(11)If the thermal equilibrium between ionization and recombination is reached instantaneously, it is possible to compute an analytic expression of the time evolution of the ionization front (Spitzer 1978) 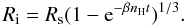 (12)The development of the ionized sphere before hydrodynamic starts to matter is shown in Fig. 2. Two cases were treated numerically, first the thermal equilibrium is reached instantaneously and the gas temperature is switched at 7736 K when the ionization fraction exceeds 0.5. This allowed us to compare our numerical solution to the analytic formula given in Eq. (12): the error is less than 0.5%. Second we resolved numerically the time evolution of the temperature given by the balance between Eqs. (9) and (10). The ionization front is slowed down by the explicit treatement of cooling owing to recombination. The recombination rate increases when the temperature decreases, leading to a lower penetration of ionizing photons.
(12)The development of the ionized sphere before hydrodynamic starts to matter is shown in Fig. 2. Two cases were treated numerically, first the thermal equilibrium is reached instantaneously and the gas temperature is switched at 7736 K when the ionization fraction exceeds 0.5. This allowed us to compare our numerical solution to the analytic formula given in Eq. (12): the error is less than 0.5%. Second we resolved numerically the time evolution of the temperature given by the balance between Eqs. (9) and (10). The ionization front is slowed down by the explicit treatement of cooling owing to recombination. The recombination rate increases when the temperature decreases, leading to a lower penetration of ionizing photons.
 |
Fig. 3 Density (top) and temperature (bottom) profiles of the expansion of an HII region in a homogenous medium (nH = 500 cm-3, T ≈ 25 K, S∗ = 1050γionizing/s). Solid lines correspond to an adiabatic cold phase and dashed lines to a cooled cold phase with the cooling described in Sect. 2.3 |
After this first step the energy deposited by the ionizing photons creates a spherical region with a high pressure. This region will therefore start expanding and pushes the surrounding interstellar matter away, creating a shock front ahead of the ionization front. This process creates an expanding ionized cavity and a shell of compressed gas. Typical density and temperature profiles are given in Fig. 3. Solid lines correspond to the adiabatic case for the cold gas and the dashed lines to the cooling function described in Sect. 2.3. The shock front is cooled down by the thermal processes and the shell is compressed up to two orders of magnitude. This phenomenon is at the origin of the idea of the collect-and-collapse scenario for triggered star formation around HII regions proposed by Elmegreen & Lada (1977).
We can derive the equations governing the density, the speed and the thickness of the shell in the approximation of an isothermal D-critical shock following Elmegreen & Lada (1977) and Spitzer (1978). The density and the pressure when the HII region has a radius r can be derived from the equilibrium between ionization and recombination in the sphere and are given by  α is equal to 1/3 and rs to
α is equal to 1/3 and rs to 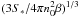 in spherical geometry while in the plan-parallel limit, α is equal to 1/2 and rs to
in spherical geometry while in the plan-parallel limit, α is equal to 1/2 and rs to 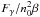 . The parameters of the shell can be computed using Eq. (13) and assuming a shell temperature Tshell and the corresponding sound speed cshell (for details, see Elmegreen & Lada 1977). They are given by Eq. (15), in which nshell is the maximum density in the shell, vshell the shock speed, and lshell the typical width of the shell
. The parameters of the shell can be computed using Eq. (13) and assuming a shell temperature Tshell and the corresponding sound speed cshell (for details, see Elmegreen & Lada 1977). They are given by Eq. (15), in which nshell is the maximum density in the shell, vshell the shock speed, and lshell the typical width of the shell  Assuming a temperature in the shell of 10 K and a radius of 20 parsecs for the HII region, we obtain a shell density of 3.2 × 104 cm-3, a speed of 3.2 km s-1, and a width of 0.5 parsec. These values agree well with the shell parameters we obtained in the 1D simulation in Fig. 3, the maximum density when the HII-region radius is 20 parsecs is 2.9 × 104 cm-3, the shell speed 4.4 km s-1, and the shell width 0.27 parsec. We can see that our code can follow the ionization front and the subsequent evolution of the dense shell with very high accuracy. We will therefore now turn our attention to more interesting 3D cases.
Assuming a temperature in the shell of 10 K and a radius of 20 parsecs for the HII region, we obtain a shell density of 3.2 × 104 cm-3, a speed of 3.2 km s-1, and a width of 0.5 parsec. These values agree well with the shell parameters we obtained in the 1D simulation in Fig. 3, the maximum density when the HII-region radius is 20 parsecs is 2.9 × 104 cm-3, the shell speed 4.4 km s-1, and the shell width 0.27 parsec. We can see that our code can follow the ionization front and the subsequent evolution of the dense shell with very high accuracy. We will therefore now turn our attention to more interesting 3D cases.
3. Forming pillars
The interstellar medium has a very complex structure with considerable inhomogeneities and high density fluctuations. The passage from 1D to 3D brings many new degrees of freedom. It allows us to study how the shell resulting from the collect and collapse scenario may be perturbed. The possibility to have localized density gradients has been extensively studied with the radiation-driven-implosion scenario (Mackey & Lim 2010; Bisbas et al. 2011; Gritschneder et al. 2009) and more recently within a turbulent media (Gritschneder et al. 2010). In this work, we first want to focus on more simple and schematic situations in which the physical processes at work can be identified and studied more easily. We will therefore study two idealized cases. First we will look at the interaction of the ionization front with a medium of constant density having a modulated interface. Then we will consider a flat interface with overdense clumps in the medium.
 |
Fig. 4 Three-dimensional snapshot of density at 500 ky of an ionization front propagation with a modulated interface. The UV flux at the top of the box is 109 photons per second per square centimetre, the box is 4 × 2 × 2 parsecs. The dense gas is initially at 500 H/cm3 at a temperature around 25 K (thermal equilibrium from Fig. 1). The (base width)/height ratios (w/h ratios hereafter) of the modulation is w/h = 0.9. |
 |
Fig. 5 Density cuts of four simulations of an ionization front propagation with a modulated interface. The UV flux at the top of the box is 109 photons per second per square centimetre, the box is 4 × 2 × 2 parsecs (half of the cut is shown). The dense gas is initially at 500 H/cm3 at a temperature around 25 K (thermal equilibrium from Fig. 1). The (base width)/height ratios of the modulations are respectively 2 for case (a), 1.4 for case (b), 0.9 for case (c) and 0.5 for case (d). |
 |
Fig. 6 Monitoring of the size (top) and the mass (bottom) of pillars identified in Fig. 5. The size is calculated by the difference of the average position of the ionization front and its position at the centre of the y-z plane (head of the initial structure). The mass is calculated in a box between the two vertical positions that are defined to calculate the size and whose width is defined by the width of the initial structure and is normalized by the mass in the initial modulation. |
3.1. From interface modulations to pillars
We first studied the interaction between the ionization front and an interface modulated by an axisymmetric sinus mode with constant heigh (amplitude of 0.5 parsec) and four different base widths (see Figs. 4 and 5). The size of the computational domain was adapted to the typical observed length scale of pillars, 4 × 2 × 2 pc3, at a resolution of 400 × 200 × 200 corresponding to spatial resolution of 1 × 10-2 pc. The boundary conditions were periodic in the directions perpendicular to the ionization propagation direction, imposed where the flux is incoming and free flow at the opposite. Ionization processes introduced in Sect. 2.2 were taken in the plan-parallel limit. The snapshots around 500 ky show that the narrower the initial structures, the longer the resulting pillars. With a (base width)/heigh ratio (w/h ratio hereafter) of 0.5 we obtained a structure whose size was almost multiplied by 3.5 in 500 ky. In addition to this, the initial structures have less and less mass with decreasing widths and still manage to form longer pillars, as can be seen in Fig. 5. High densities or high initial mass are not needed to form structures that are going to resist the ionization. The important factor here is how matter is distributed in space and interacts with the propagating shock. Very little and low-density material well distributed in space can result in a long pillar-like structure. We will call these structures pillars hereafter, but a detailed comparison with observations is needed to see whether these structures emerging from idealized scenarii are a good approximation of the reality or not.
To study the properties of the pillars, we monitor their sizes and masses in Fig. 6. The size gain identified previously is a continuous process in time at an almost constant speed which depends very strongly on the width/heigh ratio. Narrow initial modulation have a very fast growth while larger one grow slowly, if at all. The mass increase relative to the initial mass of the structure is almost the same in all simulations and does not seem to depend on the initial w/h ratio. It reaches a factor of 5–6 in 500 ky.
 |
Fig. 7 Mass profiles (top) and vertical velocity profiles (bottom) at three different times of the pillar in the w/h = 0.9 simulation. These profiles were obtained within the boxes defined in Fig. 6. |
Vertical profiles of the mass in the pillars (see Fig. 7) show that the mass gain identified in Fig. 6 is accumulated at the base. The mass of the head of the pillar slightly increases and then remains stable during the simulation while the central part connecting the head and the base is stretched and its mass decreases. The profiles of the vertical speed show that the bases of the pillars have a roughly constant speed and the size variations are caused by the vertical speed difference of the heads. The differences between the sizes of the pillars can be directly deduced from the velocity differences of the heads: a velocity difference of 0.5 km s-1 during 500 ky gives a spatial difference of 0.25 pc, which is approximatively the differences observed between the simulations with a width/heigh ratio of 2 and the one with a ratio of 1.4.
 |
Fig. 8 Zoom on the ionization of convex and concave zone in the w/h = 0.9 simulation between 22 and 132 ky. Arrows represent the velocity field projected in the x-y plane. |
 |
Fig. 9 Two-dimensional plot of the mass fraction at a given density and pressure for the w/h = 0.9 simulation at the end of the simulation (554 ky). Blue to black contours are increasing mass fraction contours (blue: 1E-6, green: 1E-5, yellow: 5E-5, orange: 1E-4, red: 5E-4, black: 2E-3). The dashed red line is the maximum density achieved in a plan-parallel 1D simulation : 4.8 × 104 cm3. The total mass at a density above this limit is around 10 solar masses. |
A closer look at the simulations (see Fig. 8) shows that the motions perpendicular to the propagation direction are shaping the structures. These motions are triggered by the initial curvature of the structure, two cases are distinguished, an initially convex zone and a initially concave zone. A shock front in a convex zone will trigger its collapse; this is the phenomenon that takes place in the radiation-driven-implosion scenario and here at the head of the initial structure. The curvature of the initial structure leads to lateral converging shocks that collide with themselves. However, the ionization of a concave zone is quite different, it will dig a hole in the medium, and the gas is pushed away lateraly. The velocity fields in Fig. 8 illustrate these phenomena; for an initially convex zone the velocities point inwards and lead to the collapse of the central structure, whereas in the initially concave zone at the base they point outwards and dig a hole in the media. These phenomena are at the origin of the size and mass increase. Indeed, the collapse of the structure takes more time if the structure is wide, therefore it will be accelerated longer, which explain the difference of the vertical speed of the pillar heads seen in Fig. 7. Additionally, the holes in each side of the pillar (see Fig. 8) gather the gas at the base of the pillar, which explains the mass increase in Fig. 7.
In addition to the mass increase there is an important density gain. The mass histogram in the pressure-density plane in Fig. 9 shows that the compression caused by the heating from UV radiation increases the pressure by one order of magnitude from the initial state, which is at a density of 500/cm3 and at a pressure of 10-12 erg/cm3. The gas is then distributed in two phases at equilibrium, hot-ionized in the green-dashed straight line and cold-dense-unionized in the blue dashed curve. The gas in transition between them is depicted with the blue contour. A 1D simulation of the collect-and-collapse process can increase the density by up to 5 × 104/cm3; this limit is drawn with the red dashed line in Fig. 9. The mass at the base of the pillar, caused by the holes from the initial concave parts and from the collapse of the lateral shocks, leads to a density enhancement of 1–2 orders of magnitude. Although the structures in our simulations are still slightly below their Jeans lengths, this process has a better chance to trigger star formation at the base of the pillars than the simple collect-and-collapse scenario.
3.2. From density modulations to pillars
Clouds have irregular shapes, but they also have unhomogeneities. Therefore, after this study of interface modulations we considered density modulations that we call clumps hereafter (with no reference to an observational definition). We define them as regions of constant overdensity. Figure 10 shows the different cases we studied. The three first cases are clumps in a homogeneous cold cloud, with a density contrast of 2, 3.5 and 5 respectively, and the last one corresponds to the radiation-driven-implosion scenario, where the clump is “isolated” in a hot low-density medium so that the shock forms directly in the structure. The density in the clump is the same as the one with a density contrast of 5. In all cases the clumps are at pressure equilibrium with the surrounding matter.
 |
Fig. 10 Density cuts of four simulations of an ionization front propagation on clumps (0.5 parsec in diameter). The UV flux at the top of the box is 109 photons per second per square centimetre, the box is 4 × 2 × 2 parsecs (half of the cut is shown, only the central parsec of the simulation box). The last simulation (case (d)) is an isolated spherical clump of constant density 1000 cm3, the three others are clumps in a homogeneous medium of density 500 cm3. The clumps have densities of 1000 for case (a), 1750 for case (b) and 2500 cm3 for case (d). |
In the isolated case the shock forms at the surface of the clump and the shell is therefore initially curved by the shape of the clump with a w/h ratio of 2. This roughly corresponds to the wider case studied in Sect. 3.1. Because the shock is curved, it will collapse on itself and form a pillar-like structure. This case was studied in detail by Mackey & Lim (2010); Gritschneder et al. (2009). However, with a widht/heigh ratio of 2 the structure is quite small and looks quite similar to the w/h = 2 case of the previous section. However, because it is isolated, the accumulation of mass process at the base identified in the previous section cannot take place.
In the three other cases, the shell is flat when it is formed, therefore the outcomes of the simulations are not as clear. When the clump is not sufficiently dense (first case nHclump/nHcloud = 2), it will not curve the shell enough to trigger lateral colliding shocks. Therefore there is no head in the final structure in this case, which is very small (i.e. comparable to the initial clump size). In the two other simulations (nHclump/nHcloud = 3.5 and 5) the clumps curve the shell enough to trigger the collision of vertical shocks, thereby forming an elongated pillar. This is very close to what we observed previously in interface modulations. Besides, we can identify a base for the pillar-structures in the final snapshots that is formed by lateral holes in the cloud and the associated accretion mass process discussed above.
The importance of the curvature effect can be emphasized by comparing the isolated case and the nHclump/nHcloud = 5 case. In both cases the density of the clump is the same, but when the shell is formed flat on a homogeneous medium, the dense clump will resist the shock to form an elongated modulation on the shock surface. In the isolated case, the shock is formed instantaneously curved on the structure with a w/h ratio of 2. Furthermore, contrary to the isolated case, the structures will grow in mass and size because of the connection with the cloud. These effects result in a final 0.5-parsec-long pillar for the isolated case, whereas the final structure in the nHclump/nHcloud = 5 case is 1.5 parsec long. The driving process to form a pillar is the ability of the matter distribution to first curve the shell and then to feed the base of the pillar by the hole mechanism identified in Sect. 3.1 (the holes are clearly visible in the final snapshots in Fig. 10).
The size evolution and the mass evolution of the pillars are comparable to the modulated-interface case. However, the evolution is not linear because of the initial conditions. Indeed, there is a first phase in which the ionization front is curved and stretched vertically around the clump when its propagation is slowed down by the overdensity. At this point (around 200 ky) the physical situation is comparable to the interface-modulated case, the ionization front is curved around a “hill”. It also explains why we chose to do a longer simulation for the density-modulated case, it allows us to compare both cases at a “physically equivalent” state at the end. When the lateral shocks collide around the hill, the pillar captures slightly more than the mass of the initial clump and its mass increase slows down. This phase occurs around 300 ky and can be clearly identified in Fig. 11. Then the mass increases because of the accumulation of matter at the base of the pillar. The process is less linear than in the interface-modulated case.
4. Observational signature
The two sections above present how pillars can be formed in a density- or interface- modulated region of the molecular cloud. These pillars are connected to the cloud, increasing in size and mass with time. However, these variations cannot be observed. A potentially observational signature to study is the structure of the line-of-sight velocity. We used the same method as Gritschneder et al. (2010). We defined a grid of squares of 0.05 × 0.05 pc2 along the pillar and binned the line-of-sight velocity in each square (see Figs. 12–14). We used the simulation with the densest clump to study the line-of-sight velocity structure, but the following results are generic. At t = 222 ky (Fig. 12), the lateral shocks can be clearly identified in the broad line spectrum. There are two components, a positive one coming towards us and a negative one going away. At this time the shell is curved around a hill, which is comparable to the situation we encountered in the interface-modulated scenario after a short time.
 |
Fig. 11 Monitoring of the size (top) and the mass (bottom) of pillars identified in Fig. 10. The size is calculated by the difference of the average position of the ionization front and its position at the centre of the y-z plane (head of the initial structure). The mass is calculated in a box between the two vertical positions that are defined to calculated the size and whose width is defined by the width of the initial structure and is normalized by the mass of the initial clump. |
 |
Fig. 12 nHclump/nHcloud = 5 simulation at t = 222 ky. Left: column density on a 0.4 × 0.4 × 0.4 pc3 box around the pillar structure in a face-on geometry. Right: mass-weighted histogram of the line-of-sight velocity in the same box (similar to optically-thin observational line spectra). Each spectrum is made on a square of 0.05 × 0.05 pc2 drawn on the column density map. The spectra are drawn between − 4 and 4 km s-1 in 80 bins (horizontal axis) and the mass between 10-4 and 1 solar mass (vertical axis in log scale). The lateral shocks can be clearly identified in the double wing spectra, which leads to a very broad line width. |
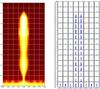 |
Fig. 13 nHclump/nHcloud = 5 simulation at t = 444 ky. Same plots as Fig. 12. The lateral shocks collided and cannot been identified anymore. |
At t = 444 ky (Fig. 13) the lateral shocks have collided, which results in a narrow line width for the histograms. The whole pillar is narrow and evacuates the pressure through radiative cooling and expansion to reach the equilibrium defined for the cold phase in Fig. 9. There are two dense parts in the pillar: the head in which the matter of the clump has been accumulated and the base at the point where the lateral shocks have closed. It will resist the ionization because it is dense enough and matter is starting to accumulate at the base.
 |
Fig. 14 nHclump/nHcloud = 5 simulation at t = 998 ky. Same plots as Fig. 12. The line width is very narrow compared to the snapshots at t = 222 ky. |
At t = 998 ky (Fig. 14) matter has accumulated at the base of the pillar based on the process that was identified in Fig. 8. The line-of-sight velocity histograms still have a narrow line width compared to Fig. 12. This phenomenon is not specific to clump simulations, the same analysis on the interface modulated simulation (aspect ratio of 0.9) in Figs. 15 and 16 shows similar results but at an earlier stage. The interface modulated simulation presents double-wing velocity spectra around t = 22.2 ky, whereas the clumpy simulation presents these spectra around t = 222 ky when the shock is curved around a hill. The double-wing structure of the velocity spectra is therefore a signature of the lateral shocks that are going to collide and a signature of the early stage of a forming pillar.
 |
Fig. 15 w/h = 0.9 simulation at t = 22.2 ky (first column in Fig. 8). The shock just formed on the modulation, the line width and the double-wing structure is comparable to Fig. 12. |
 |
Fig. 16 w/h = 0.9 simulation at t = 133.2 ky (third column in Fig. 8). The shock collided laterally and the line width is narrow as in Fig. 13. |
The previous analysis can be applied to the different simulations presented in this paper without noticable change to our conclusion. We also changed some physical conditions and parameters. We added a constant external gravitational field, included self-gravity, doubled the resolution without general changes in the morphology of the final structures. We also changed the flux to a higher value (from 109 to 5 × 109 photons/s/cm2) and the structures are similar, but evolve faster, as seen by Gritschneder et al. (2009). The shell speed cshell is proportional to 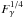 (see Eqs. (13) and (15)), therefore when the flux is multiplied by five the shell increases speed by 50%, and the whole simulation evolves faster by 50%. In all these situations, pillars form through the lateral collision of a curved shocked surface, and the double-wing spectrum is always visible before the shocks collide.
(see Eqs. (13) and (15)), therefore when the flux is multiplied by five the shell increases speed by 50%, and the whole simulation evolves faster by 50%. In all these situations, pillars form through the lateral collision of a curved shocked surface, and the double-wing spectrum is always visible before the shocks collide.
5. Conlusion and discussion
We have presented a new scenario for the formation of structures at the edge of HII regions and have shown that
-
i
A curved shock ahead of an ionization front can lead to a pillar if it is sufficiently curved to collide laterally with itself.
-
ii
This pocess is very efficient for forming stable growing pillars, and the narrower the initial structure, the more curved the front and the longer the pillar.
-
iii
Lateral gas flows can result in a density enhancement at the base of the pillars of 1–2 orders of magnitude compared to the-collect and-collapse scenario.
-
iv
When the shock is first formed flat, it can be curved by sufficiently dense clumps and leads to pillars. In isolated clumps (radiation-driven implosion) the shock is naturally curved by the form of the clump, but the resulting structure has a constant size and mass.
-
v
The double-wing line spectra of the line-of-sight velocity is a signature of the lateral collision of the shock, and hence is a signature of the early stage of a pillar formation. It can be used as an observational signature for this new scenario.
At the edge of HII regions the structure of the line-of-sight velocity can be investigated using radiotelescopes and suitable molecules that trace the dynamic to detect the double-wing spectra on gas hills and thus nascent pillars. If a gas overdensity is detected at the top of the hill (e.g. using Herschel data), the shock curvature could be attributed to the presence of an initial clump, if not to the curvature of an initial interface.
We generated curved shocks using either density or interface modulations on a parsec scale and in a very simplified situation. However, we expect that the physical processes discussed in this paper can also be applied to more realistic situations where the ionization front interacts with a turbulent interstellar medium. In this case the density fluctuations are much more complex, but the same mechanism should be at work to describe pillar formation. These turbulent situations will be studied in a forthcoming paper where we will study the interplay between shock curvature and turbulence to see its impact on star-formation rates at the edge of HII regions.
References
- Andersen, M., Knude, J., Reipurth, B., et al. 2004, A&A, 414, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arthur, S. J., Henney, W. J., Mellema, G., De Colle, F., & Vázquez-Semadeni, E. 2011, MNRAS, 414, 1747 [NASA ADS] [CrossRef] [Google Scholar]
- Audit, E., & Hennebelle, P. 2005, A&A, 433, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bertoldi, F. 1989, ApJ, 346, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Bisbas, T. G., Wünsch, R., Whitworth, A. P., Hubber, D. A., & Walch, S. 2011, ApJ, 736, 142 [Google Scholar]
- Black, J. H. 1981, MNRAS, 197, 553 [NASA ADS] [Google Scholar]
- Bowler, B. P., Waller, W. H., Megeath, S. T., Patten, B. M., & Tamura, M. 2009, AJ, 137, 3685 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Theys, J. C. 1975, ApJ, 195, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., & Bonnell, I. 2011, MNRAS, 414, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Bonnell, I. A., & Whitworth, A. P. 2007, MNRAS, 375, 1291 [NASA ADS] [CrossRef] [Google Scholar]
- Deharveng, L., Schuller, F., Anderson, L. D., et al. 2010, A&A, 523, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G., & Lada, C. J. 1977, ApJ, 214, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Kimura, T., & Tosa, M. 1995, ApJ, 451, 675 [NASA ADS] [CrossRef] [Google Scholar]
- González, M., Audit, E., & Huynh, P. 2007, A&A, 464, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gritschneder, M., Naab, T., Burkert, A., et al. 2009, MNRAS, 393, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Gritschneder, M., Burkert, A., Naab, T., & Walch, S. 2010, ApJ, 723, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, Z., Yao, Y., Yang, J., et al. 2002, ApJ, 577, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Kessel-Deynet, O., & Burkert, A. 2003, MNRAS, 338, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Kimura, T., & Tosa, M. 1990, MNRAS, 245, 365 [NASA ADS] [Google Scholar]
- Krumholz, M. R., Stone, J. M., & Gardiner, T. A. 2007, ApJ, 671, 518 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., & Lazareff, B. 1994, A&A, 289, 559 [NASA ADS] [Google Scholar]
- Lefloch, B., Cernicharo, J., Rodriguez, L. F., et al. 2002, ApJ, 581, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Lora, V., Raga, A. C., & Esquivel, A. 2009, A&A, 503, 477 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, J., & Lim, A. J. 2010, MNRAS, 403, 714 [NASA ADS] [CrossRef] [Google Scholar]
- Mellema, G., Arthur, S. J., Henney, W. J., Iliev, I. T., & Shapiro, P. R. 2006, ApJ, 647, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., & Bate, M. R. 2009, MNRAS, 398, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Purcell, C. R., Minier, V., Longmore, S. N., et al. 2009, A&A, 504, 139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reach, W. T., Rho, J., Young, E., et al. 2004, ApJ, 154, 385 [Google Scholar]
- Schneider, N., Motte, F., Bontemps, S., et al. 2010, A&A, 518, L83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smith, N., Egan, M. P., Carey, S., et al. 2000, ApJ, 532, L145 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium (Wiley-VCH) [Google Scholar]
- Strömgren, B. 1939, ApJ, 89, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Maíz-Apellániz, J., & Barbá, R. H. 2002, AJ, 124, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, R. J. R., Ward-Thompson, D., & Whitworth, A. P. 2001, MNRAS, 327, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Thermodynamic equilibrium in the pressure-density plane for the highly and weakly ionized phases. |
| In the text | |
 |
Fig. 2 Expansion of an HII region in a homogenous medium (nH = 500 cm-3, T ≈ 25 K, S∗ = 1050γionizing/s). Case 1 is a simulation where the gas temperature is instantaneously at 7736 K if the ionization fraction is exceeds 0.5. Case 2 takes into account the time evolution of the temperature given by Eqs. (9) and (10). The analytic solution is computed from Eq. (12) if the thermal equilibrium is reached instantaneously. The Strömgren radius is given by Eq. (11). |
| In the text | |
 |
Fig. 3 Density (top) and temperature (bottom) profiles of the expansion of an HII region in a homogenous medium (nH = 500 cm-3, T ≈ 25 K, S∗ = 1050γionizing/s). Solid lines correspond to an adiabatic cold phase and dashed lines to a cooled cold phase with the cooling described in Sect. 2.3 |
| In the text | |
 |
Fig. 4 Three-dimensional snapshot of density at 500 ky of an ionization front propagation with a modulated interface. The UV flux at the top of the box is 109 photons per second per square centimetre, the box is 4 × 2 × 2 parsecs. The dense gas is initially at 500 H/cm3 at a temperature around 25 K (thermal equilibrium from Fig. 1). The (base width)/height ratios (w/h ratios hereafter) of the modulation is w/h = 0.9. |
| In the text | |
 |
Fig. 5 Density cuts of four simulations of an ionization front propagation with a modulated interface. The UV flux at the top of the box is 109 photons per second per square centimetre, the box is 4 × 2 × 2 parsecs (half of the cut is shown). The dense gas is initially at 500 H/cm3 at a temperature around 25 K (thermal equilibrium from Fig. 1). The (base width)/height ratios of the modulations are respectively 2 for case (a), 1.4 for case (b), 0.9 for case (c) and 0.5 for case (d). |
| In the text | |
 |
Fig. 6 Monitoring of the size (top) and the mass (bottom) of pillars identified in Fig. 5. The size is calculated by the difference of the average position of the ionization front and its position at the centre of the y-z plane (head of the initial structure). The mass is calculated in a box between the two vertical positions that are defined to calculate the size and whose width is defined by the width of the initial structure and is normalized by the mass in the initial modulation. |
| In the text | |
 |
Fig. 7 Mass profiles (top) and vertical velocity profiles (bottom) at three different times of the pillar in the w/h = 0.9 simulation. These profiles were obtained within the boxes defined in Fig. 6. |
| In the text | |
 |
Fig. 8 Zoom on the ionization of convex and concave zone in the w/h = 0.9 simulation between 22 and 132 ky. Arrows represent the velocity field projected in the x-y plane. |
| In the text | |
 |
Fig. 9 Two-dimensional plot of the mass fraction at a given density and pressure for the w/h = 0.9 simulation at the end of the simulation (554 ky). Blue to black contours are increasing mass fraction contours (blue: 1E-6, green: 1E-5, yellow: 5E-5, orange: 1E-4, red: 5E-4, black: 2E-3). The dashed red line is the maximum density achieved in a plan-parallel 1D simulation : 4.8 × 104 cm3. The total mass at a density above this limit is around 10 solar masses. |
| In the text | |
 |
Fig. 10 Density cuts of four simulations of an ionization front propagation on clumps (0.5 parsec in diameter). The UV flux at the top of the box is 109 photons per second per square centimetre, the box is 4 × 2 × 2 parsecs (half of the cut is shown, only the central parsec of the simulation box). The last simulation (case (d)) is an isolated spherical clump of constant density 1000 cm3, the three others are clumps in a homogeneous medium of density 500 cm3. The clumps have densities of 1000 for case (a), 1750 for case (b) and 2500 cm3 for case (d). |
| In the text | |
 |
Fig. 11 Monitoring of the size (top) and the mass (bottom) of pillars identified in Fig. 10. The size is calculated by the difference of the average position of the ionization front and its position at the centre of the y-z plane (head of the initial structure). The mass is calculated in a box between the two vertical positions that are defined to calculated the size and whose width is defined by the width of the initial structure and is normalized by the mass of the initial clump. |
| In the text | |
 |
Fig. 12 nHclump/nHcloud = 5 simulation at t = 222 ky. Left: column density on a 0.4 × 0.4 × 0.4 pc3 box around the pillar structure in a face-on geometry. Right: mass-weighted histogram of the line-of-sight velocity in the same box (similar to optically-thin observational line spectra). Each spectrum is made on a square of 0.05 × 0.05 pc2 drawn on the column density map. The spectra are drawn between − 4 and 4 km s-1 in 80 bins (horizontal axis) and the mass between 10-4 and 1 solar mass (vertical axis in log scale). The lateral shocks can be clearly identified in the double wing spectra, which leads to a very broad line width. |
| In the text | |
 |
Fig. 13 nHclump/nHcloud = 5 simulation at t = 444 ky. Same plots as Fig. 12. The lateral shocks collided and cannot been identified anymore. |
| In the text | |
 |
Fig. 14 nHclump/nHcloud = 5 simulation at t = 998 ky. Same plots as Fig. 12. The line width is very narrow compared to the snapshots at t = 222 ky. |
| In the text | |
 |
Fig. 15 w/h = 0.9 simulation at t = 22.2 ky (first column in Fig. 8). The shock just formed on the modulation, the line width and the double-wing structure is comparable to Fig. 12. |
| In the text | |
 |
Fig. 16 w/h = 0.9 simulation at t = 133.2 ky (third column in Fig. 8). The shock collided laterally and the line width is narrow as in Fig. 13. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


