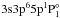| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 11 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201117758 | |
| Published online | 01 February 2012 | |
Extensive spectroscopic data for multiply ionized scandium: Sc III to Sc XXI⋆
1
CNRS, UMR 5574, Centre de Recherche Astrophysique de Lyon,
69364
Lyon
France
2
Université de Lyon, 69003 France; Université Lyon I, Observatoire
de Lyon, 69230
Saint-Genis-Laval,
France
e-mail: gmassacr@ens-lyon.fr
3
Université de Lyon, 69003
France ; Ecole Normale Supérieure de Lyon,
69007
Lyon,
France
e-mail: artru@ens-lyon.fr
Received: 24 July 2011
Accepted: 7 December 2011
Context. Spectroscopic data for scandium is sparse, while an extensive set is needed to introduce this element into stellar opacity calculations and, more importantly, into stellar models dealing with radiative diffusion.
Aims. Our goal is to provide extensive energy levels and radiative transitions data for nineteen ionization stages of scandium relevant to stellar interiors, namely from Sc iii to Sc xxi.
Methods. We used the FAC code. This code provides ab initio theoretical values for energy levels in jj-coupling and oscillator strengths of all permitted transitions. Detailed correspondences are established with compiled data from the National Institute of Standards and Technology (NIST) database, to locate as much as possible the observed levels and lines at their experimental values and to estimate the quality of our data. Comparison were also made with the spectroscopic data delivered by Kurucz.
Results. The theoretical data retained in tables include 21 842 levels and more than two millions transtions. By comparison, the NIST compilation gives a total of 820 levels and 677 gf-values. The good agreement obtained when comparing the new data with those of the NIST compilation demonstrates their quality. This work on scandium shows that the FAC code is efficient in providing spectrocopic data that are unavailable from laboratory analyses but necessary for accurate simulations of stellar plasmas.
Key words: stars: abundances / stars: chemically peculiar / atomic data / opacity
Full Tables 4–6 and extensive line lists for each ion are only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/538/A52
© ESO, 2012
1. Introduction
Atomic and spectroscopic data are an essential and basic ingredient of studies in a wide range of research fields including astrophysics. In particular, stellar structure and evolution studies depend critically on these data. Significant theoretical and experimental efforts continuously aim to provide data of high accuracy, although there is also a need to expand the extent of data, as much-needed data are often absent from databanks. Though much progress has been made in terms of computing power, a compromise is still necessary between high accuracy, which is time consuming even for a few levels or transitions of one given ion, and completeness.
This work is motivated by advances in the description of the radiative diffusion in stars, owing in particular to this increasing amount of available atomic data. The importance of atomic inputs in obtaining correct opacities is widely recognized, but stellar models including radiative diffusion, initially aimed at understanding chemically peculiar stars, depend even more on the quality and completeness of these atomic input data. The data currently used are taken from the Opacity Project (Seaton et al. 1992, 1994), or sometimes provided by OPAL (Rogers & Iglesias 1992). In an attempt to quantify whether abundance anomalies in Am stars originate from just below the superficial hydrogen convection zone or from below a (possible) deeper iron one, LeBlanc & Alecian (2008) highlighted the key role of scandium and calcium. However, as pointed out by these authors, the available atomic data for scandium are quite sparse, or even absent from atomic databanks. A far more complete set is required to assess the validity of their conclusions.
In this paper, we present the results of a comprehensive computation of energy levels and transition data for nineteen ions of scandium, namely Sc iii to Sc xix, utilizing the Flexible Atomic Code (Gu 2003, 2008). Several thousands of fine-structure levels and millions of transitions have been computed, many of which have been made available electronically in the form of tables. Much of this effort has actually been made to assess the quality of the delivered data. The data itself was validated by means of an exhaustive comparison of our theoretical results with all available experimental data from the National Institute for Standards and Technology (NIST), which attests to the accuracy of the present work. This also allows us to assign exact wavelength values to the observed lines.
This paper is organized as follows. Section 2 explains our strategy to construct the atomic structure of each ion and select configurations. The comparison with experimental data and discussion of the accuracy of our results is performed in Sect. 3. Section 4 describes the final selected data and the content and organization of the delivered tables, and our Conclusions are given in Sect. 5.
2. Procedure for theoretical calculations
Our aim in the present work is to build a representation of the atomic structure and spectrum of scandium that is as complete as possible in view of astrophysical applications. We intend to deliver data for all energy levels lying below the first ionization threshold of a given ion, except for the principal Rydberg series, which is computed up to the principal quantum number n = 10. This is in contrast to usual atomic structure computations, which concentrate on a few configurations and their transitions. Even for a not-too-heavy element such as scandium, our procedure generates and processes thousands of levels and millions of transitions in a sensible and controlled way.
The Flexible Atomic Code (FAC) is a relativistic configuration interaction program based on jj-coupling that allows these large-scale computations with the inclusion of up to thousands of fine-structure energy levels for each ion (Gu 2003, 2008). Though quite recent, FAC has become of widespread use in various research fields, and its precision has been widely tested by experiments (for instance: Aggarwal et al. 2010; Aggarwal et al. 2011; Clementson et al. 2010; Hahn et al. 2010; Wei et al. 2010). The versatility and speed of FAC allowed us by running numerous test cases to systematically construct a coherent and homogeneous set of data for nineteen ions of scandium.
Our strategy was to reconstruct stage by stage recombined ions starting from H-like Sc xxi down to Sc iii. Once the atomic structure of an ion is settled an electron is added to its low lying configurations so as to determine whether the levels of the recombined ion fall below or above the ionization limit. All configurations leading to some levels below the ionization limit are retained. Supplemented with some of the above-threshold configurations, they are used in a single run including configuration interactions. Several test minimizations are performed using the ground configuration, as well as some excited ones to obtain the losest match to experimental data (see below). Once the energy level structure is set, radiative data for bound-bound transitions are computed. Only electric dipole (E1) transitions are considered.
Table 1 describes the configuration set involved in our representation of each scandium ion. The configurations that are included in the computation of electronic states but lead to energy levels above the limit are not mentioned. We note that some electronic states are highly mixed with no clear prominent contribution from a single given configuration. In addition to its Rydberg series, an ion may require several dozens of configurations to be described completely. Some of them have several open subshells and may generate a broad range of fine structure levels: for instance, in Sc vi the configuration 3s3p33d2 consists of 202 levels with a total degeneracy of 1390; those levels are spread over more than 47 eV of which 34 eV lie below the ionization limit. These configurations are loosely connected to ground states through one electron jump transitions and are consequently absent from experimental databases. They do however matter because of the configuration interaction. Owing to their statistical weight, one may also anticipate some influence in the calculation of population equilibrium.
List of configurations of Sc ions generating fine-structure levels below the first ionization threshold.
3. Comparison with available experimental data
To assess the quality of our computations, we performed systematic comparisons with the reference data obtained from the National Institute of Standards and Technology website1 (Ralchenko et al. 2010). The NIST atomic spectra database provides a compilation of (mainly) experimental levels and wavelengths for all scandium ions. Reference papers describing this compilation are Sugar & Corliss (1980) and Kaufman & Sugar (1988). A limited number of oscillator strength values with given accuracy can also be found. They were supplemented with the gf-values computed by Kurucz for Sc iii to Sc ix, which are based on the same energy levels as in the NIST compilation. Papers that have adressed scandium include Wilson et al. (2000) (Sc v) and Sossah et al. (2008) (Sc iii and Sc iv). We first examine the energy structure.
3.1. Correspondence between FAC and NIST levels
Number of levels, ground states, and ionization energies (in eV) for the nineteen ions of scandium according to NIST and our calculations (FAC).
Our results for the electronic ground states given in Table 2 agree with those of NIST in terms of the configuration and the total angular momentum. We took the term assignments 2S+1L from NIST because FAC uses jj-coupling. The ionization energies for the nineteen ions are compared in this same table. The difference from FAC amounts to a few tenths of percent for Sc xxi to Sc v reaching a maximum of 0.5% for the closed shell ion Sc xii, an exception being Sc vii (with 1.2%). The relative difference is 1.7% for the other closed shell ion Sc iv, and for the least ionized Sc iii it reaches 3.9%. We note that the NIST ionization energy uncertainties derived by Sugar & Corliss (1980) amount to a few units in the last digit of the quoted value, and are often of the order of the differences with FAC. Our results compare favourably with the systematic calculations of Rodrigues et al. (2004), which are reported in the last columns of Table 2, in particular for Sc xviii and the lower ionization stages. However, in Rodrigues et al. (2004) almost all the periodic table was investigated, precluding any peculiar improvements, while we performed some adjustments in choosing the levels to minimize on.
 |
Fig. 1 Energy levels below the ionization threshold for Sc ix, calculated by FAC. Abscissa is the total angular momentum degeneracy 2J + 1 multiplied by + 1/−1 for even/odd levels, respectively. Black dots represent the levels from the NIST database. The lowest levels configurations are named according to their parent core: nl means 3s2nl (blue); nl′ means 3s3pnl (green); nl′′ means 3p2nl (magenta). First ionization thresholds (levels of Sc x) are also shown. |
The NIST database contains 820 levels2. They are distributed among ions according to the second column of Table 2 with 30% of them being in Sc v and Sc iv. Our large-scale computation leads to much more levels (exactly 21 842 below the first thresholds, for a total of 28 928), with the largest number of levels corresponding to ions with nearly half-filled 2p or 3p sub-shells in their ground state (third column). The reason for such a large number is somewhat different for the two cases, as can be seen by comparing the structure of Sc xv and Sc vii in Table 1. In addition to the Rydberg series converging to the first threshold, the most ionized Sc xv has a series for which the external electron extends to the n = 9 shell. In Sc vii, the external electron remains below n = 6 but many complex configurations are permitted by exciting electrons from 3s or 3p to 3d.
A principal objective of this work was to map the 820 NIST levels to FAC ones so as to compare the energy spectra and evaluate the accuracy of the calculated energies. The natural approach is to match their configuration designation and their exact symmetries – total momentum J and parity. However, these lone parameters do not ensure uniqueness. The classification in NIST utilizes LS-coupling, which is meaningful for most of the levels of scandium. FAC uses jj-coupling, thus the term designation, particularly for the parent core of a configuration, is not of direct help. We plotted in Fig. 1 the Sc ix levels obtained from our calculations and from NIST. This case, which is not particularly difficult (26 levels in NIST), will be used as an illustration in the following general discussion.
As long as a given configuration is complete in NIST, there is no ambiguity in assigning the levels. Indeed the results of FAC confidently reproduce fine structure splitting, such that a global energy shift of the configuration suffices. This situation occurs generally for the ground configurations and the first few excited ones, obviously the most commonly observed experimentally, such as 3s23p, 3s3p2, and 3s23d in Sc ix (Fig. 1). It also occurs for some high lying configurations, which are perhaps embedded in a dense energy pattern, but with a simple structure (such as 3s24s, 4d, 4f, 5s, 5d, 5f in Sc ix; note that 4p and 5p are missing in NIST).
For some configurations that are incomplete in NIST, the correspondence is obvious thanks again to the fidelity of FAC in reproducing the fine-structure energy pattern. Examples are the three levels out of seven of the configuration 3s3p4s (labelled 4s’ in Fig. 1). In some complex cases, we used the original literature. Figure 2 shows the example of the 2s22p33d configuration in Sc xiv with its 38 fine structure levels (FAC) and 18 experimental levels (NIST, black dots). For the J = 2 and J = 3 symmetries, there is some ambiguity in assigning the third from the top NIST levels. This ambiguity is removed when referring to the data in Bromage & Fawcett (1977c, red diamonds). We note the quality of the theoretical FAC results: when shifted down by 0.55 eV (one thousandth of the excitation energy), the standard deviation from the experimental data (Bromage & Fawcett 1977c) is 0.32 eV, which should be compared with a spread of 37 eV for the whole configuration and a distance of 0.48 eV for the closest levels.
 |
Fig. 2 Comparison of the energy levels of the 2s22p33d in Sc xiv configuration. Blue: as calculated by FAC; black dots: from the NIST database; red diamonds: from the original paper Bromage & Fawcett (1977c). Also shown (green, triangles) are the close levels from the 2s2p43p configuration. |
When several configurations lead to levels of the same symmetries in a narrow energy range, the situation becomes more difficult as one might expect for a configuration interaction. For highly ionized ions, this generally involves simple configurations and the correspondence is often evident. For the least ionized ions (14 to 18 electrons), the rich configuration 3s23pn−13d often interacts with the 3s23pn−14s or 3s3pn+1 configurations. These configurations are connected through one-electron jump to the ground state 3s23pn, thus they have been partially observed and recorded in NIST. The mixing of 3s23pn−1 4p with 3s3pn3d and 3s23pn−23d2 is still more intricate, but this group of levels is only observed in Sc v and Sc iv. We had to carefully check these levels when assessing the assignement. In a few cases3, we had to use the transition data to discriminate between several candidates.
We were finally able to establish a correspondence for all the levels contained in the NIST database. For most of them, the NIST designation was confirmed. A very few states are highly mixed and the FAC dominant contribution appears to differ from the NIST one. This is unimportant in as much as the level energies and the transition probabilities are correctly reproduced. More details and comments concerning the electronic structure of individual scandium ions may be found in the appendix.
3.2. Comparison of theoretical and experimental energies and adjustment
The differences in the level excitation energies between NIST and our results are plotted in Fig. 3 as a function of the NIST excitation energies. Differences in ionization energies are also drawn. The accuracy4 reported by NIST for its energy values is most often below 0.1 eV and at most 1 eV for a very few levels, hence irrelevant in this figure. Though these panels show all NIST levels, they contain fewer than 4% of the FAC levels (see last line of Table 2). The NIST databank is complete only for the lowest energy range of an ion electronic structure. Most of the excited states are embedded in a background of levels that are missing from the database (Fig. 1 is a clear illustration for the Sc ix case).
The vertical scale in Fig. 3 is the same in all the panels, while the abscissa is roughly adjusted to the ionization energies. As expected, the global trend is a decrease in accuracy as one goes from the highly ionized ions to the near-to-neutral ones, when the nucleus attraction no longer dominates electron-electron interactions. Our excitation energies are usually above NIST ones with the exception of Sc xx, Sc xii, Sc xi, and Sc iii. These ions have a simple ground state, either with closed shells (1s2 and 2s22p6) or one electron above closed shells (3s and 3s23p63d). For these ions and some others (notably Sc iv), the ionization energy difference is consistent with an extrapolation from excited levels. This is certainly not the case for Sc xvii, Sc xv, and Sc vii. The NIST ionization energies are extrapolated from bound level series, which stop far from the limit for these ions. Moreover, these ions have several ionization thresholds close to their ionization limit. As the FAC series are consistent by construction (the first series converges to the limit), it is tempting to attribute the inconsistency in ionization energy differences to a difficulty of NIST in determining the correct limit. The accuracy for the ionization potentials given in Kaufman & Sugar (1988) is less than 2000 cm-1 (0.2 eV) for Sc iii to Sc xii, and increases from 12 000 cm-1 to 20 000 cm-1 (from 1.5 eV to 2.5 eV) for ions Sc xiii to Sc xviii. This makes the differences in ionization energies between FAC and NIST much less critical for this last series of ions, and in particular for Sc xvii and Sc xv.
 |
Fig. 3 Excitation energy differences (in eV) between our results and NIST data for all the levels of the nineteen scandium ions in the NIST database, as a function of the NIST excitation energy (in eV). The differences between ionization energies are also plotted as a larger symbol with a drop line to the zero axis and the ion name nearby. |
Excitation energies assume that the ground state is the reference level. An error in the ground state absolute energy would result in a shift in all the excitation energies. To judge the quality of our results, we computed the variance, i.e. the rms of the deviation between the differences in excitation energies and their mean value (when given in relative values, the variance is relative to the ionization energy). This quantifies the extent to which the FAC and NIST energy spectra can be adjusted by shifting one of them relative to the other as a block.
For the H-like ion Sc xxi, the agreement is excellent with a variance of 12 meV (100 cm-1). This is almost entirely due to the ground state. When the latter is raised by 0.063 eV, the variance becomes 1.8 meV (14 cm-1). For comparison, the 2s1/2−2p1/2 splitting is 2200. cm-1. We note that NIST energies are also theoretical for this ion. The variance is smaller than 0.15% from Sc xx to Sc x. Systematic discrepancies appear for the lowest levels of L-shell ions Sc xix to Sc xiii with ground configurations of the type 1s22lq, q = 1 to 7. These levels (below 200 eV in the left column of Fig. 1) include the excitation of one or two of the electrons 2s to 2p. They are systematically calculated to be too high by a few eV, the difference increasing with energy. The FAC code uses a single adjusted potential to generate one electron wavefunctions, which might explain the difficulty in representing at the same time the ground configuration and the core-excited ones. Though it is possible to slightly improve the accuracy by playing with the configurations to be minimized, obtaining results accurate to a few tenths of eV would require far more sophisticated approaches. For instance, Gu (2005) supplemented configuration interaction calculations with a many-body perturbation theory (MBPT) to perform a systematic study of the previous levels in L-shell ions.
The variance is smaller than 0.5% for Sc ix to Sc vii, smaller than 1% for Sc vi to Sc iv, and 1.5% for Sc iii. The calculation encounters some difficulties in precisely determining the level energies of Sc vii to Sc iv of medium ionization charge and with the ground states of the form 3s23pq, q = 3 to 6. In addition to the aforementioned reasons, these cases contain a number of large configuration interactions, as can be verified from the output of the code. For example, in Sc vi the J = 1 levels of the even configurations 3s3p43d and 3s23p23d2 are mixed with maximum leading percentages lower than 40%.
Number of transitions in scandium spectra (first column) available from three sources: NIST database, Kurucz linelist (CD-ROM No. 23) and present calculations with FAC.
These comparisons with experimental data show that as a whole our results are of medium accuracy when compared to high precision atomic studies found in the literature (see for instance Hibbert et al. 2010, and the associated Special Issue on High precision atomic physics). The latter are however tailored to the cases under scrutiny and generally address a very limited number of levels. Our goal is in contrast to produce a large-scale database for scandium atomic structure that includes high lying levels as well and remains accurate, homogeneous, and consistent. The previous comparison with experimental data has shown that our results fullfill this aim.
To take advantage of our mapping between calculated results and NIST data, we performed some a posteriori adjustments to the FAC level energies. We found that it was unsatisfactory to simply set the excitation energies to the NIST values for all the states with a correspondence in NIST. As shown in Figs. 1−3, the corrections are minor for individual levels. However, for many excited configurations that are incomplete in NIST and surrounded with numerous predicted levels, it would be misleading to displace only a few levels. We adjusted to NIST values the levels of the lowest configurations that are complete, except for when the corresponding energy range includes other levels without any correspondence in NIST. Levels of higher energy were displaced as a few blocks (usually one or two) with an energy shift adjusted to compensate for the mean difference between the FAC and NIST energies. Some lower isolated but incomplete configurations were also individually adjusted as a block. Though somewhat arbitrary, this procedure preserves the FAC level splittings within incomplete configurations and allows us to obtain realistic patterns of predicted lines in individual multiplets. More details for each ion are given in the appendix. In any case, the data we deliver in the electronic tables allow one to go back to the original calculated values. Ionization energies were also adjusted for consistency.
3.3. Comparison of theoretical and experimental oscillator strengths
We used FAC to calculate in a second step the electric dipole transition data for the nineteen ionization stages. The FAC capabilities allow us to work in the complete configuration spaces described in Sect. 2. From a total number of transitions of around six million for all the ions, three and a half connect the levels below the limits. The ions Sc xv and Sc vii have the richest spectra, which reflects their large number of levels (see Table 2). The ion Sc vii has eight hundred times more transitions than the ions with a closed core, most of them between high levels. A census of the lines according to various selection criteria is given in the last four columns of Table 3. With a threshold of 10-4 for the weighted oscillator strength gf, the number of lines is divided by two (Col. 7). After increasing the threshold to 10-3, the number is further reduced by half (Col. 8). As the weighted transition probability gA scales as gf multiplied by the square of the transition energy, applying thresholds using gA put transitions connecting high levels at a disavantage. Retaining lines with a transition probability smaller by five orders than the strongest one, one gets fewer transitions than with gf > 10-3 (Col. 9). A Bolztmann factor can also decrease the weight of high levels. With a factor mimicking a thermal population at a temperature equal to one fifth of the ionization potential, one third of the transitions are retained than with the same threshold (compare Cols. 10 and 7).
As all the levels in NIST were identified within our level list, we were able to test the reliability of our results by comparing our transition data with all5 the NIST transitions. The second to fifth columns in Table 3 describe the distribution of the transitions among ions in the NIST database, according to whether they are given with an oscillator strength value or not, and whether they are experimentally observed or deduced by Ritz predictions from two observed levels. The 677 transitions with gf values represent 35% of a total of 1930. A little more than half of them are observed. The ions Sc v and Sc iv contain 45% of the transitions, but only 4% of those have gf values. Among the latter, some 17% belong to Sc xi, and most of them belong to the higher ionization stages with the exception of Sc iii (14%). This is likely due to their electronic structure being easier to analyse. Both Sc xxi and Sc vi have no oscillator strength in NIST.
 |
Fig. 4 Scandium weighted oscillator strengths gf for the 677 transitions in the NIST database as a function of our calculated values. Filled and open symbols refer, respectively, to transitions that are observed, or not observed and predicted from two observed levels. NIST has no oscillator strength for Sc xxi and Sc vi. The two grey lines delineate the values gfNIST/gfFAC = 2 or 1/2. |
In Fig. 4, we compare the oscillator strengths given by NIST with our results for all the studied ions. Observed transitions are marked as filled symbols, while open symbols denote the predicted Ritz transitions. The two lines delineate the limit of the range 0.5 < gfNIST/gfFAC < 2. Most of the 677 transitions definitely fall between these lines, in particular the numerous transitions of Sc xi and Sc iii. In view of the number of lines involved, this constitutes a reassuring indication of reliability. We emphasize that the connection between the NIST levels and our levels was based on symmetry and configuration characteristics, and used transition data for only a few levels (see footnote 3). Two transitions show divergent gf values in Sc xviii (upper left panel). We are confident that this is an error in NIST as those two lines imply a two-electron jump (see Appendix). In addition to the data for Sc xxi and Sc vi that have no oscillator strengths with which to compare, Sc iv is in desperately short supply of test data (lower right panel).
 |
Fig. 5 Scandium weighted oscillator strengths gf for the 1840 transitions in the Kurucz linelist (excluding Sc v) as a function of our calculated values. Large symbols refer to the transitions that are also common to NIST. |
The Kurucz linelist6 for spectra Sc ix to Sc iii provides a set of gf-values that are ten times larger than NIST (see sixth column in Table 3). Kurucz data, which is widely used in the stellar community, was the largest available source of data for scandium. They are based on the same set of levels as in NIST, hence the NIST wavelengths are reproduced in the Kurucz linelist. The Kurucz oscillator strengths are either duplicated from NIST, or independently computed. We excluded the Kurucz data for Sc v, which appeared obsolete (see Appendix). Figure 5 compares our calculated oscillator strengths with Kurucz ones. Any disagreements appear significantly larger than in Fig. 4, depending on the ion. For Sc viii, Sc vi, and most of the lines in Sc iii, the comparison is satisfactory. For the ions Sc ix, Sc vii, and Sc iv, there are large discrepancies. To trace the origin of these discrepancies, we plotted in the figure as bigger symbols the transitions that have a gf value in NIST. From Fig. 4, we know that our values match NIST ones. It appears that Kurucz miscalculated the gf value of a number of lines of Sc ix and Sc vii (upper panels). The problem seems linked to the quadruplet system in Sc ix and an inverted identification of some levels in Sc vii (see Appendix). In the case of Sc iv (lower left panel), it is difficult to draw any strong conclusion as only 4 transitions have gf values in NIST. For Sc iii, our calculations clearly match the 97 gf values for transitions shared with NIST and we are confident in our results.
Excerpt of the table of lines restricted to gf > 10-3 (see text for explanations).
Excerpt for the level list table (see text for explanations).
These comparisons utilized the transition data that we generated with FAC. These data have also been corrected to take into account the adjustments performed on the level energies as explained in Sect. 3.2. Wavelengths, oscillator strengths, and transition probabilities were scaled according to their energy dependences7. Owing to the quality of the calculated level energies and our procedure for the energy corrections, modifications to the radiative data are minor.
4. Description of the data tables
Our results regarding atomic structure and transition data for the nineteen ions Sc iii to Sc xxi are available at CDS in the form of electronic tables. The first table gives a wavelength-ordered list of lines for successive spectra from Sc iii to Sc xxi. Only transitions with weighted oscillator strength gf > 10-3 are listed. Our data refers to the corrected values that we adopted. The total number of transitions is slightly above one million (see eighth column in Table 3). The format is similar to the Kurucz data in order to allow a easy implementation into astrophyical codes. An except of the electronic table is given is Table 4. For each transition: Col. 1 gives the wavelength (in nm unit, all in vacuum); Col. 2 the weighted oscillator strength; Col. 3 the identification of the spectrum, that is the decimal code (nuclear and ionic charge) and spectroscopic notation; Cols. 3 to 6 the energy8 (in cm-1) and the total angular momentum J for successively the lower and upper levels; and Cols. 7 and 8, the electronic subshell nl of the outer electron for the lower and upper state of the transition. Additional data in the following columns are given to help the comparison with the experimental data compiled in the NIST database. For transitions between two levels that both correspond to an experimental one, the related NIST data are added: wavelength (Col. 11), log (gf) if present (Col. 12), and level energies (in cm-1, Cols. 13 and 14). These energies are given with their number of digits as found in NIST. A tag in Col. 10 characterizes the data. The label “No” or “Nr” indicates that the NIST wavelength is either observed or deduced from the Ritz combination. The label “P” indicates a predicted wavelength from two experimental levels, without any corresponding line in NIST, and the label “gf” is added when the gf value is given in NIST.
A second table gives an energy-ordered list of all levels from Sc xxi to Sc iii. The correspondence with NIST levels is also given, when it exists, as well as data allowing to go back to our original results. An excerpt is given in Table 5. Column 1 is the level index that will be used in the extended transition file. Column 2 is the adopted level energy (in cm-1), and Col. 3 is the degeneracy 2J + 1 multiplied by −1 for odd levels. The leading configuration of the level is given in Col. 4. Column 5 gives the difference between the adopted value for the energy and the value calculated by FAC. The following columns are present when there is a correspondence to a NIST level: Col. 6 gives the difference between the adopted value and NIST energy (0.00 when the level is set to NIST value). Column 7 gives the NIST energy found in the database with its conventions (“[...]”: theoretical; “+x”: for systems not connected to the ground state). The NIST level name (configuration, term, and angular momentum) are coded in Col. 8.
Excerpt of the extended linelists for each ion (see text for explanations).
Extensive linelists for individual ions are given in separate tables. They provide data for transitions selected with gA/gAmax > 10-7, where gA is the weighted transition probability and gAmax is the maximum probability for the ion. This amounts to a total of lines of around two million. Transitions are sorted first according to the energy of the upper level, then of the lower level. An excerpt is given in Table 6. Columns 1 to 4 give the index and the degeneracy of the upper level, then of the lower level. The index refers to the entry in the level list table for this ion. Column 5 gives the energy of the transition (in cm-1) and Col. 6 its gf value. The tag in Col. 7 gives the same information as in the previous linelist. The wavenumber of the NIST transition is given in Col. 8 (in cm-1), its gf value when it exists in Col. 9.
5. Conclusion
We computed extensive atomic and radiative data for nineteen ions of scandium using the FAC code. We have identified thousands of levels and millions of lines, which have been made available electronically, including in particular highly excited states that are seldom considered. We took special care to compare our results with the reference data obtained from the NIST databank. Our comparisons show that FAC is able to provide large-scale data of good quality, thus can fill existing gaps in the atomic data at hand for astrophysical purposes. Radiative data have also been compared to the Kurucz linelist for scandium, for which we detected some flaws. We plan in the near future to extend our approach to other poorly studied ions or elements, such as nickel.
Available: http://physics.nist.gov/asd
Acknowledgments
We acknowledge financial support from the “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, France, for this work. Part of this work used data obtained from 1995 Atomic Line Data (R. L. Kurucz and B. Bell) Kurucz CD-ROM No. 23. Cambridge, Mass.: Smithsonian Astrophysical Observatory.
References
- Aggarwal, K. M., Keenan, F. P., & Heeter, R. F. 2010, Phys. Scripta, 81, 015303 [NASA ADS] [CrossRef] [Google Scholar]
- Aggarwal, K. M., Kato, T., Keenan, F. P., & Murakami, I. 2011, Phys. Scripta, 83, 015302 [Google Scholar]
- Bromage, G. E., & Fawcett, B. C. 1977a, MNRAS, 178, 605 [NASA ADS] [Google Scholar]
- Bromage, G. E., & Fawcett, B. C. 1977b, MNRAS, 179, 683 [NASA ADS] [Google Scholar]
- Bromage, G. E., & Fawcett, B. C. 1977c, MNRAS, 178, 591 [NASA ADS] [Google Scholar]
- Clementson, J., Beiersdorfer, P., & Gu, M. F. 2010, Phys. Rev. A, 81, 012505 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. F. 2003, ApJ, 582, 1241 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M. 2005, Atomic Data and Nuclear Data Tables, 89, 267 [Google Scholar]
- Gu, M. F. 2008, Canadian J. Phys., 86, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, M., Bernhardt, D., Lestinsky, M., et al. 2010, ApJ, 712, 1166 [NASA ADS] [CrossRef] [Google Scholar]
- Hibbert, A., Johnson, W., & Wiese, W. 2010, J. Phys. B: Atom. Mol. Opt. Phys., 43, 070201 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman, V., & Sugar, J. 1988, J. Phys. Chem. Ref. Data, 17, 1679 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, R., & Palumbo, L. 1973, Naval Research Laboratory Report, No 7599 [Google Scholar]
- LeBlanc, F., & Alecian, G. 2008, A&A, 477, 243 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ralchenko, Y., Kramida, A., Reader, J., & NIST ASD Team. 2010, NIST Atomic Spectra Database (version 4.0), Tech. rep., National Institute of Standards and Technology, Gaithersburg, MD. [Google Scholar]
- Rodrigues, G. C., Indelicato, P., Santos, J. P., Patté, P., & Parente, F. 2004, Atomic Data and Nuclear Data Tables, 86, 117 [Google Scholar]
- Rogers, F. J., & Iglesias, C. A. 1992, ApJ, 401, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J., Zeippen, C. J., Tully, J. A., et al. 1992, Rev. Mex. Astron. Astrofis., 23, 19 [NASA ADS] [EDP Sciences] [Google Scholar]
- Seaton, M. J., Yan, Y., Mihalas, D., & Pradhan, A. K. 1994, MNRAS, 266, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Smitt, R., & Ekberg, J. O. 1985, Phys. Scr, 31, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Sossah, A. M., Zhou, H., & Manson, S. T. 2008, Phys. Rev. A, 78, 053405 [NASA ADS] [CrossRef] [Google Scholar]
- Sugar, J., & Corliss, C. 1980, J. Phys. Chem. Ref. Data, 9, 473 [Google Scholar]
- Wei, H. G., Shi, J. R., Zhao, G., & Liang, Z. T. 2010, A&A, 522, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wilson, N. J., Hibbert, A., & Bell, K. L. 2000, Phys. Scripta, 61, 603 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Comments about specific ions
A.1. Sc XXI
The H-like ion has not been observed, and NIST gives theoretical energies and predicted wavelengths without oscillator strengths. For this simple electronic structure, theoretical data are accurate. The FAC code easily reproduces the 25 levels listed by NIST. Besides a shift of 0.063 eV to match the absolute ground level (6033.755 eV), the relative energies are consistent within 0.007 eV (rms of the differences: 0.002 eV).
A.2. Sc XX
This highly ionized ion has only two observed lines (not in NIST database). As for
other He-like structures, this spectra has been the subject of numerous theoretical
works. All published energies and transitions are derived from calculations. The NIST
data include 25 levels. They show mixing between the
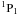 and
and
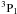 systems of about 5% in the
1snp configurations. The FAC calculation includes 199 levels, the 25
lowest energies being consistent with the NIST data. The largest discrepancy (2.2 eV
or 0.05% of the excitation energy) occurs for the
systems of about 5% in the
1snp configurations. The FAC calculation includes 199 levels, the 25
lowest energies being consistent with the NIST data. The largest discrepancy (2.2 eV
or 0.05% of the excitation energy) occurs for the
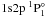 level, which is affected by the
level, which is affected by the
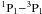 mixing. The 1s2l level
energies were adjusted to those of NIST, the 1s3l and
1s 4l ones being increased by 0.7 eV and 1.1 eV, respectively, and
all others by 1.2 eV.
mixing. The 1s2l level
energies were adjusted to those of NIST, the 1s3l and
1s 4l ones being increased by 0.7 eV and 1.1 eV, respectively, and
all others by 1.2 eV.
A.3. Sc XIX and Sc XVIII
For Sc xix (ground state 1s22s), we found excellent agreement between the calculated and experimental data. The 27 experimental levels of the Li-like configurations 1s2nl are reproduced well by the FAC calculation, the rms of the energy deviation being 0.73 eV, which is 0.06% of the ionization energy. The 8 lower levels were adjusted to NIST values and the 1s2 4l levels raised by 0.3 eV. For Sc xviii (ground state 1s22s2), the variance in the deviation from NIST is 0.07%. The 9 lower excited levels belonging to the configurations 1s22s2p and 1s22p2 were fixed to the experimental energies and the upper levels shifted down by 1 eV. The present list of 99 levels for Sc xix and 676 levels for Sc xviii help to complete the experimental level list in the low energy part.
For these two simple spectra, the FAC gf values are in good agreement with the compiled ones from NIST. The two Sc xviii Ritz lines at λ = 2.068 nm and 2.147 nm are given in NIST as 1s22p2 − 1s22s3p transitions with log gf = −1.008 and 0.21, respectively. Our calculations give log gf = −1.88 and −3.10, which corresponds more closely to a two-electron jump.
A.4. Sc XVII to Sc XII
The ground state of theses six ions belongs to configurations 1s22s22pn (n = 1 to 6). The FAC calculation delivers much more levels than present in the NIST lists (see Table 2). It may show significant discrepancy (up to 4 eV) for the first core-excited configurations of the type 1s22s2pn + 1 and 1s22pn + 2. For Sc xvi, Sc xv, and Sc xiv, the theoretical results of Bromage & Fawcett (1977c,a,b) were used to confirm the correspondence between the FAC and NIST level identifications, specifically for the levels in the 2s22pn3d (n = 1, 2, 3) configurations, which are perturbed by the configuration interaction with 2s2pn + 13p. The Sc xv NIST level 2s22p2(1P)3d2P3/2 surely does not exist. It is duplicated from the level 2s22p2(1D)3d2P3/2. We also note that the NIST level of Sc xiii labelled 2s22p4(3P)3d4F5/2 (at 492.01 eV) does not appear in any experimental line.
The levels from the configurations 2s22pn, 2s2pn+1 and 2pn+2 were fixed to their experimental values for all these ions, with the levels from 2s22p2(1S)3d2D for Sc xv, from 2s22p43s for Sc xiii, and from 2s22p53l for Sc xii. Other levels were shifted down by 1.2, 1.0, 1.0, and 0.8 eV for Sc xvii, Sc xvi, Sc xv and Sc xiv respectively, and raised by 0.4 eV for Sc xiii.
A.5. Sc XI and Sc X
The n = 2 shell remains closed for these Na-like and Mg-like ions. The
Sc xi level 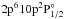 is not in the NIST line list. For this
same ion, the NIST level
is not in the NIST line list. For this
same ion, the NIST level 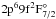 departs from the general behaviour of
the f-series. The Sc xi levels up to 5f are adjusted to NIST, the 5g raised by
0.1 eV, and upper levels by 0.3 eV. For Sc x, the levels from the
configurations 3s2 to 3s4s, 3p2 and 3p3d are fixed to NIST; those
from 3d2, 3s4p to 3s5p, and 3p4s to 3p4f were shifted down by 0.3 eV, and the
upper levels raised by 0.2 eV.
departs from the general behaviour of
the f-series. The Sc xi levels up to 5f are adjusted to NIST, the 5g raised by
0.1 eV, and upper levels by 0.3 eV. For Sc x, the levels from the
configurations 3s2 to 3s4s, 3p2 and 3p3d are fixed to NIST; those
from 3d2, 3s4p to 3s5p, and 3p4s to 3p4f were shifted down by 0.3 eV, and the
upper levels raised by 0.2 eV.
A.6. Sc IX to Sc VI
The ground state of these four ions belongs to configurations of the type 3s23pn (n = 1 to 4). Perturbations occur from configuration interactions that mix some of the 3s3pn+1 and 3s23pn−13d states. When dominant compositions are close to 50%, the assigned configuration is indicative only. For instance in Sc vii, the level computed by FAC at 32.612 eV with even parity and J = 1/2 is labelled 3s23p23d, but it could equally well be the 3s3p4 configuration (as it appears in NIST).
Kurucz provides line data for these ions. They are based on the level list given in the
NIST database but extended to a number of predicted lines that are given with Ritz
wavelengths and theoretical gf-values. For Sc ix, Kurucz
clearly miscalculates 3 out of the 15 gf-values found in the NIST data.
These three lines all involve the 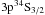 level of the quadruplet system, which is
not connected to the doublet one. In the case of Sc vii, it appears that the
calculated gf-values given by Kurucz differ significantly from 16 out
of the 20 NIST lines and from the FAC ones, the two latter ones being in reasonable
agreement. The error in the Kurucz data can be explained from inverted identifications
for levels of the perturbed configurations with three electrons in the
n = 3 shell. We note that NIST gives the
3s23p2(1D)3d2F5/2
level of Sc vii (at 46.876 eV) without any corresponding line.
level of the quadruplet system, which is
not connected to the doublet one. In the case of Sc vii, it appears that the
calculated gf-values given by Kurucz differ significantly from 16 out
of the 20 NIST lines and from the FAC ones, the two latter ones being in reasonable
agreement. The error in the Kurucz data can be explained from inverted identifications
for levels of the perturbed configurations with three electrons in the
n = 3 shell. We note that NIST gives the
3s23p2(1D)3d2F5/2
level of Sc vii (at 46.876 eV) without any corresponding line.
The list of experimental levels for Sc vi is incomplete for many configurations and there is no gf-value in NIST. For the 3s23p33d, configuration NIST gives 12 levels among the 38 expected ones calculated by FAC. The only observed transitions are from the ground state. They allow us to determine levels up to J = 3 only, hence the high-J levels are missing. From the FAC results, we can predict numerous strong transitions 3s23p33d−3s23p34f between high-J levels (J = 4 to 6) in the wavelength range 20−30 nm. Other strong predicted transitions in 3s23p33d−3s23p23d2 appear in the same range, owing to the interaction between the overlapping configurations 3s23p34f and 3s23p23d2. NIST lists 4 unclassified lines of Sc vi that could be due to 3s23p33d−3s23p34f. Such a tentative classification is reported by the Kelly compilation (Kelly & Palumbo 1973), but the corresponding levels values are unreliable because of the lack of connection to known levels of J-values lower than 3.
For Sc ix, the energies of the twelve levels from 3s23p,
3s3p2 and 3s23d were adjusted to the values of NIST, and the
upper levels shifted down by 0.3 eV (see Fig. 1).
For Sc viii, levels from 3s23p2, 3s3p3 and
3s23p3d were adjusted to NIST, except for the missing levels
3s 3p3 5S2 (shifted down by 0.6 eV) and
3s2 3p 3d 1D2,
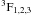 (shifted down by 1.4 eV). For
Sc vii, all levels with a correspondence to NIST were adjusted to their NIST
value, the remaining levels from 3s23p23d shifted down by 2.0 eV,
and other levels by 0.5 eV. For Sc vi, all levels from
3s23p4, 3s3p5, 3s23p33d and
3s23p34s, with a correspondence to NIST were adjusted to the
energies given by NIST, and the remaining levels from 3s23p33d
were shifted down by 1.0 eV, and other levels by 2.5 eV.
(shifted down by 1.4 eV). For
Sc vii, all levels with a correspondence to NIST were adjusted to their NIST
value, the remaining levels from 3s23p23d shifted down by 2.0 eV,
and other levels by 0.5 eV. For Sc vi, all levels from
3s23p4, 3s3p5, 3s23p33d and
3s23p34s, with a correspondence to NIST were adjusted to the
energies given by NIST, and the remaining levels from 3s23p33d
were shifted down by 1.0 eV, and other levels by 2.5 eV.
A.7. Sc V
The NIST database gives 118 Sc v energy levels and 454 electric dipolar transitions, derived from the analysis of Smitt & Ekberg (1985). Theoretical oscillator strengths for K iii, Ca iv, and Sc v iosoelectronic spectra were published by Wilson et al. (2000). We note that the Kurucz data for Sc v should be updated: the 36 listed lines are based on only 22 levels. Kurucz denominations for the parent terms 3p4(3P) and 3p4(1D) in the 3p43d configuration should be inverted. The four levels from 3p45s do not match any NIST level.
We established a complete level correspondence between FAC and NIST for the two overlapping odd configurations 3s23p44p and 3s3p53d, which have 21 and 23 levels, respectively. Smitt & Ekberg (1985) highlighted their mixed composition, with additional perturbation by the numerous unobserved levels of the 3s23p33d2 configuration. The NIST level 3s3p5(3P)3d4D5/2 is labelled 4p by FAC, the mixing being calculated as 48%−34% by Smitt & Ekberg (1985). On the even side, the 72 levels from the configurations 3s3p6, 3s23p43d, 3s23p44s, 3s23p44d, and 3s23p45s are observed and matched to the FAC levels, except for the 3s23p4(3P)5s4P5/2 level, which is unobserved. The energies of all the levels with a correspondence were adjusted to the values of NIST, and other levels shifted down by 2.0 eV, except for the level 3s23p45s4P5/2 which was shifted down by 1.6 eV.
A.8. Sc IV
All the 127 NIST levels were related to the FAC levels (the NIST level
3s3p65p1P ∗ , above the ionization limit, is not
considered). The theoretical excitation energies from the closed ground state
configuration 3s23p6 are systematically higher than experimental
ones by about 2 eV. An exception is the highest level
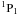 of the 3p53d configuration,
which deviates from the observed one by 4 eV. This level is separated from the rest of
its configuration by the 4 levels of 3p54s. The unobserved configuration
3p43d2 is predicted to overlap with the 3p55p and
3p54f ones. The NIST level 3p54d1P ∗ is
given by FAC as an extra 3p55s level, the label being meaningless in the case
of large mixing. Kurucz 1204 gf values differ substantially from our
results. No clear conclusion can be drawn as only 4 NIST transitions are available. The
energies of the levels from 3p6 to 3p55p and
3s 3p6 3d are adjusted to NIST, and those of other levels were shifted
down by 1.45 eV.
of the 3p53d configuration,
which deviates from the observed one by 4 eV. This level is separated from the rest of
its configuration by the 4 levels of 3p54s. The unobserved configuration
3p43d2 is predicted to overlap with the 3p55p and
3p54f ones. The NIST level 3p54d1P ∗ is
given by FAC as an extra 3p55s level, the label being meaningless in the case
of large mixing. Kurucz 1204 gf values differ substantially from our
results. No clear conclusion can be drawn as only 4 NIST transitions are available. The
energies of the levels from 3p6 to 3p55p and
3s 3p6 3d are adjusted to NIST, and those of other levels were shifted
down by 1.45 eV.
A.9. Sc III
The structure of this simple ion is based on the closed core 3s23p6. The 97 NIST gf values are nicely reproduced by FAC. In contrast the gf values given by FAC and Kurucz differ for many of the supplementary 129 lines provided by Kurucz. All NIST energies were used to adjust those FAC levels where a correspondence was found and other levels were raised by 1.2 eV.
All Tables
List of configurations of Sc ions generating fine-structure levels below the first ionization threshold.
Number of levels, ground states, and ionization energies (in eV) for the nineteen ions of scandium according to NIST and our calculations (FAC).
Number of transitions in scandium spectra (first column) available from three sources: NIST database, Kurucz linelist (CD-ROM No. 23) and present calculations with FAC.
Excerpt of the table of lines restricted to gf > 10-3 (see text for explanations).
All Figures
 |
Fig. 1 Energy levels below the ionization threshold for Sc ix, calculated by FAC. Abscissa is the total angular momentum degeneracy 2J + 1 multiplied by + 1/−1 for even/odd levels, respectively. Black dots represent the levels from the NIST database. The lowest levels configurations are named according to their parent core: nl means 3s2nl (blue); nl′ means 3s3pnl (green); nl′′ means 3p2nl (magenta). First ionization thresholds (levels of Sc x) are also shown. |
| In the text | |
 |
Fig. 2 Comparison of the energy levels of the 2s22p33d in Sc xiv configuration. Blue: as calculated by FAC; black dots: from the NIST database; red diamonds: from the original paper Bromage & Fawcett (1977c). Also shown (green, triangles) are the close levels from the 2s2p43p configuration. |
| In the text | |
 |
Fig. 3 Excitation energy differences (in eV) between our results and NIST data for all the levels of the nineteen scandium ions in the NIST database, as a function of the NIST excitation energy (in eV). The differences between ionization energies are also plotted as a larger symbol with a drop line to the zero axis and the ion name nearby. |
| In the text | |
 |
Fig. 4 Scandium weighted oscillator strengths gf for the 677 transitions in the NIST database as a function of our calculated values. Filled and open symbols refer, respectively, to transitions that are observed, or not observed and predicted from two observed levels. NIST has no oscillator strength for Sc xxi and Sc vi. The two grey lines delineate the values gfNIST/gfFAC = 2 or 1/2. |
| In the text | |
 |
Fig. 5 Scandium weighted oscillator strengths gf for the 1840 transitions in the Kurucz linelist (excluding Sc v) as a function of our calculated values. Large symbols refer to the transitions that are also common to NIST. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.