| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A141 | |
| Number of page(s) | 6 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117577 | |
| Published online | 16 February 2012 | |
Search for radial velocity variations in eight M-dwarfs with NIRSPEC/Keck II
1 Institut de Ciencies de l’Espai (IEEC-CSIC), Campus UAB, Torre C5 – parell – 2 a planta, 08193 Bellaterra, Spain
e-mail: frodler@iac.es
2 Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, 38205 La Laguna, Spain
3 Universidad de La Laguna, Avda. Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Tenerife, Spain
4 Center for Exoplanets and Habitable Worlds, The Pennsylvania State University, University Park, PA 16802, USA
5 Department of Astronomy and Astrophysics, The Pennsylvania State University, University Park, PA 16802, USA
6 Centro de Astrobiología (CSIC-INTA), Ctra. Ajalvir km. 4, 28850 Torrejón de Ardoz, Madrid, Spain
7 University of Central Florida, Physics Department, PO Box 162385, Orlando, FL 32816, USA
8 UNINOVA-CA3, Campus da Caparica, 2825-149 Caparica, Portugal
Received: 27 June 2011
Accepted: 7 December 2011
Context. Radial velocity (RV) measurements from near-infrared spectra have become a potentially powerful tool to search for planets around cool stars and sub-stellar objects. As part of a large survey to characterize M-dwarfs using NIRSPEC at Keck II, we obtained spectra of eight late M-dwarfs (spectral types M5.0–M8.0) during two or more observing epochs per target. These spectra were taken with intermediate spectral resolving powers (R ~ 20 000) in the J-band.
Aims. We search for relative RV variability in these late M-dwarfs and test the NIRSPEC capability of detecting short-period brown dwarf and massive planetary companions around low-mass stars in the J-band (≈1.25 μm). Additionally, we reanalyzed the data of the M8-type star vB10 (one of our targets), which had been presented in another article.
Methods. To achieve a precise RV measurement stability, the NIRSPEC spectra were self-calibrated by making use of the telluric absorption lines, which are present in the observed spectra and were used as a long-term stable reference. In the modeling process a multi-parameter χ2-optimization was employed to generate an accurate description of the observation. The telluric lines allowed us to model the instrumental profile of the spectrograph and the determination of the Doppler shift of the stellar absorption lines.
Results. For the entire M-dwarf sample, we found no evidence of relative RV variations induced by a short-period brown dwarf or massive planetary companion. The typical RV precision of the measurements is between 180 and 300 m s-1, which is sufficient to detect hot Neptunes around M-dwarfs. Moreover, we found that the spurious RV shift detected previously of the star VB10 was caused by asymmetries in the instrumental profile between different observing epochs, which were not taken into account in the previous analysis.
Key words: stars: late-type / stars: low-mass / brown dwarfs / techniques: radial velocities / planetary systems
© ESO, 2012
1. Introduction
The search for extrasolar planets has led to more than 700 confirmed discoveries1 by using all detection techniques. Up to now, most of the extrasolar planets have been detected by means of the radial velocity (RV) technique using high-resolution spectrographs (R = λ/Δλ ≥ 40 000) at optical wavelengths. Most discoveries are giant gaseous planets (typically hot Neptunes and Jupiters) of short-periods (of a few days) around stars of spectral types F, G and K.
As potential hosts to rocky planetary companions, M-dwarfs have become increasingly popular as targets for RV searches (e.g. Endl et al. 2006; Charbonneau et al. 2009; Mayor et al. 2009; Zechmeister et al. 2009). Very cool stars such as M-dwarfs are the most abundant type (~70%) of stars in the solar neighborhood and the Milky Way in general (Henry et al. 1997). The effective temperatures and masses of M-dwarfs are in the range 3700 to 2200 K and 0.5 to 0.07 solar masses for the M0 to M9.5 spectral types. They exhibit prominent absorption features corresponding to strong neutral atoms, H20, FeH, VO, CO, and TiO. Owing to the low masses of these objects, the reflex motion of the host star caused by the gravitational pull of the extrasolar planet is higher and more easily detectable than for more massive host stars. Because M-dwarfs are very cool stars compared with solar-type stars, short-period planets would more likely be situated in the habitable zone.
M-dwarfs emit most of their energy around 1.1−1.3 μm, in the near-infrared (NIR), while they appear very faint at optical wavelengths. First attempts to measure RV variations among very cool M-dwarfs at NIR wavelengths were made by Martín et al. (2006). They achieved an RV precision of around 300 m s-1 for the M9.5-dwarf LP944-20 by using the spectrograph NIRSPEC, which is mounted on the Keck II telescope in Hawaii (McLean et al. 1998). Recently, several research groups have reported high-precision RV measurements taken in the NIR with CRIRES (Käufl et al. 2004), mounted at the UT1/VLT in the Paranal Observatory of ESO in Chile. Bean et al. (2010a) collected high-resolution spectroscopic data of over 60 M-dwarfs (spectral types M4–M9) and used a NH3 gas cell spectrum as a stable reference. They report an RV precision of better than 5 m s-1. Figueira et al. (2010) took observations of the planetary candidate TW Hya and achieved an RV precision better than 10 m s-1 by adopting telluric lines as a stable reference. Blake et al. (2010) report RV measurements of 59 M- and L-dwarfs using the Keck/NIRSPEC spectrograph, with the aim to detect low-mass companions. They made use of strong CO absorption features around 2.3 μm in M- and L-dwarfs and achieved RV precisions between 50 and 200 m s-1. Tanner et al. (2010) report preliminary results of a late M-dwarf survey by using Keck/NIRSPEC with RV precisions between 150–300 m s-1.
In 2009, Pravdo & Shaklan (2009) announced a massive planet around the M-dwarf vB10 discovered by means of astrometrical data. Zapatero Osorio et al. (2009, hereafter ZO09) made use of our NIRSPEC data set and found evidence for RV variations, which supported the planet hypothesis. They achieved an RV precision of about 300 m s-1. However, this planet was later refuted by different groups: by Bean et al. (2010b), who took high-resolution spectra (R = λ/Δλ ~ 100 000) with CRIRES and who achieved an RV precision of ~10 m s-1, and by Anglada-Escudé et al. (2010). Additionally, Lazorenko et al. (2011) carried out an astrometric survey using the FORS2 camera of the ESO/VLT on Cerro Paranal, Chile, but found no evidence for the existence of a massive planet orbiting vB10. As part of this work, we aimed at finding out what had caused the spurious RV variations in the data analysis of ZO09.
Here, we report relative RV measurements of eight late M-dwarfs with NIRSPEC, and we support the capability of this instrument to detect giant planetary companions with short orbital periods. In Sect. 2 we describe our M-dwarf sample, our observations and data reduction. In Sect. 3 we outline the details of the data analysis, followed by the results and discussion (Sect. 4).
Journal of target observations. The average S/N values in the stellar continua are given.
Properties of the M-dwarfs.
2. Observations and data reduction
As part of our M-dwarf survey (Deshpande et al., in prep.), we observed eight M-dwarfs (2M2331, GJ1156, GJ406, GJ905, LHS1363, RXJ2208.2, and vB10) at two or more epochs (Table 1) using the NIRSPEC instrument, mounted on the Keck II telescope on the summit of Mauna Kea in Hawaii (McLean et al. 1998). We aimed at conducting RV precision tests, and searching for RV drifts that could be interpreted as massive planets orbiting those M-dwarfs. Our sample comprised dwarfs with spectral types of M5.0–M8.0 and masses between 0.14 and 0.075 M⊙. Table 2 provides a list of the spectral types, J-band magnitude and the projected stellar rotational broadening vsini of the targets.
NIRSPEC is a cross-dispersed, cryogenic echelle spectrometer employing a 1024 × 1024 ALADDIN InSb array detector. In the echelle mode, we selected the NIRSPEC-3 (J-band) filter and an entrance slit width of 0.432″ (i.e. 3 pixels along the dispersion direction of the detector), except for the 2001 June observations of vB10, where we used an entrance slit width of 0.576″. The corresponding spectral resolving powers were R = λ/Δλ ≈ 22 700 and R ≈ 17 800 for the 0.432″ and the 0.576″ slit, respectively. The length of both slits was 12″. All observations were carried out at an echelle angle of ~63°. This instrumental setup provided a wavelength coverage from 1.148 to 1.346 μm split into 10 different echelle orders, a nominal dispersion ranging from 0.164 (blue) to 0.191 Å pix-1 (red wavelengths). Weather conditions (seeing and atmospheric transparency) were fine during the observations, except for the 2008 epoch, which was hampered by cirrus and strong wind. Table 1 lists the individual exposure times and the signal-to-noise ratios (S/Ns) on average per spectral pixel in the stellar continua for each observing epoch.
For each target, the spectra were collected at two different positions along the entrance slit. This nodding allowed the later removal of the OH sky emission lines. For the identification of atmospheric telluric absorption, near-infrared featureless stars of spectral types A0-A2 were observed close in time (on average 3 min before or after the target observations) and position to our targets.
Raw data were reduced using the echelle package within IRAF2. Nodded images were subtracted to remove sky background and dark current. White-light spectra obtained with the same instrumental configuration and for each target observation were used to flat-field the data. By adopting the apall task, we first identified and optimally centered the echelle orders in the two individual nodding frames for each target and traced these orders by adopting a second-order Legendre polynomial along the dispersion axis. In the next step, we extracted the one-dimensional spectra for each echelle order adopting the same aperture/trace parameters for the target and an arc-lamp exposure of Ar, Kr, and Xe, which was always acquired after observing the target and before pointing the telescope at the next star. The air wavelengths of the arc lines were identified using the NIST3 database, and we produced preliminary wavelength calibration fits using a third-order Legendre polynomial along the dispersion axis and a second-order one perpendicular to it. The mean rms of the fits was 0.03 Å, or 0.7 km s-1.
3. Relative radial velocity method
We measured the RV of the stars relative to the telluric lines present in the spectra and to a selected epoch of the star, employing a self-calibration approach. The RV of the telluric lines is constant in all wavelengths down to a level of 10 m s-1 (e.g., Figueira et al. 2010; Seifahrt & Käufl 2008), which is about a magnitude smaller than the velocity precision we can achieve with NIRSPEC. The basics of the self-calibration method have been extensively described (e.g. Valenti et al. 1995; Endl et al. 2000; Bean et al. 2010a), so that we just give a concise description of the method here and point out the important aspects of its implementation.
Briefly, the main idea is to model the observations and thereby determine the relative RV shift, and perform a fine-tuning of the wavelength solution at the same time. Basically, the model spectrum is the product of a high-resolution telluric spectrum with a Doppler-shifted version of a high-resolution reference spectrum of the star. The product of those two spectra is convolved with the instrumental profile (IP) of the spectrograph, and finally binned to the sampling of the observed data. By variation of the free parameters of the model (Table 3), the best-fit model is evaluated by χ2 statistics. The input Doppler-shift that yields the best fit represents the measured RV.
Since our method requires the presence of telluric lines in the spectra, we restricted the analysis to the echelle orders 66, 60, 58, and 57, which were heavily contaminated mainly by absorption lines of water vapor. These four orders correspond to the wavelength ranges of λ ~ 1.147 to 1.163 μm, 1.261 to 1.279 μm, 1.304 to 1.323 μm, and 1.327 to 1.346 μm, respectively. For the echelle order numbering we refer to McLean et al. (2007). Subsequently, we subdivided each spectral order into five equidistant pixel chunks of 200 pixel each (i.e. for all four orders together we have 20 chunks). This step was made to simplify the process of improving the model, to speed up the calculations and to account for variations of the IP throughout each spectral order. Each of the following steps was carried out on each chunk individually, and the S/N was determined by 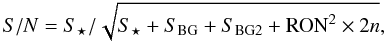 (1)where S ⋆ denotes the signal level from a star in electrons, integrated over an aperture of n pixels, SBG is the signal level of the sky background, SBG2 is the signal level from the sky background of the frame taken at the other nodding position, and RON denotes the read-out-noise level per pixel in rms electrons (for NIRSPEC, RON = 65e-1). The noise errors were propagated in the following data analysis steps.
(1)where S ⋆ denotes the signal level from a star in electrons, integrated over an aperture of n pixels, SBG is the signal level of the sky background, SBG2 is the signal level from the sky background of the frame taken at the other nodding position, and RON denotes the read-out-noise level per pixel in rms electrons (for NIRSPEC, RON = 65e-1). The noise errors were propagated in the following data analysis steps.
3.1. Step 1: Telluric template spectrum and determination of the instrumental profile
For the calculation of the atmospheric transmission spectrum, we used the line-by-line radiative transfer model (LBLRTM) code, which is based on the FASCODE algorithm (Clough et al. 1992). LBLRTM is available as fortran source code4 and runs on various platforms. As molecular database we adopted HITRAN (Rothman et al. 2005), which contains the 42 most prominent molecules and isotopes present in the atmosphere of the Earth. Following the approach presented by Seifahrt et al. (2010), we created a high-resolution theoretical telluric spectrum for each observed spectrum by accounting for the air mass of the star as well as the weather conditions (water vapour density column, temperature and pressure profiles) during the observations. We retrieved the weather information from the Global Data Assimilation System (GDAS). GDAS models are available in 3 h intervals for any location around the globe5.
Free parameters in the model per chunk.
 |
Fig. 1 Comparison between the observed telluric spectrum (points), and the theoretical model (line). The observed telluric spectrum was taken by using a featureless A-star (HD 181414), which was observed with NIRSPEC in the J-band on 2007-06-25. The rms of the telluric model fit to the observed data is about 1%. |
To calculate a first version of the instrumental profile (IP) of the spectrograph, we used the A-star observations next to our targets. First of all, we normalized the spectrum in a way that the flux in the telluric continuum was at one. Next, we refined the wavelength solution of the observed telluric spectrum with the appropriate high-resolution theoretical telluric spectrum by adopting a second order polynomial. We then determined a preliminary version of the IP as the sum of seven Gaussian profiles in a similar way as described in Valenti et al. (1995): around a central Gaussian we grouped three Gaussians on each side of it, which allowed us to account for asymmetries in the IP. Free parameters were the height and width of the central Gaussian, plus the heights of the six satellite Gaussians (cf. Table 3). To reduce the number of free parameters per chunk, and to ensure that the method works robustly, the positions and the widths of these satellites were fixed and set a priori in a way that their half-widths overlapped.
Next, we convolved the high-resolution theoretical spectrum with the determined preliminary IP and compared the resulting spectrum with the observed A-star spectrum. For a few telluric lines, we realized that the theoretical spectrum under- or overestimated the line-depths. To produce a better match between theory and observation, we iteratively carried out a fine-tuning of the line-depths in the high-resolution theoretical telluric spectrum, then again convolved the modified telluric spectrum with the IP and evaluated the result with the observation by means of χ2-statistics. The iterations were carried out until the reduced χ2 reached 1. Figure 1 shows a comparison between an A-star spectrum (HD 181414) and the fit of the refined theoretical telluric spectrum as well as the residuals of the model fit to the A-star spectrum. The rms of the telluric model fit to the observed data is about 1% on average. The refined high-resolution telluric model spectrum from now on served the purpose of the telluric template spectrum. In the final step, we refined the wavelength solution of the observed spectrum, and then re-calculated the IP by adopting this new telluric template spectrum.
3.2. Step 2: Stellar template spectrum
Owing to the lack of appropriate theoretical model spectra that fit the stellar absorption features in the J-band, we created the stellar template spectrum for one selected reference epoch by calculating an IP-free and telluric-free version of the target spectrum. Concerning the reference epoch, we selected that epoch in which the stellar spectrum showed the highest S/N. To produce the stellar template, we first applied the refined wavelength solution of the A-star spectrum (which was taken – on average – 3 min before or after the target observations) to the observed target spectrum of the same epoch. Because the telluric lines were present in the target spectrum, we needed to remove them from the spectrum. In preparation for this, we convolved the appropriate theoretical telluric spectrum with the IP. Then, we divided the target spectrum by the convolved theoretical telluric spectrum (Fig. 1). Similar to Bean et al. (2010a) and Blake et al. (2010), we found that this approach led to smaller uncertainties than when the usual method of the telluric lines removal was carried out, where the target spectrum is simply divided by the appropriate A-star spectrum.
To create the final stellar template spectrum, we deconvolved the telluric-free target observation by the IP by employing the maximum-entropy method (MEM) with 5 times oversampling of the output spectrum. In the final step, we applied the refined wavelength solution that we had obtained for the A-star spectrum to the 5 times oversampled IP-free stellar spectrum, which from then on served the purpose of the stellar template.
 |
Fig. 2 Example model components and fit for the radial velocity measurements. The components are given in the two top panels: the spectrum of the high-resolution theoretical telluric spectrum (top), and the deconvolved and RV-shifted version of the telluric free stellar spectrum (bottom). We note that the scale of the flux is different in each panel for better visibility. In the lower panel, we show the observed spectrum (points) and the best-fit model (line). |
3.3. Step 3: Fitting the observed data
For each target, we first determined the barycentric velocity differences Δvbc,t for all observation epochs t with respect to that one of the stellar template epoch. This correction was calculated by using the JPL ephemeris DE200 (Standish 1990).
We constructed the model of the observation by multiplying the telluric template with the stellar template, where its Doppler shift is one of the free parameters. The resulting combination spectrum was subjected to a convolution with the IP that was determined in step 1, and a new wavelength solution was calculated. Subsequently, all free parameters (i.e. line-depths in the models, IP, ...; see Table 3) were refined by employing Brent’s optimization algorithm, and the fit to the observed data was evaluated using χ2 statistics. The search range for the Doppler shift was Δvbc,t ± 15 km s-1 with a step width of 10 m s-1. We note that such a large interval would also allow us to detect strong relative RV variations caused by an unseen massive companions such as low-mass stars and brown dwarfs. We calculated the χ2 values for each Doppler shift and then determined the exact χ2-minimum by using a Gaussian fit. That Doppler shift which led to the overall best-fit model (χ2-minimum) constituted the measured RV of the star in the chunk, relative to the stellar template.
To determine the overall (i.e. all chunks together) RV measurement, we combined all the RV measurements in all chunks into one by considering the following restrictions: each chunk was given a specific weight that was determined from the average S/N in the stellar continuum, plus the number of telluric lines and stellar absorption lines that were present in that chunk, plus the depths of the stellar lines. Furthermore, we rejected chunks in which the RV-measurement clearly constituted an outlier (3σ above/below average of all RV measurements) by adopting sigma-clipping. No chunks were rejected for the stars GJ905, GJ1156, LHS1363, RXJ2208.2, and vB10. For 2MJ2331-2749 and LP412-31, one chunk was rejected each, while for GJ406 two chunks were rejected. All those rejected chunks were located in noisy areas with S/N levels lower than 40 on average. We attribute these spurious RV shifts to improper stellar templates which contained artifacts coming from the deconvolution of low-S/N data.
The overall RV measurement was then determined as the arithmetic weighted mean of the approved chunks. The error of the overall RV measurement was determined as the weighted standard deviation of the RV measurements in the chunks.
4. Results and discussion
We analyzed the data sets with our relative RV measurement approach and determined the relative RV measurements with respect to the selected reference epoch. For none of the eight M-dwarfs in our sample we found significant evidence of relative RV variations at the level of 3σ (Table 4), where σ stands for the measurements uncertainty. The RV precisions are on the order of 180–300 m s-1, except for the observations in July 2008, which were taken at low S/N.
We investigated the period and mass range of companions that we were able to detect with this RV precision. We determined the minimum mass of the planet by employing a Monte-Carlo analysis, thereby probing planetary orbits with different parameters and investigating how many of these orbits could be recovered for the five measurements of vB10. We considered only the case of a circular orbit and the mass of vB10, which is m⋆ = 0.078 M⊙. Figure 3 shows the 3σ detection limit. We found that for companions with only a few days period, even planets with minimum masses of mpsini ≥ 0.3 MJup can be detected with an RV precision of ~220 m s-1.
 |
Fig. 3 Monte-Carlo analysis for the five vB10 measurements. For the mass of vB10, we adopted 0.078 M⊙ from Pravdo & Shaklan (2009). Obviously, with an RV precision of ~220 m s-1 even hot Jupiters with minimum masses mpsini > 0.3 MJup can be detected around late M-dwarfs with 3σ confidence. We note that for a larger number of measurements the number of aliasing peaks can be significantly decreased. |
Relative radial velocity measurements.
In Fig. 4 we show our relative RVs of vB10 and the measurements by ZO09. We note that for a proper comparison, we adopted the same reference epoch as in ZO09. The agreement between ZO09 and our measurements is within 1σ of the quoted uncertainties for all epochs except for the 2001 epoch (BJD = 2 452 076). We now explain the discrepancy of this one measurement. Similar to our data analysis, ZO09 used the telluric lines present in the target spectra as a stable reference, but in contrast to our analysis they did not account for any IP variations in their analysis, but calculated the RVs by cross-correlation. In our analysis, we see no RV shift exceeding the RV-precision for any measurement. We obtained evidence that the different instrumental setting used on 2001-Jun.-15 (0.576′′ slit instead of the standard setting of 0.432′′) produced an asymmetric instrumental profile (Fig. 5), which led to a significant RV shift when a simple cross-correlation is adopted for the RV determination. Our results clearly demonstrate the importance of modeling the IP, especially when observations are carried out with different instrumental settings.
 |
Fig. 4 Our RV measurements of vB10 (crosses) vs. the measurements of ZO09 (open circles). The RV precision given by our analysis is about 220 m s-1, except for the last epoch in 2008, which was hampered by bad weather. We prove that the RV shift in the work of ZO09 in the first 2001 epoch (BJD = 2 452 076) originates from unaccounted asymmetries in the IP and not from a planetary companion. |
 |
Fig. 5 Instrumental profiles (IPs) of NIRSPEC for two different observing epochs of vB10. On 2001-06-15, a broader slit was used (0.576′′; solid line) than for the reference epoch (0.432′′; 3007-06-25; dashed line). To visualize the asymmetries between both IPs, we calculated the ratio between both IPs and scaled the resulting function for better visibility (dotted line). ZO09 did not account for these asymmetries between both IPs, which led to a spurious RV shift of about 1 km s-1 for the 2001-06-15 measurement in their data analysis. |
We compared our results to the work of Blake et al. (2010), who searched for companions to M- and L-dwarfs by using NIRSPEC at a spectral resolving power of ~25 000 in the K-band. They adopted one spectral order covering the wavelength range from 2.285 to 2.318 μm to measure the dense and strong CO-absorption line pattern present in those dwarfs. As a stable wavelength reference, they used the CH4 telluric absorption lines present in the observations. Similarly to us, they employed a self-calibrating approach, with the difference that they adopted theoretical models for M- and L-dwarfs, which well-described the observations.
Blake et al. obtained measurements with S/Ns in the range of 50 to 100 in the pseudo stellar continua, and they report RV precisions of 100–300 m/s for slowly rotating late-M and L dwarfs. The uncertainty of Blake et al. in the K-band agrees with our derivation of 180–300 m/s in view of our S/Ns. However, our wavelength coverage is about twice that in Blake et al. According to the relative RV precision formulae, we should have obtained better velocity precision in terms of wavelength coverage, which is not the case. We conclude that the larger number of deep lines (more than 30 lines with a line depth of more than 50%) in the CO-band region as compared to the J-band (only a few lines with a depth of more than 25%) as well as the use of theoretical template spectra instead of deconvolved stellar spectra appear to compensate for the shorter wavelength coverage in a similar factor (cf. Eq. (6) in Butler et al. 1996).
We note that Reiners et al. (2010) and Rodler et al. (2011) carried out theoretical RV precision studies of M- and L-dwarfs by adopting theoretical models of M-dwarfs (e.g. del Burgo et al. 2009). As result, they found that the highest RV precision for M-dwarfs is attained in the Y-band around 1 μm and not in the J-, H- or K-band. For L-dwarfs, however, Rodler et al. (2011) reported that the highest RV precision is attained in the J-band.
We conclude that for an accurate relative RV determination with NIRSPEC, a self-calibrating approach, which accounts for changes in the instrumental setting, produces the best measurements in terms of RV precision. Although with our RV precision we would be able to detect massive hot Neptunes around late M-dwarfs, we have not found any brown dwarf or massive planetary companion in our survey. Additionally, the re-analysis of the data of the M8-dwarf vB10 presented in ZO09 now clearly confirms the non-existence of a massive planet orbiting that dwarf and agrees with the results by other research groups (e.g. Anglada-Escudé et al. 2010; Bean et al. 2010b; Lazorenko et al. 2011).
The Extrasolar Planets Encyclopedia; http://www.exoplanet.eu; 2011-Nov.-15.
Source code and manuals are available under http://rtweb.aer.com/lblrtm_description.html
GDAS webpage: http://ready.arl.noaa.gov/READYamet.php
Acknowledgments
We thank those of the Hawaiian ancestry on whose sacred mountain we are privileged to be guests. We are grateful to H. Bouy, N. Dello-Russo, P.-B. Ngoc, R. Tata, and R. Vervack for helping to obtain the 2007 and 2008 NIRSPEC spectra. F.R. thanks to A. Seifahrt for his help with LBLRTM, and to M. Zechmeister and M. Endl for discussions on the self-calibrating approach. This work has been supported by the Spanish Ministerio de Eduación y Ciencia through grant AYA2007-67458. Partial support for this research was provided by RoPACS, a Marie Curie Initial Training Network funded by the European Commission’s Seventh Framework Programme. The Center for Exoplanets and Habitable Worlds is supported by the Pennsylvania State University, the Eberly College of Science and the Pennsylvania Space Grant Consortium. This work was partly funded by the Fundação para a Ciência e a Tecnologia (FCT)-Portugal through the project PEst-OE/EEI/UI0066/201. We would furthermore like to thank the anonymous referee for valuable comments that substantially improved the article.
References
- Anglada-Escudé, G., Shkolnik, E., Weinberger, A., et al. 2010, ApJ, 711, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Seifahrt, A., Hartman, H., et al. 2010a, ApJ, 713, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Bean, J. L., Seifahrt, A., Hartman, H., et al. 2010b, ApJ, 711, 19 [Google Scholar]
- Blake, C. H., Charbonneau, D., & White, R. J. 2010, ApJ, 723, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Butler, R. P., Marcy, G. W., Williams, E., et al. 1996, PASP, 108, 500 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonneau, D., Berta, Z. K., Irwin, J., et al. 2009, Nature, 462, 891 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Clough, S. A., Iacono, M. J., & Moncet, J.-L. 1992, J. Geophys. Res., 97, 15761 [NASA ADS] [CrossRef] [Google Scholar]
- del Burgo, C., Martín, E. L., Zapatero Osorio, M. R., & Hauschildt, P. 2009, A&A, 501, 1059 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endl, M., Kürster, M., & Els, S. 2000, A&A, 362, 585 [Google Scholar]
- Endl, M., Cochran, W. D., Kürster, M., et al. 2006, ApJ, 649, 436 [Google Scholar]
- Figueira, P., Pepe, F., Melo, C. H. F., et al. 2010, A&A, 511, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, T., Ianna, P., Kirkpatrick, D., et al. 1997, ApJ, 114, 388 [Google Scholar]
- Martín, E. L., Guenther, E., Zapatero Osorio, M. R., et al. 2006, ApJ, 644, 75 [Google Scholar]
- Mayor, M., Bonfils, X., Forveille, T., et al. 2009, A&A, 507, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLean, I. S., Becklin, E. E., Bendiksen, O., et al. 1998, Proc. SPIE, 3354, 566 [NASA ADS] [CrossRef] [Google Scholar]
- McLean, I. S., Prato, L., McGovern, M. R., et al. 2007, ApJ, 658, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Mohanty, S., & Basri, G. 2003, ApJ, 583, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Käufl, H.-U., Ballester, P., Biereichel, P., et al. 2004, SPIE, 5492, 1218 [Google Scholar]
- Lazorenko, P. F., Sahlmann, J., Ségransan, D., et al. 2011, A&A, 527, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pravdo, S. H., & Shaklan, S. B. 2009, ApJ, 700, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Basri, G. 2010, ApJ, 710, 924 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Bean, J. L., Huber, K. F., et al. 2010, ApJ, 710, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Rodler, F., del Burgo, C., Martín, E. L., et al. 2011, A&A, 532, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L. S., Jacquemart, D., Barbe, A., et al. 2005, JQSRT, 96, 139 [Google Scholar]
- Seifahrt, A., & Käufl, H. U. 2008, A&A, 491, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifahrt, A., Käufl, H. U., Zängl, G., et al. 2010, A&A, 524, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Standish, E. M., Jr. 1990, A&A, 233, 252 [NASA ADS] [Google Scholar]
- Tanner, A., White, R., Bailey, J., et al. 2010 [arXiv:1012.4882] [Google Scholar]
- Valenti, J. A., Butler, R. P., & Marcy, G. W. 1995, PASP, 107, 966 [NASA ADS] [CrossRef] [Google Scholar]
- Zapatero Osorio, M. R., Martín, E. L., del Burgo, C., et al. 2009, A&A, 505, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Kürster, M., & Endl, M. 2009, A&A, 505, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Journal of target observations. The average S/N values in the stellar continua are given.
All Figures
 |
Fig. 1 Comparison between the observed telluric spectrum (points), and the theoretical model (line). The observed telluric spectrum was taken by using a featureless A-star (HD 181414), which was observed with NIRSPEC in the J-band on 2007-06-25. The rms of the telluric model fit to the observed data is about 1%. |
| In the text | |
 |
Fig. 2 Example model components and fit for the radial velocity measurements. The components are given in the two top panels: the spectrum of the high-resolution theoretical telluric spectrum (top), and the deconvolved and RV-shifted version of the telluric free stellar spectrum (bottom). We note that the scale of the flux is different in each panel for better visibility. In the lower panel, we show the observed spectrum (points) and the best-fit model (line). |
| In the text | |
 |
Fig. 3 Monte-Carlo analysis for the five vB10 measurements. For the mass of vB10, we adopted 0.078 M⊙ from Pravdo & Shaklan (2009). Obviously, with an RV precision of ~220 m s-1 even hot Jupiters with minimum masses mpsini > 0.3 MJup can be detected around late M-dwarfs with 3σ confidence. We note that for a larger number of measurements the number of aliasing peaks can be significantly decreased. |
| In the text | |
 |
Fig. 4 Our RV measurements of vB10 (crosses) vs. the measurements of ZO09 (open circles). The RV precision given by our analysis is about 220 m s-1, except for the last epoch in 2008, which was hampered by bad weather. We prove that the RV shift in the work of ZO09 in the first 2001 epoch (BJD = 2 452 076) originates from unaccounted asymmetries in the IP and not from a planetary companion. |
| In the text | |
 |
Fig. 5 Instrumental profiles (IPs) of NIRSPEC for two different observing epochs of vB10. On 2001-06-15, a broader slit was used (0.576′′; solid line) than for the reference epoch (0.432′′; 3007-06-25; dashed line). To visualize the asymmetries between both IPs, we calculated the ratio between both IPs and scaled the resulting function for better visibility (dotted line). ZO09 did not account for these asymmetries between both IPs, which led to a spurious RV shift of about 1 km s-1 for the 2001-06-15 measurement in their data analysis. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


