| Issue |
A&A
Volume 538, February 2012
|
|
|---|---|---|
| Article Number | A149 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201117480 | |
| Published online | 17 February 2012 | |
The chemistry of C3 and C2 in cometary comae
I. Current models revisited⋆
Dept. d’Astronomia i Meteorologia, Institut de Ciències del Cosmos (ICC),
Universitat de Barcelona (IEEC-UB), c/ Martí i Franquès 1, 08028
Barcelona, Spain
e-mail: mweiler@am.ub.es
Received: 15 June 2011
Accepted: 7 October 2011
Context. It is widely accepted that C3 and in particular C2 play an important role in the compositional classification of comets, and the most well-established classification scheme to date is indeed based on the Haser production rates of these two radicals. A link between both C3 and C2 and their actual parent molecules would therefore be desirable to allow both a physical and chemical interpretation of the compositional classification of comets. A first detailed study was performed by Helbert and collaborators for comet C/1995 O1 (Hale-Bopp), which suggested a link between these two radicals and the parent species C2H2, C2H6, and C3H4.
Aims. We extend previous studies of the formation of C3 and C2 to other comets at smaller heliocentric distances. The proposed model for the formation of these two radicals is tested for these comets.
Methods. We compare the observed radial column densities of C3 and C2 in the comae of the comets C/2001 Q4 (NEAT), C/2002 T7 (LINEAR), and 9P/Tempel 1 with the results of a one-dimensional multi-fluid coma chemistry model. The shape of the modelled radial column density profiles are compared with the observed profiles, and the production rates of the parent species are computed by fitting the observational data with the model.
Results. We do not find that C2H6 is a significant parent species of the observed cometary C2. Furthermore, electron impact reactions do not play an important role in the formation of C3. The model for the formation of C3 and C2 derived from comet Hale-Bopp is inconsistent with observations of these radicals in other comets.
Key words: comets: general
© ESO, 2012
1. Introduction
1.1. The role of cometary C3 and C2
Emissions from the radicals C3 and C2 are among the most well-known types of optical emission from cometary comae (Hunaerts 1950; Douglas 1951). By comparing the Haser parent production rates of these two species in a number of comets with the Haser parent production rates of CN and OH, A’Hearn et al. (1995) derived a classification scheme of comets that is strongly based on the production rate ratio of C2/OH or, alternatively, C2/CN. This classification was confirmed by Schleicher (2008) and Langland-Shula & Smith (2011). According to this classification scheme, comets fall into two groups of “typical” comets displaying a correlation between the Haser production rates of C2 and CN, and the “depleted” comets, showing no such correlation and having in general much lower C2/OH and C2/CN ratios.
The formation of C3 and C2 from their parent species remained unexplained for a long time. This lack of knowledge prevents an interpretation of the compositional classification scheme with respect to the true chemical and physical properties of the comets. Without knowing how the classification of comets based on C3 and C2 is linked to the abundances of their parent species in the coma, we cannot draw conclusions about their formation regions in the pre-planetary disc. Furthermore, no connection between the observations of C3 and C2, and the emerging classification schemes based on infrared observations of species such as C2H6 and C2H2, can be established. It is therefore desirable to understand the origins and chemical processes linked to these two species in the cometary coma.
1.2. Current models for the production of cometary C3 and C2
It is generally believed that C3 photochemically decays towards C2, thus coupling the formation of these two radicals, which are both formed from hydrocarbons. The most detailed analysis to date of the formation of C2 and C3 was performed by Helbert et al. (2005, H05 hereafter), who presented a study of comet Hale-Bopp at heliocentric distances (rh) larger than 2.8 AU. They proposed a formation model according to which C3 is formed from either allene or propyne (the two isomers of C3H4), that did not distinguish between these two species. According to this study, C2 is formed from the decay of C3, as well as from acetylene (C2H2) and, to a smaller amount, from ethane (C2H6). In the formation pathway of this model, photochemical reactions as well as electron impact reactions play an important role. The proposed chemical network to understand the formation of C3 and C2 is presented in Fig. 1.
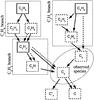 |
Fig. 1 Scheme of the formation of C3 and C2 according to H05. Species in solid boxes are parent species. Solid arrows represent photochemical reactions, dashed arrows electron impact reactions. By-products of the reactions (e.g. H, C, ...) are not included in this simplified scheme. |
1.3. Scope of this work
We present a model for the chemistry in cometary comae that allows the simulation of all kinds of chemical reactions relevant to the formation of C3 and C2. The model is used to attempt to reproduce the observed profiles of C3 and C2 column densities with projected nucleocentric distance in three comets. These comets were observed at heliocentric distances (rh) between 1 AU and 1.5 AU, thus at smaller rh than for comet Hale-Bopp studied before. The range of heliocentric distances in the observations analysed in this work is more typical of the majority of cometary observations. The three comets cover a broad range of water production rates, from moderate to high outgassing. As the electron impact reactions are linked to the density of water in the cometary coma (see Sect. 3.3), the data set analysed in this work is well-suited to studying the chemical processes involved in the formation of C3 and C2.
2. The data set
The radial column density profiles of three comets, C/2001 Q4 (NEAT), C/2002 T7 (LINEAR), and 9P/Tempel 1, are analysed. All three comets were observed by means of optical low-resolution long-slit spectroscopy with ESO telescopes. In all observations, the long-slit was placed on the nucleus position in the sky and aligned along the projected solar-antisolar direction. The heliocentric distances at which these comets were observed are in the narrow range from 1 AU to 1.5 AU. Furthermore, the degrees of solar activity at the times of observations were similar. They were also comparable to the solar activity at the time of observations of comet Hale-Bopp, thus did not introduce major uncertainties when comparing analyses of different comets. All three comets are typical of their C2/CN ratio according to the classification of A’Hearn et al. (1995), as described in Sect. 2.5. Details of the observations and data reduction are presented in the following.
Overview of the observational set-ups for the comets in the data set of this work.
2.1. Comet C/2001 Q4 (NEAT)
Comet C/2001 Q4 was discovered in August 2001, and observed on the night April 29/30, 2004, using the ESO 3.6 m/EFOSC2. The heliocentric and geocentric (Δ) distances at the time of observation were 1.00 AU and 0.39 AU, respectively. The relatively small geocentric distance allowed a high spatial resolution to be achieved in these observations. Details of the observational set-ups are provided in Table 1. This comet is the most active comet in our data set, having a water production rate of about 2.6 × 1029 s-1 at the time of observation.
2.2. Comet C/2002 T7 (LINEAR)
This comet was discovered in October 2002, and observed using the ESO 3.6 m/EFOSC2 on June 12/13, 2004. At this time, rh = 1.20 AU and Δ = 1.03 AU. With a water production rate of 6.9 × 1028 s-1, at the time of observation, this comet was less active than C/2001 Q4. Table 1 summarizes the observational set-ups.
2.3. Comet 9P/Tempel 1
Comet 9P/Tempel 1 was observed with the VLT UT1/FORS2 within the framework of the ESO Deep Impact observing campaign (Meech et al. 2005). In this paper, we analyse observations performed in the night June 3/4, 2005, thus of the undisturbed coma before the Deep Impact event. The heliocentric and geocentric distances at that time were 1.51 AU and 0.89 AU, respectively. At the time observed, Küppers et al. (2005) reported a water production rate of 3.4 × 1027 s-1, making this comet a low activity one. However, Mumma et al. (2005) present a somewhat higher water production rate of 1.21 × 1028 s-1. We applied both values. However, the difference between these two values of water production does not affect the qualitative results obtained. Details on the observational set-ups are presented in Table 1.
2.4. Data reduction
All data were reduced according to standard procedures, including the removal of cosmic ray hits, bias subtraction, flatfielding, wavelength calibration, sky background subtraction, extinction correction, absolute flux calibration, and subtraction of the continuum of sunlight scattered by cometary dust particles. In the case of comet 9P/Tempel 1, a contribution of coherent noise was also subtracted from the data. For the comets C/2001 Q4 and C/2002 T7, the subtraction of the sky background contribution was impossible. For these two comets, the sky contribution had to be subtracted with the solar continuum in a single calibration step.
The region of the long-slit spectra closest to the nucleus position is strongly affected by uncertainties in the continuum subtraction. Furthermore, the shape of the emission profiles is affected by seeing effects close to the nucleus, where the brightness gradient in the coma is very strong. Therefore, the near-nucleus region of the long-slit spectra was excluded from the analysis of both the C3 and C2 emissions.
In a following step, the fluxes of the C3 comet head group, the
C2(Δv = 0) emission, and the CN (1–1) emission were
integrated to obtain the corresponding emission profiles along the slit. The fluxes were
then converted into column densities using the corresponding fluorescence efficiencies.
For C3 and C2, the fluorescence efficiencies presented by Cochran
et al. (1992) were applied and scaled with 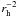 . For CN, the Swings effect has to be taken
into account. To do so, the g-factors presented by Schleicher (1983) were linearly
interpolated to the radial component of the heliocentric velocity of the comets at the
time of observation, and scaled with
. For CN, the Swings effect has to be taken
into account. To do so, the g-factors presented by Schleicher (1983) were linearly
interpolated to the radial component of the heliocentric velocity of the comets at the
time of observation, and scaled with 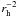 .
.
2.5. Haser production rates
To classify the comets studied in this work according to the scheme established by A’Hearn et al. (1995), we computed the Haser production rates of CN, C3, and C2 by fitting Haser profiles to the observed column density profiles, and varying the Haser parent production rate, and both the parent and daughter scale lengths. For CN, the daughter scale length, which is expected to be about 2 × 105km (A’Hearn et al. 1995), thus large compared to the spatial coverage of the observations of this work, was poorly constrained by the available observations. Thus, for a number of profiles the best-fit value was approaching infinity. However, as the CN daughter scale lengths provided in the literature (e.g. by A’Hearn et al. 1995) were clearly too small to fit the observations of CN in comet C/2001 Q4, we adopted the results of the fits to the data of these work even in cases where their values were extremely large. A gas expansion velocity of 1 km s-1 was assumed throughout. This value is probably overestimates the gas expansion velocity. However, a scaling of the production rates to any other expansion velocity can be performed by multiplying their values by that expansion velocity. The production rates resulting with these assumptions are presented in Table 2, together with the ratios of C3 and C2 to CN. According to their ratios of C2/CN, all three comets studied in this work clearly fall within the “typical” range.
Haser production rates for CN, C3, and C2.
3. The model
We develop a model capable of treating different kinds of chemical reactions in the cometary coma. Among these kinds of reactions are, as already described, photochemical and electron impact reactions. Furthermore, various collisional reactions between neutrals and ions are listed by Helbert (2002) in the formation network of C3 and C2. Although these reactions were not found to be significant, they should nevertheless be included in the study of other comets, as we attempt in this work. The rates of these reactions depend on the densities of the reactants, as well as their temperatures. As the rate of collisions decreases as the density in the coma decreases with increasing distance from the nucleus, the chemical energy released during reactions is not necessarily homogeneously distributed among all species. This effect can result in different temperatures for different species in the coma. For this reason, a multi-fluid model is required to describe the coma appropriately. At the same time, the computational effort has to be sufficiently small to allow for the large number of coma simulations required to fit the observational data. Therefore, strong simplifying assumptions have to be made. In this study, we decided to compromise between accuracy and computational effort in accordance with the model of Rodgers & Charnley (2002). The primary aim of the model we present here is to include all effects identified to be of importance to the formation of C3 and C2 in previous work, while being as simple as possible at the same time. To achieve this, three individual fluids, comprising the neutral species, the ionic species, and the electrons, respectively, are included in the model. These fluids have different temperatures and densities, but are all assumed to move with the same bulk velocity, v. The temperatures of these fluids are used to compute the reaction rates of the different species included in the model. For each species in the model, their densities are computed individually as a function of the nucleocentric distance. A spherical symmetric coma is assumed throughout. The different aspects of this model, separated into the hydrodynamical and chemical aspects, are presented in more detail in the following.
3.1. Hydrodynamics
3.1.1. Basic equations
The density, temperature, and velocity of the fluids in the model were obtained from
the equations of conservation of particle numbers, mass, momentum, and energy. Assuming
spherical symmetry, these equations can be used to obtain expressions for the number
density Nj for each species
j in the model of the form 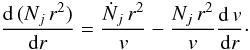 (1)In this equation,
Ṅj represents the source term for
species j, discussed in the next section on the chemical reactions.
This differential equation is written in terms of
(Nj r2)
instead of Nj, as this expression varies
less strongly with nucleocentric distance r than
Nj itself, hence permits a more stable
integration. Neglecting the loss of fast particles from the coma in his work, for the
velocity one obtains (Rodgers & Charnley 2002)
(1)In this equation,
Ṅj represents the source term for
species j, discussed in the next section on the chemical reactions.
This differential equation is written in terms of
(Nj r2)
instead of Nj, as this expression varies
less strongly with nucleocentric distance r than
Nj itself, hence permits a more stable
integration. Neglecting the loss of fast particles from the coma in his work, for the
velocity one obtains (Rodgers & Charnley 2002) 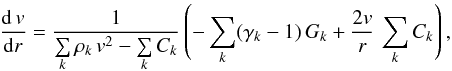 (2)where the index k runs
over all fluids in the model, and the abbreviation
Ck = γk Nk kBTk,
and Nk is the density of fluid
k and can be computed from the densities of the individual species
included in the model. The parameter γk is
the adiabatic exponent of fluid k: we assume for the neutral and ionic
fluid a value of 4/3, whereas for the electronic fluid we assume a value of 5/3 for
point-like particles. The energy source terms
Gk is discussed in more detail in
Sect. 3.3. For the temperature, the
corresponding equation is (Rodgers & Charnley 2002)
(2)where the index k runs
over all fluids in the model, and the abbreviation
Ck = γk Nk kBTk,
and Nk is the density of fluid
k and can be computed from the densities of the individual species
included in the model. The parameter γk is
the adiabatic exponent of fluid k: we assume for the neutral and ionic
fluid a value of 4/3, whereas for the electronic fluid we assume a value of 5/3 for
point-like particles. The energy source terms
Gk is discussed in more detail in
Sect. 3.3. For the temperature, the
corresponding equation is (Rodgers & Charnley 2002) 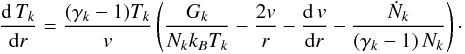 (3)A detailed discussion of the derivation of
these equations, as well as their motivation and range of validity, was provided by
Rodgers & Charnley (2002). Equations (1)–(3) represent the system of differential equations that has to be solved to
obtain the densities of the species of interest as a function of nucleocentric distance.
(3)A detailed discussion of the derivation of
these equations, as well as their motivation and range of validity, was provided by
Rodgers & Charnley (2002). Equations (1)–(3) represent the system of differential equations that has to be solved to
obtain the densities of the species of interest as a function of nucleocentric distance.
3.1.2. Simplifying assumptions of the model
The model presented here uses two major simplifying assumptions, compared to the model by Rodgers & Charnley (2002) and, in particular, Schmidt et al. (1988), which was used in previous work on this topic by H05.
The first of these simplifications is the use of only three individual fluids, but neglect of any light chemical species, such as atomic and molecular hydrogen, as individual fluids. This treatment was introduced in other models of the cometary coma, e.g. Schmidt et al. (1988) and Rodgers & Charnley (2002). The reason for this approach is that light species absorb a larger fraction of the excess energy released by chemical reactions forming these species. As the density on the coma decreases outwards to values a which no efficient thermalisation occurs, these species no longer transfer their excess energy to the bulk neutral species. Two notable effects occur, which we describe below.
The first effect is that the highly energetic species can trigger chemical reactions that are energetically prohibited for thermalised species. However, a study of this effect by Rodgers & Charnley (2005) showed that the influence of suprathermal species upon the chemical processes in the coma is in general low. Furthermore, using a model that includes separate fluids for each of the suprathermal species, H05 do not report any effect of these species on the formation of C3 and C2. Therefore, the neglect of this effect is acceptable as far as chemical reactions are concerned.
The second effect is that the reduced thermalisation of the light species in the outer coma reduces the energy input to the neutral fluid, which in turn reduces the increase in the gas expansion velocity in the outer coma. Our model therefore overestimates the gas velocity at large distances from the nucleus. This effect causes the predicted column density profiles to be too steep in the outermost coma. However, the species C3 and C2 are in all cases observed at relatively small projected nucleocentric distances anyway. Furthermore, our model is able to reproduce the shape of the radial column density profiles of C3 and C2, which were computed including suprathermal species, quite well in the projected nucleocentric distance range of interest, as shown in Sect. 4. Therefore, the neglect of suprathermal species is also acceptable.
The second simplification that we make is the neglect of interactions between the cometary plasma and the solar wind. The model of Schmidt et al. (1988) includes a three-dimensional magnetohydrodynamical (MHD) simulation. It allows for the computation of a two-dimensional distribution of ions in the coma. The density of electrons is coupled to the density of ions to ensure large-scale charge neutrality. For the computation of C3 and C2 column densities, the electron density in the coma is of importance, as electron impact reactions are important to the formation of these species. The lack of MHD simulations in our model therefore potentially affects the results. To estimate the influence of that simplification, in Sect. 4 we present a detailed comparison between the output of the models of this work and Schmidt et al. (1988). As shown there, good qualitative agreement between the outputs of the two different models can be obtained, justifying the neglect of MHD in this work.
3.2. Chemical reactions
3.2.1. Reactions and reaction rates
Several different types of reactions are taken into account in this work. Among these
are photochemical reactions such as photodissociation, photoionisation, and dissociative
photoionisation. Furthermore, neutral-neutral and neutral-ion rearrangements are
included. Among the reactions involving electrons, we include dissociative
recombination, electron impact ionisation, electron impact dissociation and radiative
recombination reactions. The general mathematical description of these reactions is
given by (Schmidt et al. 1988)
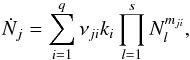 (4)where
Ṅj is the source term in Eq. (1),
Nj is the density of species
j, and q and s give the numbers of
reactions and species in the reaction network, respectively. The parameter
νji is the stoichiometric coefficient of
species j in reaction i,
ki is the rate coefficient of reaction
i, and mji is the order
of the reaction.
(4)where
Ṅj is the source term in Eq. (1),
Nj is the density of species
j, and q and s give the numbers of
reactions and species in the reaction network, respectively. The parameter
νji is the stoichiometric coefficient of
species j in reaction i,
ki is the rate coefficient of reaction
i, and mji is the order
of the reaction.
For photochemical reactions, the dependence of the reaction rate coefficients
ki on the solar radiation field was taken
into account by scaling the rate coefficients taken from the literature for a
heliocentric distance of 1 AU with 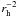 .
.
The dependence of the rate coefficients in the chemical reactions on temperature,
ki(T) was taken into
account by using an Arrhenius parameterisation 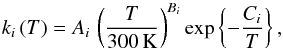 (5)were,
Ai,
Bi, and
Ci are the Arrhenius coefficients for
reaction i. For photochemical reactions, only the parameter
Ai differs from zero. For collisional
reactions, Bi describes the influence of
the particle velocity on the collision frequency. For collisional reactions, the
parameter Ci describes the minimum energy
in a collision required to trigger a reaction. This parameter introduces a strong
dependence of the reaction rate on the temperature, T, of the reactants
(Connors 1990).
(5)were,
Ai,
Bi, and
Ci are the Arrhenius coefficients for
reaction i. For photochemical reactions, only the parameter
Ai differs from zero. For collisional
reactions, Bi describes the influence of
the particle velocity on the collision frequency. For collisional reactions, the
parameter Ci describes the minimum energy
in a collision required to trigger a reaction. This parameter introduces a strong
dependence of the reaction rate on the temperature, T, of the reactants
(Connors 1990).
For collisional reactions between particles from different fluids (e.g. ion-neutral
collisions), the effective temperature according to Flower et al. (1985) 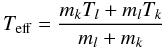 (6)was used when computing the reaction rate,
were mk and
ml are the masses of the reactants
belonging to the fluids with index l and k,
respectively. Owing to the low mass of an electron, for electron impact reactions we
assume that Teff ≈ Te, where
Te is the temperature of the electron fluid.
(6)was used when computing the reaction rate,
were mk and
ml are the masses of the reactants
belonging to the fluids with index l and k,
respectively. Owing to the low mass of an electron, for electron impact reactions we
assume that Teff ≈ Te, where
Te is the temperature of the electron fluid.
All reactions identified as important to the formation of C3 and C2 in the previous work were included in the reaction network of this work. Furthermore, important background reactions determining the velocity and temperature of the fluids, as well as providing electrons for electron impact reactions, had to be considered. In this respect, the most abundant species in the coma, such as water and carbon oxides (CO and CO2), are the most important. In this work, all reactions included in the study of H05, and listed with their Arrhenius coefficients in the appendix of Helbert (2002), were included when computing the column densities of C3 and C2. Furthermore, all reactions presented by Schmidt et al. (1988), with updates from Huebner et al. (1992), were also included as background reactions in the reaction network used in this work. A complete list of reactions included in this work was provided by Weiler (2007).
3.2.2. Optical density effects
Optical density effects are important to the chemical processes in the coma in two respects. First, the reduction in the solar flux in the inner coma by the shielding of the outer coma can reduce the rates of the photochemical reactions in the inner coma. Second, the absorption of the infrared emission from the inner coma by the outer parts of the coma can reduce the effectiveness of radiative cooling mechanisms. This mechanism is called radiative trapping.
When including optical density effects in the model of this work, we made simplifying assumptions according to Schmidt et al. (1988): a dependence of the density of all species on the nucleocentric density of r-2 was assumed throughout. Furthermore, the optical density was computed only along the nucleus – Sun line-of-sight. To compute the wavelength-dependent optical density for a particular photo reaction, the wavelength interval from 1 Å to 5255 Å was considered in this work. For 71 reactions in the reaction network, the wavelength-dependent photo cross sections from Huebner et al. (1992) are available. On the basis of these, the optical density as a function of wavelength was computed. Then, the shielded reaction rates for the 71 reactions were computed, using the wavelength-dependend reaction cross-sections. For reactions where no information about the wavelength-dependence of the photochemical reaction cross-sections was available, the average cross-sections for H2O, CO, and CO2 were used and the optical density was computed by taking only these three species into account. The total reaction rate, integrated over all wavelengths, was then corrected for this optical density.
For the computation of the infrared optical thickness of the coma, as required for the radiative trapping, we adopted a constant infrared cross-section of 4 × 10-19 m2 (Schmidt et al. 1988).
3.3. Energy source terms
The source terms Gk for the fluids k (Eqs. (2) and (3)) are composed of different additive contributions. We followed the approach by Rodgers & Charnley (2002), discussed in detail in their work, and provide only a brief description at this point.
For all three fluids, one summand of Gk represents the chemical source term, describing the energy either introduced to or subtracted from the inner energy of fluid k owing to chemical reactions. Two mechanisms are of importance in this respect. First, if a particle changes its fluid owing to a reaction (e.g. from neutral fluid to ion fluid by ionisation), it takes its thermal energy with it into the new fluid. Second, chemical reactions can release an excess energy that is distributed between the different fluids involved in the reaction, depending on the reactants, products, and their masses. The values of these excess energies were adopted from Schmidt et al. (1988) and Huebner et al. (1992). The distribution of the energies between different fluids involved in a reaction was described in detail by Draine (1986) and Rodgers & Charnley (2002).
For the electronic and neutral species, an energy source term describing the energy
exchange caused by elastic collisions was included in our model. This source term is of
particular interest, as it couples the temperature of the electrons with the temperature
of the neutral fluid, as long as collisions in the coma are sufficiently frequent. As
water has the highest elastic-collision cross-section for electrons among all major
species in the neutral fluid, this source term depends basically on the density of water,
and electrons, in the coma. To describe this effect we used the expression given by
Rodgers & Charnley (2002)
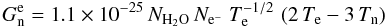 (7)in units of erg cm-3
s-1. This term was added to the total energy source term of the neutral fluid,
Gn, and subtracted from the total energy source term of the
electron fluid, Ge.
(7)in units of erg cm-3
s-1. This term was added to the total energy source term of the neutral fluid,
Gn, and subtracted from the total energy source term of the
electron fluid, Ge.
Furthermore, we included an energy source term describing the energy exchange caused by elastic collisions of electrons with ions, taken from Draine (1980), in addition to another energy source term that takes inelastic collisions of electrons with water into account. To achieve this, we incorporated the analytic parametrisation of Cravens & Korosmezey (1986) for the rotational and vibrational excitation of the water molecule in our model. As described in Sect. 3.2.2, optical density effects were taken into account, causing radiational trapping in the inner coma.
Inelastic collisions between water molecules in the coma can also lead to the cooling of the coma. In inelastic collisions, thermal energy is transferred into the excitation of water molecules, which can then be emitted as thermal radiation. This effect was included in our model using the empirical relation of Schmidt et al. (1988). For this mechanism, optical density effects were also included.
The cooling of the coma by the inelastic collisions of electrons with CO was not included as an individual contribution to the energy source term. Collisional excitation and radiative de-excitation of CO are instead included as reactions in the reaction network, and their cooling effect is included in the chemical energy source term. The Arrhenius coefficients and excess energies for these reactions were taken from Schmidt et al. (1988).
Energy exchange caused by collisions between neutral species and ions were not included
in the energy source terms, but by introducing pseudo-reactions of the type 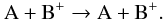 (8)For A, the most abundant neutral species
H2O, CO, and CO2 were used, for the ions B+ the
species H3O+,
(8)For A, the most abundant neutral species
H2O, CO, and CO2 were used, for the ions B+ the
species H3O+, 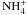 , and H2CO+ were
taken into account. These species do not undergo chemical reactions with each other, but
pseudo-reactions similar to Eq. (8) allow
the computation of the energy transfer between the neutral and the ion fluid in the model.
The rates of these pseudo-reactions are computed from hard-sphere collision theory
(Connors 1990), i.e.
, and H2CO+ were
taken into account. These species do not undergo chemical reactions with each other, but
pseudo-reactions similar to Eq. (8) allow
the computation of the energy transfer between the neutral and the ion fluid in the model.
The rates of these pseudo-reactions are computed from hard-sphere collision theory
(Connors 1990), i.e.
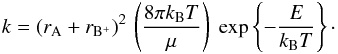 (9)In this equation, μ means
the reduced mass of the reactants. Using typical molecular radii for
rA and rB+, and
assuming that the energy barrier E is zero, one obtains the Arrhenius
coefficients Bj = 0.5,
Cj = 0, and the estimated
Aj ≈ 10-10 cm3
s-1.
(9)In this equation, μ means
the reduced mass of the reactants. Using typical molecular radii for
rA and rB+, and
assuming that the energy barrier E is zero, one obtains the Arrhenius
coefficients Bj = 0.5,
Cj = 0, and the estimated
Aj ≈ 10-10 cm3
s-1.
Summary of the initial values.
3.4. Numerical approach
The system of ordinary differential equations defined by Eqs. (1)–(3) includes parameters, such as the reaction rate coefficients, that change on scales differing by many orders of magnitude. It is therefore highly stiff, requiring an implicit or semi-implicit integration scheme. We adopted two of these publicly available integrators, LSODE (Hindmarsh 1983) and METAN1 (Bader & Deuflhard 1983). The LSODE uses an implicit Gear method (Gear 1971) for integration, whereas METAN1 makes use of a semi-implicit mid-point rule. Both approaches were suitable for solving the model presented here, and within the desired accuracy, both algorithms provided identical results.
The integration of the system of differential equations was performed from the nuclear radius as the inner boundary to an outer nucleocentric distance that was 100 times larger than the largest projected nucleocentric distance for which data were available. This choice ensured that the simulated densities could be converted into meaningful column densities for all projected nucleocentric distances where the computations have to be compared to observations. An increase in the outer limit of integration did not significantly change the resulting column densities.
3.5. Initial values
We define as initial values the densities of the parent species, and the densities,
temperatures and velocities of the three different fluids. We computed the densities of
the parent species from gas production rates taken from the literature, using the relation
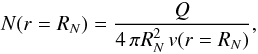 (10)where
RN is the nuclear radius,
N and Q the density and the production rate,
respectively, and v the gas velocity. The nuclear radii of the comets in
out data set were also taken from the literature. The values adopted are presented in
Table 3. However, the value assumed for the
nuclear radius has only a weak impact upon the computational results. Even a variation by
a factor of five does not significantly change the resulting column densities of
C3 and C2 at the projected nucleocentric distances of interest.
(10)where
RN is the nuclear radius,
N and Q the density and the production rate,
respectively, and v the gas velocity. The nuclear radii of the comets in
out data set were also taken from the literature. The values adopted are presented in
Table 3. However, the value assumed for the
nuclear radius has only a weak impact upon the computational results. Even a variation by
a factor of five does not significantly change the resulting column densities of
C3 and C2 at the projected nucleocentric distances of interest.
The gas temperature was computed from a very simple sublimation model of the nucleus.
From the energy budget of incoming solar radiation, reflection, thermal irradiation, and
sublimation, we derived first the temperature of the nucleus at the heliocentric distance
of the observation. We adopted a mean solar zenith angle of 60°, a geometric albedo of
0.04, and a thermal emissivity of 0.9. Furthermore, we used the thermodynamical parameters
of water presented by Fanale & Salvail (1984).
From the temperature of the ice surface, we inferred the temperature of the gas above the
surface. These two temperatures are different, because the velocity vectors of the gas
molecules leaving the surface with a temperature Tsurface are
only directed into half space, away from the surface. Thus, the velocities of the gas
molecules cannot be described bt a Maxwell distribution at the moment they are released
from the solid ice. The temperature after reaching a Maxwell distribution,
T, is computed using a reservoir outflow analogy (Knollenberg 1993)
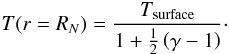 (11)In this equation, γ is the
adiabatic exponent of the neutral fluid, which we assumed to be 4/3. As the Maxwell
distribution is reached after a few collisions between the molecules, and the mean free
path of the molecules is small compared to the size of the nucleus for the comets in our
data set, we do not distinguish between the nuclear radius and the radial position at
which a Maxwell distribution is reached.
(11)In this equation, γ is the
adiabatic exponent of the neutral fluid, which we assumed to be 4/3. As the Maxwell
distribution is reached after a few collisions between the molecules, and the mean free
path of the molecules is small compared to the size of the nucleus for the comets in our
data set, we do not distinguish between the nuclear radius and the radial position at
which a Maxwell distribution is reached.
The initial gas expansion velocity was then computed by assuming that at the nucleus surface it has the local sonic speed. This assumption was justified by the observation that the cometary coma extends to infinity, requiring a supersonic flow. In case of a stationary supersonic flow, the local Mach number of one is reached at the location of maximal flux density (Landau & Lifshitz 1987), which in the case of the spherical symmetry of the coma is assumed to be at the nuclear surface. The values applied to the three comets in the data set of this work are presented in Table 3. We note that these initial velocities are smaller than the typical mean expansion velocity in the cometary coma assumed when using Haser models. Within the process of adiabatic expansion, the velocity increases in the model of this work quickly to values of about 0.7 to 0.8 km s-1. In the outer coma, this velocity increases further owing to heating by chemical processes, mainly the photodissociation of water.
3.6. Comparison with observations
To compare the model predictions with observed radial column density profiles, we first computed the densities of all species of interest as a function of nucleocentric distance. These densities were then converted into column densities, by applying again the assumption of a spherically symmetric coma. This conversion by integration over a line of sight was performed using of a Romberg integration scheme. The computed radial column densities were interpolated to the projected nucleocentric distances at which observational data points were available.
To fit the model parameters, i.e. the parent species production rates, to the
observations, the total χ2 value of the C3 and
C2 column densities was minimised. For this purpose, a downhill-simplex
algorithm (Nelder & Mead 1965) was used. This
algorithm allows for the localisation of the minimum of a function in a multi-dimensional
space. We minimised χ2 in the three-dimensional space given by
the C3 and C2 parent species production rates of
C3H4, C2H2, and C2H6.
This approach differs from the fitting procedure applied by H05, where in a first step the
column densities of C3 were fitted varying only the production rate of
C3H4. This best fitting production rate was then kept fixed, and
the observed C2 column densities were fitted by varying the production rates of
C2H2 and C2H6. This two-step fitting
procedure uses the assumption that no significant influence of the C2 parent
species C2H2 and C2H6 on the observed
C3 column densities exists. For realistic production rates of
C2H2 and C2H6, this assumption is justified.
However, if the production rates of these parent species reach unrealistically high
values, their densities in the innermost coma become sufficiently high to build up species
bearing three carbon atoms via collisional ion-neutral reactions included in the model of
Helbert (2002). This effect could be important for
C2H6 in particular. As C2 is produced from
C2H6 in several intermediate steps (see Fig. 1), it is expected that C2H6 has a relatively
small effect on C2 at the projected nucleocentric distances covered by the
observations of C2 (see Sect. 4). Very
high production rates of C2H6 might therefore agree with the
observed C2. In these cases, C2H6 can contribute to the
formation of 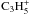 in the inner coma via a number of
neutral-ion rearrangement reactions with comparable importance, including
in the inner coma via a number of
neutral-ion rearrangement reactions with comparable importance, including
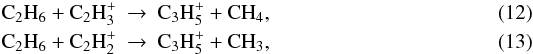 where
where 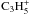 then forms C3 via the
dissociative recombination
then forms C3 via the
dissociative recombination 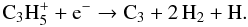 (14)Thus, for very high
C2H6 production rates, the influence of this C2 parent
species upon the computed C3 column densities is incorporated into the model.
This effect is illustrated in test computations in Sect. 4.2. However, this influence cannot be taken into account by fitting
C3 independently of C2. In effect, when excluding unrealistically
high production rates of C2H6 a priori, one becomes insensitive to
good fits that might be possible for such unrealistically high production rates. The
simultaneous fitting of C2 and C3 performed in this work does not
require such a priori constraints, thus provides an opportunity for a more stringent test
of the model.
(14)Thus, for very high
C2H6 production rates, the influence of this C2 parent
species upon the computed C3 column densities is incorporated into the model.
This effect is illustrated in test computations in Sect. 4.2. However, this influence cannot be taken into account by fitting
C3 independently of C2. In effect, when excluding unrealistically
high production rates of C2H6 a priori, one becomes insensitive to
good fits that might be possible for such unrealistically high production rates. The
simultaneous fitting of C2 and C3 performed in this work does not
require such a priori constraints, thus provides an opportunity for a more stringent test
of the model.
The shape of the radial column density profiles is affected not only by chemical processes, but also by other effects that were not included in our model. These effects are anisotropies in outgassing, resulting in a deviation from the assumed spherical symmetry of the coma, or non-steady activity (i.e. outbursts). To estimate the influence of these effects on the results of this work, fits to the column density profiles were performed independently on the projected sunward and the tailward sides of the nucleus, instead of averaging the profiles from different position angles for the fitting procedure. Differences in the best-fit model parameters between the two different position angles then provides a rough estimate of the uncertainties introduced by the violation of the simplifying assumptions made in this work.
4. Model validation
Helbert et al. (2005) presented the most elaborate study of the formation of C3 and C2, and the only one making use of a detailed chemical modeling of the cometary coma. The natural first step is therefore to compare the performance of the simpler model described above with the results presented there for comet Hale-Bopp. To do so, we selected the observed column density profiles from the night of December 19/20, 1997, at a heliocentric distance of 3.78 AU. For these observations, the solar activity was on a similar level those at the times of observation of the comets studied in this work. This was confirmed using the values of the solar 10.7 cm radio flux, and the Brussels International Sunspot Number, as provided by the Space Environment Center of the National Oceanic and Atmospheric Administration1. Furthermore, these observations have a relatively low level of noise and were the easiest to be digitised from the figure presented in Helbert (2002). As the error bars of the different data points overlap, the errors could not be digitised as well. Therefore, we used the data, for test reasons only, assuming the same absolute error in each data point (i.e. no weighting of the data points). In this particular case, for the sake of comparison of the results we followed the same approach as H05 and fitted the combined data obtained in the projected sunward and tailward side of the nucleus.
4.1. Comparison of the outputs of the two models
We first compared the C3 and C2 column density profiles obtained with the two different models, using the same input parameters and reaction network. Thus, this first step of testing did not include a direct comparison to the observational data. The results are presented in Fig. 2. The black lines in this figure show the column densities extracted from H05. The dashed red lines show the results obtained in this work for comparison. The results clearly quantitatively disagree. Qualitatively, the profiles are however in good agreement. The blue lines show the results of the model developed in this work, multiplied by a factor of 2.4 for C2 and a factor of 2.2 for C3.
The qualitative agreement, i.e. the agreement in the shapes of the column density profiles obtained with the two models, supports the conclusion that the model used in this work is capable of reproducing the results of the previous work. No effects on the shape of the radial column density profiles are neglected when setting up the model of this work, although it is simplified compared to the model by Schmidt et al. (1988) used by H05. The reason for the difference in absolute units between the modelled column density profiles, when using the same input parameters, remains unknown. Rauer et al. (2003) present Haser production rates for C3 and C2, together with the assumed scale lengths and gas expansion velocities, that were derived from the same data used in H05. The corresponding Haser column density profiles of C3 and C2 are also presented in Fig. 2 for comparison. Any differences between the shapes of the profiles obtained using a Haser model and the corresponding column density profiles of this work are caused by the different assumptions about the chemical reactions and their rates. The Haser model column densities of Rauer et al. (2003) quantitatively differ, i.e. differ in absolute value, from the data presented by H05. To match the data, the Haser production rates of Rauer et al. (2003) have to be increased by an amount very similar to the difference between production rates found in this work and H05. This suggests that the reason for the different production rates in this work and H05 might not be found within the model of this work. We are unable to clearly establish the origin of the remaining small differences in shape between the column densities by H05 and the scaled column densities in this work. The differences could be caused by differences in the models used in the two different works. However, since the differences in the absolute values of the column densities of C3 and C2 might be caused by the parent species production rates differing from the nominal values, the small differences in the shape of the profiles might also be due to the different production rates of C2H2, C2H6, and C3H4.
 |
Fig. 2 Comparison of the column densities derived for comet Hale-Bopp on Dec. 19/20, 1997, by H05 and this work, computed with the same parameters. Black lines: column densities of C3 and C2 taken from H05. Dashed red lines: column densities computed by the model of this work. Blue lines: column densities of this work, scaled to match the profiles of H05. The dashed green lines show the Haser profiles of C2 and C3 according to Rauer et al. (2003). |
Mixing ratios of the C3 parent species and the C2 parent species for comet Hale-Bopp (Dec. 19/20, 1997).
4.2. Comparison of the model output with the data
In a second step, we fitted our model to the digitised data points from the night of Dec.
19/20, 1997, using the reaction network of H05 and the initial values given by Helbert
(2002). The production rates obtained by these
fits are presented in Table 4. For comparison,
values derived from direct observations of C2H2 and
C2H6 by DelloRusso et al. (2001) are also presented. The production rates of these species were scaled to
the heliocentric distance of the observations of Hale-Bopp analysed here, i.e. 3.78 AU,
and then divided by the water production rate of 4 × 1028 s-1, as
assumed for the computations. For C2H6 we used the scaling with
rh presented by DelloRusso et al. (2001). As this scaling is based on a large number of
C2H6 observations between heliocentric distances of about 0.9 AU
and 3.0 AU, the prediction of C2H6 at
rh = 3.78 AU in this way might be acceptable. For
C2H2, only production rates around
rh = 1 AU are available, and a scaling with
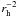 was applied. This scaling is only very
crude, as the dependence of the C2H2 production on
rh might differ from the “canonical” exponent of −2, as in
the case of C2H6. This value has therefore to be regarded as only a
rough proxi. The resulting best fits to the observed column density profiles of
C3 and C2 are presented in Fig. 3. Two observations can be made:
was applied. This scaling is only very
crude, as the dependence of the C2H2 production on
rh might differ from the “canonical” exponent of −2, as in
the case of C2H6. This value has therefore to be regarded as only a
rough proxi. The resulting best fits to the observed column density profiles of
C3 and C2 are presented in Fig. 3. Two observations can be made:
-
the shape of the radial column density profiles, both for C3 and C2, can be reproduced well by our model and the reaction network by H05;

Fig. 3 Observed column densities of C3 (filled symbols) and C2 (open symbols) versus projected nucleocentric distance for comet Hale-Bopp on Dec. 19/20, 1997, according to H05. Solid black lines show the best fits obtained in his work, using the reaction network of H05. The dashed line shows the C2 and C3 column density profiles for a C2H6 production rate that has been raised by a factor of 10 relative to the best-fit result, the dashed-dotted line for an increase by a factor of 100 (for a change by a factor of 10 no difference can be seen for C3). The red lines are the corresponding column density profiles obtained for the production rates of H05.
-
the production rates of the parent species C3H4, C2H2 and C2H6 derived in this work clearly differ. The production rate of C2H6 derived in this work is lower, while the values for C3H4 and C2H2 are higher than in H05.
We first address the observation of the lower production rate of C2H6 obtained in this work is addressed. As no error bars on the observed column densities are available for the production rate determination performed for this work, a stringent error discussion can be provided here. However, when varying the production rate of C2H6 over a wide range of values, it becomes obvious that this parameter has only a very weak influence upon the C2 column density profiles. This is illustrated by the dashed and dashed-dotted lines in Fig. 3, showing the computed C2 column density profiles for a C2H6 production rate increased by a factor of 10 and 100 with respect to the best-fit result, respectively. All other model parameters are kept fixed. Comparing the change in the C2 column density profile for the different C2H6 production rates with the scatter in the data points, an increase in the production by a factor of 10 is completely insignificant. A change by a factor of 100 might be significant. Reducing the C2H6 production to zero leads to a C2 column density profile that is indistinguishable from the best-fit profile on the scale of Fig. 3. This very small influence of the C2H6 production rate upon the fit to the observations is caused by C2 being produced from C2H6 in three or four steps, as illustrated in Fig. 1. The production of C2 from C2H6 therefore occurs significantly slower than from C2H2, and the contribution of C2H6 becomes significant only at very large projected nucleocentric distances. The range of projected nucleocentric distances covered by the observations of C2 is too small for the observed C2 to be significantly influenced by C2H6. The error in the C2H6 production rate inferred from the fit to the observations, previously assumed to be 10%, therefore appears to be strongly underestimated. From the observations, only an upper limit to the C2H6 production rate can be derived. Judging from the scatter in the data points in Fig. 3, this upper limit is likely to be of the order of some tens of percent of the water production rate. Since the production rate, as obtained from direct observations, is expected to be one order of magnitude lower than this upper limit, observations of C2 do not provide access to any useful constraint.
 |
Fig. 4 Results of the fitting of the C3 (crosses, lower curves) and C2 (diamonds, upper curves) column density profiles of the comets in our data set, using the reaction network by H05. The results for the sunward and tailward side of the nucleus are presented separately. For comet 9P/Tempel 1, the solid lines are the results obtained with the water production rate according to Küppers et al. (2005), the dashed lines according to Mumma et al. (2005). |
Figure 3 also shows the impact of C2H6 upon the column density profiles of C3. An increase by a factor of 10 in the C2H6 production rate does not noticeably affect the C3 profiles. When increasing the C2H6 production by a factor of 100, C3 also is affected, which may improve the fit to the C3 observations.
The second observation of the higher production rates of C2H2 and C3H4 found here than in H05, reflects the differences between the absolute values of the C3 and C2 column density profiles already discussed in Sect. 4.1. As the column densities computed in this work tend to be lower, higher parent species production rates are obtained in this work to compensate for this difference.
Overview of the best-fit model parameters.
To conclude, the model that we have used here can closely reproduce the of observed column densities of C3 and C2 in comet Hale-Bopp. However, the production rates of the parent species significantly differ from the values derived in the previous study. The large uncertainty in the C2H6 production rate, caused by the very weak influence of C2H6 upon the C2 column densities at projected nucleocentric distances accessible by ground-based observations, implies that it is questionable whether the production of C2H6 can be constrained from these observations of C2 at all. The production rate of C2H2 agrees with the values derived from direct observations of C2H2 of DelloRusso et al. (2001), which are listed in Table 4. However, owing to the large uncertainty caused by the scaling of the results by DelloRusso et al. (2001) over a wide range of heliocentric distances, this measurement only provides a weak constraint of the model.
5. Results with current reaction network
We then proceeded to fit the radial column density profiles of C3 and C2 of the comets in the data set considered here. Figure 4 shows the closest simultaneous fits to the observed column density profiles for all three comets. Table 5 presents the best-fit model values of the production rates of C3H4, C2H2, and C2H6. In general, no satisfying fit of the observations could be obtained using the reaction network of H05. The values in Table 5 cannot therefore be considered as reliable predictions of the production rates of these comets. For comet 9P/Tempel 1, the best fitting profiles are slightly steeper than but still close to the observed profiles. For C/2002 T7, both the computed profiles for C3 and C2 are flatter than the observed profiles. For comet C/2001 Q4, the computed profiles of C2 are only slightly flatter. However, the shape of the computed C3 profiles clearly differs from the shape of the observed C3 column density profiles. The main reason for the difference between the observed and the modelled C3 column density profiles is an increase in the computed C3 column densities at some 103 km projected nucleocentric distance. This increase, which appears as a kind of “bump” in the computed profiles, is not observed in any of the three comets in the data set.
The reason for this “bump” in the modelled column densities of C3 is the onset
of the electron impact reaction, producing C3 from
C3H4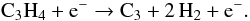 (15)The rate of this reaction has a strong
dependence on the temperature of the electrons. The corresponding Arrhenius coefficients in
Eq. (5) are
A = 3.80 × 10-8 cm3 s-1,
B = 0.5, and C = 40618. In particular, owing to the
large coefficient C, this reaction becomes effective only at high electron temperatures in
the order of 104K. In the inner cometary coma, the temperature of the electron
fluid in our model is strongly coupled to the temperature of the neutral fluid, as the
electrons exchange their energy very effectively in collisions with water molecules (see
Sect. 3.3). Thus, even if the electrons absorb a
high excess energy as they are produced by the photochemical reactions, this energy is
transferred to the neutral fluid, keeping the temperature of the electron fluid low. Only at
larger distances from the nucleus does the density of water in the coma become sufficiently
low to ensure that the energy exchange between electrons and water is ineffective. At such
large distances, the temperature of the electron fluid increases to significant values,
causing the reaction given in Eq. (15) to
become efficient in producing C3. The distances from the nucleus at which the
temperature of the electron fluid decouples from the temperature of the neutral fluid
depends on the water production rate of a comet. The higher the water production rate is,
the further out from the nucleus the density of water remains high enough to permit an
efficient collisional energy exchange between electrons and water molecules. This effect is
illustrated in Fig. 5. For comet 9P/Tempel 1, which has
the lowest water production rate of all the comets in our data set, the decoupling of the
electron temperature from the neutral temperature and its increase to some 104 K
occurs at a distance of some 102 km from the nucleus. For comet C/2002 T7 and
C/2001 Q4 with their high water production rates, the increase in the temperature of the
electronic fluid occurs further out from the nucleus, at a distance of some
103 km.
(15)The rate of this reaction has a strong
dependence on the temperature of the electrons. The corresponding Arrhenius coefficients in
Eq. (5) are
A = 3.80 × 10-8 cm3 s-1,
B = 0.5, and C = 40618. In particular, owing to the
large coefficient C, this reaction becomes effective only at high electron temperatures in
the order of 104K. In the inner cometary coma, the temperature of the electron
fluid in our model is strongly coupled to the temperature of the neutral fluid, as the
electrons exchange their energy very effectively in collisions with water molecules (see
Sect. 3.3). Thus, even if the electrons absorb a
high excess energy as they are produced by the photochemical reactions, this energy is
transferred to the neutral fluid, keeping the temperature of the electron fluid low. Only at
larger distances from the nucleus does the density of water in the coma become sufficiently
low to ensure that the energy exchange between electrons and water is ineffective. At such
large distances, the temperature of the electron fluid increases to significant values,
causing the reaction given in Eq. (15) to
become efficient in producing C3. The distances from the nucleus at which the
temperature of the electron fluid decouples from the temperature of the neutral fluid
depends on the water production rate of a comet. The higher the water production rate is,
the further out from the nucleus the density of water remains high enough to permit an
efficient collisional energy exchange between electrons and water molecules. This effect is
illustrated in Fig. 5. For comet 9P/Tempel 1, which has
the lowest water production rate of all the comets in our data set, the decoupling of the
electron temperature from the neutral temperature and its increase to some 104 K
occurs at a distance of some 102 km from the nucleus. For comet C/2002 T7 and
C/2001 Q4 with their high water production rates, the increase in the temperature of the
electronic fluid occurs further out from the nucleus, at a distance of some
103 km.
 |
Fig. 5 Temperature of the electronic fluid as a function of the nucleocentric distance for the three comets in the data set of this work. Solid lines: 9P/Tempel 1, for the water production rate according to Küppers et al. (2005) (left) and according to Mumma et al. (2005) (right). Dashed line: C/2002 T7. Dashed-dotted line: C/2001 Q4. |
This effect explains the shape of the computed radial column density profiles of C3. For comet 9P/Tempel 1, the increase in the electron temperature, and with it the onset of the reaction given in Eq. (15), occurs at nucleocentric distances so small that they are not covered by our observations. In this case, fairly acceptable fits to the observed C3 and C2 column density profiles can be obtained. For comets C/2002 T7, and even more so for comet C/2001 Q4, the increase in the electron temperature and the onset of the reaction in Eq. (15) occurs at nucleocentric distances at which C3 is observed. The onset of the reaction in Eq. (15) manifests itself as an increase in C3, hence a “bump” in the radial column density profiles of C3. In this case, no acceptable fit of the observations can be obtained. From the observations of C/2002 T7 and C/2001 Q4 it can therefore be concluded that the assumed production of C3 via the reaction in Eq. (15) is unrealistic.
This result agrees with the results found from an analysis of the column densities of C3 and C2 in comet Hale-Bopp by H05. Comet Hale-Bopp was a very active comet, but at the heliocentric distances larger than 2.8 AU at which the analysis was performed, the water production rate in absolute units was already low. The model used by H05 predicts an increase in the electron temperature by means of the same mechanism included in our model. The nucleocentric distances at which this increase occurs are smaller than 103 km in all cases studied by them (Fig. 12.1 in Helbert 2002). Owing to the large geocentric distances of comet Hale-Bopp during all observations, and the consequently low spatial resolution of the observations, this distance is not covered by the available observations. The situation is therefore analogous to the situation for comet 9P/Tempel 1 in this work. Acceptable fits to the observed C3 and C2 column density profiles can be obtained in this case, because the “bump” in the C3 column density profiles predicted by the model is fully outside the range of projected nucleocentric distances covered by the observations.
6. Reaction networks revised
The unobserved “bump” in the modelled C3 column densities, caused by the
reaction presented in Eq. (15), suggests
that we should revise the reaction rate coefficients, in particular for the electron impact
reactions of hydrocarbons. A detailed study of these reactions was presented by Alman et al.
(2000), which provides estimates of the electron
impact cross-sections, σ(E), for various reactions,
parameterised as a function of impact energy. We used these values to determine the
Arrhenius coefficients of the corresponding reactions. To do so, we computed the rate
coefficients at 1000 equidistant temperature steps between 40 K and 4 × 104 K,
using the relation (Connors 1990)
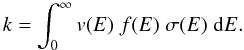 (16)In this equation,
v(E) is the electron velocity,
(16)In this equation,
v(E) is the electron velocity,
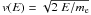 , where me is the
electron mass. For the frequency distribution of the electrons,
f(E), we assumed a Maxwell distribution for the
temperature T. The computed rate coefficients for the different
temperatures were then fitted by the Arrhenius parameterisation given in Eq. (5).
, where me is the
electron mass. For the frequency distribution of the electrons,
f(E), we assumed a Maxwell distribution for the
temperature T. The computed rate coefficients for the different
temperatures were then fitted by the Arrhenius parameterisation given in Eq. (5).
Among the reactions for which new rate coefficients are available is the reaction
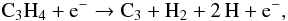 (17)which was used to replace the reaction in
Eq. (15). The Arrhenius coefficients of
this reaction are A = 10.3 × 10-9 cm3 s-1,
B = 0.369, and C = 116 800. Thus, mainly because of
the much larger value of C than the previously assumed value, this electron
impact dissociation reaction becomes far less important. The electrons in the cometary coma
do not reach high enough temperatures to make this reaction important.
(17)which was used to replace the reaction in
Eq. (15). The Arrhenius coefficients of
this reaction are A = 10.3 × 10-9 cm3 s-1,
B = 0.369, and C = 116 800. Thus, mainly because of
the much larger value of C than the previously assumed value, this electron
impact dissociation reaction becomes far less important. The electrons in the cometary coma
do not reach high enough temperatures to make this reaction important.
Furthermore, a number of additional electron impact dissociation, ionisation, dissociative ionisation, and dissociative recombination reactions were newly introduced into the reaction network from Alman et al. (2000). However, these reactions have no significant effect upon the formation of C3 and C2. A number of dissociative recombination reactions were also introduced into the reaction network from the UMIST data base (Woodall et al. 2007). Arrhenius coefficients for reactions already included in the reaction network by H05 were updated if new values were available from Alman et al. (2000) and the UMIST data base.
7. Results with revised reaction networks
The best-fit column density profiles of C3 and C2, computed with the revised reaction network for the three comets of our data set, are presented in Fig. 6. The corresponding best-fit production rates are listed in Table 5. For comet C/2001 Q4, the most optimal fits are achieved, but for the other two comets, the fits are clearly unacceptable. In general, the decrease in the C3 and C2 column densities with increasing projected nucleocentric distance is insufficiently steep relative to the observations. However, the “bump” observed in the radial C3 column density profiles is no longer produced by the model. This is in agreement with the lower electron impact rates that follow from the updated Arrhenius coefficients, in particular for the production of C3 from the electron impact dissociation of C3H4.
 |
Fig. 6 Results of the fitting of the C3 (crosses, lower curves) and C2 (diamonts, upper curves) column density profiles of the comets in our data set, using the revised reaction network. The results for the sunward and tailward side of the nucleus are presented separately. For comet 9P/Tempel 1, the solid lines are the results obtained with the water production rate of Küppers et al. (2005), and the dashed lines for that of Mumma et al. (2005). |
8. Summary and conclusions
We have found that the influence of C2H6 on the observed C2 in cometary comae is extremely very weak. Consequently, one is able to determine only an upper limit to the production rate of C2H6 from observations of C2 with currently available signal-to-noise ratios. This upper limit is likely to be so large that it places no meaningful constraint on the production of C2H6.
We have also discovered that the reaction network for the formation of C3 and C2 by H05, when constrained to reproduce the observations of these species in comet Hale-Bopp at large heliocentric distances, is unable to reproduce the observations of these species in other comets at smaller heliocentric distances. The reason for the failure is related to the electron impact reactions. Assuming a reaction rate for an electron impact reaction able to produce C3 from C3H4 as in H05, one would expect to see features in the radial column density profiles of C3 that are not observed in the comets studied in this work. For comet Hale-Bopp, these features remained undetectable at the large heliocentric distances for which the comet was observed. We have found that when we use updated reaction rates for electron impact reactions these reactions have a smaller influence on the formation of C3, but do not allow a reasonable fit to the observed column densities.
For the radial column density profiles of C3 and C2 in the comets that we have studied here, no indications have been found that electron impact reactions play a significant role in the formation of these species. Electron impact reactions, which tend to have a high energy barrier as reflected in the C-Arrhenius coefficient, will show a turn-on effect in the coma when the electron temperature decouples from the temperature of the neutral species. If electron impact reactions were of important to the production of C3 and C2 in the cometary coma, they would probably cause a kind of “bump” in the radial column density profiles. This feature in the radial column density profile is not observed in any comet studied in this work. This suggests that electron impact reactions do not play an important role in the formation of C3 and C2. Further studies of the formation of C3 and C2 may therefore safely neglect this class of reactions.
The formation of C3 and C2 in the cometary coma remains unexplained. Any future analysis should study the influence of the reactions rates assumed in the reaction networks used to explain the formation of these radicals. Furthermore, other potential parent molecules have to be considered, such as HC3N, C3H2O, and C4H2. Significant simplifications of the model may also be introduced when neglecting electron impact reactions. These simplifications would open the way for more elaborate analysis methods. The next paper of this series will be dedicated to such a study.
Acknowledgments
This work was supported by the MICINN (Spanish Ministry of Science and Innovation) – FEDER through grant AYA2009-14648-C02-01 and CONSOLIDER CSD2007-00050. It is based on work started as a PhD thesis prepared at the Institute for Planetary Research of the German Aerospace Center (Berlin, Germany) and submitted to the Technische Universität Berlin.
References
- A’Hearn, M. F., Millis, R. L., Schleicher, D. G., Osip, D. J., & Birch, P. 1995, Icarus, 118, 223 [NASA ADS] [CrossRef] [Google Scholar]
- A’Hearn, M. F., Belton, M. J. S., Delamere, W. A., et al. 2005, Science, 310, 258 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Alman, D. A., Ruzic, D. N., & Brooks, J. N. 2000, Phys. Plasmas, 7, 1421 [NASA ADS] [CrossRef] [Google Scholar]
- Bader, G., & Deuflhard, P. 1983, Numer. Math., 41, 373 [CrossRef] [Google Scholar]
- Biver, N., Bockelée-Morvan, D., Colom, P., et al. 2009, A&A, 501, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bockelee-Morvan, D., & Crovisier, J. 2003, in Cometary Science after Hale-Bopp, Vol. I, ed. H. Boehnhardt et al. (Kluwer Academic Publishers), 53 [Google Scholar]
- Connors, K. A. 1990, Chemical Kinetics (Weinheim: VCH) [Google Scholar]
- Cravens, T. E., & Korosmezey, A. 1986, Planet. Space Sci., 34, 961 [NASA ADS] [CrossRef] [Google Scholar]
- Dello Russo, N., Mumma, M. J., Disanti, M. A., Magee-Sauer, K., & Novak, R. 2001, Icarus, 153, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Despois, D., Biver, N., Bockelée-Morvan, D., & Crovisier, J. 2005, IAUS, 231, 469 [Google Scholar]
- Douglas, A. E. 1951, ApJ, 114, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1980, ApJ, 241, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Fanale, F. P., & Savail, J. R. 1984, Icarus, 60, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, P. D., Weaver, H. A., Christian, D., et al. 2004, BAAS, 36, 1121 [NASA ADS] [Google Scholar]
- Feldman, P. D., Lupu, R. E., McCandliss, S. R., et al. 2006, ApJ, 647, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., Pineau des Forets, G., Hartquist, T. W., et al. 1985, MNRAS, 216, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Friedel, D. N., Remijan, A. J., Snyder, L. E., et al. 2005, ApJ, 630, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Gear, C. W. 1971, Numerical Initial-Value Problems in Ordinary Differential Equations (Prentice-Hall: Englewood Cliffs) [Google Scholar]
- Helbert, J. 2002, Ph.D. Thesis, Freie Universität Berlin, Germany [Google Scholar]
- Helbert, J., Rauer, H., Boice, D. C., & Huebner, W. F. 2005, A&A, 442, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hindmarsh, A. C. 1983, Scientific Computing (Amsterdam: North-Holland), 55 [Google Scholar]
- Howell, E. S., Lovell, A. J., & Schloerb, F. P. 2004, IAU Circ., 8329 [Google Scholar]
- Huebner, W. F., Keady, J. J., & Lyon, S. P. 1992, Astrophys. Space Sci., 195, 1 [Google Scholar]
- Hunaerts, J. 1950, AnOB, 5, 1 [NASA ADS] [Google Scholar]
- Knollenberg, J. 1993, Ph.D. Thesis, Georg-August-Universität zu Göttingen, Germany [Google Scholar]
- Küppers, M., Bertini, I., Fornasier, S., et al. 2005, Nature, 437, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1987, Course of theoretical physics, Vol. 6: Fluid Dynamics, Butterworth-Heinemann [Google Scholar]
- Langland-Shula, L. E., & Smith, G. H. 2011, Icarus, 213, 280 [CrossRef] [Google Scholar]
- Meech, K. J., Ageorges, N., A’Hearn, M. F., et al. 2005, Science, 310, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Milam, S. N., Remijan, A. J., Womack, M., et al. 2006, ApJ, 649, 1169 [NASA ADS] [CrossRef] [Google Scholar]
- Mumma, M. J., DiSanti, M. A., Magee-Sauer, K., et al. 2005, Science, 310, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Nelder, J., & Mead, R. 1965, Comp. J., 7, 308 [Google Scholar]
- Rauer, H., Helbert, J., Arpigny, C., et al. 2003, A&A, 397, 1109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remijan, A. J., Shiao, Y.-S., Friedel, D. N., Meier, D. S., & Snyder, L. E. 2004, ApJ, 643, 567 [Google Scholar]
- Rodgers, S. D., & Chanley, S. B. 2002, MNRAS, 330, 660 [NASA ADS] [CrossRef] [Google Scholar]
- Rodgers, S. D., & Chanley, S. B. 2005, MNRAS, 356, 1542 [NASA ADS] [CrossRef] [Google Scholar]
- Schleicher, D. G. 2008, AJ, 136, 2204 [Google Scholar]
- Schmidt, H. U., Wegmann, R., Huebner, W. F., & Boice, D. C. 1988, Comp. Phys. Commun., 49, 17 [Google Scholar]
- Tozzi, G. P., Boehnhardt, H., & Curto, G. L. 2003, A&A, 398, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiler, M. 2007, Ph.D. Thesis, Technische Universität Berlin, Germany [Google Scholar]
- Weiler, M., Rauer, H., & Sterken, C. 2007, Icarus, 190, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Weiler, M., Rauer, H., Knollenberg, J., & Sterken, C. 2011, Icarus, 351, 366 [Google Scholar]
- Woodall, J., Agúndez, M., Markwick-Kemper, A. J., & Millar, T. J. 2007, A&A, 466, 1197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Overview of the observational set-ups for the comets in the data set of this work.
Mixing ratios of the C3 parent species and the C2 parent species for comet Hale-Bopp (Dec. 19/20, 1997).
All Figures
 |
Fig. 1 Scheme of the formation of C3 and C2 according to H05. Species in solid boxes are parent species. Solid arrows represent photochemical reactions, dashed arrows electron impact reactions. By-products of the reactions (e.g. H, C, ...) are not included in this simplified scheme. |
| In the text | |
 |
Fig. 2 Comparison of the column densities derived for comet Hale-Bopp on Dec. 19/20, 1997, by H05 and this work, computed with the same parameters. Black lines: column densities of C3 and C2 taken from H05. Dashed red lines: column densities computed by the model of this work. Blue lines: column densities of this work, scaled to match the profiles of H05. The dashed green lines show the Haser profiles of C2 and C3 according to Rauer et al. (2003). |
| In the text | |
 |
Fig. 3 Observed column densities of C3 (filled symbols) and C2 (open symbols) versus projected nucleocentric distance for comet Hale-Bopp on Dec. 19/20, 1997, according to H05. Solid black lines show the best fits obtained in his work, using the reaction network of H05. The dashed line shows the C2 and C3 column density profiles for a C2H6 production rate that has been raised by a factor of 10 relative to the best-fit result, the dashed-dotted line for an increase by a factor of 100 (for a change by a factor of 10 no difference can be seen for C3). The red lines are the corresponding column density profiles obtained for the production rates of H05. |
| In the text | |
 |
Fig. 4 Results of the fitting of the C3 (crosses, lower curves) and C2 (diamonds, upper curves) column density profiles of the comets in our data set, using the reaction network by H05. The results for the sunward and tailward side of the nucleus are presented separately. For comet 9P/Tempel 1, the solid lines are the results obtained with the water production rate according to Küppers et al. (2005), the dashed lines according to Mumma et al. (2005). |
| In the text | |
 |
Fig. 5 Temperature of the electronic fluid as a function of the nucleocentric distance for the three comets in the data set of this work. Solid lines: 9P/Tempel 1, for the water production rate according to Küppers et al. (2005) (left) and according to Mumma et al. (2005) (right). Dashed line: C/2002 T7. Dashed-dotted line: C/2001 Q4. |
| In the text | |
 |
Fig. 6 Results of the fitting of the C3 (crosses, lower curves) and C2 (diamonts, upper curves) column density profiles of the comets in our data set, using the revised reaction network. The results for the sunward and tailward side of the nucleus are presented separately. For comet 9P/Tempel 1, the solid lines are the results obtained with the water production rate of Küppers et al. (2005), and the dashed lines for that of Mumma et al. (2005). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


